苏教版初三数学《锐角三角函数》章末重难点题型

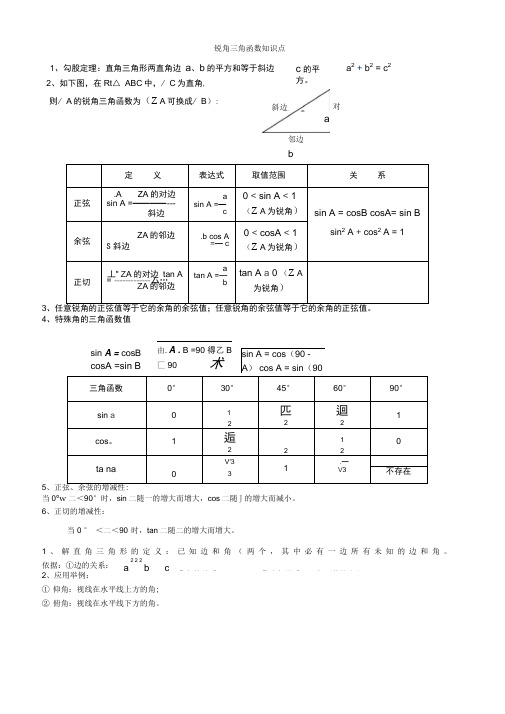
2、如下图，在Rt△ ABC中，/ C为直角,定义表达式取值范围关系正弦.A ZA的对边sin A =————---斜边asin A =—c0 < sin A < 1（Z A为锐角）sin A = cosB cosA= sin Bsin2 A + cos2 A = 1余弦ZA的邻边S斜边.b cos A=—c0 < cosA < 1（Z A为锐角）正切丄“ Z A的对边tan A= ------------- 厶…,Z A的邻边atan A =—btan A a 0 （Z A为锐角）34、特殊角的三角函数值三角函数0°30°45°60°90°sin a012匹2迴21cos。

1逅2212ta naV'31.—03V3不存在5当0°w二＜90°时，sin二随一的增大而增大，cos二随J的增大而减小。

6、正切的增减性：当0 ° ＜二＜90°时，tan二随二的增大而增大。

1、解直角三角形的定义：已知边和角（两个，其中必有一边所有未知的边和角。

依据：①边的关系：2 2 2a b c;②角的关系：A+B=90°;③边角关系：三角函数的定义。

2、应用举例：①仰角：视线在水平线上方的角;②俯角：视线在水平线下方的角。

锐角三角函数知识点1、勾股定理：直角三角形两直角边a、b的平方和等于斜边c的平方。

a2+ b2 = c2则/ A的锐角三角函数为（Z A可换成/ B）:sin A = cosB cosA =sin B 由.A .B =90 得乙B匚90 术sin A = cos（90 -A） cos A = sin（90斜边a邻边b对5、如图，在厶 ABC 中，/ ACB=90 , CD! AB 于 D,若AC二 5 6 , AB =5，则 tan / ACD 的值为()③ 坡面的铅直高度 h 和水平宽度I 的比叫做坡度（坡比）。

苏教版九年级下册数学重难点突破知识点梳理及重点题型巩固练习锐角三角函数—知识讲解【学习目标】1．结合图形理解记忆锐角三角函数定义；2．会推算30°、45°、60°角的三角函数值，并熟练准确的记住特殊角的三角函数值； 3．理解并能熟练运用“同角三角函数的关系”及“锐角三角函数值随角度变化的规律”.【要点梳理】要点一、锐角三角函数的概念如图所示，在Rt △ABC 中，∠C ＝90°，∠A 所对的边BC 记为a ，叫做∠A 的对边，也叫做∠B 的邻边，∠B 所对的边AC 记为b ，叫做∠B 的对边，也是∠A 的邻边，直角C 所对的边AB 记为c ，叫做斜边．锐角A 的对边与斜边的比叫做∠A 的正弦，记作sinA ，即sin A aA c ∠==的对边斜边；锐角A 的邻边与斜边的比叫做∠A 的余弦，记作cosA ，即cos A bA c ∠==的邻边斜边；锐角A 的对边与邻边的比叫做∠A 的正切，记作tanA ，即tan A aA A b∠==∠的对边的邻边.同理sin B b B c ∠==的对边斜边；cos B aB c∠==的邻边斜边；tan B b B B a ∠==∠的对边的邻边．要点诠释：(1)正弦、余弦、正切函数是在直角三角形中定义的，反映了直角三角形边与角的关系，是两条线段的比值．角的度数确定时，其比值不变，角的度数变化时，比值也随之变化． (2)sinA ，cosA ，tanA 分别是一个完整的数学符号，是一个整体，不能写成，，，不能理解成sin 与∠A ，cos 与∠A ，tan 与∠A 的乘积．书写时习惯上省略∠A 的角的Ca b记号“∠”，但对三个大写字母表示成的角(如∠AEF)，其正切应写成“tan∠AEF”，不能写成“tanAEF”；另外，、、常写成、、．(3)任何一个锐角都有相应的锐角三角函数值，不因这个角不在某个三角形中而不存在．(4)由锐角三角函数的定义知：当角度在0°<∠A<90°间变化时，，，tanA＞0．要点二、特殊角的三角函数值(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值，它的另一个应用就是：如果知道了一个锐角的三角函数值，就可以求出这个锐角的度数，例如：若，则锐角．(2)仔细研究表中数值的规律会发现：、、的值依次为、、，而、、的值的顺序正好相反，、、的值依次增大，其变化规律可以总结为：①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)；②余弦值随锐角度数的增大(或减小)而减小(或增大)．要点三、锐角三角函数之间的关系如图所示，在Rt△ABC中，∠C=90°．(1)互余关系：，；(2)平方关系：；(3)倒数关系：或；(4)商数关系：．要点诠释：锐角三角函数之间的关系式可由锐角三角函数的意义推导得出，常应用在三角函数的计算中，计算时巧用这些关系式可使运算简便．【典型例题】类型一、锐角三角函数值的求解策略1．（2016•安顺）如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC 的正切值是（）A．2 B．C．D．【思路点拨】根据勾股定理，可得AC、AB的长，根据正切函数的定义，可得答案．【答案】D．【解析】解：如图：，由勾股定理，得AC=，AB=2，BC=，∴△ABC为直角三角形，∴tan∠B==，故选：D．【总结升华】本题考查了锐角三角函数的定义，先求出AC、AB的长，再求正切函数．举一反三：【课程名称：锐角三角函数395948：例1（1）-（2）】【变式】在RtΔABC中，∠C=90°，若a=3，b=4，则c=，sinA=，cosA=，sinB=，cosB=．a【答案】c = 5 ，sinA = 35 ， cosA =45，sinB =45， cosB =35．类型二、特殊角的三角函数值的计算2．求下列各式的值：(1)（2015•茂名校级一模） 6tan 230°﹣sin60°﹣2sin45°；(2)（2015•乐陵市模拟） sin60°﹣4cos 230°+sin45°•tan60°；(3)（2015•宝山区一模） +tan60°﹣．【答案与解析】 解：（1）原式==12(2) 原式=×﹣4×（）2+×=﹣3+3；(3) 原式=+﹣=2+﹣=3﹣2+2【总结升华】熟记特殊角的三角函数值或借助两个三角板推算三角函数值，先代入特殊角的三角函数值，再进行化简．举一反三：【课程名称： 锐角三角函数 395948 ：例1（3）-（4）】 【变式】在Rt ΔABC 中，∠C =90°，若∠A=45°，则∠B = ，sinA=，cosA=，sinB=，cosB=．【答案】∠B=45°，sinA=，cosA=，sinB=cosB=．类型三、锐角三角函数之间的关系3．（2015•河北模拟）已知△ABC中的∠A与∠B满足（1﹣tanA）2+|sinB﹣|=0（1）试判断△ABC的形状．（2）求（1+sinA）2﹣2﹣（3+tanC）0的值．【答案与解析】解：（1）∵|1﹣tanA）2+|sinB﹣|=0，∴tanA=1，sinB=，∴∠A=45°，∠B=60°，∠C=180°﹣45°﹣60°=75°，∴△ABC是锐角三角形；（2）∵∠A=45°，∠B=60°，∠C=180°﹣45°﹣60°=75°，∴原式=（1+）2﹣2﹣1=．【总结升华】本题考查的是特殊角的三角函数值，熟记各特殊角度的三角函数值是解答此题的关键．类型四、锐角三角函数的拓展探究与应用4．如图所示，AB是⊙O的直径，且AB＝10，CD是⊙O的弦，AD与BC相交于点P，若弦CD＝6，试求cos∠APC的值．【答案与解析】连结AC，∵ AB是⊙O的直径，∴∠ACP＝90°，又∵∠B＝∠D，∠PAB＝∠PCD，∴△PCD∽△PAB，∴PC CDPA AB=． 又∵ CD ＝6，AB ＝10， ∴ 在Rt △PAC 中，63cos 105PC CD APC PA AB ∠====．【总结升华】直角三角形中，锐角的三角函数等于两边的比值，当这个比值无法直接求解，可结合相似三角形的性质，利用对应线段成比例转换，间接地求出这个比值．锐角的三角函数是针对直角三角形而言的，故可连结AC ，由AB 是⊙O 的直径得∠ACB ＝90°，cos PC APC PA ∠=，PC 、PA 均为未知，而已知CD ＝6，AB ＝10，可考虑利用△PCD ∽△PAB 得PC CDPA AB=．5．通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对(sad)．如图1①，在△ABC 中，AB ＝AC ，顶角A 的正对记作sadA ，这时sadA BCAB==底边腰．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：(1)sad60°＝________．(2)对于0＜A ＜180°，∠A 的正对值sadA 的取值范围是_______．(3)如图1②，已知sinA ＝35，其中∠A 为锐角，试求sadA 的值．【答案与解析】(1)1； (2)0＜sadA ＜2；(3)如图2所示，延长AC 到D ，使AD ＝AB ，连接BD ．设AD ＝AB ＝5a ，由3sin 5BC A AB ==得BC ＝3a ，∴ 4AC a ==，∴ CD ＝5a-4a ＝a ，BD ==，∴ sadA BD AD == 【总结升华】(1)将60°角放在等腰三角形中，底边和腰相等，故sadA ＝1；(2)在图①中设想AB ＝AC的长固定，并固定AB 让AC 绕点A 旋转，当∠A 接近0°时，BC 接近0，则sadA 接近0但永远不会等于0，故sadA ＞0，当∠A 接近180°时，BC 接近2AB ，则sadA 接近2但小于2，故sadA ＜2；(3)将∠A 放到等腰三角形中，如图2所示，根据定义可求解．。

一、锐角三角函数真题与模拟题分类汇编（难题易错题）1．如图，反比例函数() 0k y k x=≠ 的图象与正比例函数 2y x = 的图象相交于A (1,a ),B 两点，点C 在第四象限，CA ∥y 轴，90ABC ∠=︒.(1)求k 的值及点B 的坐标；(2)求tanC 的值.【答案】（1）2k =，()1,2B --；（2）2.【解析】【分析】（1）先根据点A 在直线y=2x 上，求得点A 的坐标，再根据点A 在反比例函数()0k y k x=≠ 的图象上，利用待定系数法求得k 的值，再根据点A 、B 关于原点对称即可求得点B 的坐标；（2）作BH ⊥AC 于H ，设AC 交x 轴于点D ，根据90ABC ∠=︒ ， 90BHC ∠=︒ ，可得C ABH ∠∠=，再由已知可得AOD ABH ∠∠=，从而得C AOD ∠∠=，求出C tan 即可.【详解】（1）∵点A (1，a )在2y x =上，∴a =2，∴A (1，2)，把A (1，2)代入 k y x =得2k =， ∵反比例函数()0k y k x=≠ 的图象与正比例函数 2y x = 的图象交于A ，B 两点， ∴A B 、 两点关于原点O 中心对称，∴()12B --， ； （2）作BH ⊥AC 于H ，设AC 交x 轴于点D ，∵90ABC ∠=︒ ， 90BHC ∠=︒ ，∴C ABH ∠∠=，∵CA ∥y 轴，∴BH ∥x 轴，∴AOD ABH ∠∠=，∴C AOD ∠∠=， ∴AD 22OD 1tanC tan AOD =∠===.【点睛】本题考查了反比例与一次函数综合问题，涉及到待定系数法、中心对称、三角函数等知识，熟练掌握和应用相关知识是解题的关键，（2）小题求出∠C=∠AOD是关键.2．如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB 的延长线于切点为G，连接AG交CD于K．（1）求证：KE=GE；（2）若KG2=KD•GE，试判断AC与EF的位置关系，并说明理由；（3）在（2）的条件下，若sinE=，AK=，求FG的长．【答案】（1）证明见解析；（2）AC∥EF，证明见解析；（3）FG= ．【解析】试题分析：（1）如图1，连接OG．根据切线性质及CD⊥AB，可以推出∠KGE=∠AKH=∠GKE，根据等角对等边得到KE=GE；（2）AC与EF平行，理由为：如图2所示，连接GD，由∠KGE=∠GKE，及KG2=KD•GE，利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似，又利用同弧所对的圆周角相等得到∠C=∠AGD，可推知∠E=∠C，从而得到AC∥EF；（3）如图3所示，连接OG，OC，先求出KE=GE，再求出圆的半径，根据勾股定理与垂径定理可以求解；然后在Rt△OGF中，解直角三角形即可求得FG的长度．试题解析：（1）如图1，连接OG．∵EG为切线，∴∠KGE+∠OGA=90°，∵CD⊥AB，∴∠AKH+∠OAG=90°，又∵OA=OG，∴∠OGA=∠OAG，∴∠KGE=∠AKH=∠GKE，∴KE=GE．（2）AC∥EF，理由为连接GD，如图2所示．∵KG2=KD•GE，即，∴，又∵∠KGE=∠GKE，∴△GKD∽△EGK，∴∠E=∠AGD，又∵∠C=∠AGD，∴∠E=∠C，∴AC∥EF；（3）连接OG，OC，如图3所示，∵EG为切线，∴∠KGE+∠OGA=90°，∵CD⊥AB，∴∠AKH+∠OAG=90°，又∵OA=OG，∴∠OGA=∠OAG，∴∠KGE=∠AKH=∠GKE，∴KE=GE．∵sinE=sin∠ACH=，设AH=3t，则AC=5t，CH=4t，∵KE=GE，AC∥EF，∴CK=AC=5t，∴HK=CK-CH=t．在Rt△AHK中，根据勾股定理得AH2+HK2=AK2，即（3t）2+t2=（2）2，解得t=．设⊙O半径为r，在Rt△OCH中，OC=r，OH=r-3t，CH=4t，由勾股定理得：OH2+CH2=OC2，即（r-3t）2+（4t）2=r2，解得r= t=．∵EF为切线，∴△OGF为直角三角形，在Rt△OGF中，OG=r=，tan∠OFG=tan∠CAH=，∴FG=【点睛】此题考查了切线的性质，相似三角形的判定与性质，垂径定理，勾股定理，锐角三角函数定义，圆周角定理，平行线的判定，以及等腰三角形的判定，熟练掌握定理及性质是解本题的关键．3．如图，矩形OABC 中，A(6，0)、C(0，23)、D(0，33)，射线l 过点D且与x 轴平行，点P 、Q 分别是l 和x 轴的正半轴上的动点，满足∠PQO ＝60º．(1)点B 的坐标是 ，∠CAO ＝ º，当点Q 与点A 重合时，点P 的坐标为 ；(2)设点P 的横坐标为x ，△OPQ 与矩形OABC 重叠部分的面积为S ，试求S 与x 的函数关系式和相应的自变量x 的取值范围．【答案】（1）（6，23）． 30．（3，33）（2）()()()()243x 430x 3331333x x 3x 5S {23x 1235x 93543x 9+≤≤-+-<≤=-+<≤> 【解析】解：（1）（6，23）． 30．（3，33）．（2）当0≤x≤3时，如图1，OI=x ，IQ=PI•tan60°=3，OQ=OI+IQ=3+x ；由题意可知直线l ∥BC ∥OA ，可得EF PE DC31==OQ PO DO333==，∴EF=13（3+x），此时重叠部分是梯形，其面积为：EFQO14343S S EF OQ OC3x x43 233==+⋅=+=+梯形（）（）当3＜x≤5时，如图2，()HAQEFQO EFQO221S S S S AH AQ243331333x43x3=x x32232∆=-=-⋅⋅=+---+-梯形梯形。

初中数学九年级下册锐角三角函数专题重难点汇总锐角三角函数重点知识关键词：锐角三角函数、三角函数值之间的关系、解直角三角形必须清晰知道的基本概念：锐角三角函数：在直角三角形Rt▲ABC中，∠C为直角，∠A或∠B的锐角三角函数为：1.正弦sinA=∠A的对边/斜边（取值范围为0≤sinA≤1）2.余弦cosA=∠A的邻边/斜边（取值范围为0≤cosA≤1）3.正切tanA=∠A的对边/∠A的邻边（取值范围为0≤tanA）4.余切cotA=∠A的邻边/∠A的对边（取值范围为0≤cotA）基本三角函数之间的关系：1.sinA=cosB2.cosA=sinB3.Sin^2A+cos^2A=14.tanA=cotB（写成tanA=cot(90°-A)可能更好）5.cotA=tanB6.tanA=sinA/cosA7.tanA=1/cotA8.tanA*cotA=1勾股定理：直角三角形两个直角边的平方之和等于斜边的平方。

即a^2+b^2=c^2。

一些特殊角的函数值：要记住0°、30°、45°、60°这些特殊的角的各个三角函数值。

计算题中要直接拿来使用的。

解直角三角形：在直角三角形中，除了直角外，还有五个元素：三条边和两个锐角。

根据已知的元素求解其余未知的元素的过程就是解直角三角形。

五个元素中，最少知道多少个就算解出来了呢？请大家先思考一下。

只要知道了两个元素，就可以将其他三个元素解出来了。

1.已知直角三角形的两条边：1.根据勾股定理求出第三条边；2.根据两条边求出一个锐角的三角函数值；3.根据三角函数求出锐角。

则所有元素都解出了。

1.已知直角三角形的一个锐角和一条边：大家自行演算一下吧。

比较简单，但是一定要多演变几遍，达到熟练为止。

这些都是基本功。

一些测量术语：仰角：视线在水平线上方的角；俯角：视线在水平线下方的角；坡度（坡比）：坡面的铅直高度和水平宽度的比。

第7章《锐角三角函数》易错疑难易错点1 对三角函数的符号理解不透彻1. 在Rt ABC ∆中，90C ∠=︒，4AB =，BC =sin 2A= . 易错点2 忽视直角三角形作为前提2. 已知等腰三角形ABC 中，10,12AB AC BC ===，则sin ACB ∠的值为 .3. 在ABC ∆中，,,A B C ∠∠∠的对边分别为,,a b c ，且::3:4:5a b c =，求证：7s i n s i n 5A B +=.4. 已知ABC ∆中，,,A B C ∠∠∠的对边分别为,,a b c ，且13,12,5a b c ===，求si n B 的值.易错点3 受思维定式的影响5. 在ABC ∆中，90B ∠=︒，3,5BC AB ==，求tan ,cos A A 的值.6. 在Rt ABC ∆中，90C ∠=︒，1,2AC BC ==，求sin ,tan A A 的值.易错点4 题目中没有给出图形时，忽视分类讨论7. 已知等腰三角形ABC 中，AB AC ==30°，动点P 从点B 向点C 运动，当运动到PA 与一腰垂直时，BP 的长为( ) A. 1 B. 1或3C. 1或2 8. 在Rt ABC ∆中，已知3,4AB AC ==，求tan C 的值.疑难点1 作辅助线构造直角生角形1. 如图，ABD ∆和BDC ∆且30BAD ∠=︒，45DBC ∠=︒，则 tan DAC ∠的值为( )A.3 B. 33+ C. 413+ D.132. 如图，在Rt ABC ∆C 中，90ACB ∠=︒，延长AB 到点D ，使BD AB =，连接CD ，若3tan 2A =t ，试求1tan BCD∠的值.疑难点2 解直角三角形的实际应用3. 如图1，某超市从一楼到二楼有一自动扶梯，图2是其侧面示意图.已知自动扶梯AB 的坡度为1:2.4，AB 的长度是13米，MN 是二楼楼顶，//MN PQ ，C 是MN 上自动扶梯顶端B 点正上方的一点，BC MN ⊥，在自动扶梯底端A 处测得C 点的仰角为42°，则二楼的层高BC 约为(精确到0. 1米，sin 420.67︒≈，tan 420.90︒≈( )A. 10.8米B. 8.9米C. 8. 0米D. 5.8米4. 太阳能光伏发电因其清洁、安全、便利、高效等特点，已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面图，其中的粗线表示支撑角钢，太阳能电池板与支撑角钢AB 的长度相同，均为300 cm ，AB 的倾斜角为30°，50BE CA ==cm ，支撑角钢CD ，EF 与底座地基台面接触点分别为,D F ，CD 垂直于地面，FE AB ⊥于点E .两个底座地基高度相同(即点,D F 到地面的垂直距离相同)，均为30 cm ，点A 到地面的垂直距离为50 cm ，求支撑角钢CD 和EF 的长度各是多少cm.(结果保留根号)疑难点3 三角函数与其他知识的综合应用5. 已知，如图，在平面直角坐标系xOy 中，直线y =-与x 轴、y 轴分别交于,A B两点，P 是直线AB 上一动点，⊙P 的半径为1.(1)判断原点O 与⊙P 的位置关系，并说明理由; (2)当⊙P 过点B 时，求⊙P 被y 轴所截得的劣弧的长; (3)当⊙P 与x 轴相切时，求出切点的坐标.参考答案易错1.12 2. 453. 设3,4,5(0)a k b k c k k ===>∵222222(3)(4)25a b k k k c +=+== ∴ABC ∆是以c 为斜边的直角三角形 ∴90C ∠=︒则33sin 55a k A c k ===，44sin 55b k Bc k === ∴7sin sin 5A B +=4. 因为22222125169b c a +=+== 所以ABC ∆是直角三角形，且90A ∠=︒所以12sin 13b B a == 5. 在Rt ABC ∆中，90B ∠=︒∵AC === ∴3tan 5BC A AB ==c o s34AB A AC ===6. 在Rt ABC ∆中，90C ∠=︒∴AB ==∴sinBC A AB ===2tan 21BC A AC === 7. C8. 根据题意，分两种情况讨论:①当AB 与AC 都是直角边时，3tan 4AB C AC == ②当AB 为直角边，AC 为斜边时，另一条直角边BC =则tanAB C AC ===综上，tan C 的值是34疑难 1. C2. 如图，过点D 作DE AC ⊥交AC 的延长线于点E 则//BC DE由BD AB =，得AC CE = 在Rt ADE ∆中，3tan 2DE A AE == ∴322DE CE = ∴3DECE= 在Rt CDE ∆中，1tan 3CE CDE DE ∠== ∵//BC DE∴BCD CDE ∠=∠113tan tan BCD CDE==∠∠3. D4. 如图，过点A 作AG CD ⊥，垂足为G则30CAG ∠=︒ 在Rt ACG ∆中1sin 3050252CG AC =︒=⨯=g (cm) 由题意，得503020GD =-=(cm) ∴252045CD CG GD =+=+=(cm)连接FD ，并延长与BA 的延长线交于点H 由题意，得30H ∠=︒在Rt CDH ∆中，290sin 30CDCH CD ===︒(cm)∴300505090290EH EC CH AB BE AC CH =+=--+=--+=(cm)在Rt EFH ∆中，tan 30290EF EH =︒==g答：支撑角钢CD 的长为45 cm ，EF cm. 5. (1)原点O 在⊙P 外.理由如下:由直线AB 的函数表达式y =-，得其与两坐标轴的交点分别为:(2,0),(0,A B -.在Rt OAB ∆中，tanOBA ∠==∴30OBA ∠=︒如图1，过点O 作OH AB ⊥交AB 于点H在Rt OBH ∆中， sin OH OB OBA =∠=g1>∴原点O 在⊙P 外(2)如图2，当OP 过点B ，点P 在y 轴右侧时，⊙P 被y 轴所截得的劣弧所对圆心角为120︒∴弧长为120121803ππ⨯⨯=同理，当OP 过点B ，点P 在y 轴轴左侧时，弧长同样为23π，故当OP 过点B 时，⊙P 被y 轴所截得的劣弧长为23π (3)如图3，当⊙P 与x 轴相切，且位于x 轴下方时，设切点为D在Rt DAP ∆中，tan 1tan 303AD DP DPA =∠=⨯︒=g此时点D 的坐标为(2当⊙P 与x 轴相切，且位于x 上方时，根据对称性可以求出切点坐标为(2综上，当⊙P 与x 轴相切时，切点坐标为(2，(2。

专题11锐角的三角函数重难点题型专训（7大题型）【题型目录】题型一正弦、余弦与正切的概念辨析题型二求角的正弦值题型三已知正弦值求边长题型四求角的余弦值题型五已知余弦值求边长题型六求角的正切值题型七已知正切值求边长【知识梳理】知识点1：正切与余切1.正切直角三角形中一个锐角的对边与邻边的比叫做这个锐角的正切（tangent ）．锐角A 的正切记作tan A ．tan A BC a A A AC b锐角的对边锐角的邻边．2.余切直角三角形中一个锐角的邻边与对边的比叫做这个锐角的余切（cotangent ）．锐角A 的余切记作cot A ．cot A AC b A A BC a锐角的邻边锐角的对边．ac A BC b知识点2：正弦与余弦1.正弦直角三角形中一个锐角的对边与斜边的比叫做这个锐角的正弦（sine ）．锐角A 的正弦记作sin A ．sin A BC a A AB c锐角的对边斜边．2.余弦直角三角形中一个锐角的邻边与斜边的比叫做这个锐角的余弦（cosine ）．锐角A 的余弦记作cos A ．cos A AC b A AB c 锐角的邻边斜边．a c A BC b【经典例题一正弦、余弦与正切的概念辨析】1．（2023上·福建泉州·九年级校考期中）若A 是锐角，下列说法正确的是（）A ．tan sin A AB ． 2sin 1sin 1A AC ． cos tan 90A AD ．sin cos 1A A 【答案】A【分析】本题考查三角函数．根据三角函数的定义和性质，逐一进行判断即可．【详解】解：如图，90C ，则：tan ,sin a a A A b c，∵b c ，∴tan sin A A ；故A 正确；∵0sin 1A ，∴ 2sin 11sin A A ；故B 错误；∵ cos ,tan 90tan b b A A B c a，∴ cos tan 90A A ；故C 错误；∵sin ,cos a b A A c c ，35BC AB ，设3BC k ，由勾股定理得：cos AC A AB 故选：C ．【点睛】本题考查了锐角三角函数，勾股定理，熟练掌握锐角三角函数的定义是解题关键．3．（2021上格点上，则，得出∵CD是斜边AB∴A ACD(1)利用锐角三角函数的定义求证：(2)若tan 2 ，求sin cos sin cos 【答案】(1)见解析(2)3【经典例题二求角的正弦值】A．12【答案】B【分析】本题考查网格中求三角函数值，三角函数定义，勾股定理及其逆定理，连接设小正方形边长为22AB24A ．34【答案】C【分析】本题考查圆周角定理，求角的正弦值．连接OBF ACD ，得到∵F 为弦BC 的中点，∴,OF BC BOF ∴90OBF BOF ∵CD AB ，是解题的关键．由题意知，22AC BC AB ∴222222sin sin BC AC A B AB AB 故答案为：1．4．（2023上·广西贵港·九年级统考期中）如图，在【答案】55/155【分析】本题考查正方形的性质，E 、C 、B 共线，再根据角三角形解决问题．【详解】解：如图，连接设正方形的边长为a ，由题意得∴AEC AEF ∴E 、C 、B 共线，【经典例题三已知正弦值求边长】A．2【答案】C【分析】连接OB、OC求出【点睛】本题考查了圆周角定理，等腰三角形的性质，特殊角的三角函数，解题关键是利用圆周角定理和等腰三角形的性质求出 3．（2023上·重庆万州·九年级重庆市万州第二高级中学校考期中）则cos A 的值为．【答案】215【分析】本题考查了三角函数：则5AB k ，由勾股定理可求得【详解】解：如图，∵sin 52BC A AB，∴设2BC k ，其中k 由勾股定理得AC AB =54．（2023下·九年级课时练习）在【答案】21或11【详解】如下图，过点AD AB Bsin满足的条件是两边一角，【易错点分析】条件中ABC所以对三角形的形状、大小进行确定性判断是不漏解的重要方法．5．（2023上·上海崇明·九年级校联考期中）如图，在(1)求BC的长．(2)若点D在BC边上，且在Rt ABE △中，∵3sin 5AE B AB，AB ∵:3:2BD CD ，BC ∴6BD ，4CD ，在Rt DHC △中，tan C【经典例题四求角的余弦值】则23BC AC ，23BC AC ，∴22223AB AC AC B C∵ 1,2A，【答案】2 2【分析】连接AF，由矩形的性质可得中点可得DE CE∵四边形ABCD是矩形，2AB CD，AD∵点E是CD的中点，11DE CE CD(1)求AC的长；(2)求cos OCA与tan B 的值．【答案】(1)AC的长为12(2)12cos13OCA，tan B【分析】本题考查了直角三角形中，斜边的上的中线等于斜边的一半，勾股定理，求角的余弦和正切等知识点．熟记相关几何结论是解题关键．（1）由“斜边的上的中线等于斜边的一半（2）由“斜边的上的中线等于斜边的一半定义即可求解．【详解】（1）解：ACB∵213AB CO.5BC∵，【经典例题五已知余弦值求边长】A．212B．9【答案】C【分析】根据题意得出CD边上一点，A ．94B ．125【答案】A【分析】根据4AC ，4cos 5A，可求出【详解】∵Rt ABC △，4AC ，cos A【点睛】本题考查了锐角三角函数，勾股定理，圆周的侧面积，熟练掌握圆锥的侧面积公式是解题关键．4．（2022秋·九年级单元测试）如图所示，在四边形2BE ，则sin DBE【答案】255/255【分析】先根据余弦的定义可得AD AB AE BE可求出x的值，从而可得(1)求证；BEA ADC∽(2)求证：··CD AD AC BE(3)若2AD 5，cos ABE 【答案】(1)见解析【经典例题六求角的正切值】A ．27【答案】C【分析】证明ABE △A．13B【答案】A【分析】根据题意，先证明CDE ADE ADC，【答案】12/0.5【分析】根据折叠的性质可得Rt AED△，再利用正切函数的定义求解．【答案】1174【分析】由题意可知，90CAH ACB，可得，∵EF BC，∴AH EF∴CAH CEF ，∴BCD CEF ，ABCD (1)求证：CDE CBF △△≌；(2)求CF 的长；(3)求tan BCF 的值．【答案】(1)见解析(2)35CF∵CDE CBF △△≌，∴45FBR EDC ，∴BRF △是等腰直角三角形，RF RB ，【经典例题七已知正切值求边长】在边AD A ．53B ．2【答案】A【分析】连接AP ，根据折叠的性质和平行线的性质，求得DF 的长度，根据勾股定理即可求得答案．【详解】如图所示，连接AP 根据折叠的性质可知AE EF ∴1tan 3EF FBE BF ．∵FP AD ∥，∴AEB EPF ．∴FEB EPF ．∴PF EF ．∴AE EF AP PF ．∵180DEF DFE D ∴DEF BFC ．又D C ，∴DEF CFB △∽△．∴13EF DF BF BC ．A．4033B．3340【答案】A【分析】作BH AD于H，延长∵4tan 3BH BAD AH ，∴令4BH x ，3AH x ，∴255AB BH DH x ，【答案】313【分析】点G 为求出AD ，利用正切的定义求出∵点G 为ABC ∴BD 是中线，∴132AD AC ∵1tan ABG90PQO ，∵4tan 3O ，43PQ OQ ， 设4PQ x ，则3OQ x ，同理可求3OQ ，1MQ ，4OM OQ MQ ；综上所述：2OM 或4．故答案：2或4．(1)求证：四边形BCEF (2)BG CE 于点G ，连结①求CG 的长．②求平行四边形BCEF 【答案】(1)见解析BG的结论，勾股定理求得∵是CE的中点，GEC EG CG，22∵四边形BCEF是平行四边形，，EF BCFB EC设EG CG x，则FB【重难点训练】九年级校考阶段练习）如图，融创乐园彩虹滑梯的高度为A ．cos h【答案】D∵90,BCA CD 是∴5CD AD BD ∴10,AB ACD ∵6BC ，A ．BDBC B ．BCAB 【答案】C【分析】此题主要考查了锐角三角函数的定义，得出【详解】解：∵AC BC CD AB ，∵四边形ABCD 是菱形，∴AC BD AB BC ，∴22OB AB AO∵3PC AP ，∴118422AP AC ，∴448OP AO AP ，∴3tan 8OB BPC OP，【答案】55/155【分析】题目主要考查勾股定理解三角形及其逆定理，余弦函数的定义，先根据勾股定理的逆定理判断出ABC 的形状，再由锐角三角函数的定义即可得出结论．【详解】解：∵由图可知，【答案】2【分析】本题考查了三角形内角和定理，作垂线，正弦．熟练掌握作垂线，由作图可知，CF是BD的垂直平分线，根据【答案】5 8【分析】此题主要考查了正方形性质，全等三角形的判定和性质，相似三角形的判定和性质，解直角三角形，求出BM是解本题的关键．根据正方形性质，证明（1）tan FEC（2）若15AB ，则CF【答案】377/37【答案】②③【分析】本题考查了三角形综合．交BD于点H，由2sin3D 即可求出由勾股定理即可求解，④过点在PDC中，利用三角形的三边关系即可求出∵2sin 3D ，2AD ，∴24sin 233AH AD D∴1144223ABD S BD AH △③∵2AD ，4BD ，1AD ∵90ABC ，1tan 2BAC ∴1tan tan 2DAP BAC，∴12DP AD ，【答案】菱形的边长为26cm 【分析】本题考查菱形的性质、，得出(1)以O 点为旋转中心，将ABC 逆时针方向旋转(2)画出A 关于直线1BB 的对称点D ；(3)在1AC 上画点P ，使1tan 3ACP【答案】(1)画图见解析，131C , (2)画图见解析(3)画图见解析，延长∴ 131C , ；（2）如图，D 即为所求，（3）如图，P 即为所求；【点睛】本题考查的是复杂作图，旋转的性质，轴对称的性质，全等三角形的判定与性质，平行线分线段成比例的应用，锐角三角函数的应用，掌握扎实的基础知识并应用于作图是解本题的关键．15．（2023上·安徽六安·九年级统考阶段练习）如图，于E ，点M 在AC 上，且AM AD ，连接(1)求证：2CF GE AE (2)求FM MG的值；(3)求tan CMF 的值．【答案】(1)证明见解析(2)222FM MG，再由等腰三角形的性质得。

2018年中考数学《锐角三角函数》复习精讲一、重点、难点梳理本单元学习的重点是锐角三角函数的概念、特殊角的三角函数值、解直角三角形的方法以及它的实际应用.要正确理解其概念和意义，并能推出特殊角的三角函数值，会运用“转化”思想化斜三角形为直角三角形.通过建立解直角三角形的数学模型，解决距离、高度、角度等计算问题.在解决实际问题时，要正确理解俯角、仰角、方位角、方向角及坡角、坡度等常用术语.注意把握各类图形的特征，综合运用全等三角形、相似三角形和三角形的边角关系解决问题.学习的难点是构造直角三角形，从复杂的几何图形中找出基本图形，综合运用相关知识以及转化的思想、方程的思想、变与不变的思想等解决生产、生活中的实际问题.二、易混、易错点剖析不能准确把握直角三角形中边角之间的关系，张冠李戴，不管是否是直角三角形就盲目套用锐角三角函数的定义求解;不能正确迅速地从比较复杂的图形中找出基本图形，未能掌握“遇斜化直”的基本方法致使解题受阻;在求解直角三角形的应用问题时，不能正确理解常用术语的含义，出现计算、推理错误等等. 三、中考命题解读中考对锐角三角函数的概念及简单性质、特殊角的三角函数值、已知三角函数值求角等知识点的考查，多以中低难度客观题的形式呈现;解直角三角形实际应用的题目几乎是每卷必考，一般是中等难度的解答题，背景公平，贴近生活，颇具时代性，且与全等三角形、平行四边形等知识适度融合，具有一定的综合性.围绕直角三角形边角关系的探索规律、猜想验证、知识拓展等创新性题目近年来也悄然兴起，成为中考试卷一道亮丽的风景. 四、考点题型精讲考点1 锐角三角函数的概念例1 (2017·兰州)如图1，一个斜坡长130 m ，坡顶离水平地面的距离为50 m ，那么这个斜坡与水平地面夹角的正切值等于( ) A.513 B. 1213 C. 512 D. 1312 解析:如图1，在Rt ABC ∆中，90,130ACB AB ∠=︒=Q m, 50BC =m,120AC ∴==m.505tan 12012BC BAC AC ∴∠===, 故选C.例2 (2016·荆州)如图2，在4X4的正方形方格图形中，小正方形的顶点称为格点，ABC ∆的顶点都在格点上，则ABC ∠的余弦值是( )A.2B.C. 12D. 解析:首要的问题是确定ABC ∆的形状，可以根据图形信息，尝试运用勾股定理的逆定理判断.易知，在ABC ∆中. 22220,5,25AC BC AB ===. ABC ∴∆是直角三角形，且90ACB ∠=︒.cos BC ABC AB ∴∠==故选D. 评注:锐角三角函数是在直角三角形中定义的，在求锐角三角函数值时，一定不能忽略这一点.例3 (2016·攀枝花)如图3，点(0,3),(0,0),(4,0)D O C 在⊙A 上，BD 是⊙A 的一条弦，则sin OBD ∠=( )A.12 B. 34 C. 45 D. 35解析:依题意，易知3,4OD OC ==.90,5C O D C D ∠=︒∴=Q .如图3，连接CD ,由圆周角定理，得OBD OCD ∠=∠. 3s i ns i n 5OD OBD OCD CD ∴∠=∠==.故选D. 评注:求一个角的三角函数值，通常有两种方法，找出(或构造)所求角所在的直角三角形，直接利用定义来求，如上面的例1，例2;抑或把所求角转化为直角三角形中与它相等的角间接求解，如本例和下面的例4等.例4 (2017·无锡)在如图4的正方形方格纸中，每个小的四边形都是相同的正方形，,,,A B C D 都在格点处，AB 与CD 相交于O ，则tan BOD ∠的值等于 .解析:解题的关键是构造直角三角形.平移CD 到C D ''交AB 于O '(还有其他的平移方法吗?)，如图4所示，则BO D BOD ''∠=∠.tan tan BOD BO D ''∴∠=∠.设每个小正方形的边长为a ，则,,3O B O D BD a ''''=====.作BE O D ''⊥于点E ，则BD O F BE O D ''⋅===''2O E '∴===. tan 3BEBO E O E'∴∠=='，故tan 3BOD ∠=.故填3.评注:在求解涉及直角三角形边角关系的问题时，如果题中没有可用的直角三角形，需要添加辅助线构造直角三角形来解决.常见辅助线的作法有作高或作平行线两种.本题综合运用了这两种方法.其中体现的转化思想十分重要，需要同学们用心体悟. 考点2 求特殊角的三角函数值 例5 (2017·平凉)计算:0113tan 30(4)()2π-︒+--.解析:原式312121=-=-=. 评注:对特殊角的三角函数值的考查，一般有两种方式:一是在难度较低的混合运算题中，将其和二次根式化简、零指数幂、负整数指数幂等一并考查;二是在解直角三角形时，需要求出特殊角的三角函数值解决问题. 考点3 已知三角函数值求(锐)角例6 (2016·潍坊)若关于x 的一元二次方程2sin 0x α+=有两个相等的实数根，则锐角α等于( )A.15ºB.30 ºC.45 ºD.60 º解析: Q 关于x 的一元二次方程2sin 0x α+=有两个相等的实数根，2(4sin 24sin 0αα∴∆=-=-=，解得1sin 2α=. αQ 为锐角，30α∴=︒.故选B.评注:解题的关键是借助一元二次方程根的判别式得到一个关于sin α的等式，进而在sin α为锐角的约束条件下求解. 考点4 解直角三角形例7 (2016·西宁)⊙O 的半径为1，弦AB =AC BAC ∠的度数为 .解析:因为题目中没有给出弦,AB AC 的位置关系，所以需分情况讨论:①如图5，连接OA ，过O 作OE AB ⊥于,E OF AC ⊥于F .90OEA OFA ∴∠=∠=︒.由垂径定理，得AE AE BE AF CF OAE OA ====∠==, cos AF OAF OA ∠==, 30,45,304575OAE OAF BAC ∴∠=︒∠=︒∠=︒+︒=︒;②如图6所示，仿①中的方法，可求得30,45.453015OAE OAF BAC ∠=︒∠=︒∴∠=︒-︒=︒.综上，答案为75º或15º.评注:忽视分类讨论，就有可能造成漏解.例8 (2017·徐州)如图7，已知AC BC ⊥，垂足为,4,C AC BC ==将线段AC 绕点A 按逆时针方向旋转60º，得到线段AD ,连接,DC DB . (1)线段DC = ;(2)求线段DB 的长度.解析:(1)∵AC AD =，60CAD ∠=︒， ∴ACD ∆是等边三角形， 故4DC AC ==.(2)为构造直角三角形，作DE BC ⊥于点E . ∵ACD ∆是等边三角形， ∴60ACD ∠=︒. 又∵AC BC ⊥，∴906030DCE ACB ACD ∠=∠-∠=︒-︒=︒∴在Rt CDE ∆中，122DE DC ==，cos30CE DC =︒=∴BE BC CE =-=在Rt BDE ∆中，BD 评注:本题需要综合运用旋转、等边三角形以及直角三角形中的边角关系等知识和转化的思想方法解决问题.考点5解直角三角形的应用.例9 (2017·新疆建设兵团)如图8，甲、乙为两座建筑物，它们之间的水平距离BC 为30 m ，在A 点测得D 点的仰角EAD ∠为45︒，在B 点测得D 点的仰角CBD ∠为60︒，求这两座建筑物的高度(结果保留根号).解析:在Rt BCD ∆中，60CBD ∠=︒，30BC =m ， ∵tan CDCBD BC=∠，∴tan CD BC CBD =∠=g (m)，即乙建筑物的高度为m. 如图8，过A 作AF CD ⊥于点F ， 在Rt AFD ∆中，45FAD ∠=︒， ∴30DF AF BC ===m ，∴1)AB CF CD DF ==-=(m)，即为甲建筑物的高度.评注:解题的关键在于一是正确理解仰角、俯角等术语的含义，二是对特殊角的三角函数值能够了然于心.其实，特殊角的三角函数的取值和变化是有规律可循的，记忆起来并不难.如，正弦值逐渐增大，角度:(0)30456090α︒→︒→︒→︒→︒，01sin :(0)22α=→1=→=. 例10 (2017·庆阳)美丽的黄河宛如一条玉带穿城而过，沿河两岸的滨河路风景线是兰州最美的景观之一，数学课外实践活动中，小林在南滨河路上的,A B 两点处，利用测角仪分别对北岸的一观景亭D 进行了测量.如图9，测得45DAC ∠=︒，65DBC ∠=︒，若132AB =米，求观景亭D 到南滨河路AC 的距离约为多少米?(结果精确到1米，参考数据: sin 650.91︒≈，cos 650.42︒≈，tan 65 2.14︒≈)图 9解析:易知，若过点D 作DE AC ⊥，垂足为E ， 则可出现两个直角三角形. 设BE x =，在Rt DE ∆中，tan DEDBE BE∠=， ∵65DBC ∠=︒， ∴tan 65DE x =︒g . 又∵45DAC ∠=︒， ∴AE DE =∴132tan 65x x +=︒g ， 解得115.8x ≈. ∴248DE ≈(米). 答:(略).评注:本题的解答体现了方程思想.当三角形中的线段不易直接求出时，需要依托方程求解.运用三角函数的定义建立方程，选好三角函数是关键.其一般规律是，当已知或求解中有斜边时，可用正弦或余弦，无斜边时，就用正切，即所谓的“有斜用弦，无斜用切”.还应注意，当所求元素既可用乘法算式又可用除法算式表示时，尽量用乘法算式;既可用已知数值又可用中间数值运算时，尽量用已知数值;不要企求每一步都得出具体数值，“能拖则拖”，尝试整体处理，尽量缩小误差，降低运算的繁杂程度.例11 (2017·泸州)如图10，海中一渔船在A 处且与小岛C 相距70. n mile ，若读刨nb 由西向东航行30 n mile 到达B 处，此时测得小岛C 位于B 的北偏东30º方向上，求该渔船此时与小岛C 之间的距离.解析:过点C 作CD AB ⊥于点D .由题意，得30BCD ∠=︒. 设BC x =，则在Rt BCD ∆中，1sin 302BD BC x =︒=g ，cos30CD BC x =︒=g .∴1302AD x =+. ∵222AD CD AC +=，即2221(30))702x x ++=， 解得50x =(舍去负值).答:(略).评注:通过添加辅助线，构造两个直角三角形，借助于勾股定理，建立起了已知量与未知量之间的相互联系，使问题顺利得以解决.例12 (2017·江西)如图11，研究发现，科学使用电脑时，望向荧光屏幕画面的“视线角”α约为20º，而当手指接触键盘时，肘部形成的“手肘角” β约为100º.图11②是其侧面简化示意图，其中视线AB 水平，且与屏幕BC 垂直.(1)若屏幕上下宽20BC =cm ，科学使用电脑时，求眼睛与屏幕的最短距离AB 的长; (2)若肩膀到水平地面的距离100DG =cm ，上臂30DE =cm ，下臂EF 水平放置在键盘上，其到地面的距离72FH =cm.请判断此时β是否符合科学要求的100º?(参考数据:14sin 6915︒≈，14cos 2115︒≈，4tan 2011︒≈，14tan 4315︒≈，所有结果精确到个位) 解析:(1)∵在Rt ABC ∆中，tan BCA AB=，∴20554tan tan 2011BC BC AB A ==≈=︒(cm).(2)延长FE 交DG 于点I ，则2007228DI DG FH =-=-=(cm ).在Rt DEI ∆中，2814sin 3015DI DEI DE ∠===， ∵14sin 6915︒≈，∴69DEI ∠=︒，180********β∠=︒-︒=︒≠︒，故此时β不符合100º的科学要求.评注:本题取材既具有时代性，又十分贴近生活，还顺便普及了科学使用电脑的知识.命题者通过从现实场景中抽象出几何图形，用分数表出参考数据等举措，有效地降低了题目的难度.例13 (2017·威海)图12①是太阳能热水器装置的示意图，利用玻璃吸热管可以把太阳能转化为热能，玻璃吸热管与太阳光线垂直时，吸收太阳能的效果最好，假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太光线与玻璃吸热管垂直)，请完成以下计算:①②③图12如图12②，AB BC⊥，垂足为点B，EA AB⊥垂足为点A，//CD AB，10CD=cm，120DE=cm，FG DE⊥，垂足为点G.(1)若3750'θ∠=︒，则AB的长约为cm.(参考数据: sin3750'0.61︒≈，cos3750'0.79︒≈，tan3750'0.78︒≈)(2)若30FG=cm，60θ∠=︒，求CF的长.解析:(1)如图123，作EP BC⊥于点P，作DQ EP⊥于点Q，则10CD PQ==，2390∠+∠=︒.∵190θ∠+∠=︒，且12∠=∠，∴33750'θ∠=∠=︒，则sin3120sin3750'EQ DE=∠=︒g g，∴120sin3750'1083.2AB EP EQ PQ==+=︒+≈g(cm).(2)如图12③，延长ED，BC交于点K，由(1)知360Kθ∠=∠=∠=︒.在Rt CDK∆中，tanCDCKK==∠，在Rt KGF∆中，sinGFKFK===∠，则CF KF KC=-===，即为所求.评注:正确添加辅助线构造直角三角形，善于从复杂的图形中找出可用的简单图形和数量关系，是顺利解题的先决条件.考点6其他创新题型例14 (2017·嘉兴)如图13，把n个边长为1的正方形拼接成一排，求得1tan1BAC∠=，21tan3BA C∠=，31tan7BA C∠=，计算4tan BA C∠=，…按此规律，写出tannBA C∠=(用含n的代数式表示).解析:如图13，过点C作4CE A B⊥于E，易得441A BC BA A∠=∠，∴4411tan tan4A BC BA A∠=∠=.在Rt BCE∆中，由41tan4A BC∠=，得4BE CE=，而1BC=，则CE=BE=而4A B==∴44A E AB BE=-=.在4Rt A EC∆中，441tan13CEBA CA E∠==.又∵11tan1101BAC∠==⨯+，211tan3211BA C∠==⨯+，31tan 7BA C ∠=1321=⨯+， 411tan 13431BA C ∠==⨯+，…，由此规律，不难得出211tan (1)11n BA C n n n n ∠==⨯-+-+ 故答案为113，211n n -+. 评注:本题属于规律探究型问题，需运用定义，求出锐角三角函数的值，并结合已知数值，探求数字规律，现在的问题是，题目中与求解关联度很高的三角形都是斜三角形，需要“遇斜化直”，引垂线构造直角三角形，综合运用其中的边角关系解决问题.例15 (2017·福建)小明在某次作业中得到如下结果:2222sin 7sin 830.120.990.9945︒+︒≈+= 2222sin 22sin 680.370.93 1.0018︒+︒≈+= 2222sin 29sin 610.480.870.9873︒+︒≈+= 2222sin 37sin 530.600.80 1.0000︒+︒≈+=2222sin 45sin 45(()122︒+︒=+= 据此，小明猜想:对于任意锐角α，均有22sin sin (90)1αα+︒-=.(1)当30α=︒时，验证22sin sin (90)1αα+︒-=是否成立;(2)小明的猜想是否成立?若成立，请给予证明;若不成立，请举出一个反例.解:(1)当30α=︒时，22sin sin (90)αα+︒-22sin 30sin 60=︒+︒221()2=+ 1=∴22sinsin (90)1αα+︒-=成立.(2)小明的猜想成立，证明如下:如图14，在ABC ∆中，90C ∠=︒，设A α∠=，则90B α∠=︒- ∴22sinsin (90)αα+︒-22()()BC AC AB AB=+ 222BC AC AB +=22AB AB=1= 评注:本题属于归纳猜想型问题，证明猜想的思路是，回到锐角三角函数的定义，在直角三角形中，借助勾股定理进行推证.本例的结论揭示了直角三角形中两个互余锐角的同名函数(正弦、余弦)之间存在的一种平方关系，它又可表述为22sin cos 1αα+=，这是一个非常有用的结论. 【中考演练】1.(2017·烟台)在Rt ABC ∆中，90C ∠=︒，2AB =，BC ，则sin2A= . 2.(2016·陕西)已知抛物线223y x x =--+与x 轴交于,A B 两点，将这条抛物线的顶点记为C ，连接,AC BC ，则tan CAB ∠的值为( )A.12 B. 5 C. 5D. 23.(2017·衢州)计算:0(1)2tan 60π+⨯--︒.4.(2017·台州)如图15是一辆小汽车与墙平行停放的平面示意图，汽车靠墙一侧与墙MN 平行且距离为0.8米，已知小汽车车门AO 宽为1.2米，当车门打开角度AOB ∠为40︒时，车门是否会碰到墙?请说明理由.(参考数据:sin 400.64︒≈，cos 400.77︒≈，tan 400.84︒≈)图 155.(2017·宜宾)如图16，为了测量某条河的宽度，现在河边的一岸边任意取一点A ，又在河的另一岸边取两点B ，C ，测得30α∠=︒，45β∠=︒，量得BC 长为100米，求河的宽度(结果保留根号).6.(2017·黔东南州)如图17，某校教学楼AB 后方有一斜坡，已知斜坡CD 的长为12米，坡角α为60º，根据有关部门的规定，39α∠≤︒时，才能避免滑坡危险，学校为了消除安全隐患，决定对斜坡CD 进行改造，在保持坡脚C 不动的情况下，学校至少要把坡顶D 向后水平移动多少米才能保证教学楼的安全?(结果取整数)(参考数据:sin 390.63︒≈，cos390.78︒≈，tan 390.81︒≈ 1.41≈ 1.73≈ 2.24≈)7.(2017·河南)如图18所示，我国两艘海监船,A B 在南海海域巡航，某一时刻，两船同时收到指令，立即前往救援遇险抛锚的渔船C .此时，B 船在A 船的正南方向5海里处，A 船测得渔船C 在其南偏东45º方向，B 船测得渔船C 在其南偏东53º方向.已知A 船的航速为30海里/时，B 船的航速为25海里/时，问C 船至少要等待多长时间才能得到救援?(参考数据: 4sin 535︒≈，3cos535︒≈，4tan 533︒≈)8. ( 2017·常德)图19和图20分别是某款篮球架的实物图与示意图，已知底座0.60BC =米，底座BC 与支架AC 所成的角75ACB ∠=︒，支架AF 的长为2.50米，篮板顶端F 点到篮筐D 的距离 1.35FD =米，篮板底部支架HE 与支架AF 所成的角60FHE ∠=︒，求篮筐D 到地面的距离(精确到0.01米).(参考数据:cos 750.2588︒≈，sin 750.9659︒≈，tan 75 3.732︒≈ 1.732≈ 1.414≈)图 19 图 209.(2017·舟山)如图21是小强洗漱时的侧面示意图，洗漱台(矩形ABCD )靠墙摆放，高80AD =cm ，宽48AB =cm ，小强身高166cm ，下半身100FG =cm ，洗漱时下半身与地面成80︒ (80FGK ∠=︒)，身体前倾成125︒(125EFG ∠=︒)，脚与洗漱台距离15GC = cm(点,,,D C G K 在同一直线上).(1)此时小强头部E 点与地面DK 相距多少？(2)小强希望他的头部E 恰好在洗漱盆AB 的中点O 的正上方，他应向前进或后退多少?(sin 800.98︒≈，cos800.18︒≈ 1.41≈，结果精确到0.1)10. (2017年赤峰)如图22，在ABC ∆中，设A ∠，B ∠，C ∠的对边分别为a ，b ，c ，过点A 作AD BC ⊥，垂足为D ，会有sin AD C AC =，则12ABC S BC AD ∆=g 11sin sin 22BC AC C ab C ==g ，即1sin 2ABC S ab C ∆=. 艺同理，1sin 2ABC S bc A ∆=，1sin 2ABC S ac B ∆=.通过推理还可以得到另一个表达三角形边角关系的定理一余弦定理:如图23，在ABC ∆中，若A ∠，B ∠，C ∠的对边分别为a ，b ，c ，则2222cos a b c bc A =+-， 2222cos b a c ac B =+- 2222cos c a b ab C =+-用上面的三角形面积公式和余弦定理解决问题:(1)如图24，在DE F ∆中，60F ∠=︒，D ∠，E ∠的对边分别是3和8.求DEF S ∆和2DE . 1sin 2DEF S EF DF F ∆==g ;2222cos DE EF DF EF DF F =+-=g .(2)如图25，在ABC ∆中，已知AC BC >，60C ∠=︒，'ABC ∆，'BCA ∆，'ACB ∆分别是以AB ，BC ，AC 为边长的等边三角形，设ABC ∆，'ABC ∆，'BCA ∆，'ACB ∆的面积分别为1234,,,S S S S ，求证:1234S S S S +=+.答案:1. 122. D3.0(1)2tan 60π+⨯--︒122=⨯=4. 依题意，过A 作AC OB ⊥于点C ， 在Rt AOC ∆中，40AOC ∠=︒， ∴sin 40ACOA︒=. ∵ 1.2OA =，∴sin 40 1.20.640.768AC OA =︒≈⨯=(米). ∵0.7680.8AC =<， ∴车门不会碰到墙.5.过点A 作AD BC ⊥于点D . ∵45β∠=︒，90ADC ∠=︒， ∴AD CD =.设AD CD x ==m ，则tan 30100x x ︒==+，解得1)x =.答：(略)6.如图27，假设点D 移到'D 的位置时，恰好39α∠=︒，过点D 作DE AC ⊥于点E ，作''D E AC ⊥于点'E .∵ 1.2CD =米，60DCE ∠=︒，∴sin 6012DE CD =︒==米)， 1cos 601262CE CD =︒=⨯=(米). ∵DE AC ⊥，''D E AC ⊥，'//'DD CE ， ∴四边形''DEE D 是矩形.∴''DE D E ==米) ∵''39D CE ∠=︒，∴'''12.8tan 39D E CE =≈≈︒，∴''12.86 6.8EE CE CD =-=-=(米). 答:(略).7. 过点C 作CD AB ⊥交AB 的延长线于点D ， 则90CDA ∠=︒.已知45CAD ∠=︒，设CD x =， 则AD CD x ==.∴5BD AD AB x =-=-.在Rt BDC ∆中，tan 53CD BD =︒g ， 即(5)tan53x x =-︒g ，∴455tan 533204tan 53113x ⨯︒=≈=︒--. ∴20254sin 53sin 535CD x BC ==≈=︒︒∴B 船到达C 船处约需时间:25251÷=(小时).在Rt ADC ∆中，AC ==0.94=. 故C 船至少要等待0.94小时才能得到救援.8.如图28，过点E 作EP BC ⊥于P ，过点A 作AQ FP ⊥于Q . 在Rt ABC ∆中，∵tan ABACB CB∠=∴tan 750.60 3.732 2.239AB CB =︒≈⨯=g (米)，易知四边形ABPQ 是矩形. ∴ 2.239PQ =米.又∵HE FP ⊥，AQ FP ⊥， ∴//HE AQ ，60FAQ FHE ∠=∠=︒. 在Rt FAQ ∆中，sin FQFAQ FA∠=，∴ 2.50 2.1652FQ =⨯≈(米). ∴ 2.165 1.350.815DQ FQ FD =-=-=(米)，0.815 2.239 3.05DP DQ PQ =+=+≈(米).答:(略).9.(1)如图29，过点F 作FN DK ⊥于点N ，过点E 作EM FN ⊥于点M . ∵166,100EF FG FG +==， ∴66EF =.∵80FGK ∠=︒，∴100sin8098FN =︒≈. 又∵125EFG ∠=︒，∴1801251045EFM ∠=︒-︒-︒=︒.∴66cos4546.53FM =︒=≈.∴144.5MN FN FM =+≈.故此时小强头部E 点与地面DK 相距约144.5 cm.(2)如图29，过点E 作EP AB ⊥于点P ，延长OB 交MN 于点H . ∵48AB =，O 为AB 的中点， ∴24AO BO ==.∵66sin 4546.53EM =︒≈，即46.53PH ≈，100cos8018GN =︒≈，15CG =， ∴24151857OH =++=，5746.5310.4710.5OP OH PH =-=-=≈. 故小强应向前讲约10.5 cm.10.(1)在DEF ∆中，60F ∠=︒，D ∠，E ∠的对边分别是3和8，∴11sin 38sin 6022DEF S EF DF F ∆==⨯⨯⨯︒=g 222222cos 38238cos6049DE EF DF EF DF F =+-=+-⨯⨯︒=g(2)证明:如题图25， ∵60C ∠=︒，∴222222cos60AB AC BC AC BC AC BC AC BC =+-︒=+-g g ， 即222AB AC BC AC BC =+-g两边同乘以告1sin 602︒， 得2221111sin 60sin 60sin 60sin 602222AB AC BC AC BC ︒=︒+︒-︒g ， 即2221111sin 60sin 60sin 60sin 602222AC BC AB AC BC ︒+︒=︒+︒g . 又∵'ABC ∆，'BCA ∆，'ACB ∆都是等边三角形，∴11sin 602S AC BC =︒g221sin 602S AB =︒，231sin 602S BC =︒，241sin 602S AC =︒，故1234S S S S +=+.。

—第一学期初三数学期终复习要点四第7章 锐角三角函数知识点：锐角三角函数（正切、正弦、余弦），特殊角的三角函数，由三角形值求锐角，解直角三角形，用锐角三角函数解决问题。

典型例题：例1．如图，在Rt △ABC 中，∠C =90°，AC =1，∠B =30°，则AB 的长为（ ）A ．2B ．3C ．12D ．3 例2．在Rt △ABC 中，∠C =90°，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，那么c 可以表示为A ．a 2＋b 2B ．a ⋅cos B ＋b ⋅cos AC ．a ⋅sin B ＋b ⋅sin AD ．sin sin a b A B+ 例3．在Rt △ABC 中，已知∠C =90°，CD ⊥AB ，AC =8，AB =10，则tan ∠ACD= ． 例4．计算：()102cos601212-+︒⎛⎫-- ⎪⎝⎭ 例5．如图，为了测量旗竿CD 的高度，在平地上选择点A ，用测角仪测得旗竿顶D 的仰角为30°，再在A 、C 之间选择一点B （A 、B 、C 三点在同一直线上）进行测量，已知AB =40m ．(1)若测得∠DBC =60°，则CD = m ；(2)若测得∠DBC =75°，求旗竿CD 的高度（以上结果均保留根号）．例6．如图，点A 、B 在⊙O 上，直线AC 是⊙O 的切线，OC ⊙OB ，连接AB 交OC 于点D ．(1)求证：AC ＝CD ； (2)如果OD ＝1，tan ⊙OCA ＝，求AC 的长．52A C B（第1题） A B C D 30°当堂练习：1．5．在Rt △ABC 中，∠C ＝90°，∠A 、∠B 、∠C 所对的边分别为a 、b 、c ，下列等式一定能成立的有（ ）A ．sinA ＝sinB B ．a ＝c ．sinBC ．sin 2A ＋cos 2B ＝1D ．sin A ＝tanA ．cosA2．如图，AB 是⊙O 的弦，半径OA ＝2， sinA 35=，则弦AB 的长为（ ） A ．45 B ．213 C ．4 D ．25 （第2题）（第3题）3．如图，在顶角为30°的等腰△ABC 中，AB ＝AC ，若过点C 作CD ⊥AB 于点D ．根据图形计算tan ∠BCD ＝ ．4．计算：2cos30° － tan45°－()21tan 60+︒．5. 如图，在Rt △ABC 中，∠C ＝90°，∠A ＝30°，BD 是∠ABC 的平分线，AD ＝20．(1)求BC 的长；(2)求BCD ABCS S ∆∆的值．6. 小美和同学一起到游乐场游玩．游乐场的大型摩天轮的半径为20 m ，匀速旋转1周需要12 min ．小美乘坐最底部的车厢(离地面约0.5 m)开始1周的观光，请回答下列问题：（参考数据：≈1.414，3≈1.732）(1)1.5min 后小美离地面的高度是 ▲ m ；(精确到0.1m)(2)摩天轮启动多长时间后，小美离地面的高度将首次达到10.5 m?(3)摩天轮转动一周，小美在离地面10.5m 以上的空中有多长时间？ 2课后作业：1．如图，在△ABC中，∠C＝90°，AB＝5，BC＝3，则sinA的值为（）A．34B．43C．35D．45（第1题）（第2题）2. （•鄂州）如图，在矩形ABCD中，AB=8，BC=12，点E是BC的中点，连接AE，将⊙ABE沿AE折叠，点B落在点F处，连接FC，则sin⊙ECF=（）A．B．C．D．3．计算：－222cos60°＋1 13-⎛⎫⎪⎝⎭4. 如图，某校教学楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，教学楼在建筑物的墙上留下高2m的影子CE；而当光线与地面的夹角是45°时，教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上)．求教学楼AB的高度．（参考数据：sin22°≈38，cos22°≈1516，tan22°≈25）5. （•鄂州）已知点P是半径为1的⊙O外一点，PA切⊙O于点A，且PA=1，AB是⊙O的弦，AB=，连接PB，则PB= 。

苏教版九年级下册数学重难点突破知识点梳理及重点题型巩固练习锐角三角函数—巩固练习【巩固练习】一、选择题1. （2016•乐山）如图，在Rt △ABC 中，∠BAC=90°，AD ⊥BC 于点D ，则下列结论不正确的是（ ）A ．B ．C ．D ．2.（2015•山西）如图，在网格中，小正方形的边长均为1，点A ，B ，C 都在格点上，则∠ABC 的正切值是（ ）A ．2B ．C ．D ．3. 已知锐角α满足sin25°＝cos α，则α＝( )A ．25°B ．55°C ．65°D ．75°4．如图所示，直径为10的⊙A 经过点C(0，5)和点O(0，0)，B 是y 轴右侧⊙A 优弧上一点，则∠OBC 的余弦值为 ( )A ．12B ．34C ．45第4题 第5题5．如图，在△ABC 中，∠A ＝120°，AB ＝4，AC ＝2，则sinB 的值是( )A B C D 6．在Rt △ABC 中，∠C ＝90°，若将各边长度都扩大为原来的2倍，则∠A 的正弦值( )A ．扩大2倍B ．缩小2倍C ．扩大4倍D ．不变7．如图所示是教学用具直角三角板，边AC ＝30cm ，∠C ＝90°，tan ∠BAC BC 的长为( )A ．cmB ．．．第7题 第8题8. 如图所示，在Rt △ABC 中，∠ACB ＝90°，CD ⊥AB ，垂足为D ，若AC ，BC ＝2，则sin ∠ACD 的值为( )A ．3B ．3C ．2D ． 23二、填空题9．（2016•临夏州）如图，点A （3，t ）在第一象限，OA 与x 轴所夹的锐角为α，tan α=，则t 的值是 ．10. 用不等号连接下面的式子．(1)cos50°________cos20° (2)tan18°________tan21°11．在△ABC 中，若2sin cos 0A B ⎫-+-=⎪⎪⎝⎭，∠A 、∠B 都是锐角，则∠C 的度数为 . 12．如图所示，△ABC 的顶点都在方格纸的格点上，则sinA ＝________．13．已知：正方形ABCD 的边长为2，点P 是直线CD 上一点，若DP ＝1，则tan ∠BPC 的值是________．第12题 第15题14．如果方程2430x x -+=的两个根分别是Rt △ABC 的两条边，△ABC 的最小角为A ，那么tanA 的值为________．15．如图所示，△ABC 的内心在y 轴上，点C 的坐标为(2，0)，点B 的坐标是(0，2)，直线AC 的解析式为112y x =-，则tanA 的值是________． 16.（2014•高港区二模）若α为锐角，且，则m 的取值范围是 ．三、解答题17．如图所示，△ABC 中，D 为AB 的中点，DC ⊥AC ，且∠BCD ＝30°，求∠CDA 的正弦值、余弦值和正切值．18. 计算下列各式的值．(1) （2015•普陀区一模）；(2) （2015•常州模拟）sin45°+tan45°﹣2cos60°． (3) （2015•奉贤区一模）﹣cos60°．19．如图所示，在矩形ABCD 中，E 是BC 边上的点，AE ＝BC ，DF ⊥AE ，垂足为F ，连接DE ．(1)求证：AB ＝DF ；(2)若AD ＝10，AB ＝6，求tan ∠EDF 的值．20. 如图所示，已知⊙O 的半径为2，弦BC 的长为A 为弦BC 所对优弧上任意一点(B 、C 两点除外)．(1)求∠BAC 的度数；(2)求△ABC 面积的最大值．(参考数据：sin 602=°，cos302=°，tan 303=°．【答案与解析】一、选择题1.【答案】C.【解析】在Rt △ABC 中，∠BAC=90°，sinB=， ∵AD ⊥BC ，∴sinB=，sinB=sin ∠DAC=， 综上，只有C 不正确故选：C ．2.【答案】D ；【解析】如图：由勾股定理得，AC=，AB=2，BC=，∴△ABC 为直角三角形， ∴tan∠B==， 故选：D ．3. 【答案】C ；【解析】由互余角的三角函数关系，cos sin(90)αα=-°，∴ sin25°-sin(90°-α)，即90°-α＝25°，∴ α＝65°．4.【答案】C ；【解析】设⊙A 交x 轴于另一点D ，连接CD ，根据已知可以得到OC ＝5，CD ＝10，∴ OD == ∠OBC ＝∠ODC ，∴ cos OB cos 102OD C ODC CD ∠=∠===．5.【答案】D ；【解析】如图所示，过点C 作CD ⊥AB 于D ，∵ ∠BAC ＝120°，∴ ∠CAD ＝60°，又∵ AC ＝2，∴ AD ＝1，CD ，∴ BD ＝BA+AD ＝5，在Rt △BCD 中，BC ===∴ sin 14CD B BC ===．6.【答案】D ； 【解析】根据锐角三角函数的定义，锐角三角函数值等于相应边的比，与边的长度无关，而只与边的比值或角的大小有关．7.【答案】C ；【解析】由tan BC BAC AC ∠==，∴ 30BC AC ===8. 【答案】A ；【解析】 ∵ 3AB =，∴ sin sin 3AC ACD B AB ∠=∠==二、填空题9.【答案】．【解析】过点A 作AB ⊥x 轴于B ，∵点A （3，t ）在第一象限，∴AB=t ，OB=3，又∵tan α===， ∴t=． 故答案为：．10.【答案】(1)＜； (2)＜；【解析】当α为锐角时，其余弦值随角度的增大而减小，∴ cos50°＜cos20°；当α为锐角时，其正切值随角度的增大而增大，∴ tan18°＜tan21°．11．【答案】105°；【解析】∵ 2sin cos 0A B ⎫+-=⎪⎪⎝⎭，∴ sin 02A -=cos 0B -=即sin 2A =，cos B =又∵ ∠A 、∠B 均为锐角，∴ ∠A ＝45°，∠B ＝30°，在△ABC 中，∠A+∠B+∠C ＝180°，∴ ∠C ＝105°．12．【解析】假设每一个小正方形的边长为1，利用网格，从C 点向AB 所在直线作垂线CH ．垂足为H ，则∠A 在直角△ACH 中，利用勾股定理得AC ==∴sin 5CH A AC ===． 13．【答案】2或23【解析】此题为无图题，应根据题意画出图形，如图所示，由于点P 是直线CD 上一点，所以点P 既可以在边CD 上，也可以在CD 的延长线上，当P 在边CD 上时，tan 2BC BPC PC ∠==；当P 在CD 延长线上时，2tan 3BC BPC PC ∠==．14．【答案】13或4； 【解析】由2430x x -+=得11x =，23x =，①当3为直角边时，最小角A 的正切值为1tan 3A =；②当3为斜边时，=∴ 最小角A的正切值为tan 4A ==. 故应填13或4． 15．【答案】13； 【解析】由△ABC 的内心在y 轴上可知OB 是∠ABC 的角平分线，则∠OBA ＝45°，易求AB 与x 轴的交点为(-2，0)，所以直线AB 的解析式为：2y x =+， 联立2112y x y x =+⎧⎪⎨=-⎪⎩可求A 点的坐标为(-6，-4)， ∴AB ==OC ＝OB ＝2，∴ BC＝．在Rt △ABC中，1tan 3BC A AB ===．16.【答案】 ； 【解析】∵0＜cos α＜1， ∴0＜＜1， 解得.三、解答题17.【答案与解析】过D 作DE ∥AC ，交BC 于点E ．∵ AD ＝BD ，∴ CE ＝EB ，∴ AC ＝2DE ．又∵ DC ⊥ AC ，DE ∥AC ，∴ DC ⊥DE ，即∠CDE ＝90°．又∵ ∠BCD ＝30°，∴ EC ＝2DE ，DC DE ．设DE ＝k ，则CD ，AC ＝2k ．在Rt △ACD 中，AD ．∴ sinAC CDA AD ∠===cos 7CD CDA AD ∠===．tanAC CDA CD ∠===．18.【答案与解析】解：（1）原式=4×﹣×+× =1+3． (2) 原式=×+1﹣2× =1+1﹣1=1．(3) 原式=﹣× =﹣=14． 19.【答案与解析】(1)证明：∵ 四边形ABCD 是矩形，∴ AD ∥BC ，AD ＝BC∴ ∠DAF ＝∠AEB又∵ AE ＝BC ，∴ AE ＝AD又∵ ∠B=∠DFA ＝90°，∴ △EAB ≌△ADF ．∴ AB ＝DF ．(2)解：在Rt △ABE 中，8BE =∵ △EAB ≌△ADF ，∴ DF ＝AB ＝6，AF ＝EB ＝8，∴ EF ＝AE-AF ＝10-8＝2．∴ 21tan 63EF EDF DF ∠===．20.【答案与解析】(1)连接BO 并延长，交⊙O 于点D ，连接CD ．∵ BD 是直径，∴ BD ＝4，∠DCB ＝90°．在Rt △DBC 中，sin 42BC BDC BD ∠=== ∴ ∠BDC ＝60°，∴ ∠BAC ＝∠BDC ＝60°．(2)因为△ABC 的边BC 的长不变，所以当BC 边上的高最大时，△ABC 的面积最大，此时点A 应落在优弧BC 的中点处．过O 作OE ⊥BC 于点E ，延长EO 交⊙O 于点A ，则A 为优孤BC 的中点．连结AB ，AC ， 则AB ＝AC ，∠BAE 12=∠BAC ＝30°．在Rt △ABE 中，∵ BE =BAE ＝30°，∴3tan303BEAE===°，∴132ABCS=⨯=△答：△ABC面积的最大值是。