江苏省南通市2001-2012年中考数学试题分类解析 专题6 函数的图像与性质
- 格式:doc
- 大小:2.09 MB
- 文档页数:42

2001-2012年江苏南通中考数学试题分类解析汇编(12专题)专题3:方程(组)和不等式(组)锦元数学工作室 编辑一、选择题1. (江苏省南通市2002年3分)用换元法解方程2220x 3x 8x 3x=+-+,若设x 2+3x=y ,则原方程可化为【 】A .20y 2+8y -1=0B .8y 2-20y +1=0C .y 2+8y -20=0D .y 2-8y -20=0 【答案】D 。
【考点】换元法解分式方程。
【分析】根据原方程的特点,把x 2+3x 看作整体,用y 代替,转化为关于y 的分式方程20y 8y=-,去分母并整理得一元二次方程y 2-8y -20=0。
故选D 。
2. (江苏省南通市2002年3分)某厂今年3月份的产值为50万元,5月份上升到72万元,这两个月平均每月上升的百分率是多少?若设4、5月份平均每月上升的百分率为x ,则列出的方程是【 】A .50(1+x )=72B .50(1+x )+50(1+x )2 = 72C .50(1+x )×2=72D .50(1+x )2 = 72【答案】D 。
【考点】由实际问题抽象出一元二次方程(增长率问题)【分析】设4、5月份平均每月上升的百分率为x ,4月份的产值为50(1+x),则5月份的产值为50(1+x) (1+x) =50(1+x)2。
据此列出方程50(1+x)2=72。
故选D 。
3. (江苏省南通市2004年3分)一列列车自2004年全国铁路第5次大提速后,速度提高了26千米/时,现在该列车从甲站到乙站所用的时间比原来减少了1小时,已知甲、乙两站的路程是312千米,若设列车提速前的速度是x 千米,则根据题意所列方程正确的是【 】A 、126312312=--x x B 、131226312=-+x xC 、126312312=+-x xD 、131226312=--xx 【答案】C 。
【考点】由实际问题抽象出分式方程【分析】关键描述语为:“现在该列车从甲站到乙站用的时间比原来减少了1h .”;等量关系为:提速前所用的时间-提速后用的时间=1。

2001-2012年某某某某中考数学试题分类解析汇编(12专题)专题1:实数一、选择题1.(2001某某某某3分)用小数表示3×10-2,结果为【 】A 、-0.03B 、-0.003【答案】C 。
【考点】负整指数幂。
【分析】根据负整指数幂直接计算得:3×10-2=3×0.01=0.03。
故选C 。
2.(某某省某某市2002年3分)16的平方根是【 】A .±4 B.±2 C.4 D . 2【答案】A 。
【考点】平方根。
【分析】根据平方根的定义,求数a 的平方根,也就是求一个数x ,使得x 2=a ,则x 就是a 的一个平方根。
∵(±4)2=16,∴16的平方根是±4。
故选A 。
3. (某某省某某市2003年3分)计算3258 的结果是【 】A .3B .7C .-3D .-7【答案】A 。
【考点】实数的运算【分析】先根据算术平方根、立方根的定义去掉根号,从而化简再相减:原式=5-2=3。
故选A 。
4. (某某省某某市2003年3分)《2002年某某市国民经济和社会发展统计公报》显示,2002年某某市完成国内生产总值890.08亿元,这个国内生产总值用科学记数法表示为【 】A .8.9008×108元B .8.9008×109元C .8.9008×1010元D .8.9008×1011元【答案】C 。
【考点】科学记数法。
【分析】根据科学记数法的定义,科学记数法的表示形式为a×10n ,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值。
在确定n 的值时,看该数是大于或等于1还是小于1。
当该数大于或等于1时,n 为它的整数位数减1;当该数小于1时,-n 为它第一个有效数字前0的个数(含小数点前的1个0)。
890.08亿=89008000000一共11位,从而890.08亿=89008000000=8.9008×109。

【中考12年】某某省某某市2001-2012年中考数学试题分类专题6函数的图像与性质选择题1. (2002年某某某某3分)已知关于x的一次函数y mx1=+,如果y随x的增大而增大,则m的取值X围是【】A.m>0 B.m<0 C.m≥0 D.m≤02. (2002年某某某某3分)二次函数2y x2x2=-+有【】A.最大值1 B.最大值2 C.最小值1 D.最小值23. (2002年某某某某3分)设A(x1,y1)、B (x2,y2)是反比例函数2yx=-图象上的两点.若x1<x2<0,则y1与y2之间的关系是【】A.y1<y2<0 B.y2<y1<0 C.y2>y1>0 D.y1>y2>04. (2004年某某某某3分)若反比例函数()ky k 0x =≠ (k≠0)的图象经过点(-1,2),则k 的值为【 】A .-2B .-21C .2D .217. (2007年某某某某3分)关于函数1yx=-的图象,下列说法错误的是【】A.经过点(1,-1) B.在第二象限内,y随x的增大而增大C.是轴对称图形,且对称轴是y轴 D.是中心对称图形,且对称中心是坐标原点8. (2011年某某某某3分)如图,反比例函数ky=x的图象经过点A(-1,-2).则当x>1时,函数值y的取值X围是【】A.y>1 B.0<y<1 C. y>2 D.0<y<29. (2012年某某某某3分)已知反比例函数m1yx-=的图象如图所示,则实数m的取值X围是【】A、m>1B、m>0C、m<1D、m<0二、填空题1. (2009年某某省3分)反比例函数1yx=-的图象在第▲ 象限.【答案】二、四。
【考点】反比例函数的性质。
【分析】根据反比例函数()ky=k 0x ≠的性质:当k 0>时,图象分别位于第一、三象限;当k 0<时,图象分别位于第二、四象限:∵反比例函数1y x =-的系数k=10<-,∴图象两个分支分别位于第二、四象限。

2001-2012年某某某某中考数学试题分类解析汇编(12专题)专题5:数量和位置变化一、选择题1.(2001某某某某3分)点P(-3,4)关于原点对称的点的坐标是【】A、(3,-4)B、(-3,-4)C、(3,4)D、(-4,3)【答案】A。
【考点】关于原点对称的点的坐标特征。
【分析】关于原点对称的点的坐标是横、纵坐标都互为相反数,从而点P(-3,4)关于原点对称的点的坐标是(3,-4)。
故选A。
2.(某某省某某市2003年3分)在函数x1yx+=中,自变量x的取值X围是【】A.x≠-1 B.x≠0 C.x≥-1 D.x≥-1,且x≠0【答案】D。
【考点】函数自变量的取值X围,二次根式和分式有意义的条件。
【分析】根据二次根式被开方数必须是非负数和分式分母不为0的条件,要使 x1x+在实数X围内有意义,必须x10x1x0x0+≥≥-⎧⎧⇒⎨⎨≠≠⎩⎩。
故选D。
3. (某某省某某市2004年2分)点M(1,2)关于x轴对称点的坐标为【】A、(-1,2)B、(-1,-2)C、(1,-2)D、(2,-1)【答案】C。
【考点】关于x轴对称的点的坐标【分析】关于x轴对称点的坐标是横坐标不变纵坐标变为原来的相反数,可知,A(1,2)关于x轴对称点的坐标是(1,-2)。
故选C。
4.(2012某某某某3分)线段MN在直角坐标系中的位置如图所示,线段M1N1与MN关于y轴对称,则点M的对应的点M1的坐标为【】A.(4,2)B.(-4,2)C.(-4,-2)D.(4,-2)【答案】D。
【考点】平面坐标系与坐标,关于y轴对称的点的坐标特征。
【分析】关于y轴对称的点的坐标特征是纵坐标不变,横坐标互为相反数,从而点M(-4,-2)关于y轴对称的点M1的坐标是(4,-2)。
故选D。
二、填空题1. (2001某某某某2分)函数y=1x1-中,自变量x的取值X围是▲ 。
【答案】x1≠。
【考点】函数自变量的取值X围,二次根式和分式有意义的条件。

江苏省宿迁市2001-2012年中考数学试题分类解析 专题06 函数的图像与性质一、选择题1. (2001年江苏宿迁4分)若反比例函数ky=x的图象过点(1,6),则在这个反比例函数图象上的点是【 】A 、 )2,3(B 、)3,2(--C 、)1,6(--D 、(2 , 3)2. (2004年江苏宿迁4分)抛物线2y x 2x 2+-=的顶点坐标是【 】A.(2,-2)B.(1,-2)C.(1,-3)D.(-1,-3)3. (2004年江苏宿迁4分)如果点(a ,-2a )在双曲线ky x=上,则此双曲线的图象在【 】A. 第一、二象限B. 第一、三象限C. 第二、四象限D. 第三、四象限4. (2005年江苏宿迁3分)如图,直线y 2x =与双曲线ky x=的图象的一个交点坐标为(2,4).则它们 的另一个交点坐标是【 】A .(-2,-4)B .(-2,4)C .(-4,-2)D .(2,-4)5. (2007年江苏宿迁3分)设A(x 1,y 1)、B(x 2,y 2)是反比例函数y 2x=-图象上的任意两点,且y 1<y 2 ,则x 1 ,x 2可能满足的关系是【 】A. x 1>x 2>0B. x 1<0<x 2C. x 2<0<x 1D. x 2<x 1<06. (2008年江苏宿迁3分)在平面直角坐标系中,函数y x 1=-+与23y (x 1)2=--的图象大致是【 】7. (2011年江苏宿迁3分)已知二次函数()2y ax bx c a 0++≠=的图象如图,则下列结论中正确的是【 】A .a >0B .当y 随x 的增大x >1时,y 随x 的增大而增大C .c <0D .3是方程2ax bx c 0++=的一个根8. (2012年江苏宿迁3分)在平面直角坐标系中,若将抛物线y=2x 2- 4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是【 】 A.(-2,3)B.(-1,4)C.(1,4)D.(4,3)二、填空题1. (2001年江苏宿迁4分)已知一次函数的图象如图所示,则当x=10时,y= ▲ 。
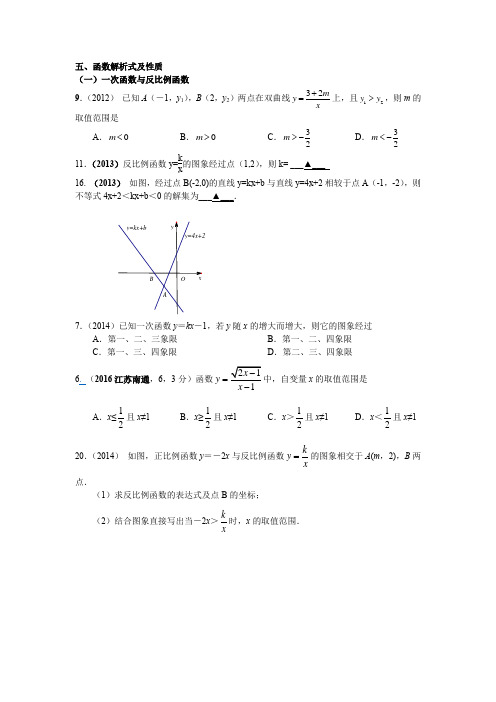
五、函数解析式及性质(一)一次函数与反比例函数9.(2012) 已知A (-1,y 1),B (2,y 2)两点在双曲线32my x+=上,且12y y >,则m 的取值范围是A .0m <B .0m >C .32m >-D .32m <-11.(2013)反比例函数y=kx的图象经过点(1,2),则k= ___▲___16. (2013) 如图,经过点B(-2,0)的直线y=kx+b 与直线y=4x+2相较于点A (-1,-2),则不等式4x+2<kx+b <0的解集为___▲___.7.(2014)已知一次函数y =kx -1,若y 随x 的增大而增大,则它的图象经过A .第一、二、三象限B .第一、二、四象限C .第一、三、四象限D .第二、三、四象限 6. (2016江苏南通,6,3分)函数1y x =-中,自变量x 的取值范围是 A .x ≤12且x ≠1 B .x ≥12且x ≠1C .x >12且x ≠1 D .x <12且x ≠1 20.(2014) 如图,正比例函数y =-2x 与反比例函数ky x=的图象相交于A (m ,2),B 两点. (1)求反比例函数的表达式及点B 的坐标;(2)结合图象直接写出当-2x >kx时,x 的取值范围.23.(2015)如图,直线y=mx+n与双曲线y=kx相交于A(-1,2),B(2,b)两点,与y轴相交于点C.(1)求m,n的值;(2)若点D与点C关于x轴对称,求△ABD的面积.10.(2016)平面直角坐标系xOy中,已知A(-1,0),B(3,0),C(0,-1)三点,D(1,m)是一个动点,当△ACD的周长最小时,△ABD的面积为A.13B.23C.43D.83(二次函数)26.(2013)某公司营销A,B两种产品,根据市场调研,发现如下信息:根据以上信息,解答下列问题:(1)求二次函数解析式;(2)该公司准备购进A,B两种产品共10吨,请设计一个营销方案,使销售A,B两种产品获得的利润之和最大,最大利润是多少?(第23题)14.(2014)已知抛物线y=ax2+bx+c与x轴的公共点是(-4,0),(2,0),则这条抛物线的对称轴是直线______________.26.(2015)某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元.设顾客一次性购买服装x件时,该网店从中获利y元.(1)求y与x的函数关系式,并写出自变量x的取值范围;(2)顾客一次性购买多少件时,该网店从中获利最多?26. (2016)平面直角坐标系xoy中,已知抛物线y=x2+bx+c经过(-1,m2+2m+1))、(0,m2+2m+2)两点,其中m为常数.(1)求b的值,并用含m的代数式表示c.(2)若抛物线y=x2+bx+c与x轴有公共点,求m的值.(3)设(a,y1)、(a+2,y2)是抛物线y=x2+bx+c上的两点,试比较y2-y1与0的大小,并说明理由.26.(2018南通,10分)在平面直角坐标系xOy中,已知抛物线y=x2﹣2(k﹣1)x+k2﹣k(k为常数).(1)若抛物线经过点(1,k2),求k的值;(2)若抛物线经过点(2k,y1)和点(2,y2),且y1>y2,求k的取值范围;(3)若将抛物线向右平移1个单位长度得到新抛物线,当1≤x≤2时,新抛物线对应的函数有最小值﹣,求k的值.。
江苏省南通市2012年中考数学试卷数学答案解析323x x=-)+【考点】同底数幂的乘法.-=,故选32,∴∠18032148【提示】根据互为补角的和等于180列式计算即可得解.70180250+=,故选B.【提示】先利用三角形内角与外角的关系,得出12∠+∠=∠120,∴18012060∠=-,,01,903∠==B AC ,∴顺时针旋转到①,可得到点P ,此时=AP三次一循环,按此规律即可求解.【考点】旋转的性质.二、填空题11.【答案】3【解析】解:2233=x y x y ,其中数字因式为3,则单项式的系数为3.【提示】把原题单项式变为数字因式与字母因式的积,其中数字因式即为单项式的系数.【考点】单项式.12.【答案】5≠x【解析】解:根据题意得50-≠x ,解得5≠x .【提示】求函数自变量的取值范围就是求函数解析式有意义的条件,分式有意义的条件是:分母不等于0.【考点】函数自变量的取值范围,分式有意义的条件.13.【答案】165.【解析】解:数据163,165,167,164,165,166,165,164,166中165出现了3次,且次数最多,所以众数是165.【提示】根据众数是一组数据中出现次数最多的数据解答即可.【考点】众数.14.【答案】23【解析】解:∵O 中,46∠=AOB ,∴12124623∠=∠=⨯=ACB AOB .【提示】由O 中,46∠=AOB ,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠ACB 的度数.【考点】圆周角定理.15.【答案】20.【解析】解:设购买甲电影票x 张,乙电影票y 张,由题意得,40+=x y ,2015700+=x y ,解得:20 20==,x y ,即甲电影票买了20张.【提示】设购买甲电影票x 张,乙电影票y 张,则根据总共买票40张,花了700元可得出方程组,解出即可得出答案.【考点】二元一次方程组的应用.16【答案】2【解析】解:作∥DE BC 于E 点,则∠=∠DEA B ,∵90∠+∠=A B ,∴90∠+∠=A DEA ,∴⊥ED AD ∵3cm 4cm ==,BC AD ,∴5=EA ,∴752cm ==-=-=CD BE AB AE ,故答案为2.90,得到(1)(3⎤-+⎥+⎦x x x (1)(13-+⎤⎥+⎦x x x 3(1)(1)13-++x x x 25-=.906030-==,AE 100cos30503⨯=海里,=BE EP 30的角所对的直角边(2)根据从中随机抽取一张牌,接着再抽取一张,列树状图如下:【提示】(1)利用数字2,3,4,8中一共有3个偶数,总数为4,即可得出点数偶数的概率. (2)利用树状图列举出所有情况,让点数都是偶数的情况数除以总情况数即为所求的概率.【考点】列表法与树状图法,概率公式.25.【答案】解:(1)利用图象可得:线段CD 表示轿车在途中停留了2.520.5-=小时;(2)根据D 点坐标为:(2.5,80),E 点坐标为:(4.5,300),代入=+y kx b ,得:880 2.5300 4.5=+⎧⎨=+⎩k b k b ,解得:110195=⎧⎨=-⎩k b ,故线段DE 对应的函数解析式为:110195=-y x . (3)∵A 点坐标为:(5,300),代入解析式=y ax 得,3005=a ,解得:60=a ,故60=y x , 当60110195=-x x ,解得: 3.9=x 小时.【提示】(1)利用图象得出CD 这段时间为22.520.5-=,得出答案即可;(2)利用D 点坐标为:(2.5,80),E 点坐标为:(4.5,300),求出函数解析式;(3)利用OA 的解析式得出,当60110195=-x x 时,即为轿车追上货车时.【考点】一次函数的应用.26.【答案】证明:(1)如图1,连接AC ,∵菱形ABCD 中,60∠=B ,∴==AB BC CD ,180120∠=-∠=C B ,∴△ABC 是等边三角形,∵E 是BC 的中点,∴⊥AE BC ,∵60∠=AEF ,∴9030∠=-∠=FEC AEF ,∴1801803012030∠=-∠-∠=--=CFE FEC C ,∴∠=∠FEC CFE ,∴=EC CF ,∴=BE DF ;(2)如图2,连接AC ,∵四边形ABCD 是菱形,60∠=B ,∴=AB BC ,60∠=∠=D B ,∠=∠ACB ACF ,∴△ABC 是等边三角形,∴60=∠=,AB AC ACB ,∴60∠=∠=B ACF ,60+∠FAD60,∴△AEF是等边三角形.60,根据菱形的性质,易得CFE,即可得60,然后利用平=AF24∴不存在实数a,使得点P在∠ACB的平分线上.45;,即∠ONB而12∠=∠=∠BM A BM A ABN ,∴12226642===-=-=,OM OM AM OM OA .综上,AM 的长为6或2.【提示】(1)该抛物线的解析式中只有两个待定系数,只需将,A B 两点坐标代入即可得解.(2)首先根据平移条件表示出移动后的函数解析式,进而用m 表示出该函数的顶点坐标,将其代入直线,AB AC 的解析式中,即可确定P 在△ABC 内时m 的取值范围.(3)先在OA 上取点N ,使得∠=∠ONB ACB ,那么只需令∠=∠NBA OMB 即可,显然在y 轴的正负半轴上都有一个符合条件的M 点;以y 轴正半轴上的点M 为例,先证△,△ABN AMB 相似,然后通过相关比例线段求出AM 的长.【考点】二次函数综合题.。
江苏省苏州市2001-2012年中考数学试题分类解析专题6:函数的图像与性质2001-2012年江苏苏州中考数学试题分类解析汇编(12专题)专题6:函数的图象与性质锦元数学工作室编辑一、选择题1. (2001江苏苏州3分)如图,L甲、L乙分别是甲、乙两弹簧的长ycm与所挂物体质量xkg之间函数关系的图象,设甲弹簧每挂1kg物体伸长的长度为k甲cm,乙弹簧每挂1kg物体伸长的长度为k乙cm,则k甲与k乙的关系是【】A.k甲>k乙B.k甲=k乙C.k甲<k乙D.不能确定【答案】A。
【考点】一次函数的应用。
【分析】∵直线的倾斜程度与它的斜率有直接关系,斜率的绝对值越大,直线越倾斜,∴根据图示可知,L甲的倾斜程度大于L乙的倾斜程度,所以k甲>k乙。
故选A。
2.(江苏省苏州市2003年3分) 已知a 1<-,点()()()123a 1y a y a 1y -+,,,,,都在函数2y=x 的图像上,则【 】 A. 123y yy << B. 132y yy << C. 321y yy << D.213y y y <<【答案】C 。
【考点】二次函数图象上点的坐标特征。
【分析】根据函数2y=x 的图象的特点,函数2y=x 图象的开口向上,对称轴是y 轴,在y 轴的左侧y 随x 的增大而减小,在y 轴的右侧y 随x 的增大而增大:∵a<-1,∴a-1<a <a +1<0,即点()()()123a 1y a y a 1y -+,,,,,都在y 轴左侧。
∵2y=x 的图象在对称轴x=0的左侧,y 随x的增大而减小,∴321y yy <<。
故选C 。
3.(江苏省苏州市2004年3分)已知正比例函数y=(3k —1)x ,若y 随x 的增大而增大,则的取值范围是【 】A k <0B k > 0C k <31D k >31【答案】D。
【考点】正比例函数的性质。
某某省某某市2001-2012年中考数学试题分类 专题6 函数的图像与性质一、选择题1. (2002年某某某某3分)抛物线2y x 4x 3=--与x 轴交于点A ,B ,顶点为P ,则△PAB 的面积为【 】A .77B .714C .73D . 122. (2003年某某某某4分)如图,抛物线2y=x bx c ++与x 轴交于A 、B 两点,与y 轴交于点C ,∠OBC=450, 则下列各式成立的是【 】A .b c 1=0--B .b c 1=0+-C .b c 1=0-+D .b c 1=0++ 【答案】D 。
【考点】二次函数综合题,等腰直角三角形的性质,曲线上点的坐标与方程的关系。
【分析】∵∠OBC=450,∴OB=OC =c 。
∴B(c ,0)。
将B (c ,0)代入2y=x bx c ++得:2c bc c=0++,∵c 不等于0,∴两边同除以c ,得: b +c +1=0。
故选D 。
3. (2005年某某某某课标卷3分)小明、小亮、小梅、小花四人共同探究代数式2x 4x 5-+的值的情况.他们作了如下分工:小明负责找值为1时x 的值,小亮负责找值为0时x 的值,小梅负责找最小值,小花负责找最大值.几分钟后,各自通报探究的结论,其中错误的是【 】A .小明认为只有当x=2时,2x 4x 5-+的值为1B .小亮认为找不到实数x ,使2x 4x 5-+的值为0C .小梅发现2x 4x 5-+的值随x 的变化而变化,因此认为没有最小值D .小花发现当x 取大于2的实数时,2x 4x 5-+的值随x 的增大而增大,因此认为没有最大值4. (2006年某某某某3分)若双曲线6y=x-经过点A (m ,3),则m 的值为【 】 A .2 B .-2 C .3 D .-3 【答案】B 。
【考点】曲线上点的坐标与方程的关系。
【分析】将A (m ,3)代入6y=x -,得:63=m-,解得:m=-2。
2001-2012年江苏南通中考数学试题分类解析汇编(12专题)专题5:数量和位置变化一、选择题1.(2001江苏南通3分)点P(-3,4)关于原点对称的点的坐标是【】A、(3,-4)B、(-3,-4)C、(3,4)D、(-4,3)【答案】A。
【考点】关于原点对称的点的坐标特征。
【分析】关于原点对称的点的坐标是横、纵坐标都互为相反数,从而点P(-3,4)关于原点对称的点的坐标是(3,-4)。
故选A。
2.(江苏省南通市2003年3分)在函数y中,自变量x的取值范围是【】A.x≠-1 B.x≠0 C.x≥-1 D.x≥-1,且x≠0【答案】D。
【考点】函数自变量的取值范围,二次根式和分式有意义的条件。
【分析】根据二次根式被开方数必须是非负数和分式分母不为0的条件,要使x在实数范围内有意义,必须x10x1x0x0+≥≥-⎧⎧⇒⎨⎨≠≠⎩⎩。
故选D。
3. (江苏省南通市2004年2分)点M(1,2)关于x轴对称点的坐标为【】A、(-1,2)B、(-1,-2)C、(1,-2)D、(2,-1)【答案】C。
【考点】关于x轴对称的点的坐标【分析】关于x轴对称点的坐标是横坐标不变纵坐标变为原来的相反数,可知,A(1,2)关于x轴对称点的坐标是(1,-2)。
故选C。
4.(2012江苏南通3分)线段MN在直角坐标系中的位置如图所示,线段M1N1与MN关于y轴对称,则点M的对应的点M1的坐标为【】A.(4,2) B.(-4,2) C.(-4,-2) D.(4,-2)【答案】D。
【考点】平面坐标系与坐标,关于y轴对称的点的坐标特征。
【分析】关于y轴对称的点的坐标特征是纵坐标不变,横坐标互为相反数,从而点M(-4,-2)关于y轴对称的点M1的坐标是(4,-2)。
故选D。
二、填空题1. (2001江苏南通2分)函数y=1x1-中,自变量x的取值范围是▲ 。
【答案】x1≠。
【考点】函数自变量的取值范围,二次根式和分式有意义的条件。
2001-2012年江苏南通中考数学试题分类解析汇编(12专题)专题6:函数的图象与性质一、选择题1.(江苏省南通市2002年3分)抛物线y=2x 2-4x +7的顶点坐标是【 】A .(-1,13)B .(-1,5)C .(1,9)D .(1,5) 【答案】D 。
【考点】二次函数的性质。
【分析】利用公式法或利用配方法可求出y=2x 2-4x +7=2(x -1)2+5的顶点的坐标(1,5)。
故选D 。
2. (江苏省南通市2003年3分)已知反比例函数ky x=的图象如图所示,则二次函数22y 2kx x k =-+的图象大致为 【 】A .B .C .D .【答案】D 。
【考点】二次函数的图象,反比例函数的图象。
【分析】由反比例函数的图象得到k 的正负,再与二次函数的图象相比较看是否一致:∵函数ky x=的图象经过二、四象限,∴k<0。
∴抛物线开口向下,对称轴b 1x 02a 4k=-=<,即对称轴在y 轴的左边。
故选D 。
3. (江苏省南通市2004年3分)抛物线21y x x 44=-+-的对称轴是【 】A 、x =-2B 、x =2C 、x =-4D 、x =4【答案】B 。
【考点】二次函数的性质。
【分析】可以用配方法将抛物线的一般式写成顶点式,或者用对称轴公式bx 2a=-求解: ∵抛物线()2211y x x 4=x 2344=-+----,∴抛物线21y x x 44=-+-的对称轴是直线x=2。
故选B 。
4. (江苏省南通市大纲卷2005年3分)二次函数2y ax bx c =++的图象如图所示, 若42,M a b c =++N a b c =-+,42P a b =+,则【 】A 、0,0,0M N P >>>B 、0,0,0M N P ><>C 、0,0,0M N P <>>D 、0,0,0M N P <><【答案】D 。
【考点】二次函数图象与系数的关系。
【分析】∵当 x =2时,420y a b c <=++,∴可以判断420M a b c <=++;∵当x =-1时,0y a b c >=-+,∴可以判断0N a b c >=-+; ∵抛物线的开口向上,对称轴在x =1右侧,∴a >0,对称轴=12bx >a-,即20a b <+。
∴可以判断()42=220P a b a b <=++。
故选D 。
5. (江苏省南通市课标卷2005年3分)已知抛物线2y x bx c =++的部分图象如图所示,若y <0,则x 的取值范围是【 】A .-1<x <4B .-1<x <3C .x <-1或 x >4D .x <-1或 x >3【答案】B 。
【考点】二次函数的图象。
【分析】根据图象,已知抛物线的对称轴x=1,与x 轴的一个交点(-1,0),根据抛物线的对称性可知,另一交点为(3,0)。
因为抛物线开口向上,所以当y <0时,-1<x <3。
故选B 。
6. (江苏省南通市大纲卷2006年3分)已知二次函数y=2x 2+9x+34,当自变量x 取两个不同的值x 1,x 2时,函数值相等,则当自变量x 取x 1+x 2时的函数值与【 】 A 、x=1时的函数值相等B 、x=0时的函数值相等C 、x=14时的函数值相等 D 、x=94-时的函数值相等【答案】B 。
【考点】抛物线与x 轴的交点,二次函数的对称性。
【分析】∵当自变量x 取两个不同的值x 1、x 2时,函数值相等,则以x 1、x 2为横坐标的两点关于直线x=94-对称,∴12x x 9=24+-,所以129x x =2+-。
∵根据抛物线的对称性可知x=92-与x=0时函数值相等。
故选B 。
7. (江苏省南通市课标卷2006年3分)如图,设直线y=kx (k <0)与双曲线5y x=-相交于A (x 1,y 1)B (x 2,y 2)两点,则x 1y 2-3x 2y 1的值为【 】A .-10B .-5C .5D .10 【答案】A 。
【考点】反比例函数图象的对称性,曲线上点的坐标与方程的关系。
【分析】根据关于原点对称的点的坐标特点找出A 、B 两点坐标的关系,再根据反比例函数图象上点的坐标特点解答即可:由题意知,直线y=kx (k >0)过原点和一、三象限,且与双曲线5y=x-交于两点,则这两点关于原点对称,∴x1=﹣x2,y1=﹣y2。
又∵点A、点B在双曲线5y=x上,∴x1y1=-5,x2y2=-5。
∴原式=﹣2x2y2+7x2y2=﹣2×(-5)+7×(-5)=-10。
故选A。
8. (江苏省南通市2007年4分)如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(m,n),且2m+n=6,则直线AB的解析式是【】.A、y=-2x-3B、y=-2x-6C、y=-2x+3D、y=-2x+6【答案】D。
【考点】一次函数图象与平移变换。
【分析】平移时k的值不变,只有b发生变化.再把相应的点代入即可:∵原直线的k=-2,向上平移后得到了新直线,∴新直线的k=-2。
∵直线AB经过点(m,n),且2m+n=6,即n=6-2 m,∴直线AB经过点(m,6-2 m)。
设新直线的解析式为y=-2x+b1,∴6-2 m =-2 m +b1,则b1=6。
∴直线AB的解析式是y=-2x+6。
故选D。
9.(江苏省南通市2008年4分)用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是【】A.203210x yx y+-=⎧⎨--=⎩B.2103210x yx y--=⎧⎨--=⎩C.2103250x yx y--=⎧⎨+-=⎩D.20210x yx y+-=⎧⎨--=⎩【答案】D。
【考点】一次函数与二元一次方程(组),待定系数法,直线上点的坐标与方程的关系。
【分析】由于函数图象交点坐标为两函数解析式组成的方程组的解,因此本题应先用待定系数法求出两条直线的解析式,联立两个函数解析式所组成的方程组即为所求的方程组:根据给出的图象上的点的坐标,(0,-1)、(1,1)、(0,2);分别求出图中两条直线的解析式为y=2x-1,y=-x+2,因此所解的二元一次方程组是20210x yx y+-=⎧⎨--=⎩。
故选D。
10. (江苏省南通市2010年3分)在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO 是等腰三角形,则满足条件的点Q共有【】A.5个B.4个C.3个D.2个【答案】B。
【考点】等腰三角形的判定,坐标与图形性质。
【分析】根据题意,画出图形,由等腰三角形的判定找出满足条件的Q点,选择正确答案,注意求解有关等腰三角形问题时一定要注意分情况讨论:如图:满足条件的点Q共有(0,2)(0,2 2 )(0,-2 2 )(0,4)。
故选B。
11. (江苏省南通市2011年3分)甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法正确的是【】A .甲的速度是4km/hB .乙的速度是10km/hC .乙比甲晚出发1hD .甲比乙晚到B 地3h 【答案】C 。
【考点】一次函数的图象。
【分析】根据所给的一次函数图象有:A.甲的速度是205/4km h =,选项错误;B. 乙的速度是2020/1km h =,选项错误;C .乙比甲晚出发101h -=,选项正确;D .甲比乙晚到B 地422h -=,选项错误。
故选C 。
12.(2012江苏南通3分)已知点A(-1,y 1)、B(2,y 2)都在双曲线y = 3+2mx 上,且y 1>y 2,则m 的取值范围是【 】A .m <0B .m >0C .m >- 3 2D .m <- 32【答案】D 。
【考点】曲线上点的坐标与方程的关系,解一元一次不等式。
【分析】将A (-1,y 1),B (2,y 2)两点分别代入双曲线y= 3+2mx ,求出 y 1与y 2的表达式:1232my 2m 3 y 2+=--=, 。
由y 1>y 2得,2m2m 323>+--,解得m <- 3 2。
故选D 。
13.(2012江苏南通3分)无论a 取什么实数,点P(a -1,2a -3)都在直线l 上,Q(m ,n)是直线l 上的点,则(2m -n +3)2的值等于 ▲ . 【答案】16。
【考点】待定系数法,直线上点的坐标与方程的关系,求代数式的值。
【分析】∵由于a 不论为何值此点均在直线l 上,∴令a=0,则P 1(-1,-3);再令a=1,则P 2(0,-1)。
设直线l 的解析式为y=kx+b (k≠0),∴ k b 3b 1-+=-⎧⎨=-⎩,解得k 2 b 1=⎧⎨=-⎩ 。
∴直线l 的解析式为:y=2x -1。
∵Q(m ,n )是直线l 上的点,∴2m-1=n ,即2m -n=1。
∴(2m-n +3)2=(1+3)2=16。
二、填空题1. (2001江苏南通2分)抛物线2y x 4x 5=-+的顶点坐标是 ▲ _。
【答案】(2,1)。
【考点】二次函数的性质。
【分析】将抛物线2y x 4x 5=-+变为项点式即可求出顶点坐标(或用公式计算): ∵()22y x 4x 5x 21=-+=-+,∴抛物线2y x 4x 5=-+的顶点坐标是(2,1)。
2.(2001江苏南通3分)设点P 1(x 1,y 1)和P (x 2,y 2)都在反比例函数y=2x-的图象上,且x 1<x 2<0,则y 1 ▲ _y 2(填“<”或“>”。
【答案】<。
【考点】反比例函数图象上点的坐标特征。
【分析】结合已知条件和反比例函数的性质,画出函数图象,根据反比例函数图象上点的特性,即可看出y1与y2的大小关:∵双曲线y=2x-中k=-2<0, ∴函数图象如图在第二、四象限内,在每个象限内,y 随x 的增大而增大。
∵点P 1(x 1,y 1)和P (x 2,y 2)都在反比例函数y=2x-的图象上,且x 1<x 2<0, ∴P 1,P 2两点在第二象限的曲线上。
∴0<y 1<y 2。
故填<。
3.(江苏省南通市2002年2分)写出具有性质“图象的两个分支分别在第二、四象限内,在每个象限内,y 随x 的增大而增大”的一个反比例函数 ▲ . 【答案】2y x=-(答案不唯一)。
【考点】反比例函数的性质。
【分析】对于反比例函数()ky k 0 x-≠,当k >0时,图象是位于一、三象限;当k <0时,图象是位于二、四象限。