湘教版二次根式知识点总结

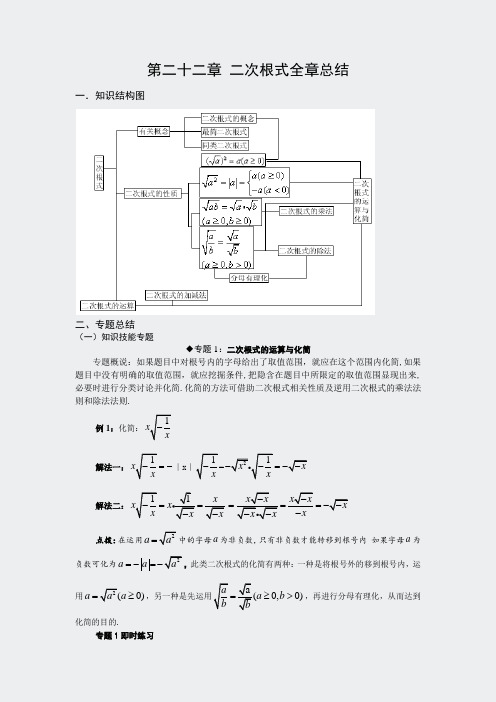
第二十二章 二次根式全章总结一．知识结构图二、专题总结（一）知识技能专题◆专题1：二次根式的运算与化简专题概说：如果题目中对根号内的字母给出了取值范围，就应在这个范围内化简,如果题目中没有明确的取值范围，就应挖掘条件,把隐含在题目中所限定的取值范围显现出来,必要时进行分类讨论并化简.化简的方法可借助二次根式相关性质及逆用二次根式的乘法法则和除法法则.例1：化简：1x x-解法一：1x x -=-∣x ∣1x-=21x x x--=-- 解法二：11x x x x x x -==--x x x x x x x x--===-----点拨：在运用2a a =中的字母a 为非负数，只有非负数才能转移到根号内 如果字母a 为负数可化为2a a a =-=-，此类二次根式的化简有两种：一种是将根号外的移到根号内，运用2(0)a a a =≥，另一种是先运用a(0,0)a a b b b=≥>，再进行分母有理化，从而达到化简的目的.专题1即时练习1. 阅读下面的文字后，回答问题：小明和小芳解答题目：先化简下式，再求值：221a a a +-+，其中a ＝9时，得出了不同的答案．小明的解答是：原式＝1)1()1(2=-+=-+a a a a ；小芳的解答是：原式＝1719212)1()1(2=-⨯=-=--=-+a a a a a ． (1)______的解答是错误的；(2)说明错误的原因． 2.把根式()131--x x 中根号外的因式适当改变后移到根号内______________. 过程与方法：◆专题2：分母有理化专题概说：分母有理化的关键是确定有理化因式，其基本形式有：（１）m a 的有理化因式是a ；（２）m a n b ±的有理化因式是m a n b ,分母有理化有时也可通过约分的办法来解决．例2：在进行二次根式化简时，我们有时会碰上如，，一样的式子，其实我们还可以将其进一步化简：＝；（一） ＝（二） ＝ ＝ （三） 以上这种化简的步骤叫做分母有理化。

第三章 二次根式 3.1 二次根式Ⅰ.核心知识点扫描1．二次根式的定义：形如a （a ≥0）的式子叫做二次根式. 2．二次根式的性质： （1）非负性：)0(0≥≥a a（2）平方关系：)0()(2≥=a a a（3）与绝对值结合：⎩⎨⎧<-≥==)0()0(2a a a a a aⅡ.知识点全面突破知识点1：二次根式的概念（重点）一般地，我们把形如a （a ≥0）的式子叫做二次根式，“”称为二次根号，二次根号下的a 叫做被开方数.【拓展延伸】（1）二次根式都含有二次根号“”.（2）在二次根式中，被开方数a 必须满足a ≥0，当a<0时，根式无意义.（3）在二次根式中，被开方数a 既可以是具体的数，也可以是单项式或多项式. （4）二次根式a （a ≥0）是a 的算术平方根，所以0≥a . 例：不论x 取何值，下列式子一定是二次根式的是（ ）A.2--xB.xC.22+x D.22-x解：根据定义，形如)0≥a a （的式子为二次根式. 因为22+x 一定为正数，所以22+x 一定是二次根式，故选C .点拨：判断一个式子是否是二次根式，要看它是否具备两个特征：□C （1）带二次根号“”；(2) 被开方数为非负数.知识点2：二次根式的性质（难点）性质1：二次根式的双重非负性：（1）a 是非负数；（2）a 的被开方数a 是非负数.性质2：2()a a =（a ≥0），即一个非负数的算术平方根的平方等于它本身；性质3：⎩⎨⎧<-≥==)0()0(2a a a a a a .例1：计算：(1)23()5，(2)2(22)- ，(3))0()2(2≥x x ，(4)222)(y x +. 解：(1) 23()5=35. (2)2(22)-= 2(22)=8.(3))0(2)2(2≥=x x x .(4) 222)(y x +=22y x +.点拨：二次根式a 是一个非负数，2()a a =（a ≥0），这个性质是逆用平方根的意义得出结论，要注意结论成立的条件是a ≥0.例2：对下列各式进行化简.（1）2)6(-；（2）26；（3）22)4(+a ；（4）)1(122≥+-x x x解：（1）2)6(-=6-=6. (2) 26=6.(3) 22)4(+a =42+a . (4))1(1)1(1222≥-=-=+-x x x x x .点拨：□C 化简二次根式的结果一定要符合非负性.Ⅲ.提升点全面突破提升点1：二次根式有意义的条件例：当x 是多少时，23x +＋11x +在实数范围内有意义？ 解：依题意，得23010x x +≥⎧⎨+≠⎩由①得：x ≥-32由②得：x ≠-1当x ≥－32且x ≠－1时，23x +＋11x +在实数范围内有意义． 点拨：求函数自变量的取值范围或使一个代数式有意义的未知数的取值范围通常有□C 三种情况：一是分母不为零，二是偶次方根的被开方数是非负数，三是零次幂的底数不为零.提升点2：利用二次根式的非负性化简例1：实数a b ，在数轴上的对应点如图所示，化简2244a ab b a b -+++的结果为 ．解：由数轴可知 0b a <<，所以20a b ->，0a b +<，所以bb a b a b a b a b a b a b a b ab a 322)2(44222-=---=++-=++-=+++-点拨：解决本题的关键是灵活运用数轴与实数的关系、二次根式的性质和绝对值的意义.例2：若y x 、为实数，且,22112+-+-<x x y 化简22--y y .解：∵21122y x x <-+-+，∴210,120.x x -≥⎧⎨-≥⎩故210x -=，∴12x =， 代入原不等式得2,y <∴22 1.22y yy y --==--- 点拨：要化简22y y --关键是确定y 的取值范围，从而去掉绝对值符号。

期末复习（五）二次根式考点一、二次根式的概念 例1.要使1213-+-x x 有意义，则x 应满足（ ）A.321≤≤x B.3≤x 且21≠x C.321<<x D.321≤<x[方法归纳]：要使二次根式有意义，则被开方数必须是非负数，若有分数，则分母还应不等于0 巩固练习：1、x 31-在实数范围内有意义，则x 的取值范围是2、使代数式xx --312有意义的x 的取值范围是考点二、二次根式的性质例2.计算：（1）2)52(＝ （2）2)3(π-＝[方法归纳]：（1）先利用乘方性质222)(b a ab =变形，再利用)0()(2≥=a a a 公式计算； （2）利用⎩⎨⎧<-≥=)0()0(2a a a a a 化简。

例3.已知0)53(322=--+-+y x y x ，则=x y 。

[方法归纳]：根据非负数的性质建立方程组，即：非负数的和等于0，这几个非负数都是0。

巩固练习：1、计算：（1）=-2)2( （2）=-2)33( 2、若0)4(322=-+-+-c b a ，则=+-c b a 3、已知1<x，则122+-x x 化简的结果是（ ）A. 1-x B.1+x C.1--x D.x -14、已知322+-+-=x x y ，求yx 的值。

考点三、二次根式的计算例4.计算：b a aab ab 33110848-+ )2132(50-⨯)0,0(815274932>>⋅⎪⎪⎭⎫ ⎝⎛-÷b a ab a b b a[方法归纳]：在进行二次根式运算时，要根据二次根式的运算顺序，先乘除再加减，有括号的先进行括号里的计算，且最后结果必须化成最简二次根式。

巩固练习：计算：（1）)323)(63()22(2-++- （4）72233162142732+--考点四、二次根式的化简求值 例5.已知1212,1212+-=-+=y x ，求223y xy x +-的值[方法归纳]：巧用完全平方公式，利用整体代入的思想可使计算简便。

《二次根式》知识全解课标要求1.理解二次根式的概念，了解被开方数必须是非负数的理由.2.了解最简二次根式的概念.3.理解二次根式的性质：()0≥a a 是非负数；()()02≥=a a a ；()02≥=a a a .知识结构内容解析1.二次根式的定义：一般地，我们把形如()0≥a a 的式子叫做二次根式.这里特别要注意的是：对于判断一个代数式是否为二次根式并不需要深究，而应侧重于二次根式有意义的条件——被开方数为非负数．2．二次根式的性质：()0≥a a 是非负数；()()02≥=a a a ；()02≥=a a a . 注意：二次根式的性质不一定非要直接从算术平方根的意义得到，也可以先由特殊到一般归纳出结论，再通过算术平方根的意义来分析证明.重点难点本节的重点是：明确二次根式()0≥a a 具有双重非负性，会确定被开方数中字母的取值范围；会利用二次根式的性质做相关计算．教学重点的解决方法：循序渐进，逐步深入，从学生已有的开方知识点出发，引导学生理解被开方数中字母的取值范围；根据从特殊到一般的数学思想，引导学生从一些特殊的举例中自主总结归纳出二次根式的一般性质．本节的难点是：二次根式的取值范围．教学难点的解决方法：通过合作探究的方式，进行小组讨论学习，容易深入问题本质，掌握透彻．教法导引教学活动的本质是一种合作、一种交流．学生是数学学习的主人，教师是数学学习的组织者、引导者与合作者．依据学生的年龄特点和已有的知识基础，本节课注重加强知识间的纵向联系，拓展学生探索的空间，体现由具体到抽象的认识过程．为了为后续学习打下坚实的基础（例如在“锐角三角函数”一章中，会遇到很多实际问题），在解决实际问题的过程中，要遇到对二次根式进行条件约束等问题，本课适当加强练习，让学生养成联系和发展的观点学习数学的习惯．学法建议学生已学习了平方根、算术平方根以及勾股定理等相关知识，具备了学习二次根式的基础．在教授新课的过程中，注重从特殊到一般数学思考问题方法，发展学生的抽象思维和概括能力，从而得到二次根式的概念，进而深入得出二次根式有意义的条件及性质．新课程标准指出：学生是学习的主体．要让学生成为真正的主人，需要在数学教学的过程中，让老师引导学生自主思考、合作探究、共同总结，从而体现学生学习的主体地位．本节课主要采用自主学习、合作探究、引领提升的方式，启发式、讲练结合的方法展开教学．先提出问题，让学生探讨、分析问题，师生共同归纳，得出概念；再对概念的内涵进行分析，得出几个重要结论，并运用这些重要结论进行二次根式的计算和化简的学习．通过对本节课的学习，使学生们的发散性思维得以启发,学生们的观察、分析、发现问题的能力得以锻炼，学生的辩证唯物主义观点得以培养．。

初二数学第四章二次根式复习与小结湘教版【本讲教育信息】一. 教学内容：第四章二次根式复习与小结二. 教学目标：1. 了解二次根式有意义的条件，发展学生的符号感。

2. 经历探索掌握积的算术平方根性质及商的算术平方根的性质，并会用性质来化简。

3. 掌握二次根式的乘法、除法法则，并会进行二次根式的乘除运算。

4. 会进行二次根式的加、减运算。

5. 会把实数运算律及乘法公式应用于二次根式的混合运算中。

三. 教学重点和难点：重点：二次根式意义及二次根式的运算。

难点：二次根式的化简及运用乘法公式和实数运算律进行二次根式运算。

四. 本章知识要点归纳：1. 二次根式的定义：形如的式子叫二次根式，其中叫作被开方数，是一个非负数时，a a a ()≥0 a 才有意义2. 二次根式的性质：①②()()||()()()a a a a a a a a a a 2200000=≥==>=-<⎧⎨⎪⎩⎪ ③·，④，ab a b a b a b a b a b =≥≥=≥>()()00003. 二次根式的运算①二次根式的乘法：·，a b ab a b =≥≥()00②二次根式的除法：，a ba b a b =≥>()00 ③二次根式的加减：需要先把二次根式化简，然后把被开方数相同的二次根式（即同类二次根式）的系数相加减，被开方数不变。

④二次根式的混合运算：先乘方（或开方），再乘除，最后加减，有括号的先算括号里面的；能利用运算律或乘法公式进行的，可适当改变运算顺序进行简便运算。

⑤有理化因式：一般常见的互为有理化因式有如下几类：1)a a 与2)a b a b +-与3)a b a b +-与4)m a n b m a n b +-与利用有理化因式的特点可以将分母有理化。

五. 方法规律指点：①如果是二次根式，则一定有a a ≥0当时，必有a a ≥≥00②当时，表示的算术平方根，因此有，反过来，也可将a a a a a ≥=02() 一个非负数写成的形式a a ()2③表示的算术平方根，因此有，可以是任意实数a a a a a 222=||④区别和的不同：()||a a a a 22==a a a a a 22中的可以取任意实数，中的只能是一个非负数，否则无意() 义。

湘教版初中数学重点知识精选掌握知识点，多做练习题，基础知识很重要！湘教版初中数学和你一起共同进步学业有成！5.1 二次根式第1课时 二次根式的概念及性质【教学目标】1.了解二次根式的意义，掌握二次根式的定义；能根据定义确定被开方数中字母的取值范围.2.理解并掌握二次根式的性质：.()20a a =≥()0a a =≥⒊经历二次根式的定义的形成过程及二次根式性质的探究过程，提高数学探究能力及归纳能力.【教学重点】二次根式的概念和相关性质.【教学难点】运用二次根式的性质：进行计算.()20a a =≥()0a a =≥【教学过程】一、新课引入我们学习了平方根和算术平方根的意义，请同学们思考并回答下面3个问题：1.5的平方根是 ，0的平方根是 ，正实数的平方根是 .a2. 需要满足什么条件？为什么？ a)0a ≥二、自主探究1.二次根式的概念：⑴我们把.⑵由于在实数范围内，负实数没有平方根，因此只有当被开方数是非负实数时，二次根式才在实数范围内有意义.即：被开方数.0a ≥⑶ 是不是二次根式.))00a a <<⑷根据已有的知识，说说你对二次根式的认识.①表示的算术平方根.②可以是数，也可以是式.③从形式上看，含有二次根号.④a a0a ≥≥2.二次根式的性质：⑴对于非负实数的一个平方根，因此：a a ()20a a =≥， ， … ===结论：当0a ≥=三、应用迁移（一）典例精析例1 当 x例2 计算：⑴⑵ ⑷ 2;(2;（二）变式运用的值.的值. 0,= (三)综合运用已知实数 0,0,a b <>四、归纳小结⑴二次根式的定义：①形如 ②被开方数a②=(0)a ≥2=(0)a ≥五、巩固提升★⒈当 时，在实数范围内有意义.x★★⒉已知，求的值. 2y =+,x y★★★⒊在实数范围内，把下列多项式分解因式：⑴ ⑵ 213;x -2312.x -相信自己，就能走向成功的第一步教师不光要传授知识，还要告诉学生学会生活。

第五章 二次根式有关二次根式的化简与运算是初中数学的重、难点之一，由于这类题目形式灵活，同时对整式、分式的运算和性质有着密切的联系，所以成为考察学生综合运用能力的“试金石”，现将一些常见的运算错误归纳如下，希望同学们加以注意，并引以为戒．一、概念不清例1．下列各式中，哪些是二次根式？哪些不是二次根式？为什么？π都是二次根式；,π剖析：对二次根式的定义理解不透，认为只要带二次根号，即为二次根式，忽视了二a ≥0的条件，所以同学们在平时做题中必须特别注意理解二次根式的被开方数是非负数．都是二次根式；,π二、违背运算顺序例22)÷⨯错解：原式1÷=剖析：由于乘除是同一级运算，因此按顺序除在前，就要先算除法．正解：原式2(27==-=-三、错用运算法则例3+．错解：原式11+=剖析：本题乱套乘法分配律，应注意：()a b c a b a c ÷+≠÷+÷．正解：原式4==．四、错用根式性质例4．计算：（1；（2错解：（1）原式1306664-=-=；（2）原式==0,0)a b =≥≥0,0)a b =≥>；=正解：（1）原式148112===⨯=．五、忽视字母范围 例5错解：原式a b=-．-a =b ，错在没有注意a =b 的情形．正解：（1）当a ≠b 时，原式a b=-；（2）当a =b 时，原式22ab=或．六、忽视隐含条件例6．化简：错解：原式=．剖析：本题隐含着10a->，所以a ＜0，这个条件．正解：原式==-七、忽视限制条件例7．已知a +b =-2,ab =1错解：原式)2a baba b+=+==-．剖析：应用二次根式的运算性质：0,0)a b =≥≥；0,0)a b=≥>时，必须这样括号里的条件，本题由a+b=-2,ab=1可知a ＜0，b ＜0，不满足性质的条件造成错误．正解：由条件可知a ＜0，b ＜0，所以原式=2aba b+=--=-=．八、忽视题设条件例8（32-≤x ≤52）．错解：原式232542x x x =++-=-．剖析：这里忽视了32-≤x ≤52这个条件，当有附加条件时，a =的应用．正解：因为32-≤x ≤52，所以-3≤x ≤5，所以2x +3≥0，2x -5≤0，所以，原式23258x x =+-+=．九、忽视分类讨论例9．2121x x x +=++-=+．。