2018年高考数学一轮复习课时跟踪检测51文新人教A版!
- 格式:doc
- 大小:175.50 KB
- 文档页数:9

课时跟踪检测(三十二)1.若等差数列{a n }的前5项之和S 5=25,且a 2=3,则a 7=( ) A .12 B .13 C .14 D .15答案:B 解析:由S 5=a 2+a 42⇒25=+a 42⇒a 4=7,所以7=3+2d ⇒d =2,所以a 7=a 4+3d =7+3×2=13.2.已知数列{a n }是等差数列,a 1+a 7=-8,a 2=2,则数列{a n }的公差d 等于( ) A .-1 B .-2 C .-3 D .-4答案:C解析:解法一:由题意,可得⎩⎪⎨⎪⎧a 1+a 1+6d=-8,a 1+d =2,解得a 1=5,d =-3.解法二:a 1+a 7=2a 4=-8,∴a 4=-4, ∴a 4-a 2=-4-2=2d ,∴d =-3.3.设S n 为等差数列{a n }的前n 项和,若a 1=1,公差d =2,S n +2-S n =36,则n =( ) A .5 B .6 C .7 D .8答案:D解析:解法一:由等差数列的前n 项和公式,可得S n +2-S n =(n +2)a 1+n +n +2d -⎣⎢⎡⎦⎥⎤na 1+n n -2d =2a 1+(2n +1)d =2+4n +2=36,∴n =8,故选D.解法二:由S n +2-S n =a n +2+a n +1=a 1+a 2n +2=36,因此a 2n +2=a 1+(2n +1)d =35,解得n =8,故选D.4.已知数列{a n }满足a n +1=a n -57,且a 1=5,设{a n }的前n 项和为S n ,则使得S n 取得最大值的序号n 的值为( )A .7B .8C .7或8D .8或9答案:C解析:由题意可知,数列{a n }是首项为5,公差为-57的等差数列,所以a n =5-57(n -1)=40-5n7,该数列前7项是正数项,第8项是0,从第9项开始是负数项,所以S n 取得最大值时,n =7或8,故选C.5.已知数列{a n }满足a 1=15,且3a n +1=3a n -2.若a k ·a k +1<0,则正整数k =( ) A .21 B .22 C .23 D .24答案:C解析:3a n +1=3a n -2⇒a n +1=a n -23⇒{a n }是等差数列,则a n =473-23n .∵a k +1·a k <0,∴⎝ ⎛⎭⎪⎫473-23k ⎝ ⎛⎭⎪⎫453-23k <0,∴452<k <472,∴k =23. 6.数列{a n }的前n 项和S n =2n 2+3n (n ∈N *),若p -q =5,则a p -a q =( ) A .10 B .15 C .-5 D .20答案:D解析:当n ≥2时,a n =S n -S n -1=2n 2+3n -=4n +1, 当n =1时,a 1=S 1=5,符合上式, ∴a n =4n +1,∴a p -a q =4(p -q )=20.7.现给出以下几个数列:①2,4,6,8,…,2(n -1),2n ;②1,1,2,3,…,n ;③常数列a ,a ,a ,…,a ;④在数列{a n }中,已知a 2-a 1=2,a 3-a 2=2.其中等差数列的个数为( )A .1B .2C .3D .4答案:B解析:①由4-2=6-4=…=2n -2(n -1)=2,得数列2,4,6,8,…,2(n -1),2n 为等差数列;②因为1-1=0≠2-1=1,所以数列1,1,2,3,…,n 不是等差数列; ③常数列a ,a ,a ,…,a 为等差数列;④当数列{a n }仅有3项时,数列{a n }是等差数列,当数列{a n }的项数超过3项时,数列{a n }不一定是等差数列.故等差数列的个数为2.8.设等差数列{a n }的前n 项和为S n ,且a 1>0,a 3+a 10>0,a 6a 7<0,则满足S n >0的最大自然数n 的值为( )A .6B .7C .12D .13答案:C解析:∵a 1>0,a 6a 7<0,∴a 6>0,a 7<0,等差数列的公差小于零,又a 3+a 10=a 1+a 12>0,a 1+a 13=2a 7<0,∴S 12>0,S 13<0,∴满足S n >0的最大自然数n 的值为12.9.正项数列{a n }满足a 1=1,a 2=2,2a 2n =a 2n +1+a 2n -1(n ∈N *,n ≥2),则a 7=________. 答案:19解析:由2a 2n =a 2n +1+a 2n -1(n ∈N *,n ≥2),可得数列{a 2n }是等差数列,公差d =a 22-a 21=3,首项a 21=1,所以a 2n =1+3(n -1)=3n -2,∴a n =3n -2,∴a 7=19.10.已知等差数列{a n }的公差d ≠0,且a 3+a 9=a 10-a 8.若a n =0,则n =________. 答案:5解析:∵a 3+a 9=a 10-a 8,∴a 1+2d +a 1+8d =a 1+9d -(a 1+7d ), 解得a 1=-4d ,∴a n =-4d +(n -1)d =(n -5)d . 令(n -5)d =0(d ≠0),可解得n =5.11.在等差数列{a n }中,a 1>0,a 10·a 11<0,若此数列的前10项和S 10=36,前18项和S 18=12,则数列{|a n |}的前18项和T 18的值是________.答案:60解析:由a 1>0,a 10·a 11<0可知,d <0,a 10>0,a 11<0, ∴T 18=a 1+…+a 10-a 11-…-a 18=S 10-(S 18-S 10)=60.12.设等差数列{a n },{b n }的前n 项和分别为S n ,T n ,若对任意自然数n 都有S n T n =2n -34n -3,则a 9b 5+b 7+a 3b 8+b 4=________.答案:1941解析:∵{a n },{b n }为等差数列, ∴a 9b 5+b 7+a 3b 8+b 4=a 92b 6+a 32b 6=a 9+a 32b 6=a 6b 6. ∵S 11T 11=a 1+a 11b 1+b 11=2a 62b 6=2×11-34×11-3=1941,∴a 6b 6=1941.1.设等差数列{a n }满足a 1=1,a n >0(n ∈N *),其前n 项和为S n ,若数列{S n }也为等差数列,则S n +10a 2n的最大值是( ) A .310 B .212 C .180 D .121答案:D解析:设数列{a n }的公差为d , 依题意,得2S 2=S 1+S 3, 因为a 1=1,所以22a 1+d =a 1+3a 1+3d , 化简可得d =2a 1=2,所以a n =1+(n -1)×2=2n -1,S n =n +n n -2×2=n 2,所以S n +10a 2n =n +2n -2=⎝⎛⎭⎪⎫n +102n -12=⎣⎢⎢⎡⎦⎥⎥⎤12n -+2122n -12=14⎝⎛⎭⎪⎫1+212n -12≤121.2.设数列{a n }的前n 项和为S n ,若S nS 2n为常数,则称数列{a n }为“吉祥数列”.已知等差数列{b n }的首项为1,公差不为0,若数列{b n }为“吉祥数列”,则数列{b n }的通项公式为( )A .b n =n -1B .b n =2n -1C .b n =n +1D .b n =2n +1答案:B解析:设等差数列{b n }的公差为d (d ≠0),S nS 2n=k , 因为b 1=1,则n +12n (n -1)d =k ⎣⎢⎡⎦⎥⎤2n +12×2nn -d ,即2+(n -1)d =4k +2k (2n -1)d ,整理得(4k -1)dn +(2k -1)(2-d )=0. 因为对任意的正整数n 上式均成立, 所以(4k -1)d =0,(2k -1)(2-d )=0,解得d =2,k =14.所以数列{b n }的通项公式为b n =2n -1.3.设S n 为等差数列{a n }的前n 项和,(n +1)S n <nS n +1(n ∈N *).若a 8a 7<-1,则( ) A .S n 的最大值是S 8 B .S n 的最小值是S 8 C .S n 的最大值是S 7 D .S n 的最小值是S 7答案:D解析:由条件,得S n n <S n +1n +1,即n a 1+a n 2n<n +a 1+a n +1n +,所以a n <a n +1,所以等差数列{a n }为递增数列.又a 8a 7<-1,所以a 8>0,a 7<0,即数列{a n }前7项均小于0,第8项大于零,所以S n 的最小值为S 7,故选D.4.在等差数列{a n }中,a 9=12a 12+6,则数列{a n }的前11项和S 11等于________.答案:132 解析:S 11=a 1+a 112=11a 6,设公差为d ,由a 9=12a 12+6,得a 6+3d =12(a 6+6d )+6,解得a 6=12,所以S 11=11×12=132.5.已知数列{a n }满足2a n +1=a n +a n +2(n ∈N *),它的前n 项和为S n ,且a 3=10,S 6=72,若b n =12a n -30,设数列{b n }的前n 项和为T n ,求T n 的最小值.解:∵2a n +1=a n +a n +2, ∴数列{a n }为等差数列.设数列{a n }的首项为a 1,公差为d ,由a 3=10,S 6=72,得⎩⎪⎨⎪⎧a 1+2d =10,6a 1+15d =72,解得⎩⎪⎨⎪⎧a 1=2,d =4.∴a n =4n -2,则b n =12a n -30=2n -31.令⎩⎪⎨⎪⎧b n ≤0,b n +1≥0,即⎩⎪⎨⎪⎧2n -31≤0,n +-31≥0,解得292≤n ≤312,∵n ∈N *,∴n =15,即数列{b n }的前15项均为负值,∴T 15最小. ∵数列{b n }的首项是-29,公差为2, ∴T 15=-29+2×15-2=-225,∴数列{b n }的前n 项和T n 的最小值为-225.6.设数列{a n }的前n 项和为S n,4S n =a 2n +2a n -3,且a 1,a 2,a 3,a 4,a 5成等比数列,当n ≥5时,a n >0.(1)求证:当n ≥5时,{a n }成等差数列; (2)求{a n }的前n 项和S n . (1)证明:由4S n =a 2n +2a n -3, 4S n +1=a 2n +1+2a n +1-3,得 4a n +1=a 2n +1-a 2n +2a n +1-2a n , 即(a n +1+a n )(a n +1-a n -2)=0. 当n ≥5时,a n >0,所以a n +1-a n =2, 所以当n ≥5时,{a n }成等差数列.(2)解:由4a 1=a 21+2a 1-3,得a 1=3或a 1=-1, 又a 1,a 2,a 3,a 4,a 5成等比数列, 所以a n +1+a n =0(n ≤5),q =-1, 而a 5>0,所以a 1>0,从而a 1=3,所以a n =⎩⎪⎨⎪⎧-n -1,1≤n ≤4,2n -7,n ≥5,所以S n =⎩⎪⎨⎪⎧32[1--n ],1≤n ≤4,n 2-6n +8,n ≥5.。
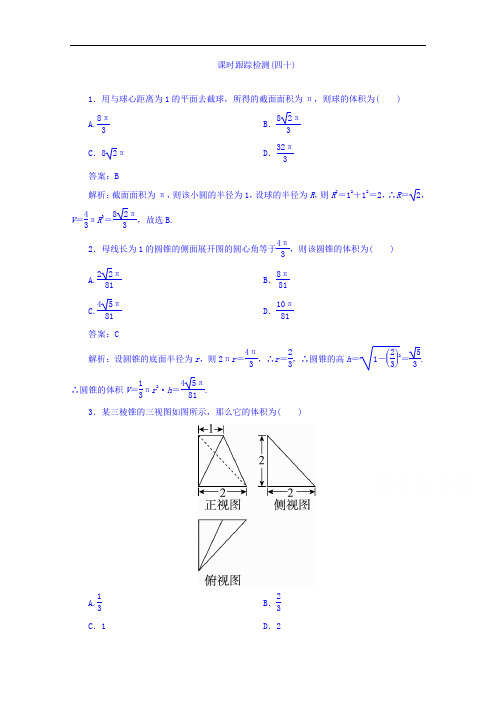
课时跟踪检测(四十)1.用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( ) A.8π3B .82π3C .82πD .32π3答案:B解析:截面面积为π,则该小圆的半径为1,设球的半径为R ,则R 2=12+12=2,∴R =2,V =43πR 3=82π3,故选B. 2.母线长为1的圆锥的侧面展开图的圆心角等于4π3,则该圆锥的体积为( )A.22π81 B .8π81C.45π81D .10π81答案:C解析:设圆锥的底面半径为r ,则2πr =4π3,∴r =23,∴圆锥的高h =1-⎝ ⎛⎭⎪⎫232=53.∴圆锥的体积V =13πr 2·h =45π81.3.某三棱锥的三视图如图所示,那么它的体积为( )A.13 B .23 C .1D .2答案:B解析: 构造棱长为2的正方体,由三视图知,该三棱锥为如图所示的三棱锥P -ABC .所以其体积V P -ABC =13S △ABC ×2=13×⎝ ⎛⎭⎪⎫12×1×2×2=23,故选B.4.如图是一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的表面积为( )A .2+3π+4 2B .2+2π+4 2C .8+5π+2 3D .6+3π+2 3答案:A解析:由三视图可知,该几何体是半个圆柱和侧棱垂直于底面的三棱柱组成的几何体,该几何体的表面积S =π×2×1+42+2×⎝ ⎛⎭⎪⎫12π+1=3π+42+2,故选A.5.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是( )A .17πB .18πC .20πD .28π答案:A解析:由三视图知,该几何体为球去掉了18所剩的几何体(如图),设球的半径为R ,则78×43πR 3=28π3,故R =2,从而它的表面积S =78×4πR 2+34×πR 2=17π.故选A.6.若几何体的三视图如图所示,则该几何体的外接球的表面积为 ( )A .34πB .35πC .36πD .17π答案:A解析:由几何体的三视图知,它是底面是正方形且有一侧棱垂直于底面的四棱锥,可把它补成一个长、宽、高分别为3,3,4的长方体,该长方体的外接球即为原四棱锥的外接球,所以4R 2=32+32+42=18+16=34(其中R 为外接球的半径),外接球表面积为S =4πR 2=34π.故选A.7.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为( )A.26 B .36 C.23D .22答案:A解析:设△ABC 外接圆的圆心为O 1,则 |OO 1|=OC 2-O 1C 2=1-13=63. 三棱锥S -ABC 的高为2|OO 1|=263.所以三棱锥S -ABC 的体积V =13×34×263=26.故选A.8.有一根长为3π cm ,底面直径为2 cm 的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为________ cm.答案:5π解析:把圆柱侧面及缠绕其上的铁丝展开,在平面上得到矩形ABCD (如图),由题意知BC =3π cm ,AB =4π cm ,点A 与点C 分别是铁丝的起、止位置,故线段AC 的长度即为铁丝的最短长度.AC =AB 2+BC 2=5π(cm).故铁丝的最短长度为5π cm.9.如图,网格纸上的小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积是________.答案:8+6π解析:该几何体是一个放倒的半圆柱上面加一个四棱锥的组合体,故该几何体的体积V =V 四棱锥+V 半圆柱=13×2×3×4+12×π×22×3=8+6π.1.某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则xy 的最大值为( )A .32B .327C .64D .647答案:C解析:由三视图知,三棱锥如图所示,底面ABC 是直角三角形,AB ⊥BC ,PA ⊥平面ABC ,BC =27,PA 2+y 2=102,(27)2+PA 2=x 2,因此xy =x 102-[x 2-72]=x 128-x 2≤x 2+-x22=64,当且仅当x 2=128-x 2,即x =8时取等号, 因此xy 的最大值是64.故选C.2.如图,四棱柱ABCD -A 1B 1C 1D 1是棱长为1的正方体,四棱锥S -ABCD 是高为1的正四棱锥,若点S ,A 1,B 1,C 1,D 1在同一个球面上,则该球的表面积为( )A.9π16 B .25π16C.49π16D .81π16答案:D解析:按如图所示作辅助线,其中O 为球心,设OG 1=x ,则OB 1=SO =2-x , 由正方体的性质知B 1G 1=22, 则在Rt △OB 1G 1中,OB 21=G 1B 21+OG 21, 即(2-x )2=x 2+⎝ ⎛⎭⎪⎫222, 解得x =78,所以球的半径R =OB 1=98,所以球的表面积为S =4πR 2=81π16,故选D.3.已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是________.答案:33解析:由题意及正视图可知,三棱锥的底面等腰三角形的底长为23,三棱锥的高为1,则三棱锥的底面积为12×22-32×23=3,∴该三棱锥的体积为13×3×1=33.4.已知E ,F 分别是棱长为a 的正方体ABCD -A 1B 1C 1D 1的棱AA 1,CC 1的中点,则四棱锥C 1-B 1EDF 的体积为________.答案:16a 3解析:解法一:如图所示,连接A 1C 1,B 1D 1交于点O 1,连接B 1D ,EF ,过O 1作O 1H ⊥B 1D 于H .因为EF ∥A 1C 1,且A 1C 1⊄平面B 1EDF ,EF ⊂平面B 1EDF , 所以A 1C 1∥平面B 1EDF .所以C 1到平面B 1EDF 的距离就是A 1C 1到平面B 1EDF 的距离. 易知平面B 1D 1D ⊥平面B 1EDF , 又平面B 1D 1D ∩平面B 1EDF =B 1D , 所以O 1H ⊥平面B 1EDF ,所以O 1H 等于四棱锥C 1-B 1EDF 的高. 因为△B 1O 1H ∽△B 1DD 1, 所以O 1H =B 1O 1·DD 1B 1D =66a . 所以V C 1-B 1EDF =13S 四边形B 1EDF ·O 1H=13·12·EF ·B 1D ·O 1H =13·12·2a ·3a ·66a =16a 3. 解法二:连接EF ,B 1D .设B 1到平面C 1EF 的距离为h 1,D 到平面C 1EF 的距离为h 2,则h 1+h 2=B 1D 1=2a . 由题意得V C 1-B 1EDF =V B 1-C 1EF +V D -C 1EF=13·S △C 1EF (h 1+h 2)=16a 3.5.一几何体按比例绘制的三视图如图所示(单位:m).(1)试画出它的直观图; (2)求它的表面积和体积. 解:(1)直观图如图所示:(2)由三视图可知,该几何体是长方体被截去一个三棱柱,且该几何体的体积是以A 1A ,A 1D 1,A 1B 1为棱的长方体的体积的34,在直角梯形AA 1B 1B 中,作BE ⊥A 1B 1于E ,则四边形AA 1EB 是正方形,∴AA 1=BE =1,在Rt △BEB 1中,BE =1,EB 1=1, ∴BB 1=2, ∴几何体的表面积S =S 正方形ABCD +S 矩形A 1B 1C 1D 1+2S 梯形AA 1B 1B +S 矩形BB 1C 1C +S 正方形AA 1D 1D=1+2×1+2×12×(1+2)×1+1×2+1=7+2(m 2).∴几何体的体积V =34×1×2×1=32(m 3),∴该几何体的表面积为(7+2) m 2,体积为32m 3.。

课时跟踪检测(六十一)[高考基础题型得分练]1.(2017·海南海口模拟)某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解答下列问题.(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动.①求所抽取的2名同学中至少有1名同学来自第5组的概率;②求所抽取的2名同学来自同一组的概率.解:(1)由题意可知,样本总人数为80.16=50,∴b=250=0.04,∴y =b10=0.004,a =16,x =0.032.(2)①由题意可知,第4组共有4人,记为A ,B ,C ,D ,第5组共有2人,记为X ,Y . 从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学有AB ,AC ,AD ,BC ,BD ,CD ,AX ,AY ,BX ,BY ,CX ,CY ,DX ,DY ,XY ,共15种情况.设“随机抽取的2名同学中至少有1名同学来自第5组”为事件E ,有AX ,AY ,BX ,BY ,CX ,CY ,DX ,DY ,XY ,共9种情况.∴P (E )=915=35.②设“随机抽取的2名同学来自同一组”为事件F ,有AB ,AC ,AD ,BC ,BD ,CD ,XY ,共7种情况.∴P (F )=715.2.某足球队两名主力队员各进行了5组罚点球训练,每组罚10次,罚中次数如下表:场?(2)若从这两名队员的5组中各随机抽取一组分析罚点球的技术和心理因素,求选出的一组中甲恰好罚中次数多于乙的罚中次数的概率.解:(1)计算甲、乙的罚中次数的平均值得x 甲=6+5+7+9+85=7,x乙=4+8+9+7+75=7,所以两人罚中次数的平均值相等,s 2甲=-2+-2+-2+-2+-25=2,s 2乙=-2+-2+-2+-2+-25=145,s 2甲<s 2乙,甲罚中次数的方差较小,相对更稳定,应派甲队员出场.(2)记甲队员的5组次数分别为A 1,A 2,A 3,A 4,A 5,乙队员的5组次数分别为B 1,B 2,B 3,B 4,B 5,随机抽取各一组所有可能的情况有25种,分别为:(A 1,B 1),(A 1,B 2),(A 1,B 3),(A 1,B 4),(A 1,B 5),(A 2,B 1),…,(A 5,B 5),其中甲恰好罚中次数多于乙的罚中次数的有(A 1,B 1),(A 2,B 1),(A 3,B 1),(A 4,B 1),(A 5,B 1),(A 4,B 2),(A 4,B 4),(A 4,B 5),(A 5,B 4),(A 5,B 5),共10种情况,故所求概率为P =1025=25.3.在等差数列{a n }和等比数列{b n }中,a 1=b 1=1,b 4=8,{a n }的前10项和S 10=55.(1)求a n 和b n ;(2)现分别从{a n }和{b n }的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值相等的概率.解:(1)设数列{a n }的公差为d ,数列{b n }的公比为q . 依题意得S 10=10+10×92d =55,b 4=q 3=8,解得d =1,q =2,所以a n =n ,b n =2n -1.(2)分别从{a n }和{b n }的前3项中各随机抽取一项,得到的基本事件有9个:(1,1),(1,2),(1,4),(2,1),(2,2),(2,4),(3,1),(3,2),(3,4).符合题意的基本事件有2个:(1,1),(2,2).故所求的概率P =29.[冲刺名校能力提升练]1.一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机抛掷两次,正四面体面朝下的数字分别为b ,c .(1)z =(b -3)2+(c -3)2,求z =4的概率;(2)若方程x 2-bx -c =0至少有一根x ∈{1,2,3,4},就称该方程为“漂亮方程”,求方程为“漂亮方程”的概率.解:(1)因为是抛掷两次,因此基本事件(b ,c ):(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个.当z =4时,(b ,c )的所有取值为(1,3),(3,1), 所以P (z =4)=216=18.(2)①若方程一根为x =1,则1-b -c =0, 即b +c =1,不成立.②若方程一根为x =2,则4-2b -c =0, 即2b +c =4,所以 ⎩⎪⎨⎪⎧ b =1,c =2.③若方程一根为x =3,则9-3b -c =0,即3b +c =9,所以 ⎩⎪⎨⎪⎧b =2,c =3.④若方程一根为x =4,则16-4b -c =0,即4b +c =16,所以 ⎩⎪⎨⎪⎧b =3,c =4.由①②③④知(b ,c )的所有可能取值为(1,2),(2,3),(3,4), 所以方程为“漂亮方程”的概率为P=316.2.某班甲、乙两名同学参加100米达标训练,在相同条件下两人10次训练的成绩(单位:秒)如下:稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论);(2)经过对甲、乙两位同学的若干次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率.解:(1)甲、乙两人10次训练的成绩的茎叶图:从统计图中可以看出,乙的成绩较为集中,差异程度较小,所以选派乙同学代表班级参加比赛更好.(2)设甲同学的成绩为x,乙同学的成绩为y,则|x-y|<0.8,得x-0.8<y<0.8+x,如图,阴影部分面积即为3×3-2.2×2.2=4.16,则P (|x -y |<0.8)=P (x -0.8<y <0.8+x )=4.163×3=104225.3.已知集合P ={x |x (x 2+10x +24)=0},Q ={y |y =2n -1,1≤n ≤2,n ∈N *},M =P ∪Q .在平面直角坐标系中,点A 的坐标为(x ′,y ′),且x ′∈M ,y ′∈M ,试计算:(1)点A 正好在第三象限的概率; (2)点A 不在y 轴上的概率;(3)点A 正好落在区域x 2+y 2≤10上的概率. 解:由集合P ={x |x (x 2+10x +24)=0}, 可得P ={-6,-4,0},由Q ={y |y =2n -1,1≤n ≤2,n ∈N *},可得Q ={1,3},则M =P ∪Q ={-6,-4,0,1,3}, 因为点A 的坐标为(x ′,y ′),且x ′∈M ,y ′∈M ,所以满足条件的点A 的所有情况为(-6,-6),(-6,-4),(-6,0),(-6,1),(-6,3),…,(3,3),共25种.(1)点A 正好在第三象限的可能情况为(-6,-6),(-6,-4),(-4,-6),(-4,-4),共4种,故点A 正好在第三象限的概率P 1=425.(2)点A 在y 轴上的可能情况为(0,-6),(0,-4),(0,0),(0,1),(0,3),共5种, 故点A 不在y 轴上的概率P 2=1-525=45.(3)点A 正好落在区域x 2+y 2≤10上的可能情况为(0,0),(1,0),(0,1),(3,1),(1,3),(3,0),(0,3),(1,1),共8种,故点A 落在区域x 2+y 2≤10上的概率P 3=825.。

课时跟踪检测(七十)1.若大前提是:任何实数的平方都大于0,小前提是:a∈R,结论是:a2〉0,那么这个演绎推理出错在( )A.大前提 B.小前提C.推理过程D.没有出错答案:A解析:要分析一个演绎推理是否正确,主要观察所给的大前提、小前提和结论及推理形式是否都正确,根据这几个方面都正确,才能得到这个演绎推理正确.因为大前提是:任何实数的平方都大于0,是不正确的.故选A。
2.观察(x2)′=2x,(x4)′=4x3,(cos x)′=-sin x,由归纳推理可得:若定义在R上的函数f(x)满足f(-x)=f(x),记g(x)为f(x)的导函数,则g(-x)=( )A.f(x)B.-f(x)C.g(x)D.-g(x)答案:D解析:由所给函数及其导数知,偶函数的导函数为奇函数,因此当f(x)是偶函数时,其导函数应为奇函数,故g(-x)=-g(x).3.观察一列算式:1⊗1,1⊗2,2⊗1,1⊗3,2⊗2,3⊗1,1⊗4,2⊗3,3⊗2,4⊗1,…,则式子3⊗5是第()A.22项B.23项C.24项D.25项答案:C解析:两数和为2的有1个,和为3的有2个,和为4的有3个,和为5的有4个,和为6的有5个,和为7的有6个,前面共有21个,3⊗5是和为8的第3项,所以为第24项,故选C.4.已知△ABC中,∠A=30°,∠B=60°,求证:a〈b.证明:∵∠A=30°,∠B=60°,∴∠A〈∠B。
∴a〈b。
其中,画线部分是演绎推理的( )A.大前提 B.小前提C.结论 D.三段论答案:B解析:由三段论的组成可得画线部分为三段论的小前提.5.将圆的一组n等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录k(k≤n)个点的颜色,称为该圆的一个“k阶色序",当且仅当两个k阶色序对应位置上的颜色至少有一个不相同时,称为不同的k阶色序.若某国的任意两个“k阶色序”均不相同,则称该圆为“k阶魅力圆".“3阶魅力圆”中最多可有的等分点个数为()A.4 B.6C.8 D.10答案:C解析:因“3阶色序”中每个点的颜色有两种选择,故“3阶色序”共有2×2×2=8种,一方面,n个点可以构成n个“3阶色序”,故“3阶魅力圆”中的等分点的个数不多于8个;另一方面,若n=8,则必须包含全部共8个“3阶色序”,不妨从(红,红,红)开始按逆时针确定其它各点颜色,显然(红,红,红,蓝,蓝,蓝,红,蓝)符合条件.故“3阶魅力圆”中最多有8个等分点,故选C.6.观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10=( )A.28 B.76C.123 D.199答案:C解析:从给出的式子特点观察可推知,等式右端的值,从第三项开始,后一个式子的右端值等于它前面两个式子右端值的和,照此规律,则a10+b10=123。

课时跟踪检测(七十四)1.若(1+i)+(2-3i)=a +b i(a ,b ∈R ,i 是虚数单位),则a ,b 的值分别等于( ) A .3,-2 B .3,2 C .3,-3 D .-1,4 答案:A解析:(1+i)+(2-3i)=3-2i =a +b i ,∴a =3,b =-2,故选A.2.已知i 为虚数单位,则复数z =(-1-2i)i 在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 答案:D解析:z =(-1-2i)i =2-i ,对应的点Z (2,-1)在第四象限. 3.复数53+4i 的共轭复数为( )A .3-4iB .3+4iC.35-45iD.35+45i 答案:D 解析:z =53+4i =-+-=35-45i , ∴z =35+45i.4.设z 是复数,则下列命题中的假命题是( ) A .若z 2≥0,则z 是实数 B .若z 2<0,则z 是虚数 C .若z 是虚数,则z 2≥0D .若z 是纯虚数,则z 2<0 答案:C解析:举反例说明,若z =i ,则z 2=-1<0,故选C. 5.已知复数z =1+2i2-i (i 为虚数单位),则z 的虚部为( )A .-1B .0C .1D .i答案:C 解析:∵z =1+2i2-i=++-+=5i5=i ,故虚部为1.6.若复数z =i(3-2i)(i 是虚数单位),则z 等于( ) A .2-3i B .2+3i C .3+2i D .3-2i答案:A解析:因为z =i(3-2i)=2+3i ,所以z =2-3i ,故选A. 7.已知i 是虚数单位,则i2 0151+i =( )A.1-i 2B.1+i2 C.-1-i 2 D.-1+i2答案:C解析:i 2 0151+i =i 4×503+31+i =i 31+i =-i 1+i =--+-=-1-i 2.8.设z =11+i +i ,则|z |=( )A.12B.22C.32D .2答案:B解析:∵z =11+i +i =1-i +-+i =1-i 2+i =12+12i ,∴|z |=⎝ ⎛⎭⎪⎫122+⎝ ⎛⎭⎪⎫122=22,故选B.9.设复数z 1和z 2在复平面内的对应点关于坐标原点对称,且z 1=3-2i ,则z 1·z 2=________.答案:-5+12i解析:z 1=3-2i ,由题意知,z 2=-3+2i. ∴z 1·z 2=(3-2i)(-3+2i)=-5+12i.10.设复数z 满足z 2=3+4i(i 是虚数单位),则z 的模为________. 答案: 5解析:∵z 2=3+4i ,∴|z |2=|3+4i|=5, 即|z |= 5.11.若复数z 满足z =i(2+z )(i 为虚数单位),则z =________. 答案:-1+i解析:由已知,得z =2i +z i ,∴z (1-i)=2i ,z =2i1-i=+-+=-1+i.12.设i 是虚数单位,若复数(2+a i)i 的实部与虚部互为相反数,则实数a 的值为________.答案:2解析:(2+a i)i =-a +2i ,其实部与虚部分别为-a,2,故-a +2=0,因此a =2. 13.计算:(1)-1++i 3;(2)+2+-2+i; (3)1-i +2+1+i -2;(4)1-3i 3+2.解:(1)-1++i 3=-3+i -i =-3+-i·i=-1-3i.(2)+2+-2+i=-3+4i +3-3i 2+i =i2+i=-5=15+25i. (3)1-i+2+1+i -2=1-i 2i -1+i2i=-1. (4)1-3i 3+2=3+-3+2=-i 3+i=-3-4=-14-34i.1.复数1+2i2-i 的共轭复数是( )A.3i5B .-3i 5C .iD .-i答案:D解析:∵1+2i2-i =++-+=5i5=i , ∴共轭复数为-i.2.已知复数z =1+a i(a ∈R )(i 是虚数单位),zz =-35+45i ,则a =( ) A .2B .-2C .±2D .-12答案:B解析:∵z =1+a i ,∴z =1-a i ,zz =1-a i 1+a i =1-a 2-2a i 1+a 2=-35+45i , ∴⎩⎪⎨⎪⎧1-a 21+a 2=-35,-2a 1+a 2=45,解得a =-2.3.复数z =i -2-2(i 为虚数单位),z 在复平面内所对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限 答案:A 解析:因为z =i-2-2=i 4+4i -1=i3+4i =-25=425+325i ,所以z 在复平面内所对应的点⎝⎛⎭⎪⎫425,325在第一象限.4.如图,若向量OZ →对应的复数为z ,则z +4z表示的复数为( )A .1+3iB .-3-iC .3-iD .3+i 答案:D解析:由图可得Z (1,-1),即z =1-i ,所以z +4z =1-i +41-i =1-i ++-+=1-i +4+4i2=1-i +2+2i =3+i.5.设复数z =3+i(i 为虚数单位)在复平面中对应点A ,将OA 绕原点O 逆时针旋转90°得到OB ,则点B 在( )A .第一象限B .第二象限C .第三象限D .第四象限 答案:B解析:因为复数z 对应点的坐标为A (3,1),所以点A 位于第一象限,所以逆时针旋转π2后对应的点B 在第二象限,故选B.6.下面是关于复数z =2-1+i的四个命题:p 1:|z |=2; p 2:z 2=2i ;p 3:z 的共轭复数为1+i ; p 4:z 的虚部为-1.其中的真命题为( ) A .p 2,p 3 B .p 1,p 2 C .p 2,p 4 D .p 3,p 4答案:C解析:∵z =2-1+i =-1-i ,∴|z |=-2+-2=2,∴p 1是假命题;∵z 2=(-1-i)2=2i ,∴p 2是真命题; ∵z =-1+i ,∴p 3是假命题; ∵z 的虚部为-1,∴p 4是真命题.7.复数-1+3i1+2i (i 为虚数单位)的共轭复数为________.答案:1-i解析:因为复数-1+3i 1+2i =-1+-2+-=5+5i5=1+i ,所以其共轭复数z =1-i.8.若3+b i1-i=a +b i(a ,b 为实数,i 为虚数单位),则a +b =________.答案:3 解析:由3+b i1-i =+b +-+=3-b ++b2=a +b i ,得a =3-b 2,b =3+b2,解得b =3,a =0,所以a +b =3.9.复数z 满足(3-4i)z =5+10i ,则|z |=________. 答案: 5解析:由(3-4i)z =5+10i 知,|3-4i|·|z |=|5+10i|,即5|z |=55,解得|z |= 5. 10.已知复数z =i +i 2+i 3+…+i 2 0141+i ,则复数z 在复平面内对应的点为________.答案:(0,1) 解析:∵i 4n +1+i4n +2+i4n +3+i4n +4=i +i 2+i 3+i 4=0,而2 013=4×503+1,2 014=4×503+2,∴z =i +i 2+i 3+…+i 2 0141+i =i +i 21+i =-1+i1+i=-1+-+-=2i2=i , 对应的点为(0,1). 11.定义运算⎪⎪⎪⎪⎪⎪a b cd =ad -bc .若复数x =1-i 1+i ,y =⎪⎪⎪ 4i2⎪⎪⎪x i x +i ,则y =________. 答案:-2 解析:因为x =1-i1+i=-22=-i ,所以y =⎪⎪⎪ 4i2⎪⎪⎪ x i x +i =⎪⎪⎪ 4i2⎪⎪⎪10=-2. 12.复数z 1=3a +5+(10-a 2)i ,z 2=21-a +(2a -5)i ,若z 1+z 2是实数,求实数a 的值. 解:z 1+z 2=3a +5+(a 2-10)i +21-a+(2a -5)i =⎝ ⎛⎭⎪⎫3a +5+21-a +i =a -13a +a -+(a 2+2a -15)i.∵z 1+z 2是实数,∴a 2+2a -15=0,解得a =-5或a =3. ∵a +5≠0,∴a ≠-5,故a =3.。

课时跟踪检测(五十一)1.椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的两倍,则m的值为()A.错误!B。
错误!C.2 D.4答案:A解析:由题意知,a2=错误!,b2=1,且a=2b,∴错误!=4,∴m=错误!。
2.已知实数4,m,9构成一个等比数列,则圆锥曲线错误!+y2=1的离心率为( )A.错误!B。
错误!C.错误!或错误!D.错误!或错误!答案:C解析:因为实数4,m,9构成一个等比数列,所以可得m2=36,解得m=6或m=-6.当圆锥曲线为椭圆时,即错误!+y2=1的方程为错误!+y2=1,所以a2=6,b2=1,则c2=a2-b2=5,所以离心率e=错误!=错误!=错误!。
当曲线是双曲线时,可求得离心率为错误!.3.椭圆错误!+错误!=1的焦点为F1,F2,点P在椭圆上,如果线段PF2的中点在y轴上,那么|PF2|是|PF1|的()A.7倍B.5倍C.4倍D.3倍答案:A解析:设线段PF2的中点为D,则|OD|=错误!|PF1|且OD∥PF1,OD⊥x轴,∴PF1⊥x轴.∴|PF1|=错误!=错误!=错误!.又∵|PF1|+|PF2|=4错误!,∴|PF2|=43-错误!=错误!.∴|PF2|是|PF1|的7倍.4.已知椭圆C:错误!+错误!=1的左、右焦点分别为F1,F2,椭圆C上的点A满足AF2⊥F1F2。
若点P是椭圆C上的动点,则F1P→·错误!的最大值为( )A。
错误!B。
错误!C.错误!D.错误!答案:B解析:设向量F1P,→,F2A,→的夹角为θ.由条件知,|AF2|为椭圆通径的一半,即|AF2|=错误!=错误!,则错误!·错误!=错误!|错误!|cos θ,于是错误!·错误!要取得最大值,只需错误!在错误!上的投影值最大,易知此时点P为椭圆短轴的上顶点,所以错误!·错误!=错误!×|错误!|cos θ≤错误!.故选B。
温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时分层提升练十一函数与方程(25分钟50分)一、选择题(每小题5分,共20分)1.若函数f(x)=ax+b有一个零点是2,那么函数g(x)=bx2-ax的零点是( )A.0,2B.0,C.0,-D.2,-【解析】选C.由题意知2a+b=0,即b=-2a.令g(x)=bx2-ax=0得x=0或x==-.2.(2017·成都模拟)若函数f(x)的零点与g(x)=4x+2x-2的零点之差的绝对值不超过0.25,则f(x)可以是( )A.f(x)=8x-2B.f(x)=(x+1)2C.f(x)=e x-1D.f(x)=ln【解析】选A.因为g(0)=-1<0,g=1>0,所以g(0)·g<0,所以g(x)的零点在内,因为f(x)=8x-2的零点为,故选A.3.(2017·定州模拟)函数f(x)=e x+3x的零点个数是( )A.0B.1C.2D.3【解析】选B.由已知得f′(x)=e x+3>0,所以f(x)在R上单调递增,又f(-1)=e-1-3<0,f(1)=e+3>0,所以f(x)的零点个数是1.【加固训练】函数f(x)=2x|log0.5x|-1的零点个数为( )A.1B.2C.3D.4【解析】选B.当0<x<1时,f(x)=2x log0.5x-1,令f(x)=0,则log0.5x=.由y=log0.5x,y=的图象知,在(0,1)内有一个交点,即f(x)在(0,1)上有一个零点.当x>1时,f(x)=-2x log0.5x-1=2x log2x-1,令f(x)=0得log2x=,由y=log2x,y=的图象知在(1,+∞)上有一个交点,即f(x)在(1,+∞)上有一个零点.4.已知三个函数f(x)=2x+x,g(x)=x-2,h(x)=log2x+x的零点依次为a,b,c,则( )A.a<b<cB.a<c<bC.b<a<cD.c<a<b【解析】选B.由于f(-1)=-1=-<0,f(0)=1>0,且f(x)为R上的增函数.故f(x)=2x+x的零点a∈(-1,0).因为g(2)=0,所以g(x)的零点b=2;因为h=-1+=-<0,h(1)=1>0,且h(x)为(0,+∞)上的增函数,所以h(x)的零点c∈,因此a<c<b.【一题多解】本题还可以采用如下方法:选B.由f(x)=0得2x=-x;由h(x)=0得log2x=-x,作出函数y=2x,y=log2x和y=-x的图象(如图).由图象易知a<0,0<c<1,而b=2,故a<c<b.二、填空题(每小题5分,共10分)5.(2017·九江模拟)函数f(x)对一切x∈R都有f=f,并且方程f(x)=0有三个实根,则这三个实根的和为.【解析】因为函数f(x)的图象关于直线x=对称,所以方程f(x)=0有三个实根时,一定有一个根是,另外两个根关于直线x=对称,且和为1,故方程f(x)=0的三个实根的和为.答案:【加固训练】(2017·漳州模拟)已知函数f(x)=若函数g(x)=f(x)-m有3个零点,则实数m的取值范围是.【解析】画出f(x)=的图象,如图.由于函数g(x)=f(x)-m有3个零点,结合图象得:0<m<1,即m∈(0,1). 答案:(0,1)6.若函数f(x)=lnx+2x-6的零点x0∈(k,k+1),则整数k的值为.【解析】因为f(2)=ln2-2<0,f(3)=ln3>0,所以f(x)=lnx+2x-6存在零点x0∈(2,3).因为f(x)=lnx+2x-6在定义域(0,+∞)上单调递增,所以f(x)=lnx+2x-6存在唯一的零点x0∈(2,3),则整数k=2.答案:2三、解答题(每小题10分,共20分)7.(2017·石家庄模拟)已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x 的定义域为区间.(1)求g(x)的解析式.(2)判断g(x)的单调性.(3)若方程g(x)=m有解,求m的取值范围.【解析】(1)因为f(a+2)=18,即3a+2=18,所以3a=2,所以g(x)=2x-4x.(2)g′(x)=2x ln2-4x ln4=2x ln2(1-2x+1).因为x∈,所以2x+1∈,所以1-2x+1≤0,又2x>0,ln2>0,所以g′(x)≤0(仅当x=-1时取“=”),所以g(x)在上是减函数.(3)由m=g(x)=2x-4x,得g(1)≤m≤g(-1),所以-2≤m≤.【加固训练】已知函数f(x)=4x+m·2x+1有且仅有一个零点,(1)求m的取值范围.(2)求函数的零点.【解析】(1)因为f(x)=4x+m·2x+1有且仅有一个零点,即方程(2x)2+m·2x+1=0仅有一个实根.设2x=t(t>0),则t2+mt+1=0.当Δ=0时,即m2-4=0,所以m=-2时,t=1;m=2时,t=-1(不合题意,舍去). 所以2x=1,x=0符合题意.当Δ>0时,即m>2或m<-2时,t2+mt+1=0有两正或两负根,即f(x)有两个零点或没有零点.所以这种情况不符合题意.综上可知:当m=-2时,f(x)有唯一零点.(2)由(1)可知,该函数的零点为x=0.8.(2017·徐州模拟)已知y=f(x)是定义域为R的奇函数,当x∈[0,+∞)时,f(x)=x2-2x.(1)写出函数y=f(x)的解析式.(2)若方程f(x)=a恰有3个不同的解,求a的取值范围.【解析】(1)当x∈(-∞,0)时,-x∈(0,+∞).因为y=f(x)是奇函数,所以f(x)=-f(-x)=-[(-x)2-2(-x)]=-x2-2x,所以f(x)=(2)当x∈[0,+∞)时,f(x)=x2-2x=(x-1)2-1,最小值为-1;当x∈(-∞,0)时,f(x)=-x2-2x=1-(x+1)2,最大值为1.所以据此可作出函数y=f(x)的图象(如图所示),根据图象,若方程f(x)=a 恰有3个不同的解,则a的取值范围是(-1,1).(20分钟40分)1.(5分)(2017·荆州模拟)f(x)是定义在R上的奇函数,且当x∈(0,+∞)时,f(x)=2016x+log2016x,则函数f(x)的零点的个数是( ) A.1 B.2 C.3 D.4【解析】选C.因为f(x)是定义在R上的奇函数,所以f(0)=0.结合函数的图象,可知函数y=2016x和函数y=-log2016x的图象在第一象限有一个交点,所以函数f(x)有一个正的零点,根据奇函数图象的对称性,有一个负的零点,所以函数有三个零点.2.(5分)已知a是函数f(x)=2x-lo x的零点,若0<x 0<a,则f(x0)的值满足( )A.f(x0)=0B.f(x0)<0C.f(x0)>0D.f(x0)的符号不确定【解析】选B.函数f(x)=2x+log2x在(0,+∞)上是增函数,故零点是唯一的,又0<x0<a,则f(x0)<f(a)=0.3.(5分)(2017·邯郸模拟)已知f(x)=且函数y=f(x)+ax恰有3个不同的零点,则实数a的取值范围是. 【解析】当x<0时,f(x)=(x+1)2-,把函数f(x)在[-1,0)上的图象向右平移一个单位即得函数y=f(x)在[0,1)上的图象,继续右移可得函数f(x)在[0,+∞)上的图象.如果函数y=f(x)+ax恰有3个不同的零点,即函数y=f(x),y=-ax的图象有三个不同的公共点,实数a应满足-a<-或≤a<,即a>或-<a≤. 故实数a的取值范围是∪.答案:∪4.(12分)已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.(1)求k的值.(2)设g(x)=log4,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.【解析】(1)由函数f(x)是偶函数可知:f(x)=f(-x),所以log4(4x+1)+kx=log4(4-x+1)-kx,log4=-2kx,即x=-2kx对一切x∈R恒成立,所以k=-.(2)函数f(x)与g(x)的图象有且只有一个公共点,即方程log4(4x+1)-x=log4有且只有一个实根,化简得:方程2x+=a·2x-a有且只有一个实根,令t=2x>0,则方程(a-1)t2-at-1=0有且只有一个正根.①a=1⇒t=-,不合题意;②a≠1,Δ=0⇒a=或-3,若a=⇒t=-2,不合题意;若a=-3⇒t=;③一个正根与一个负根,Δ>0且<0⇒a>1.综上:实数a的取值范围是{-3}∪(1,+∞).5.(13分)(2017·石家庄模拟)已知函数f(x)=-x2+2ex+m-1,g(x)=x+(x>0).(1)若y=g(x)-m有零点,求m的取值范围.(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.【解析】(1)因为g(x)=x+≥2=2e,等号成立的条件是x=e,故g(x)的值域是[2e,+∞),因而只需m≥2e,则y=g(x)-m就有零点.【一题多解】本题还可以采用以下方法:作出g(x)=x+(x>0)的大致图象如图.可知若使y=g(x)-m有零点,则只需m≥2e.(2)若g(x)-f(x)=0有两个相异实根,即g(x)与f(x)的图象有两个不同的交点,作出g(x)=x+(x>0)的大致图象如图.因为f(x)=-x2+2ex+m-1=-(x-e)2+m-1+e2.所以其图象的对称轴为x=e,开口向下,最大值为m-1+e2.故当m-1+e2>2e,即m>-e2+2e+1时,g(x)与f(x)有两个交点,即g(x)-f(x)=0有两个相异实根.所以m的取值范围是(-e2+2e+1,+∞).关闭Word文档返回原板块。
所以 a 2= 6, b 2= 1, 则 c 2= a 2-b 2= 5.课时跟踪检测(四十九)[高考基础题型得分练]1.椭圆x 2 + my = 1的焦点在y 轴上,长轴长是短轴长的两倍,贝U m 的值为(1A.4B.C. 2D.答案: 解析: 2 1 2由题意知,a = m b = 1,且a = 2b ,1•m=4,X 22.已知实数4, m,9构成一个等比数列,则圆锥曲线-+ y = 1的离心率为(B. .7答案:C解析:因为实数4, m,9构成一个等比数列, 所以可得m = 36, 解得m= 6或m=- 6.当圆锥曲线为椭圆时,即2 2m / =1的方程为x + y =1所以离心率e =a =5 _30 6= 当曲线是双曲线时可求得离心率为 .7. 2 23. [2017 •河北邯郸一模]椭圆12 + 3 = 1 的焦点为F i , F 2,点P 在椭圆上,如果线段PF 2的中点在y 轴上,那么|PB |是|PF |的( A. 7倍 B. 5倍 C. 4倍 D. 3倍答案:A解析:设线段PF 的中点为D,1 则 |0D = 2I PF 1I 且 OD/ PF , ODL x 轴,••• PF 丄 x 轴,••• |PF | = b =△=€•a 2、p 2又••• |PF | + I PF = 4西,• |PE|= 4 .3_f= =-2.■■- | PFJ 是| PF | 的 7倍.2 2x y4•已知椭圆C : ; + £= 1的左、右焦点分别为 F l , F 2,椭圆C 上的点A 满足AF 丄F 1F 2.43若点P 是椭圆C 上的动点,贝U F i P- F 2A 勺最大值为于2贝y c 的方程是()2土=12x 2D -+y =14B.3<3 2_ 9C.4D. 15 ~4答案:B解析:设向量FP, F 2A 的夹角为0 . 由条件知| AR|为椭圆通径的一半,b 2 3即 | AF = - = ©T T 3 T则 F 1P - F 2A = ?| F 1P COS 0 ,于是FP-只需FP 在 F 2A 上的投影值最大,易知此时点P 在椭圆短轴的上顶点,T T 3 T所以 FP- F 2A = x| F 1P |cos 3.3故选B.5. [2017 •陕西西安质量检测 ]已知中心在原点的椭圆 C 的右焦点为F (1,0),离心率等—1,=—1,点与线段AB 中点的直线的斜率为■,则b 的值为( 2 aB.2*3 3 C症C.2D.2,3 27答案:B解析:设 A (X 1, yj , B (X 2, ax 2 + by 1 = 1, ax 2+ by ! = 1,y 2),则即 ax 1 — ax 2=— ( by 2 — by 2), 22by 1 — by 22 2 = ax 1 — ax 2.b y — y 2y 1 + y 2 a X 1 — X 2 X 1 + X 2答案:A解析:设椭圆C 的焦距为2c (c <a ), 由于直线 AB 的方程为bx + ay — ab = 0,ab•/ b 2 = a 2 — c 2,「. 3a 4— 7a 2c 2+ 2c 4= 0,解得a 2= 2c 2或3a 2= c 2(舍去)」e =#答案:C 解析:依题意,所求椭圆的焦点位于c1x轴上,2 2因此其方程是++警=X 故选C.6. [2017 •甘肃兰州诊断]已知椭圆 C:2 2x y 云+令=1( a >b >0)的左、右焦点分别为 F 1, F 2, 右顶点为A,上顶点为B,若椭圆C 的中心到直线AB 的距离为半| F 1F 2I ,则椭圆C 的离心率e =( )B.~2D.7. [2 017 •江西师大附中模拟]椭圆ax 2+ by 21与直线y = 1 — x 交于A , B 两点,过原••• a x(-1)x• b=孚,故选B.2 2& [2017 •山东青岛模拟]设椭圆m2+ £= 1(m>0, n>0)的右焦点与抛物线y2= 8x的焦点1相同,离心率为2,则此椭圆的方程为 ________ .2 2答案:16+务=1解析:抛物线y2= 8x的焦点为(2,0),•吊—n2= 4,①• m= 4,n2= 12,2 2•椭圆方程为~+12= 1.2 29. _________ [2017 •湖南长沙一模]椭圆r :争+碁=1(a>b>0)的左、右焦点分别为F1, F2,焦距为2c,若直线y=J3(x+ c)与椭圆r的一个交点M满足/ MFF2= 2/ MFF,则该椭圆的离心率等于_________________ .答案:3 —1解析:依题意得/ MFF2= 60°,/ MFF1 = 30°,/ RMF= 90°,设| MF| = m则有| MF| = 3m I尸冋=2m该椭圆的离心率是e=丨田_J3_1| MF| + | MI2| = 32x10. 在平面直角坐标系xOy中,已知△ ABC的顶点A( —4,0)和C(4,0),顶点B在椭圆忑5答案:5解析:sin A+ sin C | BQ + | BA 2a a 5 sin B =|AQ = 2c= c = 4.2 2 21 2e= 2=m代入①得,2+ y9 = 1上,则S in A+ Sin C的值为sin Bxv 2 y11. [2017 •山东三校联考]椭圆C:孑+話=1(a>b>0)的右焦点为F,双曲线x -3 = 1的一条渐近线与椭圆C交于A, B两点,且AF丄BF则椭圆C的离心率为____________ .答案:3 —12解析:不妨取双曲线x2—V3 = 1的一条渐近线的方程为y= .3x,记椭圆C的左焦点为F1,由题意得| OA = | OB = | OF = | OF| = c,•••四边形AFBF为矩形,△ AFC是正三角形,••• | AF = c, | AF| = Q3c,c 2c•椭圆C的离心率e=a=亦=l FF l = % = 3_1= |AF + |AF| = c+ 3c = 3_12. 已知椭圆的左焦点为R,右焦点为冃,若椭圆上存在一点P,满足线段PR相切于以椭圆的短轴为直径的圆,切点为线段 __________________________ PF的中点,则该椭圆的离心率为.答案:£设| F1F2| = 2c, |PF| = 2|CM = 2b, 由椭圆的定义,得|PF a| = 2a_ 2b.2 2 2由勾股定理,得4b + (2 a—2b) = 4c ,2 yl5解得b= 3a, c = -ya,所以椭圆的离心率e =靑[冲刺名校能力提升练]2 21. [2017 •广东汕头一模]已知椭圆X +吕=1上有一点P , F i , F 2是椭圆的左、右焦点, 若厶F i PR 为直角三角形,则这样的点P 有( )A. 3个B. 4个C. 6个D. 8个答案:C解析:当/ PF 1F 2为直角时,根据椭圆的对称性知,这样的点 P 有2个;同理当/ PF 2F 1为直角时,这样的点 P 有2个;当P 点为椭圆的短轴端点时,/ F i PR 最大,且为直角,此时这样的点P 有2个.故符合要求的点 P 有6 个.+ y =0的对称点A 是椭圆C 上的点,则椭圆 C 的离心率为( 1 A.- 1 BYC© C.2D. 3 — 1答案:D解析:解法一:设A (m n ),则—/3 =— 1,解得A |,彳-,-2 3-2代入椭圆C 中,有石+ 4b 2=1,.22只 2 2 , 2. 2「•be + 3a - = 4a b ,/ 22、 2 小22 ,2,2 2、/• (a — c )c + 3a c = 4a (a — c ),4介 2 2 ,4…c — 8a c + 4a = 0,二 e — 8e + 4 = 0,2. [2017 •河北唐山模拟m- - n+ 2=0,]椭圆C:2 2F ,若F 关于直线e = 4±2 , 3,•/ 0<e<1,二e= . 3— 1.解法二:借助于椭圆的定义,本题还有如下简捷解法:设F '是椭圆的右焦点,连接 AF, AF . 由已知得厶AFF 是直角三角形,其中/ A = 90°,/ AFF = 30°,2c—— =3— 1,故选D.c + 3c '2 2x y3.已知F 1, F 2是椭圆G 尹^2= 1(a >b >0)的两个焦点,P 为椭圆答案:3••• I FF I = 2c ,. | AF | =0c , |AF | = c , 2c|FF |e= 2a = | AF | + | AF IC 上的一点,且 PF丄PF 2.若厶PFF 2的面积为 9,则 b =解析:设| PF| = r1, | PF| =「2,则r 1+「2= 2a,2,2 2r 1+「2= 4c ,2 22「1「2= (「1 +「2) —(r 1 +r ) =4a2—4c2= 4b2,1 2又S PF_,F2=歹1r2= b = 9,「. b= 3.4. [2017 •河北保定一模]与圆C: (x+ 3)2+ y2= 1外切,且与圆 2 2G: (x —3) + y = 81内切的动圆圆心P的轨迹方解析:设动圆的半径为r,圆心为F(x, y),则有|PG| = r + 1, | PG| = 9- r.所以| PG| + | PG| = 10> | CC ,即P在以2x P的轨迹方程为去+255.已知椭圆G的对称中心为原点O,焦点在x轴上,左、右焦点分别为F1和F2,且|尸冋=2,点1, 2在该椭圆上.(1)求椭圆G的方程;⑵过F1的直线I与椭圆C相交于A, B两点,若△ AFB的面积为^2#,求以F2为圆心且与直线I相切的圆的方程.解:(1)由题意知c = 1,2 a=gj + p gj + 22= 4,解得a= 2,故椭圆G的方程为x(2)①当直线I 丄x 轴时,可取A — 1, — 2 , B — 1, 2 , △ AFB 的面积为3,不符合题意.②当直线I 与x 轴不垂直时,设直线I 的方程为y = k (x + 1),代入椭圆方程得(3 + 4k 3 4 5)x 22 2+ 8k x + 4k — 12= 0,显然△ >0 成立,设 A (X 1, y 1), B (X 2, y 2),3 求椭圆C 的方程;4 在x 轴上是否存在定点经过以 MN 为直径的圆?若存在, 求定点坐标;若不存在,请说明理由.X 1+ X 2= — 8 k 2 3 +4k 2,X 1X 2 = 4k 2— 123+ 4k 2,可得| AB = 1 + k2—X1 + X2 2—4x1X212 k2+l=3 + 4k2,又圆F2的半径r =2| k|_ 1 + k2'•••△ AFB的面积为12| k| .. k2+ 1 12 2 r= 3+ 4k2=十,化简得17k4+ k2—18= 0,得k=± 1,• r = 2,圆的方程为(x —1)2+ y2= 2.2 2x y6. [2017 •湖南四校联考]在平面直角坐标系xOy中,椭圆C:二+ 2= 1(a>b>0)的离心a b率e= 1,且过点(0 , 3),椭圆C的长轴的两端点为A B,点P为椭圆上异于A, B的动点, 1| AB. 2 2 22 c a — b 1解:⑴ a a 4 b 2= 32 2 x y•••椭圆C 的方程为匚+石=1. 4 3y oy o 则 k l =,k 2=x^, 2 y ok i k 2= ―22 X o — 4x o — 42 4 — x o 3X 4 3x 2— 4 =— 4,由 I PA :y = k i (x + 2)知 M 4,6 k i ), 由 l PB : y = k 2(x — 2)知 N (4,2 k 2), • MN 的中点Q4,3总+ k 2),1•••以 MN 为直径的圆的方程为(x — 4)2+ (y — 3k 1— k 2)2=二(6k 1 — 2k ?)2 = (3k 1 — k"2, 4 令y = o ,得x — 8x + 16+ 9k 1 + 6k 〔k 2+ k 2=9k 1— 6k 1 k 2 + k 2,2•- x — 8x + 16+ 12k 1k 2= o , • x 2 — 8x + 16+ 12X-3 = o ,2 即 x — 8x + 7 = o ,解得 x = 7 或 x = 1,•••存在定点(1,o) , (7,o)经过以MN 为直径的圆. ⑵设PA PB 的斜率分别为 k i , k 2, F (x o , y o ),31 - 42 2 T。
课时跟踪检测(五) 组合与组合数公式1.[多选]下列问题是组合问题的是( )A.10个朋友聚会,每两人握手一次,一共握手多少次?B.平面上有2 020个不同的点,它们中任意三点不共线,连接任意两点可以构成多少条线段?C.集合{a 1,a 2,a 3,…,a n }的含有四个元素的子集有多少个?D.从高三(19)班的54名学生中选出2名学生分别参加校庆晚会的独唱、独舞节目,有多少种选法?解析:选ABC 组合问题与次序无关,排列问题与次序有关,D 项中,选出的2名学生,如甲、乙,其中“甲参加独唱、乙参加独舞”与“乙参加独唱、甲参加独舞”是两个不同的选法,因此不是组合问题,A 、B 、C 均是组合问题. 2.若C 2n =28,则n =( ) A.9 B .8 C.7D .6解析:选B 由C 2n =n ×n -12=28,解得n =8.3.把三张游园票分给10个人中的3人,分法有( ) A.A 310种 B .C 310种 C.C 310A 310种D .30种解析:选B 三张票没区别,从10人中选3人即可,即C 310,故选B. 4.下列计算结果为21的是( ) A.A 24+C 26 B .C 37 C.A 27D .C 27解析:选D C 27=7×62×1=21.5.甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有( ) A.36种 B .48种 C.96种D .192种解析:选C 甲选修2门有C 24=6种选法,乙、丙各有C 34=4种选法.由分步乘法计数原理可知,共有6×4×4=96种选法.6.6个朋友聚会,每两人握手1次,一共握手________次.解析:每两人握手1次,无顺序之分,是组合问题,故一共握手C 26=15次.答案:157.若C 4n >C 6n ,则n 的集合是________.解析:∵C 4n >C 6n ,∴⎩⎪⎨⎪⎧C 4n >C 6n ,n ≥6,即⎩⎪⎨⎪⎧n !4!n -4!>n !6!n -6!,n ≥6⇒⎩⎪⎨⎪⎧n 2-9n -10<0,n ≥6⇒⎩⎪⎨⎪⎧-1<n <10,n ≥6.∵n ∈N *,∴n =6,7,8,9. ∴n 的集合为{6,7,8,9}.答案:{6,7,8,9}8.按ABO 血型系统学说,每个人的血型为A 、B 、O 、AB 四种之一,依血型遗传学,当且仅当父母中至少有一人的血型是AB 型时,子女一定不是O 型,若某人的血型为O 型,则父母血型的所有可能情况有________种.解析:父母应为A 或B 或O,共有C 13·C 13=9种情况. 答案:99.(1)解不等式:2C x -2x +1<3C x -1x +1; (2)计算C 3n13+n +C 3n -112+n +C 3n -211+n +…+C 17-n 2n ; (3)求证:C m n =nn -mC mn -1.解:(1)∵2C x -2x +1<3C x -1x +1, ∴2C 3x +1<3C 2x +1, ∴2×x +1x x -13×2×1<3×x +1x2×1.∴x -13<32,∴x <112,∵⎩⎪⎨⎪⎧x +1≥3,x +1≥2,∴x ≥2,∴2≤x <112,又x ∈N *,∴x =2,3,4,5.∴不等式的解集为{2,3,4,5}.(2)由题意,⎩⎪⎨⎪⎧3n ≤13+n ,17-n ≤2n ,得173≤n ≤132, 又n ∈N *,故n =6.∴原式=C 1819+C 1718+C 1617+…+C 1112 =C 119+C 118+C 117+…+C 112 =19+18+17+…+12=124. (3)证明:∵nn -mC mn -1=nn -m ·n -1!m !n -1-m !=n !m !n -m !=C mn ,∴原式成立.10.在6名内科医生和4名外科医生中,现要组成5人医疗小组送医下乡,依下列条件各有多少种选派方法?(1)有3名内科医生和2名外科医生; (2)既有内科医生,又有外科医生.解:(1)先选内科医生有C 36种选法,再选外科医生有C 24种选法,故有C 36C 24=120种选派方法.(2)既有内科医生,又有外科医生,正面思考应包括四种情况,内科医生去1人,2人,3人,4人,有C 16C 44+C 26C 34+C 36C 24+C 46C 14=246种选派方法.若从反面考虑,则有C 510-C 56=246种选派方法.1.从6名男生和3名女生中选出4名代表,其中必须有女生,则不同的选法种数为( ) A.168 B .45 C.60D .111解析:选D 选出的代表中女生有1,2,3名时,男生相应有3,2,1名,则不同的选法种数为C 13C 36+C 23C 26+C 33C 16=111.2.若A3m=6C4m,则m的值为( )A.6 B.7 C.8 D.9解析:选B 由A3m=6C4m得m!m-3!=6·m!4!m-4!,即1m-3=14,解得m=7.3.某城市纵向有6条道路,横向有5条道路,构成如图所示的矩形道路网(图中黑线表示道路),则从西南角A地到东北角B地的最短路线共有________条.解析:要使路线最短,只能向右或向上走,途中不能向左或向下走.因此,从A地到B地归结为走完5条横线段和4条纵线段.设每走一段横线段或纵线段为一个行走时段,从9个行走时段中任取4个时段走纵线段,其余5个时段走横线段,共有C49C55=126种走法,故从A地到B地的最短路线共有126条.答案:1264.从1,2,3,4,5,6六个数字中任选3个后得到一个由这三个数组成的最小三位数,则可以得到多少个不同的这样的最小三位数?解:从6个不同数字中任选3个组成最小三位数,相当于从6个不同元素中任选3个元素的一个组合,故所有不同的数的个数为C36=6×5×43×2×1=20.5.某市工商局对35种商品进行抽样检查,鉴定结果有15种假货,现从35种商品中选取3种.(1)恰有2种假货在内的不同取法有多少种?(2)至少有2种假货在内的不同取法有多少种?(3)至多有2种假货在内的不同取法有多少种?解:(1)从20种真货中选取1件,从15种假货中选取2件,有C120C215=2 100(种),所以恰有2种假货在内的不同取法有2 100种.(2)选取2件假货有C120C215种,选取3件假货有C315种,共有选取方法C120C215+C315=2 555(种).(3)选取3件的种数有C335,因此有选取方法C335-C315=6 090(种).所以至多有2种假货在内的不同的取法有6 090种.。
课时跟踪检测(五十一)[高考基础题型得分练]1.已知抛物线C :y 2=x 的焦点为F ,A (x 0,y 0)是C 上一点,|AF |=54x 0,则x 0=( )A .4B .2C .1D .8答案:C解析:由y 2=x ,得2p =1,即p =12,因此焦点F ⎝ ⎛⎭⎪⎫14,0,准线方程为l :x =-14.设A 点到准线的距离为d ,由抛物线的定义可知d =|AF |,从而x 0+14=54x 0,解得x 0=1,故选C.2.[2017²山西运城期末]已知抛物线x 2=ay 与直线y =2x -2相交于M ,N 两点,若MN 中点的横坐标为3,则此抛物线方程为( )A .x 2=32yB .x 2=6y C .x 2=-3y D .x 2=3y答案:D解析:设点M (x 1,y 1),N (x 2,y 2).由⎩⎪⎨⎪⎧x 2=ay ,y =2x -2消去y ,得x 2-2ax +2a =0, 所以x 1+x 22=2a2=3,即a =3,因此所求的抛物线方程是x 2=3y .3.设F 为抛物线C :y 2=3x 的焦点,过F 且倾斜角为30°的直线交C 于A ,B 两点,O 为坐标原点,则△OAB 的面积为( )A.334 B .938C.6332D .94答案:D解析:易知抛物线中p =32,焦点F ⎝ ⎛⎭⎪⎫34,0,直线AB 的斜率k =33, 故直线AB 的方程为y =33⎝ ⎛⎭⎪⎫x -34,代入抛物线方程y 2=3x , 整理得x 2-212x +916=0.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=212.由抛物线的定义可得弦长|AB |=x 1+x 2+p =212+32=12,结合图象可得O 到直线AB 的距离d =p 2²sin 30°=38,所以△OAB 的面积S =12|AB |²d =94.4.[2017²吉林长春一模]过抛物线y 2=2px (p >0)的焦点F 且倾斜角为120°的直线l 与抛物线在第一、四象限分别交于A ,B 两点,则|AF ||BF |的值等于( )A.13 B .23 C.34 D .43答案:A解析:记抛物线y 2=2px 的准线为l ′,如图,作AA 1⊥l ′,BB 1⊥l ′,AC ⊥BB 1,垂足分别是A 1,B 1,C , 则有cos ∠ABB 1=|BC ||AB |=|BB 1|-|AA 1||AF |+|BF |=|BF |-|AF ||AF |+|BF |,即cos 60°=|BF |-|AF ||AF |+|BF |=12,由此得|AF ||BF |=13.5.[2017²河南洛阳一模]过抛物线y 2=4x 的焦点F 的直线交抛物线于A ,B 两点,若|AF |=5,则|BF |=( )A.14 B .1 C.54 D .2答案:C解析:由题意,设A (x 1,y 1),B (x 2,y 2), 则|AF |=x 1+1=5⇒x 1=4,y 21=4x 1=16, 不妨取y 1=4,∴直线AB :y =43x -43,代入抛物线方程可得,4x 2-17x +4=0, ∴x 1+x 2=174,即x 2=14,∴|BF |=x 2+1=54.6.[2017²湖北武汉调研]已知抛物线y 2=2px (p >0)上一点M (x 0,4)到焦点F 的距离|MF |=54x 0,则直线MF 的斜率k MF =( ) A .2 B .43 C.34 D .12答案:B解析:由抛物线的定义知,|MF |=x 0+p 2=54x 0,所以p =x 02,所以y 2=2px =x 0x .因为点M (x 0,4)在抛物线上,所以x 20=16,即x 0=4(x 0=-4舍去), 所以M (4,4),F (1,0), 所以k MF =43,故选B.7.[2017²安徽六校素质测试]若抛物线C :y 2=2x cos A (其中角A 为△ABC 的一个内角)的准线过点⎝ ⎛⎭⎪⎫25,4,则cos 2A +sin 2A 的值为( )A .-825B .85 C.825D .1-2625答案:A解析:因为抛物线C :y 2=2x cos A (其中角A 为△ABC 的一个内角)的准线过点⎝ ⎛⎭⎪⎫25,4,所以抛物线C :y 2=2x cos A 的准线方程为x =25,所以cos A 2=-25,即cos A =-45.因为角A 为△ABC 的一个内角, 所以sin A =35.cos 2A +sin 2A =cos 2A +2sin A cos A =⎝ ⎛⎭⎪⎫-452+2³35³⎝ ⎛⎭⎪⎫-45=-825.8.[2017²湖北七校2月联考]已知抛物线的方程为y 2=-4x ,直线l 的方程为2x +y -4=0,在抛物线上有一动点A ,点A 到y 轴的距离为m ,点A 到直线l 的距离为n ,则m +n 的最小值为________.答案:655-1解析:如图,过A 作AH ⊥l ,垂足为H ,AN 垂直于抛物线的准线,垂足为N ,则|AH |+|AN |=m +n +1,连接AF ,则|AF |+|AH |=m+n+1,由平面几何知识,得当A,F,H三点共线时,|AF|+|AH|=m+n+1取得最小值,最小值为F到直线l的距离,即65=655,则m+n的最小值为655-1.9.如图是抛物线形拱桥,当水面在l时,拱桥离水面2 m,水面宽4 m,水位下降1 m 后,水面宽________ m.答案:2 6解析:建立如图所示的平面直角坐标系,A,B是抛物线与水面的交点.据题意,点A的坐标为(-2,-2).设抛物线的方程为x2=ay,把A的坐标代入得a=-2,即抛物线的方程为x2=-2y.当水位下降1(单位:m)时,水面的纵坐标为-3,把y=-3代入抛物线的方程得x=± 6.∴水位下降1 m后,水面宽为2 6 m.10.已知抛物线C的方程为y2=2px(p>0),⊙M的方程为x2+y2+8x+12=0,如果抛物线C的准线与⊙M相切,那么p的值为________.答案:12或4解析:将⊙M 的方程化为一般方程:(x +4)2+y 2=4,圆心坐标为(-4,0),半径r =2,又抛物线的准线方程为x =-p2,故⎪⎪⎪⎪⎪⎪4-p 2=2,解得p =12或4.[冲刺名校能力提升练]1.已知抛物线x 2=4y 上一点A 的纵坐标为4,则点A 到抛物线焦点的距离为( ) A.10 B .4 C.15 D .5答案:D解析:由题意知,抛物线的准线方程为y =-1,所以由抛物线的定义知,点A 到抛物线焦点的距离为5.2.已知抛物线C :y 2=8x 的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若FP →=4FQ →,则|QF |=( )A.72 B .52 C .3 D .2答案:C解析:过点Q 作QQ ′⊥l 交l 于点Q ′,因为FP →=4FQ →,所以|PQ |∶|PF |=3∶4, 又焦点F 到准线l 的距离为4, 所以|QF |=|QQ ′|=3.3.设F 为抛物线y 2=6x 的焦点,A ,B ,C 为该抛物线上三点.若FA →+FB →+FC →=0,则|FA→|+|FB →|+|FC →|=( )A .4B .6C .9D .12答案:C解析:由题意得,抛物线的焦点为F ⎝ ⎛⎭⎪⎫32,0,准线方程为x =-32.设A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),∵FA →+FB →+FC →=0,∴点F 是△ABC 的重心, ∴x 1+x 2+x 3=92.由抛物线的定义可得|FA |=x 1-⎝ ⎛⎭⎪⎫-32=x 1+32, |FB |=x 2-⎝ ⎛⎭⎪⎫-32=x 2+32,|FC |=x 3-⎝ ⎛⎭⎪⎫-32=x 3+32, ∴|FA →|+|FB →|+|FC →| =x 1+32+x 2+32+x 3+32=9.4.过抛物线y 2=4x 的焦点F 的直线交该抛物线于A ,B 两点,O 为坐标原点.若|AF |=3,则△AOB 的面积为________.答案:322解析:由题意设A (x 1,y 1),B (x 2,y 2)(y 1>0,y 2<0),如图所示,|AF |=x 1+1=3,∴x 1=2,y 1=2 2. 设AB 的方程为x -1=ty ,由⎩⎪⎨⎪⎧y 2=4x ,x -1=ty ,消去x 得y 2-4ty -4=0.∴y 1y 2=-4,∴y 2=-2, ∴S △AOB =12³1³|y 1-y 2|=322.5.双曲线y 2a 2-x 24=1(a >0)的离心率为5,抛物线C :x 2=2py (p >0)的焦点在双曲线的顶点上.(1)求抛物线C 的方程;(2)过M (-1,0)的直线l 与抛物线C 交于E ,F 两点,又过E ,F 作抛物线C 的切线l 1,l 2,当l 1⊥l 2时,求直线l 的方程.解:(1)双曲线的离心率e =1+4a2=5,又a >0,∴a =1,双曲线的顶点为(0,1), 又p >0,∴抛物线的焦点为(0,1), ∴抛物线C 的方程为x 2=4y . (2)由题知,直线l 的斜率必存在,设直线l 的方程为y =k (x +1),E (x 1,y 1),F (x 2,y 2), ∵y =14x 2,∴y ′=12x ,∴切线l 1,l 2的斜率分别为x 12,x 22.当l 1⊥l 2时,x 12²x 22=-1,∴x 1x 2=-4.由⎩⎪⎨⎪⎧y =k x +1 ,x 2=4y ,得x 2-4kx -4k =0,∴Δ=(-4k )2-4(-4k )>0, ∴k <-1或k >0.①由根与系数的关系,得x 1x 2=-4k =-4, ∴k =1,满足①,即直线的方程为x -y +1=0.6.[2017²广东汕尾调研]抛物线C 关于y 轴对称,它的顶点在坐标原点,并且经过点(-22,2).(1)求抛物线C 的方程;(2)过抛物线C 的焦点作直线l 交抛物线C 于M (x 1,y 1),N (x 2,y 2)两点,且x 1<x 2,y 1≠y 2,点M 与点P 关于y 轴对称.求证:直线PN 恒过定点,并求出该定点的坐标.(1)解:由抛物线C 关于y 轴对称,可设抛物线方程为x 2=2py (p >0).因为抛物线过点(-22,2), 所以8=4p ,解得p =2. 故抛物线C 的方程为x 2=4y .(2)证明:由(1)知,C 的焦点为(0,1).因为抛物线开口向上,直线l 交抛物线C 于M (x 1,y 1),N (x 2,y 2)两点,且x 1<x 2,y 1≠y 2, 所以l 的斜率一定存在,设为k ,则直线l 方程为y =kx +1(k ≠0). 因为M 与P 关于y 轴对称,所以P (-x 1,y 1).联立方程⎩⎪⎨⎪⎧x 2=4y ,y =kx +1,消去y ,得x 2-4kx -4=0,所以⎩⎪⎨⎪⎧x 1+x 2=4k ,x 1x 2=-4.所以x 2-x 1= x 1+x 2 2-4x 1x 2=4k 2+1,y 1+y 2=k (x 1+x 2)+2=4k 2+2.所以k PN =y 2-y 1x 2+x 1=k x 2-x 1 x 2+x 1=4k k 2+14k=k 2+1.又PN 的中点为⎝⎛⎭⎪⎫x 2-x 12,y 1+y 22,即(2k 2+1,2k 2+1),所以直线PN 的方程为y -(2k 2+1)=k 2+1(x -2k 2+1),即y =k 2+1x -1. 故直线PN 恒过定点(0,-1).。