ch1-2&3 描述质点运动的物理量及两种类型
- 格式:ppt
- 大小:340.50 KB
- 文档页数:12


习题及参考解答(Ch1-2)原教科书上个别题目有误,此处已作修改,此外题号也有所变更,请注意。
第1章习题:1-1两种产品x 和y 唯一需要的要素投入是劳动L 。
一单位x 产品需要的劳动投入量是8,一单位y 产品需要的劳动投入量是1。
假设可投入的劳动量总共为48, 1) 写出生产可能集Z 的代数表达式; 2) 写出生产(隐)函数; 3) 在(,)x y 平面上显示生产边界。
1-2试画出Leontief 生产函数121122(,)min{,}f x x x x b =的等产量线。
1-3 对Cobb-Douglas 生产函数1212(,)f x x A x x a b= (0,,0A a b >>)1) 证明1122,MP y MP y x a b ==; 2) 求技术替代率TRS 12;3) 当y 或21x 变化时,TRS 12如何随之变化? 4) 画出等产量曲线。
1-4 对CES 生产函数11122()y A x x aa a d d =+, 121,0A d d +=>,1) 证明边际产出1[]i i i MP A y x a a d -=; 2) 求技术替代率TRS 12;3) 当y 或21x x 变化时,TRS 12如何随之变化? 4) 证明技术替代弹性1)s a =-。
1-5 证明:CES 生产函数在1a =时变为线性函数,在0a ®时变为Cobb-Douglas 函数,在a ? 时变为Leontief 生产函数。
1-61) 试证明欧拉定理:对任何k 次(0k ³)齐次生产函数()f x ,总有()i i ifkf x x ¶=¶åx2) 用生产函数1212(,)f x x A x x a b= (0,,0A a b >>)验证欧拉定理。
1-7 下列生产函数的规模收益状况如何?1) 线性函数:1212(,),,0f x x ax bx a b =+>;2) Leontief 生产函数; 3) Cobb-Douglas 生产函数; 4) CES 生产函数。

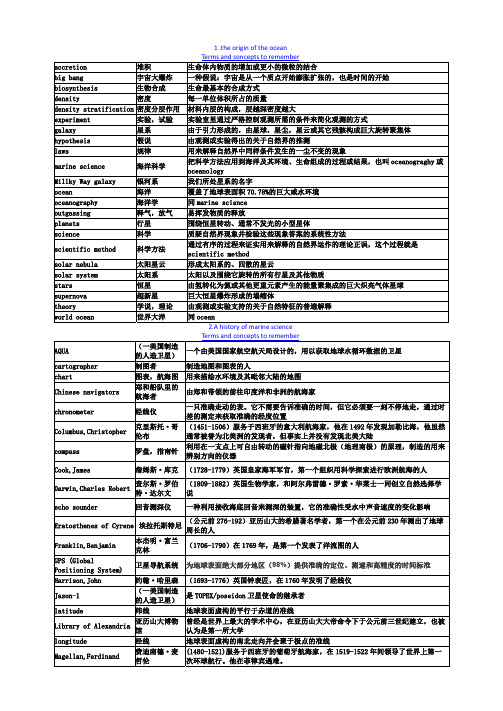
1 .the origin of the oceanTerms and concepts to rememberaccretion 堆积 生命体内物质的增加或更小的微粒的结合big bang 宇宙大爆炸 一种假说:宇宙是从一个质点开始膨胀扩张的,也是时间的开始 biosynthesis 生物合成 生命最基本的合成方式density 密度 每一单位体积所占的质量density stratification 密度分层作用 材料内层的构成,层越深密度越大experiment 实验,试验 实验室里通过严格控制观测所需的条件来简化观测的方式galaxy 星系 由于引力形成的,由星球,星尘,星云或其它残骸构成巨大旋转聚集体 hypothesis 假说 由观测或实验得出的关于自然界的推测laws 规律 用来解释自然界中同样条件发生的一尘不变的现象marine science 海洋科学 把科学方法应用到海洋及其环境、生命组成的过程或结果,也叫oceanograghy或oceanologyMillky Way galaxy 银河系 我们所处星系的名字ocean 海洋 覆盖了地球表面积70.78%的巨大咸水环境 oceanography 海洋学 同marine scienceoutgassing 释气,放气 易挥发物质的释放planets 行星 围绕恒星转动、通常不发光的小型星体science 科学 质疑自然界现象并检验这些现象答案的系统性方法scientific method 科学方法 通过有序的过程来证实用来解释的自然界运作的理论正误,这个过程就是scientific methodsolar nebula 太阳星云 形成太阳系的、四散的星云solar system 太阳系 太阳以及围绕它旋转的所有行星及其他物质stars 恒星 由氢转化为氦或其他更重元素产生的能量聚集成的巨大炽亮气体星球 supernova 超新星 巨大恒星爆炸形成的塌缩体theory 学说,理论 由观测或实验支持的关于自然特征的普遍解释world ocean 世界大洋 同ocean2.A history of marine scienceTerms and concepts to rememberAQUA (一美国制造的人造卫星)一个由美国国家航空航天局设计的,用以获取地球水循环数据的卫星cartographer 制图者 制造地图和图表的人chart 图表,航海图 用来描绘水环境及其毗邻大陆的地图Chinese navigators 郑和船队里的航海者由郑和带领的前往印度洋和非洲的航海家chronometer 经线仪 一只准确走动的表。


第二讲Ⅰ.授课题目(章节)§1.1 数列的极限 §1.3 函数的极限 Ⅱ.教学目的与要求1. 理解数列极限与函数极限的概念;明确极限是描述变量的变化趋势;了解极限的X N ---εδεε,,定义中的X N ,,,δε的含义2. 理解极限的性质 Ⅲ.教学重点与难点:重点:数列极限与函数极限的概念 难点:极限的定义 Ⅳ.讲授内容:§1.1数列极限的定义 一. 列极限的定义定义:设{}n x 为一数列,如果存在常数a ,对于任意给定的正数ε(不论它多么小),总存在正整数N ,使得n>N 时,不等式ε<-a x n 都成立,那么就常数a 是数列{}n x 的极限,或者称数列{}n x 收敛与a,记为)(lim∞→→=∞→n a x a nn n x 或.如果不存在这样的常数a,就说数列{}n x 没有极限,或者说数列{}n x 是 发散的,习惯上也说nx n ∞→lim 不存在.例1.证明数列2, ,)1(,,43,34,211nn n --+的极限是1.证:a x nnn a x n n n -=--+=--为了使,11)1(1小于任意给定的正数ε,只要εε111><nn或.所以,,1,0⎥⎦⎤⎢⎣⎡=>∀εεN 取则当n>N 时,就有n n n 1)1(--+<ε,即1)1(1lim=-+-∞→nn n n例2.设,1<q 证明等比数列 ,,,,,112-n q q q 的极限是0. 证:)1,0<>∀εε(设,因为,0011--=-=-n n n qqx 要使εε<<--1,0n n qx 只要取自然对数,得qn q q q n ln ln 1,0ln ,1.ln ln )1(εε+><<<-故因,取N n q N <⎥⎥⎦⎤⎢⎢⎣⎡+=则当,ln ln 1ε时,就有0lim ,011=<--∞→-n n n q q 即ε.二. 敛数列的性质定理1(极限的唯一性):如果{}n x 收敛,则它的极限唯一证明 用反证法.假设同时有2.,b a b a b x a x n n -=<→→ε取且及.因为11,,lim N n N a x n n <∃=∞→当正整数故时,不等式2a b a x n -<-都成立.同理,因为22,,lim N n N b x n n <∃=∞→当正整数故时,不等式2a b b x n -<-都成立.取{}21,max N N N =(这式子表示21N N N 和是中较大的那个数),则当N n <时,(2)式及(3)式会同时成立.但由(2)式有,2b a x n +<由(3)式有,2b a x n +>,这是不可能的.这矛盾证明了本定理的断言. 数列的有界性概念定义:对于数列{}n x ,如果存在着正数M,使得对于一切n x 都满足不等式M x n ≤,则称数列{}n x 是有界的;如果这样的正数M 不存在,就说数列{}n x 是无界的.定理2(收敛数列的有界性) 如果{}n x 收敛,则数列{}n x 一定有界 定理3:(收敛数列的保号性)如果a x n n =∞→lim 且a>0(或a<0)那么存在正整数N>0,当n>N 时,都有n x >0(或n x <0)推论:如果{}n x 从某项起有n x ≥0(或n x ≤0)且)0(0,lim ≤≥=∞→a a a x n n 或则子数列的概念:在数列{}n x 中任意抽取无限多项并保持这些项在原数列{}n x 中的先后次序,这样得到的一个数列称为原数列{}n x 的子数列(或子列).设在数列{}n x 中,第一次抽取1n x ,第二次在1n x 后抽取2n x ,第三次在2n x 后抽取⋅⋅⋅3n x ,这样无休止地抽取下去,得到一个数列1n x ,2n x , ,kn x ,这个数列{}n x 就是{}n x 的一个子数列.定理4.(收敛数列与其子数列间的关系)如果{}n x 收敛于a ,则它的任一子数列也收敛,且极限也是a §1.3 函数的极限 一、函数极限的定义1.自变量趋于有限值时函数的极限定义1:设函数0)(x x f 在点的某一去心邻域内有定义.如果存在常数A,对于任意给定的正数ε(不论它多么小),总存在正数δ,使得当x 满足不等式δ<-<00x x 时,对应的函数值)(x f 都满足不等式ε<-A x f )(,那么常数A 就叫做函数0)(x x x f →当时的极限,记作)()()(lim 00x x A x f A x f x x →→=→当或.例1. 证明211lim21=--→x x x证明:这里,函数在点x=1是没有定义的饿,但是函数当1→x 是的极限存在或不存在与它并无关系.事实上,εε<-->∀11,02x x 不等式约去非零因子x-1,就化为ε<-=-+121x x ,因此,只要取εδ=,那么当ε<-<10x 时,就有ε<---2112x x所以 211lim21=--→x x x单侧极限的概念:上述0x x →时函数)(x f 的极限概念中,x 是既从0x 的左侧也从0x 的右侧趋于0x 的.但有时只能或只需考虑x 仅从0x 的左侧趋于0x (记作-→0x x )的情形,或x 仅从0x 的右侧趋于0x (记作+→0x x )的情形.在-→0x x 的情形,x 在0x 的左侧,0x x <.在A x f x x =→)(lim 0的定义中,把δ<-<00x x 改为00x x x <<-δ,那么A 就叫做函数)(x f 当0x x →时的左极限,记作A x f x x =-→)(lim 0或A x f =-)(0.类似的,在A x f x x =→)(lim 0的定义中,把δ<-<00x x 改为δ+<<00x x x ,那么A 就叫做函数)(x f 当0x x →时的右极限,记作A x f x x =+→)(lim 0或A x f =+)(0.右极限与左极限统称为单侧极限.解:仿例3可证当0→x 时)(x f 的左极限1)1(lim )(lim 0-=-=--→→x x f x x x而右极限1)1(lim )(lim 0=+=++→→x x f x x x ,因为左极限和右极限存在但不相等,所以)(lim 0x f x →不存在.2.自变量趋于无穷大时函数的极限定义2:设函数)(x f 当x 大于某一正数时有定义.如果存在常数A,对于任意给定的正数ε(不论它多么小),总存在着正数X,使得当x 满足不等式X x >时,对应的函数值)(x f 都满足不等式ε<-A x f )(,那么常数A 就叫做函数)(x f 当∞→x 时的极限,记作A x f x =∞→)(l i m 或)(当∞→→x A x f )(.定义2可简单地表达为:A x f x =∞→)(lim X x X >>∃>∀⇔当,0,0ε时有ε<-A x f )(.例3:证明.01lim=∞→xx证:X x X >>∃>∀,当要证0,0ε时,不等式ε<-01x成立.因这个不等式相当于ε<x1或ε1>x由此可知,如果取ε1=X ,那么当<-=>01,1xX x 不等式时εε成立.这就证明了.01lim=∞→x x一. 数极限的性质:定理1(函数极限的唯一性):如果)(lim 0x f x x →存在,则这极限必唯一定理2(函数极限的局部有界性):如果A x f x x =→)(lim 0,那么存在常数M>0和0>δ,使得当M x f x x ≤<-<)(时,有δ00.证:因为)(lim 0x f x x →=A,所以取ε=1,则当,0>∃δδ<-<00x x 时,有1)()(1+<+-≤⇒<-A A A x f x f A x f )(,记,1+=A M 则定理2就获证明.定理3(函数极限的局部保号性):如果A x f x x =→)(lim 0,而且)0(0<>A A 或,那么存在常数0>δ,使得当δ<-<00x x 时,有00)(<>)((或x f x f ).如果)(lim 0x f x x →=A ,而且A>0(或A<0),那么存在常数ξ>0,使得当ξ<-<00x x 时,有f (x )>0 ( 或f (x ) <0 )推论:如果在0x 的某去心邻域内)0)((0)(≤≥x f x f 或而且A x f x x =→)(lim 0,那么)0(0≤≥A A 或,定理4(函数极限与数列极限的关系)如果极限)(lim 0x f x x →存在,{}n x 为函数f (x)的定义域内任意收敛于0x 的数列,且满足:)(0+≠∈N n x x n ,那么相应的函数列{})(n x f 必收敛,且)(lim )(lim 0x f x f x x n n →∞→=Ⅴ. 小结与提问:小结:极限定义是本讲的难点,必须结合极限的直观描述和集合解释弄懂其本质。
第1章大气概况一.简答题1、简述大气的主要成分,并说明二氧化碳、臭氧和水汽的分布于作用。
2、简述大气的垂直分层概况。
3、简述对流层的主要特征。
二.选择题1.1 大气概述1.天气是指某一特定区域:A.在较短时间内各种气象要素的综合表现B.在较长时间内各种气象要素的综合表现C.气象要素的多年平均特征(包括极值)D.气象要素的一年平均特征(包括极值)2.表征大气状态的物理量和物理现象的气象术语称为:A.天气B.气候C.气象要素D.天气系统3.气候是指某一特定区域:A.在较短时间内各种气象要素的综合表现B.气象要素的多年平均特征(包括极值)C.气象要素的一年平均特征(包括极值)D.天气形势4.下列属于气象要素的是:A 风云雾霜沙尘暴B 气压高气压台风C 风云雨冷峰暖锋D 气温气压冷锋暖锋5.气象要素主要包括:I、气压、气温; II、雾、气团、锋面; III、相对湿度、沙尘暴; IV、风、云、能见度; V、温度、高压、低压;VI、雨、雪、雷暴A.I、III、IV、VI B. I、II、IV ~VI C.II~IV、VI D. II、IV~VI1.2 大气的组成1.大气的主要成分为:A.氮气、氧气、二氧化碳、惰性气体 B.干洁空气、水汽、气溶胶质粒C.氮气、氧气、二氧化、水汽 D. 氮气、氧气、二氧化碳、惰性气体、水汽2.干洁空气中的主要成分为:A.氮气、氧气、二氧化碳 B. 氮气、氧气、氩气C.氩气、氧气、二氧化 D. 氮气、氧气、氩气、二氧化碳、3.在气压相同的情况下,密度较小的空气是:A.暖湿空气B.冷湿空气C.干热空气D.干冷空气4.在气压相同的情况下,密度较大的空气是:A.暖湿空气B.冷湿空气C.干热空气D.干冷空气5.在气压相同的情况下,密度较小的空气是:A.暖湿空气B.冷湿空气C.干热空气D.干冷空气6.在气压相同的情况下,密度较大的空气是:A.暖湿空气B.冷湿空气C.干热空气D.干冷空气7.影响天气及气候变化的主要大气成分包括:A.二氧化碳、臭氧和惰性气体B.氮气、二氧化碳和惰性气体C.二氧化碳、臭氧和水汽D.氧气、臭氧和惰性气体8.大气中能够透过太阳短波辐射、强烈吸收和放射长波辐射的主要气体成分为:A.臭氧B.氮气C.氧气D.二氧化碳9.在大气成分中,主要吸收太阳紫外线的气体成分为:A.臭氧B.二氧化碳C.氧气D.氮气10.在自然界的温度和压力条件下,哪种大气成份能在气态、液态和固态三者之间互相转化(即发生相变的唯一大气成份)?A.氮气B.氧气C.水汽D.二氧化碳11.在下列大气成分中,能产生温室效应的大气成分是:A.氧气 B.氮气 C.氩气 D.二氧化碳12.通常在90千米高度以下,可将干空气作为单一成分的理想气体处理,其平均分子量为:A.16摩尔B.18摩尔C.29摩尔D.32摩尔13.近地面层空气的平均密度为:A.1.01~1.03克/厘米3B.1.00克/厘米3C.1293克/厘米3D.0.86~0.92克/厘米314.从地面向上随着高度的增加,空气密度:A.缓慢递减B.迅速递减C.缓慢递增D.迅速递增15.从高空到地面向下随着高度的减小,空气密度:A.缓慢递减B.迅速递减C.缓慢递增D.迅速递增16.在自然条件下能发生相变的唯一大气成分是:A.氧 B.氮 C.水汽 D.氩17.一般而言,大气中的水汽分布A 低空多于高空B 海洋多于陆地,低纬多于高纬C 夏季多于冬季,白天多于夜间D ABC都对18.在水汽相变过程中,大气固体杂质可以充当:A.凝结核,不利于相变过程发生B.催化剂,不利于水汽凝结C.凝结核,有利于相变过程发生D.催化剂,有利于水汽凝结19.对大气温度有较大影响的大气成分:Ⅰ.氮气;Ⅱ.臭氧;Ⅲ.二氧化碳;Ⅳ.氧气;Ⅴ.水汽;Ⅵ.氢气。
§1—2 原子光谱一. 光谱光谱:电磁辐射的强度随频率(或波长)的分布 吸收光谱:具有连续光谱分布的光,通过吸收介质之后,某些波段或某 些波长成分的光能量被介质部分或全部吸收,原来连续分布的光谱中将 出现一些暗区或暗线。
发射光谱与吸收光谱:物质在较高温度下的发射光谱与在较低温度下的吸 收光谱对应。
前者表现为暗背景下的一组亮带或亮线,后者则表现为 连续光谱下的一组暗带或暗线。
带状光谱:由于物质分子或原子间相互作用的影响,一般情况下,流体、 固体物质的吸收波段很宽,吸收光谱为具有一定宽度的带状分布。
线状光谱:稀薄气体的吸收波段很窄,吸收光谱为一系列明锐的暗线。
二. 氢原子光谱氢原子受到激发后,可以发出线状光谱,光谱从远红外区延伸到紫外区。
其中可见光区最著名的光谱线有以下四条名称 波长(nm) 颜色Hδ 410.17 紫Hγ 434.05 青Hβ 486.13 深绿Hα 656.28 红氢的Balmer线系1885年Balmer发现,对于已知的14条氢的光谱线,可以用一个简单的 公式表示其波长分布n2 λn = B 2 , n −4其中 B = 364 .56 nmn = 3,4,5,LBalmer公式 线系限波长n → ∞ , λ ∞ = B = 364 .56 nm1896年里德伯(Rydberg)将Balmer公式改写用波数表示2 1 n −4 ⎡1 1⎤ ~ ν = = = R H ⎢ 2 − 2 ⎥, 2 λ B n ⎣2 n ⎦1n = 3,4,5,LHδ HγHβHα连续光谱区Balmer线系λ氢原子的光谱线系氢原子的其它谱线系• Lyman系 • Balmer系 • Paschen系 • Brackett系1 1 ~ ν = RH [ 2 − 2 ], n = 2,3,4, L 1 n1 1 ~ ν = RH [ 2 − 2 ], n = 3,4,5,L 2 n 1 1 ~ ν = RH [ 2 − 2 ], n = 4,5,6, L 3 n1 1 ~ ν = RH [ 2 − 2 ], n = 5,6,7,L 4 n1 1 ~ ν = RH [ 2 − 2 ], n = 6,7,8,L 5 n• Pfund系4 RH = = 1.0967758 × 107 m −1 B里德伯常量氢原子的谱线系的组合法则1 1 ~ ν = RH [ 2 − 2 ] m n其中m = 1,2,3, Ln = m + 1, m + 2, m + 3, L对于其中的每一个m,n=m+1, m+2, ……可以构成一个谱线系 上述方法称为“组合法则”,即每一条光谱线的波数可以表示为两个与 整数有关的谱项之差。