下载文档原格式
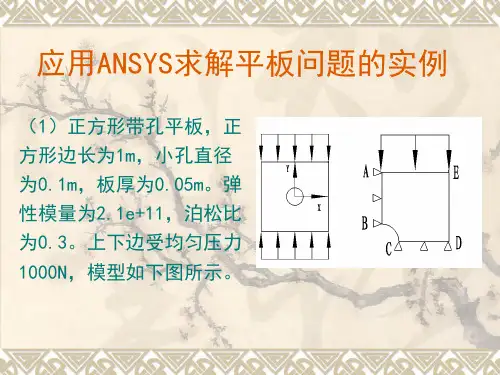
第二章 弹性力学平面问题有限单元法§2-1 三角形单元(triangular Element)三角形单元是有限元分析中的常见单元形式之一，它的优点是:①对边界形状的适应性较好，②单刚形式及其推导比较简单,故首先介绍之。
一、结点位移和结点力列阵设右图为从某一结构中取出的一典型三角形单元。
在平面应力问题中，单元的每个结点上有沿x 、y 两个方向的力和位移，单元的结点位移列阵规定为： 相应结点力列阵为: (式2-1-1)二、单元位移函数和形状函数前已述及，有限单元法是一种近似方法，在单元分析中，首先要求假定（构造）一组在单元内有定义的位移函数作为近似计算的基础。
即以结点位移为已知量，假定一个能表示单元内部（包括边界）任意点位移变化规律的函数。
构造位移函数的方法是：以结点(i,j,m)为定点。
以位移(u i ,v i ,…u m v m )为定点上的函数值，利用普通的函数插值法构造出一个单元位移函数。
在平面应力问题中，有u,v 两个方向的位移,若假定单元位移函数是线性的,则可表示成:(,)123u u x y x y ααα==++546(,)v v x y x y ααα==++ (2-1-2)a{}⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=m j i m ed d d d m j j i v u v u v u i {}ii j j m X Y X (2-1-1)Y X Y iej m m F F F F ⎧⎫⎪⎪⎪⎪⎧⎫⎪⎪⎪⎪⎪⎪==⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎪⎪⎪⎪⎪⎪⎩⎭式中的6个待定常数α1 ,…, α6 可由已知的6个结点位移分量(3个结点的坐标)确定。
将3个结点坐标(x i,y i ),(x j,y j ),(x m,y m )代入上式得如下两组线性方程:123i i i u x y ααα=++123j j j u x y ααα=++ (a)123m m m u x y ααα=++和546i i i v x y ααα=++546j j j v x y ααα=++ (b)546m m m v x y ααα=++利用线性代数中解方程组的克来姆法则,由(a)可解出待定常数1α 、2α 、3α :11A Aα=22A Aα=33A Aα=式中行列式:1i i i j j j m m m u x y A u x y u x y =2111i i j j m mu y A u y u y =3111i i j jm mx u A x u x u =2111i i j j m mAx y A x y x y ==A 为△ijm 的面积,只要A 不为0,则可由上式解出:11()2m m i ij j a u a u a u A α=++ 21()2m m i ij j bu b u b u A α=++ （C ）31()2m mi i j j c u c u c u A α=++式中:m m i j j a x y x y =- m m j i i a x y x y =- m i j j i a x y x y =-m i j b y y =- m j i b y y =- m i j b y y =- （d ）m i j c x x =- m j i c x x =- m j i c x x =-为了书写方便，可将上式记为:m m i j i a x y x y =-m ij by y =- (,,)i j mm i jc x x =-(,,)i j m表示按顺序调换下标,即代表采用i,j,m 作轮换的方式便可得到(d)式。
Mmm3 弹性力学平面问题的有限元法本章包括以下的内容：3.1弹性力学平面问题的基本方程3.2单元位移函数3.3单元载荷移置3.4单元刚度矩阵3.5单元刚度矩阵的性质与物理意义3.6整体分析3.7约束条件的处理3.8整体刚度矩阵的特点与存储方法3.9方程组解法3.1弹性力学平面问题的基本方程弹性力学是研究弹性体在约束和外载荷作用下应力和变形分布规律的一门学科。
在弹性力学中针对微小的单元体建立基本方程，把复杂形状弹性体的受力和变形分析问题归结为偏微分方程组的边值问题。
弹性力学的基本方程包括平衡方程、几何方程、物理方程。
弹性力学的基本假定如下：1）完全弹性，2）连续，3）均匀，4）各向同性，5）小变形。
3.1.1基本变量弹性力学中的基本变量为体力、面力、应力、位移、应变，各自的定义如下。
体力体力是分布在物体体积内的力，例如重力和惯性力。
面力面力是分布在物体表面上的力，例如接触压力、流体压力。
应力物体受到约束和外力作用，其内部将产生内力。
物体内某一点的内力就是应力。
图3.1如图3.1假想用通过物体内任意一点p 的一个截面mn 将物理分为Ⅰ、Ⅱ两部分。
将部分Ⅱ撇开，根据力的平衡原则，部分Ⅱ将在截面mn 上作用一定的内力。
在mn 截面上取包含p 点的微小面积A ∆，作用于A ∆面积上的内力为Q ∆。
令A ∆无限减小而趋于p 点时，Q ∆的极限S 就是物体在p 点的应力。
S A QA =∆∆→∆0lim应力S 在其作用截面上的法向分量称为正应力，用σ表示；在作用截面上的切向分量称为剪应力，用τ表示。
显然，点p 在不同截面上的应力是不同的。
为分析点p 的应力状态，即通过p 点的各个截面上的应力的大小和方向，在p 点取出的一个平行六面体，六面体的各楞边平行于坐标轴。
图3.2将每个上的应力分解为一个正应力和两个剪应力，分别与三个坐标轴平行。
用六面体表面的应力分量来表示p 点的应力状态。
应力分量的下标约定如下：第一个下标表示应力的作用面，第二个下标表示应力的作用方向。
xy τ，第一个下标x 表示剪应力作用在垂直于X 轴的面上，第二个下标y 表示剪应力指向Y 轴方向。
正应力由于作用表面与作用方向垂直，用一个下标。
x σ表示正应力作用于垂直于X 轴的面上，指向X 轴方向。
应力分量的方向定义如下：如果某截面上的外法线是沿坐标轴的正方向，这个截面上的应力分量以沿坐标轴正方向为正；如果某截面上的外法线是沿坐标轴的负方向，这个截面上的应力分量以沿坐标轴负方向为正。
剪应力互等：xz zx zy yz yx xy ττττττ===,,物体内任意一点的应力状态可以用六个独立的应力分量x σ、y σ、z σ、xy τ、yz τ、zxτ来表示。
位移位移就是位置的移动。
物体内任意一点的位移，用位移在x ，y ，z 坐标轴上的投影u 、v 、w 表示。
应变物体的形状改变可以归结为长度和角度的改变。
各线段的单位长度的伸缩，称为正应变，用ε表示。
两个垂直线段之间的直角的改变，用弧度表示，称为剪应变，用γ表示。
物体内任意一点的变形，可以用zx yz xy z y x γγγεεε、、、、、六个应变分量表示。
3.1.2平面应力和平面应变问题弹性体在满足一定条件时，其变形和应力的分布规律可以用在某一平面内的变形和应力的分布规律来代替，这类问题称为平面问题。
平面问题分为平面应力问题和平面应变问题。
1）平面应力问题设有很薄的等厚薄板，只在板边上受到平行于板面并且不沿厚度变化的面力，体力也平行于板面且不沿厚度变化。
图3.3设板的厚度为t ，在板面上：()02=±=tz z σ，()02=±=t z zx τ， ()02=±=t z zy τ由于平板很薄，外力不沿厚度变化，因此在整块板上有，0=z σ，0=zx τ， 0=zy τ剩下平行于XY 平面的三个应力分量xy y x τσσ、、未知。
2）平面应变问题设有很长的柱形体，支承情况不沿长度变化，在柱面上受到平行于横截面而且不沿长度变化的面力，体力也如此分布。
图3.4以柱体的任一横截面为XY 平面，任一纵线为Z 轴。
假定该柱体为无限长，则任一截面都可以看作对称面。
由对称性，0=zx τ，0=zy τ，0=w由于没有Z 方向的位移，Z 方向的应变0=z ε。
未知量为平行于XY 平面的三个应力分量xy y x τσσ、、，物体在Z 方向处于自平衡状态。
3.1.3平衡方程弹性力学中，在物体中取出一个微小单元体建立平衡方程。
平衡方程代表了力的平衡关系，建立了应力分量和体力分量之间的关系。
对于平面问题，在物体内的任意一点有，00=+∂∂+∂∂=+∂∂+∂∂Y xy X yx xyy yxx τστσ（3-1）3.1.4几何方程由几何方程可以得到位移和变形之间的关系。
对于平面问题，在物体内的任意一点有，xv y u y vx u xy y x ∂∂+∂∂=∂∂=∂∂=γεε （3-2）刚体位移由位移u=0，v=0可以得到应变分量为零，反过来，应变分量为零则位移分量不为零。
应变分量为零时的位移称为刚体位移。
刚体位移代表了物体在平面内的移动和转动。
由 000=∂∂+∂∂=∂∂=∂∂xv y u y vx u可以得到刚体位移为以下形式，xv v y u u ωω+=-=00由0,0=∂∂=∂∂yvx u 可得， )(),(21x f v y f u ==将21,f f 代入0=∂∂+∂∂xvy u 可得， ω==-dxx df dy y df )()(21积分后得到，xv x f y u y f ωω+=-=0201)()(得到位移分量，xv v y u u ωω+=-=00当0,0,000==≠ωv u 时，物体内任意一点都沿x 方向移动相同的距离，可见0u 代表物体在x 方向上的刚体平移。
当0,0,000=≠=ωv u 时，物体内任意一点都沿y 方向移动相同的距离，可见0v 代表物体在y 方向上的刚体平移。
当0,0,000≠==ωv u 时，可以假定0>ω，此时的物体内任意一点P （x ，y ）的位移分量为，x v y u ωω=-=,P 点位移与y 轴的夹角为α，θωωαtg xyx y tg ===P 点合成位移为，r y x x y v u ωωωω=+=+-=+222222)()(r 为P 点到原点的距离，可见ω代表物体绕z 轴的刚体转动。
3.1.5物理方程弹性力学平面问题的物理方程由广义虎克定律得到。
1）平面应力问题的物理方程()y x x Eμσσε-=1()x y y Eμσσε-=1（3-3）xy xy Eτμγ)1(2+=平面应力问题有，0=z σ()y xz Eσσμε+-=2）平面应变问题的物理方程⎪⎪⎭⎫ ⎝⎛---=y x x Eσμμσμε112⎪⎪⎭⎫ ⎝⎛---=x y y Eσμμσμε112（3-4）xy xy Eτμγ)1(2+=平面应变问题有，0=z ε()y x z σσμσ+=在平面应力问题的物理方程中，将E 替换为21μ-E 、μ替换为μμ-1，可以得到平面应变问题的物理方程；在平面应变问题的物理方程中，将E 替换为2)1()21(μμ++E 、μ替换为μμ+1，可以得到平面应力问题的物理方程。
图3.5求解弹性力学平面问题，可以归结为在任意形状的平面区域Ω内已知控制方程、在位移边界u S 上约束已知、在应力边界σS 上受力条件已知的边值问题。
然后以应力分量为基本未知量求解，或以位移作为基本未知量求解。
如果以位移作为未知量求解，求出位移后，由几何方程可以计算出应变分量，得到物体的变形情况；再由物理方程计算出应力分量，得到物体的内力分布，就完成了对弹性力学平面问题的分析。
3.2单元位移函数根据有限元法的基本思路，将弹性体离散成有限个单元体的组合，以结点的位移作为未知量。
弹性体内实际的位移分布可以用单元内的位移分布函数来分块近似地表示。
在单元内的位移变化可以假定一个函数来表示，这个函数称为单元位移函数、或单元位移模式。
对于弹性力学平面问题，单元位移函数可以用多项式表示，...26524321++++++=y a xy a x a y a x a a u ...26524321++++++=y b xy b x b y b x b b v（3-5）多项式中包含的项数越多，就越接近实际的位移分布，越精确。
具体取多项，由单元形式来确定。
即以结点位移来确定位移函数中的待定系数。
图3.6如图3.6所示的3结点三角形单元，结点I 、J 、M 的坐标分别为),(i i y x 、),(j j y x 、),(m m y x ，结点位移分别为i u 、i v 、j u 、j v 、m u 、m v 。
六个节点位移只能确定六个多项式的系数，所以3结点三角形单元的位移函数如下，⎭⎬⎫++=++=y a x a a y a x a a u 654321v（3-6）将3个结点上的坐标和位移分量代入公式（3-6）就可以将六个待定系数用结点坐标和位移分量表示出来。
将水平位移分量和结点坐标代入（3-6）中的第一式，mm m j j j i i i y a x a a u y a x a a u y a x a a u 321321321++=++=++= 写成矩阵形式，⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧321111a a a y xy x y x u u u m m j j i i m j i（3-7）令[]T 111=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡m mj j i iy x y xy x ，则有[]⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-m j i u u u a a a 1321T （3-8）T]T []T [*1=- A 2T =，A 为三角形单元的面积。
[T]的伴随矩阵为，[]T*T ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---------=i j ji i j j i m i i m mi i m j m m j jm m j x x y y y x y x x x y y y x y x x x y y y x y x （3-9）令 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=m ji m ji m j i m mmj jj i i ic c c b b b a a a c b a c b a c b a T*]T [ （3-10）则 ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧m j i m jim j im j i u u u c c c b b b a a a A a a a 21321（3-11）同样，将垂直位移分量与结点坐标代入公式（3-6）中的第二式，可得，⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧m j i m jim j im j i v v v c c c b b b a a a A a a a 21654（3-12）将（3-11）、（3-12）代回（3-6）整理后可得，])()()[(21m m m m j j j j i i i i u y c x b a u y c x b a u y c x b a Au ++++++++= ])()()[(21m m m m j j j j i i i i v y c x b a v y c x b a v y c x b a Av ++++++++=令)(21y c x b a AN i i i i ++=（下标i ，j ，m 轮换）可得⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡=⎭⎬⎫⎩⎨⎧m m j j i i m jim j i v u v u v u N N N N N N v u 0000 （3-13）单元内的位移记为{}⎭⎬⎫⎩⎨⎧=v u f 单元的结点位移记为{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=m m j j ii m j i ev u v u v u δδδδ 单元内的位移函数可以简写成，{}[]{}e N f δ=（3-14）把[N]称为形态矩阵，N i 称为形态函数。
