受控源电路的分析演示课件

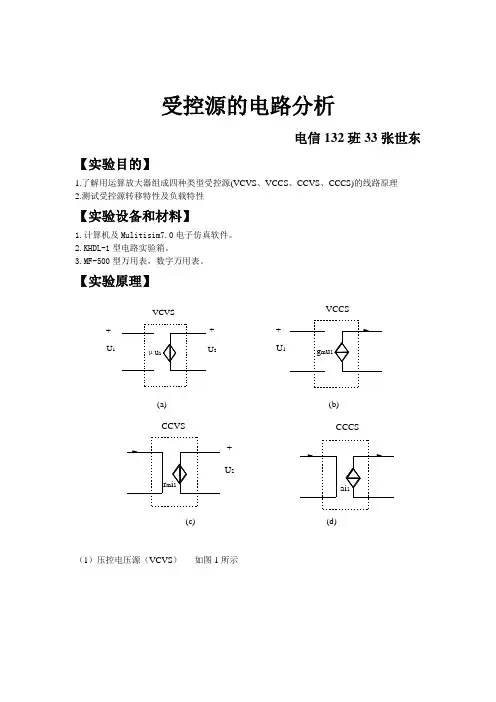
受控源的电路分析电信132班33张世东【实验目的】1.了解用运算放大器组成四种类型受控源(VCVS、VCCS、CCVS、CCCS)的线路原理2.测试受控源转移特性及负载特性【实验设备和材料】1.计算机及Mulitisim7.0电子仿真软件。

2.KHDL-1型电路实验箱。

3.MF-500型万用表，数字万用表。

【实验原理】VCVSU1 + _2+__+U1VCCS(a) (b)CCVS_+U2CCCS(c) (d)（1）压控电压源（VCVS）如图1所示U1+_图1由于运放的输入“虚短”路特性，即 1u u u n p == 所以有 2122R u R u i n == 又因运放内阻为∞，有21i i = 因此121212121222112)1()()(u R R R R R u R R i R i R i u +=+=+=+= 即运放的输出电压2u 只受输入电压1u 的控制而与负载L R 大小无关，电路模型如图（a ）所示。

转移电压比21121R Ru u +==μ μ为无量纲，又称为电压放大系数。

这里的输入、输出有公共接地点，这种联接方式称为共地联接。

（2）压控电流源（VCCS ） 将图2的1R 看成一个负载电阻L R ，如图2所示，即成为压控电流源VCCS 。

U 1U 2+_+_图2此时，运放的输出电流 Ru R u i i n R L 1===。

即运放的输出电流L i 只受输入电压1u 的控制，与负载L R 大小无关。

电路模型如图（b ）所示。

转移电导 )(11s Ru i g L m ==这里的输入、输出无公共接地点，这种联接方式称为浮地联接 （３） 流控电压源（CCVS ） 如图3所示由于运放的“+”端接地，所以0=p u ，“—”端电压n u 也为零，此时运放的“—”端称为虚接地点。

显然，流过电阻R 的电流1i 就等于网络的输入电流S i 。

此时，运放的输出电压R i i u S R -=-=12，即输出电压2u 只受输入电流S i 的控制，与负载L R 大小无关，电路模型如图（c ）所示。

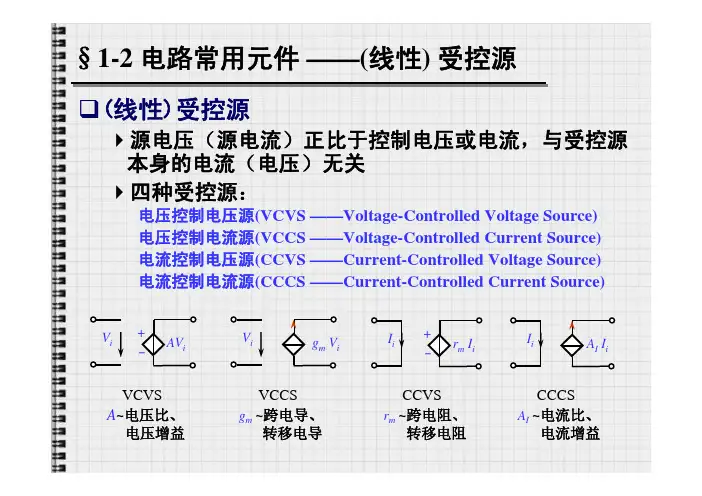
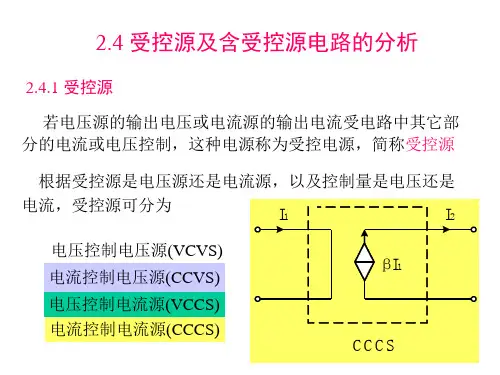
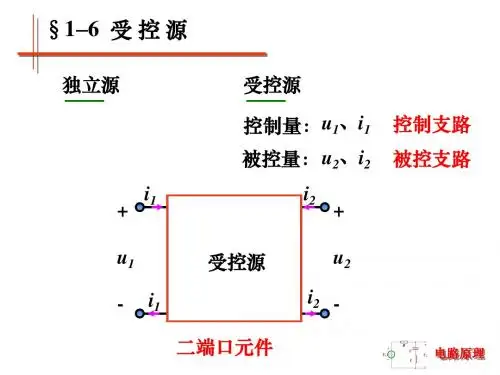
§1-2 电路常用元件——(线性) 受控源(线性)受控源源电压（源电流）正比于控制电压或电流，与受控源本身的电流（电压）无关四种受控源：电压控制电压源(VCVS ——Voltage-Controlled Voltage Source)电压控制电流源(VCCS ——Voltage-Controlled Current Source)电流控制电压源(CCVS ——Current-Controlled Voltage Source)电流控制电流源(CCCS ——Current-Controlled Current Source)V i AVi-+VCVSA~电压比、电压增益V i gmVVCCSg m~跨电导、转移电导I i-+r m I iCCVSr m~跨电阻、转移电阻I i AII iCCCSA I~电流比、电流增益独立源与受控源：几个名词的内涵“源”：指具备向外界提供能量/功率的能力。

“独立/受控”：源电压/电流是由自身属性决定还是由别的信号决定。

“理想/非理想”：输出电压/电流是否与输出电流/电压有关（即内阻是否为零）。

通常所说的电压/电流源是指独立理想电压/电流源；通常所说的受控电压/电流源是指受控理想电压/电流源。

(线性)受控源例：集成差分放大器(运算放大器)差分跨导放大器……V iAV i-+RI V 电阻变换电路()RV A R AV V I i i i -=-=1iV V =AR I V R -==1等效若A <1，等效电阻为正阻若A >1，等效电阻为负数——线性负阻受控源应用举例——电阻变换电路§1-2 电路常用元件——集总参量与分布参量❑集总参量将电场、磁场看成是集中于某一类元件内部电容～电场电感～磁场电阻～耗能适用于低频电路（元件尺寸远小于电磁波波长） 集总电路——只包含集总参量元件。

ε(t )-+R L简单电路-+ε(t )R L集总参量电路dldRdL dCdG传输线的分布参量❑分布参量分布于电路各个部分的微参量——更接近于实际 通常用于高频电路(元件尺寸与电磁波波长可比拟)第一章：线性电路的复数解法§1-1 电路分析导论§1-2 电路常用元件§1-3 常参量线性电路的复数解法常参量线性电路的时域解法简谐函数的复数表示复阻抗和复导纳§1-4 滤波器常参量线性电路的时域解法例1：RC充放电电路Et RI t V =+)()(dtt dV Cdt t dQ t I )()()(==E dtt dV RC t V =+)()(～1阶常微分方程)()(=+dt t dV RC t V 求通解：RCt e C t V /1)(-=通解Edtt dV RC t V =+)()(求特解：Et V =)(特解解=特解+通解：()()Ee C t V t V t V RC t +=+=-/1)(特解通解代入初值：()E C V CQ +==1)0(0()E CQ C -=01EQ (0)V (t )+_+_RCI (t )t=0常参量线性电路的时域解法例1：RC充放电电路()()RCt e E C Q E t V //0)(--+=()()[]()∞+∞-=-Y eY Y t Y t τ/0)(一阶RC或RL 电路的通解E tV Q (0)/CEtV Q (0)/CEV =∞)(～稳态～暂态t =4τ，暂态部分衰减为1.8%t =5τ，暂态部分衰减为0.67%RL RC /或=τ～时间常数例2：RL串联电路t A t RI t I dtdL ωcos )()(=+()t C t C eC t I LtR ωωsin cos )(21/0++=-特解通解A R L L C A R L RC 22222221,+=+=ωωωA RL RI C C C I 222010)0()0(+-=→+=ω()t C t C t I t ωωsin cos )(21+→∞→时，当～稳态R L /=τ～时间常数Acos ωt+_RLI (t )I (0)例3：RLC串联电路()()()()t E dt t I Ct RI t I dt dL =++⎰1E (t )Q (0)V (t )+_+_RCLI (t )I (0)()()()()dt t dE t I C t I dt d R t I dtd L =++122一般形式:N阶常系数微分方程(或方程组)X (t )→与激励源有关的函数Y (t )→待求解的电压或者电流函数a i→常系数,取决于电路元件及连接关系()()t X t Y a dt d a dt d a dt d a n n n n n n =⎪⎪⎭⎫ ⎝⎛++++---01111N阶常系数微分方程解法(复习一下高数):()()t X t Y a dt d a dt d a dt d a n n n n n n =⎪⎪⎭⎫ ⎝⎛++++---01111 Y (t )的解= 齐次方程的通解+ 特解 求通解:()001111=⎪⎪⎭⎫ ⎝⎛++++---t Y a dt d a dt d a dt d a n n n n n n ())(0111=++++=--a s a s a s a s F n n n n 定义特征方程:特征方程的第i 个(n i 重)复根:nnj S pi ii i i =+=∑=1,βαS i ——固有频率齐次方程的通解:()()()∑∑=--=--+++=+++=p i tj t i i n n i pi tS i i n n i i i i i i i i ee b t b tb eb t b tb t Y 10,1,11,10,1,11,βα 通解当所有的Re (S i )<0时,通解将随时间呈指数或者近似指数衰减,因此只要经过足够长的时间,初值的作用就可以小到忽略不计，电路的响应将主要由激励信号决定，这类电路叫做稳定电路。