含四种受控源电路的节点导纳矩阵系统列写法
- 格式:docx
- 大小:37.10 KB
- 文档页数:4

目录摘要 (1)1 题目 (1)2 节点导纳矩阵的计算原理 (2)2.1节点方程 (2)2.2节点导纳矩阵元素的物理意义 (5)3 计算过程 (6)4 用MATLAB计算 (7)4.1程序清单: (7)4.2 输出结果与分析 (9)5 小结 (10)参考文献 (11)成绩评定表节点导纳矩阵的计算1 题目电力系统如下图所示,图中所有串联支路参数均为阻抗标幺值,所有对支路参数均为导纳标幺值。
求设网络的节点导纳矩阵。
图一2 节点导纳矩阵的计算原理2.1节点方程在图2中的简单电力系统中,若略去变压器的励磁功率和线路电容,负荷用阻抗表示,便可得到一个有5个基点(包括零电位点)和7条支路的等值网络,如图3所示。
图2图3将接于节点1和4的电势源和阻抗的串联组合变换成等值的电流源和导纳的并联组合,便得到图4的等值网络。
其中:••=1101E y I ••图4以零电位点作为计算节点电压的参考点,根据基尔霍夫电流定律,可以写出4个独立节点的电流平衡方程如下上述方程组经过整理可以写成:式中:⎪⎪⎪⎭⎪⎪⎪⎬⎫=+-+-=-+-=-+-++-=-+•••••••••••••••••••••4440343424244324232342243223220121212112110)()(0)()(0)()()()(I V y V V y V V y V V y V V y V V y V V y V y V V y I V V y V y ⎪⎪⎪⎭⎪⎪⎪⎬⎫=++=++=+++=+•••••••••••••4444343242434333232424323222121212111000I V Y V Y V Y V Y V Y V Y V Y V Y V Y V Y V Y V Y 34433424422423322312211234244044342440443423331224232022121011;;;;;;;;y Y Y y Y Y y Y Y y Y Y y y y Y y y y Y y y Y y y y y Y y y Y -==-==-==-==++=++=+=+++=+=一般地,对于有n 个独立节点的网络,可以列写n 个节点方程:也可以用矩阵写成:或缩写成:YV=I矩阵Y 称为节点导纳矩阵。

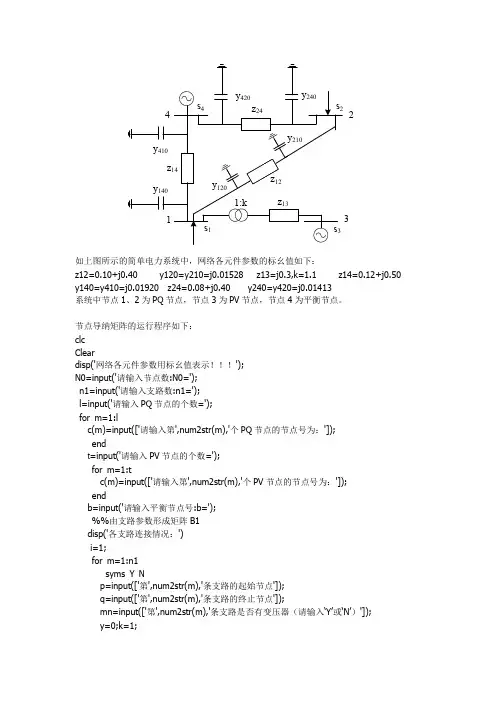
23yy如上图所示的简单电力系统中,网络各元件参数的标幺值如下:z12=0.10+j0.40 y120=y210=j0.01528 z13=j0.3,k=1.1 z14=0.12+j0.50 y140=y410=j0.01920 z24=0.08+j0.40 y240=y420=j0.01413系统中节点1、2为PQ节点,节点3为PV节点,节点4为平衡节点。
节点导纳矩阵的运行程序如下:clcCleardisp('网络各元件参数用标幺值表示');N0=input('请输入节点数:N0=');n1=input('请输入支路数:n1=');l=input('请输入PQ节点的个数=');for m=1:lc(m)=input(['请输入第',num2str(m),'个PQ节点的节点号为:']);endt=input('请输入PV节点的个数=');for m=1:tc(m)=input(['请输入第',num2str(m),'个PV节点的节点号为:']);endb=input('请输入平衡节点号:b=');%%由支路参数形成矩阵B1disp('各支路连接情况:')i=1;for m=1:n1syms Y Np=input(['第',num2str(m),'条支路的起始节点']);q=input(['第',num2str(m),'条支路的终止节点']);mn=input(['第',num2str(m),'条支路是否有变压器(请输入‘Y’或‘N’)']);y=0;k=1;if mn=='Y';k=input('请输入变压器变比(标幺值):');z=input(['请输入第',num2str(m),'条支路的线路阻抗']);elsez=input(['请输入第',num2str(m),'条支路的线路阻抗:']);y=input(['请输入第',num2str(m),'条支路线路的对地阻抗:']);endB1(i,1)=p;B1(i,2)=q;B1(i,3)=z;B1(i,4)=y;B1(i,5)=1/k;i=i+1;enddisp('由支路参数形成的矩阵B1')B1%求节点导纳矩阵Y=zeros(N0);e=zeros(1,N0);f=zeros(1,N0);for i=1:n1p=B1(i,1);q=B1(i,2);Y(p,q)=Y(p,q)-1./(B1(i,3)*B1(i,5));Y(q,p)=Y(p,q);Y(q,q)=Y(q,q)+1./(B1(i,3)*B1(i,5)^2)+B1(i,4)./2;Y(p,p)=Y(p,p)+1./B1(i,3)+B1(i,4)./2;Enddisp('导纳矩阵Y=');disp(Y)程序运行结果:。


电力网节点导纳矩阵计算例题与程序————————————————————————————————作者:————————————————————————————————日期:电力网节点导纳矩阵计算例题与程序佘名寰 编写用计算机解算电力网潮流电压和短路电流问题首先需确定电力网的节点导纳矩阵或节点阻抗矩阵。
本文通过例题介绍用网络拓扑法计算节点导纳矩阵的方法和程序,程序考虑了线路并联电容和变压器支路标么变比不为1时的影响。
程序用MATLAB 语言编写,线路参数均采用标么值。
本文稿用office word 2007 版编写,可供电气专业人员计算相关问题时参考。
1.用网络拓扑计算节点导纳矩阵 1.1网络拓扑矩阵:【例1.1】 例图1-1是有5 个节点和5条支路的网络,节点5作为基准参考点,1 ,2, 3, 4为独立节点,支路编号和方向图中已标识。
例图1-1对于具有n 个节点b 条支路的有向图,它的关联矩阵为一个N ×B 的矩阵A a :A a =[a ij ]若支路j 与节点i 相关,且箭头背离节点i ,则a ij =1,若箭头指向节点则a ij =-1,若支路j 与节点i 无关,则a ij =0, 图1-1所示的有向图的关联矩阵为① ② ③ ④ ⑤ 支路编号A ij =行编号从上到下为1 2 3 4 5节点编号(5为参考节点) 去掉第5行即为独立节点的关联矩阵。
以下介绍生成网络关联矩阵的M 函数文件 ffm.m :% M FUNCTION ffm.m②③①YYY④⑤1:1 1.042315Z21=0.04+J0.25Z23=0.08+J0.30Z13=0.1+J0.35 Z42=J0.015 Z53=J0.03 YC1=J0.25% Np is number of node point,Nb is number of braches% nstart--the start point of branches ,nend -- the end point,% A -- network incidence matrixfunction[A]=ffm(nstart,nend)global Np Nbn=length(nstart);A=zeros(Np,Nb);for i=1:nA(nstart(i),i)=1;A(nend(i),i)=-1;end以例图1-1网络为例调用ffm.m文件求其关联矩阵运算以上程序可得关联矩阵 mm ij如下:mm =-1 0 1 0 01 1 0 -1 00 -1 -1 0 -10 0 0 1 00 0 0 0 1Mm ij明显与A ij是相同的。



为了提供一个例题,我将使用一个简单的电路图来说明如何编写一个支路节点导纳矩阵。
假设我们有以下电路图:
```
+--- R1 ---+
| |
V1 -+--- R2 ---+--- R3 --- V2
| |
+--- R4 ---+
```
在这个电路中,V1和V2是电压源,R1、R2、R3和R4是电阻器。
我们将电路分解为四个支路:支路1包含V1和R1,支路2包含R1和R2,支路3包含R2和R3,支路4包含R3、R4和V2。
首先,我们给每个支路节点编号,并确定电流的流向。
在这个例子中,我们将支路1的节点编号为节点1,支路2的节点编号为节点2,支路3的节点编号为节点3,支路4的节点编号为节点4。
然后,我们可以根据支路的电导值来创建支路节点导纳矩阵。
在这个例子中,我们假设电导值为G1、G2、G3和G4。
支路节点导纳矩阵的形式是一个4x4的矩阵,其中每个元素表示两个节点之间的导纳值。
在这个例子中,支路节点导纳矩阵可以表示为:
```
G1+G2 -G1 0 0
-G1 G1+G2 -G2 0
0 -G2 G2+G3 -G3
0 0 -G3 G3+G4
```
这样的支路节点导纳矩阵描述了电路中各个节点之间的导纳关系,可以用于进一步的电路分析和计算。
请注意,具体的导纳值取决于电阻值和电压源的数值。



一、概述
在电力系统分析中,受控源是一种被广泛使用的模型,在各种电路和系统的分析中都有重要的应用。
受控源电路的节点导纳矩阵系统列写法是一种用来表示受控源电路的方法,能够方便地进行分析和计算。
本文将重点介绍含四种受控源电路的节点导纳矩阵系统列写法,包括其原理、方法和应用。
二、含四种受控源电路的节点导纳矩阵
1. 受控电压源
受控电压源是一个电压源,其输出电压由电路中的某个变量控制。
在节点导纳矩阵系统列写法中,受控电压源可以表示为:
$I_k = -G_{NK}V_k + H_{NK}V_m$
其中,$I_k$为电流,$V_k$为电压,$G_{NK}$为导纳矩阵的元素,$H_{NK}$表示受控源的系数。
2. 受控电流源
受控电流源是一个电流源,其输出电流由电路中的某个变量控制。
在节点导纳矩阵系统列写法中,受控电流源可以表示为:
$V_k = -B_{NK}I_k + E_{NK}I_m$
其中,$V_k$为电压,$I_k$为电流,$B_{NK}$为导纳矩阵的元素,$E_{NK}$表示受控源的系数。
3. 受控电压源的双向连接
受控电压源的双向连接是一种复杂的受控源模型,其输出电压由电路中的两个变量控制。
在节点导纳矩阵系统列写法中,受控电压源的双向连接可以表示为:
$I_k = -G_{NK}V_k + H_{NK}V_m$
$I_m = -G_{NM}V_m + H_{NM}V_k$
其中,$I_k$和$I_m$分别为电流,$V_k$和$V_m$分别为电压,$G_{NK}$、$H_{NK}$、$G_{NM}$、$H_{NM}$为导纳矩阵的元素。
4. 受控电流源的双向连接
受控电流源的双向连接是一种更为复杂的受控源模型,其输出电流由电路中的两个变量控制。
在节点导纳矩阵系统列写法中,受控电流源的双向连接可以表示为:
$V_k = -B_{NK}I_k + E_{NK}I_m$
$V_m = -B_{NM}I_m + E_{NM}I_k$
其中,$V_k$和$V_m$分别为电压,$I_k$和$I_m$分别为电流,$B_{NK}$、$E_{NK}$、$B_{NM}$、$E_{NM}$为导纳矩阵的元素。
三、节点导纳矩阵系统列写法的计算方法
节点导纳矩阵系统列写法的计算方法主要包括以下步骤:
1. 建立节点电压方程
根据电路的拓扑结构,建立节点电压方程,将电路中所有的元件用导纳矩阵表示,得到整个电路的节点导纳矩阵方程。
2. 定义受控源的系数
根据电路中的受控源的类型,定义相应的系数,将受控源的影响加入到节点导纳矩阵方程中。
3. 构建整体矩阵方程
将受控源的系数加入到节点导纳矩阵方程中,得到整体的节点导纳矩阵方程。
4. 解方程求解
通过数值计算或符号计算的方法,求解整体的节点导纳矩阵方程,得到电路中各个节点的电压和电流。
四、节点导纳矩阵系统列写法的应用
1. 电路分析
通过节点导纳矩阵系统列写法,可以方便地进行电路的分析和计算,
得到各个节点的电压和电流,从而对电路的性能和稳定性进行评估。
2. 电力系统仿真
在电力系统的仿真和计算中,节点导纳矩阵系统列写法可以有效地描
述各种复杂的电路和系统,对系统的各种参数和运行情况进行模拟和
分析。
3. 控制系统设计
在控制系统的设计和分析中,受控源的模型是一个常见的方法,节点
导纳矩阵系统列写法可以有效地描述受控源对系统的影响,为系统的
控制和稳定性分析提供便利。
五、总结
节点导纳矩阵系统列写法是一种用来描述含四种受控源电路的方法,
通过对各种受控源的模型和系数进行定义和加入,可以方便地对复杂
的电路和系统进行分析和计算。
节点导纳矩阵系统列写法在电路分析、电力系统仿真和控制系统设计中有着重要的应用价值,是电力系统分
析中的重要工具之一。