五年级上册三角形、平行四边形和梯形面积计算

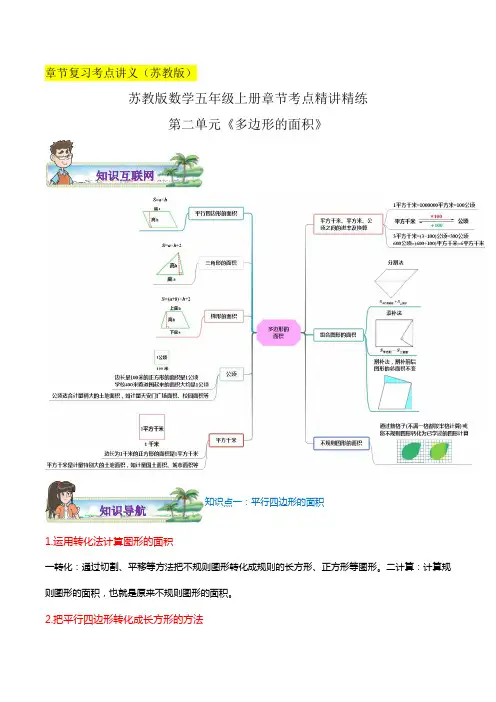
章节复习考点讲义（苏教版）苏教版数学五年级上册章节考点精讲精练第二单元《多边形的面积》知识点一：平行四边形的面积1.运用转化法计算图形的面积 一转化：通过切割、平移等方法把不规则图形转化成规则的长方形、正方形等图形。

二计算：计算规则图形的面积，也就是原来不规则图形的面积。

2.把平行四边形转化成长方形的方法知识导航知识互联网沿着平行四边形的任意一条边上的任意一条高剪成两个图形后，通过平移都可以把平行四边形转化成一个长方形。

3.平行四边形的面积计算公式平行四边形的面积=底×高，用字母表示为S=a×h。

知识点二：三角形的面积1.三角形和平行四边形之间的关系两个完全一样的三角形可以拼成一个平行四边形，每个三角形的面积是两个完全一样的三角形所拼成的平行四边形的面积的一半，即三角形的面积=平行四边形的面积÷2或平行四边形的面积=三角形的面积×2。

2.三角形的面积计算公式三角形的面积等于与它等底等高的平行四边形面积的一半。

三角形的面积=底×高÷2，用字母表示为S=a×h÷2。

知识点三：梯形的面积1.梯形面积计算中的“转化”两个完全一样的梯形可以拼成一个平行四边形，梯形的面积是两个完全一样的梯形所拼成的平行四边形的面积的一半，也就是：梯形的面积=平行四边形的面积÷2或平行四边形的面积=梯形的面积×2。

2. 梯形的面积梯形的面积=（上底＋下底）×高÷2。

用字母表示：S=（a＋b）×h÷2。

知识点四：认识公顷和平方千米1.公顷的认识测量或计量土地面积，通常用公顷作单位，公顷可以写成hm²。

边长100米的正方形土地，面积是1公顷。

公顷和平方米之间的进率是10000，1公顷=10000平方米。

2. 平方千米的认识测量或计量大面积的土地，通常用平方千米作单位。

平方千米可以写成km²。

五年级上册数学教案第五单元（多边形面积的计算）西师大版教案：五年级上册数学教案第五单元（多边形面积的计算）西师大版一、教学内容本节课我将会讲解五年级上册数学的第五单元，主要内容是多边形面积的计算。

我们将学习如何计算三角形、平行四边形和梯形的面积。

二、教学目标通过本节课的学习，我希望学生能够掌握三角形、平行四边形和梯形的面积计算方法，并能够灵活运用这些方法解决实际问题。

三、教学难点与重点本节课的重点是让学生掌握三角形、平行四边形和梯形的面积计算公式。

难点在于如何引导学生理解并运用这些公式。

四、教具与学具准备为了更好地进行课堂教学，我准备了一些实物模型和多媒体教具，包括三角形、平行四边形和梯形的模型，以及相关的PPT和动画演示。

五、教学过程1. 引入：我会在课堂上展示一些实际的多边形物体，如三角形桌子、平行四边形窗户和梯形屋顶，引导学生思考如何计算这些物体的面积。

2. 讲解：然后我会利用多媒体教具，分别展示三角形、平行四边形和梯形的面积计算过程，解释相关的公式和计算方法。

3. 练习：在讲解完每个多边形的面积计算方法后，我会给出一些例题，让学生分组讨论和解答，巩固所学的内容。

六、板书设计板书设计将会包括三角形、平行四边形和梯形的面积计算公式，以及相关的符号和步骤。

七、作业设计八、课后反思及拓展延伸本节课的教学目标是让学生掌握三角形、平行四边形和梯形的面积计算方法。

通过实际的多边形物体引入，多媒体教具的演示和例题的练习，学生能够更好地理解和运用这些计算方法。

在课堂上，我注意引导学生积极参与，鼓励他们提出问题和解答问题。

通过板书设计，学生能够清晰地了解每个多边形的面积计算公式。

作业的设计也符合学生的认知水平，能够巩固所学的内容。

然而，我也注意到一些学生在理解和运用这些计算方法时还存在一些困难。

在课后，我将会针对这些学生进行个别辅导，帮助他们克服困难，提高他们的数学能力。

我也会通过一些拓展延伸的活动，让学生进一步探索多边形的面积计算问题，激发他们的学习兴趣。

多边形的面积一、计算公式注：S表示面积，a表示底，h表示高，底和高必须对应！在梯形的面积公式里，a表示上底，b表示下底，一般来说，短的是上底，长的是下底。

在计算面积时，要找准对应的量。

求三角形和梯形的面积时，不要忘了除以2。

二、其他知识点1、计算多边形的面积，要代入公式计算。

2、推导平行四边形的面积，将平行四边形转化成长方形。

（割补法）3、平行四边形的周长＝相邻两边长之和×2 三角形的周长＝三条边之和梯形的周长＝上底＋下底＋两条腰4、把一个长方形拉成平行四边形，周长不变，面积变小（平行四边形的高比原来长方形的宽小）。

反之，把平行四边形拉成一个长方形，周长不变，面积变大。

5、两个完全一样的三角形可以拼成一个平行四边形。

（拼摆法）6、等底等高的平行四边形和三角形，平行四边形的面积是三角形面积的2倍，三角形面积是平行四边形面积的一半。

等面积等底的平行四边形和三角形，三角形的高是平行四边形的高的2倍，平行四边形的高是三角形的高的一半。

7、在直角三角形里，两条直角边就是对应的底和高，斜边最长。

8、两个完全一样的梯形可以拼成一个平行四边形。

（拼摆法）9、计算堆成梯形形状的圆木、钢管等的个数，通常用下面的方法：（顶层个数＋底层个数）×层数÷2＝总个数。

注意：只有下一层物体比上一层物体数多1时，才有“层数＝底层个数－顶层个数＋1”10、求组合图形的面积时，一定要找准所分成的图形的相关数据。

11、不规则图形的面积可以转化成学过的图形来估算，也可以通过数方格的方法来估算。

三、解答方法1、计算面积时，分清是算哪种图形的面积，直接利用相应的面积公式，一定要找准公式里所需的每个量，注意单位是否一致，算出结果后记得写单位，面积单位有“平方”两个字。

2、计算底、高、上底或下底时，同样看清是哪种图形，直接利用相应面积公式的变式。

（熟记和熟练运用上面表格的计算公式。

）3、计算组合图形的面积时，利用割补法，看清组合图形是由哪几个简单图形（所谓简单图形，就是我们学过的长方形、正方形、平行四边形、三角形、梯形）组成的，分别算出每个简单图形的面积，最后不要忘了再相加（分割法，图形是凸的）或相减（添补法，图形是凹的）。

第二单元复习一、填空1. 360000平方米=（）公顷2平方千米=（）公顷=（）平方米2.把一个长20厘米，宽10厘米的长方形剪成两个完全相同的三角形，每个三角形的面积是（）平方分米。

3.一个平行四边形和一个三角形面积相等，高也相等，平行四边形的底是6米，三角形的底是（）。

4、一个梯形的上底是6厘米，下底是8厘米，高是10厘米，这个梯形的面积是（），从中剪下一个最大的三角形的面积是（）。

5、一个直角三角形的三条边分别是60厘米，80厘米，100厘米，它的面积是（）平方厘米，斜边上的高是（）厘米。

6、一个三角形和一个平行四边形的面积相等，高也相等，三角形的底是6厘米，则平行四边形的底是（）厘米；若平行四边形的底是10厘米，则三角形的底是（）厘米。

7、一个梯形上下底的平均长度是40厘米，高12厘米，这个梯形的面积是（）平方厘米。

8.一个梯形的上底是5厘米，下底是7厘米，如果把下底延长2厘米，则梯形的面积增加4平方厘米。

原梯形的面积是（）平方厘米。

9、如右图，用4个完全一样的等腰直角三角形拼成一个梯形，这个梯形的面积是（）平方厘米。

10.一个平行四边形的面积是60平方米，如果高不变，底扩大两倍，面积是（）平方米，如果高扩大为原来的4倍，底缩小为原来的1/4，面积是（）平方米。

二、判断：（1）平行四边形的面积是三角形面积的两倍。

（）（2）任何一个平行四边形都可以分成两个完全一样的三角形。

（）（3）两个完全一样的梯形一定能拼成一个平行四边形，一个平行四边形一定能分成两个完全一样的梯形。

（）（4）将两个直角边分别为3厘米、4厘米，斜边为5厘米的三角形拼成平行四边形，周长最大是16厘米。

（）（5）两个面积相等的平行四边形不一定是等底等高的。

（）（6）用同样长的铁丝围成一个长方形和一个平行四边形，长方形与平行四边形的周长相等，面积不相等。

（）三、选择：（1）右图是两个完全相同的长方形，其中阴影部分的面积是相比，甲（）乙。

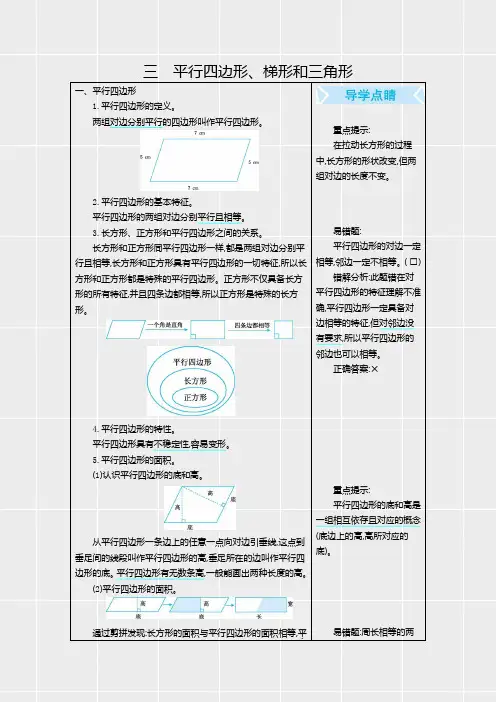
三平行四边形、梯形和三角形一、平行四边形1.平行四边形的定义。

两组对边分别平行的四边形叫作平行四边形。

2.平行四边形的基本特征。

平行四边形的两组对边分别平行且相等。

3.长方形、正方形和平行四边形之间的关系。

长方形和正方形同平行四边形一样,都是两组对边分别平行且相等,长方形和正方形具有平行四边形的一切特征,所以长方形和正方形都是特殊的平行四边形。

正方形不仅具备长方形的所有特征,并且四条边都相等,所以正方形是特殊的长方形。

4.平行四边形的特性。

平行四边形具有不稳定性,容易变形。

5.平行四边形的面积。

(1)认识平行四边形的底和高。

从平行四边形一条边上的任意一点向对边引垂线,这点到垂足间的线段叫作平行四边形的高,垂足所在的边叫作平行四边形的底。

平行四边形有无数条高,一般能画出两种长度的高。

(2)平行四边形的面积。

通过剪拼发现:长方形的面积与平行四边形的面积相等,平．重点提示:在拉动长方形的过程中,长方形的形状改变,但两组对边的长度不变。

易错题:平行四边形的对边一定相等,邻边一定不相等。

( )错解分析:此题错在对平行四边形的特征理解不准确,平行四边形一定具备对边相等的特征,但对邻边没有要求,所以平行四边形的邻边也可以相等。

正确答案:✕重点提示:平行四边形的底和高是一组相互依存且对应的概念(底边上的高,高所对应的底)。

易错题:周长相等的两行四边形的底等于长方形的长．．．．．．．．．．．．．;．平行四边形的高等于长方形的．．．．．．．．．．．．．宽．。

长方形的面积=长×宽平行四边形的面积=底×高如果用S表示平行四边形的面积,a和h分别表示平行四边形的底和高,那么平行四边形的面积的字母公式为S=ah。

二、梯形1.梯形的定义。

只有一组对边平行的四边形叫作梯形。

2.平行四边形和梯形的异同点。

相同点:都是四边形;都有平行的对边。

不同点:平行四边形的两组对边分别平行且相等;梯形只有一组对边平行,且平行的这组对边不相等。

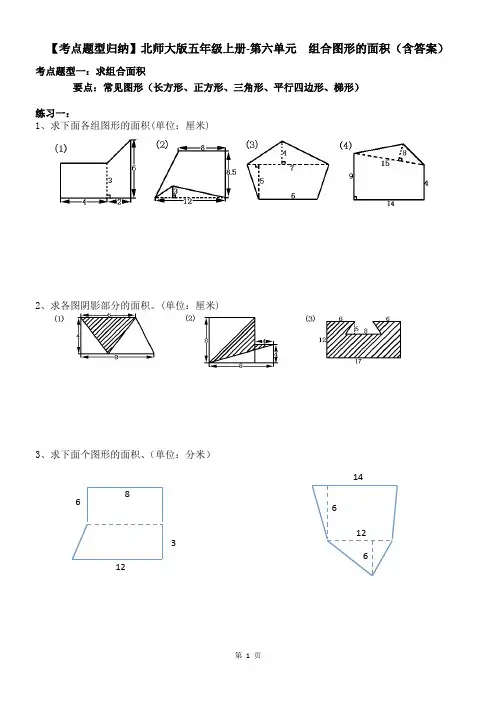
【考点题型归纳】北师大版五年级上册-第六单元 组合图形的面积（含答案）考点题型一：求组合面积要点：常见图形（长方形、正方形、三角形、平行四边形、梯形）练习一：1、求下面各组图形的面积(单位：厘米)2、求各图阴影部分的面积。

(单位：厘米)3、求下面个图形的面积、（单位：分米）812366612 14考点题型二：两个正方形要点：①阴影部分是常见图形可尝试直接求出②阴影部分切割法③整体减去部分得到阴影部分练习二：1、先观察图形特点，再求图形中阴影部分的面积．（单位：厘米）5.44.26431.52.5 82、求阴影部分的面积．（单位：厘米）3、图中两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积。

4、大小正方形如图放置，阴影部分为重叠部分，求空白部分面积。

（单位：厘米）1577225、求下图阴影部分的面积（单位：厘米）考点题型三：平行四边形与三角形练习三：1、下图的平行四边形面积是40平方厘米，求阴影部分的面积.(单位：厘米)2、平行四边形的面积是320平方厘米，求梯形面积．3、已知平行四边形的面积是48平方分米，求阴影部分的面积。

3dm8dm4、如图所示，一个平行四边形被分成A、B两份，A的面积比B的面积打40平方米，A的上底是多少？B8米A5、如图，平行四边形面积240平方厘米，求阴影部分面积。

考点题型四：梯形和三角形练习四：1、阴影部分面积是40平方米，求空白部分面积。

（单位：米）2、求阴影部分的面积．（单位：厘米）3、如图所示，梯形的周长是52厘米，求阴影部分的面积。

1014164、下图直角梯形的面积是49平方分米，求阴影部分的面积。

5、图中梯形中空白部分是直角三角形，它的面积是45平方厘米，求阴影部分面积。

6、阴影部分面积是40平方米，求空白部分面积。

（单位：米）7、下图ABCD是梯形，它的面积是140平方厘米，已知AB＝15厘米，DC＝5厘米。

求阴影部分的面积。

8、求梯形的面积。

（单位：厘米）9、如图，已知梯形ABCD的面积为37.8平方厘米，BE长7厘米，EC长4厘米，求平行四边形ABED 的面积。

小学数学三角形平行四边形梯形面积练习题篇一：五年级上册三角形、平行四边形和梯形面积练习(1) 三角形、平行四边形和梯形的面积长方形面积= 平行四边形面积=正方形面积= 三角形面积= 梯形面积= 求下列图形的面积：（单位：cm）835典型例题1：一个等腰直角三角形，最长的边是10厘米，这个三角形的面积是多少平方厘米？【巩固练习1】：如图正方形中套着一个长方形，正方形的边长是12厘米，长方形的四个角的顶点把正方形的四条边各分成两段，其中长的一段是短的2倍。

求中间长方形的面积。

典型例题2：求右面平行四边形的周长。

612【巩固练习2】：求右面三角形的AB上的高。

典型例题3：求右图等腰直角三角形中阴影部分的面积。

（单位：厘米）【巩固练习3】：求四边形ABCD的面积。

（单位：厘米）5B典型例题4：有一种将正方形内接于等腰直角三角形。

已知等腰直角三角形的面积是72平方厘米，正方形的面积分别是多少？【巩固练习4】：有一种将正方形内接于等腰直角三角形。

已知等腰直角三角形的面积是72平方厘米，正方形的面积分别是多少？典型例题5：图中两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积。

【巩固练习5】：图中两个正方形的边长分别是6厘米和4厘米，求阴影部分的面积。

典型例题6：如图，用40m长的篱笆靠墙围了一个梯形养鸡场，求养鸡场的面积？【巩固练习6】求右图等腰直角三角形中阴影部分的面积。

（单位：厘米）典型例题7：在一个直角三角形铁皮上剪下一块正方形，剩下两个三角形，已知AD=3cm，DB=4cm，两个三角形面积和是多少？2、已知正方形ABCD的边长是7厘米，求正方形EFGH的面积。

3、求下图长方形ABCD的面积（单位：厘米）。

4、如图，用48m长的篱笆靠墙围了一个梯形养鸡场，求养鸡场的面积？5、在一个直角三角形铁皮上剪下一块正方形，剩下两个三角形，已知AD=4cm，DB=6cm，两个三角形面积和是多少？一、填空（每题3分）1、一个平行四边形的底长8厘米，是高的2倍，它的面积是（），与它等底等高的三角形面积是（）。

专题04 多边形的面积知识点一：平行四边形、三角形的面积1、平行四边形的面积公式：底×高 S=ah2、平行四边形的面积公式推导：平行四边形可以转化成一个长方形；长方形的长相当于平行四边形的底；长方形的宽相当于平行四边形的高；长方形的面积等于平行四边形的面积。

因为长方形面积=长×宽，所以平行四边形面积=底×高。

在同一个平行四边形中，不同的底与它对应的高的乘积是不变的。

3、三角形的面积公式：底×高÷2 S=ah÷24、三角形面积公式推导：两个完全一样的三角形可以拼成一个平行四边形，平行四边形的底相当于三角形的底，平行四边形的高相当于三角形的高；平行四边形的面积等于三角形面积的2倍。

因为平行四边形面积=底×高，所以三角形面积=底×高÷25、等底等高的三角形的面积是平行四边形面积的一半。

真题讲练：一、填空题1．（2022·广东广州·五年级期末）一个平行四边形的面积是17.5cm2，它的高是2.5cm，底是( )cm。

2．（2022·广东广州·五年级期末）如图，一块三角形交通标志牌的面积是236dm，它的高是( )dm。

3．（2021·广东广州·五年级期末）一块三角形土地的面积是160m2，底是32m，高是( )m。

4．（2022·广东广州·五年级期末）一个平行四边形的面积是36cm2，和它等底等高的三角形的面积是( )cm2。

5．（2021·广东广州·五年级期末）一个三角形的高是5cm，底是高的1.4倍。

这个三角形的底是( )dm，面积是( )dm2。

6．（2021·广东广州·五年级期末）一个平行四边形的面积是36平方分米，底是9分米，它的高是( )分米，与它等底等高的三角形面积是( )平方分米。

平行四边形、三角形和梯形的面积计算一、填空。

(每空2分，共16分)1．一个平行四边形的底是9分米，高是底的2倍，它的面积是()平方分米。

2．一个三角形和一个平行四边形等底等高，如果平行四边形的面积是128平方米，那么三角形的面积是()平方米。

3．一个直角三角形，它的两条直角边分别是4 cm和3 cm，它的面积是()cm2。

4．三角形的一条边长4分米，这条边上的高是6分米，另一条边长3分米，则这条边上的高是()。

5．三角形和平行四边形的高相等，面积也相等，三角形的底是16 cm, 平行四边形的底是()cm。

6．一个平行四边形的面积是9平方分米，底扩大为原来的4倍，高不变，扩大后平行四边形的面积是()平方分米。

7．一个梯形的上底与下底的平均长度是30厘米，高是12厘米，这个梯形的面积是()平方厘米。

8．一个梯形，如果上底增加4厘米，就成为一个边长10厘米的正方形，这个梯形的面积是()平方厘米。

二、判断。

(对的在括号里打“√”，错的打“×”)(每题2分，共10分) 1．平行四边形的面积一定比三角形的面积大。

() 2．把一个长方形的框架拉成一个平行四边形，面积减少了。

()3．任意一个平行四边形都可以分成两个大小和形状都相同的梯形。

() 4．两个等底等高的平行四边形，形状不一定完全相同。

() 5．三角形的高越大，面积就越大。

()三、选择。

(把正确答案的字母填在括号里)(每题3分，共15分) 1．小玲想算一个上底是a，下底是b，高是3的梯形的面积，她应该使用的公式是()。

A．S＝ab B．S＝3(a＋b)÷2C．S＝3ab÷2 D．S＝ab÷22．两个()可以拼成一个平行四边形。

A．面积相等的梯形B．周长相等的梯形C．等腰梯形D．完全相同的梯形3．如下图，用剪、拼的方法，把一个平行四边形转化成一个长方形，原来的平行四边形与现在的长方形相比，()。

A．周长不变，面积变小B．周长变了，面积变大C．周长不变，面积变大D．周长变了，面积不变4．一个梯形，如果高不变，上底增加2厘米，下底减少2厘米，则面积()。

计算面积公式长方形的长＝面积÷宽长方形的宽＝面积÷长2、长方形的周长＝（长＋宽）×2 字母表示：L＝（a＋b）×2长方形的长＝周长÷2－宽长方形的宽＝周长÷2－长二、正方形的面积和周长1、正方形的面积＝边长×边长字母表示：S＝a×a2、正方形的周长＝边长×4 字母表示：L＝4×a正方形的边长＝周长÷4三、认识底和高1、口诀：一横一竖加直角，分别就是底和高。

2、直角三角形的两条直角边，分别就是它的底和高。

3、三角形有3条高。

平行四边形有无数条高。

梯形有无数条高。

平行四边形的底＝S平÷高字母表示：a＝S平÷h平行四边形的高＝S平÷底字母表示：h＝S平÷a三角形的底＝S三×2÷高字母表示：a＝S三×2÷h三角形的高＝S三×2÷底字母表示：h＝S三×2÷a梯形的高＝S梯×2÷（上底＋下底）字母表示：h＝S梯×2÷（a＋b）梯形的上底＝＝S梯×2÷高－下底字母表示：a＝S梯×2÷h－b）梯形的下底＝＝S梯×2÷高－上底字母表示：b＝S梯×2÷h－a→等底等高的三角形的面积是等底等高平行四边形的一半，即2S三＝S平2、两个完全相同的梯形可以拼成一个平行四边形。

→这两个梯形的面积等于拼成的平行四边形的面积，即2S梯＝S平1、直角三角形的一条直角边与底重合，那么另外一条直角边就是高。

平行四边形的高锐角三角形的高（在里面）梯形的高2、三角形的高（1）锐角三角形：三条高都在里面。

（2）直角三角形：一条高在里面，两条直角边是另外两条高。

（3）钝角三角形：一条高在里面，另外两条高在外面（需要画出底的延长线）。

五年级数学多边形的面积计算公式汇总+练习题（附答案）面积计算公式1、长方形的面积=长×宽字母表示：S=ab长方形的长=面积÷宽 a=S÷b长方形的宽=面积÷长b=S÷a2、正方形的面积=边长×边长字母表示: S= a²3、平行四边形的面积=底×高字母表示：S=ah平行四边形的高=面积÷底 h=S÷a平行四边形的底=面积÷高 a=S÷h4、三角形的面积=底×高÷2字母表示：S=ah÷2三角形的高= 2×面积÷底h=2S÷a三角形的底= 2×面积÷高a=2S÷h5、梯形的面积=（上底+下底）×高÷2字母表示：S=(a+b)·h ÷2梯形的高=2×面积÷（上底+下底）h=2S÷(a+b)梯形的上底=2×面积÷高—下底a=2S÷h-b梯形的下底=2×面积÷高—上底b=2S÷h-a1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方米=10000平方厘米1米=10分米=100厘米多边形面积同步试题一、填空1．完成下表。

考查目的：平行四边形、三角形和梯形的面积计算及变式练习。

答案：解析：直接利用公式计算这三种图形的面积，对于学生来说完成的难度不大。

对于已知平行四边形的面积和高求底、已知三角形的面积和底求高这两个变式练习，可引导学生进行比较，理解并强化三角形和梯形的类似计算中需要先将“面积×2”这一知识点。

2．下图是一个平行四边形，它包含了三个三角形，其中两个空白三角形的面积分别是15 平方厘米和25 平方厘米。

中间涂色三角形的面积是（）。

考查目的：等底等高的三角形和平行四边形的面积之间的关系。

章节测试题1.【答题】一个三角形三个内角的比是3：3：6，且最短边长为10厘米，则它的面积是（）A.100平方厘米B.50平方厘米C.25平方厘米【答案】B【分析】先依据三角形的内角和是180°，利用按比例分配的方法，求出最大角和最小角的度数，即可判定出这个三角形的类别，从而可以求出其面积。

【解答】180°×[3÷（3+3+6）]=45°，180°×[6÷（3+3+6）]=90°，所以这个三角形是等腰直角三角形，且其直角边为10厘米，则其面积为：10×10÷2，=100÷2，=50（平方厘米）；这个三角形的面积是50平方厘米.。

2.【答题】两个完全一样的长方形内有①和②两个三角形，比较①和②的面积（）.A.三角形①的面积＞三角形②的面积B.三角形①的面积=三角形②的面积C.三角形①的面积＜三角形②的面积【答案】B【分析】由题意可知：这两个三角形底和高都相等，根据等底等高的三角形的面积相等即可解答.【解答】因为三角形①和三角形②等底等高，由等底等高的三角形的面积相等可知，它们的面积也相等.选B.3.【答题】两个等底、等面积的三角形，它的高一定（）.A.相等B.不相等C.无法比较【答案】A【分析】本题主要考查三角形的面积公式，抓住题目条件，即可判断．三角形的面积=底×高÷2，得出高=面积×2÷底，如果两个三角形等底等面积，则其高一定相等．【解答】根据三角形的面积=底×高÷2，得出高=面积×2÷底，所以两个三角形若底相等、面积相等，则高一定相等．选A.4.【答题】一个等腰直角三角形，最长边是12厘米，这个三角形的面积是（）平方厘米。

A.144B.72C.36D.36或72【答案】C【分析】先画出此图（如下）：最长的边即斜边，画出斜边上的高，然后根据“三角形的面积=底×高÷2”进行解答即可．【解答】由图可知：以斜边为底，底是12厘米，高是12÷2=6厘米，12×6÷2，=72÷2，=36（平方厘米）；答：这个三角形的面积是36平方厘米．5.【答题】在一个长方形内画一个最大的三角形，这个三角形的面积（）长方形面积的一半．A.大于B.小于C.等于D.不一定【答案】C【分析】在一个长方形内画一个最大的三角形，最大的三角形的底=长方形的长，最大的三角形的高=长方形的宽；根据长方形的面积公式和三角形的面积公式即可求解．【解答】在一个长方形内画一个最大的三角形，最大的三角形的底=长方形的长，最大的三角形的高=长方形的宽，故三角形的面积=三角形的底×三角形的高÷2=长方形的长×长方形的宽÷2=长方形面积的一半.选C.6.【答题】一个三角形和一个平行四边形等底等高，它们的面积比是（）.A. 3：1B. 1：3C. 2：1D. 1：2【答案】D【分析】本题主要考查等底等高的三角形于平行四边形面积之间的关系即等底等高的三角形的面积是平行四边形面积的．根据等底等高的三角形的面积是平行四边形面积的，因此，一个三角形和一个平行四边形等底等高，它们的面积比是1：2；因此解答．【解答】因为等底等高的三角形的面积是平行四边形面积的，所以，一个三角形和一个平行四边形等底等高，它们的面积比是1：2．选D.7.【答题】三角形中空白部分的面积是12平方厘米，蓝色部分的面积是______平方厘米.【答案】8【分析】此题考查的是有关三角形面积的计算.根据三角形面积＝底×高÷2，得出高＝面积×2÷底，三角形中空白部分的面积是12平方厘米，底为6厘米，求高为多少，代入数据即可.图中蓝色部分为三角形，蓝色部分的高与空白部分的高相等，所以再根据三角形的面积公式求出蓝色部分的面积即可.【解答】空白部分的高为：12×2÷6=4（厘米），蓝色部分的底为4厘米，蓝色部分的高与空白部分的高相等，为4厘米，求蓝色部分面积为多少，列式计算为：4×4÷2=8（平方厘米）.故此题的答案是8.8.【答题】一个平行四边形与一个三角形等底等高，平行四边形与三角形的面积之和为36平方厘米，那么三角形的面积是（）A. 18平方厘米B. 24平方厘米C. 6平方厘米D. 12平方厘米【答案】D【分析】本题主要考查平行四边形的面积与等底等高的三角形的面积的关系．依据三角形面积是与其等底等高的平行四边形面积的一半即可求解．【解答】解：设三角形的面积为x平方厘米，则平行四边形的面积为2x平方厘米.答：三角形的面积是12平方厘米．选D.9.【答题】一个三角形的底是4分米，高是3分米，面积是______平方分米.【答案】6【分析】此题考查的是三角形的面积.【解答】三角形的面积＝底×高÷2.一个三角形的底是4分米，高是3分米，面积是：4×3÷2＝6（平方分米）.故此题的答案是6.10.【答题】一个三角形的面积是22平方厘米，它的底是5.5厘米，高是（）厘米.A. 4B. 6C. 8D. 2【答案】C【分析】本题主要考查三角形面积公式的灵活应用．由“三角形的面积=底×高÷2”可得“高=三角形的面积×2÷底”，三角形的面积和底已知，代入公式即可求解．【解答】22×2÷5.5=8（厘米），这个三角形的高是8厘米．选C.11.【答题】在下图中，平行四边形的面积是阴影部分面积的（）.A. 3倍B. 4倍C. 6倍【答案】B【分析】从平行四边形的底边中点到对边中点连线，这样就把平行四边形分成了相等的两个小平行四边形，再根据平行四边形与它等底等高的三角形（阴影部分）面积的关系计算选出即可．【解答】从平行四边形的底边中点到对边中点连线，这样就把平行四边形分成了相等的两个小平行四边形，阴影部分是三角形，它的面积等于和它等底等高的小平行四边形面积的一半，所以大平行四边形的面积是阴影部分面积的2×2=4倍．选B.12.【答题】一个三角形和一个平行四边形的底相等，面积也相等，平行四边形的高是6厘米，那么三角形的高是12厘米．（）【答案】✓【分析】根据平行四边形的面积=底×高及三角形的面积=底×高÷2，推导一个平行四边形和一个三角形的面积相等，底边长相等时，三角形的高是平行四边形的高的2倍，再列式解答即可．【解答】因为一个三角形和一个平行四边形的底相等，面积也相等，所以三角形的高是平行四边形的高的2倍，即三角形的高为：6×2=12（厘米）．故此题是正确的.13.【答题】三角形的底边扩大到原来的2倍，高扩大到原来的3倍，它的面积（）.A.扩大到原来的3倍B.扩大到原来的5倍C.扩大到原来的6倍【答案】C【分析】根据三角形的面积=底×高÷2和积的变化规律进行解答即可.【解答】因为三角形的面积=底×高÷2，所以根据积的变化规律，一个三角形的底边扩大到原来的2倍，高扩大到原来的3倍，2×3=6，那么面积扩大到原来的6倍，选C.14.【答题】一个三角形的底和面积与一个平行四边形的底和面积分别相等，平行四边形的高是10cm，三角形的高是（）.A. 10cmB. 20cmC. 5crn【答案】B【分析】三角形的面积＝底×高÷2，平行四边形面积＝底×高.若三角形和平行四边形面积相等，底相等，则三角形的高的一半和平行四边形的高相等，即三角形的高是平行四边形的高的2倍，由此解答即可.【解答】平行四边形和三角形的面积相等，底也相等，平行四边形的高是10cm，那么三角形的高是10×2=20（cm）.选B.15.【答题】如果平行四边形比与它等底等高的三角形的面积大10平方厘米，那么这个三角形的面积是（）A.5平方厘米B.10平方厘米C.20平方厘米【答案】B【分析】依据三角形的面积是与它等底等高的平行四边形的面积的一半，由平行四边形比与它等底等高的三角形的面积大10平方厘米，可知大的部分就是平行四边形面积的一半，即三角形的面积，据此解答．【解答】根据题意，平行四边形比与它等底等高的三角形的面积大10平方厘米，即这个三角形的面积就是10平方厘米.选B.16.【答题】两个三角形的面积相等，底不相等，这两个三角形的高（）相等．A.可能B.一定C.不可能【答案】C【分析】根据三角形的面积=底×高÷2，得出底×高=面积×2，两个面积相等的三角形，则面积的2倍也相等，也就是底乘高相等；再根据积不变的性质即可求解．【解答】因为两个面积相等的三角形，则面积的2倍也相等，也就是底乘高相等；根据积不变的性质，所以说这两个三角形的底不相等，高不可能相等．选C.17.【答题】一个三角形的底是21分米，高是10分米，这个三角形的面积是（）平方分米．A.210B.105C.21【答案】B【分析】根据三角形的面积=底×高÷2，代数计算即可．【解答】21×10÷2=105（平方分米）．所以这个三角形的面积是105平方分米．选B.18.【答题】一个三角形的底和高都扩大到原来的10倍，那么面积（）.A.不变B.扩大到原来的20倍C.扩大到原来的100倍【答案】C【分析】根据三角形的面积=底×高÷2和积的变化规律进行解答即可.【解答】因为三角形的面积=底×高÷2，所以根据积的变化规律，一个三角形的底和高都扩大到原来的10倍，10×10=100，那么面积扩大到原来的100倍，选C.19.【答题】一个三角形的面积是25平方厘米，高是5厘米，它的底是（）厘米．A.4B.8C.10D.16【答案】C【分析】根据三角形的面积=底×高÷2，得出底＝面积×2÷高，据此代入数据即可求解．【解答】底是：25×2÷5=10（厘米）选C.20.【答题】图中，左边三角形的面积（）右边三角形的面积．A.＞B.＜C.=【答案】C【分析】根据中点的定义和等底同高的三角形面积相等的性质即可求解.【解答】因为中线将三角形分成两部分，所以左边三角形和右边三角形是等底同高的两个三角形，所以左边三角形的面积=右边三角形的面积.选C.。

保密★启用前第四单元多边形的面积（拓展卷）答案解析1．D【分析】设三个图形的高都是hcm，根据“三角形的面积＝底×高÷2”求出三角形的面积；根据“平行四边形的面积＝底×高”求出平行四边形的面积；根据“梯形的面积＝（上底＋下底）×高÷2”求出梯形的面积；进而比较即可得出结论。

【详解】三角形面积：6×h÷2＝3h（cm2）平行四边形面积：3h（cm2）梯形面积：（4＋2）×h÷2＝6h÷2＝3h（cm2）三角形面积＝平行四边形面积＝梯形面积。

比较图中的3个图形的面积大小，发现面积一样大。

故答案为：D【点睛】熟练掌握三角形面积公式、平行四边形面积公式、梯形面积公式是解答本题的关键。

2．A【分析】根据等腰直角三角形的特征，可知等腰直角三角形的两条直角边相等，分别是这个三角形的底和高，根据三角形的面积＝底×高÷2，代入数据解答即可。

【详解】6×6÷2＝18（平方厘米）它的面积是18平方厘米。

故答案为：A【点睛】本题主要考查了三角形的面积公式的灵活应用，要熟练掌握相关公式。

3．C【分析】等底等高的三角形面积等于平行四边形面积的一半，由此可知，阴影部分是三角形，用阴影部分面积×2，即可求出这个平行四边形的面积，据此解答。

【详解】66×2＝132（cm2）一个平行四边形（如图），阴影部分的面积是66cm2。

这个平行四边形的面积是132cm2。

故答案为：C【点睛】明确等底等高的三角形面积与平行四边形面积之间的关系是解答本题的关键。

4．C【分析】三角形面积＝底×高÷2，梯形面积＝（上底＋下底）×高÷2＝上下底的和×高÷2，观察可知，篱笆长度没变，三角形的高＝梯形的高，三角形的底＝梯形上底＋下底，根据三角形和梯形面积公式，举例说明即可。