概率论与数理统计公式整理(超全免费版)
- 格式:doc
- 大小:1.15 MB
- 文档页数:30

概率论与数理统计公式大全一、概率基本公式1.事件的概率:对于事件A,在随机试验中发生的次数记为n(A),则事件A的概率为P(A)=n(A)/n,其中n为试验总次数。
2.互斥事件的概率:对于互斥事件A和B,有P(A∪B)=P(A)+P(B)。
3.事件的余事件概率:设事件A为必然事件,全集的概率为P(S)=1,事件A的余事件为A',则有P(A')=1-P(A)。
4.条件概率:对于两个事件A和B,假设事件B已经发生,事件A发生的概率记为P(A,B),则P(A,B)=P(A∩B)/P(B)。
二、随机变量及其概率分布1.离散型随机变量:设X是一个离散型随机变量,其概率函数为P(X=k),其中k为X的取值,概率函数满足P(X=k)≥0,且∑P(X=k)=12. 连续型随机变量:设X是一个连续型随机变量,其概率密度函数为f(x),概率密度函数满足f(x)≥0,且∫f(x)dx = 13. 随机变量的数学期望:对于离散型随机变量X,其数学期望为E(X) = ∑k*P(X=k);对于连续型随机变量X,其数学期望为E(X)=∫xf(x)dx。
4. 随机变量的方差:对于离散型随机变量X,其方差为Var(X) =E(X^2) - [E(X)]^2;对于连续型随机变量X,其方差为Var(X) = E(X^2) - [E(X)]^2三、常见的概率分布1.伯努利分布:表示一次实验成败的概率分布,概率函数为P(X=k)=p^k(1-p)^(1-k),其中0≤p≤12.二项分布:表示n次独立重复的伯努利试验中成功次数的概率分布,概率函数为P(X=k)=C(n,k)*p^k(1-p)^(n-k),其中C(n,k)为组合数。
3. 泊松分布:表示单位时间或单位面积内发生事件次数的概率分布,概率函数为P(X=k) = (lambda^k)/(k!)*e^(-lambda),其中lambda为平均发生率。
4.均匀分布:表示在一个区间内取值相等的概率分布,概率密度函数为f(x)=1/(b-a),其中[a,b]为区间。

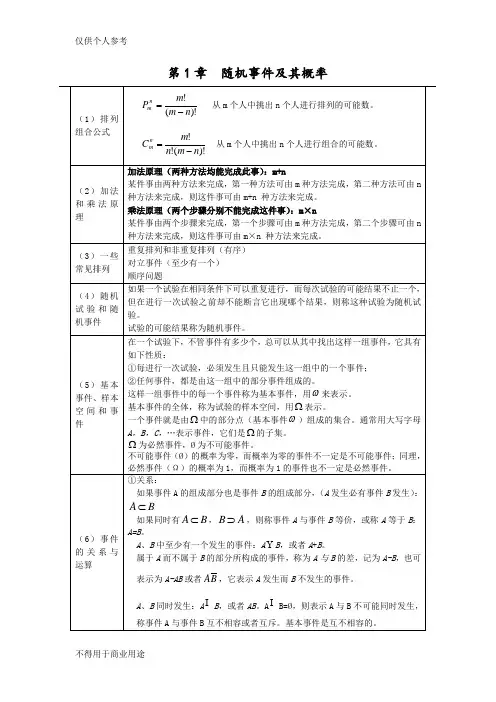


概率论与数理统计公式(全)2011-1-1第1章随机事件及其概率1概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-1第二章随机变量及其分布1概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-1第三章二维随机变量及其分布1概率论与数理统计公式(全)2011-1-1概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-1第四章随机变量的数字特征(1)离散型连续型1概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-1第五章大数定律和中心极限定理1概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-1第六章样本及抽样分布1概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-1第七章参数估计1概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-1第八章假设检验1概率论与数理统计公式(全)2011-1-11概率论与数理统计公式(全)2011-1-1单正态总体均值和方差的假设检验1。

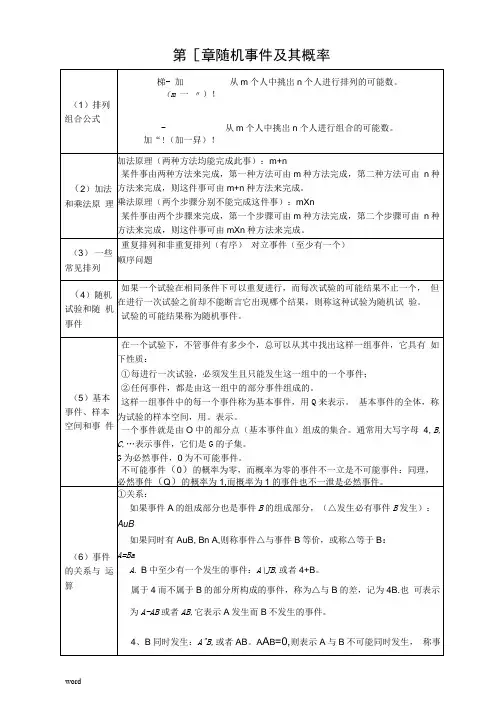
第[章随机事件及其概率第二章随机变量及其分布第三童二维随机变量及其分布个有序对<x,y),则称g 为离散型随机量。
设纟二(X, Y)的所有可能取值为(m )(ij = 12…), 且事件{纟=a,儿)}的概率为PH ,,称P{ (X, Y)=(兀,儿)}= “沁 J = 1,2,…)为疔=(X, 丫)的分布律或称为X 和丫的联合分布律。
联合分这里內具有下而两个性质:(1) P&0 (i,j=1,2,-): (2)工工 P'6i J(1)联合离散型分布如果二维随机向量纟(X, Y)的所有可能取值为至多可列设n 个随机变量…、X.相互独立,且服从标准正态分 布,可以证明它们的平方和的分布密度为“1 S1— -------- H - e 2 u > 0,y (w )= J 2I r I'{2) 0,u < 0.我们称随机变星w 服从自由度为n 的力2分布,记为w 〜 Z 2(n)>英中所谓自由度是指独立正态随机变量的个数,它是随机变量 分布中的一个重要参数。
力2分布满足可加性:设kZ+〃2 +・ • +代)・/-I*分布X ~AW )V ~F S ),可以证明函数T 亠 ylYIn的概率密度为我们称随机变量F 服从第一个自由度为山,第二个自由度为n 2 的F 分布,记为F-f(n b n 2).第四章随机变量的数字特征(1)离散型 连续型t 分布 设X, 丫是两个相互独立的随机变量.且H +I―(-co<r <+oc ).F 分布我们称随机变量T 服从自由度为n 的t 分布,记为T 〜t(n).设X ~力2(/“)丁~力2(心),且X 与丫独立,可以证明 尸=土仙的概率密度函数为Yin,t 2 + — n第五章大数定律和中心极限定理特姝情形:若X2,…具有相同的数学期望E(X I )=M , 则上式成为设u 是n 次独立试验中事件A 发生的次数,p 是事件A 在每次试验中发生的概率,则对于任意的正数£ •有lim;?->x伯努利大数左律说明,当试验次数n 很大时,事件A 发生 的频率与概率有较大判别的可能性很小,即这就以严格的数学形式描述了频率的稳立性。

概率论与数理统计完整公式概率论与数理统计是数学的一个分支,研究随机现象和随机变量之间的关系、随机变量的分布规律、经验规律及参数估计等内容。
在概率论与数理统计的学习中,有许多重要的公式需要掌握。
以下是概率论与数理统计的完整公式。
一、概率论公式:1.全概率公式:设A1,A2,…,An为样本空间S的一个划分,则对任意事件B,有:P(B)=P(B│A1)·P(A1)+P(B│A2)·P(A2)+…+P(B│An)·P(An)2.贝叶斯公式:对于样本空间S的一划分A1,A2,…,An,其中P(Ai)>0,i=1,2,…,n,并且B是S的任一事件,有:P(Ai│B)=[P(B│Ai)·P(Ai)]/[P(B│A1)·P(A1)+P(B│A2)·P(A2)+…+P (B│An)·P(An)]3.事件的独立性:若对事件A,B有P(AB)=P(A)·P(B),则称事件A,B相互独立。
4.概率的乘法公式:对于独立事件A1,A2,…,An,有:P(A1A2…An)=P(A1)·P(A2)·…·P(An)5.概率的加法公式:对事件A,B有:P(A∪B)=P(A)+P(B)-P(AB)6.条件概率的计算:对事件A,B有:P(A,B)=P(AB)/P(B)7.古典概型的概率计算:设事件A在n次试验中发生k次的次数服从二项分布B(n,p),则其概率可表示为:P(X=k)=C(n,k)·p^k·(1-p)^(n-k),其中C(n,k)=n!/[k!(n-k)!]二、数理统计公式:1.样本均值的期望和方差:样本的均值X̄的期望和方差分别为: E(X̄) = μ,Var(X̄) = σ^2 / n,其中μ 为总体的均值,σ^2 为总体方差,n 为样本容量。
2.样本方差的期望:样本方差S^2的期望为:E(S^2)=σ^2,其中σ^2为总体方差。