概率论与数理统计公式定理整理汇编
- 格式:doc
- 大小:406.49 KB
- 文档页数:10

概率论与数理统计公式大全一、概率基本公式1.事件的概率:对于事件A,在随机试验中发生的次数记为n(A),则事件A的概率为P(A)=n(A)/n,其中n为试验总次数。
2.互斥事件的概率:对于互斥事件A和B,有P(A∪B)=P(A)+P(B)。
3.事件的余事件概率:设事件A为必然事件,全集的概率为P(S)=1,事件A的余事件为A',则有P(A')=1-P(A)。
4.条件概率:对于两个事件A和B,假设事件B已经发生,事件A发生的概率记为P(A,B),则P(A,B)=P(A∩B)/P(B)。
二、随机变量及其概率分布1.离散型随机变量:设X是一个离散型随机变量,其概率函数为P(X=k),其中k为X的取值,概率函数满足P(X=k)≥0,且∑P(X=k)=12. 连续型随机变量:设X是一个连续型随机变量,其概率密度函数为f(x),概率密度函数满足f(x)≥0,且∫f(x)dx = 13. 随机变量的数学期望:对于离散型随机变量X,其数学期望为E(X) = ∑k*P(X=k);对于连续型随机变量X,其数学期望为E(X)=∫xf(x)dx。
4. 随机变量的方差:对于离散型随机变量X,其方差为Var(X) =E(X^2) - [E(X)]^2;对于连续型随机变量X,其方差为Var(X) = E(X^2) - [E(X)]^2三、常见的概率分布1.伯努利分布:表示一次实验成败的概率分布,概率函数为P(X=k)=p^k(1-p)^(1-k),其中0≤p≤12.二项分布:表示n次独立重复的伯努利试验中成功次数的概率分布,概率函数为P(X=k)=C(n,k)*p^k(1-p)^(n-k),其中C(n,k)为组合数。
3. 泊松分布:表示单位时间或单位面积内发生事件次数的概率分布,概率函数为P(X=k) = (lambda^k)/(k!)*e^(-lambda),其中lambda为平均发生率。
4.均匀分布:表示在一个区间内取值相等的概率分布,概率密度函数为f(x)=1/(b-a),其中[a,b]为区间。

概率论与数理统计公式定理全总结一、概率论公式:1.基本概率公式:对于随机试验E,事件A的概率可以表示为P(A)=事件A的样本点数/所有样本点数。
2.条件概率公式:对于事件A和事件B,若P(B)>,则事件A在事件B发生的条件下的概率可以表示为P(A,B)=P(A∩B)/P(B)。
3.全概率公式:对于互不相容事件A1,A2,...,An,它们的和事件为全样本空间S,且概率P(Ai)>,则对于任意事件B有P(B)=Σ(P(Ai)×P(B,Ai))。
4.贝叶斯公式:对于互不相容事件A1,A2,...,An,它们的和事件为全样本空间S,且概率P(Ai)>,则对于任意事件B,有P(Ai,B)=(P(B,Ai)×P(Ai))/Σ(P(B,Ai)×P(Ai))。
二、数理统计公式:1.期望:随机变量X的期望E(X)=Σ(Xi×P(Xi)),其中Xi为随机变量X的取值,P(Xi)为随机变量X取值为Xi的概率。
2. 方差:随机变量X的方差Var(X) = Σ((Xi - E(X))^2 ×P(Xi)),其中Xi为随机变量X的取值,E(X)为随机变量X的期望,P(Xi)为随机变量X取值为Xi的概率。
3. 协方差:随机变量X和Y的协方差Cov(X,Y) = E((X - E(X))(Y - E(Y))),其中E(X)和E(Y)分别为随机变量X和Y的期望。
4. 相关系数:随机变量X和Y的相关系数ρ(X,Y) = Cov(X,Y) / √(Var(X) × Var(Y)),其中Cov(X,Y)为随机变量X和Y的协方差,Var(X)和Var(Y)分别为随机变量X和Y的方差。
三、概率论与数理统计定理:1.大数定律:对于独立同分布的随机变量X1,X2,...,Xn,它们的均值X̄=(X1+X2+...+Xn)/n,当n趋向于无穷大时,X̄趋向于X的期望E(X)。
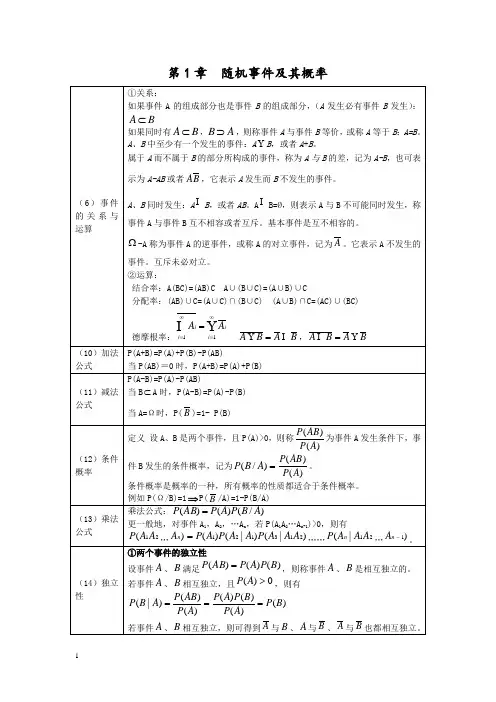

「 ef(x) w0,其中 0,则称随机变量X 服从参数为X 的分布函数为1xe, xF(x)'0,x<0。
记住积分公式:x ne xdx n!指数分布的指数分布如果二维随机向量(X, Y)的所有可能取值为至多可列个有序对(x,y),则称为离散型随机(1)联合分离散型布设=(X,Y)的所有可能取值为(X i,y j)(i,j 1,2,),且事件{ =(X i,y j)}的概率为P ij,,称P{(X,Y) (X i,y j)} P j(i,j 1,2,)为=(X,Y)的分布律或称为X和Y的联合分布律。
联合分布有时也用下面的概率分布表来表示:这里P ij具有下面两个性质(1)P ij>0 (i,j=1,2,…);(2)P j 1.i j(1)大数定律X 切比雪夫大数定律设随机变量冶,X2,…相互独立,均具有有限方差,且被同一常数C所界:D (X i) <C(i=1,2,…),则对于任意的正数£,有limnPLx,丄n i 1 n° E(X i)i 11特殊情形: 若X1,X2,…具有相同的数学期望 E (X)=「则上式成为lim Pn1n X i大数定辛钦大数定律1.设卩是n次独立试验中事件A发生的次数,p是事件A在每次试验中发生的概率,则对于任意的正数£,有limn伯努利大数定律说明,当试验次数小,即limn这就以严格的数学形式描述了频率的稳定性。
很大时,事件1.A发生的频率与概率有较大判别的可能性很0.设X1, X2,…,Xi,…是相互独立同分布的随机变量序列,且 E ( X n) =g,则对于任意的正数£有lim Pn1 nX in i 11.(2)中心极限定理2X N(,)n 格定理设随机变量X1,X2,…相互独立,服从同一分布,且具有相同的数学期望和方差:E(X k) ,D(X k) 0(k 1,2, ),则随机变量的分布函数F n(x)对任意的实数X,Y nnX k nk 1X k nlim F n(x) limn n此定理也称为独立同分布的中心极限定理。

概率论与数理统计公式大全概率论和数理统计作为数学的两个重要分支,被广泛应用于各个领域。
无论是在学术研究还是实际应用中,熟悉并掌握相关的公式是非常重要的。
本文将为您提供概率论与数理统计公式的大全,帮助您更好地理解和应用这两门学科。
一、概率论公式1. 概率公式- 概率的定义:P(A) = N(A) / N(S),其中P(A)表示事件A发生的概率,N(A)代表事件A的样本点个数,N(S)表示样本空间中的样本点总数。
- 加法法则:P(A∪B) = P(A) + P(B) - P(A∩B),其中P(A∪B)表示事件A或事件B发生的概率,P(A∩B)表示事件A和事件B同时发生的概率。
- 乘法法则:P(A∩B) = P(A) × P(B|A),其中P(B|A)表示在事件A 发生的条件下,事件B发生的概率。
2. 条件概率公式- 条件概率的定义:P(A|B) = P(A∩B) / P(B),其中P(A|B)表示在事件B发生的条件下,事件A发生的概率。
- 全概率公式:P(A) = ∑[P(Bi) × P(A|Bi)],其中Bi为样本空间的一个划分,P(Bi)表示事件Bi发生的概率,P(A|Bi)表示在事件Bi发生的条件下,事件A发生的概率。
3. 事件独立性公式- 事件A和事件B独立的定义:P(A∩B) = P(A) × P(B),即事件A和事件B同时发生的概率等于事件A发生的概率乘以事件B发生的概率。
- 事件的相互独立:若对于任意的事件A1,A2,...,An,有P(A1∩A2∩...∩An) = P(A1) × P(A2) × ... × P(An),则称事件A1,A2,...,An相互独立。
4. 随机变量- 随机变量的定义:随机变量X是样本空间到实数集的映射。
- 随机变量的分布函数:F(x) = P(X≤x),表示随机变量X小于等于x的概率。
- 随机变量的概率密度函数(连续型随机变量):f(x)是非负函数,且对于任意实数区间[a, b],有P(a≤X≤b) = ∫[a, b]f(x)dx。

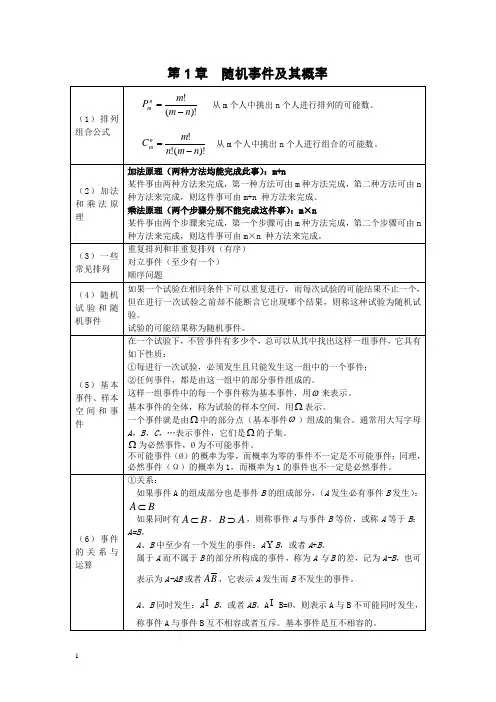

概率论与数理统计公式大全一、概率论公式1.概率的基本性质:-非负性:对于任意事件A,有P(A)>=0;-规范性:对于必然事件S,有P(S)=1;-可列可加性:对于互不相容的事件Ai(i=1,2,...),有P(A1∪A2∪...)=P(A1)+P(A2)+...。
2.条件概率:-事件B发生的条件下,事件A发生的概率:P(A,B)=P(A∩B)/P(B);-乘法公式:P(A∩B)=P(A,B)*P(B)。
3.全概率公式:-事件A的概率:P(A)=ΣP(A,Bi)*P(Bi),其中Bi为样本空间的一个划分。
4.贝叶斯公式:-事件Bi发生的条件下,事件A发生的概率:P(Bi,A)=P(A,Bi)*P(Bi)/ΣP(A,Bj)*P(Bj),其中Bj为样本空间的一个划分。
5.独立性:-事件A与事件B相互独立的充要条件是P(A∩B)=P(A)*P(B)。
二、数理统计公式1.随机变量的概率分布:-离散型随机变量的概率分布函数:P(X=x);-连续型随机变量的概率密度函数:f(x)。
2.数理统计的基本概念:-样本均值:X̄=ΣXi/n;-样本方差:s^2=Σ(Xi-X̄)^2/(n-1);-样本标准差:s=√s^2;- 样本协方差:sxy = Σ(Xi-X̄)(Yi-Ȳ) / (n-1)。
3.大数定律:-样本均值的大数定律:当样本容量n趋向于无穷大时,样本均值X̄趋向于总体均值μ。
4.中心极限定理:-样本均值的中心极限定理:当样本容量n足够大时,样本均值X̄服从近似正态分布。
5.参数估计:-点估计:用样本统计量对总体参数进行估计;-置信区间估计:用样本统计量构造一个区间,以估计总体参数的范围。
6.假设检验:-假设检验的基本步骤:提出原假设H0和备择假设H1,选择适当的检验统计量,计算拒绝域,进行假设检验。
以上只是概率论与数理统计中的一些重要公式和定理,还有很多其他的公式和定理没有一一列举。
掌握这些公式和定理,可以帮助我们更好地理解和应用概率论与数理统计的知识。

第1章随机事件及其概率例1.16 设某人从一副扑克中(52张)任取13张,设A 为“至少有一张红桃”,B 为“恰有2张红桃”,C 为“恰有5张方块”,求条件概率P (B |A ),P (B |C )解135213391352135213391)(1)(C C C C C A P A P -=-=-=13521139213)(C C C AB P ⋅=13391352113921313521339135213521139213)()()(C C C C C C C C C C A P AB P A B P -=-==1352839513)(C C C C P =1352626213513)(C C C C BC P =83962621313528395131352626213513)()()(C C C C C C C C C C C P BC P C B P ===例1.21 某工厂生产的产品以100件为一批,假定每一批产品中的次品最多不超过4件,且具有如下的概率:一批产品中的次品数0 1 2 3 4概率0.1 0.2 0.4 0.2 0.1现进行抽样检验,从每批中随机抽取10件来检验,若发现其中有次品,则认为该批产品不合格。
求一批产品通过检验的概率。
4()()()kk k P B P AP B A ==∑解设B 表示事件“一批产品通过检验”,A i (i =0,1,2,3,4)表示“一批产品含有i 件次品”,则A 0,A 1, A 2, A 3, A 4组成样本空间的一个划分,00()0.1,()1P A P B A ==10991110100()0.2,()0.900C P A P B A C ===10982210100()0.4,()0.809C P A P B A C ===10973310100()0.2,()0.727C P A P B A C ===10964410100()0.1,()0.652C P A P B A C ===814.0652.01.0727.02.0809.04.0900.0.021.0≈⨯+⨯+⨯+⨯+=顾客买到的一批合格品中,含次品数为0的概率是0004()(|)0.11(|)0.1230.814()(|)ii i P A P B A P A B P A P B A =⋅⨯==≈⋅∑类似可以计算顾客买到的一批合格品中,含次品数为1、2、3、4件的概率分别约为0.221、0.398、0.179、0.080。
概率论与数理统计常用公式整理1. 概率论公式(1)概率定义:对于随机事件A,概率P(A)的定义为:P(A) = N(A) / N,其中N(A)为事件A发生的次数,N为试验总次数。
(2)加法定理:对于两个事件A和B,有:P(A ∪B) = P(A) + P(B) - P(A∩B)。
(3)乘法定理:对于两个独立事件A和B,有:P(A ∩B) = P(A) ×P(B)。
(4)条件概率:对于事件A和B,且P(A) > 0,条件概率P(B|A)定义为:P(B|A) = P(A ∩B) / P(A)。
(5)全概率公式:对于一组互斥事件A1, A2, ..., An,且它们的并集构成了样本空间,有:P(B) = Σ[P(B|Ai) ×P(Ai)],其中Σ表示求和。
(6)贝叶斯公式:对于一组互斥事件A1, A2, ..., An,且它们的并集构成了样本空间,有:P(Ai|B) = [P(B|Ai) ×P(Ai)] / P(B)。
2. 数理统计公式(1)样本均值:对于样本x1, x2, ..., xn,样本均值定义为:x̄= (x1 + x2 + ...+ xn) / n。
(2)样本方差:对于样本x1, x2, ..., xn,样本方差定义为:s^2 = [(x1 - x̄)^2+ (x2 - x̄)^2 + ... + (xn - x̄)^2] / (n - 1)。
(3)样本标准差:对于样本x1, x2, ..., xn,样本标准差定义为:s = √[s^2]。
(4)期望值:对于随机变量X,其期望值定义为:E(X) = Σ[x ×P(X =x)],其中Σ表示求和。
(5)方差:对于随机变量X,其方差定义为:Var(X) = E[(X - E(X))^2]。
(6)协方差:对于两个随机变量X和Y,其协方差定义为:Cov(X, Y) = E[(X- E(X))(Y - E(Y))]。
概率论与数理统计公式集锦HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】概率论与数理统计公式集锦一、随机事件与概率二、随机变量及其分布1、分布函数2、离散型随机变量及其分布3、续型随机变量及其分布4、随机变量函数Y=g(X)的分布 离散型:()(),1,2,j ii j g x y P Y y p i ====∑,连续型:①分布函数法,②公式法()(())()(())Y X f y f h y h y x h y '=⋅=单调三、多维随机变量及其分布1、离散型二维随机变量及其分布 分布律:(,),,1,2,i j ij P Xx Y y p i j ====分布函数(,)i i ijx x y yF X Y p ≤≤=∑∑边缘分布律:()i i ij jp P X x p ⋅===∑ ()j j ij ip P Y y p ⋅===∑条件分布律:(),1,2,ij i j jp P X x Y y i p ⋅====,(),1,2,ij j i i p P Y y X x j p ⋅====2、连续型二维随机变量及其分布①联合分布函数及性质分布函数:⎰⎰∞-∞-=xydudvv u f y x F ),(),(=P (X<=x,Y<=y )性质:2(,)(,)1,(,),F x y F f x y x y∂+∞+∞==∂∂((,))(,)GP x y G f x y dxdy ∈=⎰⎰②边缘分布函数与边缘密度函数分布函数:⎰⎰∞-+∞∞-=xX dvdu v u f x F ),()( 密度函数:⎰+∞∞-=dv v x f x f X ),()(③条件概率密度+∞<<-∞=y x f y x f x y f X X Y ,)(),()(,+∞<<-∞=x y f y x f y x f Y Y X ,)(),()( 3、随机变量的独立性随机变量X 、Y 相互独立(,)()()X Y F x y F x F y ⇔=,离散型:..ij i j p p p = ,连续型:(,)()()X Y f x y f x f y =4、二维随机变量和函数的分布 离散型:()(,)i j kk i j x y z P Z z P X x Y y +=====∑连续型:()(,)(,)Z f z f x z x dx f z y y dy +∞+∞-∞-∞=-=-⎰⎰四、随机变量的数字特征1、数学期望①定义:离散型∑+∞==1)(k k k p x X E ,连续型⎰+∞∞-=dx x xf X E )()(②性质:(),E C C =)()]([X E X E E =,)()(X CE CX E =,)()()(Y E X E Y X E ±=±b X aE b aX E ±=±)()( ,当X 、Y 相互独立时:)()()(Y E X E XY E =2、方差①定义:222()[(())]()()D X E X E X E X E X =-=-②性质:0)(=C D ,)()(2X D a b aX D =±,),(2)()()(Y X Cov Y D X D Y X D ±+=±当X 、Y 相互独立时:)()()(Y D X D Y X D +=±3、协方差与相关系数①协方差:(,)()()()Cov X Y E XY E X E Y =-,当X 、Y 相互独立时:0),(=Y X Cov ②相关系数:XY ρ,当X 、Y 相互独立时:0=XY ρ(X,Y 不相关)③协方差和相关系数的性质:)(),(X D X X Cov =,),(),(X Y Cov Y X Cov =),(),(),(2121Y X Cov Y X Cov Y X X Cov +=+,),(),(Y X abCov d bY c aX Cov =++4、常见随机变量分布的数学期望和方差五、大数定律与中心极限定理1、切比雪夫不等式若,)(,)(2σμ==X D X E 对于任意0>ε有2)(})({εεX D X E X P ≤≥-2、大数定律: ①切比雪夫大数定律:若n X X 1相互独立,2)(,)(i i i i X D X E σμ==且C i ≤2σ,则:∑∑==∞→−→−ni iPni i n X E nX n11)(),(11②伯努利大数定律:设n A 是n 次独立试验中事件A 发生的次数,p 是事件A 在每次试验中发生的概率,则0ε∀>,有:lim 1A n n P p n ε→∞⎛⎫-<= ⎪⎝⎭③辛钦大数定律:若1,,n X X 独立同分布,且μ=)(i X E ,则μ∞→=−→−∑n P ni iXn113、中心极限定理①列维—林德伯格中心极限定理:独立同分布的随机变量(1,2,)i X i =,均值为μ,方差为02>σ,当n充分大时有:1((0,1)~nn k k Y X n N μ==-−−→∑ ②棣莫弗—拉普拉斯中心极限定理:随机变量),(~p n B X ,则对任意x 有:③近似计算:1()nk k P a X b =≤≤≈Φ-Φ∑ 概率论与数理统计公式整理1、总体和样本的分布函数 设总体()XF x ,则样本的联合分布函数)(),(121k nk n x F x x x F =∏=2、统计量样本均值:∑==ni i X nX 11,样本方差:∑∑==--=--=ni i ni i X n X n X X n S 122122)(11)(11 样本标准差:∑=--=ni i X X n S 12)(11 ,样本k 阶原点距: 2,1,11==∑=kXnA ni ki k样本k 阶中心距:11(),1,2,3n k k i i B X X k n ==-=∑3、三大抽样分布(1)2χ分布:设随机变量(0,1)i X N (1,2,,)i n =且相互独立,则称统计量222212n X X X ++=χ服从自由度为n 的2χ分布,记为)(~22n χχ性质:①n n D n n E 2)]([,)]([22==χχ②设)(~),(~22n Y m X χχ且相互独立,则)(~2n m Y X ++χ(2)t 分布:设随机变量)(~),1,0(~2n Y N X χ,且X 与Y 独立,则称统计量:nY X T =服从自由度为n 的t 分布,记为)(~n t T性质:①()0(1),()(2)2n E T n D T n n =>=>-②22lim ()()x n n f x x ϕ-→∞== (3)F 分布:设随机变量22~(),~()X m Y n χχ,且X 与Y 独立,则称统计量(,)X mF m n Y n=服从第一自由度为m ,第二自由度为n 的F 分布,记为~(,)F F m n ,性质:设~(,)F F m n ,则1~(,)F n m F七、参数估计1.参数估计①定义:用12(,,,)n X X X θ∧估计总体参数θ,称12(,,,)n X X X θ∧为θ的估计量,相应的12(,,,)n x x x θ∧为总体θ的估计值。
第1章随机事件及其概率
我们作了n次试验,且满足
每次试验只有两种可能结果,A发生或A不发生;
n次试验是重复进行的,即A发生的概率每次均一样;
每次试验是独立的,即每次试验A 发生与否与其他次试验A 发生与否是互不影响的。
这种试验称为伯努利概型,或称为n 重伯努利试验。
用p 表示每次试验A 发生的概率,则A 发生的概率为q p =-1,用)(k P n 表示n 重伯努利试验中A 出现)0(n k k ≤≤次的概率,
k n k k
n n q p k P C -=)(,n k ,,2,1,0 =。
第二章 随机变量及其分布
第三章二维随机变量及其分布
第四章随机变量的数字特征
第五章大数定律和中心极限定理
第六章样本及抽样分布
第七章参数估计
第八章假设检验
单正态总体均值和方差的假设检验。
概率论与数理统计公式集锦
一、随机事件与概率
二、随机变量及其分布
1、分布函数性质
()()(),()()()
()k k x x
x P X x F x P X x P a X b F b F a f t dt
2、离散型随机变量及其分布
3、连续型随机变量及其分布
4、随机变量函数Y=g(X)的分布 离散型:()(),1,2,j i
i j g x y P Y y p i
L ,
连续型:①分布函数法,②公式法()(())()(())Y X f y f h y h y x h y 单调
三、多维随机变量及其分布
1、离散型二维随机变量及其分布
分布律:(,),,1,2,i j ij P X x Y y p i j L 分布函数(,)i i ij
x x y y
F X Y p
边缘分布律:()i i ij j
p P X x p ()j j ij
i
p P Y y p
条件分布律:(),1,2,ij i j j
p P X x Y y i p
L ,(),1,2,ij j i i p P Y y X x j p
L
2、连续型二维随机变量及其分布 ①分布函数及性质 分布函数:
x y
dudv v u f y x F ),(),(
性质:2(,)
(,)1,(,),F x y F f x y x y
((,))(,)G
P x y G f x y dxdy
②边缘分布函数与边缘密度函数 分布函数:
x
X dvdu v u f x F ),()(密度函数:
dv v x f x f X ),()(
y
Y dudv v u f y F ),()(
du y u f y f Y ),()(
③条件概率密度
y x f y x f x y f X X Y ,)(),()(, x y f y x f y x f Y Y X ,)
()
,()(
3、随机变量的独立性
随机变量X 、Y 相互独立(,)()()X Y F x y F x F y , 离散型:..ij i j p p p ,连续型:(,)()()X Y f x y f x f y 4、二维随机变量和函数的分布 离散型:()(,)i j k
k i j x y z P Z z P X x Y y
连续型:()(,)(,)Z f z f x z x dx f z y y dy
四、随机变量的数字特征
1、数学期望
①定义:离散型
1
)(k k k p x X E ,连续型
dx x xf X E )()(
②性质:(),E C C )()]([X E X E E ,)()(X CE CX E ,)()()(Y E X E Y X E b X aE b aX E )()(,当X 、Y 相互独立时:)()()(Y E X E XY E
2、方差
①定义:222()[(())]()()D X E X E X E X E X
②性质:0)( C D ,)()(2X D a b aX D ,),(2)()()(Y X Cov Y D X D Y X D 当X 、Y 相互独立时:)()()(Y D X D Y X D 3、协方差与相关系数
①协方差:(,)()()()Cov X Y E XY E X E Y ,当X 、Y 相互独立时:0),( Y X Cov ②相关系数:
XY
,当X 、Y 相互独立时:0 XY
(X,Y 不相关)
③协方差和相关系数的性质:)(),(X D X X Cov ,),(),(X Y Cov Y X Cov ),(),(),(2121Y X Cov Y X Cov Y X X Cov ),(),(Y X abCov d bY c aX Cov
4、随机变量分布的期望和方差
五、大数定律与中心极限定理
1、切比雪夫不等式
若,)(,)(2 X D X E 对于任意0 有2
)
(})({
X D X E X P
2、大数定律:①切比雪夫大数定律:若n X X 1相互独立, 2
)
(,)(i i i i X D X E 且C i 2
,则:
n
i i
P
n
i i n X E n
X n
1
1
)(),(1
1
②伯努利大数定律:设n A 是n 次独立试验中事件A 发生的次数,p 是事件A 在每次试验中发生的概率,则0 ,有:lim 1A n n P p n
③辛钦大数定律:若1,,n X X L 独立同分布,且 )(i X E ,则
n P
n
i i X n
1
1
3、中心极限定理
①独立同分布的中心极限定理:均值为 ,方差为02 的独立同分布时,
当n 充分大时有:)1,0(~1
N n n X
Y n
k k
n
②拉普拉斯定理:随机变量),(~p n B X 则对任意x 有:
x
t x x dt
e
x p np np X P )(21})
1({
lim 22
③近似计算:
)(
)(
)(
)(1
1
n n a n n b n n b n n X
n n a P b X
a P n
k k
n
k k
六、数理统计的基本概念
1、总体和样本
总体X 的分布函数)(x F 样本),(21n X X X 的联合分布为)(),(121k n
k n x F x x x F
2、统计量 (1)样本均值:
n
i i X n
X 1
1
(2)样本方差:
n
i i n
i i X n X n X X n S 1
22122
)(11
)(11 (3)样本标准差:
n
i i X X n S 12)(11 (4)样本k 阶距: 2,1,1
1
k
X
n
A n
i k
i k
(5)样本k 阶中心距:
n
i k i
k k k X X
n
M B 1
3,2,)(1
3、三大抽样分布
(1)2 分布:设随机变量n X X X 21,相互独立,且都服从标准正态分布)1,0(N ,则随机变量
2
22212n X X X 所服从的分布称为自由度为n 的2 分布,记为)(~22n
性质:①n n D n n E 2)]([,)]([22 ②设)(~),(~22n Y m X 且相互独立,则)(~2n m Y X
(2)t 分布:设随机变量)(~),1,0(~2n Y N X ,且X 与Y 独立,则随机变量:n
Y X T
所服
从的分布称为自由度的n 的t 分布,记为)(~n t T
性质:①()0(1),()(2)2n E T n D T n n
②2
2lim ()()x n n f x x
(3)F 分布:设随机变量)(~),(~2212n V n U ,且U 与V 独立,则随机变量2
1
21),(n V n U n n F
所服从的分布称为自由度),(21n n 的F 分布, 记为),(~21n n F F ,性质:设12~(,)X F n n ,则
211
~(,)F n n X
七、参数估计
1.参数估计
(1) 定义:用),,(21n X X X
估计总体参数 ,称),,(21n X X X
为 的估计量,相应的
12(,,,)n x x x
L 为总体 的估计值。
(2) 当总体是正态分布时,未知参数的矩估计值=未知参数的极大似然估计值 2.点估计中的矩估计法:(总体矩=样本矩) 样本均值:
n
i i X n
X E X 1
1)(或dx x xf X E X
),()(
求法步骤:设总体X 的分布中包含有未知参数12,,,k L ,它的前k 阶原点矩
()(1,2,,)
i i E X i k L 中包含了未知参数
12,,,k
L ,即
12(,,,)(1,2,,)i i k g i k L L 。
又设n x x x ,,,21 为总体X 的n 个样本值,用样本矩
1
1(1,2,,)n i
i j j A X i k n L 代替i ,在所建立的方程组中解出的k 个未知参数即为参数
12,,,k L 的矩估计量12,,,k
L
3.点估计中的极大似然估计
极大似然估计法:n X X X ,,21取自X 的样本,设),(~ x f X 或~(,)X P x , 求法步骤: ①似然函数:])([),()(1
1
n
i i
n i i
P x f L 或
②取对数:1
ln ()ln (,)n i
i L f x
或1
ln ()ln ()n
i
i L p
③解方程:0ln ,,0ln 1 k L
L ,解得:111212(,,,)(,,,)
n k k n x x x x x x
L L L
L 4.估计量的评价标准
5. 单正态总体参数的置信区间
八
假设
检
验
1.假设检验的基本概念
2.单正态总体均值和方差的假设检验。