3.2 闭环系统的传递函数

一个反馈控制系统在工作过程中，一般会受到两类信号的作用，统称外作用。

一类是有用信号或称输入信号、给定值、指令等，用)(t r 表示。

通常)(t r 是加在控制系统的输入端，也就是系统的输入端；另一类则是扰动，或称干扰)(t n ，而干扰)(t n ，可以出现在系统的任何位置，但通常，最主要的干扰信号是作用在被控对象上的扰动，例如电动机的负载扰动等。

一、系统的开环传递函数系统反馈量与误差信号的比值，称为闭环系统的开环传递函数，二、系统的闭环传递函数1、输入信号)(s R 作用下的闭环传递函数令0)(=s D ，这时图1可简化成图2(a)。

输出)(s C 对输入)(s R 之间的传递函数，称输入作用下的闭环传递函数，简称闭环传递函数，用)(s Φ表示。

而输出的拉氏变换式为2、干扰)(s D 作用下的闭环传递函数同样，令0)(=s R ，结构图1可简化为图3(a)。

以)(s D 作为输入，)(s C 为在扰动作用下的输出，它们之间的传递函数，用)(s n Φ表示，称为扰动作用下的闭环传递函数，简称干扰传递函数。

系统在扰动作用下所引起的输出为三、系统的误差传递函数系统的误差信号为)(s E ,误差传递函数也分为给定信号作用下的误差传递函数和扰动信号作用下的传递函数。

前者表征系统输出跟随输入信号的能力，后者反映系统抗扰动的能力。

1、输入信号)(s R 作用下的误差传递函数为了分析系统信号的变化规律，寻求偏差信号与输入之间的关系，将结构图简化为如图2)(b 。

列写出输入)(s R 与输出)(s ε之间的传递函数，称为控制作用下偏差传递函数。

用表示。

)()()()()()()()(21s H s G s H s G s G s E s B s G K ===)()()(21s G s G s G =)()(1)()()()(1)()()()()(2121s H s G s G s H s G s G s G s G s R s C s +=+==Φ)()()()(1)()()(2121s R s H s G s G s G s G s C +=)()(1)()()()(1)()()()(2212s H s G s G s H s G s G s G s N s C s n +=+==Φ)()()()(1)()(212s N s H s G s G s G s C +=)()()(s R s s εΦε=2、干扰)(s D 作用下的误差传递函数同理，干扰作用下的偏差传递函数，称干扰偏差传递函数。

已知单位反馈系统的开环传递函数求闭环传递函数为了求解单位反馈系统的闭环传递函数，我们需要先了解单位反馈系统和闭环传递函数的一些基本概念。

单位反馈系统是一种常见的控制系统结构，由三个主要部分组成：开环传递函数、比例增益和反馈信号。

开环传递函数是指系统输出与输入之间的关系，也被称为系统的传输函数。

它表示在没有反馈的情况下，输入信号对输出信号的影响。

通常用H(s)表示，其中s是复变量。

比例增益是一个常数，用来调整输入信号对输出信号的影响，通常用K表示。

反馈信号是系统输出的一部分，用来校正系统的行为。

在单位反馈系统中，反馈信号等于系统的输出信号。

闭环传递函数是反馈控制系统中最重要的性能指标之一，它表示反馈控制系统中输入信号对输出信号的影响。

闭环传递函数可以通过将开环传递函数与比例增益进行组合来计算。

现在，我们将通过以下步骤来求解单位反馈系统的闭环传递函数。

步骤1：给定开环传递函数H(s)，计算比例增益K。

步骤2：使用单位反馈系统的定义，建立闭环传递函数Y(s)/X(s)的表达式。

步骤3：将开环传递函数H(s)替换为相应的表达式，计算闭环传递函数。

下面是对每个步骤的详细说明。

步骤1：给定开环传递函数H(s)，计算比例增益K。

比例增益K是一个常数，可以通过将开环传递函数的极点值代入到单位反馈系统的传递函数中进行计算。

假设开环传递函数H(s)的极点是p1，p2，...，pn，那么比例增益K可以计算为K = 1 / (p1 * p2 * ... * pn)。

步骤2：使用单位反馈系统的定义，建立闭环传递函数Y(s)/X(s)的表达式。

根据单位反馈系统的定义，闭环传递函数Y(s)/X(s)可以表示为Y(s)/X(s)=K*H(s)/(1+K*H(s))。

步骤3：将开环传递函数H(s)替换为相应的表达式，计算闭环传递函数。

将开环传递函数H(s)替换为相应的表达式后，闭环传递函数可以进一步简化为Y(s)/X(s)=K*(表达式)/(1+K*(表达式))。

机电控制工程基础综合练习解析一、填空1. 自动控制就是 没有 人直接参与的情况下， 使生产过程的输出量按照给定的规律运行或变化 。

2．系统的稳定性取决于 系统闭环极点的分布 。

3. 所谓反馈控制系统就是的系统的输出 全部或部分 地返回到输入端。

积分环节的相频特性)(ωϕ为 90°。

4. 给定量的变化规律是事先不能确定的，而输出量能够准确、迅速的复现给定量，这样的系统称之为随动系统 。

5. 在 零初始条件 下，输出量的拉氏变换与输入量的拉氏变换之比称为线性系统（或元件）的 传递函数 。

6. 单位积分环节的传递函数为 1/s 。

7．一阶系统11+Ts ，则其时间常数为 T 。

8．系统传递函数为W(s)，输入为单位阶跃函数时，输出拉氏变换Y (s)为 ss W )( 。

9．单位负反馈系统开环传函为)1(9)(+=s s s G ，系统的阻尼比ξ=0.167、无阻尼自振荡角频率ωn 为 3 ，调节时间ts （5％）为 6 秒。

10．反馈信号(或称反馈)：从系统(或元件)输出端取出信号，经过变换后加到系统(或元件)输入端，这就是反馈信号。

当它与输入信号符号相同，即反馈结果有利于加强输入信号的作用时叫 正反馈 。

反之，符号相反抵消输入信号作用时叫 负反馈 。

11．Ⅰ型系统 不能 无静差地跟踪单位斜坡输入信号。

12. 某环节的传递函数为2s ，则它的幅频特性的数学表达式是 ，相频特性的数学表达式是 。

2ω；90o13.单位反馈系统的开环传递函数为)3)(2()(*++=s s s K s G ，根轨迹的分支数为 3 。

14. 负反馈结构的系统，其前向通道上的传递函数为G(s)，反馈通道的传递函数为H(s)，则该系统的开环传递函数为 ，闭环传递函数为 。

G(s)H(s)，)()(1)(s H s G s G +15. 函数f(t)=2t 的拉氏变换为 。

22s16．单位负反馈结构的系统，其开环传递函数为)2(+s s K则该系统为 型系统，根轨迹分支数为 。

3-1 设系统的微分方程式如下：（1） )(2)(2.0t r t c= （2） )()()(24.0)(04.0t r t c t c t c=++ 试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。

已知全部初始条件为零。

解：（1） 因为)(2)(2.0s R s sC =闭环传递函数ss R s C s 10)()()(==Φ 单位脉冲响应：s s C /10)(= 010)(≥=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(≥=t t t c（2）)()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C `闭环传递函数124.004.01)()()(2++==s s s R s C s φ单位脉冲响应：124.004.01)(2++=s s s C t e t g t 4sin 325)(3-= 单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s C t e t e t c t t 4sin 434cos 1)(33----=3-2 温度计的传递函数为11+Ts ，用其测量容器内的水温，1min 才能显示出该温度的98%的数值。

若加热容器使水温按10ºC/min 的速度匀速上升，问温度计的稳态指示误差有多大解法一 依题意，温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知：o o T c 98)4(=，因此有 min 14=T ，得出 min 25.0=T 。

视温度计为单位反馈系统，则开环传递函数为Tss s s G 1)(1)()(=Φ-Φ=⎩⎨⎧==11v TK ！用静态误差系数法，当t t r ⋅=10)( 时，C T Ke ss ︒===5.21010。

解法二 依题意，系统误差定义为 )()()(t c t r t e -=，应有 1111)()(1)()()(+=+-=-==ΦTs TsTs s R s C s R s E s e C T sTs Ts ss R s s e s e s ss ︒==⋅+=Φ=→→5.210101lim )()(lim 203-3 已知二阶系统的单位阶跃响应为)1.536.1sin(5.1210)(2.1o tt et c +-=-试求系统的超调量σ％、峰值时间ｔp 和调节时间ｔs 。

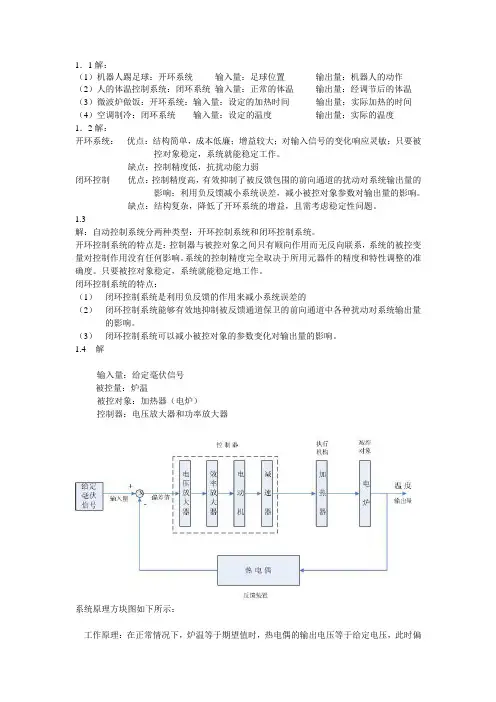
1．1解：（1）机器人踢足球：开环系统输入量：足球位置输出量：机器人的动作（2）人的体温控制系统：闭环系统输入量：正常的体温输出量：经调节后的体温（3）微波炉做饭：开环系统：输入量：设定的加热时间输出量：实际加热的时间（4）空调制冷：闭环系统输入量：设定的温度输出量：实际的温度1．2解：开环系统：优点：结构简单，成本低廉；增益较大；对输入信号的变化响应灵敏；只要被控对象稳定，系统就能稳定工作。

缺点：控制精度低，抗扰动能力弱闭环控制优点：控制精度高，有效抑制了被反馈包围的前向通道的扰动对系统输出量的影响；利用负反馈减小系统误差，减小被控对象参数对输出量的影响。

缺点：结构复杂，降低了开环系统的增益，且需考虑稳定性问题。

1.3解：自动控制系统分两种类型：开环控制系统和闭环控制系统。

开环控制系统的特点是：控制器与被控对象之间只有顺向作用而无反向联系，系统的被控变量对控制作用没有任何影响。

系统的控制精度完全取决于所用元器件的精度和特性调整的准确度。

只要被控对象稳定，系统就能稳定地工作。

闭环控制系统的特点：（1）闭环控制系统是利用负反馈的作用来减小系统误差的（2）闭环控制系统能够有效地抑制被反馈通道保卫的前向通道中各种扰动对系统输出量的影响。

（3）闭环控制系统可以减小被控对象的参数变化对输出量的影响。

1.4解输入量：给定毫伏信号被控量：炉温被控对象：加热器（电炉）控制器：电压放大器和功率放大器系统原理方块图如下所示：工作原理：在正常情况下，炉温等于期望值时，热电偶的输出电压等于给定电压，此时偏差信号为零，电动机不动，调压器的滑动触点停留在某个合适的位置上。

此时，炉子散失的热量正好等于从加热器获取的热量，形成稳定的热平衡状态，温度保持恒定。

当炉温由于某种原因突然下降时，热电偶的输出电压下降，与给定电压比较后形成正偏差信号，该偏差信号经过电压放大器、功率放大器放大后，作为电动机的控制电压加到电动机上，电动机带动滑线变阻器的触头使输出电压升高，则炉温回升，直至达到期望值。

参考答案3-1. 设温度计需要在一分钟内指示出响应值的98%，并且假设温度计为一阶系统，求时间常数T 。

如果将温度计放在澡盆内，澡盆的温度以10/min C ︒的速度线性变化，求温度计的误差。

解：()()98%c t c =∞⨯，41min t T ==，0.25T =；()10r t t =，()10()t Tc t t T e-=-+，()()()10()tTe t r t c t T e-=-=-，lim ()10 2.5ss t e e t T →∞===3-2．已知单位负反馈系统的开环传递函数为4()5G s s =+ 求系统的单位阶跃响应。

解：24()54s s s φ=++，1()R s s=， 21444133()()()(54)(4)(1)41C s s R s s s s s s s s s s φ=⋅===+-++++++； 414()133t t c t e e --=+-3-3. 已知单位负反馈系统的开环传递函数为1()(1)G s s s =+ 求系统的上升时间r t 、峰值时间p t 、超调量%σ和调整时间s t 。

解：2()1()1G s R s s s =++，2121n n ωωξ⎧=⎪⎨=⎪⎩，10.5n ωξ=⎧⎨=⎩，0.866d ω=，arccos 60βξ︒== 2.42r d t πβω-==s ， 3.63p dt πω==s，%100%16%eσ=⨯=，48s nt ξω==s3-4. 已知系统的单位阶跃响应:为6010()10.2 1.2t t c t e e --=+-，试求：（1）系统的闭环传递函数；（2）系统的阻尼比ξ和无阻尼自然振荡频率n ω。

解：10.2 1.2600()6010(60)(10)C s s s s s s s =+-=++++，1()R s s =， 2()600()70600C s R s s s =++，2600270n nωωξ⎧=⎪⎨=⎪⎩，24.51.43n ωξ=⎧⎨=⎩3-5. 已知单位负反馈系统的开环传递函数为：()(1)KG s s Ts =+当()()r t t ε=时，系统的动态性能指标%30%σ=，0.3(5%)s t s ≤∆=，求系统K 、T 值以满足动态指标。

已知闭环传递函数求开环传递函数在控制理论的世界里，闭环传递函数就像是一个聪明的老朋友，总是在你需要的时候给你建议，帮你调整各种参数，让你的系统运行得更加顺畅。

想象一下，你正在驾驶一辆车，前面是个急转弯，如果没有导航，哎呀，可能就要翻车了。

闭环传递函数就像那个贴心的导航仪，提醒你何时加速，何时刹车。

而开环传递函数呢，就是那台车本身的性能，或者说是它的基础配置。

如果你想从闭环传递函数得到开环传递函数，那可得好好琢磨琢磨。

就像你想知道为什么你的朋友总是那么乐观，想要揭开他内心的小秘密。

我们可以先回顾一下闭环传递函数的基本形式。

通常，这个传递函数看起来像个小公式，分子和分母各有一堆参数和变量，像个数学的拼图游戏，真是让人捉摸不透。

想要获得开环传递函数，首先你得明白闭环和开环之间的关系。

闭环系统就是把输出反馈到输入，然后再通过某种方式调整，确保系统保持稳定。

而开环系统嘛，就是没有那个反馈，完全按照设定的规则运行，感觉就像在公路上自由驰骋，任你飞翔。

为了从闭环传递函数得到开环传递函数，我们可以利用一些简单的数学变换。

闭环传递函数一般写成这样的形式：( G_{cl = frac{G_{ol{1 + G_{olH )。

听起来像在念咒语，其实不复杂，( G_{ol )是开环传递函数，( H )是反馈传递函数。

也就是说，闭环传递函数是由开环传递函数和反馈传递函数共同作用的结果。

这里的“1”就像是一个永远不变的基石，所有的一切都围绕着它运转。

想要从这个公式反推出开环传递函数，可以做一些简单的变换。

把上面的公式稍微变一变，我们可以得到 ( G_{ol = frac{G_{cl{1 G_{clH )。

这就像是把配方中的材料调换了一下位置，找到了另一种美味的可能。

把闭环传递函数放到一边，去寻找开环传递函数的真谛。

其实就是换个思路，看待问题。

这个过程就像在玩拼图，慢慢把每一块都放到位，突然之间，整个画面就都清晰了。

别忘了，这个反馈函数 ( H ) 的值也会影响到结果。

《自动控制原理》课程教学大纲课程编号：课程名称：自动控制原理英文名称：Automatic Control Theory课程类型:专业必修课总学时：63讲课学时：45 上机学时：18学分：2.5（0.5）适用对象：能源动力及其自动化专业先修课程：高等数学、大学物理、积分变换、电路、数字电子技术、模拟电子技术一、课程性质、目的和任务本课程为能源动力及其自动化专业的主要专业基础课程之一，目的是使学生掌握负反馈控制原理、控制系统数学模型的建立和系统性能分析、设计的基本方法，培养学生分析和设计自动控制系统性能的基本能力并能满足其它后续专业课程对自动控制理论知识的需要。

二、教学基本要求本课程采用时域法、根轨迹法和频率特性法对自动控制系统的性能进行分析和设计，学完本课程应达到以下基本要求。

1．掌握负反馈控制原理掌握负反馈控制原理，能够分析负反馈控制系统的调节过程并画出相应的控制系统方框图。

了解控制系统的基本构成和分类。

2．熟悉建立控制系统数学模型的方法熟悉用拉氏变换法求解线性系统微分方程的基本方法。

掌握控制系统传递函数、动态结构图建立和简化方法。

3．熟悉运用时域分析法分析系统性能的方法掌握典型二阶系统的单位阶跃响应以及性能指标的求取。

掌握用劳斯代数稳定判据判断系统的稳定性的方法。

掌握求系统的稳态误差及误差系数的方法。

4．熟悉用根轨迹分析法分析控制系统性能的方法掌握根据系统开环传递函数的零、极点分布绘制闭环系统根轨迹图的基本方法。

根据根轨迹图分析控制系统的性能。

了解开环零、极点对系统性能的影响。

5．熟悉频率分析法分析控制系统性能的方法熟悉典型环节频率特性的求取以及频率特性曲线，掌握系统开环对数频率特性曲线、极坐标曲线绘制的基本方法。

了解根据开环对数频率特性曲线分析闭环系统性能的方法。

熟悉用奈奎斯特稳定判据判断系统稳定性的方法。

掌握稳定裕度的计算方法。

6．熟悉非线性控制系统的分析方法了解非线性控制系统的特点和常见非线性特性。

- 1 - 已知开环传递函数求闭环传递函数 在现代控制理论中，传递函数是一种反映系统运动规律的数学表达方式，是一个系统解耦后输出和输入之间的函数关系，它不仅展示了系统结构和特性，而且可以用于系统分析与设计，因此，传递函数是研究工程控制问题的一个重要工具。 传递函数可分为开环传递函数和闭环传递函数。开环传递函数描述的是系统的输入和输出之间的关系；闭环传递函数描述的是输入和反馈的关系，是一个有效控制的重要概念。闭环传递函数可以准确地反映控制器的特性，是整个系统分析、设计与计算的基础。 因此，如何从已知的开环传递函数求闭环传递函数是广泛学习和应用的一个重要问题。本文旨在深入探讨如何从已知的开环传递函数求闭环传递函数的方法。 首先，要求闭环传递函数，必须先确定控制器，控制器是一个受控系统结构的组成部分，用于检测系统输出和设定目标值之间的差别，从而调整系统输入，以实现系统的自控加以平衡，控制器本身也具有一定的传递函数，与开环传递函数相乘就可以得到闭环传递函数。 其次，也可以通过频域变换的方法从已知的开环传递函数求闭环传递函数。首先，将开环传递函数进行频域变换，得到调节器的相位特性和幅值特性；然后对调节器的相位特性和幅值特性进行函数填充；最后，将相位特性和幅值特性进行反变换，从而求得闭环传递函数。 再次，也可以使用离散状态变换的方法从已知的开环传递函数求闭环传递函数。离散状态变换法是把控制器抽象为有限个状态，由状 - 2 -

态变换方程确定状态之间的转换机制；然后，通过状态变换矩阵来描述状态转换关系，最后，将状态变换矩阵与开环传递函数相乘，求得闭环传递函数。 最后，绝缘安全电路技术也可以从已知的开环传递函数求闭环传递函数。绝缘安全电路技术是一种新型的控制方法，它改变控制信号通过电路网络的通路，以及网络中单元元件的参数，从而改变网络传递函数，最后乘以系统原来的开环传递函数，就可以达到满足要求的闭环传递函数。 综上所述，从已知的开环传递函数求闭环传递函数的方法，主要有控制器模型法、频域变换法、离散状态变换法和绝缘安全电路技术。其中，控制器模型法的优点是结构简单易求，频域变换法的优点是可以较准确地反映控制器的性能；离散状态变换法的优点是可以求出多阶系统的闭环传递函数，而绝缘安全电路技术也是一种灵活的控制技术，可以动态调节系统的误差，从而让系统达到完全稳定。 总之，从已知的开环传递函数求闭环传递函数是现代控制理论中广泛学习和应用的一个重要问题，本文通过介绍了几种常用的技术方法，希望能够为大家寻找一条适合自己的解决方案，实现更精准的控制传递函数求解。

现代控制理论(主汽温对象模型)班级:学号:姓名:目录一. 背景及模型建立1.火电厂主汽温研究背景及意义2.主汽温对象的特性3.主汽温对象的数学模型二.分析1.状态空间表达2.化为约当标准型状态空间表达式并进行分析3.系统状态空间表达式的求解4.系统的能控性和能观性5.系统的输入输出传递函数6.分析系统的开环稳定性7.闭环系统的极点配置8.全维状态观测器的设计9.带状态观测器的状态反馈控制系统的状态变量图10.带状态观测器的闭环状态反馈控制系统的分析三.结束语1.主要内容2.问题及分析3.评价一.背景及模型建立1.火电厂主汽温研究背景及意义火电厂锅炉主汽温控制决定着机组生产的经济性和安全性。

由于锅炉的蒸汽容量非常大、过热汽管道很长，主汽温调节对象往往具有大惯性和大延迟，导致锅炉主汽温控制存在很多方面的问题，影响机组的整个工作效率。

主汽温系统是表征锅炉特性的重要指标之一，主汽温的稳定对于机组的安全运行至关重要。

其重要性主要表现在以下几个方面：(1) 汽温过高会加速锅炉受热面以及蒸汽管道金属的蠕变，缩短其使用寿命。

例如，12CrMoV 钢在585℃环境下可保证其应用强度的时间约为10万小时，而在 595℃时，其保证应用强度的时间可能仅仅是 3 万小时。

而且一旦受热面严重超温，管道材料的强度将会急剧下降，最终可能会导致爆管。

再者，汽温过高也会严重影响汽轮机的汽缸、汽门、前几级喷嘴和叶片、高压缸前轴承等部件的机械强度，从而导致设备损坏或者使用年限缩短。

(2) 汽温过低，会使得机组循环热效率降低，增大煤耗。

根据理论估计可知：过热汽温每降低10℃，会使得煤耗平均增加0.2%。

同时，汽温降低还会造成汽轮机尾部的蒸汽湿度增大，其后果是，不仅汽轮机内部热效率降低，而且会加速汽轮机末几级叶片的侵蚀。

此外，汽温过低会增大汽轮机所受的轴向推力，不利于汽轮机的安全运行。

(3) 汽温变化过大会使得管材及有关部件产生疲劳，此外还将引起汽轮机汽缸的转子与汽缸的胀差变化，甚至产生剧烈振动，危及机组安全运行。