非惯性系下力学问题
- 格式:doc
- 大小:839.00 KB
- 文档页数:31


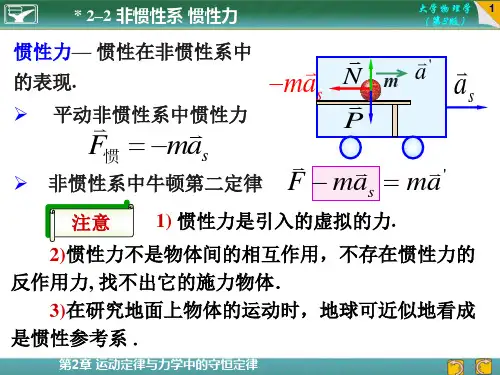
惯性力非惯性参考系中的力惯性力是指物体在非惯性参考系中受到的表观力,它并不是真实存在的力,而是由于参考系的加速度而产生的一种惯性现象。
本文将探讨在非惯性参考系中,惯性力的概念以及如何计算和应用。
一、惯性力的概念在惯性参考系中,物体的运动状态由牛顿定律描述,即物体在受力作用下产生加速度。
然而,在非惯性参考系中,观察者处于相对运动状态,该参考系具有加速度。
在这种情况下,物体看起来似乎受到了额外的力,而实际上却只是观察者与参考系之间相互作用的结果。
惯性力可以分为离心力和科里奥利力两种类型。
离心力是指物体在非惯性参考系中由于参考系加速向心的结果而产生的力,它的大小与物体的质量以及参考系的加速度成正比。
科里奥利力是指物体在非惯性参考系中由于参考系加速引发的物体自身旋转而产生的横向力,它的方向垂直于物体的速度和参考系的加速度。
二、惯性力的计算要计算非惯性参考系中的惯性力,首先需要确定参考系的加速度以及物体的质量。
对于离心力,它的计算公式可以表示为F = m * a,其中F是离心力,m是物体的质量,a是参考系的加速度。
而科里奥利力的计算公式则较为复杂,它的大小为F = 2 * m * V * W,其中V是物体的速度,W是参考系的角速度。
三、惯性力的应用惯性力是解释一些日常生活现象的重要概念。
例如,在旋转木马上,当人们靠近中心处时,他们会感到向外的力,这是离心力的结果。
另外,当我们乘坐快速转弯的车辆时,我们会感到身体向外倾斜,这同样是离心力的作用。
科里奥利力在天气现象中也有应用,例如飓风的旋转和水槽中形成的涡旋等。
需要注意的是,惯性力只是一种表观力,它并不真正参与物体的相互作用中,因此在力学问题中并不需要将其考虑为真实的力。
在实际应用中,我们通常需要将惯性力考虑进去,以便更准确地描述非惯性参考系中的物体运动状态。
总之,惯性力是非惯性参考系中物体受到的表观力,它的存在是由参考系的加速度引发的。
离心力和科里奥利力是惯性力的两种类型,它们分别与物体的质量、速度以及参考系的加速度、角速度有关。


Advances in Social Sciences 社会科学前沿, 2019, 8(6), 960-964Published Online June 2019 in Hans. /journal/asshttps:///10.12677/ass.2019.86132The Application of Non-Inertial Systemin Solving Mechanics Problemsin Senior High SchoolHuiyun Du1, Yujing Huang1, Shuiyuan Chen1, Qingying Ye1, Xueqie Yang21College of Physics and Energy, Fujian Normal University, Fuzhou Fujian2Xiamen No.1 Middle School of Fujian, Xiamen FujianReceived: May 28th, 2019; accepted: Jun. 11th, 2019; published: Jun. 18th, 2019AbstractTraining of thinking ability in physics teaching is an important way to improve students’ scientific literacy in middle school. Based on the perspective of exploring teaching strategies of high school physics methods, this paper analyzes and compares the solutions of four typical mechanical prob-lems in senior high school with those of inertial system and non-inertial system respectively. It is expected to be helpful to the improvement of physics teaching methods and the improvement of students’ thinking ability.KeywordsHigh School Mechanics, Typical Exercises, Non-Inertial Reference System非惯性系在高中力学解题的妙用杜慧云1,黄宇静1,陈水源1,叶晴莹1,杨学切21福建师范大学物理与能源学院,福建福州2厦门第一中学,福建厦门收稿日期:2019年5月28日;录用日期:2019年6月11日;发布日期:2019年6月18日摘要物理教学中思维能力训练是中学阶段提升学生科学素养的重要方式。


惯性力与非惯性系摘要惯性力是非惯性系中的非真实力,本文证明了在非惯性系中将惯性力视为真实力计入后,惯性系下的所有力学规律在非惯性系下都能成立。
当惯性力做功与路径无关时,可以引入惯性力势能,引入惯性力势能并计入系统总机械能后,机械能守恒体系中的条件与结论也仍然成立。
关键字:非惯性系; 惯性力; 惯性力势能ABSTRACTInertia force is unreal power in non-inertia system. It proves in this article that when inertia force is added as real power in non-inertia system, all the mechanical laws which apply in inertia system also do in non-inertial system. When inertia force’s doing work has nothing to do with path, potential energy can be brought in. The conditions and conclusions still apply in the system of conservation of mechanical energy when it adds potential energy to the total mechanical energy.Keywords:Non-inertial; Inertia; Inertial force potential energy1非惯性系与惯性力我们在描绘物体的运动状态时,称选作参照场的物体或物体群,为参照系。
又因为牛顿第一定律又称为惯性定律。
所以凡适用用牛顿定律的参照系都可以称作惯性参照系。
从伽俐若相对性原理中还得到:相对于惯性参照系作匀速直线运动的参照系来说,其力学过程是完全等价的。


非惯性系下的拉格朗日方程及其应用摘要本文介绍了在非惯性系中建立动力学方程的方法,惯性系中拉格朗日方程在非惯性系中的转换形式,以及非惯性系中的应用等研究成果。
关键词非惯性;拉格朗日方程;应用在运用拉格朗日方程的计算中,多是在惯性系中进行的。
诚然在惯性系中运用拉格朗日方程有很多方便之处。
但是有时会遇到在惯性系中考察则不易求出物体的动能。
例:如图,物体绕Z轴转动,不易求出转动惯量IZ,则转动动能不易求出,进而质点P的总的动能不易求出。
在惯性系下运用拉格朗日方程有困难。
此时,如果考虑在非惯性系中,采用非惯性系下的拉格朗日方程,可能使得问题容易解决,从而得到解决问题的另一条途径。
1)在非惯性系下拉格朗日方程的形式在非惯性系中,牛顿定律形式上成立,则由几个质点所形成的力学体系的动力学方程可写为或其中,为作用在第i个质点的约束反力的合力,为作用在第i个质点上的惯性力的合力,为主动力的合力。
在理想约束的条件下,则得:把不独立的等改为用广义坐标等来表示,则上式变为:(1.1式)以下的推导过程可采用《理论力学教程》第二版(作者:周衍柏)中的推导方法。
只是在末尾增添上此项:令进而推导可得:将(A)中的三个式子代入(1.1式)可得:由于相互独立,故得:(1.2式)这就是在非惯性系下的拉格朗日方程的基本形式。
2)存在属于保守力的惯性力(1)根据保守力的定义或斯巴克斯公式易证牵连惯性力是保守力;(2)由于惯性离心力是有心力,易证有心力属于保守力。
3)在非惯性系下的保守系的拉格朗日方程的形式对保守力系而言存在势能V,且:(B)式对也成立。
把(B)式代入(A)式,则:同理也可求得。
其中V1属于保守力的主动力作用于力系而具有的势能;V2为属于保守力的惯性力的作用而具有的势能。
令,即V为总的势能,则(1.2)可改写为:令,即L为非惯性系下的拉格朗日函数,则可得:(1.3)4)非惯性系下的拉格朗日方程的运用例1:一个光滑细管可在竖直平面内绕通过其一端的水平轴以匀角速转动。
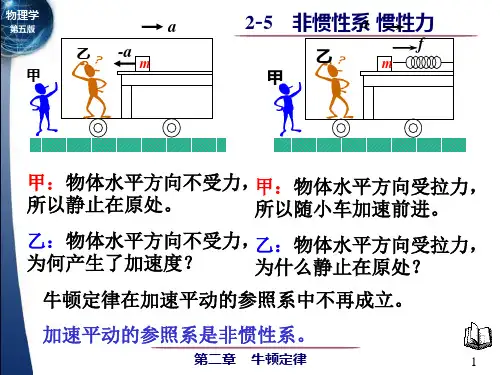
第三章 非惯性系力学引言:到目前为止,我们对质点的力学现象只是限制在惯性参考系中进行讨论的。
但是在某些实际问题中往往要求我们在非惯性系中研究力学问题。
而牛顿定律a m F =只适用于惯性系,在非惯性系中,它是不能适用的,那么相对于非惯性系中的运动定律要解决的是,质点在怎样的力作用下作怎样的运动,换句话来说,运动定律要解决的问题是,质点的受力情况与运动情况之间的联系。
1、对惯性系来说这种联系已经有了,就是牛顿第二定律a m F =。
提到了质点的受力情况,必须要明确力是物体之间的相互作用,既然力是物体间的互相作用,它与参照系的选择有没有关系?没有关系。
2、对非惯性系质点所受的力仍然为F 。
至于运动情况与参照系的选取却是有关的,对不同的参照系会给出不同的描述。
因此,质点相对惯性系和非惯性系的加速度当然是不同的,为了加以区分,就用a ' 表示质点相对非惯性系的加速度。
此时F 就不等于a m F '= ,F 虽然不等于a m F '= ,那么能不能找出F 与a ' 的关系呢?如果找到了它们之间的关系,也就等于找到了非惯性系中的运动定律,那么我们也就可以在非惯性系中讨论力学问题了。
F 与a '之间的关系总能够找到的。
3、只要能找到a 与a ' 的关系:)(a f a '=,根据运动描述的相对性,这个关系总是可以找到的。
那么根据)(a mf a m F '== 也就可以找到F 与a ' 的关系。
因此根据这条解决问题的途径,在这一章里我们准备要讲的4、内容:是①相对运动;②非惯性系动力学;③然后再做一个大题目——解决地球自转所产生的影响。
下面先讲质点相对运动的描述。
也就是讨论质点相对于两个不同参照系运动之间的关系。
§1. 作平动的参照系一、伽利略变换如右图所示,为叙述方便起见简称OX 坐标系为O 系,假定O 系为惯性系,并认为它是一个固定不动的参照系,就称它为固定坐标系。
包头师范学院本科毕业论文论文题目:非惯性系中动力学问题的讨论院系:物理科学与技术学院专业:物理学姓名:王文隆学号: 0809320007指导教师:鲁毅二〇一二年三月摘要综述了近几十年来国内外学者对非惯性系动力学方面的研究情况 ,以及对非惯性系动力学的实际应用情况。
介绍了在非惯性系中建立动力学方程的方法 ,惯性系中拉格朗日方程在非惯性系中的转换形式 ,以及非惯性系中的能量定理和能量守恒定律的应用等研究成果。
最后 ,概述了一些运用非惯性系动力学的方法来解决非惯性系中的理论和实际工程应用两方面的文献 ,并且对非惯性系的研究和应用进行了展望。
关键词:非惯性系;惯性力;动力学方程;拉格朗日方程;动量定理; 动能定律;守恒定律AbstractAnd under classical mechanics frame, the conservation law, leads into the inertial force concept according to kinetic energy theorem , moment of momenum theorem , mechanical energy in inertia department, equation having infered out now that the sort having translation , having rotating is not that inertia is to be hit by dynamics, priority explains a few representative Mechanics phenomenon in being not an inertia department.Key words:Non- inertia Inertial force Kinetic energy theorem Mechanical energy conserves Apply目录引言 (5)1非惯性系概述 (6)1.1非惯性系 (6)1.2 惯性力 (6)2 动力学方程 (7)2.1 质点动力学方程 (7)2.2 拉格朗日方程 (8)3 能量问题 (9)4 应用研究举例 (9)5 研究展望 (10)参考文献 (11)致谢 (12)非惯性系中动力学问题的讨论引言实际工程中有许多系统处于非惯性系内工作 ,如航空航天、天文和外星空探索等领域的许多转子系统。
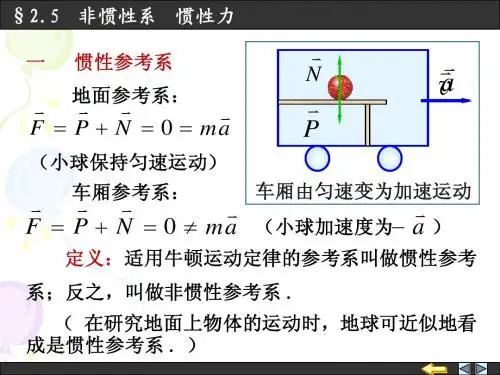
非惯性系中的力学在经典力学中,我们通常将研究对象限定在惯性系中。
惯性系是指一个不受任何外力或惯性力作用的参考系。
然而,在许多实际情况下,我们无法避免研究非惯性系中的力学。
非惯性系中的力学研究相对复杂,但它在解释许多日常生活中的现象、工程设计以及航天飞行等方面具有重要的意义。
一、引言在力学研究中,我们常常使用牛顿定律来描述物体的运动,即F=ma,其中F为物体所受合力,m为物体的质量,a为物体的加速度。
然而,牛顿定律仅在惯性系中成立,当系统处于非惯性系中时,就需要考虑惯性力的作用。
二、非惯性力的概念和作用非惯性力是指在非惯性系中对物体产生的看似存在的力,实际上是由于非惯性系的运动而产生的惯性效应。
常见的非惯性力有离心力、科里奥利力以及向心力等。
离心力是一个物体在非惯性系中沿着旋转轴的方向产生的力,它的大小与物体的质量、距离旋转轴的距离以及角速度有关。
离心力在许多日常生活场景中起着重要作用,比如旋转游乐设施中的体验、地球自转引起的地球形状畸变等。
科里奥利力是一个物体在非惯性系中由于角速度的改变所产生的力。
科里奥利力的方向垂直于运动方向和旋转轴,在天文学、航天飞行等领域有重要的应用。
例如,地球上飞行的飞机或火箭就需要考虑科里奥利力的影响。
向心力是一个物体在非惯性系中沿着旋转轴的方向产生的力,它与物体的质量、旋转角速度以及距离旋转轴的距离有关。
向心力在转弯的机动车辆、垂直旋转的过山车等情况下起着重要作用。
三、非惯性系中的运动方程在非惯性系中,我们需要修正牛顿定律,使其适用于非惯性系的情况。
修正后的运动方程为F=m(a-a'),其中a'为非惯性系的加速度。
非惯性系中的运动方程相对复杂,因为我们需要考虑添加的惯性力对物体运动所产生的影响。
四、实例分析接下来,我们通过几个实例来说明非惯性系中的力学问题。
1. 旋转地球上的自由落体在地球自转的惯性系中,物体的自由落体可以简单地由重力加速度描述。
然而,在地球自转的非惯性系中,我们需要考虑离心力和科里奥利力的影响。
渤海大学本科毕业论文题目非惯性系下力学问题的研究完成人姓名张亚楠主修专业物理学教育所在院(系)数理学院物理系入学年度2008年完成日期2011年6月1日指导教师丁文波非惯性系下力学问题的探讨张亚楠渤海大学物理系摘要:非惯性参照系就是能够对同一个被观测的单元施加作用力的观测参照框架和附加非线性的坐标系的统称。
在经典机械力学中,任何一个使得“伽利略相对性原理”失效的参照系都是所谓的“非惯性参照系”。
了解非惯性系下的力学问题很重要。
对于非惯性系的研究已经从传统的理论已经从传统的理论教学扩展到实际生活应用领域,从宏观研究深入到微观领域。
随着生活领域的不断扩大,对非惯性系下的元器件动力学行为,特别是非线性动力学行为的研究还有很大的空间。
在直升机转子等航空发动机转子的动力学研究中,应用的也主要是非惯性系动力学的理论知识。
近年来通过研究发现,在非惯性系中两体问题、摩擦力、压强以及浮力问题等都得以解决。
本文阐述了惯性系和非惯性系的区别,由惯性力着手,把牛顿第二地定律引入到非惯性系中,分析了牛顿第二定律的适用条件,并对非惯性系下的力学问题进行研究。
第一部分对非惯性系和惯性系进行概述。
第二部分对非惯性系下摩擦力的研究进行了讲述,摩擦力从动于包括惯性力在内的其它力作用。
第三部分通过分析在非惯性系中液体内部浮力和压强的变化,阐述了在不同参考系下液体浮力和压强的变化规律。
关键词:非惯性系;摩擦力;压强;浮力Mechanics Problems in the non-inertial frameZhang Ya-nan Department of Physics,Bohai University Abstract:Collectively referred to as the coordinate system of the observation frame of reference and additional non-linear non-inertial frame of reference is the ability to exert force on the same observation unit. In classical mechanics, no one makes the "failure of the principle of Galilean relativity" frame of reference is the so-called "non-inertial frame of reference. Mechanical problem is very important to understand the non-inertial frame. For non-inertial frames from the traditional theory has been expanded from the traditional teaching of the theory to real-life applications, from a macro research into micro areas. With the continuous expansion of areas of life, the dynamic behavior of non-inertial frame components, especially the study of nonlinear dynamic behavior there is a lot of space. The study of helicopter rotor aero-engine rotor dynamics, the application of theoretical knowledge of non-inertial frame dynamics. In recent years, the study found that two-body problem in the non-inertial, friction, pressure and buoyancy problems are all resolved. This paper describes the difference between inertial frames and non-inertial frames, to proceed by the inertia force, the introduction of Newton's second law of land to the non-inertial reference frame, Newton's Second Law applies to conditions, mechanical problems and non-inertial frame study. The first part an overview of the non-inertial frames and inertial frames. Thesecond part of the non-inertial friction about the friction follower force, including the inertia force. The third part through the analysis of liquid internal buoyancy and pressure change in the non-inertial reference frame on a different reference liquid buoyancy and pressure variation.Key words: Non-inertial;Friction;Pressure;Buoyancy目录引言 (1)一、非惯性系概述 (3)(一)非惯性系和惯性系 (3)(二)平动非惯性参考系 (5)1.平动的非惯性系 (5)2. 非惯性系中牛顿运动定律的应用 (7)(三)转动非惯性参考系 (11)1. 转动坐标系中的运动学问题 (11)2. 转动非惯性系中的动力学问题 (13)3. 落体偏东——地球自转的动力学效应 (13)二、非惯性系中摩擦力的研究 (14)(一)摩擦力的从动性 (14)(二)非惯性系中的摩擦力 (15)1.惯性力的具体形式 (15)2.静摩擦力 (16)3.滑动摩擦力 (16)三、非惯性系中液体内部的浮力和压强的讨论 (17)(一)惯性系中液体内部浮力和压强的表达式 (17)(二)非惯性系中液体内部浮力和压强的表达式 (18)结论 (25)参考文献 (26)非惯性系下的力学问题的研究引言经典理论认为凡是牛顿运动定律适用的参照系为惯性系,牛顿运动定律不成立的参照系为非惯性系[1]。
所有相对于惯性系做匀速直线运动的参照系都是惯性系,相对于惯性系做非匀速直线运动的参照系就不是惯性系。
在一般精度范围内,地球或静止在地面上的任一物体都可以近似看作惯性系。
同样,在地面上做匀速直线运动的物体也可以近似地看作惯性系,但在地面上做变速运动的物体就不能看作惯性系[2,3]。
可以看出,经典理论是把匀速直线运动的参照系作为惯性系,非匀速直线运动的参照系作为非惯性系[4,5]。
在研究地面上物体的运动时,为了研究问题的方便,人们通常取地球作为参照系,即惯性参照系,凡相对惯性系作变速运动的参照系就是非惯性参照系。
两者惟一的差别就是在非惯性系中存在一个引力场。
对参照系作了分类,并提出了参照系的选择原则[6]。
从相对性和绝对性对参照系和惯性系及非惯性系作了论述。
研究在惯性参照系下机械运动所遵循的规律的力学被称之为“经典力学”,因此牛顿力学只有在惯性参照系中才能成立[7,8]。
在不同参照系中观察同一物体的运动,所得的描述物体运动的结论并不相同。
但是,可以通过在非惯性参照系中引进一个假设的力———惯性力,牛顿运动定律在非惯性参照系中便能成立了[9]。
对非惯性系的理论研究,其关键点为引入牛顿力的概念,运用牛顿第二定律建立动力学运动微分方程,便可求出各个物理量。
运用能量定理及守恒定律解决非惯性系中的比较特殊的质点运动,尤其是指两质点的相对速度问题,比运用动力学方程简捷和方便得多[10]。
对于非惯性系中理想流体的动力学方程问题,在近些年来也有研究。
在非惯性系中引入惯性力和等效势能的概念,或是运用非惯性系中流体动力学方程,都可推导出非惯性系中伯努利方程的等效形式,用以解决流体动力学问题[11]。
同样,通过研究发现,在惯性系中适用的阿基米德定律,在非惯性系中也可以用来解决流体动力学问题和流体流溢的边界条件问题[12]。
一、非惯性系的概述(一)非惯性系和惯性系凡是牛顿第二定律能够适用的参照系称为惯性参照系。
经典力学的相对性原理指出,一切力学规律在相互作匀速运动而无转动的参考系中都是相同的。
在一个作匀速直线运动的密封座舱中的观察者,无法通过内部的力学实验来判断座舱相对于恒星是静止的还是在作匀速运动的,他只有朝窗外看才能知道,但仍然无法判断究竟是座舱还是恒星在运动。
另一方面,参考系在力学上的这种等效,并非对任意运动的参考系都成立。
在颠簸运行的火车里和在作匀速运动的火车里,力学运动并不服从同样的定律。
在精确地写相对于地球的运动方程时,必须考虑地球的转动。
一个参考系,如果自由质点在其中作非加速运动,就称为惯性参考系或伽利略参考系,所有相互作非加速运动而无转动的参考系都是惯性参考系。
判断一个特定参考系是不是惯性系,取决于能以多大的精确度去测出这个参考系的微小加速度效应。
在地面上的一般工程动力学中,由于地球的自转角速度较小,地面上一点的向心加速度很小,可取与地球固连的坐标系作为惯性参考系。
在一些必须把地球自转计算在内的问题中,例如研究陀螺仪表的漂移时,可采用地球中心坐标系作为近似的惯性参考系,其原点与地球中心重合,轴指向所认定的恒星。
天文学中则采用黄道坐标系或银道坐标系作为惯性参考系。
牛顿第二定律不适用的参照系称为非惯性参照系。
非惯性参考系附加引力场,考虑在高空向地球坠落的小物体,简化为不考虑空气和地球旋转的影响,那么分别选择地球和小物体为参照系情况有所不同,若以地球为参照系,由于地球近似为惯性系,所以小物体做自由落体运动,到达地面过程中动能不断增加,其动能是由势能转换而来的,能量守恒成立。
若以小物体为参照系,小物体是非惯性系,按照广义相对论,其中有一个附加引力场,引力场指向上。