第08讲 图的基本概念及最小支撑树问题
- 格式:ppt
- 大小:400.50 KB
- 文档页数:21


最小支撑树的定义最小支撑树(Minimum Spanning Tree,MST)是在一个连通图中选择一棵树,使得树上的所有边的权值之和最小且包含图中的所有顶点。
最小支撑树在许多领域中都有广泛的应用,如通信网络、电力传输、城市规划等。
本文将介绍最小支撑树的定义、构造算法以及应用场景。
一、最小支撑树的定义最小支撑树是一个连通图的子图,它是原图的一棵树,包含了原图的所有顶点,但只包含足够连接这些顶点的最小边集合。
换句话说,最小支撑树是一个连通图的生成树,其边的权值之和最小。
二、最小支撑树的构造算法1. Prim算法Prim算法是一种贪心算法,从一个初始顶点开始,每次选择一条与当前生成树相连的权值最小的边,直到生成树包含所有顶点。
具体步骤如下:(1)选择一个初始顶点v,加入生成树T;(2)在剩余的顶点中,找到与T中的顶点相连的边中权值最小的边e;(3)将边e加入生成树T中,并将与e相连的顶点加入T;(4)重复步骤2和步骤3,直到T包含所有顶点。
2. Kruskal算法Kruskal算法也是一种贪心算法,它按照边的权值从小到大的顺序选择边,并且在选择过程中避免形成环路。
具体步骤如下:(1)将图中的所有边按照权值从小到大排序;(2)依次选择权值最小的边,如果该边的两个顶点不在同一个连通分量中,则加入最小支撑树,并将两个连通分量合并;(3)重复步骤2,直到最小支撑树包含所有顶点。
三、最小支撑树的应用场景1. 通信网络规划最小支撑树可以用于通信网络的规划,例如在电信网络中,选择最小支撑树可以使得网络中的通信线路最短,从而提高通信效率和降低成本。
2. 电力传输在电力传输中,最小支撑树可以用于选择电力线路的布置方案。
通过选择最小支撑树,可以使得电力线路的总长度最短,从而减少能量损耗和电力传输成本。
3. 城市规划在城市规划中,最小支撑树可以用于规划道路系统。
通过选择最小支撑树,可以使得城市中的道路总长度最短,从而提高交通效率和减少交通拥堵。

最⼩⽀撑树这篇介绍的是最⼩⽀撑树,常见的有Prim算法和Krustal算法。
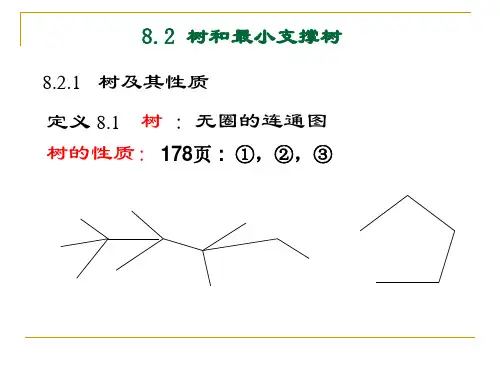
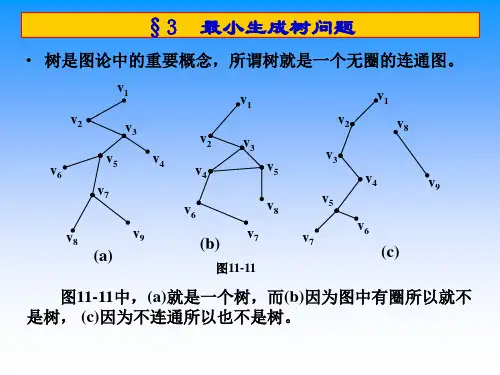
⽀撑树:连通图G的某⼀⽆环连通⼦图T若覆盖G中所有的顶点,则称作G的⼀颗⽀撑树或⽣成树(spanning tree)。
⽀撑树必须覆盖所有的顶点,并且不能有环路,因此是禁⽌环路前提下的极⼤⼦图,也是保持通路前提下的最⼩⼦图。
⼀个图可能有很多⽀撑树,它们都包含n个顶点和n-1条边。
最⼩⽀撑树:在带权⽹络G所有的⽀撑树中,成本最低的称为最⼩⽀撑树(MST)。
Prim算法割(cut):在图G=(V;E)中,顶点集V的任⼀平凡⼦集U及其补集V\U构成⼀个割。
如果边uv满⾜u属于U且v不属于U,称作是该割的⼀条跨越边(cross)。
跨边联接于V及其补集之间,也称作该割的⼀座桥。
Prim算法迭代的准则:最⼩⽀撑树总是会采⽤联接每⼀割的最短跨越边。
算法的策略是贪⼼迭代:从⼀个点出发,每次都寻找已经得到的⽀撑树⼦树T'与剩余的点构成的割的最短跨越边,并把它加⼊⽀撑树。
算法复杂度为O(n^2),适合于稠密图、考虑算法的过程,我们可以在发现⼀个顶点时,把它的优先级设置为与⼦树T’的联边的权重。
实际上,也就是把顶点的优先级设置为跨越边的权重,然后寻找那个最短的跨越边,加⼊到⼦树中。
因此,这个问题也可以归于优先级搜索的框架:1 template<typename Tv, typename Te> struct PrimPU2 {3virtual void operator()(Graph<Tv, Te>* g, int uk, int v)4 {5if (g->status(v) == UNDISCOVERED)//对于uk每个尚未被发现的邻接顶点v6if (g->priority(v) > g->weight(uk, v))7 {8 g->priority(v) = g->weight(uk, v);//更新优先级数9 g->parent(v) = uk;//更新⽗节点10 }11 }12 };只需要重写优先级更新器即可。





最小支撑树数学模型在数学和计算机科学的广袤领域中,最小支撑树数学模型是一个具有重要理论价值和广泛实际应用的概念。
它就像是一张精心编织的网络,以最经济、最有效的方式连接着各个节点。
那么,什么是最小支撑树呢?简单来说,给定一个连通的无向图,所谓的支撑树就是包含图中所有顶点的树。
而最小支撑树则是在所有可能的支撑树中,边的权值之和最小的那一个。
想象一下,有一个城市需要铺设通信线路,将各个区域连接起来。
每个区域就像是图中的一个顶点,而连接区域之间的线路成本就是边的权值。
我们的目标就是找到一种连接方式,使得线路总成本最低,同时确保每个区域都能被连通,这就是最小支撑树问题在实际生活中的一个典型应用。
为了更好地理解最小支撑树数学模型,让我们先了解一下图的基本概念。
一个图由顶点和边组成,顶点代表着对象,边则表示对象之间的关系。
边可以有权值,这个权值可以表示距离、成本、时间等各种实际意义。
在寻找最小支撑树的过程中,有几种经典的算法。
其中,最著名的当属普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法。
普里姆算法的基本思想是从一个顶点开始,逐步添加与之相邻且权值最小的边,不断扩展树的范围,直到包含所有顶点。
就好像我们在一片森林中,从一棵小树开始,一点点把周边最合适的树枝接过来,最终形成一棵完整的大树。
而克鲁斯卡尔算法则是先将所有的边按照权值从小到大排序,然后依次选取权值最小且不会形成回路的边,直到构成一棵连通的树。
这有点像是在一堆杂乱的树枝中,先挑出最短的、能用的,逐步搭建起一个稳固的结构。
这些算法在实际应用中各有优劣。
普里姆算法适用于稠密图,即边的数量相对较多的图;而克鲁斯卡尔算法在稀疏图,也就是边的数量相对较少的情况下,效率更高。
最小支撑树数学模型在交通规划、网络设计、物流配送等众多领域都发挥着关键作用。
在交通规划中,它可以帮助我们确定最优的道路建设方案,以最小的成本连接各个城市或地区;在网络设计中,能够找到最节省成本的布线方式,确保网络的连通性和稳定性;在物流配送中,优化货物运输的路线,降低运输成本。