一般粒子的波函数及其物理意义
- 格式:ppt
- 大小:859.00 KB
- 文档页数:24

波函数物理意义波函数是量子力学中的一个重要概念,也是描述微观粒子行为的核心数学工具之一。
它是一个含有时空信息的复数函数,能够描述粒子的位置、动量以及其他物理特性。
波函数的物理意义可以通过以下几个方面进行解释。
首先,波函数的模的平方代表了找到粒子在某个位置或某个状态的概率。
根据量子力学的波粒二象性,粒子既可以被看作粒子,也可以被看作波。
在波动理论中,波的振幅的平方代表了在空间中某一点上发现波的概率密度。
类似地,波函数的模的平方表示了在某个位置上找到粒子的概率密度。
其次,波函数的相位包含了有关粒子的信息,如相对相位和干涉效应。
在传统波动理论中,同频率的两个波相遇时会发生干涉,波函数中也包含了这种干涉现象。
这种干涉可以解释许多奇特的现象,如双缝干涉实验和量子隧穿等。
此外,波函数还可以描述粒子的运动和演化。
根据薛定谔方程,波函数会随着时间的变化而演化,往往呈现出类似于波动的运动形式。
根据这个方程,波函数的时间演化可以预测出粒子的位置和动量变化,从而帮助我们理解粒子在空间中的行为。
最后,波函数还可以用于描述多粒子系统的行为。
由于量子力学中存在量子纠缠现象,多粒子系统的波函数无法分解为各个粒子的波函数乘积。
相反,多粒子的波函数是所有粒子状态的组合。
这种纠缠关系导致了量子力学的非局域性和不可克隆性等独特性质。
总之,波函数在量子力学中具有重要的物理意义。
它能够描述粒子的位置、动量、演化和相位等特性。
通过对波函数的分析和计算,我们可以推导出粒子的行为和性质,进一步理解微观世界。
波函数的物理意义不仅仅是一种数学工具,更是我们认识微观世界的重要窗口。


简述波函数的物理意义波函数是量子力学中一个重要的概念,描述了处于量子状态的粒子的行为。
它是由施密特(Schmidt)、波尔(Bohr)等人引入,并得到了海森堡(Heisenberg)、薛定谔(Schrödinger)等人的进一步发展。
波函数的物理意义可以通过以下几个方面来描述。
1.粒子位置的概率分布:波函数的模的平方,即,Ψ(x,t),²,描述了粒子在时间t和位置x处的概率分布。
这意味着波函数在特定时间和位置的值越大,粒子出现在该处的概率越高。
由此可见,波函数的物理意义之一是描述了粒子位置的概率。
2.粒子的运动:波函数是随时间和位置变化的,通过薛定谔方程来描述。
这个变化过程反映了粒子的运动。
薛定谔方程表明,波函数的时间演化由哈密顿算符H控制。
波函数演化的速度由哈密顿算符中的能量项决定。
因此,波函数的物理意义之二是描述了粒子的运动。
3.粒子的角动量:波函数还可以描述粒子的角动量。
对于自旋½的粒子,波函数有两个分量,表示上下自旋。
自旋是粒子固有的性质,描述了粒子对旋转的响应。
波函数中的自旋分量决定了粒子在不同方向上的自旋测量结果。
因此,波函数的物理意义之三是描述了粒子的角动量性质。
4.粒子的态叠加和测量:波函数还可以描述粒子的量子态叠加和测量过程。
量子态叠加是指当一个粒子处于多个不同状态之一时,它可以同时处于所有这些态的叠加态。
波函数中的不同分量对应于不同的态叠加。
测量过程会导致波函数的坍缩,即从叠加态向单个确定态的转变。
波函数的物理意义之四是描述了量子态叠加和测量的过程。
5.波函数的归一化:波函数的平方的积分必须为1,即∫,Ψ(x, t),²dx=1、这是由于概率密度的归一性要求,即粒子必须出现在整个空间中。
波函数的归一化要求决定了波函数的形式和物理意义。
总的来说,波函数的物理意义是描述了量子态的性质、粒子的位置和运动、角动量等多个方面。
通过波函数可以得到与粒子相关的物理量,比如能量、动量、角动量等的平均值和概率分布。

量子力学波函数的物理意义量子力学是描述微观世界行为的理论,它提出了波粒二象性的概念,即微观粒子既可以表现出粒子的性质,又可以表现出波动的性质。
在量子力学中,波函数是一个重要的概念,它用来描述微观粒子的状态。
波函数的物理意义是什么呢?本文将从不同的角度来探讨波函数的物理意义。
1. 波函数的数学表达在量子力学中,波函数用符号ψ表示,它是一个复数函数。
波函数的平方的模的积分等于1,即∫|ψ(x)|^2dx = 1。
这意味着波函数描述的是微观粒子的概率分布。
波函数的模的平方表示在某个位置找到粒子的概率,而波函数本身则描述粒子的相位性质。
2. 波函数的物理解释:波粒二象性波函数的物理意义可以通过波粒二象性的概念理解。
在实验中,物质粒子表现出波动性质,例如干涉和衍射现象,这可以用波函数来描述。
而在其他实验中,物质粒子又表现出粒子性质,例如只在特定位置上相互作用,这可以用波函数的模的平方来解释。
3. 波函数的时间演化波函数不仅仅是描述粒子在空间中的分布,还可以随时间演化。
根据薛定谔方程,波函数随时间的演化是由哈密顿算符决定的。
波函数的时间演化描述了微观粒子的行为,例如衰变、干涉等现象。
4. 波函数与可测量物理量波函数不仅包含了微观粒子的空间和时间分布信息,还与可测量的物理量有关。
根据量子力学原理,可测量物理量的期望值可以通过波函数的数学处理得到。
例如,对于位置算符x,其期望值为<x> =∫ψ*(x)xψ(x)dx,其中ψ*(x)表示波函数的共轭复数。
波函数的物理意义是提供了可测量物理量的统计信息。
5. 波函数坍缩在测量微观粒子时,波函数会发生坍缩。
坍缩后的波函数描述了粒子被测量后的状态。
量子力学中的测量过程是波函数演化的非线性过程,而波函数的坍缩则使得测量结果是确定的而非概率性的。
波函数的坍缩保证了测量理论与实验结果的一致性。
总结起来,波函数是量子力学中描述微观粒子状态的数学工具,它具有重要的物理意义。


量子力学中的波函数及其物理意义波函数是描述量子力学中粒子性质与行为的重要概念。
它可以用数学方式表示,并提供了有关粒子位置、动量和能量等信息。
本文将探讨波函数的定义、性质以及其在量子力学中的物理意义。
一、波函数的定义与性质量子力学中的波函数用Ψ表示,它是一个复数函数,并且必须满足归一化条件。
波函数的平方值|Ψ|²表示了在给定位置上找到粒子的概率密度。
1. 归一化条件波函数必须满足归一化条件,即积分后的平方和为1。
一般来说,波函数在一定区域内的平方和代表了该粒子在该区域出现的概率。
2. 波函数的复数性质波函数是一个复数函数,其中实部和虚部分别表示了粒子的实部和虚部。
这两部分的相对大小和相位关系对波函数的演化和测量结果均有影响。
3. 波函数的连续性波函数必须在整个空间内是连续的,包括可能出现的间断点。
这个条件保证了波函数的物理意义和可解性。
二、波函数的物理意义波函数不是物理量本身,而是通过运算符作用于波函数上得到物理量的期望值。
波函数提供了以下重要信息:1. 粒子的位置分布通过波函数的平方值|Ψ|²,我们可以得到粒子在空间中出现的概率分布。
这反映了粒子的位置不确定性以及可能出现的空间区域。
2. 粒子的动量与能量波函数的动量空间表示称为动量波函数,它提供了粒子动量的概率分布。
从动量空间的角度来看,波函数的形态表现了粒子的动量空间分布。
3. 量子力学的态叠加与变化波函数可以通过超定线性组合的方式表示多个不同态的叠加状态。
这种态的叠加在量子力学中被称为叠加态,可以描述一系列可能发生的物理过程。
4. 测量与波函数塌缩当我们对粒子进行测量时,波函数会发生塌缩。
塌缩后的波函数代表了测量结果所对应的状态。
波函数的塌缩是量子力学中一种重要的随机现象。
三、波函数演化与时间依赖性波函数对时间的依赖性是量子力学中一个重要的研究方向。
根据薛定谔方程,波函数会随着时间的推移而发生演化。
波函数的时间演化可以揭示粒子的运动规律和行为。


波函数的物理意义与性质波函数是量子力学中描述物质波动性质的核心概念之一。
它既是一个数学函数,也是描述粒子在不同位置和状态下的概率振幅。
波函数的物理意义与性质对于理解量子力学的基本原理和应用非常重要。
一、物理意义1. 粒子位置的概率分布:波函数的模的平方表示了在给定时间和空间内找到粒子的概率密度分布。
在一维情况下,波函数的模的平方在坐标轴上的积分即为粒子在该一维空间内的概率。
2. 粒子动量的概率分布:波函数的复数振幅和相位包含了粒子的动量信息,其中振幅的平方与粒子的概率密度相关。
波函数变换到动量空间后,其模的平方表示了得到不同动量值的粒子概率。
3. 不确定性原理:波函数的物理意义涉及到不确定性原理。
根据不确定性原理,对一个粒子的位置和动量的准确测量是不可能的。
波函数的展宽与位置和动量的不确定性相关,展宽越大,不确定性就越小。
4. 粒子束缚态与散射态:对于定态波函数,它描述了粒子在束缚系统内的行为,如电子在原子中的运动态。
而散射态则描述了粒子在势场中遇到障碍物时的散射行为。
波函数的物理意义包括反映粒子的能量、波长、传播速度等特性。
二、性质1. 归一化:波函数的模的平方必须为1,以保证概率的和为1。
归一化条件能够确保在粒子在某一空间内的存在概率为100%。
2. 可加性:如果一个系统由多个粒子组成,系统的总波函数是各个粒子波函数的乘积。
这意味着整个系统的波函数可以通过各个粒子的波函数相乘得到,展现了波函数的可加性。
3. 观测与波函数坍缩:当我们对一个系统进行观测,测量粒子的某个性质时,波函数将会根据测量结果坍缩到对应的本征态上。
这是量子力学中观测过程的一个基本特性。
4. 可叠加性:波函数符合线性叠加原理,即若干波函数的线性组合仍然是一个有效的波函数。
这种性质使得波函数可以描述多个态的叠加情况,如叠加态和纠缠态。
总结:波函数的物理意义与性质对于理解量子力学中的基本概念和原理至关重要。
它描述了粒子的位置和动量的概率分布,反映了粒子的波动性质以及不确定性原理。

波函数解释知识点波函数解释是量子力学中重要的一个概念,它用来描述微观粒子的运动状态及其性质。
本文将介绍波函数解释的相关知识点,包括波函数的定义、波函数的物理意义、波函数的性质以及波函数的应用等。
一、波函数的定义在量子力学中,波函数用符号ψ表示,它是描述微观粒子的一种数学函数。
波函数的定义依赖于粒子所处的具体情况,比如自由粒子、束缚粒子或多粒子系统等。
波函数通常是空间坐标和时间的函数,即ψ(r,r),其中r表示位置矢量,r表示时间。
二、波函数的物理意义波函数的物理意义可以通过波函数的模的平方来描述。
波函数的模的平方|ψ(r,r)|²表示在某一时刻粒子出现在空间体积元rr内的概率。
即r(r,r)rr=|ψ(r,r)|²rr表示在空间体积元rr内发现粒子的概率。
波函数的物理意义可以通过测量得到,例如电子的位置、动量等。
三、波函数的性质1. 波函数的归一化:波函数必须满足归一化条件,即对整个空间积分结果为1。
即∫|ψ(r,r)|²rr=1,这表示粒子必定存在于空间中。
2. 波函数的连续性:波函数及其一阶导数在空间中连续,避免出现不连续点。
3. 波函数的可微性:波函数应该是可微的,以满足薛定谔方程的求解条件。
4. 波函数的奇偶性:对于具有中心对称性的体系,波函数可能是奇函数或偶函数。
四、波函数的应用1. 粒子的定态波函数:波函数的解可以得到粒子的能级、能量及角动量等相关信息,对于束缚系统,波函数的节点和能级的关系也十分重要。
2. 粒子的散射:通过波函数的解,可以计算散射截面、反射系数等散射性质,从而揭示粒子之间相互作用的性质。
3. 粒子的叠加态:多个波函数的线性叠加可以得到粒子的叠加态,这可以用来描述多粒子系统中的统计性质。
4. 量子力学中的难题:波函数的解决了一些传统力学难以解释的问题,如双缝干涉实验等。
总结:波函数解释是量子力学的核心概念之一,它描述了微观粒子的运动状态和性质。

波函数的物理意义
1 什么是波函数
波函数是一种用于描述粒子的属性的数学概念,是粒子的概括的量子物理特征的一部分。
它有助于在量子物理学中理解粒子的性质,例如能量,动量和偶极矩。
波函数既可以描述能量状态,也可以用来描述粒子的空间分布。
2 波函数的定义
按照经典物理学理论,粒子总是可以定位在一个确定的位置和状态下。
而按照量子理论,粒子是无法精确定位的,但是可以描述它们处于某种可能性状态下,称为波函数。
波函数是用来描述粒子可能存在的态的概率,它代表不同粒子的不同态的概率分布,而粒子的动量和能量对应不同的波函数表示的态。
3 力学波函数
力学波函数是求解物体状态的量子力学方程的基本解法。
它可以用来描述物体的空间分布和动量,以及物体的能量状态,以及它们的相互作用。
在力学上,其原理是:量子力学能量状态和函数必须满足力学方程和它们之间的相互作用,因此力学波函数是描述粒子状态的一种解法,即从物理角度解释物体状态。
4 波函数的物理意义
波函数是量子物理学中一种重要的概念,它可以用来描述粒子的属性和性质。
原子的波函数可以明确地说明原子的能级,因此可以用来预测原子的性质。
而波函数也正是电子结构模型的基石,它可以用来描述原子核周围电子的波动性和分布模式,以及它们之间可能存在的相互作用。
另外,波函数也可以用于求解守恒量,这也是使用量子力学分析物体状态的一种常用方法。
因此,波函数是量子物理学中一个关键概念,它可以用来描述我们宇宙中物体的特征和性质。
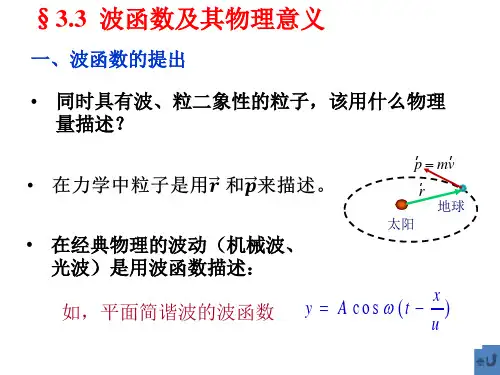
§3.3 波函数及其物理意义一、微粒的波函数描述自由粒子 ⇔ 平面波自由粒子不受力,动量不变,所以同它联系的波长(ph =λ)也不变,是单色波,设一平面波沿速度υ 的方向传播,该方向的单位矢量为n ,即n υυ=,t 时刻,代表平面单色波的波动方程:)(cos 0υωψψn p r t -= υυθυnr r r n ⋅==cos OP r = :原点到波面任意一点矢量 )t (2cos )t cos (2cos 00νλπψνλθπψ-⋅=-=nr r欧拉公式:θθθsin cos i e i ±=± 取“+”)t (20νλπψψ-⋅=nr i e――沿n 方向传播的、波长为λ、频率为ν的平面简谐波方程。
用波方程来描写实物粒子,根据德布罗意关系:νh E = n h p λ= ⇒ )(0Et p r i e -⋅=ψψ ――自由粒子的波函数,描写动量为p 、能量为E 的自由粒子。
经典力学 ⇒ 位置和速度 量子力学 ⇒ 波函数波函数体现了波粒二象性,其中的E 和p 是描写粒子性的物理量,却处在一个描写波的函数中。
二、波函数的物理意义1926年,德国物理学家玻恩:2),,,(t z y x ψ表示t 时刻、(x 、y 、z )处、单位体积内发现粒子的几率。
如图为电子衍射的强度分布图。
用粒子的观点,极大值处意味着到达的电子多,极小值处意味着到达的电子少。
从波的观点来看,极大值处表示波的强度大,极小值处表示波的强度小。
如果用玻恩的观点就能将粒子和波的概念统一起来。
因为2),,,(t z y x ψ即波的强度表示t 时刻、(x 、y 、z )处发现电子的几率密度。
如果2),,,(t z y x ψ大,则电子出现几率大,因而电子出现的数目也多,此处为衍射极大值处;反之,如果2),,,(t z y x ψ小,则电子出现几率小,电子出现的数目也少,此处为衍射极小值处。
*),,,(2ψψψ==t z y x W 表示t 时刻、(x 、y 、z )处发现粒子的几率密度。
波函数的物理意义波函数是量子力学中一个重要的概念,描述了微观粒子的状态和行为。
它是量子力学方程的解,通过对波函数的分析,我们可以揭示微观世界的一些奇妙现象和规律。
本文将探讨波函数的物理意义,从不同的角度解释其含义和应用。
1. 波函数的统计解释在量子力学中,波函数是描述微观粒子行为的概率振幅。
具体而言,波函数的模的平方给出了在某个特定状态下观测到粒子的概率分布。
例如,对于一个束缚在势阱中的电子,其波函数的模的平方表示了电子存在于不同位置的概率密度分布。
因此,波函数可以用来预测粒子的位置、动量、能量等物理量的概率分布。
2. 波函数的波动性解释与经典物理学中的粒子不同,量子力学中的粒子常常表现出波动性。
波函数既可以解释为粒子在空间中的几率分布,也可以看作是一种波动。
波函数的特点包括幅度、波长和频率等,与经典波动的描述相似。
例如,电子的波函数在空间中波动,类似于光波的传播。
这种波动性使得量子粒子在双缝实验等情况下会呈现干涉和衍射现象,形成粒子的波粒二象性。
3. 波函数的量子态解释波函数还可以解释为量子系统的量子态。
量子态用来描述系统的性质,包括能量、角动量、自旋等。
波函数是一个复数函数,描述了系统在某个特定状态下的量子态。
通过对波函数的操作和演化,我们可以计算系统的期望值和物理量的变化。
例如,利用波函数可以计算电子的能级、原子的光谱等量子化现象。
4. 波函数的求解方法波函数的求解是量子力学中的一个关键问题。
根据系统的不同特点和边界条件,我们需要使用不同的方法求解波函数。
常见的求解方法包括薛定谔方程、量子力学近似方法和数值计算方法等。
通过这些方法,我们可以得到不同系统的波函数和其对应的物理意义。
总结起来,波函数是量子力学中描述微观粒子行为的数学工具。
它既有统计解释,可以用来预测粒子的概率分布;又有波动性解释,可以描述粒子的波粒二象性;还有量子态解释,用于描述系统的性质和量子化现象。
波函数的求解是量子力学研究的核心问题之一,通过对波函数的研究,我们可以深入理解微观世界的本质和规律。
波函数的物理意义及作用波函数是量子力学中的重要概念,它描述了量子系统的状态。
在量子力学中,粒子的行为与经典物理学有很大的不同,而波函数的物理意义和作用正是用来描述这种不同之处。
波函数的物理意义可以理解为描述了粒子的概率幅。
根据波函数的模的平方,即波函数的绝对值的平方,我们可以得到粒子在某个位置上的概率密度。
这意味着波函数可以告诉我们在不同位置上找到粒子的可能性有多大。
例如,在一个一维无限深势阱中的粒子,其波函数的平方表示了粒子在不同位置上的可能性分布。
波函数还可以用来计算粒子的物理量。
根据量子力学的原理,物理量的平均值可以通过对波函数进行数学运算得到。
例如,对于一个处于定态的量子系统,其平均位置可以通过对波函数乘以位置算符并对整个空间积分来计算得到。
这意味着波函数不仅描述了粒子的概率分布,还包含了对物理量的信息。
波函数还具有一些其他的重要作用。
首先,它是解决薛定谔方程的关键。
薛定谔方程是量子力学的基本方程,描述了量子系统随时间演化的规律。
解薛定谔方程得到的波函数可以描述系统的态随时间的演变。
其次,波函数还可以用来描述量子态之间的转换。
当系统发生量子跃迁时,波函数将发生变化,从而描述了系统状态的变化。
波函数还有一些重要的性质。
首先,波函数必须满足归一化条件,即波函数的模的平方在整个空间上积分等于1。
这是因为粒子必须存在于某个位置上。
其次,波函数必须是连续可微的,这是由于薛定谔方程是一个二阶偏微分方程。
这些性质保证了波函数在物理上的合理性和可解性。
波函数在量子力学中具有重要的物理意义和作用。
它描述了粒子的概率幅,可以计算物理量的平均值,是解决薛定谔方程的关键,描述了量子态之间的转换。
波函数的物理意义和作用使得我们能够理解和描述微观世界中粒子的行为。
通过对波函数的研究和理解,我们可以揭示量子力学的奥秘,深入理解微观世界的规律。