B112-11.2全等三角形的判定(1)配套练习

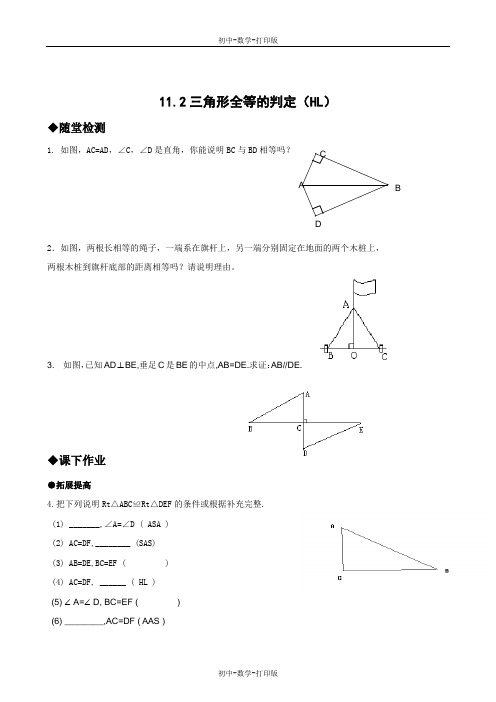
11.2三角形全等的判定（HL ）◆随堂检测1. 如图，AC=AD ，∠C ，∠D 是直角，你能说明BC 与BD 相等吗？2．如图，两根长相等的绳子，一端系在旗杆上，另一端分别固定在地面的两个木桩上， 两根木桩到旗杆底部的距离相等吗？请说明理由。

3. 如图，已知AD ⊥BE,垂足C 是BE 的中点,AB=DE.求证：AB//DE.◆课下作业●拓展提高4.把下列说明Rt△ABC≌Rt△DEF 的条件或根据补充完整. (1) _______,∠A=∠D ( ASA ) (2) AC=DF,________ (SAS)(3) AB=DE,BC=EF ( ) (4) AC=DF, ______ ( HL ) (5) ∠A=∠D, BC=EF ( ) (6) ________,AC=DF ( AAS )CD AB5.小明既无圆规，又无量角器，只有一个三角板，他是怎样画角平分线的呢？他的具体做法如下：在已知∠AOB 的两边上，分别取OM=ON ，再分别过点M 、N 作OA 、OB 的垂线交点为P,画射线OP.则OP 平分∠AOB 。

其中运用的数学道理是 。

6.如图，AB ＝AC ，CD ⊥AB 于D ，BE ⊥AC 于E ，则图中全等的三角形对数为（ ） （A ）1 （B ）2 （C ）3 （D ）47.如图，幼儿园的滑梯有两个长度相同的滑梯，左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等，(1)△ABC≌△DEF 吗?(2)两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系？8. 如图，已知∠B=∠E=90°，AC=DF ，BF=EC.求证：AB=DE.●体验中考1．(2009年浙江省湖州市)如图：已知在ABC △中，DE=DF ，D 为BC 边的中点，过点D 作DE AB DF AC ⊥，⊥，垂足分别为E F ，.求证：BED CFD △≌△2．(2009年北京市).已知：如图，在△ABC 中，∠ACB=90，CD AB 于点D,点E 在AC 上，CE=BC,过E 点作AC 的垂线，交CD 的延长线于点F .求证：AB=FCDCB EAFDABECF参考答案:随堂检测：1、要挖掘图中隐含的公共边答案：在Rt△ACB和Rt△ADB中,∵AB=AB, AC=AD∴ Rt△ACB≌Rt△ADB (HL)∴BC=BD(全等三角形对应边相等).2、两根木桩到旗杆底部的距离是否相等，也就是看OB与OC是否相等，OB、OC分别在Rt△ABO和Rt△ACO 中,只需证明这两个三角形全等。

教学内容全等三角形的判定教学目标掌握全等三角形的判定方法重点全等三角形的判定探索三角形全等的条件（5种）1边角边（重点）两边及其夹角分别分别相等的两个三角形全等，可以简写成“边角边”或“SAS”.注：必须是两边及其夹角，不能是两边和其中一边的对角.原因：如图：在A ABC和A ABD中，/ A= / A,AB=AB,BC=BD,显然这两个三角形不全等.A例 1 如图，AC=AD, / CAB= / DAB,求证：A ACB义A ADB.AD例 2 如图，在四边形 ABCD 中，AD〃BC, / ABC= /DCB, AB=DC, AE=DF 求证:BF=CE.例3.(1)如图①，根据“SAS"，如果BD=CE, =,那么即可判定4BDC24CEB； (2)如图②，已知BC=EC, NBCE二ACD,要使4ABC2△口£&则应添加的一个条件为例4. 如图，已知AD=AE,N1=N2, BD=CE,则有4ABD2，理由是△ABE义，理由是.例5.如图，在4ABC和4DEF中，如果AB=DE, BC=EF,只要找出N=N 或〃，就可得到4ABC2△DEF.A D例6.如图，已知AB〃DE, AB=DE, BF=CE,求证：4ABC24口£艮例 7.如图，点B 在线段AD 上，BC〃DE, AB=ED, BC=DB. 求证：NA二NE 例8.如图，点E, F 在BC 上，BE=CF, AB=DC, NB=NC.求证: NA=ND.2.角边角两角及其夹边分别相等的两个三角形全等（可以简写成“角边角”或“ASA”）例1.如图，在4ABC中，点D是BC的中点，作射线AD,线段AD及其延长线上分别取点E, F，连接CE，BF.添加一个条件，使得4BDF24CDE,你添加的条件是:.（不添加辅助线）例2. 如图，已知人口平分/8人&且N ABD=N ACD,则由“AAS”可直接判定△^A.B例 3.如图，在 RtA ABC 中，N ACB=90°, BC=2cm, CD^AB,在AC 上取一点E,使EC二BC, 过点E作EF^AC交CD的延长线于点F,若EF=5cm,那么AE=cm.例4.如图，AD〃BC,N ABC的角平分线BP与/8人口的角平分线AP相交于点P,作PE L AB于点E.若PE=2,则两平行线AD与BC间的距离为.例 5.如图，已知EC=AC, ZBCE=ZDCA, NA=NE.求证：BC=DC.例6.如图，在4ABC中，D是BC边上的点（不与B, C重合），F, E分别是AD及其延长线上的点，CF〃BE.请你添加一个条件，使4BDE24CDF （不再添加其他线段，不再标注或使用其他字母），并给出证明.（1）你添加的条件是：；（2）证明：例7.如图，A在DE上，F在AB上，且BC=DC,N1=N2=N3,则DE的长等于（）A. DCB. BCC. ABD. AE+AC【基础训练】1 .如图，已知 AB = DC,NABC=NDCB,则有4ABC2，理由是；且有2 .如图，已知AD=AE,N1 = N2, BD = CE,则有4ABD2，理由是；△ ABF /，理由是.3 .如图，在4ABC 和ABAD 中，因为 AB = BA,NABC=NBAD, =，根 据“SAS”可以得到4ABC2ABAD.4 .如图，要用“SAS”证4ABC2AADE,若AB=AD, AC=AE,则还需条件（ ）.5 .如图，OA=OB, OC = OD,NO=50°,N D = 35°,则NAEC 等于（ ）.A. 60°B. 50°C. 45°D. 30°A.NB = ND C.N1 = N2 BNC=NED.N3 = N4（第4皿（第56.如图，如果AE=CF, AD〃BC, AD = CB,那么^ADF和ACBE全等吗？请说明理由.律f题）7.如图，已知AD与BC相交于点O,NCAB = NDBA, AC = BD.求证: (1)NC=ND；(2)AAOC^ABOD.C第T题）8.如图，AACD和4BCE都是等腰直角三角形，NACD=NBCE=90°, AE交DC于F, BD分别交CE、AE于点G、H.试猜测线段AE和BD的位置和数量关系，并说明理由.（第8题）9.如图，在4ABC 中，AB=AC, AD 平分/BAC.求证：NDBC=NDCB.（第KJ题）10.如图，4ABC是等边三角形，D是AB边上的一点，以CD为边作等边三角形CDE,使点E、A在直线DC的同侧，连接AE.求证：AE〃BC.（第门题）角角边两角分别相等且其中一组等角的对边相等的两个三角形全等，可以简写成“角角边”或“AAS”. 例1、如图，在4ABC中，N ABC=45°, H是高AD和高BE的交点，试说明BH=AC.例 2、如图，N ACB=90°, AC二BC, BE±CE, AD±CE 于 D, AD=2.5cm, DE=1.7cm. 求BE的长.例3、如图，在4ABC中,AC±BC, CE±AB于E, AF平分/CAB交CE于点F,过F作FD〃 BC交AB于点D.求证：AC=AD.例 3.如图，AD 平分/BAC, DEXAB 于 E, DFXAC 于 F,且 DB二DC,求证：EB=FC例4.如图，在4ABC中，D是BC的中点，DELAB, DFXAC,垂足分别是E, F, BE=CF. 求证：AD 是4ABC的角平分线.例5.如图，在4ABC中，AB二CB,N ABC=90°, D为AB延长线上的一点，点E在BC 边上，连接 AE, DE, DC, AE二CD.求证：NBAE二NBCD.例6.如图，D是BC上一点，DEL AB, DF±AC, E, F分别为垂足，且AE=AF.(1)AAED与4AFD全等吗？为什么？(2)AD平分/BAC吗？为什么？例 7.如图，已知 ACLBC, BDLAD, BC 与 AD 交于 O, AC=BD.试说明：ZOAB=ZOBA.例8.如图，NACB 和/ADB都是直角，BC二BD, E是AB上任意一点.求证：CE=DE.例 9.如图，已知RtAABC^RtAADE,ZABC=Z ADE=90°, BC 与 DE 相交于点 F, CD, EB.连接(1)图中还有几对全等三角形，请你一一列举；(2)求证：CF=EF.例10.如图，在四边形ABCD中，AC 平分/BAD,并且CB=CD.求/ABC+NADC的度数.例11. (1)如图①，A, E, F, C四点在一条直线上，AE二CF,过点E, F分别作DELAC, 8尸，八0连接BD交AC于点G,若AB二CD,试说明FG=EG.(2)若将4DCE沿AC方向移动变为如图②的图形，(1)中其他条件不变，上述结论是否仍成立？请说明理由.B BD D①. ②课后练习:1.如图，点C在线段AB的延长线上，AD = AE, BD = BE, CD = CE,则图中共有对全等三角形，它们是2.如图，若AB = CD, AC=BD,则可用“SSS”证 23.如图，已知 AB = DC, BE=CF,若要利用“SSS”得到4ABE2△DCF,还需增加的一个条件是.i第3题）（第-I题）4.如图所示是一个由四根木条钉成的框架，拉动其中两根木条后，它的形状将会改变，若想固定其形状不变，需要加钉一根木条，可钉在（）.A. AE 上B. EF 上C. CF 上D. AC 上5.如图，已知E、C两点在线段BF上，BE=CF, AB=DE, AC=DF.求证：AABC2A DEF.& E C F（第三⑦6.如图，在4ABC和4DCB中，AC与BD相交于点O, AB=DC, AC=BD.(1)求证：4ABC 2ADCB；(2)AOBC的形状是.(直接写出结论，不需证明)＜第6题)7、如图，在口ABCD中，点E、F分别是AD、BC的中点，AC 与EF相交于点O.(1)过点B作AC的平行线BG,延长EF交BG于点H；(2)在(1)的图中，找出一个与4BFH全等的三角形，并证明你的结论.8、如图，已知BD±AB, DC,AC,垂足分别为点B、C, CD=BD, AD 平分/BAC吗，为什么？9.如图，四边形ABCD是正方形，点G是BC上的任意一点，DELAG于E, BF#DE,交 AG于F.那NAF与BF+EF相等吗？请说明理由.B G C10.如图，BD、CE分别是4ABC的边AC和边AB上的高，如果BD = CE,试证明AB = AC.11.如图，在RtAABC和RtABAD中，AB为斜边，AC=BD, BC、AD相交于点E (1)请说明AE=BE 的理由；(2)若N AEC=45°, AC = 1,求 CE 的长.12.如图，在4ABC中，D是BC的中点，DELAB, DFLAC,垂足分别是点E、F, BE= CF.(1)图中有几对全等的三角形？请一一列出；(2)选择一对你认为全等的三角形进行证明.4练习21.如图，已知NB = NDEF, AB=DE,要证明△ ABC2△DEF.（1）若以“ASA”为依据，还缺条件；（2）若以“AAS”为依据，还缺条件£（第1期】《第2题）2.如图，已知AD平分/BAC,且NABD=NACD,则由“AAS”可直接判定△2 △.3.如图，已知AB=AC,要根据“ASA”得到以BE2AACD,应增加一个条件是 _______________（第3 （第4（第54.如图，点P是/AOB的平分线OC上的一点，PD±OA, PE LOB,垂足分别为点D、E, 则图中有对全等三角形，它们分别是.5.如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是（）.A.带①去B.带②去C.带③去D.带①和②去6.如图，已知AC平分/8八口，/1 = /2, AB与AD相等吗？请说明理由.C£第67.如图，点B、E、F、C在同一直线上，已知NA=ND, 需要补充的一个条件是.（写出一个即可）NB = NC,要使4ABF 2ADCE,8.如图，在4ABC中，N ABC=45°, H是高AD和高BE的交点，试说明BH=AC.A9.如图，已知点A、D、B、E在同一条直线上，且AD=BE,NA=NFDE,则AABC2A DEF.请你判断上面这个判断是否正确，如果正确，请给出说明；如果不正确，请添加一个适当条件使它成为正确的判断，并加以说明.10.已知：如图，AB=AE,N1 = N2,NB = NE.求证：BC=ED.21。

前言：该同步练习题由多位一线国家特级教师针对当前最新的热点、考点、重点、难点、知识点，精心编辑而成。

以高质量的同步练习题助力考生查漏补缺，在原有基础上更进一步。

（最新精品同步练习题）12.2三角形全等的判定基础巩固1.(题型三)如图12-2-1，某同学把一块三角形玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是( )______图12-2-1A.带①去B.带②去C.带③去D.带①和②去2.(题型一)如图12-2-2，在∆ABC中，AB=AC，BE=CE，则由“SSS”可以判定( )图12-2-2A.∆ABD≌∆ACDB.∆BDE≌∆CDEC.∆ABE≌∆ACED.以上都不对3.(题型一、四)如图12-2-3，∆BDC′是将长方形纸片ABCD沿着BD折叠得到的，图中（包括实线、虚线在内）共有全等三角形( )图12-2-3A.1对B.2对C.3对D.4对4.(题型三)如图12-2-4，点B在射线AE上，∠CAE=∠DAE，∠CBE=∠DBE，AD=8，则AC= ．图12-2-45.(题型二、三、四、五)如图12-2-5，已知AB⊥CF，DE⊥CF，垂足分别为B，E，AB=DE．请你添加一个适当的条件，使∆ABC≌∆DEF．添加的条件是．图12-2-56.(题型三)如图12-2-6,AB∥CD,AD，BC交于点O,EF过点O分别交AB，CD 于点E，F，且AE=DF.求证：O是EF的中点．图12-2-67.(题型二)［福建泉州中考］如图12-2-7，∆ABC，∆CDE均为等腰直角三角形，∠ACB=∠DCE=90°，点E在AB上．求证：∆CDA≌∆CEB．图12-2-7。

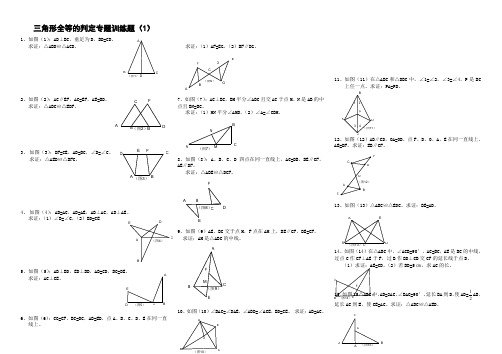
三角形全等的判定专题训练题（1）1、如图（1）：AD ⊥BC ，垂足为D ，BD=CD 。

求证：△ABD ≌△ACD 。

2、如图（2）：AC ∥EF ，AC=EF ，AE=BD 。

求证：△ABC ≌△EDF 。

3、 如图（3）：DF=CE ，AD=BC ，∠D=∠C 。

求证：△AED ≌△BFC 。

4、 如图（4）：AB=AC ，AD=AE ，AB ⊥AC ，AD ⊥AE 。

求证：（1）∠B=∠C ，（2）BD=CE5、如图（5）：AB ⊥BD ，ED ⊥BD ，AB=CD ，BC=DE 。

求证：AC ⊥CE 。

6、如图（6）：CG=CF ，BC=DC ，AB=ED ，点A 、B 、C 、D 、E 在同一直线上。

求证：（1）AF=EG ，（2）BF ∥DG 。

7、如图（7）：AC ⊥BC ，BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN=BC 。

求证：（1）MN 平分∠AMB ，（2）∠A=∠CBM 。

8、如图（8）：A 、B 、C 、D 四点在同一直线上，AC=DB ，BE ∥CF ，AE ∥DF 。

求证：△ABE ≌△DCF 。

9、如图（9）AE 、BC 交于点M ，F 点在AM 上，BE ∥CF ，BE=CF 。

求证：AM 是△ABC 的中线。

10、如图（10）∠BAC=∠DAE ，∠ABD=∠ACE ，BD=CE 。

求证：AB=AC 。

11、如图（11）在△ABC 和△DBC 中，∠1=∠2，∠3=∠4，P 是BC上任一点。

求证：PA=PD 。

12、如图（12）AB ∥CD ，OA=OD ，点F 、D 、O 、A 、E 在同一直线上，AE=DF 。

求证：EB ∥CF 。

13、如图（13）△ABC ≌△EDC 。

求证：BE=AD 。

14、如图（14）在△ABC 中，∠ACB=90°，AC=BC ，AE 是BC 的中线，过点C 作CF ⊥AE 于F ，过B 作BD ⊥CB 交CF 的延长线于点D 。

全等三角形的性质及判定练习题（1）1：下列说法，正确的是（ ）A.全等图形的面积相等B.面积相等的两个图形是全等形C.形状相同的两个图形是全等形D.周长相等的两个图形是全等形2：如图1，折叠长方形ABCD ，使顶点D 与BC 边上的N 点重合，如果AD=7cm ，DM=5cm ，∠DAM=39°，则AN =____cm ，NM =____cm ，NAB ∠= .3:如图2，已知ABC ADE ∆≅∆，AB AD =，BC DE =，那么与BAE ∠相等的角是 .4:如图3，ABC ADE ∆≅∆，则AB= ，∠E= _．若∠BAE=120°，∠BAD=40°，则∠BAC= .5：如图，在ABC ∆中，::2:5:11A B ACB ∠∠∠=，若将ACB ∆绕点C 逆时针旋转，使旋转前后的//A B C ∆中的顶点/B 在原三角形的边AC 的延长线上，求/BCA ∠的度数.图4EDCBA图2 图3MDAN BC图1BFADCE6：如图1,,,AE DB BC EF BC ==∥EF .求证:ABC DEF ∆≅∆7:已知.,,AB DF AC DE BE CF ===,求证:AB ∥DF图1ADCFBEAED B8:如图，AC=DF ，AC//DF ，AE=DB ，求证：BC//EF9:如图, AD=EB,AC ∥DF ,BC ∥EF .求证:ABC DEF ∆≅∆10:如图，在△ABC 中, M 在BC 上, D 在AM 上, AB AC =,DB DC =.问BM CM =吗?说明理由.11:如图, △ABC, AD 是它的角平分线,且BD CD =,ED 、DF 分别垂直于AB 、AC ，垂足为E 、F ，请说明BE CF =.12：已知：如图 , CE ∞AB 于E , BF ∞CD 于F , 且BF=CE13:已知：如图，∠A=∠D=90°，AC ，BD 交于O ，AC=BD.求证：OB=OC ．14：如图，AB AC =，AD AE =，EAD BAC ∠=∠.求证：△ABD ≌△ACE15:已知如图,AE ＝AC,AB ＝AD,∠EAB ＝∠CAD,试说明:∠B ＝∠D16：如图,BDA CEA ∠=∠,AE AD =.求证:AB AC =17:如图, △ABC 是等腰三角形,,AD BE 分别是,BAC ABC ∠∠的角平分线, △ABD 和△BAE 全等吗?请说明你的理由.18:已知：如图 , AB=AC , AD=AE , 求证：△OBD ≌△OCE全等三角形的性质及判定练习题（2）第一部分：选择题2．如图,已知AC和BD相交于O,且BO＝DO,AO＝CO,下列判断正确的是（）A．只能证明△AOB≌△COD B．只能证明△AOD≌△COBC．只能证明△AOB≌△COB D．能证明△AOB≌△COD和△AOD≌△COB2题4．如图,已知MB＝ND,∠MBA＝∠NDC,下列不能判定△ABM≌△CDN的条件是（）A．∠M＝∠N B．AB＝CD C．AM＝CN D．AM∥CN5．如图，已知0A=OB，OC=0D，下列结论中：①∠A=∠B；②DE=CE；③连OE，则0E平分∠0，正确的是( )A．①② B.②③C．①③D．①②③6.已知△ABC的六个元素,下面甲、乙、丙三个三角形中和△ABC全等的图形是（）A．甲和乙Ｂ．乙和丙Ｃ．只有乙Ｄ．只有丙第三部分：填空题1.如图，△ABC ≌△AED ，∠BAC=25°，∠B=35°，AB=3cm ，BC=1cm ，则∠E= , ∠ ADE= ；线段DE= cm ，AE= cm .2.已知ABC DEF ∆≅∆，若ABC ∆的周长为32，8AB =，12BC =，则DE = ，DF = . 第四部分：解答题1.如图，已知ABC AED ∆≅∆，AE AB =，AD AC =，20D E ︒∠-∠=，60BAC ︒∠=.求C ∠的度数.2.如图，已知AB=DE ，AF=DC ，BE=CF ，求证：∠A=∠D.3.已知：AB=CD ，AD=BC.试说明∠A=∠C.（公共边）ＥD CBABEDCAADB EFC DAO4.如图,在四边形ABCD中,已知BD平分∠ABC,∠A＋∠C＝180o,试说明AD＝CD.。

全等三角形的判定练习题一、选择题1. 下列哪组条件可以判定两个三角形全等？A. 两边和其中一边的对角相等B. 两角和其中一角的对边相等C. 两边和它们的夹角相等D. 两角和其中一边相等A. ∠A=∠DB. ∠B=∠EC. ∠C=∠FA. SAS（边角边）B. ASA（角边角）C. AAS（角角边）D. SSS（三边）二、填空题1. 若两个三角形的______相等，且它们的夹角相等，则这两个三角形全等。

2. 在全等三角形中，对应边______相等，对应角______相等。

3. 要判定两个三角形全等，至少需要知道它们的______个元素相等。

三、判断题1. 若两个三角形的两边和它们的夹角分别相等，则这两个三角形一定全等。

（）2. 两个等腰三角形的底角相等，则这两个三角形全等。

（）3. 两个等边三角形的边长相等，则这两个三角形全等。

（）四、解答题1. 在△ABC中，AB=AC，∠B=∠C，求证：△ABC是等腰三角形。

2. 已知△ABC和△DEF，AB=DE，BC=EF，∠B=∠E，求证：△ABC≌△DEF。

3. 在△ABC中，AB=AC，∠A=40°，∠B=70°，求∠C的度数。

4. 已知△ABC和△DEF，AB=DE，BC=EF，AC=DF，求证：△ABC≌△DEF。

5. 在△ABC中，AB=8cm，AC=10cm，∠A=60°，求BC的长度。

五、作图题1. 请作出一个三角形，使其与给定三角形全等，已知条件是两边及其夹角。

2. 请作出一个三角形，使其与给定三角形全等，已知条件是两角及其夹边。

3. 请作出一个三角形，使其与给定三角形全等，已知条件是三边。

六、综合题1. 在平面直角坐标系中，点A(2, 3)，点B(6, 3)，点C和点D在x轴上，且△ABC≌△ABD，求点C和点D的坐标。

2. 在四边形ABCD中，AB=CD，AD=BC，且∠ABC=∠CDA=90°，证明：△ABC≌△CDA。

《三角形全等的判定》同步练习及答案A等级1、指出下图中的全等三角形各有几对，分别是哪些三角形。

△ABC中，AB=AC，D为BC中点，DE⊥AB，DF⊥AC2、指出下图中的全等三角形各有几对，分别是哪些三角形。

OA=OB，OC=OD3、指出下图中的全等三角形各有几对，分别是哪些三角形。

△ABC中，AB=AC，AE=AF，AD⊥BC于D4、判断( )1.三个角对应相等的两个三角形全等.( )2.顶角及腰上的高相等的两个等腰三角形全等.( )3.全等三角形对应的中线相等.( )4.有一边相等的两个等腰直角三角形全等.5、△ABC和△A′B′C′中，已知∠A=∠B′，AB=B′C′，增加条件可使△ABC≌△B′C′A′(ASA).6、△ABC中∠C=90°,BC＞AC，E在BC上，且BE=EA. ∠CAE∶∠B=4∶7,则∠CEA=_____.7、△ABC中，∠C=90°，BE为角平分线，ED⊥AB于D，若AE+ED=5cm,则AC=_______.8、四边形ABCD中，边AB=DC，AD=BC，∠B=40°,则∠C= .9、△ABC中，AB=AC，两中线BE，CF交于O，则按条件所作图形中共有对全等三角形.10、如图，AC⊥BE,AC=CE,CB=CF，把△EFC绕点C逆时针旋转90°,E落在______点上，F落在点上.B等级11、判断( )1.全等三角形的对应角相等，反之也成立.( )2.周长为16,一边长为5的两个等腰三角形全等.( )3.有两个角及一条边相等的两个三角形全等.( )4.有锐角及斜边对应相等的两个直角三角形全等.12、BP为∠ABC平分线，D在BP上，PA⊥BA于A，PC⊥BC于C，若∠ADP=35°，则∠BDC= 。

13、若△ABC≌△A′B′C′,且AB=10cm，BC=6cm,则A′C′的取值范围为 .14、在△ABC和△DEF中，∠C=∠D，∠B=∠E，要使两三角形全等，需增加条件( )A.AB=EDB.AB=FD C,AC=FD D. ∠A=∠F15、下列条件能判断△ABC≌△DEF的是( )A. ∠A=∠D, ∠C=∠F, ∠B=∠EB. ∠A=∠D,AB+AC=DE+DFB. ∠A=∠D, ∠B=∠E,AC=DF D. ∠A=∠D,AC=DF,BC=EF16、△ABC中，∠C=90°，AD为角平分线，BC=32，BD∶DC=9∶7,则点D到AB的距离为( )A.18cmB.16cmC.14cmD.12cm17、∠MON的边OM上有两点A、C，ON上有两点B、D，且OA=OB，OC=OD，AD，BC交于E，则①△OAD≌△OBC，②△ACE≌△BDE，③连OE.则OE平分∠AOB，以上结论( )A.只有一个正确B.只有一个不正确C.都正确D.都不正确18、△ABC中，∠C=90°,AC=BC，AD为角平分线，DE⊥AB于E，且AB=6cm，则△DEB的周长为( )A.4cmB.6cmC.8cmD.10cm19、B为AC上一点，在AC同侧作等边△EAB及等边△DBC,那么下列式子错误的是( )A.△ABD≌△EBCB. ∠BDA=∠BCEC.△ABE≌△BC DD.若BE交AD于M，CE交BD于N，那么△NBC≌△MBD20、线段OD=DC，A在OC上，B在OD上，且OA=OB，OC=OD，∠COD=60°，∠C=25，AC，BC交于E，则∠BED的度数是( )A.60°B.70°C.80°D.50°C等级21、已知：△ABC中，D、E、F分别是AB、AC、BC上的点，连结DE、EF，∠ADE=∠EFC，∠AED=∠ACB，DE=FC。

前言：
该同步训练习题由多位一线国家特级教师针对当前最新的热点、考点、重点、难点、知识点，精心编辑而成。

以高质量的同步训练习题助力考生查漏补缺，在原有基础上更进一步。

（最新精品同步训练习题）
12.2三角形全等的判定
第1课时三角形全等的判定(SSS)
[学生用书P25]
1．如图12-2-6所示，在△ABC中，AB＝AC，BE＝CE，则由“SSS”可以判定( )
图12-2-6
A．△ABD≌△ACD B．△BDE≌△CDE
C．△ABE≌△ACE D．以上都不正确
2．如图12-2-7，点D，E在线段BC上，AB＝AC，AD＝AE，BE＝CD，要判定△ABD≌△ACE，较为快捷的判定依据是__ __．
图12-2-7
3．[2016·福州]一个平分角的仪器如图12-2-8所示，其中AB＝AD，BC＝DC. 求证：∠BAC＝∠DAC.
图12-2-8
4．如图12-2-9，四边形ABCD中，AB＝CD，CB＝AD.求证：△ABC≌△CDA.
图12-2-9
5．如图12-2-10，AB＝AC，AE＝AD，BD＝CE，求证：△AEB≌△ADC.
图12-2-10。

全等三角形的判定（一）1. 如图是一个平分角的简单仪器，其中AD 二AB, BC 二DC.将A 放在角的顶点，AB 和AD沿着角的两边放下，沿AC 画一条射线AE, AE 就是ZDAB 的平分线.在这个过程中AADC AABC 的根据是（A. SASB. SSSC. AASD. ASA2. 如图，AABC 的三条边全不相等，BODE ・以D 、E 为两个顶点作位置不同的三角形, 使新作的三角形与全等.这样的三角形可以作出（ ）A. 2个B. 4个C. 6个D. 8个3.如图，AB=FD, AC=FE, BD=CE,则 AABC 和 Z\FDE ()A. 一定全等B. 一定不全等4. 如图，在 Z\ABC 和 AFED 中，AC 二 FD, BC 二 ED,要利用 全等吋，下面的4个条件中：①AE=FB ；②AB=FE ；③AE 二BE ；④BF=BE,可利用的是（） A. ①或② B.②或③ C.①或③ D.①或④D、Frc上述三种情况都有可能 “SSS” 来判定△ ABC 和 ZXFED E5.如图是用圆规和直尺画己知角的平分线的示意图，该画法是根据全等三角形识别中的（7.如图，AE 二DF, CE 二BF, AB=CD 可有 AB 二CD 得 __ ,从而根据 _____ 得厶ACE^ADBF.9. _____________________________________________________ 如图，已知AB 二AC , AD 二AE , BD 二EC ,则图中有 __________________________________________ 对全等三角形，它们10. 如图，AABC 的三个顶点分别在格子的3个顶点上，请你试着再在格子的顶点上找出一个点 D,使得△【)％与全等，把这样的三角形都画出来.11. (曲靖中考)如图，已知点B, E, C, F 在一条直线上，AB 二DF, AC=DE, BE=CF.(1) 求证：AC/7DE ；(2) 若 BF=13, EC 二5,求 BC 的长.D. SAS理rh 是 ______可以 rh “sss” 判定全等的三角形是A. SSSB. ASAC. AAS BC AB 二DC ,12.（河北中考）如图，点B, F, C, E在直线1上（F, C之间不能直接测量），点A, D在1异侧，测得AB=DE, AC二DF, BF二EC・（1）求证：AABC^ADEF；（2）指出图中所有平行的线段，并说明理由.全等三角形的判定（一）课后作业参考答案1.解析：根据题目所给条件可利用SSS定理判定厶ADC^AABC,进而得到ZDAC=Z BAC.AD = AB解:•・•在ZiADC 和AABC 中\DC = BC , A AADC^ AABC （SSS）, A ZDAC=ZBAC,AC = AC・・・AC就是ZDAB的平分线.故选：B.2.解析：分别是以D为圆心，AB为半径，作圆，以E为圆心，AC为半径，作圆.两圆相交于两点（D, E上下各一个），经过连接后可得到两个；然后以D为圆心，AC为半径，作圆，以E为圆心，AB 为半径，作圆.两圆相交于两点（D, E上下各一个），经过连接后可得到两个.故选C.3.解析：由BD二CE,可得出BODE,然后利用SSS,可判定△ ABC^ AFDE.解：V BD=CE,・・・BD+DC二CE+DC,即BODE,在Z\ABC 和Z\FDE 中，AB = FDV \A C=FE,:. AABC^ AFDE （SSS）.故选A.BC = DE4.解析：要利用SSS进行AABC和AFED全等的判定，还需要条件AB=FE,结合题意给岀的条件即可作出判断.解:由题意可得，要用SSS进行AABC和AFED全等的判定，需要AB=FE,若添加①AE=FB,则可得AE+BE二FB+BE,即AB二FE,故①可以；若添加AB二FE,则可直接证明两三角形的全等，故②可以.若添加AE=BE,或BF二BE,均不能得出AB二FE,不可以利用SSS进行全等的证明，故③④不可以.故选A.5.解析：根据画图得出CD二BD, AC=AB,根据SSS推出两三角形全等，即可出答案.解：从画图中知CD二BD, AC二AB,・.・ AD=AD,・•・ AACD^ AABD (SSS),・・・ ZCAD二ZBAD,故选A.6.解析：根据已知结合隐含条件AC二AC即可得出全等三角形.解答AB = CD证明：在AABC 和Z\CDA 屮<BC = AD f:. △ABC9ACDA (SSS).故答案为：CDA, SSS.AC = AC7.解析：本题要判定△ ACE9ZXDBF,已知AB二CD, BC=BC可得AC=BD,又因为AE二DF, CE二BF,所以可根据SSS判定△ ACE^ ADBF.解：TAB二CD, BC=BC・•・AC二BDVAE=DF, CE=BFA AACE^ ADBF. (SSS)8.解析：可以由“SSS”判定全等的三角形是△ ABD^ ADCA； AABC^ ADCB；有条件AC二DB, AB二DC再加上公共边AD二AD可证明△ ABD^ ADCA；有条件AC=DB, AB二DC再加上公共边BC=BC可证明△ ABC^ ADCB.解：可以由“SSS”判定全等的三角形是AABD竺ADCA； AABC^ ADCB；AD = AD•・•在AADC 和ADAB 中\A C=DB, :. AABD^ ADCA (SSS)；AB = CDAB = DC•・•在AnBC 和ADCB 中\A C=DB, :. AABC^ ADCB (SSS),BC = BC故答案为：AABD竺ADCA； AABC^ ADCB.9.解析：此题是一道开放题，所以要求学生的思维必须严密，考虑全面各种情况，不要漏解.解：如图所示:10.解析：根据直角三角形的两个锐角互余进行解答即可.解：在RTADBC 中，ZD=65°,可得：ZDCB二25° ,在RTAACE 中，ZDCB二25°,可得：ZACF二65° ,在RTAACF 屮，ZACF二65°,可得：ZEAC二25°・AB = DF11.解析：(1)证明：TBE二CF・・・BC=FE 在Z\ABC 和ADFE 中<AC = DE, A AABC^ADFE (SSS),BC=FE:.ZACE=ZDEF, ・・・AC〃DE；(2)解：V A ABC A DEE, ABC=EF, ・・.CB-EC 二EF-EC, .\EB=CF, VBF=13, EO5,・・・EB二(13-5) 4-2=4, ・・.CB二4+5=9・12.解析：(1)先证明BC二EF,再根据SSS即可证明.(2)结论AB〃DE, AC〃DF,根据全等三角形的性质即可证明.(1)证明：VBF=CE,・・・BF+FC二FC+CE,即BOEF,AB = DE在/XABC 和ADEF 中，\AC = DF A AABC^ADEF (SSS).BC = EF(2)结论：AB〃DE, AC〃DF.理由：VAABC^ADEE,.\ZABC=ZDEF, ZACB=ZDFE,。