梁弯曲

梁弯曲的概念梁是一种常见的结构元素，广泛应用于建筑、桥梁、机械等领域。

在工程应用中，梁可以承受各种荷载导致的弯矩和剪力。

而梁的弯曲是指梁在承受荷载的作用下产生的曲率变化。

针对梁的弯曲问题，可以利用梁弯曲理论进行力学分析和结构设计。

梁弯曲的概念实际上涉及到两个重要的力学概念：弯矩和曲率。

弯矩是由外力作用在梁上产生的，它可以使梁产生弯曲或者使梁产生剪切变形。

曲率描述了梁的弯曲程度，是弯曲轴线的弯曲半径的倒数。

在分析梁弯曲时，通常会采用欧拉—伯努力学说，即假设梁在弯曲过程中，横截面平面仍然保持垂直于位移方向。

这个假设为了简化问题，但在一些特殊情况下可能需要引入其他理论模型。

梁弯曲的特点是在横向距离上产生剪切力和弯矩。

在梁的底部表面上，由于负弯矩的存在，会产生压应力；在梁的顶部表面上，由于正弯矩的存在，会产生拉应力。

而在距离横截面中性轴较远的位置，弯矩和曲率的值较大；而在中性轴附近位置，弯矩和曲率的值较小。

对于简单支承的梁，弯曲会导致两个基本的反应：梁曲率和梁挠度。

梁的曲率是横截面在垂直于曲线切线方向上的曲率半径的倒数。

梁的挠度是指梁在一点的纵向位移。

在分析梁弯曲时，可以利用弯曲方程和边界条件求解梁的曲率和挠度。

梁弯曲的分析可以应用不同的方法，其中最常用的方法是基于理想化梁的假设和采用弯曲方程。

对于简支梁，弯曲方程可以表示为：M = EI * d²y/dx²其中M是弯矩，E是弹性模量，I是截面惯性矩，y是梁的纵向位移，x是横向距离。

这个方程可以用来描述弯曲梁的受力和变形情况。

对于常见的梁形状，如矩形梁、T形梁或I形梁等，可以通过求解弯曲方程来得到梁的曲率和挠度分布。

这些分布信息可以用来评估梁的性能、设计合理的梁结构和验证结构的可靠性。

此外，在实际工程中，还需要考虑梁的极限弯矩和极限弯矩系数。

极限弯矩是指在不发生塑性滞后的情况下，梁能够承受的最大弯矩。

而极限弯矩系数是指实际弯矩与极限弯矩之间的比值。

梁弯曲问题的四个弯曲要素哎呀，今天咱们聊聊梁弯曲的问题，听起来可能有点枯燥，不过别担心，我保证会让你觉得轻松有趣。

先说说这四个弯曲要素，咱们可不能小看了它们，每一个都能把你绕得晕头转向。

材料特性。

想象一下，你在家里用的那根木棍和铁棍，感觉是不是差别大得很？木棍弯弯曲曲，像个小孩子的玩具，而铁棍就像个硬汉，坚韧得让人刮目相看。

材料的强度和弹性，简直就像是每个人的性格。

有的人软绵绵，有的人坚硬无比。

这材料的选择，真的是让人头疼，不过呀，选对了，能让你省下不少力气，真是事半功倍的好事儿。

再来说说负载。

负载就像是给梁加了个大包袱，试想一下，如果你一个人搬着十斤的东西，轻松自如；可要是再加个五斤，嘿，立刻就觉得吃力了。

负载不仅影响梁的弯曲程度，还影响它的承受能力。

这就像你在日常生活中，面对压力的时候，一下子被压得喘不过气，或者轻松应对，心态决定了一切。

负载越大，弯曲越明显，就像你的心情也会因为压力而大起大落。

然后咱们得提到支撑条件。

就好比你在家里搭个帐篷，底下支撑得稳，帐篷才能屹立不倒。

梁的支撑点就像这个帐篷的四个角，稳稳当当，才能承受住各种挑战。

如果支撑点不对，那梁就有可能“翘起来”，可是要是稳稳当当，那它就能安安稳稳地待着，仿佛在说：“来吧，尽管压我，我不怕！”所以，选好支撑点，就能让你的设计更加可靠。

咱们得聊聊梁的跨度。

跨度就像是一条宽宽的河流，水流过的地方越宽，挑战越大。

这条河流越宽，梁就得越强壮，才能不被冲垮。

跨度大，就得想办法增强梁的强度，才能在上面跑得更快，过得更顺。

就像生活中的一些关键时刻，挑战越大，我们越得努力去克服，才能迎来更美好的未来。

所以，梁弯曲的问题，看似简单，其实背后有很多小故事。

每一个要素都像是生活中的一部分，互相交织，缺一不可。

材料、负载、支撑条件、跨度，四个弯曲要素就像四个好朋友，只有他们齐心协力，才能创造出一个美好的结构。

就像我们生活中，有朋友的支持，才能勇往直前，无所畏惧。

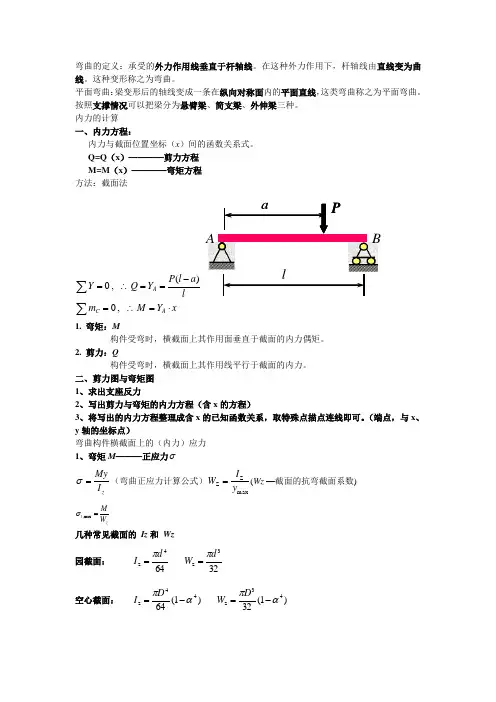
弯曲的定义：承受的外力作用线垂直于杆轴线。

在这种外力作用下，杆轴线由直线变为曲线。

这种变形称之为弯曲。

平面弯曲：梁变形后的轴线变成一条在纵向对称面内的平面直线，这类弯曲称之为平面弯曲。

按照支撑情况可以把梁分为悬臂梁、简支梁、外伸梁三种。

内力的计算一、内力方程：内力与截面位置坐标（x ）间的函数关系式。

Q=Q （x ）————剪力方程 M=M （x ）————弯矩方程 方法：截面法xY M m la l P Y Q Y A C A⋅=∴=-==∴=∑∑ , 0)( , 0PalAB1. 弯矩：M构件受弯时，横截面上其作用面垂直于截面的内力偶矩。

2. 剪力：Q构件受弯时，横截面上其作用线平行于截面的内力。

二、剪力图与弯矩图 1、求出支座反力2、写出剪力与弯矩的内力方程（含x 的方程）3、将写出的内力方程整理成含x 的已知函数关系，取特殊点描点连线即可。

（端点，与x 、y 轴的坐标点）弯曲构件横截面上的（内力）应力 1、弯矩M ———正应力σz I My=σ（弯曲正应力计算公式）maxZ Z y I W =(Wz —截面的抗弯截面系数) z t W M =max ,σ几种常见截面的 Iz 和 Wz 园截面： 644z d I π=323z d W π=空心截面： )1(6444z απ-=D I )1(3243z απ-=D W矩形截面： 123z bh I = 62z bh W =空心矩形截面： 12123300z bh h b I -= )2//()1212(03300z h bh h b W -=关于正应力的强度校核：① 校核强度： [m a xσ≤zW M② 设计截面尺寸：[m a xσM W z ≥③ 计算许可载荷：[max σz W M ≤2、剪力Q ——剪应力t*=zzbI QS 1τ其中Q 为截面剪力；S z 为y 点以下的面积对中性轴之静矩 Iz 为整个截面对z 轴之惯性矩；b 为y 点处截面宽度。

梁弯曲知识点总结一、弯曲概念在物理学和工程力学中，弯曲是指在材料受到外力作用下，产生一种曲率变化的变形形式。

在梁的情况下，当梁受到外部载荷作用时，梁将发生一种曲率变化，即梁的一部分受到压力而另一部分受到拉力，使得梁产生一种弯曲的变形形式。

梁的弯曲是梁理论研究的重要内容之一。

二、弯曲的原理梁的弯曲原理是由梁的弯矩和弯曲应力来描述的。

梁在弯曲时，横截面上的各个点受到的弯矩不同，由于弯矩的不平衡，在梁的上表面产生的张力，下表面产生的压力，产生了一种称为弯曲应力的内力形式。

弯曲应力的作用下，梁在弯曲的过程中产生了曲率变化，弯曲原理是用来描述梁在弯曲时的变形和内力情况的。

三、梁的弯曲方程梁的弯曲方程是用来描述梁在弯曲时的曲率和弯矩之间的关系的。

梁的弯曲方程可以通过力学原理和材料力学原理来推导出来。

梁的弯曲方程可以用来计算梁在受载时的弯曲变形和各个截面上的应力情况，对于工程结构的设计和分析具有非常重要的意义。

梁的弯曲方程通常包括以下几个方面：1.梁的弯曲变形方程：描述梁在弯曲时产生的曲率变化和曲线形状；2.梁的弯矩方程：描述梁在受力状况下产生的弯矩大小和分布情况；3.梁的弯曲应力方程：描述梁在弯曲状况下产生的应力大小和分布情况。

梁的弯曲方程是梁理论的核心内容，对于工程结构的设计和分析具有重要的意义。

四、梁的弯曲理论梁的弯曲理论是研究梁在受载时的弯曲变形和内力情况的理论。

梁的弯曲理论是以弹性理论和材料力学为基础的，通过对梁在弯曲时的力学原理和材料力学原理进行分析和推导，得出了梁在弯曲时的各种数学模型。

梁的弯曲理论可以应用于工程结构的设计和分析中，能够比较准确地描述梁在受载时的变形和内力情况，为工程结构的安全和稳定性提供理论依据。

梁的弯曲理论包括以下几个方面：1.梁的弯曲变形分析：描述梁在受载时产生的形状和曲率变化；2.梁的弯曲应力分析：描述梁在受载时产生的应力大小和分布情况；3.梁的弯曲挠度分析：描述梁在受载时产生的挠度大小和分布情况；4.梁的弯曲裂缝分析：描述梁在受载时产生的裂缝情况。

梁的弯曲变形应用原理简介梁是一种常见的结构元素，用于承受和传递载荷。

在实际应用中，梁常常会发生弯曲变形，这种变形有着重要的应用原理和工程意义。

本文将介绍梁的弯曲变形的应用原理，以及它在工程领域中的具体应用。

梁的弯曲变形原理当梁受到外部载荷作用时，其会发生弯曲变形。

梁的弯曲变形主要是由内力矩引起的，内力矩是梁截面上的剪力和弯矩引起的。

弯曲变形原理可以用以下几个要点来描述：1.梁撑杆法：梁在弯曲时，可以看做由无数撑杆组成的系统。

每个撑杆受到不同大小的拉伸或压缩力，整个梁发生的弯曲变形是各撑杆弹性变形的综合效果。

2.中性轴和截面旋转：梁弯曲时，存在一个中性轴，该轴是在截面内法线应力为零的位置。

梁在弯曲时，截面内部会发生旋转，上部受拉，下部受压，截面的变形呈现出弯曲的形态。

3.弯矩与曲率关系：梁的弯曲变形与弯矩和曲率有关。

弯矩是横截面上的合力矩，而曲率则是截面内部形成的曲线的曲率半径的倒数。

根据弯矩和曲率之间的关系，可以计算出梁的变形情况。

梁的弯曲变形应用梁的弯曲变形在工程领域中有着广泛的应用。

下面列举了梁的弯曲变形应用在不同工程中的具体案例：1. 建筑结构设计在建筑结构设计中，梁的弯曲变形是必须考虑的因素之一。

通过合理的梁的尺寸和形状设计，可以满足建筑物的结构强度和刚度要求，保证建筑物的安全性和稳定性。

2. 桥梁工程在桥梁工程中，梁的弯曲变形对于桥梁的承载能力和结构安全性影响重大。

通过分析梁的弯曲变形情况，可以确定桥梁的设计参数，保证桥梁承受车辆和行人的荷载，确保桥梁的正常使用和运行。

3. 机械设计梁的弯曲变形在机械设计中也有着广泛的应用。

例如，在起重机设计中，梁的弯曲变形会导致起重机的运动效果失真，因此需要精确计算梁的弯曲变形，以确保起重机的稳定性和可靠性。

4. 航天器设计在航天器设计中，梁的弯曲变形是非常重要的考虑因素。

航天器需要承受巨大的重力和惯性力，梁的弯曲变形对于航天器的结构强度和稳定性至关重要。

关于梁的弯曲中若干公式的分类讨论①
梁的弯曲是指梁在受外力作用下产生弯曲变形的过程。

在梁的弯曲中，有许多公式可以用来描述和计算梁的弯曲性能。

本文将对其中的若干公式进行分类讨论。

一、基本公式
1. 弯矩公式：在梁弯曲的过程中，弯矩是一个重要的物理量，用来描述梁受力状态的变化。

弯矩公式可以表达为M = -EI(d^2v/dx^2)，其中M表示弯矩，E表示杨氏模量，I 表示截面惯性矩，v表示横向挠曲位移，x表示沿梁的坐标方向。

二、简支梁公式
当梁两端支座固定时，称为简支梁。

对于简支梁，可以应用以下公式进行计算：
1. 弯曲刚度公式：弯曲刚度是描述简支梁抵抗弯曲变形的能力的一个重要参数。

弯曲刚度公式可以表达为EI/R = M = PL/4，其中EI/R表示弯曲刚度，M表示弯矩，P表示受力，L表示梁的长度。

2. 最大弯矩公式：最大弯矩是指梁在简支梁情况下受力状态下的最大弯矩值。

最大弯矩公式可以表达为Mmax = PL/4，其中Mmax表示最大弯矩，P表示受力，L表示梁的长度。

三、悬臂梁公式
梁的弯曲中有许多公式可以用来描述和计算梁的弯曲性能。

其中包括基本公式、简支梁公式和悬臂梁公式。

这些公式可以帮助我们更好地理解和分析梁的弯曲行为，并进行相应的工程设计和计算。