计算理论基础章7

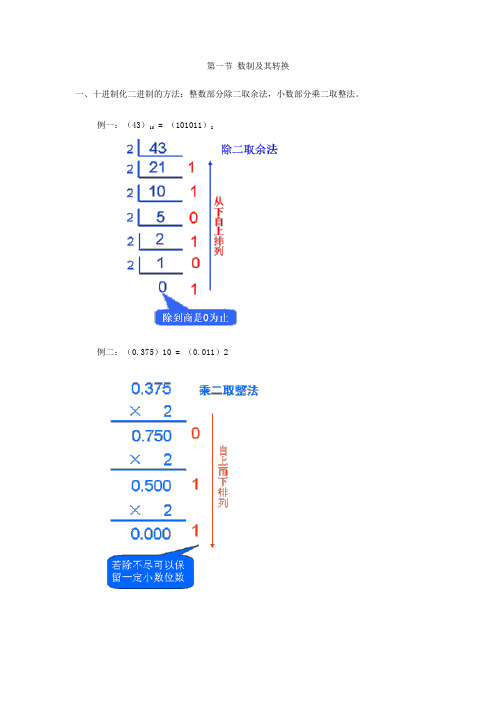
第一节数制及其转换一、十进制化二进制的方法：整数部分除二取余法，小数部分乘二取整法。

例一：（43）10 = （101011）2例二：（0.375）10 = （0.011）2第二节算术运算和逻辑运算一、二进制的算术运算1、加法运算规则：0+0=0 0+1=1 1+0=1 1+1=102、减法运算规则：0-0=0 0-1=1（向高位借1） 1-0=1 1-1=03、乘法运算规则：0×0=00×1=01×0=01×1=1第二节存储器系统三、主存储器1、特点：容量小、读写速度快、价格高2、分类：① 随机存储器（RAM）：就是我们通常称的内存② 只读存储器（ROM）：只能读不能写，一般用于存放计算机启动所需的最基本程序。

③ 缓冲存储器（Cache）：速度最快，一般集成于CPU中。

第三章网络基础知识第一节网络的组成与结构一、网络组成1、通信主体：服务器和工作站2、通信设备：传输介质、网络设备3、通信协议：通常是TCP/IP二、网络分类按传输距离分：局域网（LAN）、城域网（MAN）、广域网（WAN）按网络结构分：总线型、星型、环型、树型三、网络拓扑结构第二节网络协议第四章其他相关基础知识第一节计算机病毒一、特点寄生性、隐蔽性、非法性、传染性、破坏性第三节Internet相关知识一、IP地址每台与Internet连接的主机都必须有一个IP地址，IP地址采用分段式表示：共分4段，每段用一个字节即八个二进制位表示，实际的IP把二进制转换成十进制书写。

如61.153.238.132，因为每段时一个字节，因此IP每段的数字大小最大为255。

IP地址分类如下表：目前32位IP地址资源几近枯竭，有人提出用128位表示IP，即IPV6 。

二、域名：Internet的域名系统叫做DNS，DNS是树形结构的。

域名跟IP地址是多对一的关系1、域名分级系统：一个域名最右边的部分通常叫顶级域名，往前依次为二级域名、三级域名等。

计算理论基础知识计算理论是计算机科学的核心领域之一，它研究的是计算过程的本质和限制。

在计算机科学的发展过程中，计算理论提供了重要的理论基础和方法，为计算机科学和技术的发展奠定了坚实的基础。

本文将简要介绍计算理论的基础知识。

一、自动机理论自动机是计算理论中的重要概念之一，它用于描述计算过程的抽象模型。

自动机可以分为有限自动机和非确定性有限自动机等多种类型。

有限自动机是一种最简单的计算模型，它由状态、输入字母表、转换函数和初始状态等组成。

通过状态的转换和输入的驱动，有限自动机可以执行特定的计算任务。

非确定性有限自动机则相对更加复杂，它在进行状态转换时可以有多个可能的选项。

二、形式语言与文法形式语言和文法是计算理论中研究自动机行为规律的重要工具。

形式语言是由符号组成的集合，用于表示计算过程中的输入、输出和中间结果等信息。

文法则定义了形式语言的句子生成规则。

常见的文法类型有上下文无关文法、上下文相关文法等。

形式语言和文法的研究使得我们能够通过规则来描述和分析计算过程，从而更好地理解计算机科学中的一些重要概念和问题。

三、图灵机和可计算性理论图灵机是计算理论中最重要的概念之一，它由一个无限长的纸带和一个读写头组成。

图灵机通过读写头在纸带上的移动和改写来模拟计算过程。

图灵机的提出使得我们能够更深入地研究计算过程的本质和限制。

可计算性理论是计算理论中的一个重要分支，它研究的是什么样的问题可以通过某种计算模型解决。

根据可计算性理论，存在一些问题是不可计算的，即无法用任何计算模型来解决。

四、复杂性理论复杂性理论是计算理论中的另一个重要分支，它研究的是计算问题的复杂度。

复杂性理论主要关注计算问题的难解性和可解性。

常见的复杂性类别有P类、NP类等。

P类问题是可以在多项式时间内解决的问题，而NP类问题是可以在多项式时间内验证解的问题。

复杂性理论的研究使得我们能够更好地理解计算问题的本质，从而设计更高效的算法和方法。

五、计算复杂性和可计算性的关系计算复杂性和可计算性是计算理论中两个重要的概念。

计算基础知识点总结基础计算是人们在日常生活和工作中都会用到的一种重要的技能，它不仅对普通人来说是必不可少的，对工程师、科学家、会计师等专业人士来说更是基础中的基础。

掌握基础计算知识，对于提高工作效率、减少错误、提高工作质量等方面都是非常有帮助的。

本文将对基础计算知识进行总结，力求全面、系统地介绍基础计算知识的各个方面。

第一部分：基本数学运算1. 加法加法是最基本的数学运算之一，它是指将两个或多个数值相加得到一个和的过程。

在实际生活中，加法运算经常用到，比如购物结账、家庭账单、工程量清单等都需要用到加法运算。

2. 减法减法是与加法相对应的一种数学运算，它是指从一个数值中减去另一个数值得到差的过程。

在实际生活中，减法运算也非常常见，比如计算存款的利息、购物找零、工程量清单的结算等都需要用到减法运算。

3. 乘法乘法是一种重要的数学运算，它是指将两个或多个数值相乘得到一个积的过程。

在实际生活中，乘法运算也经常用到，比如计算工作时间与工资的关系、计算商品价格和数量的关系等都需要用到乘法运算。

4. 除法除法是数学运算中的一种重要形式，它是指将一个数值除以另一个数值得到商的过程。

在实际生活中，除法运算也非常常见，比如计算每天的平均花销、计算商品的单价等都需要用到除法运算。

5. 混合运算混合运算是指在一个数学式中同时包含多种数学运算，比如加法、减法、乘法和除法等。

在实际生活中，混合运算也经常用到，比如计算购物车的总金额、计算复杂的数学问题等都需要用到混合运算。

第二部分：整数和分数的运算1. 整数的加减乘除整数是指包括正整数、负整数和零在内的一类数，在整数的加减乘除运算中，要特别注意正负数相加减的规则、乘法和除法的特点等。

2. 分数的加减乘除分数是一种特殊的数形式，它由一个分子和一个分母组成，在分数的加减乘除运算中，要特别注意分子和分母的运算规则、分数的化简、通分等问题。

3. 整数和分数的混合运算整数和分数的混合运算是整数和分数加减乘除的混合形式，在混合运算中，要特别注意整数和分数的转换、公约数和公倍数的运用等问题。

第一章：信息技术概述1.1：信息与信息技术1.1.1信息与信息处理控诉论的创始人：维纳信息就是信息，既不是物质也不是能量。

信息的定义：客观世界中各种事物运动运动状态和变化内容的反映，是认识主体对客观事物状态和变化的感知。

客观世界的三大构成要素：信息、物质与能量。

人信息处理的过程：获取信息、传递信息、加工（处理）信息和施用信息。

缺点：算不快，记不住，传不远，看不清，听不清。

信息处理包括哪些行为和活动：A．信息的收集：信息的感知，测量，获取，输入B．信息的加工：分类，计算，分析，综合，转换，管理C．信息的存储:书写，摄影，录音，录像D．信息的传递：邮寄，出版，电话，广播电视，短息，博客，微信E．信息的施用：控制，显示，导航，机器人1.1.2信息技术和信息产业信息技术：用来扩展人们信息器官功能，协助人们更有效地进行信息处理的一门技术。

现代信息技术的主要特征：以数字技术为基础，软件与通信技术为核心，采用微电子和光电子器件。

信息产业：从事信息技术开发，设备与产品的研制生产以及提供信息服务的若干部门的总称。

A信息设备制造B信息服务C信息内容产业D信息基础设备1.1.3信息化与信息社会信息化的作用：A对传统产业进行改造，极大地提高了传统产业的劳动生产率;B孕育和催生了许多新兴产业;C推进了管理扁平化和社会的信息化；D推动经济全球化。

1.2数字技术基础1.2.1信息的基本单位——比特比特(符号b)只有两种状态“0”“1”，中文为二进位数字例如：电平的高低，电流的有无等每个字节包含八个比特（字节的符号B）1.比特的存储A比特存储在触发器里（一种双稳电子线路）一个触发器可以存储一个比特B电容器C利用盘片在光滑表面上的微小凹坑记录2.比特与二进位3.信息在计算机中的表示（1）无符号整数自然码（2）带符号整数0~2n-1；“0”表示正数（+）“1”表示（-）；正数为负的需要用补码（原码取反加1）缺点：不直观(3)文字符号的表示西文字符（ASCII码）：美国信息交换标准码，一共有128个字符，包括96个可打印字符和32个控制字符。

第七章 波浪理论及其计算原理在自然界中；常可以观察到水面上各式各样的波动，这就是常讲的波浪运动，它造成海洋结构的疲劳破坏，也影响船的航行和停泊的安全。

波浪的动力作用也常引起近岸浅水地带的水底泥沙运动，致使岸滩崩塌，建筑物前水底发生淘刷，港口和航道发生淤积，水深减小，影响船舶的通航和停泊。

为了海洋结构物、驾驶船舶和船舶停靠码头的安全，必须对波浪理论有所了解。

一般讲，平衡水面因受外力干扰而变成不平衡状态，但表面张力、重力等作用力则使不平衡状态又趋于平衡，但由于惯性的作用。

这种平衡始终难以达到，于是，水体的自由表面出现周期性的有规律的起伏波动，而波动部位的水质点则作周期性的往复振荡运动。

这就是波浪现象的特性。

波浪可按所受外界的干扰不同进行分类。

由风力引起的波浪叫风成波。

由太阳、月亮以及其它天体引起的波浪叫潮汐波。

由水底地震引起的波浪叫地震水波由船舶航行引起的波浪叫船行波。

其中对海洋结构安全影响最大的是风成波。

风成波是在水表面上的波动，也称表面波。

风是产生波动的外界因素，而波动的内在因素是重力。

因此，从受力的来看；称为重力波。

视波浪的形式及运动的情况，波浪有各种类型。

它们可高可低，可长司短。

波可是静止的一一驻波（即两个同样波的相向运动所产生的波，也可以是移动的——推进波以一定的速度将波形不变地向一个方向传播的波），可以是单独的波，也可以是一个接一个的一系列波所组成的波群。

§7-1 液体波动理论一、流体力学基础1、速度场 描述海水质点的速度随空间位置和时间的变化规律的一个矢量。

),,,(t z y x V V =它的三个分量为：x 方向的量：),,,(t z y x u u =y 方向的量：),,,(t z y x v v =z 方向的量：),,,(t z y x w w =2、速度势 对于作无旋运动的液体，存在一个函数，它能反映出速度的变化，但仅仅是反映速度大小的变化，这个函数称为速度v的势函数，简称速度势： ),,,(t z y x φφ=3、速度与速度势的关系x u ∂∂=φ， y v ∂∂=φ， zw ∂∂=φ 二、海水运动的基本假设1、海水无粘性，只有重力是唯一的外力；2、液体自由液面上的压力为常数；3、液体波动振幅相对于波长为无限小；4、液体作无旋运动。

计算理论可计算性基础知识计算理论是计算机科学的基础学科之一，研究计算问题的性质和方法。

在计算理论中，可计算性是一个重要的概念，涉及到计算问题是否可解等方面的内容。

本文将介绍计算理论中的可计算性基础知识，包括图灵机、停机问题和可计算函数等。

一、图灵机图灵机是计算理论中最基本的计算模型之一，由英国数学家阿兰·图灵在1936年提出。

图灵机由一个无限长的纸带和一个可移动的读写头组成，纸带上有一串离散的符号。

图灵机的操作包括读取纸带上的符号、根据当前符号和内部状态进行状态转移、写入符号等。

通过这些操作，图灵机可以模拟任何其他计算模型的行为。

图灵机模型的提出使得计算问题的可计算性得到了严格的定义。

一个计算问题是可计算的，即存在一个图灵机可以解决它，如果给定任何输入，图灵机要么停机并给出输出，要么永远不停机。

可计算问题可以形式化地描述为输入输出函数，即给定一个特定的输入，图灵机能够计算出相应的输出。

二、停机问题停机问题是计算理论中的一个经典问题，也是不可计算问题的例子。

停机问题是指给定一个图灵机程序和输入，判断此程序能否在有限步骤内停机。

停机问题的不可解性意味着无法找到一个通用的算法来解决所有的停机问题。

根据停机问题的不可解性，图灵机的可计算性也受到限制。

存在一些计算问题，即使使用图灵机也无法解决，这些问题被称为不可计算问题。

停机问题是其中的一个例子，因为无法判断一个程序是否会在有限步骤内停机，图灵机也无法计算出对应的输出。

三、可计算函数可计算函数是指可以使用图灵机计算的函数。

一个函数被称为可计算函数，即存在一个图灵机可以计算出给定输入下的输出。

例如，加法、减法、乘法等基本算术运算都是可计算函数。

此外，存在一些复杂的函数，如指数函数、对数函数等，也都是可计算函数。

可计算函数的概念是基于图灵机模型的计算性定义的，它提供了一种形式化的描述方式，使得计算问题的可解性可以用数学语言进行刻画。

通过研究可计算函数及其性质，我们可以深入理解计算问题的本质，并探索计算机科学的边界和限制。

定义概念题目：第三章：1. 图灵机：是一种精确的通用计算机模型，能模拟实际计算机的所有计算行为，它的核心是转移函数δ，它说明了机器如何从一个格局走到下一个格局。

对于图灵机，δ的形式如下：Q×Γ→Q×Γ{L,R},图灵机是一个7元组（Q，∑，Γ，δ，q 0,q accept,q reject）.其中Q，∑，Γ都是有穷集合，并且1）Q是状态集；2）∑是输入字母表，不包括特殊空白符号凵，3）Γ是带字母表，其中凵∈Г，∑∈Г4）δ2. 格局：图灵机的计算过程中，当前状态，当前内容和读写头当前位置组合在一起。

例如：1011q701111：当前状态q7，当前读写头位置在第二个0上。

定义3.2 如果一个语言能被某一个图灵机识别，则称该语言是图灵可识别的（递归可枚举语言）定义3.2 如果一个语言能被某一个图灵机判定，则称该语言是图灵可判定的简称可判定的（递归语言）3.图灵机的变形：多带图灵机、非确定型图灵机、枚举器。

每个4.枚举器：他是图灵机的一种变形，是带有打印机的图灵机，图灵机把打印机当作输出设备，从而可以打印串，每当图灵机想在打印序列中增加一个串时，就把此串送到打印机。

一个语言是图灵可识别的，当且仅当有枚举器枚举它。

5.图灵机的术语：形式化描述，实现描述，高水平描述。

第四章：1.可判定的语言有：（A DFA、A NFA、A REX、E DFA、EQ DFA 是正则语言）、（A CFG、E CFG 是上下无关语言）❶每个上下文无关语言都是可判定的。

2.不可判定的语言有:：EQ CFG、A TM 、停机问题、HALT TM 、E TM、REGULAR TM 、EQ TM 、 E LBA 、ALL CFG 、PCPA TM =｛<M,ω>｜M是TM，ω是串，M接受ω｝是不可判定的。

证明：假设证A TM 是可判定的，下面将由之导出矛盾。

设H是A TM 的判定器。

令M是一个TM，ω是一个串。

《计算理论》计算理论计算理论是计算机科学的一个重要分支，它研究计算的本质、计算机的局限性、算法的复杂性等问题。

计算理论不仅对计算机科学的理论研究有着重要的贡献，而且对计算机科学的实际应用也有着重要的指导意义。

本文将从计算理论的基础概念、重要方法和应用研究方面分别进行综述。

一、计算理论的基础概念计算理论的基础概念包括自动机、图灵机、可计算性、复杂性等。

1.自动机自动机是一种数学模型，描述一组有限状态与转换规则，它可以接受或拒绝输入的序列。

其种类包括有限自动机、下推自动机、图灵机等，其中图灵机是计算理论中最重要的一种自动机。

2.图灵机图灵机是由英国数学家图灵（Alan Turing）在1936年提出的，它是一种虚拟机器，可以模拟任何其他计算模型的算法，其所能解决的问题可以称之为可计算问题。

图灵机包括状态寄存器、可写磁带、读写头等组成部分，它可以读取磁带上的输入符号，根据规则执行计算，并将结果输出到磁带上。

3.可计算性可计算性是计算理论中的一个基本概念，它指的是能够通过某种计算模型进行计算的问题。

如果一个问题可以被图灵机计算，那么它就具有可计算性。

4.复杂性复杂性是计算理论中的另一个核心概念，它指的是计算的时间和空间复杂度。

时间复杂度指的是算法执行所需的时间，而空间复杂度指的是算法执行所需的空间。

通常通过渐进符号来表示算法的复杂性，如O(n)、O(nlogn)等。

二、计算理论的重要方法计算理论的重要方法包括可计算性理论、复杂性理论、自动机理论等。

1.可计算性理论可计算性理论是研究问题的可计算性的理论。

该理论主要使用图灵机等计算模型来描述问题的可计算性，其重要结论包括：（1）停机问题不可解停机问题是指给定一个程序及其输入，是否可以在有限时间内停止运行。

停机问题不可解意味着不存在一个通用算法，可以判定任意程序是否会在有限时间内停机。

（2）哥德尔不完备定理哥德尔不完备定理指的是，任何形式化的公理化系统都存在某些命题是无法通过该系统来证明的。