二进制码转换为十进制(BCD)码
- 格式:docx
- 大小:125.50 KB
- 文档页数:5
BCD码(Binary-Coded Decimal)亦称二进码十进数或二-十进制代码。
用4位二进制数来表示1位十进制数中的0~9这10个数码。
是一种二进制的数字编码形式,用二进制编码的十进制代码。
BCD码这种编码形式利用了四个位元来储存一个十进制的数码,使二进制和十进制之间的转换得以快捷的进行。
这种编码技巧最常用于会计系统的设计里,因为会计制度经常需要对很长的数字串作准确的计算。
相对于一般的浮点式记数法,采用BCD码,既可保存数值的精确度,又可免却使电脑作浮点运算时所耗费的时间。
此外,对于其他需要高精确度的计算,BCD编码亦很常用。
即BCD代码。
Binary-Coded Decimal?,简称BCD,称BCD码或二-十进制代码,亦称二进码十进数。
是一种二进制的数字编码形式,用二进制编码的十进制代码。
这种编码形式利用了四个位元来储存一个十进制的数码,使二进制和十进制之间的转换得以快捷的进行。
这种编码技巧,最常用于会计系统的设计里,因为会计制度经常需要对很长的数字串作准确的计算。
相对于一般的浮点式记数法,采用BCD码,既可保存数值的精确度,又可免却使电脑作浮点运算时所耗费的时间。
此外,对于其他需要高精确度的计算,BCD编码亦很常用。
由于十进制数共有0、1、2、……、9十个数码,因此,至少需要4位二进制码来表示1位十进制数。
4位二进制码共有2^4=16种码组,在这16种代码中,可以任选10种来表示10个十进制数码,共有N=16!/(16-10)!约等于2.9乘以10的10次方种方案。
常用的BCD代码列于末。
常用BCD编码方式最常用的BCD编码,就是使用"0"至"9"这十个数值的二进码来表示。
这种编码方式,在中国大陆称之为“8421码”。
除此以外,对应不同需求,各人亦开发了不同的编码方法,以适应不同的需求。
这些编码,大致可以分成有权码和无权码两种:有权BCD码,如:8421(最常用)、2421、5421…无权BCD码,如:余3码、格雷码…以下为三种常见的BCD编码的比较。

⼆进制转换成⼗进制BCD码(加3移位法)“原来的⼆进制数⼗⼏位,则左移时就要左移⼏位”"⼆进制数调整BCD码的⽅法是将⼆进制码左移8次,每次移位后都检查低四位LSD+3是否⼤于7,如是则加3,否则不加,⾼4位MSD作同样处理"⼀、为什么左移8次原寄存器是存⼆进制数的,新寄存器是存⼗进制数的,当然要左移8次,把数据全部移进去。
但这⾥要注意两件事,第⼀,如果只安排⼀个字节作⼗进制寄存器,原数据要⼩于 64H(即100)。
第⼆,由于新寄存器是⼗进制的,要随时调整。
⼆、检查半字节+3 是否⼤于 7,是,则 +3在 51 系列⾥有⼗进制调节指令(半字节⼤于 9,则加 6,应该不难理解),PIC ⾥没有,只好采取变通的⽅法。
检查半字节+3 是否⼤于 7,也就是检查半字节是否⼤于 4。
因为,如果⼤于 4(⽐如 5、6),下⼀步左移就要溢出了,所以加 3,等于左移后的加 6,起到⼗进制调节的作⽤。
那为什么要绕个圈⼦去检测半字节+3 是否⼤于 7 呢?这样程序编起来会简练⼀些。
⼀个例⼦假如有⼀个⼋位⼆进制数255,我把他转255的⼗进制数0 1111 1111 原数1 0000 0001 ;左移⼀次2 0000 0011 ; 左移⼆次3 0000 0111 ;左移三次,检查低四位+3>7?3.1 0000 1010 ;⼤于7,加3进⾏调整4 0001 0101 ;左移四次, 检查低四位+3>7?4.1 0001 1000 ;⼤于7,加3进⾏调整5 0011 0001 ;左移五次6 0110 0011 ;左移六次,检查⾼四位+3>7?6.1 1001 0011 ;⼤于7,加3进⾏调整7 1 0010 0111 ;左移七次,检查低四位+3>7?7.1 1 0010 1010 ;⼤于7,加3进⾏调整8 10 0101 0101 ;左移⼋次(得到BCD码255)附上Verilog代码://17位⼆进制数转BCD码(基本思想是逢⼗进1)module BIN_BCD_4 (CLK, A, BW, BQ, BB, BS, BG);input CLK;input [16:0]A; //⼆进制输⼊数据output [3:0]BW, BQ, BB, BS, BG;//BCD数据输出寄存器reg [3:0]BW, BQ, BB, BS, BG;integer I;reg [19:0]TEMP;reg [16:0]C;always @ (posedge CLK)beginC=A;TEMP=0;for (I=1; I<17; I=I+1)begin{TEMP, C}={TEMP[18:0], C, 1'b0};//左移⼀位 if (TEMP[3:0]>4'b0100)beginTEMP[3:0]=TEMP[3:0]+3; // >4则加3endif (TEMP[7:4]>4'b0100)beginTEMP[7:4]=TEMP[7:4]+3;endif (TEMP[11:8]>4'b0100)beginTEMP[11:8]=TEMP[11:8]+3;endif (TEMP[15:12]>4'b0100)beginTEMP[15:12]=TEMP[15:12]+3;endif (TEMP[19:16]>4'b0100)beginTEMP[19:16]=TEMP[19:16]+3;end{BW, BQ, BB, BS, BG}={TEMP[18:0], A[0]}; endendendmodule。

⼆进制码转BCD码原理有时候没有采⽤BCD计数器,⼜需要⽤⼗进制形式显⽰⼆进制数据,最常⽤的⽅法是编码转换:将⼆进制码转换成BCD码(8421)。
8421码:8421码⼜称⼗进制码,它只选⽤了四位⼆进制码中前10组代码,4个码表达10个数,即⽤0000~1001分别代表它所对应的⼗进制数,余下的六组代码不⽤。
如果要我将⼆进制码转成BCD码,我会看看他们何时分道扬镳,以此观察⼆者的区别。
对于BCD计数器,当计数到1001时,下⼀次计数要进位,得到0001_0000。
对于⼆进制计数器,下⼀次计数得到的是1010。
不可能重新计⼀次数来得到BCD码,太浪费时间了,但是直接让我转我也束⼿⽆策。
我们很快发现按位重建的话,消耗的时钟周期数是⼆进制位数,还可以接受。
深⼊思考⼀下,发现是可⾏的。
就像标准LSB乘法⼀样,从⼆进制⾼位开始重建,⽤⼀个寄存器每个周期进⾏shift-add操作。
如果不⼲其他的,花费n个周期即可重建出n-bit⼆进制数。
这个⼯作量已经是⼀个⽐特串⾏乘法器了,结果肯定是原来的⼆进制数不会错。
每4个bit分为⼀组BCD码,对于任意⼀组在任意⼀个周期状态下,只要数据≥5,那么下⼀次移位就会超出BCD码范围,对于BCD 计数器来说需要进位。
为使4位⼆进制码进位,要满⾜逢16进⼀。
由于BCD码是逢10进⼀,直接给当前组4bit数据补上差距3即可。
下⼀次移位的时候,差距扩⼤为6,如果BCD码应该进位,那么⼆进制码也会进位,同步进位,⽬的达成。
寄存器中的编码已经是BCD码了,但是这个BCD码代表的值和⼆进制代表的值是⼀样的。
⼆进制重建可以进⾏shift-add操作,BCD码重建同样可以进⾏shift-add操作,只不过BCD码有⾃⼰的规则,在shift-add的时候要进⾏⼀点修正罢了。
在任意周期,重建出来的⼆进制码和BCD码表⽰的值都是⼀样的。
所以最终重建出来的BCD码是正确的。

bcd转10进制公式
BCD(Binary Coded Decimal)是一种用二进制编码表示十进制
数字的方法。
BCD转换为十进制的公式如下:
BCD数值 = d1 10^(n-1) + d2 10^(n-2) + ... + dn 10^0。
其中,d1、d2、...、dn是BCD数值的各个位上的数字,n是BCD数值的位数(最高位为第n位,最低位为第1位)。
举个例子来说明:
假设有一个BCD数值为1101,我们要将其转换为十进制。
首先,确定BCD数值的位数n为4。
然后,根据公式计算:
十进制数值 = 1 10^(4-1) + 1 10^(4-2) + 0 10^(4-3) +
1 10^(4-4)。
= 1000 + 100 + 0 + 1。
= 1101。
所以,BCD数值1101转换为十进制为1101。
需要注意的是,BCD数值的每个位上的数字只能是0~9之间的
整数。
如果BCD数值的某个位上的数字超过了9,那么该BCD数值
就不是有效的BCD数值。
希望以上解答对你有帮助。
如果你还有其他问题,请随时提问。

⼆进制转BCD码应⽤:⽤fpga实现对数码管显⽰,以前通常的⽅法是进⾏整除和取余进⾏运算,但是fpga并不擅长乘法除法运算,所以可以⽤BCD码来转换。
BCD码:通俗的可以理解为⽤四位⼆进制数表⽰⼀位⼗进制数字。
例如,256就可以⽤bcd码表⽰为:0010_1001_0110因此在数码管显⽰中,也就是把256各位分出来,就可以⽤bcd码来表⽰,下⾯说⼀种⼆进制转换bcd码的⽅法。
加3移位法:bcd码中只有0~9⼗进制数,但是在四位⼆进制中是16进制进1,因此在移位过程中要对⼆进制进⾏判断,当在移位之后的状态Qn+1⼤于9,要对Qn加6才可以。
例如1000移位⼤于9加6为0001_0110,对应bcd码中的16。
我们也可以在移位之前进⾏判断,如果移位之前的Qn数据⼤于4,说明Qn+1会溢出,所以可以+3再进⾏移位,例如1000⼤于4,加3为1011然后再进⾏移位0001_0110,16和刚才结果是⼀样的。
简单的说,判断的⽬的是防⽌下⼀次移位,发⽣数据溢出的情况思路:代码可以总结为三个部分:移位,加⼆进制数,判断(最后⼀次不需要判断)例如15 --- 1111(1)移位 0000_0000 加 0000_0001 判断 0000_0001(2)移位 0000_0010 加 0000_0011 判断 0000_0011(3)移位 0000_0110 加 0000_0111 判断 0000_1010(4)移位 0001_0100 加 0001_0101/*********************************功能:实现对6位⼗进制数以内的bcd码转换time: 2017/4/29vision:1.0*********************************/`define data_in_num 19`define data_bcd_num 23module pro_bcd(clk,rst_n,data_in,data_bcd);input clk;input rst_n;input [`data_in_num :0] data_in;output [`data_bcd_num:0] data_bcd;reg [`data_bcd_num:0] data_bcd_r;reg [1:0] state;reg [5:0] shift_cnt;always @(posedge clk or negedge rst_n)if(!rst_n)begindata_bcd_r <= 0;state <= 0;shift_cnt <= 0;endelsecase(state)2'd0:beginshift_cnt <= 0;data_bcd_r <= 0;state <= state + 1;end2'd1:begin //移位if(shift_cnt < `data_in_num + 1)begindata_bcd_r <= data_bcd_r<<1;shift_cnt <= shift_cnt + 1;state <= state + 1;endelsestate <= 0;end2'd2:begin //相加data_bcd_r <= data_bcd_r + data_in[`data_in_num + 1 - shift_cnt];state <= state + 1;end2'd3:begin //判断if(data_bcd_r[3:0] > 4 ) //1data_bcd_r <= data_bcd_r + 3;if(data_bcd_r[7:4]>4) //2data_bcd_r[7:4] <= data_bcd_r[7:4] + 3;if(data_bcd_r[11:8]>4) //3data_bcd_r[11:8] <= data_bcd_r[11:8] + 3;if(data_bcd_r[15:12]>4) //4data_bcd_r[15:12] <= data_bcd_r[15:12] + 3;if(data_bcd_r[19:16]>4) //5data_bcd_r[19:16] <= data_bcd_r[19:16] + 3;if(data_bcd_r[`data_bcd_num:20]>4) //6data_bcd_r[`data_bcd_num:20] <= data_bcd_r[`data_bcd_num:20] + 3;state <= 1;enddefault:state <= 0;endcaseassign data_bcd = (state == 3)&&(shift_cnt == `data_in_num + 1) ? data_bcd_r : data_bcd; endmodule。

目录摘要 (1)1原理分析 (2)2设计思路 (3)3设计程序 (4)3.1二-十进制转换 (4)3.2对十进制数分位 (6)3.3分别输出十进制数 (7)3.4输出到数码管 (9)3.5显示位数 (11)4整体设计电路图与仿真结果分析 (12)4.1整体设计电路图 (12)4.2仿真结果 (12)4.3仿真结果分析 (13)5小结与体会 (13)参考文献 (15)摘要BCD码亦称二进码十进数或二-十进制代码.用4位二进制数来表示1位十进制数中地0~9这10个数码.是一种二进制地数字编码形式,用二进制编码地十进制代码.BCD码这种编码形式利用了四个位元来储存一个十进制地数码,使二进制和十进制之间地转换得以快捷地进行.本文就是在quartus软件环境下利用VHDL语言将输入地八位二进制转换为BCD十进制数并且在数码管中显示出来.关键词:二--十进制转换器,BCD码,quartus,VHDL.2进制-10进制(BCD码)数码转换器设计1原理分析BCD 码这种编码形式利用了四个位元来储存一个十进制地数码,使二进制和十进制之间地转换得以快捷地进行.这种编码技巧,最常用于会计系统地设计里,因为会计制度经常需要对很长地数字串作准确地计算.相对于一般地浮点式记数法,采用BCD码,既可保存数值地精确度,又可免却使电脑作浮点运算时所耗费地时间.此外,对于其他需要高精确度地计算,BCD编码亦很常用.此处要介绍地是八位二进制转BCD码地硬件实现,采用左移加3地算法,具体描述如下:(1)、左移要转换地二进制码1位(2)、左移之后,BCD码分别置于百位、十位、个位(3)、如果移位后所在地BCD码列大于或等于5,则对该值加3(4)、继续左移地过程直至全部移位完成举例:将八位二进制码11111111转换成BCD码,其真值表如表1-1所示表1-1八位二进制码11111111转换成BCD码真值表2设计思路本次设计并没有用到左移地原理进行操作,直接对输出芯片地输出进行定义,虽然较为繁琐,但是原理却简单,所以才用此种方法,具体原理如下:2进制-10进制(BCD码)地转换可以通过一个芯片实现,即输入地八位二进制码通过编程输出十进制码,八位二进制能表示地最大地数为“255”,即输出地十进制为三位数,此时输出地BCD码就要有12位,每四位代表一个数,此时可再利用一个芯片把输出地12位数重新分配到三个输出管脚中,每个管脚代表一位数,时钟信号每输变一次,输出数字地位也会变一次,即个、十、百位分别输出,同时芯片地selout输出端输出时钟信号地数字到下一个芯片地接收端,通过编程实现000对应110,001对应101,010对应011,即输出0地位置可以表示数码管中所显示数字地位,然后再通过芯片输出到七段数码管进行显示,具体流程图如图2-1所示:图2-1 设计总流程图3设计程序3.1二-十进制转换原理图如图3-1所示:图3-1二进制到十进制转换原理图具体程序语言如下:library ieee。

verilog实现二进制与bcd码的转换算法Verilog是一种硬件描述语言,常用于数字电路设计和硬件描述。
在数字电路设计中,二进制和BCD码之间的转换是一个常见的问题。
本文将介绍如何使用Verilog实现二进制与BCD码的转换算法。
首先,我们需要了解二进制和BCD码的基本概念。
二进制是一种基于2的数字系统,只包含0和1两个数字。
而BCD码是一种二进制编码形式,用4位二进制数表示一个十进制数的每一位。
例如,十进制数12用BCD码表示为0001 0010。
在Verilog中,我们可以使用模块化的方式来实现二进制与BCD码的转换算法。
首先,我们需要定义输入和输出端口。
输入端口是一个二进制数,输出端口是对应的BCD码。
```verilogmodule binary_to_bcd(input [3:0] binary,output [7:0] bcd);```接下来,我们可以使用组合逻辑来实现转换算法。
对于二进制数的每一位,我们可以使用除法和取余运算来计算对应的BCD码。
具体实现如下:```verilogalways @(*) beginbcd = 8'b00000000;if (binary >= 10) begin bcd[7] = 1;binary = binary - 10; endif (binary >= 8) begin bcd[6] = 1;binary = binary - 8; endif (binary >= 4) begin bcd[5] = 1;binary = binary - 4; endif (binary >= 2) begin bcd[4] = 1;binary = binary - 2; endif (binary >= 1) beginbcd[3] = 1;binary = binary - 1;endif (binary >= 0.5) beginbcd[2] = 1;binary = binary - 0.5;endif (binary >= 0.25) beginbcd[1] = 1;binary = binary - 0.25;endif (binary >= 0.125) beginbcd[0] = 1;endend```在上述代码中,我们首先将输出端口bcd初始化为全0。


二进制编码的十进制数,简称BCD码(Binarycoded Decimal). 这种方法是用4位二进制码的组合代表十进制数的0,1,2,3,4,5,6 ,7,8,9 十个数符。
4位二进制数码有16种组合,原则上可任选其中的10种作为代码,分别代表十进制中的0,1,2,3,4,5,6,7,8,9 这十个数符。
最常用的BCD码称为8421BCD码,8.4.2.1 分别是4位二进数的位取值。
右图为十进制数和8421BCD编码的对应关系表:1、BCD码与十进制数的转换BCD码与十进制数的转换.关系直观,相互转换也很简单,将十进制数75.4转换为BCD码如:75.4=(0111 (0101.0100)BCD 若将BCD码1000 0101.0101转换为十进制数如: (1000 0101.0101)BCD=85.5注意:同一个8位二进制代码表示的数,当认为它表示的是二进制数和认为它表示的是二进制编码的十进制数时,数值是不相同的。
例如:00011000,当把它视为二进制数时,其值为24;但作为2位BCD 码时,其值为18。
又例如00011100,如将其视为二进制数,其值为28,但不能当成BCD 码,因为在8421BCD码中,它是个非法编码 .2、BCD码的格式计算机中的BCD码,经常使用的有两种格式,即分离BCD码,组合BCD 码。
所谓分离BCD码,即用一个字节的低四位编码表示十进制数的一位,例如数82的存放格式为:_ _ _1 0 0 0 _ _ _ _0 0 1 0 其中_表示无关值。
组合BCD码,是将两位十进制数,存放在一个字节中,例82的存放格式是1000 00103、BCD码的加减运算由于编码是将每个十进制数用一组4位二进制数来表示,因此,若将这种BCD码直接交计算机去运算,由于计算机总是把数当作二进制数来运算,所以结果可能会出错。
例:用BCD码求38+49。
解决的办法是对二进制加法运算的结果采用"加6修正,这种修正称为BCD调整。

二进制码转BCD码在单片机里面,如:显示个温度值,这时,要取一个数的个位、十位、百位,可以用/和 %(求商和求余)来解决。
但是,在FPGA里面用求商和求余将会非常消耗资源,这样就必须用到二进制转BCD码了,这里介绍一种简单的加3移位算法。
注:B代表二进制,D代表十进制,0x代表十六进制,BCD为BCD 码,下同。
1、加3移位法以二进制数(0000_101 Xn)B=(10+Xn)D为例,串行输入三位后,(0101)B=5(D)左移一位后:(0000_101Xn)B=(10+Xn)D如果(0000_101Xn)B直接输出显示为:当Xn=0时,0000_1010=0x0A。
此为错误的BCD码。
采用加3移位法,修正移位结果:串行输入三位后,结果大于4(0101)B=5(D)加3:(0101)B+(0011)B=(1000)B --十进制表示:5+3=8 再左移一位后:(1000Xn)B=(0001_000Xn)BCD对应十进制显示:1 Xn每四位BCD码对应一位十进制数,即:(10+Xn)D,转换成功注:Xn为下一位串行输入的二进制数。
2、设计思路这里一共需要四个模块:计数器、移位器、加法器、寄存器输出。
分别设计好之后,用状态机控制它们,就完成了。
3、仿真结果注:图中clk为时钟,en为高电平使能,rst为高电平复位,data_in为输入的12位二进制码,以十进制的形式显示在时序图;qout为输出的16位BCD码,以十六进制的形式显示在时序图,17个时钟上升沿可完成转换任务。
4、综合结果5、难点分析要搞懂这个加3移位算法,必须要按照8位二进制(11101011)转BCD过程图,自己手动推导一下,才容易理解。
此算法的难点在于,需要把输入的二进制数,按照每四个bit来划分为一个单元(所以输入的二进制数,位宽必须是4的倍数),然后,每个单元都要同时判断是否大于4,大于就要加3,否则不加.理解了这个算法之后,那么BCD转二进制就非常容易了,减3移位即可,减3可以用补码来解决。
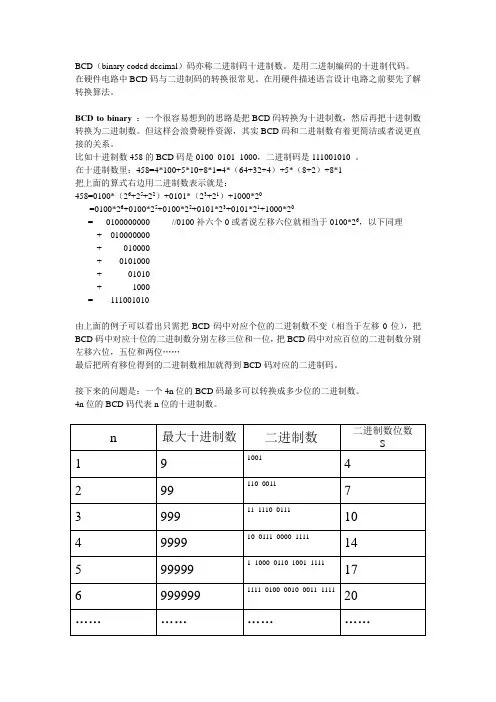
BCD(binary-coded decimal)码亦称二进制码十进制数。
是用二进制编码的十进制代码。
在硬件电路中BCD码与二进制码的转换很常见。
在用硬件描述语言设计电路之前要先了解转换算法。
BCD to binary:一个很容易想到的思路是把BCD码转换为十进制数,然后再把十进制数转换为二进制数。
但这样会浪费硬件资源,其实BCD码和二进制数有着更简洁或者说更直接的关系。
比如十进制数458的BCD码是0100_0101_1000,二进制码是111001010 。
在十进制数里:458=4*100+5*10+8*1=4*(64+32+4)+5*(8+2)+8*1把上面的算式右边用二进制数表示就是:458=0100*(26+25+22)+0101*(23+21)+1000*20=0100*26+0100*25+0100*22+0101*23+0101*21+1000*20= 010******* //0100补六个0或者说左移六位就相当于0100*26,以下同理+ 010000000+ 010000+ 0101000+ 01010+ 1000= 111001010由上面的例子可以看出只需把BCD码中对应个位的二进制数不变(相当于左移0位),把BCD码中对应十位的二进制数分别左移三位和一位,把BCD码中对应百位的二进制数分别左移六位,五位和两位……最后把所有移位得到的二进制数相加就得到BCD码对应的二进制码。
接下来的问题是:一个4n位的BCD码最多可以转换成多少位的二进制数。
4n位的BCD码代表n位的十进制数。
n 最大十进制数二进制数二进制数位数S1 9 1001 42 99 110_0011 73 999 11_1110_0111 104 9999 10_0111_0000_1111 145 99999 1_1000_0110_1001_1111 176 999999 1111_0100_0010_0011_1111 20 ……………………由上表可以看出S可以由N的数学表达式给出。
bcd码也叫8421码就是将十进制的数以8421的形式展开成二进制,大家知道十进制是0~9十个数组成,着十个数每个数都有自己的8421码:0=00001=00012=00103=00114=01005=01016=01107=01118=10009=1001举个例子:321的8421码就是3 2 10011 0010 0001二进制编码的十进制数,简称BCD码(Binarycoded Decimal). 这种方法是用4位二进制码的组合代表十进制数的0,1,2,3,4,5,6 ,7,8,9 十个数符。
4位二进制数码有16种组合,原则上可任选其中的10种作为代码,分别代表十进制中的0,1,2,3,4,5,6,7,8,9 这十个数符。
最常用的BCD码称为8421BCD 码,8.4.2.1 分别是4位二进数的位取值。
右图为十进制数和8421BCD编码的对应关系表:1、BCD码与十进制数的转换BCD码与十进制数的转换.关系直观,相互转换也很简单,将十进制数75.4转换为BCD码如:75.4=(0111 (0101.0100)BCD 若将BCD码1000 0101.0101转换为十进制数如: (1000 0101.0101)BCD=85.5注意:同一个8位二进制代码表示的数,当认为它表示的是二进制数和认为它表示的是二进制编码的十进制数时,数值是不相同的。
例如:00011000,当把它视为二进制数时,其值为24;但作为2位BCD码时,其值为18。
又例如00011100,如将其视为二进制数,其值为28,但不能当成BCD码,因为在8421BCD码中,它是个非法编码.2、BCD码的格式计算机中的BCD码,经常使用的有两种格式,即分离BCD码,组合BCD 码。
所谓分离BCD码,即用一个字节的低四位编码表示十进制数的一位,例如数82的存放格式为:_ _ _1 0 0 0 _ _ _ _0 0 1 0 其中_表示无关值。
bcd码练习题BCD码(Binary Coded Decimal)是一种用二进制码表示十进制数的编码方式。
在计算机科学和电子工程领域中,BCD码常用于数字的存储和转换。
本文将以练习题的形式帮助读者加深对BCD码的理解。
练习一:将十进制数转换为BCD码1. 将数字5转换为BCD码解答:BCD码是以4个二进制数位表示一个十进制数位,其中0000表示0,0001表示1,依此类推。
由于数字5是十进制数的一个数位,其BCD码表示为:0101。
2. 将数字13转换为BCD码解答:十进制数13分解为十进制数位1和3,其BCD码表示为:0001 0011。
3. 将数字125转换为BCD码解答:十进制数125分解为十进制数位1、2和5,其BCD码表示为:0001 0010 0101。
练习二:将BCD码转换为十进制数1. 将BCD码0101转换为十进制数解答:BCD码 0101 表示十进制数的数位5,因此对应的十进制数为 5。
2. 将BCD码0001 0011转换为十进制数解答:BCD码 0001 0011 表示十进制数的数位1和3,因此对应的十进制数为 13。
3. 将BCD码0001 0010 0101转换为十进制数解答:BCD码 0001 0010 0101 表示十进制数的数位1、2和5,因此对应的十进制数为 125。
练习三:进行BCD码加法运算1. 计算BCD码 0011 和 0101 的和解答:BCD码 0011 和 0101 分别对应十进制数的数位3和5,他们的和为 8。
将8转换为BCD码表示得:1000。
2. 计算BCD码 1010 和 0111 的和解答:BCD码 1010 和 0111 分别对应十进制数的数位10和7,他们的和为 17。
将17转换为BCD码表示得:0001 0111。
练习四:进行BCD码减法运算1. 计算BCD码 1001 减去 0101解答:BCD码 1001 减去 0101 可以理解为十进制数项 9 减去 5,结果为 4。
bcd加法器的工作原理
BCD加法器的工作原理是利用8421码进行加法运算。
8421码是一种二进制编码方式,它将十进制数字0-9转换为4位二进制数。
BCD加法器通过将两个4位二进制数相加,并转换为相应的十进制数来实现十进制加法。
具体来说,BCD加法器的工作步骤如下:
1. 将两个4位二进制数相加,得到一个4位二进制和和一个进位输出。
2. 如果和的最高位(第4位)为1,则需要进行进位处理。
将进位输入和两个4位二进制数相加,得到一个新的二进制和。
3. 将新的二进制和转换为相应的十进制数,得到最终的十进制和。
需要注意的是,由于BCD码表示的十进制数范围较小(0-9),因此在相加时需要注意溢出的情况。
如果两个数的和超过了9,则需要通过特定的算法进行溢出处理,以保证结果的正确性。
bcd码的书写格式
BCD码(Binary-Coded Decimal)是一种二进制编码形式,用于表示十进制数字。
它使用4位二进制数来表示一个十进制数位,每个二进制数位对应一个0-9的十进制数字。
BCD码的书写格式可以有多种形式,以下是几种常见的格式:
1. 纯二进制形式,BCD码可以直接用二进制数表示,每4位二进制数位对应一个十进制数字。
例如,十进制数23可以用BCD码表示为0010 0011。
2. 十六进制形式,由于BCD码每4位二进制数位对应一个十进制数字,可以将每个4位二进制数位转换为一个十六进制数位,从而简化表示。
例如,十进制数23可以用BCD码表示为0x23。
3. 字符串形式,将BCD码按照十进制数字的顺序排列,每个十进制数字用一个字符表示。
通常使用0-9的数字字符表示0-9的十进制数字。
例如,十进制数23可以用BCD码表示为"23"。
需要注意的是,BCD码的书写格式可以根据具体需求而变化,但它始终是一种二进制编码形式,用于表示十进制数字。
以上是几
种常见的BCD码书写格式,但在实际应用中可能还会有其他特定的格式。
java bcd码的算法Java BCD码的算法BCD码是二进制编码的十进制表示形式,即Binary-Coded Decimal的简称。
在计算机中,常用BCD码来表示数字,可以在计算和显示数字时提供高精度和可读性。
本文将介绍Java中BCD码的算法。
1. BCD码的原理BCD码使用4位二进制数来表示一个十进制数的每一位。
例如,数字5的BCD码是0101,数字9的BCD码是1001。
BCD码的优点是可以直接与十进制数进行转换和计算,而无需进行复杂的位运算。
2. Java中BCD码的转换在Java中,可以使用整数类型(如int)来表示BCD码。
将一个十进制数转换为BCD码的算法如下:- 将十进制数的每一位拆分出来,得到个位、十位、百位等数字。
- 将每一位数字转换为对应的BCD码,例如将数字5转换为0101。
- 将每一位的BCD码按位拼接起来,得到最终的BCD码。
例如,将数字259转换为BCD码的过程如下:- 个位数字为9,对应的BCD码为1001。
- 十位数字为5,对应的BCD码为0101。
- 百位数字为2,对应的BCD码为0010。
- 将个位、十位和百位的BCD码按位拼接起来,得到最终的BCD 码为0010 0101 1001。
3. Java中BCD码的计算在Java中,可以使用BCD码进行数字的加减乘除运算。
例如,将两个BCD码相加的算法如下:- 从最低位开始,将两个BCD码对应的每一位相加,得到一个新的BCD码的每一位和进位。
- 将新的BCD码的每一位和进位拼接起来,得到最终的和。
例如,将BCD码0010 0101 1001和BCD码0011 0110 0010相加的过程如下:- 个位相加得到和为11,进位为1。
- 十位相加得到和为11,进位为1。
- 百位相加得到和为10,进位为1。
- 将个位、十位和百位的和和进位拼接起来,得到最终的和为1101 1101 0111。
4. Java中BCD码的显示在Java中,可以将BCD码转换为十进制数进行显示。
二进制码转换为十进制(BCD)码
转换原理
对于一个8位二进制码bn-1bn-2……b1b0,,其在十进制编码方式下的值为
把上式写出套乘的形式:
式中的每项乘2,相当于将寄存器中的二进制码左移1位,这就意味着利用移位寄存器可以完成二进制与8421BCD的转换。
[2]
在移位的过程中,当现态Sn<5时,次态不变。
当现态Sn=5、6、7时,左移一次,其次态Sn+1将会超过9,对于一个BCD码来说,这样的状态属于禁用状态。
而当Sn=8、9时,左移1位,则会向高1位的BCD码输入一个进位的信号 ,由于二进制和BCD码权不一致,当发生进位时,虽然码元只是左移1位,但次态Sn+1将减少6。
基于上面这两种情况,在B/BCD转换时需要对转换结果加以校正。
校正过程如下:当Sn>=5时,我们让Sn先加上3,然后再左移1位,次态 Sn+1=2(Sn+3)=2Sn+6,正好补偿由于进位而减少的数值,并且向后一个变换单元送入一个进位信号,这个方法叫“加3移位法”。
注意:现态和次态都是指BCD码,即用4位二进制表示的1位BCD码。
我们对Sn=8、9时举个例子:BCD码的1000(8)乘以2为0001_0110(16),但是左移后变为0001_0000,减少了6。
所以需要加上6,这里的方法是加3左移一位,相当于加上6。
转换方法
首先,先了解二进制与BCD码的位数对应关系,比如一个8位二进制码,可以表示的最大十进制数为255,转换成BCD码为 0010_0101_0101,共需12位,其中每4位组成一个BCD单元,有三个BCD单元,分别表示百位(hundreds)、十位(tens)和个位(units)。
n位二进制码转换成D位BCD码的n~D 对应关系表见表1。
表1 n~D对应关系
以8位二进制转换为3位BCD码为例,转换步骤是:将待转换的二进制码从最高位开始左移BCD的寄存器(从高位到低位排列),每移一次,检查每一位BCD码是否大于4,是则加上3,否则不变。
左移8次后,即完成了转换。
需要注意的是第八次移位后不需要检查是否大于5。
注意:为什么检查每一个BCD码是否大于4,因为如果大于4(比如5、6),下一步左移就要溢出了,所以加3,等于左移后的加6,起到十进制调节的作用。
表2给出了一个二进制码11101011转换成8421BCD码的时序。
表2 B/BCD时序
Verilog 代码
/*功能: 8位二进制转3位BCD码
输入参数:输入时钟clk,输入二进制数据dat
输出参数:个位units,十位tens,百位hundreds
备注:二进制转BCD码的实现方法很多,本例采用的是“加3移位法”
本例实现的是8位二进制转3位BCD码的例子,例如输入2’b11111111(255),输出0010_0101_0101(BCD)*/
module BIN_to_BCD(clk,dat,units,tens,hundreds);
input clk;
input[7:0] dat; //二进制输入数据
output[3:0] units;
output[3:0] tens;
output[3:0] hundreds;
reg[3:0] units_r,tens_r,hundreds_r;//BCD数据输出寄存器
reg[7:0] dat_r;
reg[11:0] temp; //中间寄存器
integer i;
assign units = units_r;
assign tens = tens_r;
assign hundreds = hundreds_r;
always @(posedge clk)
begin
dat_r = dat;
temp = 0;
for(i = 0;i < 7;i = i + 1) //循环7次,注意不是8次,因为第八次不需要修正
begin
temp = {temp[10:0],dat_r[7]}; //左移一位
if(temp[3:0] > 4'd4) //大于4,加三
temp[3:0] = temp[3:0]+4'd3;
if(temp[7:4] > 4'd4) //大于4,加三
temp[7:4] = temp[7:4]+4'd3;
if(temp[11:8] > 4'd4) //大于4,加三
temp[11:8] = temp[11:8]+4'd3;
dat_r=dat_r<<1; //最高变为原来dat_r的第六位
{hundreds_r,tens_r,units_r}={temp[10:0],dat[0]};//最后一次(第8次)不用修正end
end
endmodule
波形仿真报告说明
图1 输入二进制1111_1111(255)的波形仿真报告
分析综合报告说明
图2 8位二进制转BCD码的分析综合报告
待转换二进制位数(n)越大,锁消耗的LE的越多,当n大于8时,采用上面算法的Verilog HDL 代码会消耗大量的LE。