二进制数到BCD码的转换

⼆进制转换成⼗进制BCD码（加3移位法）“原来的⼆进制数⼗⼏位，则左移时就要左移⼏位”"⼆进制数调整BCD码的⽅法是将⼆进制码左移8次,每次移位后都检查低四位LSD+3是否⼤于7,如是则加3,否则不加,⾼4位MSD作同样处理"⼀、为什么左移8次原寄存器是存⼆进制数的，新寄存器是存⼗进制数的，当然要左移8次，把数据全部移进去。

但这⾥要注意两件事，第⼀，如果只安排⼀个字节作⼗进制寄存器，原数据要⼩于 64H（即100）。

第⼆，由于新寄存器是⼗进制的，要随时调整。

⼆、检查半字节+3 是否⼤于 7，是，则 +3在 51 系列⾥有⼗进制调节指令（半字节⼤于 9，则加 6，应该不难理解），PIC ⾥没有，只好采取变通的⽅法。

检查半字节+3 是否⼤于 7，也就是检查半字节是否⼤于 4。

因为，如果⼤于 4（⽐如 5、6），下⼀步左移就要溢出了，所以加 3，等于左移后的加 6，起到⼗进制调节的作⽤。

那为什么要绕个圈⼦去检测半字节+3 是否⼤于 7 呢？这样程序编起来会简练⼀些。

⼀个例⼦假如有⼀个⼋位⼆进制数255,我把他转255的⼗进制数0 1111 1111 原数1 0000 0001 ;左移⼀次2 0000 0011 ; 左移⼆次3 0000 0111 ;左移三次,检查低四位+3>7?3.1 0000 1010 ;⼤于7,加3进⾏调整4 0001 0101 ;左移四次, 检查低四位+3>7?4.1 0001 1000 ;⼤于7,加3进⾏调整5 0011 0001 ;左移五次6 0110 0011 ;左移六次,检查⾼四位+3>7?6.1 1001 0011 ;⼤于7,加3进⾏调整7 1 0010 0111 ;左移七次,检查低四位+3>7?7.1 1 0010 1010 ;⼤于7,加3进⾏调整8 10 0101 0101 ;左移⼋次(得到BCD码255)附上Verilog代码://17位⼆进制数转BCD码(基本思想是逢⼗进1)module BIN_BCD_4 (CLK, A, BW, BQ, BB, BS, BG);input CLK;input [16:0]A; //⼆进制输⼊数据output [3:0]BW, BQ, BB, BS, BG;//BCD数据输出寄存器reg [3:0]BW, BQ, BB, BS, BG;integer I;reg [19:0]TEMP;reg [16:0]C;always @ (posedge CLK)beginC=A;TEMP=0;for (I=1; I<17; I=I+1)begin{TEMP, C}={TEMP[18:0], C, 1'b0};//左移⼀位 if (TEMP[3:0]>4'b0100)beginTEMP[3:0]=TEMP[3:0]+3; // >4则加3endif (TEMP[7:4]>4'b0100)beginTEMP[7:4]=TEMP[7:4]+3;endif (TEMP[11:8]>4'b0100)beginTEMP[11:8]=TEMP[11:8]+3;endif (TEMP[15:12]>4'b0100)beginTEMP[15:12]=TEMP[15:12]+3;endif (TEMP[19:16]>4'b0100)beginTEMP[19:16]=TEMP[19:16]+3;end{BW, BQ, BB, BS, BG}={TEMP[18:0], A[0]}; endendendmodule。

16位二进制数转换成BCD码的的快速算法－51单片机2010-02-18 00:43在做而论道上篇博文中，回答了一个16位二进制数转换成BCD码的问题，给出了一个网上广泛流传的经典转换程序。

程序可见：/%D7%F6%B6%F8%C2%DB%B5%C0/blog/item/6154551f93ba561440341732. html中的HEX2BCD子程序。

.说它经典，不仅是因为它已经流传已久，重要的是它的编程思路十分清晰，十分易于延伸推广。

做而论道曾经利用它的思路，很容易的编写出了48位二进制数变换成16位BCD码的程序。

但是这个程序有个明显的缺点，就是执行时间太长，转换16位二进制数，就必须循环16遍，转换48位二进制数，就必须循环48遍。

上述的HEX2BCD子程序，虽然长度仅仅为26字节，执行时间却要用331个机器周期。

.单片机系统多半是用于各种类型的控制场合，很多时候都是需要“争分夺秒”的，在低功耗系统设计中，也必须考虑因为运算时间长而增加系统耗电量的问题。

为了提高整机运行的速度，在多年前，做而论道就另外编写了一个转换程序，程序的长度为81字节，执行时间是81个机器周期，（这两个数字怎么这么巧！）执行时间仅仅是经典程序的1/4！.近来，在网上发现了一个链接：/news/Article/uc/uc8051/200803/4751.html，也对这个经典转换程序进行了改进，话是说了不少，只是没有实质性的东西。

这篇文章提到的程序，一直也没有找到，也难辩真假。

这篇文章好像是选自某个著名杂志，但是在术语的使用上，有着明显的漏洞，不像是专业人员的手笔。

比如说文中提到的：“使用51条指令代码，但执行这段程序却要耗费312个指令周期”，就是败笔。

51条指令代码，真不知道说的是什么，指令周期是因各种机型和指令而异的，也不能表示确切的时间。

.下面说说做而论道的编程思路。

;-----------------------------------------------------------------------;已知16位二进制整数n以b15~b0表示，取值范围为0~65535。

1.在片内RAM 30H单元有-个8位二进制数，将其转换成压缩BCD码，存于片内RAM 41H（高位）40H（低位）中。

方法：2^8=256,所以8位二进制A<=256,A/100商是百位数，存放到41h单元，余数再除以10，再得商是10位数,高低位互换，) ORG 0100HSTART:MOV A,30H ;取来8位二进制数MOV B,#100DIV AB ;除以100MOV 41H,A ;商是百位数，存放到41h单元MOV A,B ;取回余数MOV B,#10DIV AB ;再除以10SWAP A ;商是10位数,高低位互换ORL A,BMOV 40H,A ;将十位数与个位位数存入40hSJMP $END2.一个字节（8位）BCD码转换为二进制数（方法：先将高半字节乘以10，再加上低半字节）设待转换的BCD码存放于R2中DTOB:MOV A,R2ANL A,#0F0HSWAP AMOV B,#0AHMUL ABMOV R3,AMOV A,R2ANL A,#0FHADD A,R3RET3.二进制数转换为ASCII码设(30H)=4BH,将高4位的ASCII码放在31H单元,低4位的ASCII码放在32H单元,程序具有通用性,向入口参数30H存入任何数,都能将其变成相应的ISCII 码.ORG 0000HLJMP MAINORG 0030HMAIN:MOV SP,#60HMOV 30H,#4BHMOV R2,30HMOV A,R2ANL A,#0FHCJNE A,#0AH,NEQNEQ: JC LOOPADD A,#37HJMP LOOP3LOOP:ADD A,#30HLOOP3:MOV 31H,AMOV A,R2SWAP AANL A,#0FHCJNE A,#0AH,NE1NE1: JC LOOP1ADD A,#37HJMP LOOP4LOOP1:ADD A,#30HLOOP4:MOV 32H,AA1: SJMP A1END4.已知R0的低半个字节为一个四位的二进制数，要求将其转换为ASCAII码后送回R0中。

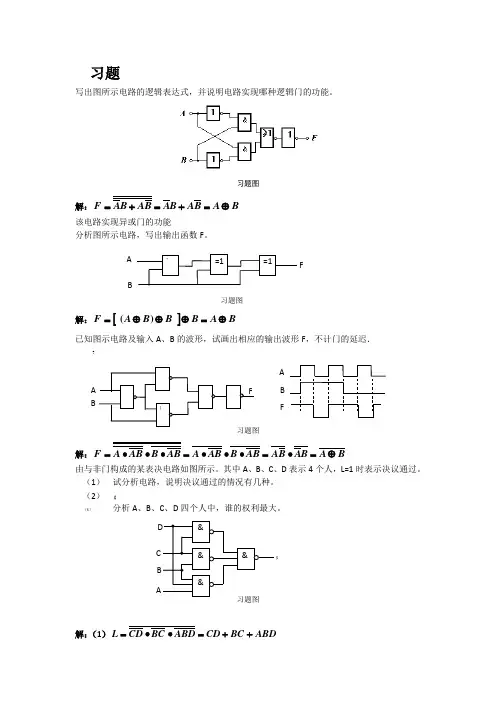
习题写出图所示电路的逻辑表达式，并说明电路实现哪种逻辑门的功能。

习题图解：B A B A B A B A B A F ⊕=+=+= 该电路实现异或门的功能分析图所示电路，写出输出函数F 。

习题图 解：[]B A B BB A F ⊕=⊕⊕⊕=)(已知图示电路及输入A 、B 的波形，试画出相应的输出波形F ，不计门的延迟．?解：B A B A B A AB B AB A AB B AB A F ⊕=•=•••=•••=由与非门构成的某表决电路如图所示。

其中A 、B 、C 、D 表示4个人，L=1时表示决议通过。

（1） 试分析电路，说明决议通过的情况有几种。

（2） 【 （3） 分析A 、B 、C 、D 四个人中，谁的权利最大。

习题图解：（1）ABD BC CD ABD BC CD L ++=••=C & && & D $ L B A " =1=1 =1FFA B[FB A（2）(3)根据真值表可知，四个人当中C 的权利最大。

分析图所示逻辑电路，已知S 1﹑S 0为功能控制输入，A ﹑B 为输入信号，L 为输出，求电路所具有的功能。

&习题图解：（1）011011)(S S B S A S S B S A L ⊕⊕+⊕=⊕⊕•⊕= (2)(3)当S 1S 0=00和S 1S 0=11时，该电路实现两输入或门，当S 1S 0=01时，该电路实现两输入或非门，当S 1S 0=10时，该电路实现两输入与非门。

(2)1￥电路逻辑功能为：“判输入ABC 是否相同”电路。

已知某组合电路的输入A 、B 、C 和输出F 的波形如下图所示，试写出F 的最简与或表达式。

习题图:解：（1）根据波形图得到真值表：，(2)由真值表得到逻辑表达式为C AB BC A C B A F ++=、设∑=)14,12,10,9,8,4,2(),,,(m D C B A F ，要求用最简单的方法，实现的电路最简单。

BCD码转换成二进制什么是BCD码？BCD（Binary-Coded Decimal）码是一种用二进制编码的十进制数表示方法。

在BCD码中，每个十进制数的每位都用4位二进制数表示，称为“BCD位”。

比如，十进制数23的BCD码为00100011，其中“0010”表示2，“0011”表示3。

BCD码可以用于数字显示、计算机存储和传输等领域。

BCD码的转换方法将BCD码转换成二进制的方法非常简单。

对于每一个BCD位，只需要将其转换成对应的4位二进制数即可。

以十进制数23的BCD码为例，我们需要将其转换成二进制数。

1.首先，将BCD码的第一个BCD位“0010”转换成4位二进制数“0010”；2.接下来，将BCD码的第二个BCD位“0011”转换成4位二进制数“0011”；3.最后，将这两个4位二进制数连接起来，得到十进制数23的二进制表示：“0010 0011”。

BCD码转换成二进制的算法为了更好地理解BCD码转换成二进制的算法，我们可以先将十进制数转换成BCD码，然后再将BCD码转换成二进制。

下面是BCD码转换成二进制的算法：1.将BCD码的第一个BCD位转换成4位二进制数；2.将BCD码的第二个BCD位转换成4位二进制数；3.重复上述步骤，直到所有的BCD位都被转换成4位二进制数；4.将所有的4位二进制数连接起来，得到最终的二进制表示。

BCD码转换成二进制的示例让我们通过一个具体的例子来演示BCD码转换成二进制的过程。

假设我们要将十进制数27转换成BCD码，然后再将BCD码转换成二进制。

1.将十进制数27转换成BCD码，得到BCD码的表示为“0010 0111”；2.将BCD码的第一个BCD位“0010”转换成4位二进制数“0010”；3.将BCD码的第二个BCD位“0111”转换成4位二进制数“0111”；4.将这两个4位二进制数连接起来，得到最终的二进制表示：“0010 0111”。

总结BCD码是一种用二进制编码的十进制数表示方法。

bcd转换为二进制BCD码（Binary-Coded Decimal，二进制编码十进制）是一种用二进制数码来表示十进制数的方法，即将0-9十个数字分别进行二进制编码，可以被计算机直接处理。

由于它的特殊性质，使得BCD码不同于其他的编码方式，同时也使得BCD码可以被应用于很多领域，例如金融、准确度要求高的计算等。

然而，很多时候我们需要将BCD码转换成二进制数，在本篇文章中将详细讲述BCD码转换成二进制码的方法。

一、什么是BCD码？BCD码是一种二进制编码，可以用于表示数字0-9。

使用BCD码表示一个数时，将这个数的每一位数字转换成BCD码（即用4位二进制数来表示），拼接而成。

例如，数字29的BCD码是0010 1001。

二、BCD码转二进制码的基本方法将BCD码转换为二进制码，只需要将每一位的BCD码拆分后转换成二进制码，再将这些二进制码按位拼接在一起即可。

具体操作步骤如下：1. 选中一个BCD码。

2. 查看BCD码最高位（MSB，即最左边那一位），如果是1，则表示这个十进制数字大于或等于5；如果是0，则表示这个十进制数字小于5。

因此，可以根据最高位的值，做出递归处理。

3. 如果MSB是1，那么将这个BCD码减去5，然后按照步骤1和步骤2递归处理。

4. 如果MSB是0，那么将这个BCD码乘以2，然后按照步骤1和步骤2递归处理。

5. 递归处理这个BCD码的每个数字，把它们的二进制码连接成一个二进制数。

6. 完成后得到的就是BCD码转换后的二进制码。

三、实例讲解以BCD码1001（即数字9的BCD码）为例，通过上述步骤，将其转换为二进制码的过程如下：1. 选中BCD码1001。

2. 最高位为1，表示这个十进制数字大于等于5。

3. 1001 - 0101 = 0100。

减去5，得到4，然后对这个数字应用上述步骤。

4. 选中BCD码0100。

5. 最高位为0，表示这个十进制数字小于5。

6. 0100 * 2 = 1000。

一、8421BCD码二进制编码的十进制数，简称BCD码(Binarycoded Decimal). 这种方法是用4位二进制码的组合代表十进制数的0，1，2，3，4，5，6 ，7，8，9 十个数符。

4位二进制数码有16种组合，原则上可任选其中的10种作为代码，分别代表十进制中的0，1，2，3，4，5，6，7，8，9 这十个数符。

最常用的BCD码称为8421BCD码，8.4.2.1 分别是4位二进数的位取值。

点击此处将给出十进制数和8421BCD编码的对应关系表。

1、BCD码与十进制数的转换BCD码与十进制数的转换.关系直观，相互转换也很简单，将十进制数75.4转换为BCD码如: 75.4=(0111 (0101.0100)BCD 若将BCD码1000 0101.0101转换为十进制数如: (1000 0101.0101)BCD＝85.5注意:同一个8位二进制代码表示的数，当认为它表示的是二进制数和认为它表示的是二进制编码的十进制数时，数值是不相同的。

例如：00011000，当把它视为二进制数时，其值为24；但作为2位BCD码时，其值为18。

又例如00011100，如将其视为二进制数，其值为28，但不能当成BCD码，因为在8421BCD 码中，它是个非法编码.2、BCD码的格式计算机中的BCD码，经常使用的有两种格式，即分离BCD码，组合BCD码。

所谓分离BCD码，即用一个字节的低四位编码表示十进制数的一位，例如数82的存放格式为：_ _ _1 0 0 0 _ _ _ _0 0 1 0 其中_表示无关值。

组合BCD码，是将两位十进制数，存放在一个字节中，例82的存放格式是1000 00103、BCD码的加减运算由于编码是将每个十进制数用一组4位二进制数来表示，因此，若将这种BCD码直接交计算机去运算，由于计算机总是把数当作二进制数来运算，所以结果可能会出错。

例：用BCD码求38+49。

解决的办法是对二进制加法运算的结果采用"加6修正,这种修正称为BCD调整。

河南科技大学课程设计说明书课程名称 EDA技术题目八位二进制转化为BCD码及余三码、BCD码转化为余三码学院车辆与动力工程学院班级学生姓名指导教师日期2012年7月14号八位二进制码转化为BCD码及余三码、BCD码转化余三码摘要八位二进制数转化为BCD码和余三码的转换在计算机语言中起到了非常重要的作用，通过这次的课程设计让我们更好地掌握二进制数转化为BCD 码和余三码。

二进制转化为余三码不能直接转化，只能通过BCD码为中介进而转化成余三码。

余三码（余3码）是由8421BCD码加上0011形成的一种无权码，由于它的每个字符编码比相应的8421BCD码多3，故称为余三码。

BCD码的一种。

余三码是一种对9的自补代码，因而可给运算带来方便。

其次，在将两个余三码表示的十进制数相加时，能正确产生进位信号，但对“和”必须修正。

修正的方法是：如果有进位，则结果加3；如果无进位，则结果减3。

如，（526）10进制=（0101 0010 0110）8421BCD码=（1000 0101 1001）余3码EDA技术打破了软件和硬件间的壁垒，使计算机的软件技术与硬件实现、设计效率与产品性能合二为一，它代表了电子设计技术和应用技术的发展方向。

VHDL主要用于描述数字系统的接口，结构和功能，它的语法简单易懂，移植性好。

本设计采用VHDL，Altera公司的Quartus II软件仿真，来实现八位二进制到BCD和BCD到余三码的转换。

由于八位二进制的最大范围是0~255，而八位BCD码的范围是0~99，故在转换时输入信号只能取99以内的数。

关键词：八位二进制、BCD码、余三码、VHDL目录第一章绪论 (1)§1.1 课程设计题目 (1)§1.2 设计目的 (2)§1.3 课程设计要求 (2)第二章EDA、VHDL简介 (3)§2.1 EDA简介 (3)§2.2 VHDL简介 (3)第三章设计过程 (5)§3.1设计规划 (5)§3.2各个模块设计及原理图 (5)§3.2.1八位二进制码转化为八位BCD码 (5)§3.2.2八位BCD码转化为八位余三码 (6)§3.2.3八位二进制码转化为8位余三码 (7)第四章系统仿真 (9)§4.1八位二进制码转化为八位BCD码仿真及分析 (9)§4．2八位BCD码转化为八位余三码仿真及分析 (9)§4.3八位二进制码转化为八位余三码仿真及分析 (10)第五章总结 (11)参考文献 (12)第一章绪论随着计算机科学与技术突飞猛进地发展，用数字电路进行信号处理的优势也更加突出，自20世纪70年代开始，这种用数字电路处理模拟信号的所谓“数字化”浪潮已经席卷了电子技术几乎所有的应用领域EDA是电子设计自动化（Electronic Design Automation）的缩写，在20世纪90年代初从计算机辅助设计（CAD）、计算机辅助制造（CAM）、计算机辅助测试（CAT）和计算机辅助工程（CAE）的概念发展而来的。