下载文档原格式
%**********************%实验二：图像点运算%********************%一.使用函数imadjust实现图像灰度变换I=imread('C:\Documents and Settings\Administrator\桌面\数值图像处理实验\16学时实验\实验二\fig0222b.jpg');g1= imadjust (I, [ 0.31875 0.7 ], [ 0 0.7 ], 0.5 );g2= imadjust (I, [ 0.31875 0.7], [ 0 0.7 ], 1 );g3= imadjust (I, [ 0.31875 0.7], [ 0 0.7 ], 2 );g4= imadjust (I, [ 0 0.7 ], [ 0.7 0.0078431], 1 );figure(1)subplot(221);imshow(g1);subplot(222); imshow(g2);subplot(223);imshow(g3);subplot(224); imshow(g4);clear;%二。
观察并记录均衡前后的差别f2=imread('C:\Documents and Settings\Administrator\桌面\数值图像处理实验\16学时实验\实验二\fig0305.tif');g5= im2uint8(mat2gray(log(1+double (f2))));figure(2)subplot(121);imshow(f2);subplot(122);imshow(g5);clear;%三。
使用函数imhist绘制灰度直方图，观察四种直方图的差别f3=imread('C:\Documents and Settings\Administrator\桌面\数值图像处理实验\16学时实验\实验二\fig0222b.jpg');h = imhist( f3 );figure(3)subplot(221);imhist( f3 );subplot(222); plot( h );subplot(223);stem( h );subplot(224); bar( h );clear;%四。
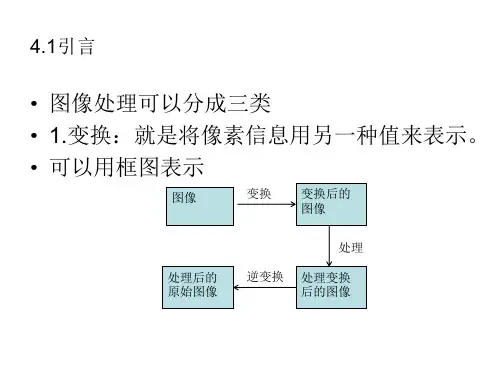
第四章点运算4.1 引言在图像处理中，点运算是—种简单却很重要的技术．它能让用户改变图像数据占据的灰度范围，当显示一幅图像时，点运算的作用尤其明显。
对于一幅输入图像，经过点运算(point operation)将产生一幅输出图像，后者的每个像素点的灰度值仅由相应输入像素点的值决定(这种方法与局部运算的差别在于，后者每个输出像素的灰度值由对应输入像素的一个邻域内几个像素的灰度值决定)。
因此，点运算不可能改变图像内的空间关系。
点运算有时又被称为对比度增强、对比度拉伸或灰度变换。
它是图像数字化软件和图像显示软件的重要组成部分。
点运算以预定的方式改变一幅图像的灰度直方图。
除了灰度级的改变是根据某种特定的灰度变换函数进行之外，点运算可看作是“从像素到像素”的复制操作。
若输入图像为A(x，y)，输出图像为B(x，y)，则点运算可表示为：（1）B x y f A x y(,)[(,)]点运算可完全由灰度变换(gray-scale transformation，GST)函数f(D)确定，后者描述了输入灰度级和输出灰度级之间的映射关系。
4.1.1 点运算的应用在真正开始对图像进行处理之前，有时用点运算来克服图像数字化器的局限性。
点运算对于改善图像显示，也同样重要。
光度学标定人们常希望数字图像的灰度能反映某些物理特性，如光照强度、光密度等。
通过去掉图像传感器的非线性的影响．点运算可达到该目的。
例如。
假设一幅图像被一个对光照强度呈非线性反应的仪器所数字化，点运算可以变换灰度级．使之反映光照强度的等步长增量。
这是光度学标定(photometric calibration)的一个例子。
点运算的另一个用处是变换灰度的单位。
假定有一个图像数字化器，用来数字化一幅显微镜下观察到的图像。
其产生的灰度值与标本的透射率呈线性关系，点运算可用来产生一幅图像，该图像的灰度级可代表光学密度的等步长增量。
我们可将光度学标定作为图像数字化的软件方(面)。
实验1 点运算和直方图处理一、实验目的1. 掌握利用Matlab图像工具箱显示直方图的方法2. 掌握运用点操作进行图像处理的基本原理。
3. 进一步理解利用点操作这一方法进行图像处理的特点。
4. 掌握利用Matlab图像工具箱进行直方图均衡化的基本方法。
二、实验的硬件、软件平台硬件：计算机软件：操作系统：WINDOWS 7应用软件：MATLAB三、实验内容及步骤1. 了解Matlab图像工具箱的使用。
2. 利用Matlab图像工具箱对图像进行点操作，要求完成下列3个题目中的至少2个。
⑴图1灰度范围偏小，且灰度偏低，改正之。
⑵图2暗处细节分辨不清，使其能看清楚。
⑶图3亮处细节分辨不清，使其能看清楚。
图1 图2 图33. 给出处理前后图像的直方图。
4. 利用MatLab图像处理工具箱中函数对以上图像进行直方图均衡化操作，观察结果。
四、思考题1. 点操作能完成哪些图像增强功能？2. 直方图均衡化后直方图为何并不平坦？为何灰度级会减少？五、实验报告要求1．对点操作的原理进行说明。
2．给出程序清单和注释。
3．对处理过程和结果进行分析（包括对处理前后图像的直方图的分析）。
实验代码以及解析点操作：I = imread('POINT1.BMP'); %读入图像j=rgb2gray(I); %将图像转为灰度图像INFO=IMFINFO('POINT1.BMP') %获取图片的格式、尺寸、颜色数量、修改时间等信息[l,r]=size(j); %图片大小figure; %建立一个图形框subplot(221)imshow(j) %在两行两列的第一个位置放置图片jtitle('POINT1.BMP') %给该图片加上标题POINT1.BMPfor m=1:lfor n=1:r %从第一个像素循环到最后一个像素p1(m,n)=j(m,n)*1.2; %把各点乘上1.2得到p1图endendfor m=1:lfor n=1:rp2(m,n)=j(m,n)*2; %%把各点乘上2得到p2图endendfor m=1:lfor n=1:rp3(m,n)=j(m,n)*2+50; %把各点乘上2再加50得到p2图endendsubplot(222)imshow(p1)title('j(m,n)*1.2') %p1图放在第二个位置且冠名j(m,n)*1.2subplot(223)imshow(p2)title('j(m,n)*2') %p1图放在第三个位置且冠名j(m,n)* 2subplot(224)imshow(p3)title('j(m,n)*2+50') %p1图放在第四个位置且冠名j(m,n)*2+50figure; %建立一个新的窗口并且依次显示以上四个图的直方图subplot(221),imhist(j,64); title('原图直方图')%64代表把0-250的灰度范围分为64份subplot(223),imhist(p2,64);title('j(m,n)*2')subplot(224),imhist(p3,64);title('j(m,n)*2+50')%picture2 %这里把两个图片的点操作处理都放在了同一个程序里I2 = imread('POINT2.BMP'); %各语句意思同上j2=rgb2gray(I2);INFO2=IMFINFO('POINT2.BMP')[l2,r2]=size(j2);figure;subplot(221)imshow(j2)title('POINT1.BMP')for a=1:l2for b=1:r2q1(a,b)=j2(a,b)*1.2;endendfor a=1:l2for b=1:r2q2(a,b)=j2(a,b)*1.3;endendfor a=1:l2for b=1:r2q3(a,b)=j2(a,b)/2;endendsubplot(222)imshow(q1)title('j(m,n)*1.2')subplot(223)imshow(q2)title('j(m,n)*2')subplot(224)imshow(q3)title('j(m,n)*2+50')figure;subplot(221),imhist(j2,64);title('j2原图的直方图')subplot(222),imhist(q1,64);title('j(m,n)*1.2')subplot(223),imhist(q2,64);title('j(m,n)*2')本程序共创建了四个窗口，分别是两个原图和处理后的图像对比，以及各图对应的直方图POINT1.BMPj(m,n)*1.2j(m,n)*2j(m,n)*2+500j2原图的直方图1002000j(m,n)*1.2100200j(m,n)*2100200j(m,n)*2+50100200用函数POINT2histeqPOINT2.BMP 0100200histeq0100200思考题1.点操作能完成哪些图像增强功能？点操作可以完成的图像增强功能包括灰度变换，直方图均衡化，直方图规定化等空间域的处理2.直方图均衡化后直方图为何并不平坦？为何灰度级会减少？直方图使灰度级分布具有均匀概率密度，扩展了像素取值的动态范围但减少了灰度级。
实验二 图像点运算一、实验目的1) 掌握图像线性和非线性点运算的基本原理和算法；2) 掌握借助直方图分析点运算的基本方法；3) 掌握图像灰度直方图均衡的原理和算法；4) 掌握根据图像特点进行点运算的基本原理和方法。
5) 通过编程，上机调试程序，进一步提高编程能力及使用计算机解决问题的能力。
二、实验原理1. 图像线性点运算的基本方法图像点运算是一种基于单个像素的灰度调整方法，它通常根据一定的全局模型或像素统计值来对像素进行逐一操作，不涉及其它像素。
图像点运算方法大体可分为线性方法和非线性方法。
线性变换方法就是将图像中所有点的灰度按照线性灰度变换函数进行变换。
可用公式简单表述为(,)[(,)]g m n T f m n =。
其中[.]T 为变换函数。
一种扩展感兴趣的，牺牲其它区间的函数表达式如下[]; 0(,)(,)(,); (,);(,)255a f m n a d c g x y c f m n a a f m n b b a b b f m n ≤<⎧⎪-⎪=+-≤<⎨-⎪≤<⎪⎩ （1） 其中输入图像为(,)f m n ，输出图像为(,)g m n 。
,,,a b c d 为参数，不同的值会有较大的差异。
使用时要注意输出函数的阈值限定。
如图 1 所示，该函数对于感兴趣的[a,b)区间，采用斜率大于1的线性变换来进行扩展，而把其它区间用a 或b 来表示。
图1 扩展感兴趣的，牺牲其它区间的函数表达式2.图像非线性点运算图像非线性变换种类非常丰富，可分为分段线性变换、对数变换、幂数变换等等。
阈值分割就利用了分段线性变换函数。
对数变换常用来扩展被压缩的高值图像中的暗像素，相对的是反对数变换的调整值。
分段线性变换函数意为在某一灰度区间的变换函数为线性函数，组合形式为[][](,);0(,)(,)(,); (,)(,);(,)c f m n f m n a a d c g x y c f m n a a f m n b b a N d d f m n b b f m n M M b ⎧≤<⎪⎪-⎪=+-≤<⎨-⎪-⎪+-≤<⎪-⎩（2） 其中输入图像为(,)f m n ，输出图像为(,)g m n 。
中北大学
毕业设计开题报告
学生姓名：学号：
学院、系：
专业：
设计题目：图像的点运算技术研究及软件实现
指导教师:
2012年2月24日
毕业设计开题报告
1．结合毕业设计情况，根据所查阅的文献资料，撰写2000字左右的文献综述：
文献综述
近年来，网络技术和网络应用蓬勃发展，特别是Internet的日益普及，是得益于语音、成像技术为主体的多媒体技术成为业内人士研究的重点之一。
伴随网络兴起的视屏游戏和视屏特技都使图像处理越来越引人注目。
数字图像处理是指用计算机对图像进行的相关处理，数字图像处理技术的内容非常丰富,总的来说数字图像处理包括以下几项内容：①点运算；②几何处理；③图像增强；④图像复原；⑤图像形态学处理；⑥图像编码；⑦图像重建；⑧模式识别［1］。
本课题主要介绍点运算。
例如图像在生成、获取、传输过程中、受光源、成像系统的影响, 不可避免的要造成图像像质的降低, 这时就需要图像增强; 计算机识别目标时，就需要提取目标的形状和结构特征等，这些都可以通过点运算来实现［2］。
图像的点运算是一种既简单又重要的技术，它能让用户改变图像的灰度值。
一幅输入图像经过点运算后将产生一幅新的输出图像，由输入图像像素点的灰度值决定相应输出图像像素点的灰度值，可由灰度变换函数表示如下：B（x，y）=f[A(x,y)]［3］。
下面将依次介绍图像点运算的一些技术：图像的直方图、图像灰度的线性变换、灰度拉伸、直方图均衡化和图像的细化等。
1．灰度直方图
将图像中的像素按其灰度值大小进行组合，所构成的以像素数量为因变量、灰度值为自变量的函数，就是图像的灰度直方图［3］。
灰度直方图能给出一幅图像的概要信息，是图像处理与分析的重要依据之一。
它是数字图像处理技术中最简单、最有用的工具，它描述了一幅图像的灰度级内容。
可以说，对图像的分析与观察，直到形成一个有效的处理方法，都离不开直方图［4］。
灰度直方图是灰度的函数，它描述的是图像中具有该灰度值的像数个数，其横坐表示像素的灰度级别，纵坐标是该灰度出现的频率（像素个数）［4］。
如果大多数像素灰度值趋在较暗的区域，该图像整体视觉效果偏暗；如果大多数像素灰度值趋在较亮的区
域，该图像整体视觉效果偏亮；如果像素分布均匀，动态范围比较合适［5］。
2．灰度的线性变换（线性点运算）
灰度的线性变换是将图像中所用的点的灰度按照线性灰度变换函数进行变换。
当图像由于曝光不足或过度，或由于成像设备的非线性或图像记录设备动态范围太窄等因素，会产生对比度不足，使图像细节分辨不清，此时可以使用线性灰度变换。
该线性灰度变换函数f（x）是一个一维线性函数: f(x)=fA*x+fB，式中fA为线性函数的斜率，fB为线性函数在y轴的截距。
当fA>1时，输出图像的对比度将增大；当fA<1时，输出图像的对比度将减少；当fA=1且fB不为0时，操作仅使所有像素灰度值上移或下移，其效果是使整个图像更暗或更亮；如果fA<0，暗区域将变亮，亮区域将变暗，点运算完成了图像求补运算。
特殊情况下，当fA=1，fB=0时，输出图像和输入图像相同；当fA= -1,fB=255时，输出图像的灰度正好反转［5］。
3.灰度拉伸
灰度拉伸又叫对比度拉伸，它是一种最基本的灰度变换，使用的是最简单的分段线性变换函数，它的主要思想是提高图像处理灰度级的动态范围［6］。
灰度拉伸可以更加灵活地控制灰度直方图的分布，它可以有选择地拉伸某段灰度区间以改善输出图像。
如果一幅图像灰度集中在较暗的区域而导致图像偏暗，可以用灰度拉伸功能来拉伸（斜率>1）物体灰度区间以改善图像；同样如果图像灰度集中在较亮的区域而导致图像偏亮，也可以用灰度拉伸功能来压缩（斜率<1）物体灰度区间以改善图像质量［7］、［8］。
4.直方图均衡化
直方图均衡化也叫灰度均衡变换，它能使输入图像转换为在新图像每一灰度级上都有相同的像素点的输出图像［9］。
它是灰度变换一个重要应用，广泛应用在图像增强处理中，它是以累计分布函数变换为基础的直方图修正法，可以产生一幅灰度及分布具有均匀概率密度的图像，扩展了像素的取值动态范围，许多图像的灰度值是非均匀分布的，其中灰度值集中在一个小区域内的图像是很常见的［10］、［11］。
直方图均衡化是一种通过重新均匀地分布各灰度值来增强图像对比度的方法。
经过直方图均衡化的图像对二值化阈值选取十分有利。
一般来说，直方图修正能提高图像的主观质量，因此在处理艺术图像是非常有用［12］。
灰度均衡变换的原理如下：A[a]=(∑N[i])×255／(H·W) ［11］
中a为原图像像素灰度值（0—255），经过灰度均衡运算，a的值变为灰度均衡值A，N为原
图像各灰度值对应的像元数量，H为图像的高度（单位是像元数）。
经过灰度均衡后，图像的对比度大大提高，转换后图像的灰度分布也趋于均匀。
5.图像的细化
图像的细化，又称图像的骨骼化，是特指在保持原图像拓扑结构的情况下抽出一个单像素宽的骨骼的过程，是数字图像预处理中的重要一环，广泛用于数字、文字、指纹等的识别中［13］、［14］。
因此，图像的细化算法研究一直受到图像处理领域的关注。
近年来许多学者相继提出了各种细化算法，从考虑问题的角度，图像细化的方法有两种，即边缘点删除和内点保留［15］。
基于边缘删除的细化算法在细化过程中只对边缘点的可删除性进行判断并做出相应处理，由于受跟踪顺序及所考察领域的影响容易产生骨架的非对称性；基于内点保留的细化算法容易使所获得的骨架大于一个像素［16］。
参考文献：
[ 1 ] 阮秋琦.数字图像处理基础[M].北京：清华大学出版社，2009.8-10.
[ 2 ] 刘文耀等. 光电图像处理[M].北京：电子工业出版社 ,2002.31-37.
[ 3 ] 阮秋琦.数字图像处理基础[M].北京：清华大学出版社，2009.130.
[ 4 ] 何斌、马天予等.数字图像处理[M]（第二版）.北京：人民邮电出版社，2002.43-44. [ 5 ] 何斌、马天予等.数字图像处理[M]（第二版）.北京：人民邮电出版社，2002.46. [ 6 ] 刘文耀等. 光电图像处理[M].北京：电子工业出版社 ,2002.321-325
[ 7 ] 朱建军.用VC实现Windows下BMP位图文件的显示[J].湘潭师范学院学报，1998.19:40-43.
[ 8 ] 邓炜等.计算机图像识别系统的设计与实现[J]，计算机应用研究报，2000.13:20—22.
[ 9 ] 何斌、马天予等.数字图像处理[M]（第二版）.北京：人民邮电出版社，2002.123 [ 10 ] 邓炜等.计算机图像识别系统的设计与实现[J]，计算机应用研究报，2000.17:28—29.
[ 11 ] 杨静怡等.计算机图像处理机常用算法手册[M].南京：南京大学出版社，1997.
[ 12 ] 何斌、马天予等.数字图像处理[M]（第二版）.北京：人民邮电出版社，2002.127 [ 13 ] 苏统华.用VC开发图像处理系统[J].电脑技巧与维护，2001.10:73-78
[ 14 ] 邓炜等.计算机图像识别系统的设计与实现[J]，计算机应用研究报，2000.19:15—18.
[ 15 ] 阮秋琦.数字图像处理基础[M].北京：清华大学出版社，2009.144-146
[ 16 ] 阮秋琦.数字图像处理基础[M].北京：清华大学出版社，2009.334-337
毕业设计开题报告
２．本课题要研究或解决的问题和拟采用的研究手段（途径）：
本课题要研究或者解决的问题大致有三个：首先，学会各种常用的点运算技术，掌握这些技术的相关算法，并对这些算法进行相应的研究，比较出各自的优劣。
其次，要设计出一款可以对图像做点运算处理的图像处理软件，这种软件要囊括相关点运算处理技术，如线性点运算、灰度直方图，直方图均衡变换等，并且要尽可能地达到好的效果与效率。
最后，能用直方图对图像的加减运算、阈值滤波和线性变换及直方图均衡的效果做定量的分析与判定。
课题研究者拟采用的研究途径及过程，首先，储备大量的与本课题有关的相关资源。
去学校图书馆查阅相关内容的书籍，寻找其中有利于本课题进展的文章及算法。
同时，在网上也积极搜索与本课题有关的文章，特别是在一些正规的权威的网站，例如CNKI。
其次，对本课题进行全面的由浅入深的学习研究。
大量阅读学习点运算处理技术的相关知识，熟练掌握与本课题关联的定义、规则和算法，去劣存优，去粗存精。
再次，程序设计。
对相关点运算处理技术进行程序化，最终要完成软件的初步正确运行。
最后，对软件的效率进行分析改善，并做出一定的研究。
毕业设计开题报告
指导教师意见：
通过文献综述可见，同学明确了课题的背景、目的和意义，了解了国内外的研究现状，了解了与该课题相关的关键技术。
为开展设计打好了基础。
该同学明确该课题要完成的任务和其中要用到的关键技术，并提出了拟采用的研究手段，思路正确，手段可行。
同意该生开题。
指导教师：
2012 年2 月27 日所在系审查意见：
系主任：
2012 年2 月28 日。
