2013力学竞赛静力学练习题

判断题1．两个大小相等、方向相同的力分别作用在同一物体时，它们对物体产生的效应相同（）2．凡合力都比分力大（）3．汇交的三个力是平衡力（）4．两个力在同一轴上的投影相等，则这两个力一定相等（）5．平面力偶矩的大小与矩心点的位置有关（）6．力和力偶可以合成（）7．凡在二力作用下的约束成为二力构件（）8．两端用光滑铰链连接的构件是二力构件（）9．刚体上的力可沿作用线移动（）10．物体上的力可沿作用线移动（）11．刚体是指在外力的作用下大小和形状不变的物体。

（）12、一对等值、反向，作用线平行且不共线的力组成的力称为力偶。

（）13、力的可传性原理和加减平衡力系公理只适用于刚体。

（）(F) = FL。

（）F14、图中F对O点之矩为mO15、工程力学的研究对象是杆件和杆件结构。

()16、力系的等效力就是力系的合力。

()17、力偶只能使刚体转动，而不能使刚体移动。

（）18、二力平衡公理适用于物体。

（）19、二力平衡公理只适用于刚体。

（）20、作用与反作用公理针对一个物体而言。

（）21、三力平衡汇交定理只适用于刚体。

（）22、力的平行四边形法则只适用于刚体上的力的合成和分解。

（）23、强度指结构或构件抵抗变形的能力。

（）24、刚度指结构或构件抵抗破坏的能力。

（）25、稳定性指结构或构件保持原有平衡状态的能力。

（）26、研究物体的平衡问题时可将物体视为刚体。

（）27、对物体进行内力分析和承载能力计算时可将物体视为刚体。

（））28、对物体进行内力分析和承载能力计算时必须将物体视为变形体。

（29、按作用时间长短可将荷载分为静荷载和动荷载。

（）30、按作用性质可将荷载分为恒荷载和活荷载。

（）31、力的平移定理适用于任何物体。

（）32、力的平移定理只适用于刚体。

（）33、力对刚体的作用效应包括运动和变形。

（）34、约束反力的方向与主动力有关，而与约束类型无关。

（）35、研究对象与周围物体相接触处一定有约束反力。

（）36、约束反力的个数由约束类型决定。

一、判断题（共30分，每道3分）1.两个大小相等、方向相同的力分别作用于同一物体时，它们对物体产生的效应相同。

（）2.凡合力都比分力大。

（）3.汇交的三个力是平衡力。

（）4.当平面汇交力系平衡时，选择几个投影轴就能列出几个独立的平衡方程。

（）5.两个力F1，F2在同一轴上的投影相等，则这两个力一定相等。

（）6.在平面中任意两个力都可以简化为一个合力。

（）7.平面力偶的大小与钜心点的位置有关。

（）8.当平面任意力系向某点简化结果为力偶时，如果再向另一点简化，则其结果是一样的。

（）9.作用于刚体上的平面任意力学，若其力多边形自行封闭，则此刚体平衡。

（）10.如果某平面任意力系由多个力偶和一个力组成，该力系一定不是平衡力系。

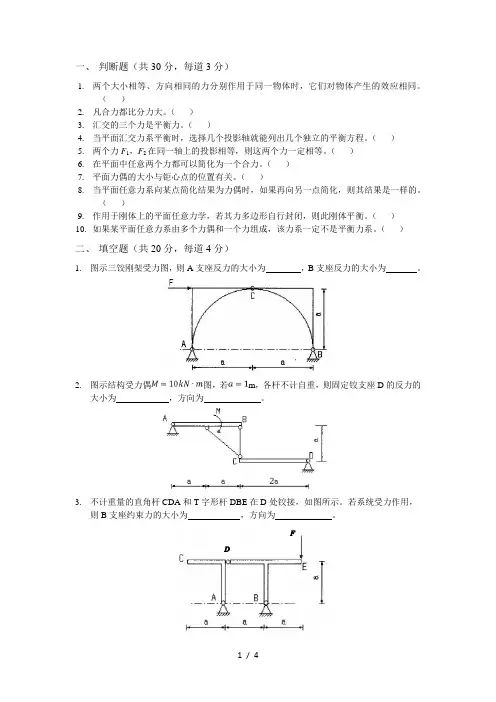
（）二、填空题（共20分，每道4分）1.图示三饺刚架受力图，则A支座反力的大小为，B支座反力的大小为。

2.图示结构受力偶图，若m，各杆不计自重，则固定铰支座D的反力的大小为，方向为。

3.不计重量的直角杆CDA和T字形杆DBE在D处铰接，如图所示。

若系统受力作用，则B支座约束力的大小为，方向为。

4. 直角弯杆ABCD 与直杆DE 及EC 铰接如图，作用在DE 杆上力偶矩，不计杆重和摩擦，尺寸如图。

则支座A的约束反力大小为 ，B 处的约束反力大小为 。

5. 图示AB 杆，不计自重，在5个力作用下处于平衡，则作用于B 点的4个力的合力F R的大小为 ，方向沿着 。

三、 计算题（共50分）1. 四连杆机构OABO 1在图示位置平衡，已知OA=0.4m ，O 1B=0.6m ，AB 处于水平位置。

作用在曲柄OA 上的力偶矩M 1，不计自重，求力偶M 2的大小及连杆AB 所受的力。

（10分）M 2O 1OABM 130°2. 图示滑道连杆机构，在滑道连杆上作用水平力F 。

已知曲柄OA=r ，滑道倾角为β，曲柄OA 与水平夹角θ，机构重量和各处摩擦力不计。

试求当机构平衡时，作用在曲柄OA 上的力偶M 的大小。

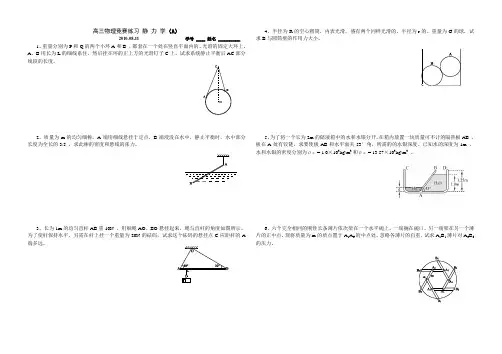
高三物理竞赛练习静力学（A）2010-08-11 学号 ____ 姓名 __________1、重量分别为P和Q的两个小环A和B ，都套在一个处在竖直平面内的、光滑的固定大环上。

A、B用长为L的细线系住，然后挂在环的正上方的光滑钉子C上。

试求系统静止平衡后AC部分线段的长度。

2、质量为m的均匀细棒，A端用细线悬挂于定点，B端浸没在水中，静止平衡时，水中部分长度为全长的3/5 ，求此棒的密度和悬线的张力。

3、长为1m的均匀直杆AB重10N ，用细绳AO、BO悬挂起来，绳与直杆的角度如图所示。

为了使杆保持水平，另需在杆上挂一个重量为20N的砝码，试求这个砝码的悬挂点C应距杆的A 端多远。

4、半径为R的空心圆筒，内表光滑，盛有两个同样光滑的、半径为r的、重量为G的球，试求B与圆筒壁的作用力大小。

5、为了将一个长为2m的储液箱中的水和水银分开，在箱内放置一块质量可不计的隔热板AB ，板在A处有铰链，求要使板AB和水平面夹53°角，所需的的水银深度。

已知水的深度为1m 、水和水银的密度分别为ρ水= 1.0×103kg/m3和ρ汞= 13.57×103kg/m3。

6、六个完全相同的刚性长条薄片依次架在一个水平碗上，一端搁在碗口，另一端架在另一个薄片的正中点。

现将质量为m的质点置于A1A6的中点处，忽略各薄片的自重，试求A1B1薄片对A6B6的压力。

静力学（A ） 提示与答案：1、提示：本题应用共点力平衡知识，正确画出两个小环的受力，做出力的矢量三角形，利用力三角形和空间几何三角形相似求解。

答案：QP Q+L 。

2、提示：本题利用力矩平衡知识求解，列方程注意转动点（或转动轴）应根据所求问题正确选取，另注意浮力的作用点在浸没段的中心点。

答案：2521ρ水；72mg 。

3、提示：本题利用刚体平衡条件求解，列出力的平衡方程和力矩平衡方程求解，列力矩平衡方程注意转动点（或转动轴）应根据所求问题正确选取。

静力学试题及答案一、单项选择题（每题2分，共20分）1. 静力学中，力的三要素是什么？A. 大小、方向、作用点B. 大小、方向、作用线C. 大小、作用点、作用线D. 方向、作用点、作用线答案：A2. 力的合成遵循什么法则？A. 牛顿第一定律B. 牛顿第二定律C. 牛顿第三定律D. 平行四边形法则答案：D3. 以下哪个不是静力学平衡条件？A. 合力为零B. 合力矩为零C. 物体静止D. 物体匀速直线运动答案：D4. 在静力学中，物体的平衡状态是指：A. 物体静止B. 物体匀速直线运动C. 物体静止或匀速直线运动D. 物体加速运动答案：C5. 以下哪个力不是保守力？A. 重力B. 弹簧力C. 摩擦力D. 电场力答案：C6. 静摩擦力的方向总是：A. 与物体运动方向相反B. 与物体运动趋势相反C. 与物体运动方向相同D. 与物体运动趋势相同答案：B7. 动摩擦力的大小与以下哪个因素有关？A. 物体的质量B. 物体的速度C. 物体间的接触面积D. 物体间的正压力答案：D8. 物体在斜面上保持静止时，斜面对物体的摩擦力方向是：A. 垂直于斜面向上B. 垂直于斜面向下C. 平行于斜面向上D. 平行于斜面向下答案：C9. 以下哪个力不是静力学中的力？A. 重力B. 弹力C. 摩擦力D. 惯性力答案：D10. 物体在水平面上静止时，其受力情况是：A. 重力与支持力平衡B. 重力与摩擦力平衡C. 支持力与摩擦力平衡D. 重力与支持力不平衡答案：A二、填空题（每题2分，共20分）1. 静力学中，物体的平衡状态是指物体处于________或________状态。

答案：静止；匀速直线运动2. 力的平行四边形法则可以用于求解两个力的______。

答案：合力3. 静摩擦力的大小与物体间的正压力______。

答案：无关4. 当物体在斜面上静止时，斜面对物体的摩擦力方向是______。

答案：平行于斜面向上5. 动摩擦力的大小与物体间的正压力______。

2013届物理竞赛第一轮复习 静力学测验(2011.10.16)姓名 满分160分 得分1.（本题6分）如图所示，物体 A 靠在光滑竖直的墙面，用带铰链的棒支住它，物体重为G ，棒重G ‘，棒和竖直方向的夹角为 ，则以下说法正确的是：（ ） A 物体A 对棒端的弹力、磨擦力的合力的方向必沿棒的方向； B 增加物重G ，物体对棒的弹力将减小；C 移动铰链的位置，使 角增大，但仍支住物体A ，则物体对棒 的弹力将增大；D 增大棒重G ‘，物体A 对棒的磨擦力将增大；2．在水平桌面M 上放置一块正方形薄板abcd ，在木板的正中央放置一个质量为m 的木板，如图所示，先以木板的ad 边为轴，将木板向上缓慢转动，使木板 a d 的ab 边与桌面的夹角为θ；在接着以木板的ab 边为轴，将木板向上缓慢转动，使木板的ad 边与桌面的夹角也为θ（ab 边与桌面的 b c 夹角θ不变），在转动过程中木板在薄木板上没有滑动，则转动以后木板受到的摩擦力的大小为（ ）A 2√2mgSin θ BmgSin2θ C √2mgSin θ D mgSin √2θ 3．（本题6分）如图所示，一个直角斜槽（两槽面间夹角为90°，两槽面跟竖直面的夹角均为45°），对水平面的倾角为θ，一个横截面积为正方形的物 块恰能沿此斜槽匀速下滑，假定两槽面的材料和槽面的情况相同， 则物块和槽面之间的动摩擦因数μ为（ ）A √2 tan θB √2/ 2 cot θC √2/ 2 tan θD √2 cot θ4. （本题6分）如图所示上细下粗的容器中盛有一定质量的水，若将它倒置，则水对容器底面的压力和压强变化的情况是（ ）A 、压力减小，压强增大B 、压力增大，压强减小C 、压力和压强都增大D 、压力和压强都减小 5．（本题6分）如图所示是单臂斜拉桥的示意图,均匀桥板ao 重为G ,三根平行钢索与桥面成30°,间距ab =bc =cd =do ,若每根钢索受力相同，左侧桥墩对桥板无作用力，则每根钢索的拉力大小 是6、（本题15分）如图1所示，一根重8牛顿的均质直棒AB ，其A 端用悬线悬挂在O 点，现用F = 6牛顿的水平恒力作用于B 端，当达到静止平衡后，试求：（1）悬绳与竖直方向的夹角α；（2）直棒与水平方向的夹角β。

静力学模拟试题及答案一、选择题1. 静力学中，力的平衡状态是指：A. 物体静止不动B. 物体速度为零C. 物体加速度为零D. 物体受力为零答案：C2. 以下哪项不是静力学中的基本概念？A. 力B. 力矩C. 动量D. 平衡答案：C二、填空题1. 根据牛顿第一定律，物体在不受外力作用时，将保持________状态。

答案：静止或匀速直线运动2. 在静力学中，当物体受到多个力作用时，若这些力的合力为零，则物体处于________状态。

答案：平衡三、简答题1. 解释什么是静力学中的二力平衡，并给出一个生活中的例子。

答案：二力平衡是指两个大小相等、方向相反、作用在同一直线上的力作用在物体上，使得物体保持静止或匀速直线运动的状态。

例如，当一个人站在水平地面上时，其受到的重力和地面的支持力就是一对二力平衡的例子。

2. 描述力矩的三要素，并说明它们是如何影响力矩的大小和方向的。

答案：力矩的三要素包括力的大小、力臂的长度以及力的作用点。

力的大小越大，力臂越长，力矩就越大；力臂长度固定时，力的作用点越远离旋转轴，力矩也越大。

力矩的方向遵循右手定则，即当力的方向从旋转轴指向力的作用点时，拇指指向的方向即为力矩的方向。

四、计算题1. 一个质量为10kg的物体，受到一个水平向右的力F=20N，求物体的加速度。

答案：根据牛顿第二定律，F=ma，所以a=F/m=20N/10kg=2m/s²。

2. 一个杠杆长2m，一端固定，另一端受到一个垂直向下的力G=100N，求杠杆的力臂长度。

答案：由于杠杆平衡，力臂长度等于杠杆长度的一半，即1m。

五、论述题1. 论述静力学在工程学中的应用，并给出至少两个具体的例子。

答案：静力学在工程学中有着广泛的应用，例如：- 在建筑设计中，通过静力学分析可以确定建筑物结构的稳定性和承载能力，确保建筑物的安全。

- 在机械设计中，通过计算零件的受力情况，可以设计出既满足功能需求又具有足够强度的机械结构。

静力学练习题及参考答案1. 问题描述：一根长度为L的均质杆以一端固定在墙上，另一端悬挂一重物。

重物造成的杆的弯曲应力最大为σ。

杆的质量可以忽略不计。

计算重物的质量m。

解答：根据静力学原理，杆的弯曲应力可以用公式计算：σ = M / S，其中M是杆的弯矩，S是杆的截面横截面积。

因为杆是均质杆，所以它的截面横截面积在整个杆上都是相等的。

设杆的截面横截面积为A。

杆的弯矩M可以通过杆的长度L和重物的力矩T计算得到：M = T * (L/2)。

代入上面的公式，我们可以得到：σ = (T * (L/2)) / A。

根据题目的描述，我们可以得到如下等式：σ = (m * g * (L/2)) / A，其中g是重力加速度。

我们可以将这个等式转换成求解未知质量m的方程。

将等式两边的A乘以m，并将等式两边的m乘以g，我们可以得到如下方程：m^2 = (2 * σ * A) / (g * L)解这个方程，我们可以求得未知质量m。

2. 问题描述：一根均质杆的长度为L，质量为M。

杆的一端固定在墙上，另一端悬挂一重物。

杆与地面的夹角为θ。

重物造成的杆的弯曲应力最大为σ。

求重物的质量m。

解答：在这个问题中，除了重物的力矩，还需要考虑到重力对杆的力矩。

由于杆是均质杆，其质量可以均匀分布在整个杆上。

假设杆上的每个微小质量元都受到与其距离一致的力矩。

重物造成的力矩可以用公式计算：M1 = m * g * (L/2) * sinθ，其中g 是重力加速度。

由于杆是均质杆，它的质心位于杆的中点。

因此重力对杆的力矩可以用公式计算：M2 = M * g * (L/2) * cosθ。

根据静力学的原理，杆的弯曲应力可以用公式计算：σ = M / S，其中M是杆的弯矩，S是杆的截面横截面积。

在这个问题中，我们可以将弯曲应力的计算公式推广到杆的中点（也就是质心）：σ = (M1 + M2) / S代入上面的公式，我们可以得到：σ = ((m * g * (L/2) * sinθ) + (M *g * (L/2) * cosθ)) / S根据题目的描述，我们可以得到如下等式：σ = ((m * g * (L/2) * sinθ) + (M * g * (L/2) * cosθ)) / (A / 2)，其中A是杆的横截面积。

第一章 静力学基础和物体的受力分析 练习题一、填空题1、理论力学的任务是研究物体作 的规律。

2、平衡是指 或 状态。

3、力是物体之间相互的 作用。

4、刚体是受力作用而 的物体。

5、刚体受到两个力作用而平衡的充分必要条件是 。

6、约束是指限制 的周围物体。

7、对刚体而言，力的三要素是 、 、 。

二、单项选择题1、图示系统受力F 作用而平衡。

欲使A 支座约束力的作用线与AB 成60º角，则斜面 的倾角α应为______________。

（A ） 0º （B ） 30º （C ） 45º （D ） 60º题1图 题2图2、如图所示的两个楔块A 、B 在m -m 处光滑接触，现在其两端沿轴线各加一个大小相 等、方向相反的力，则两个楔块的状态为 。

（A ）A 、B 都不平衡 （B ）A 平衡、B 不平衡 （C ）A 不平衡、B 平衡 （D ）A 、B 都平衡3、三力平衡定理是 。

（A ）共面不平行的三个力互相平衡必汇交于一点 （B ）共面三力若平衡，必汇交于一点（C ）三力汇交于一点，则这三个力必互相平衡。

（D ）此三个力必定互相平行4、作用和反作用定律的适用范围是。

（A）只适用于刚体（B）只适用于变形体（C）只适用于处于平衡状态的物体（D）适用于任何物体三、作图题作出下列系统中指定对象的受力图1、杆AB2、圆柱A3、杆AB、整体4、刚架AB5、杆AB6、整体7、曲杆AB、曲杆BC、整体8、每个物体；整体9、每个物体，整体10、每个物体；整体11、杆AB、杆BC；整体12、杆AB、杆BC；整体13、杆AC、杆CB、销钉C、整体第二章 平面汇交力系与平面力偶系 练习题一、填空题1、研究平面汇交力系时, 采用两种方法, 即 法和 法。

2、平面汇交力系平衡的几何条件是 。

3、一个力F G在某轴上的分力是 量、投影是 量。

4、合力投影定理在x 方向的表达式是 。

静力学和动力学练习题(含答案)静力学和动力学练题 (含答案)静力学练题1. 一个质量为10kg的物体置于水平面上。

一个力F = 50N施加在物体上，使其保持静止。

求摩擦力的大小。

解答：根据静力学的条件，物体保持静止时，合力为零。

我们可以设置以下方程：ΣF = F - F_f = 0其中，ΣF为合力，F为施加在物体上的力，F_f为摩擦力。

代入已知数据，得到：50N - F_f = 0解方程得到 F_f = 50N，因此摩擦力的大小为50N。

2. 一个质量为5kg的物体沿斜面下滑，斜面的倾角为30度。

在不考虑摩擦的情况下，求物体的加速度。

解答：根据静力学的条件，物体在斜面上保持平衡时，合力沿着斜面的方向为零。

我们可以设置以下方程：ΣF = m * g * sinθ - m * g * cosθ = 0其中，ΣF为合力，m为物体的质量，g为重力加速度，θ为斜面的倾角。

代入已知数据，得到：5kg * 9.8m/s^2 * sin30° - 5kg * 9.8m/s^2 * cos30° = 0解方程得到加速度 a = 4.9m/s^2，因此物体的加速度为4.9m/s^2。

动力学练题1. 一个质量为2kg的物体以速度4m/s沿着水平方向运动。

一个恒力F = 6N施加在物体上，与运动方向垂直。

求物体在3秒后的速度。

解答：根据动力学的条件，物体在受到恒力作用时，速度的变化可以通过牛顿第二定律来计算。

我们可以使用以下公式：F = m * a其中，F为力的大小，m为物体的质量，a为物体的加速度。

根据题目已提供的数据，可以计算出物体的加速度：6N = 2kg * a解方程得到 a = 3m/s^2。

然后，我们可以使用以下公式来计算物体的速度变化：v = u + a * t其中，v为物体的最终速度，u为物体的初始速度，a为物体的加速度，t为时间间隔。

代入已知数据，计算得到：v = 4m/s + 3m/s^2 * 3s = 4m/s + 9m/s = 13m/s因此，物体在3秒后的速度为13m/s。

静力学复习题1. 某平面任意力系向O 点简化，得到R ˊ=10N ，M 0=10 N·cm ，方向如图所示，求：该力系向A 点简化的结果。

2. 图示三铰刚架受力F 作用，求：A 、B 支座反力的大小。

3. 已知力P = 40 kN ，S =20kN ，物体与地面间的摩擦系数f = 0.5，动摩擦系数f ′= 0.4，求：物体所受的摩擦力。

4. 物块重W ，一外力F 作用在物块上，且作用线在摩擦角外，如图所示，已知ο25=θ，摩擦角ο20=m ϕ，F W =。

试确定物块的运动状态。

5. 力F 通过A （3，4，0），B （0，4，4）两点（长度单位为米），若F =100N ，求/；(1) 该力在y 轴上的投影；(2 )该力对z 轴的矩。

6. 已知力F 的大小，角度ϕ和θ，以及长方体的边长a ，b ，c ，求：（1）力F 在轴z 和y上的投影；（2）力F 对轴x 的矩)(F x m 。

7. 图示正立方体，各边长为a ，四个力1F 、2F 、3F 、4F 大小皆等于F ，如图所示，作用在相应的边上。

求：此力系简化的最终结果并在图中画出。

8. 等边三角形ABC.边长为a.己知四个力的大小相等，即F1=F2=F3=F4=F；力偶矩M=Fa, 则该力系简化的最后结果是什么？9. 图示结构，杆重不计.已知：L=4.5m. q0=3kN/m. P=6kN. M=4.5kNm.求固定端E处的反力.（作业二中4题）10 .图示结构，由杆AB、DE、BD组成，各杆自重不计，D、C、B均为铰链连接，A 端为固定端约束。

已知q（N/m），M=qa2（N·m），P=2qa（N），尺寸如图。

试列四个方程求固定端A的约束反力及BD杆所受的力。

（作业二中3题）11. .图示多跨梁由直杆AD和T字形杆DHG组成.已知：力P=2kN，q=0.5kN/m, M=4kNm，L=4m。

试列二个刚体静力学平衡方程求：支座H和支座C的反力。

工程力学——静力学部分习题 第一章 静力学公理与物体的受力分析一、判断题1．力是滑动矢量，可沿作用线移动。

（ ） 2．凡矢量都可用平行四边形法则合成。

（ ） 3．凡是在二力作用下的约束成为二力构件。

（ ） 4．两端用光滑铰链连接的构件是二力构件。

（ ） 5．凡是合力都比分力大。

（ ） 6．刚体的平衡条件是变形体平衡的必要条件，而非充分条件。

（ ） 7．若作用在刚体上的三个力的作用线汇交于一点，则该刚体必处于平衡状态。

（ ） 二、填空题1．作用力与反作用力大小 ，方向 ，作用在 。

2．作用在同一刚体上的两个力使刚体平衡的充要条件是这两个力 ， ， 。

3．在力的平行四边形中，合力位于 。

三、选择题1．在下述公理、法则、定理中，只适用于刚体的有（ ）。

A ．二力平衡公理B 力的平行四边形法则C ．加减平衡力系原理D 力的可传性E 作用与反作用定律2．图示受力分析中，G 是地球对物体A 的引力，T 是绳子受到的拉力，则作用力与反作用力指的是（ ）。

A T ′与GB T 与GC G 与G ′D T ′与G ′3．作用在一个刚体上的两个力F A 、F B ，若满足F A ＝－F B 的条件，则该二力可能是（ ）。

A 作用力与反作用力或一对平衡力 B 一对平衡力或一个力偶 C 一对平衡力或一个力或一个力偶 D 作用力与反作用力或一个力偶 四、作图题1．试画出下列各物体的受力图。

各接触处都是光滑的。

（a ） （b）2． 试画出图示系统中系统及各构件的受力图。

假设各接触处都是光滑的，图中未画出重力的构件其自重均不考虑。

（c ）ABPo30（d ）（f ）（e ）（a ）A BP 2P 1（b）第二章 平面汇交力系与平面力偶系一、判断题1. 两个力F 1、F 2在同一轴上的投影相等，则这两个力大小一定相等。

（ ）2. 两个力F 1、F 2大小相等，则它们在同一轴上的投影大小相同。

（ ）3. 力在某投影轴方向的分力总是与该力在该轴上的投影大小相同。

静力学试题及答案一、选择题1. 静力学中，力的平衡条件是什么？A. 力的大小相等B. 力的方向相反C. 力的大小相等，方向相反D. 力的大小和方向都相等答案：C2. 以下哪个不是静力学的基本概念？A. 力的合成B. 力的分解C. 力的平衡D. 力的守恒答案：D二、填空题1. 在静力学中，当一个物体处于________时，我们称其为平衡状态。

答案：静止或匀速直线运动2. 根据牛顿第一定律，物体在没有外力作用下，将保持________状态。

答案：静止或匀速直线运动三、简答题1. 简述牛顿第三定律的内容及其在静力学中的应用。

答案：牛顿第三定律指出，作用力和反作用力大小相等，方向相反，作用在两个不同的物体上。

在静力学中，这一定律用于分析物体间的相互作用，确保系统的力平衡。

2. 解释什么是静摩擦力，并说明其在物体保持静止状态时的作用。

答案：静摩擦力是阻止物体滑动的力，其大小与引起滑动的外力相等，但方向相反。

在物体保持静止状态时，静摩擦力与外力平衡，防止物体发生运动。

四、计算题1. 一个质量为10 kg的物体，受到水平方向上的两个力F1和F2的作用，F1 = 50 N，F2 = 30 N，求物体受到的合力。

答案：首先确定两个力的方向，如果F1和F2方向相反，则合力F = F1 - F2 = 50 N - 30 N = 20 N；如果F1和F2方向相同，则合力F = F1 + F2 = 50 N + 30 N = 80 N。

2. 一个斜面上的物体质量为20 kg，斜面与水平面的夹角为30°，求物体受到的重力分量在斜面方向上的分力。

答案：物体受到的重力G = m * g = 20 kg * 9.8 m/s² = 196 N。

在斜面方向上的分力 F = G * sin(θ) = 196 N * sin(30°) = 98 N。

五、分析题1. 一个均匀的直杆，长度为L，固定在水平面上的A点，B点自由悬挂，求直杆的平衡条件。

第一章 静力学例题：如图均匀带轴的直角弯杆，质量为m ，OA 段长度是AB 段长度的2倍，对杆施力F ，使杆静止在如图的位置，求F 的最小值 (在计算重力矩时，可分别计算OA 、AB 部分的重力矩。

)解： mgl l mg l F 322315+= 15F N = 例题：如图，半径为R 的匀质球体，内部挖去半径为R/2的球，求剩余部分重心的位置。

提示：设球的密度为ρ 挖去部分的质量 31432R m πρ⎛⎫= ⎪⎝⎭剩余部发的质量 33244332R m R πρπρ⎛⎫=- ⎪⎝⎭376R πρ= 则 124R m m x =（x 为m 2到球心间距） 3317266R R R x πρπρ= 14R x = 例题：一薄壁烧杯，半径为r ，质量为m ，重心位于中心线上，离杯底的距离为H ，今将水慢慢注入杯中，问烧杯连同杯内的水共同重心最低时，水面离杯底的距离等于多少？为什么？（设水的密度为ρ）解：当烧杯连同杯内的水共同重心在水面上时，就处于最低位置。

有 ()222h mgH g r hm g r h gh ρπρπ+=+ 22()2h mgH g r h mg g r h h ρπρπ+⋅⋅=+h = 例题：两个轻弹簧，劲度系数为k 1、k 2，按图所示连接，并在下面悬挂一重物G ，滑轮质量不计，把滑轮和两个弹簧等效一个弹簧，求等效弹簧的劲度系数。

解：设悬挂上重物G 后滑轮的位置比未悬挂重物G 时的位置下降了x ∆，而弹簧k 1和k 2分别伸长了1x ∆和2x ∆122x x x ∆+∆=∆而 1122k x k x ∆=∆滑轮受力平衡 1122k x k x G ∆+∆=等效弹簧的劲度系数 G k x =∆21214k k k k += 例题：如图所示，质量为m 的物体放在摩擦因数为µ的水平面上，对物体施加一和水平方向成θ的力F 的作用，要使物体运动，求力F 的大小范围？解：要使物体运动，应符合)sin (cos θμθF mg F +>mg F μθμθ>-)sin (cos若θμcot <，则θμθμsin cos ->mg F 若θμcot ≥，则用再大的力也推不动物体。

静力学竞赛习题详解1.图1—23所示的上大下小的杯中，盛有密度均匀的混合液体．其密度为ρ经过一段时间后变成密度分别为ρ1,ρ2的两层均匀液体．如果总体积不变，试讨论杯底所受液体的压强有何变化?[解]: 取以杯底为底面积的竖直水柱为研究对象,在均匀混合时,该体积内两种密度的液体各占一半.而分层后,由于密度较大的一半液体分布在杯子的底部,由于平均底面积较小,而体的总高度不变,2.底边为a θ当θ动或翻倒．试分别求出发生滑动和翻倒时的θ，并说明在什么条件下出现的是滑动情况，在什么条件下出现的是翻倒情况．[解]物体恰好沿斜面下滑的条件是:sin cos mg mg θμθ=即tan μθ=若物体不下滑而翻倒,此时重心的延长线恰好过物体的左下角如图解2-2所示.此时角θ满足tan a bθ=若a u b <, 当1tan θμ-= 时, 先开始滑动.若a u b>, 当1tan a b θ-=时,先翻倒.3．一物体质量为m ，置于倾角为的斜面上，物体与斜面间的动摩擦4.一轻绳跨过两个等高的轻定滑轮,两端分别挂上质量m l =4kg 和m 2=2kg 的物体,如图1-25所示.在滑轮之间的绳上悬挂物体m ,为使三个物体能图1-25保持平衡,求m 的取值范围． [解]:m 最大值:的夹角α接近因此1m m <+ m 的最小值m 的夹角近90由此解得: m 综合以上:5.质量为M =1多少?[解]当物体在斜面运动时,物体所受的力并不在同一平面内.在垂直斜面的平面内,物体的受力如解2-5-1所示.沿斜面平面内受力如解2-5-2所示.由图可知。

N =mg cos30°因为物体做匀速直线运动,所以在两个方向合力都为0，即有21sin F f mg f θ=⎧⎨=⎩f 1、f 2分别为物体所受摩擦力的两个分量。

f 2解2-5-2f =求得f =又由f N μ=可求得μ=6．如图1-27线的夹角为θ[解]可。

静力学考试题及答案一、选择题（每题2分，共20分）1. 静力学中，物体处于平衡状态的充要条件是（）。

A. 合力为零B. 合力矩为零C. 合力和合力矩都为零D. 合力和合力矩中至少有一个为零答案：C2. 以下哪个力不是保守力？（）。

A. 重力B. 弹簧力C. 摩擦力D. 静电力答案：C3. 一物体在水平面上受到一个斜向上的拉力F，下列关于物体受力的说法正确的是（）。

A. 物体受到的重力和支持力是一对平衡力B. 物体受到的拉力和摩擦力是一对平衡力C. 物体受到的重力和拉力是一对平衡力D. 物体受到的拉力和支持力是一对平衡力答案：A4. 一个质量为m的物体，受到一个大小为F的力作用，下列说法正确的是（）。

A. 物体的加速度一定为F/mB. 物体的加速度一定为0C. 物体的加速度可能为0D. 物体的加速度一定为F/m答案：C5. 一物体在水平面上受到一个大小为F的力作用，下列说法正确的是（）。

A. 物体的加速度一定为F/mB. 物体的加速度一定为0C. 物体的加速度可能为0D. 物体的加速度一定为F/m答案：C6. 一个质量为m的物体在水平面上受到一个大小为F的力作用，下列说法正确的是（）。

A. 物体受到的合力为FB. 物体受到的合力为0C. 物体受到的合力可能为0D. 物体受到的合力一定为F答案：C7. 一物体在水平面上受到一个大小为F的力作用，下列说法正确的是（）。

A. 物体受到的合力为FB. 物体受到的合力为0C. 物体受到的合力可能为0D. 物体受到的合力一定为F答案：C8. 一个质量为m的物体在水平面上受到一个大小为F的力作用，下列说法正确的是（）。

A. 物体受到的合力为FB. 物体受到的合力为0C. 物体受到的合力可能为0D. 物体受到的合力一定为F答案：C9. 一物体在水平面上受到一个大小为F的力作用，下列说法正确的是（）。

A. 物体受到的合力为FB. 物体受到的合力为0C. 物体受到的合力可能为0D. 物体受到的合力一定为F答案：C10. 一个质量为m的物体在水平面上受到一个大小为F的力作用，下列说法正确的是（）。

1、力系简化习题2、已知P 及长方体的边长a 、b 、c ，则力P 对AB 轴（AB 轴与长方体顶面的夹角为φ，且由A 指向B ）的力矩为 。

(sin Pa φ) `第3题图x yz AB'OO 'B 'C '1F 2F yz PABab cO第2题图φ3、如图所示正方体边长为a ，其上作用两个力1F ，2F 大小均为F ，则该力系的主矢量在OB '方向的投影为 ，力系对CA '轴之矩为 ，力系的最简形式为力螺旋，其中的力偶矩大小为 。

(答案：（1）6(0.8165)F F =；（2）0；（3）12Fa )4、如图所示，边长为a ，b ，c 的长方体，顶点A 和C 处分别作用有大小均为P 的力1F 和2F ，(1) 力2F 对AD 1轴的力矩大小为 22b c -+，(2) 力1F 和2F 所构成的力螺旋中的力偶矩矢大小为22b c -+，5、 桁架如图所示，已知力P 及尺寸ａ，求支座Ａ、B 、C 、D 处的约束反力a a aaa P AH I J K B CF G EDaBb c F 1F 2xyz C D1B 1C 1D 16、简单桁架ADKG 和BEKH 以铰K 和杆CD ，CE 相连构成组合桁架如图示。

则此桁架支座A 处的约束反力为 （5分）， B 处的约束反力为 （5分）。

（111 , 222Ax Bx By F F F F F F ==＝－；－）7、 均质杆AD 重量为G ，长为4m ，用一根短杆支撑，且处于平衡状态，如图所示。

若AC ＝BC ＝AB ＝3，且A 、B 、C 三处的摩擦角均为030，不计BC 杆的自重。

则AD 杆A 处的受力为 （3分）， AD 杆C 处的受力为 （3分）。

（2332, , 993C Ax Ay F G F G F G ===）8、在水平的桌子上放一个直径为a ，重为P 的内部绝对 光滑的均质圆筒，筒内放一根长2l ，重Q 的均质细杆。