基于遗传算法的PID整定原理及matlab仿真程序

控制理论与应用Control Theory and Applications《自动化技术与应用》2004年第23卷第7期用遗传算法实现PID 参数整定万佑红1,李新华2(1.南京邮电学院电子工程系,江苏　南京　210003; 2.安徽大学电子工程系,安徽　合肥　230001)摘要:PI D 参数整定一直是控制领域中的重要研究问题。

本文在M AT LAB 平台上将遗传算法应用于PI D 参数的自动整定,算法实例仿真取得了良好的效果,为PI D 参数整定方法提供了一种新的尝试。

关键词:PI D 参数;遗传算法中图分类号:TP27312　文献标识码:A 文章编号:100327241(2004)0720007202PID Tu nin g Bas e d O n Ge netic Alg orit h m sWAN You -hong 1,LI Xin -hua 2(1.E lectronics Department of Nanjing University of P osting T echnology ,Nanjing 210003,China ;2.E lectronics Department of AnHui University ,Hefei 230001,China )Abstract :A new method to s olve the tuning of PI D paramrters is proposed in this paper.I t is showed that g ood control effect can be obtained by usingG enetic Alg orithms (G A ).K ey w ords :PI D paramrters ;G A1　引言PI D 控制无需知道被控对象的数学模型,算法简单,鲁棒性好且可靠性高,因此成为一种获得广泛应用的控制策略。

基于MATLAB的PID控制器参数整定及仿真摘要: PID控制器结构和算法简单应用广泛，但参数整定方法复杂，通常用凑试法来确定。

文中探讨利用MATLAB实现PID参数整定及仿真的方法，并分析、比较比例控制、比例积分控制和比例微分控制，探讨了Kp, Ti, Td 3个参数对PID 控制规律的影响。

关镇词: MATLAB ; PID控制器;参数整定;仿真Parameter tuning and emulation of PID controller based on MATLAB Ahstratct; The control structure and algorithm of PID is easy and widely applicable，but its setting meth-ods of parameter are multifarious. Generally utilize guessing and trying to fix. This artical is convenient to tune PID parameters and emulate through MATLAB experiment. Analyze and compare the proportion control, the proportion integral control and the proportion differential control. Discuss the influence of three parameters KP ，Ti and Td to the PID control rules.Key words ; MATLAB;PID controller; parameter tuning; emulation引言PID控制器又称为PID调节器，是按偏差的比例P( Proportional )、积分I(Integxal)、微分D ( Differential orDerivative)进行控制的调节器的简称，它主要针对控制对象来进行参数调节。

PID控制是工业过程控制中应用最广的策略之一，因此PID控制器参数的优化成为人们关注的问题，它直接影响控制效果的好坏，并和系统的安全、经济运行有着密不可分的关系。

目前PID参数的优化方法有很多，如间接寻优法、梯度法、爬山法等，而在热工系统中单纯形法专家整定法则应用较广。

虽然这些方法都具有良好的寻优特性，但存在着一些弊端，单纯形法对初值比较敏感，容易陷入局部最优化解，造成寻优失败。

专家整定法则需要太多的经验，不同的目标函数对应不同的经验，而整理知识库则是一项长时间的工程。

因此我们选取了遗传算法来进行参数寻优，该方法是一种不需要任何初始信息并可以寻求全局最优解的、高效的优化组合方法。

采用遗传算法进行PID三个系数的整定，具有以下优点：（1）与单纯形法相比，遗传算法同样具有良好的寻优特性，且克服了单纯形法参数初值的敏感性。

在初始条件选择不当的情况下，遗传算法在不需要给出调节器初始参数的情况下，仍能寻找到合适的参数，使控制目标满足要求。

同时单纯形法难以解决多值函数问题以及在多参数寻优（串级系统）中，容易造成寻优失败或时间过长，而遗传算法的特性决定了它能很好地客服以上问题。

（2）与专家整定相比，它具有操作方便、速度快的优点，不需要复杂的规则，只通过字串进行简单地复制、交叉、变异，便可达到寻优。

避免了专家整定法中前期大量的知识库整理工作及大量的仿真实验。

（3）遗传算法是从许多点开始并行操作，在解空间进行高效启发式搜索，克服了从单点出发的弊端及搜索的盲目性，从而使寻优速度更快，避免了过早陷入局部最优解。

（4）遗传算法不仅适用于单目标寻优，而且也适用于多目标寻优，根据不同的控制系统，针对一个或多个目标，遗传算法均能在规定的范围内寻找到合适参数。

遗传算法作为一种全局优化算法，得到越来越广泛的应用。

近年来，遗传算法在控制上的应用日益增多。

二、基于遗传算法的PID整定原理1、参数的确定及表示首先确定参数范围，该范围一般是由用户给定，然后由精度的要求，对其进行编码。

控制系统PID参数整定方法的MATLAB仿真1. 引言PID控制器是一种常见的控制算法，广泛应用于自动控制系统中。

其通过调节三个参数：比例增益（Proportional gain）、积分时间常数（Integral time constant）和微分时间常数（Derivative time constant），实现对被控对象的稳态误差、响应速度和稳定性等性能指标的调节。

PID参数的合理选择对控制系统的性能至关重要。

本文将介绍PID控制器的经典整定方法，并通过MATLAB软件进行仿真，验证整定方法的有效性。

2. PID控制器的整定方法2.1 手动整定法手动整定法是根据经验和试错法来选择PID参数的方法。

具体步骤如下：1.将积分时间常数和微分时间常数设为零，仅保留比例增益，将比例增益逐渐增大直至系统产生较大的超调现象。

2.根据超调响应的情况，调整比例增益，以使系统的超调量接近所需的范围。

3.逐步增加微分时间常数，观察系统的响应速度和稳定性。

4.增加积分时间常数，以减小系统的稳态误差。

手动整定法的优点是简单易行，但需要经验和反复试验，对控制系统要求较高。

2.2 Ziegler-Nichols整定法Ziegler-Nichols整定法是一种基于试探和试错法的自整定方法，该方法通过调整系统的输入信号，观察系统的输出响应，从而确定PID参数。

具体步骤如下：1.将I和D参数设为零，仅保留P参数。

2.逐步增大P参数，直到系统的输出出现大幅度的振荡。

3.记录下此时的P参数值，记为Ku。

4.根据振荡的周期Tp，计算出系统的临界增益Kc = 0.6 * Ku。

5.根据系统的类型选择相应的整定法则：–P型系统：Kp = 0.5 * Kc，Ti = ∞，Td = 0–PI型系统：Kp = 0.45 * Kc，Ti = Tp / 1.2，Td = 0–PID型系统：Kp = 0.6 * Kc，Ti = Tp / 2，Td = Tp / 82.3 Cohen-Coon整定法Cohen-Coon整定法是基于频域曲线拟合的方法，主要应用于一阶和二阶系统的整定。

引言PID操纵器结构简单且鲁棒性强，在操纵领域一直被普遍应用。

运算机的进展为在线辩识提供了条件，从而也为在线整定PID参数提供了可能。

PID操纵是工业进程中应用最普遍的策略之一，因此PID 操纵器参数的优化成为人们关注的问题，它直接阻碍操纵成效的好坏，并和系统的平安、经济运行有着密不可分的关系。

目前PID参数的优化方式很多，如：间接寻优法，梯度法，登山法等，而在热工系统中单纯形法、专家整定法那么应用普遍。

尽管二者都具有良好的寻优特性，但却存在一些短处，单纯刑法对初值比较灵敏，容易陷入局部最优解，造成寻优失败。

专家整定法那么需要太多体会，不同的目标函数对应不同的体会，而整理知识库是一项长时刻的工程。

因此咱们选取遗传算法来进行参数寻优，该方式是一种不需要任何初始信息并能够寻求全局最优解的高效的优化组合方式。

第一章：遗传算法和PID操纵原理简介一遗传算法简介大体原理遗传算法是依照生物进化的模型提出的一种优化算法。

遗传算法是从代表问题可能潜在解集的一个群组（popuation）开始的，而一个种群那么由通过基因（gene）编码（coding）的必然数量的个体（individual）组成。

每一个个体事实上是染色体（chromosome）带有特点的实体。

染色体作为遗传物质的要紧载体，即多个基因组合，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现。

因此，在一开始需要实现从表现型到基因型的映射即编码工作。

由于仿照基因编码的工作很复杂，咱们往往进行简化，如二进制编码。

初代种群产生以后，依照适者生存和优胜劣汰的原理，逐代（genetation）演化产生出愈来愈好的近似解。

在每一代，依照问题域中个体的适应度（fitness）大小挑选（selection）个体，并借助于自然遗传学的遗传算子（genetic operator）进行组合交叉.（crossover）和变异（mutation）,产生出代表新的解集的种群。

%GA(Generic Algorithm) Program to optimize PID Parameters clear all;close all;global rin yout timefSize=30;CodeL=3;MinX(1)=zeros(1);MaxX(1)=20*ones(1);MinX(2)=zeros(1);MaxX(2)=*ones(1);MinX(3)=zeros(1);MaxX(3)=*ones(1);Kpid(:,1)=MinX(1)+(MaxX(1)-MinX(1))*rand(Size,1);Kpid(:,2)=MinX(2)+(MaxX(2)-MinX(2))*rand(Size,1);Kpid(:,3)=MinX(3)+(MaxX(3)-MinX(3))*rand(Size,1);G=100;BsJ=0;%*************** Start Running ***************for kg=1:1:Gtime(kg)=kg;%****** Step 1 : Evaluate BestJ ******for i=1:1:SizeKpidi=Kpid(i,:);[Kpidi,BsJ]=chap5_2f(Kpidi,BsJ);BsJi(i)=BsJ;end[OderJi,IndexJi]=sort(BsJi);BestJ(kg)=OderJi(1);BJ=BestJ(kg);Ji=BsJi+1e-10; %Avoiding deviding zerofi=1./Ji;% Cm=max(Ji);% fi=Cm-Ji;[Oderfi,Indexfi]=sort(fi); %Arranging fi small to biggerBestfi=Oderfi(Size); %Let Bestfi=max(fi)BestS=Kpid(Indexfi(Size),:); %Let BestS=E(m), m is the Indexfi belong to max(fi)kgBJBestS%****** Step 2 : Select and Reproduct Operation******fi_sum=sum(fi);fi_Size=(Oderfi/fi_sum)*Size;fi_S=floor(fi_Size); % Selecting Bigger fi valuer=Size-sum(fi_S);Rest=fi_Size-fi_S;[RestValue,Index]=sort(Rest);for i=Size:-1:Size-r+1fi_S(Index(i))=fi_S(Index(i))+1; % Adding rest to equal Sizeendk=1;for i=Size:-1:1 % Select the Sizeth and Reproduce firstlyfor j=1:1:fi_S(i)TempE(k,:)=Kpid(Indexfi(i),:); % Select and Reproducek=k+1; % k is used to reproduceendend%************ Step 3 : Crossover Operation ************Pc=;for i=1:2:(Size-1)temp=rand;if Pc>temp %Crossover Conditionalfa=rand;TempE(i,:)=alfa*Kpid(i+1,:)+(1-alfa)*Kpid(i,:);TempE(i+1,:)=alfa*Kpid(i,:)+(1-alfa)*Kpid(i+1,:);endendTempE(Size,:)=BestS;Kpid=TempE;%************ Step 4: Mutation Operation ************** Pm=[1:1:Size]*/Size; %Bigger fi,smaller PmPm_rand=rand(Size,CodeL);Mean=(MaxX + MinX)/2;Dif=(MaxX-MinX);for i=1:1:Sizefor j=1:1:CodeLif Pm(i)>Pm_rand(i,j) %Mutation Condition TempE(i,j)=Mean(j)+Dif(j)*;endendend%Guarantee TempE(Size,:) belong to the best individualTempE(Size,:)=BestS;Kpid=TempE;endBestfiBestSBest_J=BestJ(G)figure(1);plot(time,BestJ);xlabel(’Times’);ylabel(’Best J’);figure(2);plot(timef,rin,’r’,timef,yout,’b’);xlabel(’Time(s)’);ylabel(’rin,yout’);子程序：function [Kpidi,BsJ]=pid_gaf(Kpidi,BsJ)global rin yout timefts=;sys=tf(400,[1,50,0]);dsys=c2d(sys,ts,’z’);[num,den]=tfdata(dsys,’v’);rin=;u_1=;u_2=;y_1=;y_2=;x=[0,0,0]’;B=0;error_1=0;tu=1;s=0;P=100;for k=1:1:Ptimef(k)=k*ts;r(k)=rin;u(k)=Kpidi(1)*x(1)+Kpidi(2)*x(2)+Kpidi(3)*x(3);if u(k)>=10u(k)=10;endif u(k)<=-10u(k)=-10;endyout(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2; error(k)=r(k)-yout(k);%------------ Return of PID parameters -------------u_2=u_1;u_1=u(k);y_2=y_1;y_1=yout(k);x(1)=error(k); % Calculating Px(2)=(error(k)-error_1)/ts; % Calculating Dx(3)=x(3)+error(k)*ts; % Calculating Ierror_2=error_1;error_1=error(k);if s==0if yout(k)>&yout(k)<tu=timef(k);s=1;endendendfor i=1:1:PJi(i)=*abs(error(i))+*u(i)^2*; B=B+Ji(i);if i>1erry(i)=yout(i)-yout(i-1);if erry(i)<0B=B+100*abs(erry(i));endendendBsJ=B+*tu*10;。

2010届毕业生毕业论文题目: 基于遗传算法整定的PID控制院系名称：信息科学与工程学院专业班级：电子信息科学与技术学生姓名：学号：指导教师：教师职称：讲师2010年 6 月 2 日摘要PID控制器是在工业过程控制中常见的一种控制器，因此，PID参数整定与优化一直是自动控制领域研究的重要问题。

遗传算法是一种具有极高鲁棒性的全局优化方法，在自控领域得到广泛的应用。

针对传统PID参数整定的困难性，本文提出了把遗传算法运用于PID参数整定中。

本文首先对PID控制的原理和PID参数整定的方法做了简要的介绍。

其次介绍了遗传算法的原理、特点和应用。

再次，本文结合实例阐述了基于遗传算法的PID参数优化方法，采用误差绝对值时间积分性能指标作为参数选择的最小目标函数,利用遗传算法的全局搜索能力,使得在无须先验知识的情况下实现对全局最优解的寻优,以降低PID参数整定的难度,达到总体上提高系统的控制精度和鲁棒性的目的。

最后，本文针对遗传算法收敛速度慢、易早熟等缺点，将传统的赌盘选择法与最优保存策略结合起来，并采用改进的自适应交叉算子和自适应变异算子对PID参数进行迭代寻优整定。

采用MATLAB对上述算法进行仿真验证，仿真结果表明了遗传算法对PID 参数整定的有效性。

关键词：PID；参数控制；遗传算法；MATLABTitle Tuning of PID Parameters Based on Genetic AlgorithmAbstractPID controller is a kind of controller that is usual in industrial process control. Therefore, tuning and optimization of PID parameters are important researchable problems in the automatic control field, where Genetic algorithm is widely used because of the highly robust global optimization ability of it. Aiming at the difficulty of traditional tuning of PID parameter, this paper puts forward a method that genetic algorithm is applied to the tuning of PID parameters.Firstly, the principle of PID control and the methods of tuning of PID parameters are introduced briefly. Secondly, this paper introduces the principle, characteristics and application of genetic algorithm. Thirdly, this article expounds on the methods of tuning of PID parameters based on genetic algorithm with an example. In this paper, the performance index of time integral of absolute error serves as the minimum objective function in the tuning of PID parameters, and the global search ability of genetic algorithm is used, so the global optimal solution is obtained without prior knowledge, and the difficulty of tuning of PID parameter is reduced, so the goal is achieved which is improving the control accuracy and robustness of the system overall. Finally, aiming at the weakness of genetic algorithm, such as the slow convergence of prematurity and precocious, the traditional gambling site selection method and elitist model are united in this paper, and the paper also adopted adaptive crossover operator and adaptive mutation operator to optimize PID parameters iteratively.Use MATLAB to simulate these algorithms, and the simulation results show that PID controller tuning based on genetic algorithm is effective.Keywords: Genetic algorithm; PID control; optimum; MATLAB目次1 引言 (1)1.1 PID控制的发展与现状 (1)1.2 遗传算法的发展与现状 (1)1.3 课题研究背景和意义 (3)1.4 本文主要工作 (3)2 PID控制 (5)2.1 PID控制原理 (5)2.2 PID参数整定 (7)3 遗传算法 (9)3.1 遗传算法基本原理 (9)3.1.1 遗传算法概要 (9)3.1.2 遗传算法的应用步骤 (10)3.2 遗传算法的实现 (11)3.2.1 编码方法 (11)3.2.2 适应度函数 (12)3.2.3 选择算子 (12)3.2.4 交叉算子 (13)3.2.5 变异算子 (14)3.2.6 遗传算法控制参数选取 (14)3.3 遗传算法的仿真验证 (15)4 基于遗传算法的PID参数优化 (18)4.1 总体实现 (18)4.2 具体实现 (19)4.2.1 参数的确定及表示 (19)4.2.2 选取初始种群 (19)4.2.3 适应度函数的确定 (19)4.2.4 选择部分实现 (20)4.2.5 交叉部分实现 (20)4.2.6 变异部分实现 (21)4.3 编译及仿真 (22)4.3.1 编译环境选择 (22)4.3.2 仿真验证及结果分析 (22)5 基于改进遗传算法的PID参数优化 (24)5.1 遗传算法的改进 (24)5.1.1 选择算子的改进 (24)5.1.2 交叉与变异算子的改进 (24)5.2 仿真验证及结果分析 (25)结论 (26)致谢 (27)参考文献 (28)1 引言1.1 PID控制的发展与现状PID控制技术的发展可以分为两个阶段。

一、引言中央空调系统在现代建筑中扮演着至关重要的角色，对空调系统的控制效率和性能要求也越来越高。

PID控制器作为一种经典的控制算法，被广泛应用于中央空调系统中。

而遗传算法作为一种全局搜索和优化的方法，具有一定的优势和应用前景。

MATLAB作为一个功能强大的模拟工具，提供了丰富的工具箱和函数，可以用于模拟和优化中央空调系统的PID控制器参数。

二、MATLAB模拟中央空调PID控制器1. 使用MATLAB进行中央空调系统建模在MATLAB环境中，可以利用Simulink工具箱进行中央空调系统的建模。

建立空调系统的传递函数模型，包括室内外温度传感器、风机、制冷剂循环等部件，以及控制器的输入输出。

这一步可以帮助工程师理解系统的动态特性，并为下一步的控制器设计做准备。

2. 设计PID控制器在MATLAB中，可以利用Control System Toolbox设计PID控制器。

根据已建立的系统模型，利用PID Tuner或者手动调节的方式，得到合适的比例、积分和微分系数，使得系统能够快速、稳定地响应温度变化。

3. 仿真系统响应利用Simulink工具箱对设计的PID控制器进行仿真，观察系统的响应特性。

可以通过改变温度变化输入信号，观察系统的温度响应、控制器输出等参数，并评估PID控制器性能的优劣。

三、遗传算法在PID参数优化中的应用1. 遗传算法原理及优化遗传算法是一种模拟生物进化过程的优化方法，其基本思想是通过种群的选择、交叉和变异等操作，实现对问题的全局搜索和优化。

在PID参数优化中，可以利用遗传算法搜索合适的控制器参数，使得系统的性能指标达到最优。

2. MATLAB中的遗传算法工具MATLAB提供了遗传算法工具箱，可以方便地使用遗传算法对问题进行优化。

用户可以自定义适应度函数、遗传算子等参数，也可以选择内置的优化函数进行快速优化。

3. 将遗传算法与PID控制器相结合通过将遗传算法与PID控制器相结合，可以实现对PID参数的优化。

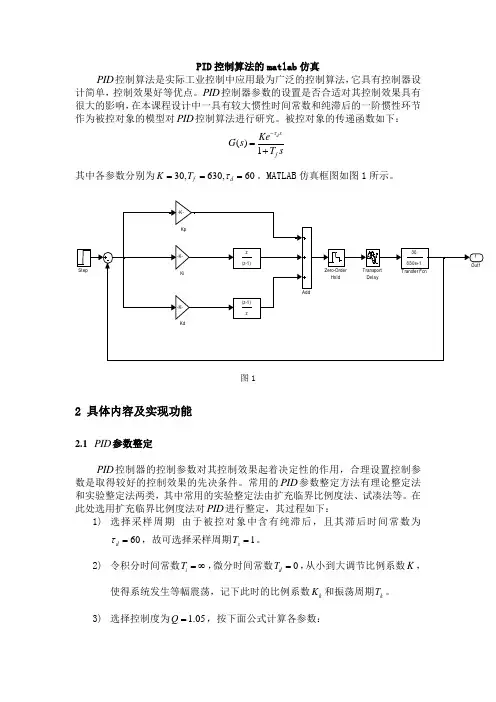
PID 控制算法的matlab 仿真PID 控制算法是实际工业控制中应用最为广泛的控制算法，它具有控制器设计简单，控制效果好等优点。

PID 控制器参数的设置是否合适对其控制效果具有很大的影响，在本课程设计中一具有较大惯性时间常数和纯滞后的一阶惯性环节作为被控对象的模型对PID 控制算法进行研究。

被控对象的传递函数如下：()1d sf Ke G s T sτ-=+ 其中各参数分别为30,630,60f d K T τ===。

MATLAB 仿真框图如图1所示。

1Out1Zero-Order HoldTransport Delay30630s+1Transfer FcnStep-K-Kp-K-Ki-K-Kdz (z-1)(z-1)zAdd图12 具体内容及实现功能2.1 PID 参数整定PID 控制器的控制参数对其控制效果起着决定性的作用，合理设置控制参数是取得较好的控制效果的先决条件。

常用的PID 参数整定方法有理论整定法和实验整定法两类，其中常用的实验整定法由扩充临界比例度法、试凑法等。

在此处选用扩充临界比例度法对PID 进行整定，其过程如下：1) 选择采样周期 由于被控对象中含有纯滞后，且其滞后时间常数为60d τ=，故可选择采样周期1s T =。

2) 令积分时间常数i T =∞，微分时间常数0d T =，从小到大调节比例系数K ，使得系统发生等幅震荡，记下此时的比例系数k K 和振荡周期k T 。

3) 选择控制度为 1.05Q =，按下面公式计算各参数：0.630.490.140.014p k i k d k s kK K T T T T T T ====通过仿真可得在1s T =时，0.567,233k k K T ==，故可得：0.357,114.17,32.62, 3.262p i d s K T T T ====0.0053.57p s i i p d d sK T K T K T K T ====按此组控制参数得到的系统阶跃响应曲线如图2所示。