4.2核外电子运动状态的描述
- 格式:ppt
- 大小:2.28 MB
- 文档页数:144



原子核外电子的空间运动状态原子核外电子的空间运动状态:(一)电子轨道1、电子轨道是电子沿着原子核外围运动的一条椭圆形轨迹。
这条椭圆形轨迹完全由电子和核间的电磁场相互作用决定。
2、电子轨道的轨道角动量是指电子在原子核外围空间运动的时候的角动量,它可以通过电磁场的膜位能准确的确定出来。
3、电子轨道的运动状态就是指电子在轨道中的运动状态,包括了单重态的电子轨道运动状态,以及双重态的电子轨道运动状态和三重态的电子轨道运动状态等。
(二)电子自旋1、电子自旋是电子在空间中自身运动的一个特征,通俗来说就是电子在原子核外围空间中以固定的角速度运动。
2、电子自旋具有两个独立的特性,即电子的线性自旋,也就是说电子的运动方向不断变化;另一个就是电子的角速度自旋,也就是说电子的具体自旋方向会一直保持不变。
3、自旋的结构包括两个自旋态,一个是有磁态,即自由自旋,它没有内部能量变化;对应的还有无磁态,即锁定自旋,它有内部能量变化。
(三)电子跃迁1、电子跃迁是指电子在原子核外围空间中运动时从一个轨道状态跃到另一个空间状态的过程,电子跃迁中包括了单重态电子跃迁,双重态电子跃迁和三重态电子跃迁等等。
2、电子跃迁的机理一般是由电磁场的膜位能决定的,这也是电子跃迁过程发生的根本原因。
电子跃迁过程中,电子原先处在的低能量状态会被电磁场膜位能引导,由低能量跃到其他的高能量状态之中。
3、电子跃迁过程还会受到外界的干扰,包括光辐射,热辐射等,外界的干扰可以使原子中电子从一个轨道跃到另一个轨道或空间状态,从而使原子转变为激发态,从而发生一系列使原子性质发生变化的现象。
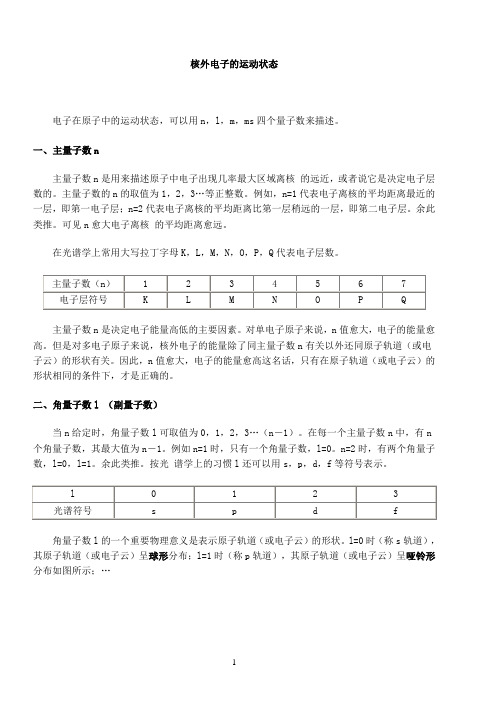
核外电子的运动状态电子在原子中的运动状态,可以用n,l,m,ms四个量子数来描述。
一、主量子数n主量子数n是用来描述原子中电子出现几率最大区域离核的远近,或者说它是决定电子层数的。
主量子数的n的取值为1,2,3…等正整数。
例如,n=1代表电子离核的平均距离最近的一层,即第一电子层;n=2代表电子离核的平均距离比第一层稍远的一层,即第二电子层。
余此类推。
可见n愈大电子离核的平均距离愈远。
在光谱学上常用大写拉丁字母K,L,M,N,O,P,Q代表电子层数。
主量子数n是决定电子能量高低的主要因素。
对单电子原子来说,n值愈大,电子的能量愈高。
但是对多电子原子来说,核外电子的能量除了同主量子数n有关以外还同原子轨道(或电子云)的形状有关。
因此,n值愈大,电子的能量愈高这名话,只有在原子轨道(或电子云)的形状相同的条件下,才是正确的。
二、角量子数l (副量子数)当n给定时,角量子数l可取值为0,1,2,3…(n-1)。
在每一个主量子数n中,有n 个角量子数,其最大值为n-1。
例如n=1时,只有一个角量子数,l=0。
n=2时,有两个角量子数,l=0,l=1。
余此类推。
按光谱学上的习惯l还可以用s,p,d,f等符号表示。
角量子数l的一个重要物理意义是表示原子轨道(或电子云)的形状。
l=0时(称s轨道),其原子轨道(或电子云)呈球形分布;l=1时(称p轨道),其原子轨道(或电子云)呈哑铃形分布如图所示;…s电子云p电子云角量子数l的另一个物理意义是表示同一电子层中具有不同状态的亚层。
例如,n=3时,l可取值为0,1,2。
即在第三层电子层上有三个亚层,分别为 s,p,d亚层。
为了区别不同电子层上的亚层,在亚层符号前面冠以电子层数。
例如,2s是第二电子层上的亚层,3p是第三电子层上的p亚层。
表4-1列出了主量子数n,角量子数l及相应电子层、亚层之间的关系。
表中为主量子数n,角量子数l及其相应电子层亚层之间的关系前已述及,对于单电子体系的氢原子来说,各种状态的电子能量只与n有关。

核外电子运动状态的描述2-2 核外电子运动状态的描述一、波函数和原子轨道1.波动方程描述宏观物体运动状态的状态方程F=ma,即牛顿第二定律。
那么对微观粒子的运动,能不能也有个状态方程呢?1926年,奥地利物理学家薛定谔根据德布罗依预言,提出了描述微观粒子运动状态的波动方程,称为薛定谔方程其基本形式是:这是个高等数学中的二阶偏微分方程,式中x、y、z为粒子在空间的直角坐标,m可近似看作是电子质量,E为总能量即电子的动能和势能之和,V是势能即核与电子的吸引能,ψ为方程的解(ψ是希腊字母,读做普赛[Psi])。
薛定谔方程是用来描述质量为m的微观粒子,在势能为V的势场中运动,其运动状态和能量关系的定态方程。
因为薛定谔方程的每一合理的解ψ,都表示该粒子运动的某一稳定状态,与这个解相应的常数E,就是粒子处于这个稳定状态的能量。
由于有很多解,说明具有多种运动状态。
对于一定体系,能量最低的状态称为基态,能量较高的状态称为激发态。
粒子由一个状态跃迁到另一状态,能量的改变量是一定的,不能取任意的数值,即能量是量子化的由于薛定谔方程是高等数学中一个微分方程,与初等数学中方程不同,它的解ψ不是一些数而是些函数。
它是波的振幅与坐标的函数,因此称作波函数。
2.波函数(ψ)如上所述,波函数ψ就是薛定谔方程的解,是描述核外电子空间运动状态的数学函数式。
如同一般函数式有常量和变量一样,它包含三个常量和三个变量,它的一般形式为式中n、l、m为三个常量,x、y、z为三个变量。
电子在核外运动,有一系列空间运动状态。
每一特定状态就有一个相应的波函数ψ和相应的能量E。
如有1s、2s、2p、3d、4f……等等核外空间状态,就有ψ1s、ψ2s、ψ2p、ψ3d、ψ4f……和E1s、E2s、E2p、E3d、E4f……与其相对应。
或者说一个确定的波函数ψ就代表着核外电子的一个空间运动状态,电子处于这个空间状态运动时就具有确定的能量和其它一些相应的物理量。