方向导数讲解
- 格式:pdf
- 大小:2.14 MB
- 文档页数:16



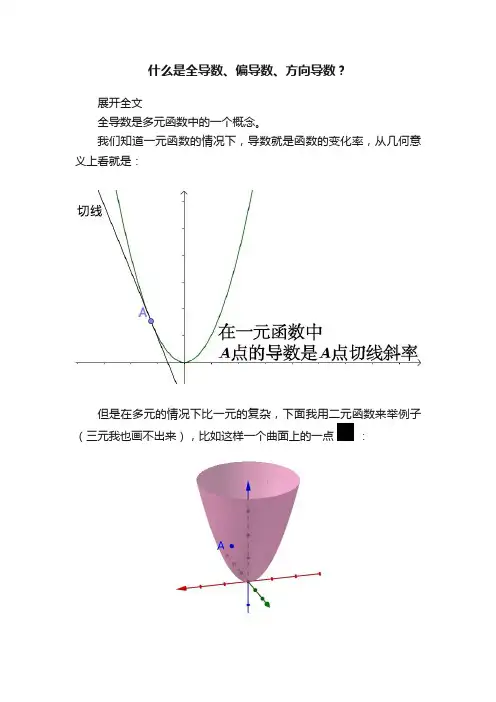
什么是全导数、偏导数、方向导数?展开全文全导数是多元函数中的一个概念。
我们知道一元函数的情况下,导数就是函数的变化率,从几何意义上看就是:但是在多元的情况下比一元的复杂,下面我用二元函数来举例子(三元我也画不出来),比如这样一个曲面上的一点:在曲面上可以做无数条过点的曲线(图上随便画了三根):每根曲线都可能可以(也有作不出来的情况,你想想一元的时候也有作不出切线的情况)作一根切线,比如(随便挑了一根切线来画,都画出来太乱了):全导数的意义:每一根切线都和一个全导数“相关”,点有无数个全导数。
最精简的回答已经完了,后面我就要讲一些细节了,主要阐述下面两个细节:•方向导数、偏导数是特殊的全导数•每一根切线都和一个全导数“相关”,这个“相关”是什么意思?难道不就是切线的斜率就是全导数吗?顺便说一下,如果所有这些切线共面的话,那么这个平面就是切平面(全微分),可以参考我之前的回答如何直观理解全微分?。
1 参数方程为了继续讲下去,我们需要了解下所需要的技术手段:参数方程。
参数方程的用处很多,下面讲解下我们需要了解的部分。
1.1 通过参数方程来描述所有的曲线要描述所有这些曲线,我们就需要一些数学手段,这就是参数方程。
我们来看一下,随便画一条过点的曲线:这条曲线也是一个关于的函数,因此它与平面上的曲线具有一一对应的关系:因此我们只需要描述上的曲线就可以达到描述曲面的曲线的目的,这时候就很自然的可以使用参数方程了。
举个具体的例子,对于这个二元函数,函数图像是这样的:注意此时的都可以自由改变:但是如果增加参数方程:这有什么意义?此时的的变化就受到的约束:我们来把这根参数方程决定的直线放到三维空间去:根据之前的描述,这根直线可以决定一根曲面上的曲线:这根曲面上的曲线就是刚才说过的:1.2 参数方程可以拍扁三维图像从另外一个角度看,参数方程可以把三维的图像一巴掌拍扁:什么意思,我们来看看,还是这个二元函数:增加参数方程约束:把代入到里面去,可以得到:这就好比把空间的立体图形拍扁到了平面,这个特性在后面会用到,所以在这里先预热下。

第八章第七节方向导数与梯度,PlϕP lαT lz =f (x ,y )•Mρ本质上,方向导数计算可归结为一元函数导数计算14 1414)e ()()e (i i f i if l l r rr rr −=−∂∂=∂∂存在,且时,当i l r r =e ;x f i f ∂∂=∂∂时,当i l r r −=e .)(xf i f ∂∂−=−∂∂)e ()()e (i i fi ifl l r r r r −=−∂∂=∂∂存在可微可偏导沿任意方向的方向导数存在处沿任意方向在)0,0(),(22y x y x f +==均不存在,)0,0()0,0(),(在从而y x f 1oα=5π/4的方向导数达沿梯度相反方向,∂f ∂l取得最小值: min (∂f ) = l ∂l− gradf (x, y)≤0f ( x, y)减小最快 .方向:是函数值增加最快的方向 grad f :模 : 等于函数的方向导数最大值2º 梯度的概念可以推广到三元函数 u = f ( x, y, z)grad f (x, y,z) = { ∂f , ∂f , ∂f } ∂x ∂y ∂z类似于二元函数,三元函数的梯度也有上述性质.例5 求函数 u = ln( x2 + y2 + z2 ) 在点 M (1,2, −2)处的梯度。
解grad uM= ⎜⎛ ⎝∂u, ∂u, ∂u ∂x ∂y ∂z⎟⎞ ⎠(1,2,−2)令r=x2 +y2 + z2,则∂u = ∂x1 r2⋅ 2x注意 x , y , z 具有轮换对称性= ⎜⎛ ⎝2 rx2,2 ry2,2z r2⎟⎞ ⎠ (1,2,−2)= 2 (1, 2, − 2) 93. 梯度的几何意义(1) 等高线z对函数 z = f ( x, y),曲线⎧ ⎨ ⎩z z= =f c(x,y)xoyL*在xOy面上的投影 L* : f ( x, y) = c称为函数 z = f (x, y)的等高(值)线 .z z =2−(x2+y2)z =c2ygrad f ( x, y)o xz =c1yf (x, y) =c1 f (x, y) =c2o x(c1 < c2 )(2) 等高线 f (x, y) = c 的法向量等高线 L∗:f ( x, y) = c⎩⎨⎧x y= =x y(x)L∗在点 P ( x, y)处的切向量:r T={1,d y } = {1, −fx }dxfy=1 fy{fy,−fx}( fy ≠ 0)L∗在点 P ( x , y )处的法向量:nr = ± { f x , f y }(nr ⋅r T=0)(3) 等高线上的法向量与梯度的关系L∗在点 P ( x, y)处的法向量为 nr, 则① nr // grad f ( x, y)②∂f=gradf ( x, y) cos(gradf(x,y)∧,nr)∂n = ± grad f ( x, y)= 0或π当 nr 与 grad f ( x, y)同方向时,∂f ∂n=gradf(x,y)=maxl∂f ∂l当 nr 与 grad f ( x, y )同方向时,∂f = ∂ngradf(x,y)=maxl∂f ∂l≥0沿梯度方向, f ( x, y)的值增加最快.故 z = f (x, y) 在点 P( x, y )的梯度恰为等高线 f (x, y) = c 在这点的一个法向量,其指向为:从数值较低的等高线到数值较高的等高线,而梯度的模等于函数沿这个法线方向的方向导数.梯度为等高线上yf ( x, y) = c2 grad f ( x, y) 的一个法向量,P其指向为:从数值较低的等高线f ( x, y) = c1到数值较高的等ox高线.(c1 < c2 )f (x, y) = c等高线同样, 对应三元函数 u = f ( x, y, z), 有等值面(等量面)f (x, y,z) = c, 当各偏导数不同时为零时, 等值面上 点P处的法向量为 grad f P . 函数在一点的梯度垂直于该点等值面,指向函数 增大的方向.类似地,设曲面c z y x f =),,(为函数),,(z y x f u = 的等量面,此函数在点),,(z y x P 的梯度的方向与 过点P 的等量面c z y x f =),,(在这点的法线的一 个方向相同,且从数值较低的等量面指向数值较 高的等量面,而梯度的模等于函数沿这个法线方 向的方向导数.4. 梯度的基本运算公式grad (1)r=C u C u C grad )(grad (2)=v u v u grad grad )(grad (3)±=±u v v u v u grad grad )(grad (4)+=uu f u f grad )()(grad (5)′=5. 梯度的应用梯度的应用非常广泛,如:(1) 计算方法中求解非线性方程组的最速下降法;(2) 在热力学中,引出热流向量:U k q grad −=r(其中U (P )为温度函数)表示物体中各点处热流动的方向和强度;(3) 在电磁场学中的电位u 与电场强度有关系:E ruE grad −=r这说明场强:垂直于等位面,且指向电位减少的方向.),z y 沿方向l (γzfβcos cos ∂∂+)沿方向l (方向角为可微时方可用。


方向导数,梯度方向导数和梯度是数学中两个重要的概念,它们在各个领域都有着广泛应用。
本文将对这两个概念进行介绍和解释。
方向导数是向量值函数在某一点沿着某一方向的导数。
简单来说,方向导数描述了函数在某一点上沿着某一方向变化的速率。
在三维空间中,方向导数可以用以下公式进行表示:$$D_{\vec{u}}f=\lim_{h\to0}\frac{f(\vec{P}+h\vec{u})-f(\vec{P})}{h}$$其中,$\vec{P}$表示函数在某一点的位置,$\vec{u}$表示某一方向,$f(\vec{P}+h\vec{u})$表示函数在点$\vec{P}+h\vec{u}$处的取值。
方向导数可以看作是梯度沿着某一方向的投影,可以用以下公式计算:方向导数在物理学、工程学、经济学等各个领域都有着广泛应用。
例如,在物理学中,方向导数可以用来描述电场、热场等物理量的变化规律。
二、梯度$$\nabla f=\frac{\partial f}{\partial x}\vec{i}+\frac{\partial f}{\partial y}\vec{j}+\frac{\partial f}{\partial z}\vec{k}$$其中,$\vec{i}$、$\vec{j}$、$\vec{k}$分别表示$x$、$y$、$z$方向的单位向量。
梯度向量的模长表示函数在该点上的变化率最大值,方向与梯度向量相同的方向是函数在该点上变化率最快的方向。
在物理学、计算机图形学、优化等领域中,梯度都有着广泛的应用。
例如,在计算机图形学中,梯度可以用来计算图像的边缘和纹理,从而实现图像的特征提取和识别。
总结:方向导数和梯度都是向量值函数中非常重要的概念。
方向导数描述了函数沿着某一方向变化的快慢,可以用来描述物理量的变化规律;梯度表示函数变化最快的方向和速率,可以用来计算图像的特征和优化问题的解。
掌握方向导数和梯度的概念和计算方法,可以为各个领域的学习和应用提供重要的数学工具。

方向导数的表达式
方向导数计算公式是方程为x=x(s),y=y(s),z=z(s),函数
u=u[x(s),y(s),z(s)]。
方向导数求解方法:先求切线斜率和法线斜率,得到内法线方向,再求z对x和y的偏导数,最后求方向导数。
方向导数
在函数定义域的内点,对某一方向求导得到的导数。
一般为二元函数和三元函数的方向导数,方向导数可分为沿直线方向和沿曲线方向的方向导数。
求解方法
首先我们要明白方向导数的定义,以三元函数为例:设绵爹三元函数f在点P0(x0,y0,z0)的某邻域内有定义英特,l为从点P0出发的射线,P(x,y,z)为l上且含于邻域内的任一点,以ρ表示P和P0两点间的距离。
若极限lim((f(P)-f(P0))/ρ)=lim(△lf/ρ)(当ρ→0时)存在,则爹肥著称此极限为函数f在点P0沿方向l的方向导数。

方向导数的相关问题方向导数是一种在几何上表示函数在特定方向上的变化率的概念,在微积分中是一个重要的概念,被广泛应用于物理、数学、工程等各个领域。
在本文中,将讨论方向导数的相关问题,包括它的概念、性质、运算方法以及在不同的领域中的应用。
概念方向导数是指在某特定方向上变化率的函数,它是某一点关于这个方向上某个变量变化量无限小时函数变化量与变量变化量的比值。
简言之,方向导数就是函数在某特定方向上的变化率,即函数f(x)在x该方向上的变化率就是f(x)。
性质方向导数的性质可以总结为以下几点:(1)向导数的值是函数在该方向上变化率的大小,它可以为正、负或零;(2)向导数的值可以大于1;(3)向导数的值的符号是函数在该方向上的变化性质的标志,正表示函数在该方向上是增函数,负表示函数在该方向上是减函数;(4)向导数的值等于1时,函数在该点处是极值。
运算方法方向导数可以使用极限运算来计算,其计算公式如下:f(x)=lim [f(x+h)-f(x)]/h其中h表示该方向上变量变化量,x表示该方向上变量的取值,f(x)表示函数在该点的值。
应用方向导数在不同的领域中有着广泛的应用,其中可以分为两大类: (1)理应用:在物理、力学、电磁学和激光等领域,方向导数经常被用来描述变化的趋势和变化率。
(2)学应用:在数学领域中,方向导数经常被用来求解微分方程,并且在几何上也被用于求解曲面上的极点等问题。
总结从上文中可以看出,方向导数是一个重要的概念,它所描述的内容不仅在几何中有着重要的作用,而且在物理、数学等不同的领域中也有着广泛的应用。
它的特性、运算方法等也有助于我们更好地了解该概念,并且在实际应用中更有效地使用它。

方向导数与梯度在多变量微积分和优化理论中,方向导数和梯度是两个重要的概念。
它们提供了函数在某一点处关于不同方向的信息,以及函数在该点处的变化率和方向。
理解这两个概念对于解决各种实际问题,如最优控制、机器学习、图像处理等都至关重要。
方向导数是函数在某一点处沿特定方向的变化率。
给定一个函数f(x)在点x0,对于任意的方向v = (h1, h2,..., hn),方向导数Df(x0)v 是f(x)在x0处沿v方向的变化率。
具体地,Df(x0)v = lim(h->0) [f(x0 + hv) - f(x0)] / h。
方向导数的重要性在于它提供了函数在某一点处对不同方向的敏感度。
例如,如果你在山峰上沿着不同的方向行走,方向导数可以告诉你哪个方向更容易攀登,哪个方向更困难。
梯度是函数在某一点处所有方向导数的向量。
给定一个函数f(x)在点x0,梯度gradf(x0)是一个向量,其方向是f(x)在x0处增加最快的方向,而其大小是f(x)在该方向的导数。
具体地,gradf(x0) = (f'(x01), f'(x02),..., f'(xn))。
梯度是一个非常重要的概念,因为它提供了函数在某一点处的最大变化率方向。
在很多实际问题中,找到这个最大变化率方向往往能够指引我们找到最优解。
例如,如果你在山峰上寻找攀登最快的方式,梯度可以告诉你应该沿着哪个方向前进。
梯度是方向导数的最大值。
换句话说,对于任意给定的方向v,方向导数Df(x0)v都不超过梯度的长度。
这是因为梯度是所有方向导数向量的范数,即||gradf(x0)|| = max{Df(x0)v : ||v|| = 1}。
这个性质表明,梯度不仅提供了函数在某一点处的最大变化率方向,还给出了沿这个方向的导数(即变化率)。
这使得梯度在优化问题中具有特别的重要性,因为它可以用来找到使函数值下降最快的方向。
方向导数和梯度是多变量微积分和优化理论中的重要概念。
方向导数知识点方向导数•方向导数的定义•方向导数的计算方法•方向导数与偏导数的关系•方向导数的几何意义方向导数的定义方向导数是指函数在某个给定点沿着某个方向的变化率。
具体而言,如果有一个函数f(x,y),在点(x0,y0)处沿着一个单位向量u=[a b]的方向上的导数,那么这个导数就是f在(x0,y0)处沿着方向u的方向导数D u f(x0,y0)。
方向导数的计算方法方向导数可以通过求函数在给定点的梯度向量与方向向量的点积来计算。
假设函数f(x,y)在(x0,y0)处可微分,那么其梯度向量为∇f(x0,y0),方向向量为u=[ab],则方向导数D u f(x0,y0)的计算公式为:D u f(x0,y0)=∇f(x0,y0)⋅u其中,⋅表示向量的点积。
注意,∇f(x0,y0)表示函数f(x,y)在(x0,y0)处的梯度向量,u=[ab]表示方向向量。
方向导数与偏导数的关系方向导数与偏导数之间存在一定的关系。
事实上,当方向向量u=[1]时,方向导数D u f(x0,y0)就是函数f(x,y)在(x0,y0)处关于x的偏导数∂f∂x (x0,y0);当方向向量u=[01]时,方向导数D u f(x0,y0)就是函数f(x,y)在(x0,y0)处关于y的偏导数∂f∂y(x0,y0)。
方向导数的几何意义方向导数的几何意义可以从梯度向量的方向来理解。
梯度向量∇f(x,y)表示函数f(x,y)在某点的最大变化方向。
当方向向量与梯度向量的方向相同时,方向导数达到最大值;当方向向量与梯度向量的方向垂直时,方向导数为0;当方向向量与梯度向量的方向相反时,方向导数达到最小值。
因此,方向导数可以用来描述函数在某点沿着某个方向的变化率及变化方向。
以上就是关于方向导数的相关知识点的整理和详解。
方向导数的定义、计算方法、与偏导数的关系以及几何意义都非常重要,对于理解多元函数的变化规律具有重要意义。
§8.7方向导数方向导数是多元函数在某一点沿着某个给定方向上的导数,它反映了函数在该方向上变化的速率。
在物理学、工程学、计算机科学等领域中,方向导数是一个非常重要的概念。
在这篇文章中,我们将学习方向导数的定义、性质和应用。
1. 方向导数的定义设函数 $z=f(x,y)$ 在点 $(x_0,y_0)$ 处有定义,$\vec{v}=(v_1,v_2)$ 是一个单位向量,则函数 $z=f(x,y)$ 沿着向量 $\vec{v}$ 的方向导数为:$$D_{\vec{v}}f(x_0,y_0)=\lim_{h\to0}\frac{f(x_0+hv_1,y_0+hv_2)-f(x_0,y_0)}{h}$$其中,$h$ 表示向量 $\vec{v}$ 的长度。
(2) 方向导数的计算方法其中,$f_x(x_0,y_0)$ 和 $f_y(x_0,y_0)$ 分别表示函数 $z=f(x,y)$ 在点$(x_0,y_0)$ 处的偏导数。
(1) 判断曲面的陡峭程度对于曲面 $z=f(x,y)$,我们可以通过计算函数沿着不同方向的方向导数来判断其陡峭程度。
如果在某个方向上的方向导数比较大,那么曲面就比较陡峭。
(2) 极小化函数在某个方向上的变化率有时候我们需要在函数 $z=f(x,y)$ 中找到一个点 $(x_0,y_0)$,使得在该点沿着某个给定方向上的方向导数最小。
这个问题可以转化为求函数在 $(x_0,y_0)$ 处的梯度与给定方向向量的点积最小的问题,具体方法可以使用 Lagrange 乘子法求解。
(3) 最速下降法最速下降法是求解无约束优化问题的一种方法,它的基本思想是沿着函数梯度的相反方向进行搜索,以达到使函数值最小的目标。
在每一次搜索中,我们可以计算函数沿着当前梯度的相反方向的方向导数,以确定最佳的搜索步长。
方向导数的表述方向导数是多元函数在某一点沿着给定方向的变化率。
它是一个重要的概念,在数学分析和应用数学中经常被使用。
在本文中,我们将详细讨论方向导数的定义、性质和计算方法,并给出一些具体的例子来帮助理解。
1. 定义设函数f(x,y)在点P(x0,y0)附近有定义。
对于任意单位向量u=(a,b),其中a和b 是实数,并且满足a2+b2=1,我们定义f(x,y)在点P沿着方向u的方向导数为:D u f(x0,y0)=limℎ→0f(x0+aℎ,y0+bℎ)−f(x0,y0)ℎ如果这个极限存在,则称之为函数f(x,y)在点P关于方向u的方向导数。
2. 性质方向导数具有以下性质:(1) 线性性质设函数f(x,y)在点P处关于方向u和v的方向导数分别为D u f(x0,y0)和D v f(x0,y0),则对于任意实数k和l,有:D ku+lv f(x0,y0)=kD u f(x0,y0)+lD v f(x0,y0)这个性质表明方向导数具有线性性质。
(2) 方向导数与梯度的关系设函数f(x,y)在点P处可微分,则函数f(x,y)在点P处沿着梯度∇f(x0,y0)的方向导数最大,并且最大值为∥∇f(x0,y0)∥。
换句话说,方向导数最大的方向是梯度的方向。
(3) 方向导数的计算公式设函数f(x,y)在点P附近有定义且可微分,则函数f(x,y)在点P关于单位向量u= (a,b)的方向导数可以通过以下公式计算:D u f(x0,y0)=∇f(x0,y0)⋅u其中,∇f(x,y)=(∂f∂x ,∂f∂y)是函数f(x,y)的梯度。
3. 计算方法计算方向导数的常用方法有以下两种:(1) 利用定义计算根据方向导数的定义,可以通过直接计算差商的极限来求解。
具体步骤如下:1.将函数f(x,y)代入方向导数的定义;2.化简表达式,并利用极限运算法则计算极限。
这种方法比较直接,但对于复杂函数和复杂方向可能会比较繁琐。
(2) 利用梯度计算根据性质(3)中给出的公式,我们可以利用梯度来计算方向导数。
方向导数
一、问题的提出
实例:一块长方形的金属板,四个顶点的坐
标是(1,1),(5,1),(1,3),(5,3).在坐标原
点处有一个火焰,它使金属板受热.假定板
上任意一点处的温度与该点到原点的距离成
反比.在(3,2)处有一个蚂蚁,问这只蚂蚁应
沿什么方向爬行才能最快到达较凉快的地点?
问题的实质:应沿由热变冷变化最骤烈的方
向(即梯度方向)爬行.
讨论函数在一点P 沿某一方向的变化率问题.),(y x f z =(如图)
它的参数方程为⎩⎨⎧+=+=βαcos cos 00t y y t x x +∞<<∞-t 方向向量的有向直线,
为
且以面上通过点是为一单位向量,
设→→→→e y x P xoy l j βi αe ),(cos +cos =00o y x
αl Q ∙x ∆y ∆∙∙P
β
二、定义
上任意一点,则有
是设l y x Q ),(,)cos ,cos (),(00→
→==--=e t t t y y x x PQ βα,t PQ =→
的有向距离。
到点为点称Q P t ),()(P f Q f z -=∆当沿着趋于时,
Q P l t
y x f t y t x f t ),()cos ,cos (lim 00000-++→βα,t z Δ考虑是否存在?
.),()cos ,cos (lim 00000),(00t
y x f t y t x f l f
t y x -++=∂∂→βα记为
定义 设函数 z=f(x,y) 在点P(00,y x )的某个邻域内有
定义,l 是一非零向量,)cos ,(cos βα=→
l e 是与l 同方
向的单位向量,如果极限 t
y x f t y t x f t ),()cos ,cos (lim 00000-++→βα存在,则称此极限为函数),(y x f z =在P 点处沿l 方向
的方向导数(directional derivative),
依定义,函数),(y x f 在点P 沿着x 轴正向}0,1{1=e 、y 轴正向}1,0{2=e 的方向导数分别为y x f f ,;
沿着x 轴负向、y 轴负向的方向导数是 y x f f --,.
所以方向导数是偏导数的推广。
定理 如果函数),(y x f z =在点),(y x P 是可微分的,
那末对于任意单位向量)cos ,(cos βα=→
l e ,函数
),(y x f z =在该点方向l 的方向导数都存在,且有 βαcos cos y
f x f l f ∂∂+∂∂=∂∂。
证明由于函数可微,则增量可表示为
)(),(),(ρo y y
f x x f y x f y y x x f +∆∂∂+∆∂∂=-∆+∆+两边同除以,t 得到
取,cos ,cos βαt y t x =∆=∆
t
t o y f x f t
y x f t y t x f )(cos cos )
,()cos ,cos (+⋅∂∂+⋅∂∂=-++βαβα故有方向导数
t y x f t y t x f t ),()cos ,cos (lim 0-++→βα.cos cos βαy
f x f ∂∂+∂∂==∂∂l
f
例1 求函数y
xe z 2=在点)0,1(P 处沿从点)0,1(P 到点)1,2(-Q 的方向的方向导数.
例2 求函数22),(y xy x y x f +-=在点(1,1)沿与x 轴方向夹角为α的方向射线l 的方向导数.并问在怎样的方向上此方向导 数有
(1)最大值; (2)最小值; (3)等于零?
对于三元函数),,(z y x f u =,它在空间一点
),,(z y x P 沿着方向)cos ,cos ,(cos γβα=→l e
的方向导数 ,可定义为
=l f ∂∂三、三元函数方向导数的定义
t
z y x f γt z βt y αt x f t ),,()cos +,cos +,cos +(lim 0→
同理:当函数在此点可微时,那末函数在该点沿任意方向L 的方向导数都存在,且有 .cos cos cos γβαz
f y f x f l f ∂∂+∂∂+∂∂=∂∂
四、小结
方向导数的概念
(注意方向导数与一般所说偏导数的区别)
方向导数的计算
(1.计算偏导数;2.计算单位向量的坐标)
(用定义计算)
讨论函数2
2),(y x y x f z +==在)0,0(点处的偏导数是否存在?方向导数是否存在?思考题
x
f x f x z
x ∆-∆=∂∂→∆)0,0()0,(lim 0)0,0(.||lim 0x
x x ∆∆=→∆ 同理:)0,0(y z ∂∂y
y y ∆∆=→∆||lim 0故两个偏导数均不存在.
思考题解答
沿任意方向},,{z y x l = 的方向导数,ρ
ρ)0,0(),(lim 0)0,0(f y x f l z
-∆∆=∂∂→1)()()()(lim 2
2220=∆+∆∆+∆=→y x y x ρ故沿任意方向的方向导数均存在且相等.。