当前位置：文档之家 › 材料力学14章静不定结构习题课

材料力学14章静不定结构习题课

  • 格式：ppt
  • 大小：2.43 MB
  • 文档页数：86

下载文档原格式

  / 86

合集下载

材料力学课件-第61讲 第十四章 静不定问题分析(2)

材料力学课件-第61讲 第十四章 静不定问题分析(2)

1
2
3
4
5
6
8
P
FN7
m
m’
FN7
求解思路讨论：
A 点在与F 垂直方向位移
例: A点位移与F 方向相同，求角
解：配置单位载荷系统
作业 14-1 14-2 14-3
谢 谢
B
M
O
R
A
B
M0
q
O
R
A
B
1
图(1)
4. 计算B端水平位移（1）
方法1
B端的水平位移为
4. 计算B端水平位移（2）
q
O
R
A
B
M0
图(二)
方法2
q
O
R
A
B
1
图(2)
结果相同！
例2：求B 端反力
1. 问题分析
静不定度
相当系统
变形协调条件
2度
相当系统
单位载荷系统 1
单位载荷系统 2
④单位载荷系统
第 14 章 静不定问题分析(2)
第六十讲知识点 力法分析静不定问题（续）
外静不定问题分析（续） 内静不定问题分析
§2 用力法分析静不定问题（续）
外静不定问题分析(续)
题1：已知外力偶 M0 ，求B端约束反力和水平位移。
q
O
R
A
B
M0
1. 问题分析
静不定度
相当系统
变形协调条件
FB
例2：求B 端反力（续）
变形协调条件
相当系统
内力静不定问题分析
分析桁架内力与qCD ，各杆EA同
1. 问题分析
几度静不定问题？

材料力学第十四章__超静定结构

材料力学第十四章__超静定结构

§14．1 超静定结构概述
整理课件
本节应用能量法求解静不定系统。 应用能量法求解静不定系统，特别是对桁 架、刚架等构成的静不定系统，将更加有效 。 求解静不定问题的关键是建立补充方程。 静不定系统，按其多余约束的情况，可以 分为外力静不定系统和内力静不定系统。
整理课件
支座反力静不定 类型反力静定内力静不定
整理课件
解静不定梁的一般步骤
(4)在求出多余约束反力的基础上，根据静 力平衡条件，解出静不定梁的其它所有支 座反力。 (5)按通常的方法（已知外力求内力、应力 、变形的方法）进行所需的强度和刚度计 算。
整理课件
例：作图示梁的弯矩图 。
整理课件
解：变形协调条件为
A 0
即
MAl2Pl2 10 2 382
A
M10 1
D
P
1
2
(d)
(e)
1 P0 2M E 1 0 M P d I s2 P E 20 2 a (I 1 c
o) s (1 )d P2(a 1 ) 2 E2 I
1102M E102IdsE aI02(1)2d2EaI
上面两式代入 正则方程：
11
X 整理课1件
Pa( 2
)
求出X1后，可得图（C）
解得
MA
3Pl 16
整理课件
3Pl MA 16
11 P
5P
16

整理课件
另解：变形协调条件为
vB 0
即
RBl2
2l Pl2
5l
0
2 386
解得
5P
RB 16
整理课件
5P
5Pl/32
16
3Pl 16

材料力学(单辉组)第十四章静不定问题分析

材料力学(单辉组)第十四章静不定问题分析

FBy F
B
F A xA
Rj
F Ay
MA
Rj
A
静定基
解：4个反力，3个平衡方程，1次外力静不定
认为B处为多余约束，移去B支座，加反力
变形协调条件: DBy=0
11
FBy F 利用截面法求弯矩
M
B
Rj
A
M j FR1 cosj FByRsinj
利用卡氏第二定理求位移
静定基
曲杆弯矩正号 使曲率增大
静定基
A
B
Dcy

V Fcy

M2
M 2 Fcy
EI dx AB
2
M1
M1 Fcx
EI dx BC
1

a2 EI

1 2
Fcx

1 3
Fcy

3 8
qa2

C
Fcx
Fcy 利用变形协调条件求支反力
由
D D
cx cy

0 0

4
3

1
2
根据多余的约束条件
几何方程 物理方程
补充方程
当杆件外形、载荷较复杂或材料为非线性弹 性时，问题难于求解
由于能量方法可较容易给出载荷与位移关系， 从而采用能量法比较容易处理静不定问题
9
EX1
F
B
Rj
A
已知：小曲率杆，半径R
不计剪力和轴力对曲杆变形影响
求解：支反力和内力？
10
FBy F
B
4
有缝 q
F Ax A F A y (a)
刚架
B
FBy

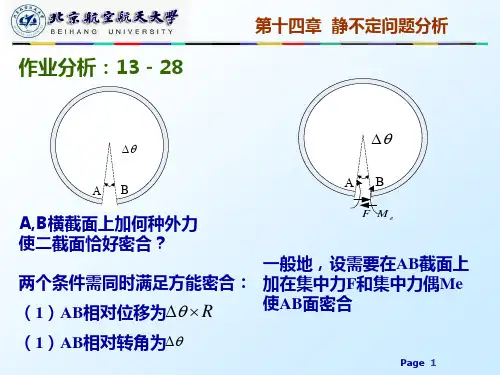
材料力学(15)第十四章 静不定问题分析

材料力学(15)第十四章 静不定问题分析
F
静不定问题分析
F
1（内）＋1（外）＝ 2 度
3（内）＋3（外）＝ 6 度
F
梁：外3 环：内3 圆环
梁环接触：1
3+3+1=7 度
Page 9
第十四章
静不定问题分析

梁杆结构的静不定问题
(b) (a) (a): 1度 (b): 2度 (c) (c): 2度
Page10
第十四章
静不定问题分析
§14-2
8
静不定问题分析
a 4 a 5 7 6 8 3
a 2
1
N i N i li m / m EA i 1 a [(2 2) N 7 (2 2) P] 0 P EA
2 N7 P 2
1 1
思考：若求加载点的水平位移，如何选择单位载荷状态
4 5
6 8 3
2 1
4 5
q
FS
M
FN
断开：内力静定
刚性连接：多了三个约束
F F
单闭口的平面刚架或曲杆 内3度静不定
内6度
Page 7
第十四章 F F
静不定问题分析
6度内力静不定
F
F
5度内力静不定 加一中间铰减 少一度静不定
F F
F F
2度内力静不定
4度内力静不定,加一根二力 杆增加一度静不定
Page 8
第十四章 混合静不定
H
利用单位载荷法建立补充方程
Page20
P
第十四章
x2
B
RB N
静不定问题分析
x1 C
N
D
真实载荷状态(相当系统)：
RB RD N 2

《材料力学》精品课程(全册)第十四章 超静定结构

《材料力学》精品课程(全册)第十四章 超静定结构

,YB
9qa 16
X
A
qa 16
,
YA
7qa 16
目录
上面我们讲的是只有一个多余约束的情况！ 那么当多余约束不止一个时，力法方程是什么样的呢？
P2
P2
P1
P1
P3
P3
X3
X1
X2
目录
变形协调条件 ：
1 2 3 0
i 表示 X作i 用点沿着 方向X的i 位移
由叠加原理：
1 1X1 1X 2 1X3 1P 0 1 11 X 1 12 X 2 13 X 3 1P 0
C
B 11
对于线弹性结构，位移与力成正比，X1是单位力“1”的X1倍，故1X1
的X1倍，即有
1X1 11 X1
也是11
所以（*）式可变为： 11 X 1 1F 0
若：
11
l3 3EI
于是可求得
1F
Fa 2 6EI
(3l a)
X1
Fa 2 2l 3
(3l
a)
目录
例14.1：试求图示平面刚架的支座反力。已知各杆 EI=常数。
可得：
12 21 23 32 0
于是正则方程可化为
11 X 1 13 X 3 1F
31 X 1 33 X 3 3F
22 X 2 0
目录
对称结构在反对称载荷作用下的情况：
F P
F P
F
X3
X2
F
X1
X3 X2
P
P
同样用图乘法可证明
当对称结构上受反对称载荷作用时，
在对称面上对称内力等于零。
目录
例如：
该体系中多出一个外部约束，为一次超静定梁

高等教育大学本科课件 材料力学 第14章 静不定问题分析

高等教育大学本科课件 材料力学 第14章 静不定问题分析

M
l
A
B
HA RA HC
相当系统
x1 l
A
l x2 C RC B
l x2 1C
单位载荷状态
真实载荷状态(相当系统)：
HA HC
RA
M l
HC
M ( x1 )
(
M l
HC
) x1
M ( x2 ) HC x2
C 0
单位载荷状态：
M( x1 ) x1 M( x2 ) x2
C
1 EI
[
l
0 M( x1 ) M( x1 )dx1
§14-2 用力法分析静不定问题
➢ 几个概念： 基本系统： 解除多余约束后的静定结构（静定基）
相当系统： 作用有载荷和多余反力的基本系统。
Page11
BUAA
MECHANICS OF MATERIALS
➢ 第一类静不定问题：存在多余的外部约束
解除多余的外部约束，代之以支反力
相当系统
在解除约束处，建立变形协调条件
Page3
BUAA
➢ 内力静不定
MECHANICS OF MATERIALS
存在多余内部约束 平面桁架：
内力静不定度 = m - 2n + 3 m: 杆数 n: 节点数
外力静定 内力静不定(一度)
几何可变
4 - 24 + 3 = -1
5 - 24 + 3 = 0
6 - 24 + 3 = 1
Page4
例1：已知EI为常数，求A
A
M l
B
解： 解静不定，求解多余未知力
l
存在1个多余外部约束：
一度外力静不定
C

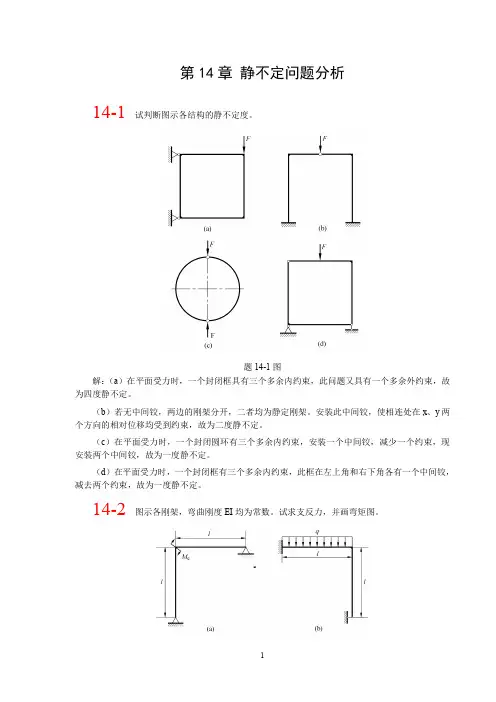
第十四章北航 材料力学 全部课件 习题答案


dM qRd R1cos( ) qR21cos( )d
所以，在切向载荷 q 与多余未知力 FBy 作用下，截面的弯矩为
6
M
(
)
0
qR2
1
cos(
)d
FBy
R
sin
qR2
(
sin
)
FBy
R
sin
(b)
在图 c 所示铅垂单位载荷作用下，截面的弯矩则为
M () Rsin
根据单位载荷法，得相当系统横截面 B 的铅垂位移为
1
9F 4
2FN1
2
3F 2
FN1
1
0
得
FN1 F
ቤተ መጻሕፍቲ ባይዱ
由此得
FN2
F 4
,
FN3
F 2
2. 角位移计算
施加单位力偶如图 d 所示，并同样以刚性杆 BC 与 DG 为研究对象，则由平衡方程
11
M B 0, 1 F N2 2a F N3 3a 0
MG 0, F N2 2a F N3 a 0
M ( ) qR2 4 sin π
在图 d 所示水平单位载荷作用下，截面的弯矩则为
M () R(1cos)
于是，得截面 B 的水平位移为
ΔBx
1 EI
π/2
R(1
0
cos )qR2
4 π
sin
Rd
qR4 EI
π2 8
π 2
2 π
1
( )
14-5 图示桁架，各杆各截面的拉压刚度均为 EA，试求杆 BC 的轴力。
MG 0, F 3a FN1 3a FN2 2a FN3 a 0
得
FN2

材料力学第14章(静不定)doc资料


应用叠加法：
11F1X1 0
由1X111X1
∴变形协调方程
1F1X 110
或： 1X 11 1F0 A ——力法正则方程
F
B
1F
1X1
X1
11
1
系数δ11和Δ1F可由莫尔定理(积分或图乘)求得(图c、d) F
1FE 1[I (1 2Pl)(6 52l)](c)
5 Pl 3
Pl
6 EI
11 E 1[I(1 22l2l)(3 22l)] (d)
X1 A
F
B
C
二、力法正则方程
1X 11 1F0
变形协调方程的标准形式，即所谓的力法正则方程。
X1——多余未知量；
11——在基本静定系上， X1取单位值时引起的在X1作用点沿
X1方向的位移； 1F——在基本静定系上， 由原载荷引起的在X1作用点沿
X1方向的位移；
力法解超静定的基本步骤：
①判定静不定次数 ②选取并去除多余约束，代以多余约束反力。 ③画出两个图：原载荷图和单位力图。
M(j1)Rsijn1
M(j2)Rsijn2
1F202M (j1)M E (j1I)Rdj1F E3R I0 2(1co j1)ssijn 1dj1
FR 3 2 EI
F
A
j2
j1 B
O
F
2
F
2
１ A j2
j1
１
O
M(j1)Rsijn1
M(j2)Rsijn2
11 202M(j1)M E(j1I)Rdj12ER3I02sin2j1dj1
FB
A
a
a
C X1
X1 D
a a

材料力学(单辉祖)第十四章静不定问题分析


求解上式可得
X1
=
1−
π2
π
4⋅ −1
P 2
=
4−π π2 −8
P
,8X2来自=π π−3
2
−1
⋅
PR 4
=
2(π
π2
− 3)
−8
PR
8
27
Example-7
在平面xy内，由k根等直杆组 y
成的杆系，在结点A处用铰连 接在一起，并受到水平载荷P1 和垂直载荷P2的作用。已知各 杆的材料相同，其拉压弹性模
∂X 1
∂X 2
Rϕ
25
Example-6
由对称截面处的约束条件， 可得变形相容性条件
Δ = ∂Uc = 0, θ = ∂Uc = 0
∂X 1
∂X 2
P/2 X2
X1 X3
Rϕ
即
∫ − 1
EI
π 2
0
⎜⎛ ⎝
PR 2
sin
ϕ
−
X 1R(1 −
cos ϕ )
−
X
2
⎟⎞ ⎠
⋅
R(1 −
cosϕ )Rdϕ
F
M (ϕ ) = FR (1− cosϕ ) − FByR sinϕ
π
∫ Δ By
=
∂Vε ∂FBy
=
2
[M
0
(ϕ ) ∂M (ϕ )][EI ]−1Rdϕ
∂FBy
8
Example-1
π
M (ϕ ) = FR (1− cosϕ ) − FByR sinϕ
∫ Δ By
=
∂Vε ∂FBy
=
2
[EI ]−1 ⎡⎣FR (1− cosϕ ) − FBy R sinϕ ⎤⎦ (−R sinϕ ) Rdϕ

14章静不定结构-习题课解析


A
B a
1
1
B
ω 1=Fa2/2
FD F
a
Fa D a2 C a2
a
D a
C
F
ω 2=Fa2/2
C
F
a
a
2 2
A
X1
X1 B
1M 1 2 M 2 1 Fa 2a Fa Δ1F a EI EI 2 3 2 EI C D 5Fa 3 a 6EI 3 1M1 2 M 2 1 a 2 2a 5 a 3 1F F 11 2 a X 1 EI EI EI 2 3 3 EI 11 2
C
f

M =-PRsinφ j[0, /4] M =Rsin(π/4+φ)
A
P C
B
C f 45 °
f A
a
B X1 B 1
M2 1 4 2 4 2 2 11 ds R sin Rd R sin j Rd j 0 0 E I EI 4 s 1 R3 4 1 1 1 4 0 cos 2 d 0 cos 2j Rdj EI 2 2 2 2 2 3 3 4 R 1 1 4 R sin 2 cos 2j EI 2 4 4 EI 0 2 4 0 C MM 1 4 1P ds R sin j PR sin j Rdj 0 EI EI 4 f s
4
2 PR 1 2 PR 3 j 1 4 cos 2j sin 2j 2 EI 4 16 EI 2 4 0
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2
2a 3
Fa2 2
a
5Fa3 6EI
X1
1P
11
F 2
F
B a
C a
F
X1 X1 B a
C a
例3：刚架的弯曲刚度为EI，承受力F。 F
F
试求：刚架多余约束反力。
F 1
a
A
A
11
1 EI
a2 8
2 3
a 2
a3 4
7a3 24EI
a a
A
B
F
F
X1 X1
a
a
A
B
Δ1F
1 EI
(A) 强度提高,刚度不变
(B) 强度不变,刚度提高
(C) 强度,刚度都提高 (D) 强度,刚度都不变 答案：(C)
三、下图所示结构是
静不定机构
(A) 0 次 (B) 2次 (C) 3次 (D) 4次
(a)图
(b)图
答案：(A)
二、下图所示结构是
静不定机构
(A) 1次 (B) 2次 (C) 3次 (D) 4次
1 F
Fa
例5：已知结构的弯曲刚度为EI， 试求对称轴上A截面的内力。
解：11
2a EI
,
Δ1F
Fa2 4EI
A
由 11X1 1F 0 得
X1
Fa 8
a
FSA 0
1
FNA
F 2
,
MA
Fa 8
A X1 F/2
a Fa
a
a
F 1
Fa/2 1
F/2
例6：已知刚架的弯曲刚度为EI。 试求截面A处弯矩。
Fa2 2
a 2
Fa3 4EI
X1
1P
11
6F 7
例4：已知刚架的弯曲刚度为EI，试求刚架内最大弯矩
及其作用位置。
a Fa
A
B
C
a
E
D
a
解：
11
2a3 EI
,
Δ1F
Fa3 3EI
由 11X1 1F 0
得
X1
F 6
()
M max
5Fa 6
作用于固定端A
a Fa
A
B
C
a
E
D
a
a
X1
a aa
PR 3 AEI
11
1 EI
2 0
R
2sin
2
j
Rdj
R 3
4EI
X
1
1P
11
P
0.318P
讨论：已知图示半圆曲杆的
Me
弯曲刚度为EI，试求曲杆支
C
座A处垂直反力FAy。
R
A
B
解：
Me /2
C R X1 A
Me /2
R
R1
例15 半圆形曲杆ACB为直杆AD、BF铰接如图。曲杆及直杆的抗弯刚度均为
1
N1
1
1
1
1
约束反力三次静不定
2）解除B点约束，建立静定基
P
X1 X 3
1 1P
M2
l
0
M
P .M1 dx EI
0
X2
3）对静定基进行受力分析， 建立相当系统
4）研究B点竖直,水平位移 和转角建立正则方程
12
l
0
M 2.M1dx EI
0
13
l
0
EI。求D、F处的反力矩MD、MF（只考虑杆件的弯曲变形）。 P
解： 由对称性知 N＝P/2。 一、 分析图。由对称性取一半研
究，求B点水平位移使用莫尔积 分，在任一横截面上，
M NR(1 cosj) FRsinj
M R sin j
VBx
MM l EI
dx
PR 3 4EI
FR 3
4EI
VBx
D
NA
1 D
D
A,B,C,D,E,F
A
A
A M ( ) 1
3) 用E,A两截面将刚架截开, 取EA(1/3)段研究:
M ( ) NA.R.(1 cos )
1P
0
3 M P ( )M ( )Rd
EI
11
0
3
M
( )M
EI
( )Rd
例21、求图示结构的约束反力
P
P
A
CB
a
b
l
MP Pa
解：1）判断静不定种类及次数
1 8
5 6
1 2
29Fa3 48EI
由 11X1 Δ1F Δ 得
X1
29F 64
3EIΔ 4 a3
例2：刚架的弯曲刚度为EI，承受力F。 A
试求：刚架多余约束反力。
F
A
B
A
Байду номын сангаас
X1 X1 B
D
a
a
FD
C
D
C
a
a
A
F
F
11
2 EI
a2 2
2a 3
a3
5a3 3EI
D
Δ1F
1 EI
Fa2
X1
1F
11
F 22
F
C
B
A
FC A
B
X
1
FC
B
φ
A
C A
B
1
φ
例8、求图示结构 C
的约束反力
EI
EA
a
A EI l
B
P 解：1）判断静不定种类及次数
约束反力一次静不定
2）解除B点约束，建立静定基
3）对静定基进行受力分析，建立相当系统 4）研究AB梁的B点与BC杆的B点的竖直相 对线位移，建立正则方程
使用莫尔积分，在任一横截面上，
M FRcos（j/4） j[/4，/2]
M R sinj
j[0，/2]
11
s
M2 ds
EI
1 EI
2 R sinj 2 Rdj R3
0
4EI
MM 1
1P
s
ds E I EI
2
4
FR
sin
j
4
R
sin
j
Rdj
FR3 8 2EI
,
ΔiF
n k 1
FNi,k FNF,k lk Ek Ak
例1：刚架的弯曲刚度为EI，承受力F后，支座C有一 下陷量Δ，试求刚架C处的反力。
a/2 F a/2
B
C
Δ a
A
解：
a/2 F a/2
F
a
B
C
Δ
Fa/2
X1
1
a
Fa/2
a
A
11
a3 EI
1 2
2 3
1
4a3 3EI
Δ1F
Fa3 EI
答案：(B)
四、下图所示结构是
静不定机构
(A) 0 次 (B) 2次 (C) 3次 (D) 4次
答案：(A)
例17、求图示结构梁DE的最大正应力σmax=?
a
B
A
1 1P 11.X1 0
X1
a
D
a
C
aE
P
1 P.a
1P
2 EI
.(1 .a.1 22
Pa.2 3
.1 2
a)
Pa3 6EI
2
解：1）判断静不定种类及次数
1 Pa
a
例20:求图示闭合圆形刚架在A截面上的弯矩 M A 因为A,E都是结构的对称截面
B
NE
所以: A,E截面上反对称的内力等于0
C
P
E
ME
E 即:A,E截面上只有轴力和弯矩 又因为CD是对称轴 NE NA且M E M A
以CD轴为Y轴: y 0
NE .cos30 N A.cos30 0
由11X1 Δ1F 0 得
X1
3qa 8
FBx 0, FAx 0,
FBy
3qa 8
FAy
11qa 8
,
M
A
qa2 8
逆时针
例13：已知刚架的弯曲刚度为EI。 q0
试求支座B处的反力。
C
解：
11
1 EI
a x12 dx1
0
a 0
a2
dx2
4a3 3EI
a A
Δ1F
1 EI
Ni .Ni EAi
.li
(7
6 2).P.a 3EA
0
0
0
0
0
0
0 0 0
11
10 Ni.Ni.li i1 EAi
(4 4 2).a EA
1
0
a
1 2Pa 3 a
2 2 2Pa 3 2 2a 1 4Pa 3 a
由正则方程
X1
即为杆AB的轴力
而原结构中其它各杆的轴力=？
2 4 2Pa 3 2 2a FNI Ni Xi.N i
a
a
q
解： 11
2a EI
,
Δ1F
qa3 EI
q
由 11X1 1F 0 得
a q A
a
M
A
X1
1 2
qa2
q
q
另解：
q
FS
2qa ,
MA
qa2 2
A X1
qa
FS
FS
例7: 1/4圆形曲杆ACB如图。半径为R，曲杆抗弯刚度为
EI。求:A、B处的反力矩（只考虑杆件的弯曲变形）。