下载文档原格式
《现代控制理论基础》课程教学大纲课程代码：090142129课程英文名称：Foundation of Modern Control Theory课程总学时：32 讲课：32 实验：0 上机：0适用专业：信息与计算科学大纲编写（修订）时间：2017.11一、大纲使用说明（一）课程的地位及教学目标本课程是信息与计算科学专业的一门专业基础课，是自动化专业重要的技术基础课。
该课程的目的是使学生熟悉控制系统的状态空间分析方法，掌握线性控制系统的状态可控性、可测性和李亚普诺夫稳定性理论，并能对线性控制系统的运动行为进行分析。
通过本课程的学习，使学生掌握建立系统状态空间模型的基本方法；掌握利用状态空间模型分析系统特性和系统设计的方法。
了解并掌握基于状态空间模型分析与设计方法。
通过运用MATLAB软件，使学生具备能用计算机软件对各类运筹学模型进行求解和对求解结果进行简单分析的能力。
培养学生利用现代控制理论和计算机技术解决控制系统的分析和综合问题，为工业控制系统开发与设计奠定理论基础。
（二）知识、能力及技能方面的基本要求1.基本知识：要求学生掌握控制系统的状态空间分析方法，线性控制系统的状态可控性、可测性和李亚普诺夫稳定性理论，并能对线性控制系统的运动行为进行分析。
掌握利用状态空间模型分析系统特性和系统设计的方法。
2.基本能力：培养学生逻辑推理能力和抽象思维能力；根据实际问题抽象出适当的状态空间模型并能分析系统特性和进行系统设计能力；运用现代控制理论的思想和方法分析、解决实际问题的能力和创新思维与应用能力。
3.基本技能：使学生获得现代控制理论的基本分析和设计技能；运用计算机软件求解基本模型和分析结果的技能。
（三）实施说明1. 本大纲主要依据信息与计算科学专业2017-2020版教学计划、信息与计算科学专业专业建设和特色发展规划和沈阳理工大学编写本科教学大纲的有关规定及全国通用《现代控制理论基础教学大纲》并根据我校实际情况进行编写的；2. 教师在授课过程中可以根据实际情况酌情安排各部分的学时，课时分配表仅供参考；3. 教师在授课过程中对内容相关的部分可以自行安排讲授顺序；4. 本课程建议采用课堂讲授、讨论、多媒体教学和实际问题的分析解决相结合的多种手段开展教学。
3.1 线性定常系统的能控性线性系统的能控性和能观测性概念是卡尔曼在1960年首先提出来的。
当系统用状态空间描述以后，能控性、能观测性成为线性系统的一个重要结构特性。
这是由于系统需用状态方程和输出方程两个方程来描述输入-输出关系，状态作为被控量，输出量仅是状态的线性组合，于是有“能否找到使任意初态转移到任意终态的控制量”的问题，即能控性问题。
并非所有状态都受输入量的控制，有时只存在使任意初态转移到确定终态而不是任意终态的控制。
还有“能否由测量到的由状态分量线性组合起来的输出量来确定出各状态分量”的问题，即能观测性问题。
并非所有状态分量都可由其线性组合起来的输出测量值来确定。
能控性、能观测性在现代控制系统的分析综合中占有很重要的地位，也是许多最优控制、最优估计问题的解的存在条件，本章主要介绍能控性、能观测性与状态空间结构的关系。
第一节线性定常系统的能控性能控性分为状态能控性、输出能控性（如不特别指明便泛指状态能控性）。
状态能控性问题只与状态方程有关，下面对定常离散系统、定常连续系统分别进行研究（各自又包含单输入与多输入两种情况）：一、离散系统的状态可控性引例设单输入离散状态方程为：初始状态为：用递推法可解得状态序列：可看出状态变量只能在+1或-1之间周期变化，不受的控制，不能从初态转移到任意给定的状态，以致影响状态向量也不能在作用下转移成任意给定的状态向量。
系统中只要有一个状态变量不受控制，便称作状态不完全可控，简称不可控。
可控性与系统矩阵及输入矩阵密切相关，是系统的一种固有特性。
下面来进行一般分析。
设单输入离散系统状态方程为：(3-1)式中，为维状态向量；为纯量，且在区间是常数，其幅值不受约束；为维非奇异矩阵，为系统矩阵；为维输入矩阵：表示离散瞬时，为采样周期。
初始状态任意给定，设为；终端状态任意给定，设为，为研究方便，且不失一般性地假定。
单输入离散系统状态可控性定义如下：在有限时间间隔内，存在无约束的阶梯控制信号，,，能使系统从任意初态转移到任意终态，则称系统是状态完全可控的，简称是可控的。
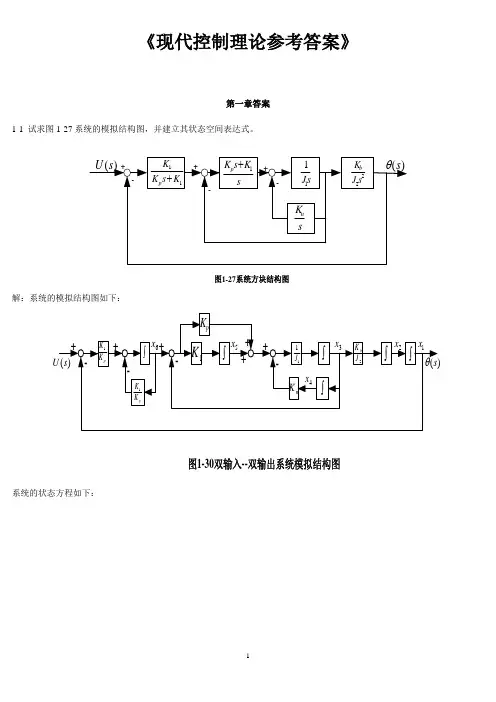
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。
图1-27系统方块结构图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
现代控制理论基础三 Prepared on 22 November 2020状态重构问题与Luenberger状态观测器前已指出，对于状态完全能控的线性定常系统，可以通过线性状态反馈任意配置闭环系统的极点。
事实上，不仅是极点配置，而且系统镇定、解耦控制、线性二次型最优控制 (LQ)问题等，也都可由状态反馈实现。
然而，在节介绍极点配置方法时，曾假设所有的状态变量均可有效地用于反馈。
但在实际情况中，并非所有的状态度变量都可用于反馈。
这时需要估计不可量测的状态变量。
迄今已有多种无需使用微分来估计不能量测状态的方法。
对不能量测状态变量的估计通常称为观测。
估计或者观测状态变量的动态系统称为状态观测器，或简称观测器。
观测器分为全维状态观测器降维状态观测器最小阶状态观测器或最小阶观测器5.5.1 问题的提法在下面有关状态观测器的讨论中，我们用x~表示被观测的状态向量。
在许多实际情况中，一般将被观测的状态向量用于状态反馈，以便产生期望的控制输入。
考虑如下线性定常系统=x+BuAxy=Cx假设状态向量x 可由如下动态方程)~(~~x C y K Bu x A x e -++=中的状态x ~来近似，则该式表示状态观测器，其中e K 称为观测器的增益矩阵。
注意到状态观测器的输入为y 和u ，输出为x ~。
式（）中右端最后一项包括可量测输出y 与估计输出x ~C 之差的修正项。
矩阵e K 起到加权矩阵的作用。
修正项监控状态变量x ~。
当此模型使用的矩阵A 和B 与实际系统使用的矩阵A 和B 之间存在差异时，由于动态模型和实际系统之间的差别，该附加修正项将减小这些影响。
图所示为带全维状态观测器的系统方块图。
图 全维状态观测器方块图5.5.2 全维状态观测器的误差方程在此讨论的状态观测器的阶数和系统的阶数相等。
假设系统由式（）和（）定义。
观测器的方程由式（）定义。
为了得到观测器的误差方程，将式（）减去式（），可得)~(~~x C Cx K x A Ax x x e ---=- )~)((x x C K A e --=定义x 与x ~之差为误差向量，即 x x e ~-=则式（）可改写为e C K A e e )(-= 由式（）可看出，误差向量的动态特性由矩阵C K A e -的特征值决定。
第一和第二讲小结一、状态空间表达式的标准形式能控标准形能观测标准形对角线标准形Jordan标准形二、矩阵的特征值及对角线化矩阵是能控标准形时的变换矩阵求法（1）特征值互异（2）重根（3）一般情形三、利用MATLAB进行系统模型之间的相互转换[A, B, C, D] = tf2ss (num, den)[num,den] = ss2tf [A,B,C,D,iu]四、时域分析的基本概念状态转移矩阵及其性质，凯莱-哈密尔顿定理最小多项式五、矩阵指数计算级数法，对角线标准形与Jordan标准形法拉氏变换法凯莱-哈密尔顿定理II、分析部分第三章线性多变量系统的能控性与能观测性分析能控性(controllability)和能观测性(observability)深刻地揭示了系统的内部结构关系，由R.E.Kalman于60年代初首先提出并研究的这两个重要概念，在现代控制理论的研究与实践中，具有极其重要的意义，事实上，能控性与能观测性通常决定了最优控制问题解的存在性。
例如，在极点配置问题中，状态反馈的的存在性将由系统的能控性决定；在观测器设计和最优估计中，将涉及到系统的能观测性条件。
在本章中，我们的讨论将限于线性系统。
将首先给出能控性与能观测性的定义，然后推导出判别系统能控和能观测性的若干判据。
3.1 线性连续系统的能控性3.1.1 概述能控性和能观测性就是研究系统这个“黑箱”的内部的状态是否可由输入影响和是否可由输出反映。
例1．给定系统的描述为u x x xx⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡2150042121 []⎥⎦⎤⎢⎣⎡-=2160x x y将其表为标量方程组的形式，有：u x x+=114 u x x2522+-= 26x y -=例3－2：判断下列电路的能控和能观测性)(t u +yCR )(t uL y23.1.2 能控性的定义考虑线性时变系统的状态方程∑:Bu x t A x+=)( ， u t D x t C t y )()()(+=，00)(x t x =，J t ∈ (3.1.1)其中，x 为n 维状态向量，u 维p 维输入向量，J 为时间定义区间，B A ,分别为n n ⨯和p n ⨯的元为t 的连续函数的矩阵。
下面给出系统能控和不能控的定义：定义1：对线性时变系统∑，如果对取定初始时刻J t ∈0的一个非零初始状态0x ，存在一个时刻J t ∈1，01t t >，和一个无约束的的容许控制)(t u ，[]10,t t t ∈，使状态由0x 转移到1t 时0)(1=t x ，则称此0x 在0t 时刻是能控的。
定义2：对线性时变系统∑，如果状态空间中的所有非零状态都是在0t 时刻为能控的，那么称系统∑在时刻t o 是能控的。
定义3：对上述线性时变系统，取定初始时刻J t ∈0，如果状态空间中存在一个或一些非零状态在时刻0t 是不能控的，则称系统∑在时刻0t 是不完全能控的。
定义的几点解释：（1） 对轨迹不加限制，是表征系统状态运动的一种定性特性；（2） 容许控制的分量幅值不加限制，且在J 上平方可积； （3） 线性系统的能控性与0t 无关；（4） 如果将上面非零状态转移到零状态，改为零状态到非零状态，则称为系统的能达性。
（5） 系统不完全能控为一中“奇异”情况。
3.1.2 能观测性的定义(3.1.1)的状态方程可以表示为⎰+=tt d u B t x t t t x 0)()(),(),()(00ττττΦΦ (3.1.2)则系统输出)()()()(),()(),()()(000t u t D d u B t t C x t t t C t y tt ++=⎰ττττΦΦ(3.1.3)若定义)()()()(),()()()(0t u t D d u B t t C t y t y tt --=⎰ττττΦ (3.1.4)这样00),()(x t t t C y Φ= (3.1.5) 所以，(3.1.5)系统的能观测性研究等价于下列系统∑: x t A x)(= x t C t y )()(= (3.1.6)定义1：如果系统的状态x (t o )在有限的时间间隔内可由输出的观测值确定，那么称系统在时刻t o 是能观测的。
定义2：对(3.16)所示系统，如果对取定初始时刻J t ∈0的一个非零初始状态0x ，存在一个有限时刻J t ∈1，01t t >，使对所有[]10,t t t ∈有0)(=t y ，则称此0x 在时刻0t 是不能观测的。
定义3：对(3.16)所示系统，如果对取定初始时刻J t ∈0，如果状态空间中存在一个或一些非零状态在时刻0x 是不能观测的，的一个非零初始状态0x ，存在一个有限时刻J t ∈1，01t t >，则称该系统在时刻0t 是不能观测的。
前已指出，在用状态空间法设计控制系统时，这两个概念起到非常重要的作用。
实际上，虽然大多数物理系统是能控和能观测的，然而其所对应的数学模型可能不具有能控性和能观测性。
因此，必须了解系统在什么条件下是能控和能观测的。
3.1节涉及到能控性，3.2节将讨论能观测性。
上面给出了系统状态能控与能观测的定义，下面我们将首先推导状态能控性的代数判据，然后给出状态能控性的标准形判据。
最后讨论输出能控性。
3.2 定常系统状态能控性判据3.2.1 定常系统状态能控性的代数判据考虑线性连续时间系统Σ： )()()(t Bu t Ax t x += (3.2.1）其中，m n nn nR B R A R t u R t x ⨯⨯∈∈∈∈,,)(,)(1，且初始条件为)0()(0x t x t ==。
如果施加一个无约束的控制信号，在有限的时间间隔10t t t ≤≤内，使初始状态转移到任一终止状态，则称由式（3.2.1）描述的系统在0t t =时为状态(完全)能控的。
如果每一个状态都能控，则称该系统为状态(完全)能控的。
引理1[格拉姆矩阵判据]线性定常系统(3.2.1)为完全能控的充分必要条件是，存在01>t ，使如下定义的格拉姆矩阵⎰--=1T 0T 1],0[t tA At c dt e BB e t W (3.2.2) 非奇异。
证明：充分性：已知],0[1t W c 非奇异，欲证系统完全能控。
采用构造法证明，构造的控制量为 011T ],0[)(T x t W e B t u c tA ---=， ],0[1t t ∈在)(t u 作用下容易解得⎰-+=111)(01)()(t t t A At dt t Bu e x et x ⎰----=1T 11011T 0],0[t c tA At At At x t dtW e BB e e x e01110],0[],0[11x t W t W ex ec c At At --=0= 充分性得证。
必要性：已知系统为完全能控，欲证],0[1t W c 非奇异。
采用反证法。
反设c W 为奇异，也即反设存在某个非零n R x ∈0， 使成立0],0[01T0=x t W x c 由此进而有dt x e BB e x x t W x t A At t c 0T 0T 001T0T 1],0[0--⎰==dt x eB t tA ⎰-=1T 020T要使上式成立，应有00T T =-x eB tA ， ],0[1t t ∈∀另一方面，因系统完全能控，对非零0x 又成立⎰-+==11101)()(0t AtAt At dt t Bu e e x et x 由此得出⎰--=100)(t Atdt t Bu e x []0T 021)(x dt t Bu e x t At⎰--= ⎰=-=100TT 0)()(t dt x t u B t u所以 00=x 。
这表明，00≠x 的假设是和系统完全能控相矛盾。
因此，反设不成立，即],0[1t W c 为非奇异。
必要性得证。
定理1[代数判据]线性定常系统(3.2.1)为完全能控的充分必要条件为 n B A AB Brank n =-][1 (3.2.3) 其中，n 为矩阵A 的维数。
][1B A AB BQ n c -= (3.2.4)称为系统的能控性判别阵。
证 充分性：已知n rankQ c =，欲证系统为完全能控。
采用反证法。
反设系统不完全能控，则格拉姆矩阵⎰--=1T 0T 1],0[t t A At c dt e BB e t W 奇异。
意味着存在某个非零向量α使成立⎰--==1T 0T T 1T],0[0t tA Atc dt eBB et W αααα⎰--=1T 0T T T ]][[t tA Atdt B eB eαα由此可得 0T =-B eAtα， ],0[1t t ∈∀现将上式求导直至)1(-n 次，再在所得结果中令0=t ，那么可得到,0T =B α 0T=AB α，02T=B A α，0,1T =-B A n α进而，表上式为 0][T 1T==-c n Q B A AB Bαα由于0≠α，所以上式意味着c Q 为行线性相关，与假设矛盾。
反设不成立，系统为完全能控。
充分性得证。
必要性：已知系统完全能控，欲证.n rankQ c =采用反证法。
反设n rankQ c <,这意味着c Q 行线性相关，因此必存在一个非零n 维常向量α，使成立 0][1TT==-B A AB BQ n c αα考虑到问题的一般性，由上式进一步得到,0T =B A iα 1,,1-=n i再据凯莱－哈密顿定理， ,,1+n n AA 均可表示为2,,A A I1,-n A 的线性组合，由此得到0T =B A iα， ,2,1=i得到B t A t A At I ]!31!21[3322T+-+-α,T B e At-=α ],0[1t t ∈∀这样⎰==--1T 01T T T 0],0[t tA At t W dt e BB e αααα表明],0[1t W 为奇异，系统不完全能控，与已知条件矛盾，反设不成立。
于是n rankQ c =, 必要性得证。
------------------------------------------------ [例3.1] 考虑由下式确定的系统：u x x x x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡1010112121 由于00011][det det ===AB B Q即Q 为奇异，所以该系统是状态不能控的。
----------------------------------------------- [例3.2] 考虑由下式确定的系统：u x x x x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡1012112121 对于该情况，01110][det det ≠-==AB B Q即Q 为非奇异，因此系统是状态能控的。
