陀螺定向测量报告记录
- 格式:doc
- 大小:1.91 MB
- 文档页数:15



陀螺逆转点法定向及精度评定摘要隧道或井巷工程测量导线布设的形式因受巷道形状的制约,若单纯采用改变导线布设形式或提高测角次数与精度等方法,往往难以满足工程施工对于测量的精度要求。
陀螺经纬仪是测量井下导线边方位角、提高测量精度的重要仪器。
尤其是在贯通测量中陀螺经纬仪的应用非常广泛。
贯通测量是一项十分重要的测量工作,必须严格按照设计要求进行。
巷道贯通后,其接合处的偏差不能超过一定限度,否则就会给采矿工程带来不利影响,甚至造成很大的损失。
本文对陀螺经纬仪工作原理介绍,以及陀螺经纬仪在贯通测量中的精度评定。
陀螺经纬仪在不同领域的贯通测量工作中运用实例的分析,总结出在贯通测量导线加测陀螺定向边的最佳位置。
关键词:陀螺定向,贯通测量,陀螺经纬仪,精度评定ABSTRACTTunnel or shaft engineering measurement wires for the form of roadway, if simple shape by changing arrangement forms or improve wires and precision Angle measurement methods, and often difficult to satisfy the measurement accuracy for engineering construction. Gyro theodolite is measured in wire edge Angle, improve the measuring precision instruments. Especially in the measurement of the photoelectric theodolite gyro breakthrough is used extensively. Through measurement is a very important measurement work, must strictly according to the design requirements. The roadway expedite, its joint deviation cannot exceed a certain limit, otherwise they will be detrimental to the mining project, and even cause great losses. This paper introduces working principle of gyro theodolite, as well as the breakthrough in the measurement of the gyro theodolite accuracy assess. Gyro theodolite in different fieldsof the measurement of the examples, this paper leads in breakthrough measurement on the edge of the directional gyro adds the best position.Key words: directional gyro; through measurement; gyro theodolite; Accuracy Assessment目录1 绪论 (1)1.1陀螺定向的研究现状 (1)1.2研究陀螺定向的目的 (1)1.3陀螺定向的应用领域及发展趋势 (2)2 陀螺经纬仪定向测量原理与方法 (3)2.1陀螺经纬仪的类型与结构 (3)2.1.1 陀螺经纬仪定向的优点及应用领域 (3)2.1.2 陀螺经纬仪的基本结构 (3)2.1.3 陀螺经纬仪的类型 (4)2.2陀螺经纬仪定向的基本步骤 (5)2.3跟踪逆转点法测定陀螺方位角的作业过程 (7)2.3.1 陀螺仪悬带零位观测 (7)2.3.2 粗略定向 (8)2.3.3 精密定向 (9)3 陀螺定向的误差分析 (13)3.1陀螺定向的误差来源 (13)3.2陀螺定向在贯通测量中的精度评定 (14)3.2.1 陀螺方位角一次测定中误差 (14)3..2.2 一次定向中误差 (14)3.3陀螺定向在贯通测量中导线的平差 (15)3.3.1 具有两条陀螺定向边导线的平差 (15)3.3.2 具有三条陀螺定向边导线的平差 (17)4 陀螺定向在贯通测量中的应用实例分析 (20)4.1陀螺定向在道路贯通测量中的应用实例分析 (20)4.1.1 工程概况 (20)4.1.2 陀螺定向技术 (20)4.1.3 精度评定 (22)4.1.4 工程分析 (23)4.2陀螺定向在矿山贯通测量中的应用实例分析 (24)4.2.1 工程概况 (24)4.2.2 陀螺定向技术 (24)4.2.3 精度评定 (26)4.2.4 工程分析 (27)4.3陀螺定向在水利贯通测量中的应用实例分析 (27)4.3.1项目概况 (27)4.3.2 陀螺定向技术 (28)4.3.3 陀螺定向精度评定 (29)4.3.4 坐标解算及成果对比分析 (30)4.3.5 工程分析 (35)5 结论 (38)参考文献 (39)致谢...................................................... 错误!未定义书签。

世界有色金属 2016年 12月上52陀螺仪在竖井定向测量的应用张石聪(云南驰宏锌锗股份有限公司,云南 曲靖 655000)摘 要:近年来,随着公司找探矿及采矿向纵深方向延伸,竖井工程已成为公司主要的运输巷道,竖井定向的精度已成为公司测量的重点和难点工程。
在实际的工程建设过程中,联系三角形定向已很难满足超深井测量定向的精度要求,因此,只有行求更为行至有效的竖井定向方法。
目前一般采用的竖井测量方法有联系三角形法、光学投点以及陀螺定向等这几种方法。
相较这几种定向方法,为了更好地确保测量时效性,满足深井测量精度的准确性,采用陀螺仪定向是目前国内及公司竖井定向的最为行之有效方法。
本文主要分析探讨陀螺仪在竖井定向测量的应用是否满足定向要求。
关键词:竖井;陀螺仪;井下定向测量中图分类号:V241.5 文献标识码:A 文章编号:1002-5065(2016)23-0052-2Application of gyroscope in vertical shaft measurementZHANG Shi-cong(Yunnan Chihong Zn&Ge Limited company,Qujing 655000,China)Abstract: In recent years, with the company looking for prospecting and mining to extend the depth, the shaft has become the company's main transport roadway, the accuracy of vertical shaft has become the focus of the company's measurement and difficult projects. In the actual process of engineering construction, connection triangle orientation has been difficult to meet the requirements of ultra deep directional precision measurement result, only for more effective methods to shaft orientation. At present, there are several methods to measure the vertical shaft, such as triangle method, optical projection and gyro orientation. Compared with these methods, in order to better ensure the timeliness of measurement, to meet the accuracy of the accuracy of the deep well measurement, the use of gyro orientation is the most effective method of the current domestic and corporate vertical orientation. This paper mainly analyzes and discusses the application of the gyro in vertical shaft measurement to meet the requirements of orientation.Keywords: shaft; gyroscope; downhole directional measurement为了进一步提高竖井定向的精度,建设单位在实际的操作过程中加强了对于竖井措施的运用,在这一过程中,为了确保竖井定向效果达到工程规范要求,相关人员加强了对于陀螺仪设备的使用。

university of science and technology of china 96 jinzhai road, hefei anhui 230026,the people's republic of china陀螺仪实验实验报告李方勇 pb05210284 sist-05010 周五下午第29组2号2006.10.22 实验题目陀螺仪实验(演示实验)实验目的1、通过测量角加速度确定陀螺仪的转动惯量;2、通过测量陀螺仪的回转频率和进动频率确定陀螺仪的转动惯量;3、观察和研究陀螺仪的进动频率与回转频率与外力矩的关系。
实验仪器①三轴回转仪;②计数光电门;③光电门用直流稳压电源(5伏);④陀螺仪平衡物;⑤数字秒表(1/100秒);⑥底座(2个);⑦支杆(2个);⑧砝码50克+10克(4个);⑨卷尺或直尺。
实验原理1、如图2用重物(砝码)落下的方法来使陀螺仪盘转动,这时陀螺仪盘的角加速度?为:?=d?r/dt=m/ip (1) 式中?r为陀螺仪盘的角速度,ip为陀螺仪盘的转动惯量。
m=f.r为使陀螺仪盘转动的力矩。
由作用和反作用定律,作用力为:f=m(g-a) (2) 式中g为重力加速度,a为轨道加速度(或线加速度)轨道加速度与角加速度的关系为:a=2h/tf2; ?=a/r (3) 式中h为砝码下降的高度,r如图1所示为转轴的半径,tf为下落的时间。
将(2)(3)代入(1)2ip?2mr2t?h2mgr可得: (4)2f测量多组tf和h的值用作图法或最小二乘法拟合数据求出陀螺仪盘的转动惯量。
2、如图3所示安装好陀螺仪,移动平衡物w使陀螺仪ab轴(x轴)在水平位置平衡,用拉线的方法使陀螺仪盘绕x轴转动(尽可能提高转速),此时陀螺仪具有常数的角动量l:l=ip.?r (5) 当在陀螺仪的另一端挂上砝码m(50g)时就会产生一个附加的力矩m*,这将使原来的角动量发生改变:dl/dt=m*=m*gr* (6) 由于附加的力矩m*的方向垂直于原来的角动量的方向,将使角动量l变化dl,由图1可见: dl=ld?这时陀螺仪不会倾倒,在附加的力矩m*的作用下将会发生进动。

测绘定向报告范文模板一、引言测绘定向是测绘工程中重要的一环,通过定向测量可以确定测量对象在空间中的方位角、仰角和距离,为后续的测量作业提供了准确的基础数据。
本报告旨在对某测绘工程项目中的定向测量进行详细的介绍与分析,以期提供参考和借鉴。
二、测绘定向工作内容1. 定向测量任务概述本次测绘定向工作的任务是确定测量对象在空间中的方位角、仰角和距离。
根据项目要求,测量对象为两个建筑物之间的距离与方位角。
2. 测量仪器与材料在本次定向测量中,采用了以下仪器和材料:- GNSS(Global Navigation Satellite System)接收机:用于接收卫星信号并测量位置坐标;- 角度测量仪:用于测量建筑物间的方位角和仰角;- 测距仪:用于测量建筑物之间的距离;- 三脚架、标尺、刷盘等辅助工具。
3. 定向测量方法本次定向测量采用了三角定位法,具体步骤如下:1. 设置测量仪器并进行初始操作,确保仪器正常工作;2. 在建筑物一上设置基准点,并使用GNSS接收机记录该点的初始坐标;3. 使用角度测量仪在基准点上测量建筑物二的方位角和仰角;4. 使用测距仪测量建筑物一与二之间的距离;5. 根据测量结果计算建筑物二的空间坐标。
三、测绘定向结果与分析1. 定向测量结果根据测量数据计算,建筑物二的空间坐标如下:- X坐标:100.00米- Y坐标:200.00米- Z坐标:30.00米2. 结果分析与评价根据测量结果可以看出,本次定向测量的准确度较高,定位误差在允许范围内。
其中,测距仪的精度对定向测量结果的影响最大,因此在测距时需要注意提高仪器使用的精度。
同时,定向测量中使用的GNSS接收机对卫星信号的接收效果也会影响定向测量的准确度。
在实际工作中,应选择合适的场地和时间进行测量,以确保接收机的性能和测量结果的精度。
四、结论与建议本次测绘定向工作顺利完成,根据测量数据计算的建筑物二的空间坐标准确无误。
为了提高测绘定向的准确性,建议在使用测距仪时更加注意仪器的精度,同时在选择测量时间和场地时要注意优化接收机的接收效果。

陀螺定向⽅法和精度评定解析陀螺逆转点法定向及精度评定摘要隧道或井巷⼯程测量导线布设的形式因受巷道形状的制约,若单纯采⽤改变导线布设形式或提⾼测⾓次数与精度等⽅法,往往难以满⾜⼯程施⼯对于测量的精度要求。
陀螺经纬仪是测量井下导线边⽅位⾓、提⾼测量精度的重要仪器。
尤其是在贯通测量中陀螺经纬仪的应⽤⾮常⼴泛。
贯通测量是⼀项⼗分重要的测量⼯作,必须严格按照设计要求进⾏。
巷道贯通后,其接合处的偏差不能超过⼀定限度,否则就会给采矿⼯程带来不利影响,甚⾄造成很⼤的损失。
本⽂对陀螺经纬仪⼯作原理介绍,以及陀螺经纬仪在贯通测量中的精度评定。
陀螺经纬仪在不同领域的贯通测量⼯作中运⽤实例的分析,总结出在贯通测量导线加测陀螺定向边的最佳位置。
关键词:陀螺定向,贯通测量,陀螺经纬仪,精度评定ABSTRACTTunnel or shaft engineering measurement wires for the form of roadway, if simple shape by changing arrangement forms or improve wires and precision Angle measurement methods, and often difficult to satisfy the measurement accuracy for engineering construction. Gyro theodolite is measured in wire edge Angle, improve the measuring precision instruments. Especially in the measurement of the photoelectric theodolite gyro breakthrough is used extensively. Through measurement is a very important measurement work, must strictly according to the design requirements. The roadway expedite, its joint deviation cannot exceed a certain limit, otherwise they will be detrimental to the mining project, and even cause great losses. This paper introduces working principle of gyro theodolite, as well as the breakthrough in the measurement of the gyro theodolite accuracy assess. Gyro theodolite in different fieldsof the measurement of the examples, this paper leads in breakthrough measurement on the edge of the directional gyro adds the best position.Key words: directional gyro; through measurement; gyro theodolite; Accuracy Assessment⽬录1 绪论 (1)1.1陀螺定向的研究现状 (1)1.2研究陀螺定向的⽬的 (1)1.3陀螺定向的应⽤领域及发展趋势 (2)2 陀螺经纬仪定向测量原理与⽅法 (3)2.1陀螺经纬仪的类型与结构 (3)2.1.1 陀螺经纬仪定向的优点及应⽤领域 (3)2.1.2 陀螺经纬仪的基本结构 (3)2.1.3 陀螺经纬仪的类型 (4)2.2陀螺经纬仪定向的基本步骤 (5)2.3跟踪逆转点法测定陀螺⽅位⾓的作业过程 (7)2.3.1 陀螺仪悬带零位观测 (7)2.3.2 粗略定向 (8)2.3.3 精密定向 (9)3 陀螺定向的误差分析 (13)3.1陀螺定向的误差来源 (13)3.2陀螺定向在贯通测量中的精度评定 (14)3.2.1 陀螺⽅位⾓⼀次测定中误差 (14)3..2.2 ⼀次定向中误差 (14)3.3陀螺定向在贯通测量中导线的平差 (15)3.3.1 具有两条陀螺定向边导线的平差 (15)3.3.2 具有三条陀螺定向边导线的平差 (17)4 陀螺定向在贯通测量中的应⽤实例分析 (20)4.1陀螺定向在道路贯通测量中的应⽤实例分析 (20)4.1.1 ⼯程概况 (20)4.1.2 陀螺定向技术 (20)4.1.3 精度评定 (22)4.1.4 ⼯程分析 (23)4.2陀螺定向在矿⼭贯通测量中的应⽤实例分析 (24)4.2.1 ⼯程概况 (24)4.2.2 陀螺定向技术 (24)4.2.3 精度评定 (26)4.2.4 ⼯程分析 (27)4.3陀螺定向在⽔利贯通测量中的应⽤实例分析 (27)4.3.1项⽬概况 (27)4.3.2 陀螺定向技术 (28)4.3.3 陀螺定向精度评定 (29)4.3.4 坐标解算及成果对⽐分析 (30)4.3.5 ⼯程分析 (35)5 结论 (38)参考⽂献 (39)致谢..................................................... 错误!未定义书签。

科学技术创新2020.26以柠条塔S1210超长隧道贯通测量为例,加入陀螺定向测量,进行贯通误差预计。
以下主要对导线网中加测陀螺定向边后的平差计算、加测最佳位置确定及实际加测情况等进行分析,提出了提高贯通精度的具体方案。
1加测陀螺边后附合导线平差及加测陀螺边最佳位置确定1.1加测陀螺边导线终点误差估计如图1,A 为起始点,AA 1为起始定向边,其坐标方位角为α0,导线测量点K 为终点,α1,αII ,…,αN 为N 条陀螺定向边,导线段数为N ,由B 点至K 点的一段为支导线。
图1导线示意图(1)由导线量边误差引起的终点K 的贯通误差(1)其中:m l :测边中误差;α':导线边与水贯通方向夹角。
(2)测角误差对贯通点误差累积影响(2)式中:η:所有导线点到重心连接线y'轴投影长;R y':支导线B 至K 各点和K 点连线y'轴投影长。
(3)陀螺定向对贯通点误差累积影响假设各条陀螺定向边精度相同为m α0时有:(3)1.2两井贯通贯通点水平方向贯通误差预计如图2,地面点P 向两竖井分布布设导线P-I-II-III 和P-IV-V-VI ,假设m β上为测角中误差,m l 上为量边中误差,陀螺定向边为α1,α2,…,α5,测定其陀螺定向方位角,陀螺定向中误差设为m α1,m α2,…,m α5,其中地下导线独立施测2次。
导线段为A-E ,E-M ,M-K ,B-C ,C-N ,N-K ,其中M-K ,B-C ,N-K 为支导线边,A-E ,E-M ,C-N 是方向附合导线边,井下测角中误差m β下,井下量边中误差m l 下。
图2导线布设示意图贯通点在x'上误差预计如下:(1)地面导线边引起贯通测量x'上的误差(4)式中:R y':地面导线各点与井下导线的起始点A 和B 的连线在y'轴上的投影长;α':地面导线各边与x'轴夹角。

陀螺仪实验陀螺仪是一种具有比较复杂的运动学和动力学现象的装置,它有一个高速旋转的定点运动转子,该转子的轴线具有定向性,这是陀螺的最大特点。
陀螺的定向性在工程中有重要用途,如舰船和导弹的导航、稳定船舶和车辆的姿态,实际上行驶的自行车能够不翻倒也是由于陀螺的定向性,这时自行车的两个轮子就是陀螺。
因此,陀螺仪实验对于学生巩固和提高所学运动学、动力学知识,对复杂运动规律的认知和分析计算都有重要作用。
一、陀螺仪的理论基础1.欧拉角如图4-9,设Oxyz 为一个正交坐标惯性系,另一个正交坐标系321x x Ox 或O ξηζ绕坐标原点O 定点转动,坐标系321x x Ox (动系)相对于Oxyz 的角位置关系可以用多种方法来描述,其中用三个欧拉(Euler )角φ,θ,ψ来描述是刚体动力学中常见的方法。
参见图4-9,坐标系321x x Ox 的当前位置,可以将坐标系Oxyz 转动三次到达,先将Oxyz 绕z 轴转φ角,记为坐标系1,其中x 轴到达节线的位置;再将坐标系1绕节线转θ角,记为坐标系2,这时z 轴变为3x 轴;最后将坐标系2绕3x 轴转ψ角就得到321x x Ox ,其中原来的x 轴变为1x 轴、y 轴变为2x 、z 轴变为3x 轴。
这三个角是相互独立的,分别称为动系的进动角(φ)、章动角(θ)和自转角(ψ)(节线绕z 轴的转动为进动,动系绕节线的转动为章动,动系绕自转轴3x 的转动为自转)。
一般情况下,它们唯一地确定动系(刚体)的瞬时角位置。
再来确定动系321x x Ox 的角速度矢量Ω。
在~t t t +∆的t ∆时间内,设动系角位置的无穷小增量为φ∆、θ∆和ψ∆,动系的这种无穷小角位置改变可以将动系分别绕z 轴转φ∆、绕节线转θ∆和绕3x 轴转ψ∆后叠加得到,且结果与转动次序无关(我们对此不作证明,但必须注意,刚体多次有限转动的结果却与转动次序有关,因此不能叠加;学生可以将一本书沿任意两条边以一种次序各转90︒,再重新按不同的次序各转90︒,结果是不同的)。
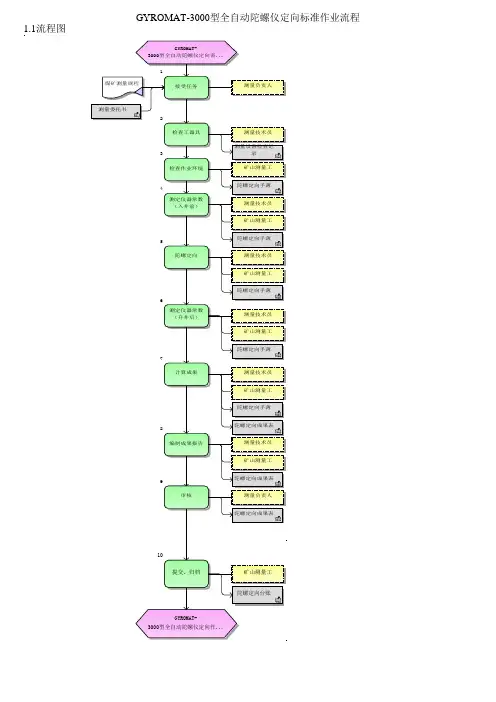
GYROMAT-3000型全自动陀螺仪定向标准作业流程
1.1流程图 1
接受任务5陀螺定向测定仪器常数
(升井后)计算成果测定仪器常数
(入井前)编制成果报告3检查作业环境9审核检查工器具GYROMAT-
3000型全自动陀螺仪定向需...
煤矿测量规程测量负责人
测量技术员
测量设备检查记
录
矿山测量工
陀螺定向手薄
测量技术员
矿山测量工
陀螺定向手薄
测量技术员
矿山测量工
陀螺定向手薄
测量技术员
矿山测量工
陀螺定向手薄
测量技术员
矿山测量工
陀螺定向手薄
测量技术员
矿山测量工
陀螺定向成果表
测量负责人
陀螺定向成果表
提交、归档GYROMAT-
3000型全自动陀螺仪定向作...
矿山测量工
陀螺定向台账。
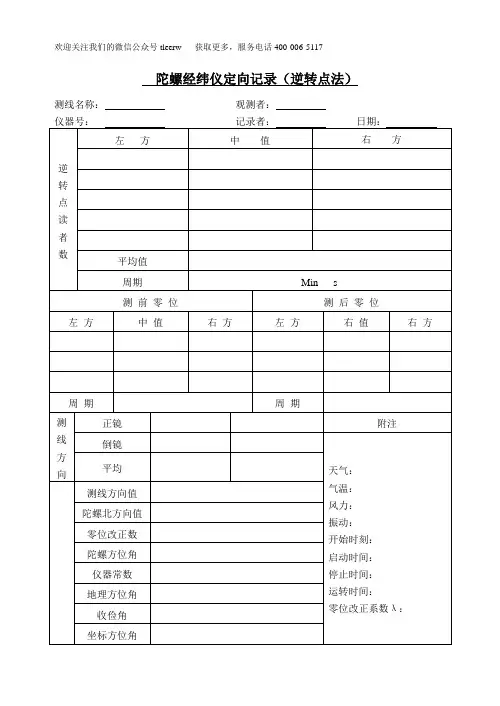
陀螺定向测量报告记录陀螺定向测量报告记录————————————————————————————————作者:————————————————————————————————日期:中国人民解放军第一〇〇一工厂陀螺仪定向报告XXX矿业1# 与3# 斜坡道实测2015年10月26日潼金矿业1#、3#斜坡道陀螺定向测量成果报告1 定向设备本次陀螺定向采用中国人民解放军第一〇〇一工厂自主研发、生产的HGG05型陀螺全站仪(1σ≤5″),编号15001,上置中翰测绘公司生产的TS-802N型全站仪。
2 数据来源点位信息由XXX矿业地勘部提供。
表1 控制点信息点位X YG3007 3816634.319 428917.073G3006 3816594.778 428824.508G3024 3811951.219 432293.488G3022 3812175.001 432187.5851053 3814565.216 430662.2291055 3814721.892 430541.139E106 3814496.765 431437.456E107 3814459.429 431541.8953083 3811452.311 431630.6633082 3811581.143 431634.860 其中地面控制点为:G3007、G3006;G3024、G3022。
α=246°52′09″,根据计算得知控制边方位角分别为:3006GG3007→α=334° 40′ 28″。
G3024→G30223 定向过程1) 在控制边进行2测回定向测量,标定仪器常数; 2) 在待定边进行3测回定向测量;3) 在原控制边进行2测回定向测量,以两次控制边测量结果检验仪器的稳定性和精度,确保陀螺定向成果准确可靠。
4 陀螺定向的限差要求1) 同一条边各测回测量结果最大互差不得超过10″; 2) 两次地面控制边测量结果均值之差不得大于15″。
陀螺经纬仪定向作业过程嘿,咱今儿就来说说这陀螺经纬仪定向作业过程。
你知道陀螺经纬仪不?那可是个厉害的家伙呢!就像一个超级精确的指南针,能给咱指引方向。
首先呢,咱得把这陀螺经纬仪好好地安置在一个合适的地方。
这就好比给一个武林高手找个好的练武场地,得平稳,不能有啥晃动干扰它发挥呀。
然后呢,咱就开始启动这个神奇的仪器啦。
想象一下,陀螺经纬仪就像一个在舞台上尽情表演的舞者,开始旋转起来啦。
它那旋转的姿态,可真是美妙又精准。
这时候,咱就得仔细观察它的一举一动,就像看着自己心爱的宝贝一样。
等它转得差不多了,咱就得进行一系列的数据测量和记录啦。
这可不能马虎,每一个数字都像是一个小宝藏,得好好地挖掘和保存起来。
这过程就像是在收集珍贵的宝石,一个都不能少,一个都不能错。
接着呢,还得进行一些计算和分析。
这可有点像解一道复杂的数学题,得动动脑筋,把那些数据都理清楚,找出正确的答案。
要是算错了一步,那可就前功尽弃啦,就好比走路走偏了方向。
在整个作业过程中,每一步都得小心翼翼,就像走在钢丝上一样。
一个不小心,就可能导致结果不准确。
这可不行呀,咱得对自己的工作负责,对最后的结果负责呀!你说这陀螺经纬仪定向作业过程是不是很有趣呢?虽然有点复杂,但是当你看到最后得出的精确结果时,那种成就感可真是无与伦比呀!就像你辛苦种的花儿终于绽放出美丽的花朵一样让人开心。
而且呀,这陀螺经纬仪定向作业可不仅仅是一项工作,它更是一种挑战呢!挑战自己的耐心,挑战自己的细心,挑战自己的专业能力。
只有通过了这些挑战,才能成为真正的高手。
你再想想,要是没有这陀螺经纬仪定向作业,那很多工程可都没法进行啦。
它就像是一个默默无闻的英雄,在背后为我们的生活提供着重要的支持。
所以呀,可别小看了这个过程哦!总之呢,陀螺经纬仪定向作业过程虽然不简单,但却是非常重要的。
咱得认真对待,用心去做,才能让它发挥出最大的作用。
让我们一起加油,把这个作业过程完成得漂漂亮亮的吧!你说是不是呢?。
陀螺进动实验报告本文主要介绍陀螺进动实验的工作原理、实验步骤和结果分析。
陀螺进动是一种非常特殊的自转运动,可以在物理学和工程学中得到广泛的应用,具有重要的研究价值。
一、实验目的本实验旨在通过实验手段深入理解陀螺进动的基本工作原理,通过观察实验现象对进动角速度等物理量进行测量。
二、实验装置实验装置主要包括:陀螺仪、杆、支架、尺子、快门、相机、计时器等实验器材。
陀螺仪是将高速旋转的陀螺静止摆放后,它的轴线会发生一个规则的圆锥进动的物理实验装置。
本次实验中采用的是普通的一体式铸钢陀螺仪。
三、实验步骤1.将陀螺在陀螺仪起始位置(竖直)灌装液压油,如蜡烛泪一样滔滔滴进。
此时液压油涂在轴承和轴肏表面,能够表面一些润滑作用,使陀螺击打出现的阻力减小。
轴承涂的太多,陀螺就阻力变大,进动现象就会比较明显,轴下涂的太多,摩擦将会导致摆动不可逆动摆摸动。
2.将陀螺安装在器材上,旋转速度要逐渐增加以避免陀螺因为力矩不均衡而抖动。
当陀螺仪外面的刻度盘转了一个圈,就将陀螺从垂直位置转到水平位置,会出现明显的进动和离心甩出现象。
3.拍摄陀螺进动照片,并用计时器测量每一次进动的周期和周期时间。
四、实验结果分析通过实验数据可得到陀螺进动的周期,进动角速度等物理量。
据此可以对陀螺进动的运动轨迹和动力学特征进行分析。
在进动过程中,陀螺的角动量守恒。
假设在竖直方向,角动量的方向为z方向,则初始状态下,角动量为-2mvlg。
当将陀螺从竖直方向转到水平方向后,由于离心力和阻力作用,陀螺会在圆锥面上运动,角速度维持原来的大小但旋转方向发生了偏转。
在进动过程中,所有的外力矩都与进动轴平行,因此进动轴角速度不断变化,在进动锥面上旋转。
总之,陀螺进动实验是一种非常重要的物理实验,在物理学和工程学研究中具有广泛的应用。
通过实验能够更深入全面地了解陀螺进动的运动特征和物理原理,同时也能够培养实验操作技能和数据分析能力。
university of science and technology of china 96 jinzhai road, hefei anhui 230026,the people’s republic of china陀螺仪实验实验报告李方勇 pb05210284 sist-05010 周五下午第29组2号2006.10.22 实验题目陀螺仪实验(演示实验)实验目的1、通过测量角加速度确定陀螺仪的转动惯量;2、通过测量陀螺仪的回转频率和进动频率确定陀螺仪的转动惯量;3、观察和研究陀螺仪的进动频率与回转频率与外力矩的关系。
实验仪器①三轴回转仪;②计数光电门;③光电门用直流稳压电源(5伏);④陀螺仪平衡物;⑤数字秒表(1/100秒);⑥底座(2个);⑦支杆(2个);⑧砝码50克+10克(4个);⑨卷尺或直尺。
实验原理1、如图2用重物(砝码)落下的方法来使陀螺仪盘转动,这时陀螺仪盘的角加速度?为:?=d?r/dt=m/ip (1) 式中?r为陀螺仪盘的角速度,ip为陀螺仪盘的转动惯量。
m=f.r为使陀螺仪盘转动的力矩。
由作用和反作用定律,作用力为:f=m(g-a) (2) 式中g为重力加速度,a为轨道加速度(或线加速度)轨道加速度与角加速度的关系为:a=2h/tf2; ?=a/r (3) 式中h为砝码下降的高度,r如图1所示为转轴的半径,tf为下落的时间。
将(2)(3)代入(1)2ip?2mr2t?h2mgr可得: (4)2f测量多组tf和h的值用作图法或最小二乘法拟合数据求出陀螺仪盘的转动惯量。
2、如图3所示安装好陀螺仪,移动平衡物w使陀螺仪ab轴(x轴)在水平位置平衡,用拉线的方法使陀螺仪盘绕x轴转动(尽可能提高转速),此时陀螺仪具有常数的角动量l:l=ip.?r (5) 当在陀螺仪的另一端挂上砝码m(50g)时就会产生一个附加的力矩m*,这将使原来的角动量发生改变:dl/dt=m*=m*gr* (6) 由于附加的力矩m*的方向垂直于原来的角动量的方向,将使角动量l变化dl,由图1可见: dl=ld?这时陀螺仪不会倾倒,在附加的力矩m*的作用下将会发生进动。
陀螺定向测量报告记录
————————————————————————————————作者:————————————————————————————————日期:
中国人民解放军第一〇〇一工厂
陀螺仪定向报告
XXX矿业1# 与3# 斜坡道实测
2015年10月26日
潼金矿业1#、3#斜坡道陀螺定向测量成果报告
1 定向设备
本次陀螺定向采用中国人民解放军第一〇〇一工厂自主研发、生产的HGG05型陀螺全站仪(1σ≤5″),编号15001,上置中翰测绘公司生产的TS-802N型全站仪。
2 数据来源
点位信息由XXX矿业地勘部提供。
表1 控制点信息
点位X Y
G3007 3816634.319 428917.073
G3006 3816594.778 428824.508
G3024 3811951.219 432293.488
G3022 3812175.001 432187.585
1053 3814565.216 430662.229
1055 3814721.892 430541.139
E106 3814496.765 431437.456
E107 3814459.429 431541.895
3083 3811452.311 431630.663
3082 3811581.143 431634.860 其中地面控制点为:G3007、G3006;G3024、G3022。
α=246°52′09″,根据计算得知控制边方位角分别为:3006
G
G3007→
α=334° 40′ 28″。
G3024→
G
3022
3 定向过程
1) 在控制边进行2测回定向测量,标定仪器常数; 2) 在待定边进行3测回定向测量;
3) 在原控制边进行2测回定向测量, 以两次控制边测量结果检验仪器的稳定性和精度,确保陀螺定向成果准确可靠。
4 陀螺定向的限差要求
1) 同一条边各测回测量结果最大互差不得超过10″; 2) 两次地面控制边测量结果均值之差不得大于15″。
5 数据处理结果
5.1 方法1数据处理方法及结果 5.1.1 仪器常数的计算
1T 1T1--A A A C γα+==控制控制
式中:∆-仪器常数;
控制α-控制边坐标方位角,即3006G G3007→α、3022G G3024→α;
1γ-控制边仪器架设点子午线收敛角;
1T A -控制边测得(含复测)的陀螺方位角均值;
子午线收敛角1γ用下式计算。
ϕλλγsin )-(1中控制=
式中:控制λ-控制边仪器架设点经度,精确到秒;
中λ-仪器架设点所处3°带中央子午线;
ϕ-仪器架设点纬度,精确到分。
标定仪器常数实测陀螺方位角结果见表2。
表2 仪器常数陀螺测定
序号控制边编号陀螺方位角均值(
1
T
A)互差
1 G3007→G3006246°25′54″
246°25′55.5″3″246°25′57″
2 G3024→G3022 334°15′54″
334°15′56″4″334°15′58″
5.1.2 待测边测量陀螺方位
待测边测定陀螺方位角结果见表3。
表3 待测边陀螺测定
序号待测边编号陀螺方位角均值(
待测
A)互差
1
1#斜坡道
1053→1055
321°53′09″
321°53′12.7″6″
321°53′15″
321°53′14″
2 1#斜坡道
E106→E107109°15′34″
109°15′35″3″109°15′34″
109°15′37″
3 3#斜坡道
3083→3082001°26′14″
001°26′18″6″001°26′20″
001°26′20″
5.1.3 复测仪器常数
仪器常数复测陀螺方位角结果见表4。
表4 复测仪器常数
序号控制边编号陀螺方位角均值两次标定常数陀螺方位角均值互差
1 G3007→G3006246°26′07″
246°26′08.5″13″246°26′10″
2 G3024→G3022334°15′46″
334°15′49.5″ 6.5″334°15′53″
经复测,两次控制边测量结果均值之差为分别为13″、6.5″,满足陀螺定向限差要求。
5.1.4 仪器常数的确定
仪器常数见表5。
表5 仪器常数
控制边
控制边坐标
方位角(控制α) 控制边子午线收敛角(1γ)
控制边测得陀螺方位角均值(1T A )
仪器常数 (C ) G3007→G3006 246°52′09″ -26′16.72″ 246°26′02″ -9.72″ G3024→G3022
334°40′28″
-24′59.47″
334°15′52.8″
-24.27″
5.1.5 数据处理
1) 待测边坐标方位角计算
2γα-+=C A 待测待测
式中:待测α-待测边坐标方位角;
待测A -待测边实测陀螺方位角;
2γ-待测边仪器架设点子午线收敛角。
子午线收敛角2γ用下式计算。
ϕλλγsin )-(2中待测=
式中:待测λ-待测边仪器架设点经度,精确到秒;
中λ-仪器架设点所处3°带中央子午线;
ϕ-仪器架设点纬度,精确到分。
2)子午线收敛角计算的说明
利用高斯坐标反算,选取与控制边相同的地球半径与扁率分母及参考椭球,由X ,Y 计算出仪器架设点(控制边、待测边)的经纬度,进而计算出相应的子午线收敛角。
5.1.5 测量结果
1)待测边(1053→1055)的坐标方位角为322°18′39.95″; 2)待测边(E106→E107)的坐标方位角为109°40′44.96″; 3)待测边(3083→3082)的坐标方位角为001°51′7.66″。
5.2 方法2数据处理方法及结果 5.2.1 仪器常数的确定
1T A -=∆控制α
其中:控制α-控制边坐标方位角;
1T A -控制点测得(含复测)陀螺方位角均值。
方法2仪器常数见表6。
表6 方法2仪器常数
控制边
控制边坐标
方位角(控制α) 控制边测得陀螺方位角均值(1T A )
仪器常数 (∆) G3007→G3006 246°52′09″ 246°26′02″ 26′07″ G3024→G3022
334°40′28″
334°15′52.8″
24′35.2″
5.2.2 数据处理
待测边坐标方位角用下式计算。
γ
α∆++∆=2T A 待
其中: ∆-仪器常数;
2T A -待测边测得陀螺方位角均值;
γ∆-控制边仪器架设点与待测边仪器架设点子午线收敛角之差。
子午线收敛角之差的计算公式用下式计算。
ϕλλγsin )-(待测控制=∆
其中:待λ-待测边仪器架设点经度,精确到秒;
控制λ-控制边仪器架设点经度,精确到秒;
ϕ-陀螺仪架设点纬度,精确到分。
5.2.3 测量结果
1)待测边(1053→1055)的坐标方位角为322°18′41.39″; 2)待测边(E106→E107)的坐标方位角为109°40′46.36″; 3)待测边(3083→3082)的坐标方位角为001°51′07.60″。
6 精度分析
1)同一条边各测回测量结果最大互差均未超过10″,详见表2、表3互差,表明仪器内符合精度符合要求;
2) 两次地面控制边测量结果均值之差均未超过15″,详见表4两次标定常数陀螺方位角均值互差,表明仪器外符合精度符合要求;
3)方法1仪器常数C 互差14.55″,表明仪器在经过运输和纬度发生
变化时仪器常数稳定性符合要求。
11
附件 测量原始数据
12
13
14
15。