ADF检验和协整检验的区别
- 格式:docx
- 大小:115.90 KB
- 文档页数:11

1.ADF单位根检验2.Engle-Granger协整检验3.Da-vdson误差修正模型4.Granger因果关系检验1、简单回归;2、工具变量回归;3、面板固定效应回归;4、差分再差分回归(difference in differnece);5、狂忒二回归(Quantile)。
大杀器就这几种,破绽最少,公认度最高,使用最广泛。
真是所谓的老少皆宜、童叟无欺。
其他的方法都不会更好,只会招致更多的破绽。
你在STATA里面还可以看到无数的其他方法,例如GMM、随机效应等。
GMM其实是一个没有用的忽悠,例如估计动态面板的diffGMM,其关键思想是当你找不到工具变量时,用滞后项来做工具变量。
结果你会发现令人崩溃的情况:不同滞后变量的阶数,严重影响你的结果,更令人崩溃的是,一些判断估计结果优劣的指标会失灵。
这GMM的唯一价值在于理论价值,而不在于实践价值。
你如果要玩计量,你就可以在GMM的基础上进行修改(玩计量的方法后面讲)。
有人会问:简单回归会不会太简单?我只能说你真逗。
STATA里面那么多选项,你加就是了。
什么异方差、什么序列相关,一大堆尽管加。
如果你实在无法确定是否有异方差和序列相关,那就把选项都加上。
反正如果没有异方差,结果是一样的。
有异方差,软件就自动给你纠正了。
这不很爽嘛。
如果样本太少,你还能加一个选项:bootstrap来估计方差。
你看爽不爽!bootstrap就是自己把脚抬起来扛在肩上走路,就这么牛。
这个bootstrap就是用30个样本能做到30万样本那样的效果。
有吸引力吧。
你说这个简单回归简单还是不简单!很简单,就是加选项。
可是,要理论推导,就不简单了。
我估计国内能推导的没几个人。
那些一流期刊上论文作者,最多只有5%的人能推导,而且大部分是海龟。
所以,你不需要会推导,也能把计量做的天花乱坠。
工具变量(IV)回归,这不用说了,有内生性变量,就用这个吧。
一旦有内生性变量,你的估计就有问题了。
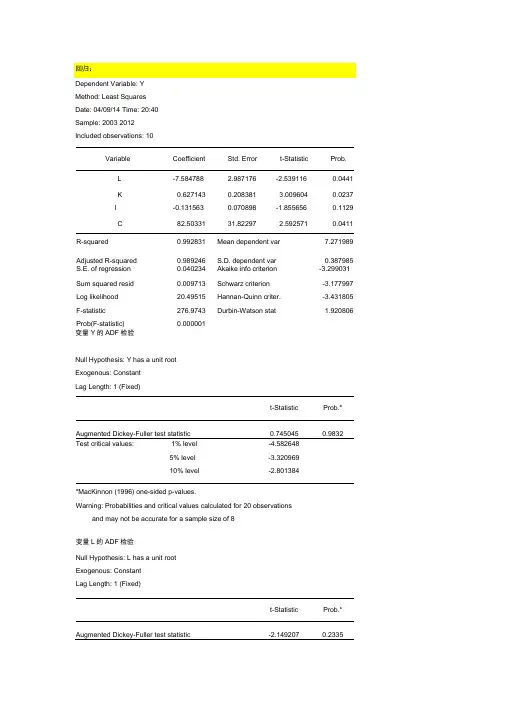

单位根检验的方法主要有以下几种:
1. ADF检验:即Augmented Dickey-Fuller检验,是对Dickey-Fuller检验的扩展,可以处理含有高阶滞后项的时间序列数据。
它通过在回归模型中加入差分滞后项来控制序列相关的干扰。
2. PP检验:即Phillips-Perron检验,与ADF检验类似,但使用非参数方法来修正序列相关的问题,对小样本性质有一定的改进。
3. KPSS检验:即Kwiatkowski-Phillips-Schmidt-Shin检验,是一种基于平稳序列的检验方法,原假设是序列是平稳的,而备择假设是序列存在单位根。
4. ERS检验:即Elliott-Rothenberg-Stock检验,是一种基于误差修正模型的单位根检验方法,适用于存在长期均衡关系的非平稳时间序列。
5. NP检验:即Nelson-Plosser检验,是一种专门用于检验宏观经济时间序列是否存在单位根的方法。
6. DF-GLS检验:即Dickey-Fuller Generalized Least Squares检验,是一种改进的Dickey-Fuller检验,使用广义最小二乘法来估计模型参数,以提高检验的功效。
7. 霍尔斯检验:即Hall测试,也是一种单位根检验方法,主要用于检测分数整合的存在。
8. 其他检验:还有一些其他的单位根检验方法,如Fisher类型的检验、Maddala-Wu检验等,它们在不同的情况下有各自的适用性和优势。

正确的计算以年为的定基指数的方法为:如果有以上一年为100的GDP指数,如何计算以某固定年份为100的GDP指数?以北京1978年为100的定基指数计算为例:第一步:(1 )将1978年的GDP指数定义为100,这样,1978年定基指数(1978=100) = 100.第二步:(2)那么1979年的定基(1978 = 100)就等于当年的同比指数,即1979年GDP定基指数(1978=100) =1979年GDP指数(以上一年为100)第三步(最关键):1980 年GDP 指数(1978=100)=1979 年GDP 指数(1978 = 100)*1980年GDP指数(以上一年为100) /100o第四步:自1981年起重复第三步,即以各上年定基指数(1978=100)分别乘以当年同比指数(上年=100的指数)再除以100,就依次可以得到所有年份以1978年为100 的定基指数。
EXCEL直接复制第三步的公式就可以计算出来。
本文来自:人大经济论坛数据交流中心版,详细出处参考:定基指数编辑1定基指数与环比指数的关系2定基指数的分类3定基指数与环比指数的区别團定基鯉即定比指数。
定基指数是指在指数数列中,各期指数都以某一固定时期为基期。
定基担数说明现象在较长时期内的发展变化情况。
定基指数与环比指数的关系编辑定基指数与环比指数可以相互换算。
定基指数等于相应时期环比指数的连乘积。
这种关系的存在要求在以下条件下:各个指数釆用的权数不变,指数值中不出现零和负数的情况。
定基指数的分类绽1.数量指标定基指数数列2.质屋指标定基指数数列定基指数与环比指数的区别编辑环比指数数列和定基指数数列各有不同用途。
若要说明各时期的现象与其前一时期对比变动的情况时,可采用环比指数数列加以分析:而要说明各时期的现象与某一固定时期对比变动情况时,就应采用定基指数数列加以分析。
根据需求约朿型经济态势下影响经济快速增长的主要是消费需求列如:消费、出口等,在此经济态势下我们构造了如下的函数:根据上表可知数据是平稳的,通过了单根检验。

adf检验通俗解释
ADF检验,即单位根检验(Augmented Dickey-Fuller Test),是一种经济学时间序列分析中常用的统计方法。
它用来判断一个时间序列数据是否存在单位根,即是否存在趋势。
通俗地说,单位根检验用来判断时间序列数据的变化趋势是否随机性的,或者说是否存在长期趋势。
如果数据存在长期趋势,就不能用简单的方法进行分析和预测,因为数据变化是有规律的。
而单位根检验可以帮助我们识别数据是否存在长期趋势,从而选择合适的模型来进行进一步分析。
ADF检验的思路是将时间序列数据拆分成趋势项、季节项、残差项等不同部分,然后分别对这些部分进行统计检验。
如果残差项(即剔除了趋势项和季节项后的数据)不存在单位根,那么我们可以认为原始数据也不存在单位根,即没有长期趋势。
通过ADF检验,我们可以得到一个统计量,根据这个统计量的显著性水平,来判断时间序列是否存在单位根。
如果统计量的值小于某个阈值,即p值小于显著性水平,那么我们可以拒绝存在单位根的假设,认为数据不存在长期趋势。
总之,ADF检验是一种用来判断时间序列数据是否存在长期趋势的方法,通过检验序列的残差项是否存在单位根,来判断原始数据是否存在单位根。


常用的协整检验方法(一)常用的协整检验方法协整检验在时间序列分析中扮演着重要的角色,它用于检测多个非平稳时间序列之间是否存在长期的关系。
本文将介绍几种常用的协整检验方法,以帮助读者更好地理解和运用这些方法。
1. 单位根检验单位根检验是协整检验的基础,常用的方法有ADF(Augmented Dickey-Fuller)检验和PP(Phillips-Perron)检验。
它们都可以用来判断一个时间序列是否是平稳的。
•ADF检验:基本思想是通过引入滞后差分来构建一个扩展的Dickey-Fuller统计量,然后进行假设检验。
•PP检验:是对ADF检验的改进,它考虑了残差自相关的情况,减少了误检的可能性。
2. Johansen检验Johansen检验是用来检验时间序列之间是否存在协整关系的方法,它基于向量自回归(VAR)模型。
Johansen检验的原假设是存在r个协整关系,其中r是一个确定的非负整数。
Johansen检验有两个主要统计量:Trace统计量和Eigenvalue统计量。
通过比较这两个统计量和对应的临界值,可以判断时间序列之间是否存在协整关系以及协整关系的个数。
3. Engle-Granger检验Engle-Granger检验是一种基于OLS回归的协整检验方法。
它首先通过引入滞后差分将非平稳时间序列转化为平稳序列,然后利用最小二乘法建立回归模型,检验残差是否平稳。
Engle-Granger检验分为两个步骤:回归阶数的确定和残差的平稳性检验。
在回归阶数的确定中,可以采用信息准则(如AIC、BIC)来选择最佳的阶数。
在残差的平稳性检验中,可以使用ADF检验或PP 检验来判断。
4. 可视化方法除了以上的统计方法,还可以运用可视化方法来辅助协整检验。
常用的可视化方法包括散点图、路径图和回归图等。
散点图可以用来观察两个时间序列之间的关系,如果它们呈现出一种趋势性的关系,可能存在协整关系。
路径图可以展示多个时间序列之间的协整关系,有助于形象地理解协整关系的存在和特征。

adf单位根检验法ADF单位根检验法(Augmented Dickey-Fuller test)是一种经济学和计量经济学领域常用的统计检验方法,用于判断一个时间序列数据是否具有单位根(unit root)。
单位根存在指示时间序列数据具有非平稳性,即呈现随机漫步(random walk)的性质,不具备长期平稳的趋势。
本文将详细介绍ADF检验的理论基础、检验过程和应用场景,并对其进行更加深入的探讨。
首先,我们来看看ADF检验的理论基础。
ADF检验是以经济学家Dickey和Fuller的名字命名的,旨在解决单位根存在导致回归分析中的问题。
单位根存在意味着时间序列数据具有非平稳性的特征,该非平稳性可能使得回归模型中的OLS(Ordinary Least Squares)估计出现偏误,导致虚假回归(spurious regression)的问题。
为了解决这个问题,Dickey和Fuller提出了ADF检验方法,通过在回归方程中引入差分变量来检验单位根的存在。
从统计学的角度来看,ADF检验是对一个自回归模型(Autoregressive model)的残差序列进行检验,并基于t统计量来判断序列是否具有单位根。
ADF检验的原假设(null hypothesis)是序列具有单位根,即存在非平稳性;备择假设(alternative hypothesis)是序列具有平稳性。
检验统计量的定义如下:ADF检验统计量:t = (β1 - 1) / SE(β1)其中,β1是线性回归方程中单位根存在与否的系数估计值,SE(β1)是其标准误。
根据统计学理论,如果序列具有单位根,则t统计量其实应该服从一个标准正态分布。
因此,我们可以利用标准正态分布的临界值来判断t统计量的显著性,从而对原假设的成立与否进行判断。
接下来,我们来看看ADF检验的实际操作过程。
ADF检验的步骤如下:1.提取时间序列数据。
首先,我们需要选择一个时间序列数据来进行检验。
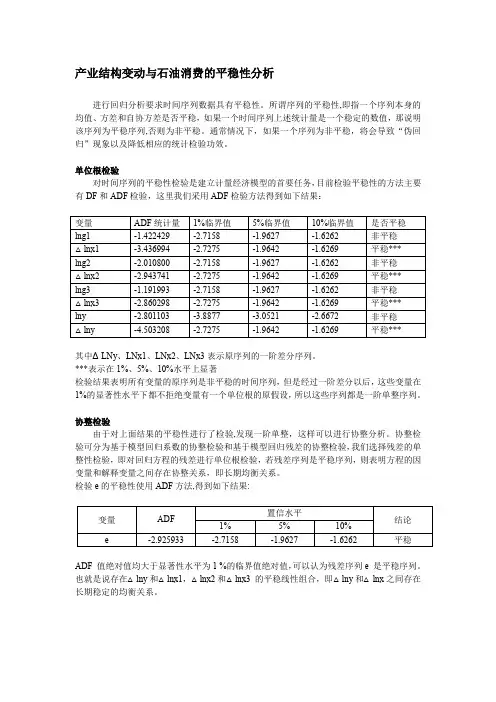
产业结构变动与石油消费的平稳性分析进行回归分析要求时间序列数据具有平稳性。
所谓序列的平稳性,即指一个序列本身的均值、方差和自协方差是否平稳,如果一个时间序列上述统计量是一个稳定的数值,那说明该序列为平稳序列,否则为非平稳。
通常情况下,如果一个序列为非平稳,将会导致“伪回归”现象以及降低相应的统计检验功效。
单位根检验对时间序列的平稳性检验是建立计量经济模型的首要任务,目前检验平稳性的方法主要有DF 和ADF 检验,这里我们采用ADF 检验方法得到如下结果:变量 ADF 统计量 1%临界值 5%临界值 10%临界值 是否平稳 lng1 -1.422429 -2.7158 -1.9627 -1.6262 非平稳 △lnx1 -3.436994 -2.7275 -1.9642 -1.6269 平稳*** lng2 -2.010800 -2.7158 -1.9627 -1.6262 非平稳 △lnx2 -2.943741 -2.7275 -1.9642 -1.6269 平稳*** lng3 -1.191993 -2.7158 -1.9627 -1.6262 非平稳 △lnx3 -2.860298 -2.7275 -1.9642 -1.6269 平稳*** lny -2.801103 -3.8877 -3.0521 -2.6672 非平稳 △lny-4.503208-2.7275-1.9642-1.6269平稳***其中ΔLNy 、LNx1、LNx2、LNx3表示原序列的一阶差分序列。
***表示在1%、5%、10%水平上显著检验结果表明所有变量的原序列是非平稳的时间序列,但是经过一阶差分以后,这些变量在1%的显著性水平下都不拒绝变量有一个单位根的原假设,所以这些序列都是一阶单整序列。
协整检验由于对上面结果的平稳性进行了检验,发现一阶单整,这样可以进行协整分析。
协整检验可分为基于模型回归系数的协整检验和基于模型回归残差的协整检验,我们选择残差的单整性检验,即对回归方程的残差进行单位根检验,若残差序列是平稳序列,则表明方程的因变量和解释变量之间存在协整关系,即长期均衡关系。

单位根检验和协整检验单位根检验和协整检验是时间序列分析中常用的两种方法。
本文将分别介绍这两种检验方法的概念、原理和应用。
一、单位根检验1.概念单位根检验,又称为ADF(Augmented Dickey-Fuller)检验,是一种用于判断时间序列是否具有平稳性的方法。
它的基本原理是通过对时间序列进行一定程度的差分,使得序列变得平稳,从而判断序列是否具有单位根。
2.原理在时间序列中,如果一个变量具有单位根,则说明它在长期内存在趋势或者周期性波动。
而如果一个变量具有平稳性,则说明它在长期内不存在趋势或者周期性波动。
因此,通过对时间序列进行差分,可以消除其中的趋势或者周期性波动,使得序列变得平稳。
ADF检验的基本原理就是通过比较差分后的时间序列与原始时间序列之间的关系来判断是否存在单位根。
具体地说,在ADF检验中,我们需要假设一个线性回归模型:ΔYt = α + βt + γYt-1 + δ1ΔYt-1 + … + δpΔYt-p + εt其中,Δ表示差分符号;Yt表示时间序列;α、β、γ、δ1~δp和εt分别表示回归系数和误差项。
如果该模型中的γ等于0,则说明时间序列具有单位根,即存在趋势或者周期性波动;如果γ小于0,则说明时间序列具有平稳性,即不存在趋势或者周期性波动。
3.应用ADF检验通常用于判断时间序列是否具有平稳性。
在金融领域中,它常被用于股票价格的分析和预测。
例如,通过对股票价格进行ADF检验,可以判断该股票是否处于上涨或下跌趋势,并进一步预测未来的走势。
二、协整检验1.概念协整检验是一种用于判断两个或多个时间序列之间是否存在长期稳定的关系的方法。
它的基本原理是通过构建线性组合,使得两个或多个时间序列之间的关系变得平稳。
2.原理在协整检验中,我们需要假设一个线性组合模型:Yt = α + βXt + εt其中,Yt和Xt分别表示两个时间序列;α、β和εt分别表示回归系数和误差项。
如果该模型中的β等于0,则说明Yt和Xt之间不存在长期稳定的关系;如果β不等于0,则说明Yt和Xt之间存在长期稳定的关系,即它们是协整的。

ADF检验通俗解释
ADF检验,全名为Augmented DickeyFuller检验,是一种用于检验时间序列数据中单位根存在性的统计检验方法。
单位根表示时间序列数据具有非平稳性,即均值或方差可能随时间变化。
以下是对ADF检验的通俗解释:
单位根的概念:在时间序列中,如果一个变量具有单位根,意味着它的变化随时间的推移而保持在某一水平上。
这使得时间序列变量呈现出一种趋势,而不是随机波动。
平稳性的重要性:在统计学和经济学中,我们通常假设数据是平稳的,即它们的均值和方差在时间上是恒定的。
如果时间序列具有单位根,就可能导致违反这个平稳性假设。
ADF检验的目的:ADF检验的目的是确定一个时间序列是否具有单位根,从而判断该序列是否是平稳的。
如果序列是平稳的,就更容易应用许多统计方法,因为这些方法通常基于数据的稳定性。
检验的步骤:
提出假设:ADF检验的零假设是序列具有单位根,即非平稳。
备择假设是序列是平稳的。
进行统计检验:通过比较计算出的检验统计量与临界值,来判断是否拒绝零假设。
如果拒绝了零假设,就认为序列是平稳的。
ADF统计量的解释:ADF检验的统计量反映了单位根的存在性。
如果ADF统计量的值小于某个阈值(即临界值),那么我们可能拒绝
零假设,认为序列是平稳的。
总体而言,ADF检验是一种用于检验时间序列平稳性的工具,它帮助我们判断一个变量是否随时间保持在某一水平上,从而影响到我们在统计建模和分析中如何处理这个变量。
金融计量学期末考试重点题型及知识点:第一大题,单项选择(主要是经典线性回归,拟合优度,协整检验,单位根检验)第二大题,名词解释1.最小二乘法:根据被解释变量的所有观测值与估计值之差的平方和最小的原则求得参数估计量2.单个变量的t检验:单总体t检验是检验一个样本平均数与一个已知的总体平均数的差异是否显着3.最小二乘估计量的统计性质:(1)在满足基本假设的情况下,多元线性模型结构参数?的普通最小二乘估计、最大或然估计及矩估计具有线性性、无偏性、有效性。
(2)同时,随着样本容量增加,参数估计量具有渐近无偏性、渐近有效性、一致性。
(3)利用矩阵表达可以很方便地证明,注意证明过程中利用的基本假设4.时间序列数据:在不同时间点上收集到的数据,这类数据反映了某一事物、现象等随时间的变化状态或程度5.多元线性回归模型的基本假设:1、关于模型设定的假设2、关于解释变量的假设3、关于随机项的假设6.拟合优度:是指回归直线对观测值的拟合程度7.可决系数:指回归平方和(SSR)在总变差(SST)中所占的比重。
可决系数可以作为综合度量回归模型对样本观测值拟合优度的度量指标。
8.脉冲响应函数定义:由于动态乘数对应每一个时期跨度j,有一个对应的动态乘数,那么如果将不同时期跨度j的动态乘数按j从小到大的顺序摆放在一起,形成一个路径,就成为了脉冲响应函数。
9.随机过程:是一系列或一组随机变量的集合,用来描绘随机现象在接连不断地观测过程中的实现结果。
对于每一次观测,得到一个观测到的随机变量10.弱平稳:是指时间序列的统计规律不会随着时间的推移而发生变化。
一个平稳的时间序列可以看作一条围绕其均值上下波动的曲线。
11.白噪音过程:一个随机过程如被称为白噪音过程,则组成该过程的所有随机序列彼此互相独立,并且均值为0,方差为恒定不变值。
12.自回归移动平均模型ARMA(p,q):13.部分自相关函数(PACF):部分自相关函数是指yt与yt+k 之间,在剔除了这两期通过中间的yt+1,yt+2,…..yt+k-1形成的线性依赖关系后,而存在的相关性。
单位根检验和协整检验一、单位根检验的概念和原理单位根检验是时间序列分析的重要工具,在经济学中广泛应用于研究时间序列数据的平稳性。
它用来判断一个时间序列是否具有单位根的存在,单位根表示一个时间序列具有非平稳的特性。
单位根检验的原理是基于自回归模型(Autoregressive Model,简称AR模型)。
AR模型是一种常用的时间序列分析模型,它假设当前观测值与过去的p个观测值存在线性关系。
在单位根检验中,通常使用的是ADF检验(Augmented Dickey-Fuller Test)和KPSS检验(Kwiatkowski-Phillips-Schmidt-Shin Test)。
ADF检验是一种常用的单位根检验方法,它基于Dickey-Fuller单位根检验,并对原检验方法进行扩展和改进。
ADF检验的原假设是存在单位根,备择假设是不存单位根。
通过ADF检验的结果,可以判断一个时间序列是否平稳。
KPSS检验是另一种常用的单位根检验方法,它的原假设是存在单位根,备择假设是不存单位根。
KPSS检验的结果与ADF检验相反,当p值小于显著性水平时,拒绝存在单位根的原假设,即序列是平稳的。
二、单位根检验的应用场景单位根检验在经济学中有着广泛的应用场景。
以下是一些常见的应用场景:1.金融市场:单位根检验可用于判断金融市场的收益率时间序列数据是否具有平稳性。
平稳的收益率序列可以用于构建有效的投资组合和预测股票价格。
2.宏观经济:在宏观经济分析中,单位根检验可用于判断经济增长率、失业率等变量是否具有平稳性。
平稳的经济变量序列可以提供有效的经济政策参考。
3.国际贸易:单位根检验可用于判断国际贸易量和汇率等变量是否具有平稳性。
平稳的贸易量和汇率序列对于制定贸易政策和汇率政策具有重要意义。
三、协整检验的概念和原理协整检验是单位根检验的一种推广,它用于判断两个或多个时间序列之间是否存在长期均衡关系。
协整关系表示两个或多个时间序列的线性组合是平稳的,即它们在长期内是相互影响的。
时间序列的平稳、非平稳、协整、格兰杰因果关系步骤:先做单位根检验,看变量序列是否平稳序列,若平稳,可构造回归模型等经典计量经济学模型;若非平稳,进行差分,当进行到第i次差分时序列平稳,则服从i阶单整(注意趋势、截距不同情况选择,根据P值和原假设判定)。
若所有检验序列均服从同阶单整,可构造VAR模型,做协整检验(注意滞后期的选择),判断模型内部变量间是否存在协整关系,即是否存在长期均衡关系。
如果有,则可以构造VEC模型或者进行Granger因果检验,检验变量之间“谁引起谁变化”,即因果关系。
1.单位根检验是序列的平稳性检验,如果不检验序列的平稳性直接OLS容易导致伪回归。
常用的ADF检验包括三个模型方程。
在李子奈的《高级计量经济学》上有该方法的全部步骤,即从含趋势项、截距项的方程开始,若接受原假设,则对模型中的趋势项参数进行t 检验,若接受则进行对只含截距项的方程进行检验,若接受,则对一阶滞后项的系数参数进行t检验,若接受,则进行差分后再ADF检验;若拒绝,则序列为平稳序列。
2.当检验的数据是平稳的(即不存在单位根),要想进一步考察变量的因果联系,可以采用格兰杰因果检验,但要做格兰杰检验的前提是数据必须是平稳的,否则不能做。
3.当检验的数据是非平稳(即存在单位根),并且各个序列是同阶单整(协整检验的前提),想进一步确定变量之间是否存在协整关系,可以进行协整检验,协整检验主要有EG两步法和JJ检验:(1)EG两步法是基于回归残差的检验,可以通过建立OLS模型检验其残差平稳性;(2)JJ检验是基于回归系数的检验,前提是建立VAR模型(即模型符合ADL模式)。
4.当变量之间存在协整关系时,可以建立ECM进一步考察短期关系,Eviews这里还提供了一个Wald-Granger检验,但此时的格兰杰已经不是因果关系检验,而是变量外生性检验,请注意识别。
5.格兰杰检验只能用于平稳序列!这是格兰杰检验的前提,而其因果关系并非我们通常理解的因与果的关系,而是说x的前期变化能有效地解释y的变化,所以称其为“格兰杰原因”。
实验报告6单位根检验和协整检验(验证性实验)实验原理:1、给定实际问题的时间序列,利用DF检验及ADF检验,检验时间序列的平稳性以及判断模型的生成形式。
2、给定两个非平稳时间序列,利用EG检验,检验它们之间是否存在协整关系。
实验题目:某地区过去38年谷物产量序列如下表所示:24.5 33.7 27.9 27.5 21.7 31.9 36.8 29.9 30.2 32.0 34.019.4 36.0 30.2 32.4 36.4 36.9 31.5 30.5 32.3 34.9 30.136.9 26.8 30.5 33.3 29.7 35.0 29.9 35.2 38.3 35.2 35.536.7 26.8 38.0 31.7 32.6这些年该地区相应的降雨量序列如下表所示:9.6 12.9 9.9 8.7 6.8 12.5 13.0 10.1 10.1 10.1 10.87.8 16.2 14.1 10.6 10.0 11.5 13.6 12.1 12.0 9.3 7.711.0 6.9 9.5 16.5 9.3 9.4 8.7 9.5 11.6 12.1 8.010.7 13.9 11.3 11.6 10.4(1)使用单位根检验,分别考察这两个序列的平稳性。
(2)选择适当模型,分别拟合这两个序列的发展。
(3)确定这两个序列之间是否具有协整关系。
(4)如果这两个序列之间有协整关系,请建立适当的模型拟合谷物产量序列的发展。
实验要求:第一步:编程建立R数据集;第二步:调用plot.ts程序对两组数据绘制时序图。
第三步:利用adf.test和pp.test检验这两个时间序列是否存在单位根?分别对这两个时间序列进行建模。
第四步:利用po.test对这对数据进行分析,考察它们是否具有协整关系。
第五步:根据这两个时间序列的相关性,利用lm建立这两个时间序列之间的回归模型。
第六步:根据输出的残差序列,判断是否平稳?同时对残差序列进行单位根检验,以验证判断是否正确,若残差序列平稳,则两个时间序列之间存在协整关系,可以建立动态回归模型。
计量经济学协整检验方法协整检验(cointegration test)是计量经济学中用于检验变量之间是否存在长期稳定的均衡关系的方法。
它的主要目的是确定变量之间的长期关系,即是否存在一个稳定的均衡关系,从而可以进行有效的经济分析和预测。
本文将介绍几种常用的协整检验方法。
1. 单位根检验方法(Unit root test)单位根检验用于检验时间序列数据是否具有非平稳性。
一般来说,如果变量是非平稳的,那么它们之间就不可能存在长期稳定的均衡关系。
常用的单位根检验方法有ADF检验(Augmented Dickey-Fuller test)和KPSS检验(Kwiatkowski–Phillips–Schmidt–Shin test)等。
ADF检验是一种参数统计方法,可以用来检验变量是否是单位根过程,从而判断是否存在协整关系;KPSS检验则是一种非参数统计方法,用于检验变量是否是平稳的。
2. Johansen协整检验方法(Johansen cointegration test)Johansen协整检验方法是一种常用的多变量协整检验方法,可以同时检验多个变量之间的协整关系。
该方法基于向量自回归模型(vector autoregressive model,VAR),通过对向量误差修正模型(vectorerror correction model,VECM)的估计,检验向量自回归参数的协整关系。
Johansen协整检验方法具有较强的参数估计效率和较好的统计性质,被广泛应用于实证研究中。
3. Engle-Granger两步法(Engle-Granger two-step method)Engle-Granger两步法是一种常用的两步骤协整检验方法。
首先,通过对变量进行单位根检验,确定哪些变量是非平稳的;然后,对非平稳变量进行协整关系的估计和检验。
该方法的优点是简单易行,适用于小样本情况,但它的估计效率相对较低。
4. 引导回归法(Bootstrap method)引导回归法是一种非参数的协整检验方法,用于解决传统统计方法在小样本情况下可能存在的偏误和低功效问题。
单位根与协整检验实验心得
1、单位根检验:单位根检验用于判断时间序列数据是否具有非平稳性。
常用的单位根检验方法有ADF(Augmented Dickey-Fuller)检验和KPSS(Kwiatkowski-Phillips-Schmidt-Shin)检验等。
通过单位根检验,可以确定时间序列数据是否需要进行差分操作以实现平稳性。
2、协整检验:协整检验用于判断多个时间序列之间是否存在长期稳定的关系。
当变量之间存在协整关系时,它们的误差项会相互修正,从而保持一个稳定的平衡状态。
常用的协整检验方法有Johansen 检验和Engle-Granger检验等。
协整关系的存在说明变量之间存在长期的均衡关系,可以应用于建立有效的统计模型。
3、实验设计:在进行单位根和协整检验前,请确保选择适当的样本时间范围和取样频率,以获取可靠的结果。
同时,还要注意样本量的充分性,样本量较小可能导致检验结果不准确。
4、结果解释:根据单位根和协整检验的结果,可以得出相应的统计量和p值。
通常,在统计显著水平(如0.05)下,如果p值小于显著性水平,则可以拒绝原假设,认为序列是平稳的或存在协整关系。
特征根迹统计量(P值)5%临界值λ_max统计量(P值)5%临界值原假设0.786230 43.63(0.02) 40.17 23.14(0.06) 24.16 0个协整向量0.659057 20.49(0.14) 24.28 16.14(0.09) 17.8 至少1个协整向量0.249925 4.35(0.66) 12.32 4.31(0.58) 11.22 至少2个协整向量0.002389 0.0023(0.88) 4.13 0.036(0.88) 4.13 至少3个协整向量正确的计算以1978年为100的定基指数的方法为:如果有以上一年为100的GDP指数,如何计算以某固定年份为100的GDP指数?以北京1978年为100的定基指数计算为例:第一步:(1)将1978年的GDP指数定义为100,这样,1978年定基指数(1978=100)=100.第二步:(2)那么1979年的定基(1978=100)就等于当年的同比指数,即1979年GDP定基指数(1978=100)=1979年GDP指数(以上一年为100)第三步(最关键):1980年GDP指数(1978=100)=1979年GDP指数(1978=100)*1980年GDP指数(以上一年为100)/100。
第四步:自1981年起重复第三步,即以各上年定基指数(1978=100)分别乘以当年同比指数(上年=100的指数)再除以100,就依次可以得到所有年份以1978年为100的定基指数。
EXCEL直接复制第三步的公式就可以计算出来。
本文来自: 人大经济论坛数据交流中心版,详细出处参考:定基指数编辑目录1定基指数与环比指数的关系2定基指数的分类3定基指数与环比指数的区别定基指数即定比指数。
定基指数是指在指数数列中,各期指数都以某—固定时期为基期。
定基指数说明现象在较长时期内的发展变化情况。
定基指数与环比指数的关系编辑定基指数与环比指数可以相互换算。
定基指数等于相应时期环比指数的连乘积。
这种关系的存在要求在以下条件下:各个指数采用的权数不变,指数值中不出现零和负数的情况。
定基指数的分类编辑1.数量指标定基指数数列2.质量指标定基指数数列定基指数与环比指数的区别编辑环比指数数列和定基指数数列各有不同用途。
若要说明各时期的现象与其前一时期对比变动的情况时,可采用环比指数数列加以分析;而要说明各时期的现象与某一固定时期对比变动情况时,就应采用定基指数数列加以分析。
此经济态势下我们构造了如下的函数:根据上表可知数据是平稳的,通过了单根检验。
对数据做回归的结果如下图:根据上表的各项指标显示出,无论从拟合优度上看,还是从t 检验、F 检验方面观察,计量模型都是不错的。
模型可以用于大略的预测。
可得三者之间的长期关系为:文献[10]庄佳强,需求因素对长期经济增长的影响研究[论文]华中科技大学博士学位论文。
(去掉了)[7][15]林哲,毛中根,中国经济平稳增长的总需求结构分析,学术月刊,2005年5月。
(去掉7)综述林哲(2005)研究表明,中国当前的最终消费需求、投资需求和进出口之间不协调。
这种不协调会带来不利的长期性影响,进而影响到长期供给潜力的实现。
庄佳强(2008)采用比较分析、统计分析、计量分析和数理建模等方法从经验和理论两方面展开论述,得出消费需求和经济长期存在相互反馈效应。
具体内容投资需求对经济的拉动作用在于:短期内投资需求是总需求的组成部分,投资增加使总产出增加;长期内投资的结果是资本存量的增加,即生产能力的增加。
居民消费与政府消费之和组成国内最终消费。
消费对经济增长的拉动作用主要体现在:一消费需求是最总需求的重要组成部分,消费增加使总产出增加;二消费(如教育和医疗保健等方面的支出)对人力资本的创造以及政府提供的生产性公共产品,为长期经济增长提供生产要素,从而推动经济增长。
进出口对于弥补国内需求不足起着非常重要的作用,因为全球化的资源流动促进经济发展[7]。
[1]作者:国家统计局,1978年以来我国经济社会发展的巨大变化[N],人民日报,2013年11月6日。
.cn/news/f53c70b6-43be-48c3-ab4b-ae4148c35c99.html重要符合要求ADF 检验和协整检验(同上)。
GDP 平减指数=现值GDP/实际GDP国内生产总值指数(上年=100)国内生产总值指数是指反映一定时期内国内生产总值变动趋势和程度的相对数,该指标是以上一年为基期计算的指数。
按不变价格计算。
GDP 环比指数:real GDP i / real GDP i-1重要(4)构造计量模型模型中各变量都是加速资本形成的,符合供给约束型经济的逻辑。
A.相关系数。
A.单根检验。
首先对这几个变量取对数,以消除数据存在的异方差。
然后对ln Y I 、ln YG、lnY M 0、ln Y M 1、ln YM 2进行ADF 检验,ADF 检验结果如下图所示: ln Y I 、ln Y G 、ln Y M 0、ln Y M 1、ln YM 2的单根检验结果 变量 差分次数 (c,t,k ) DW 值 ADF 统计值 5%临界值 1%临界值 结论 lnYI1(0,0,1)1.82-2.28-1.97-2.73ln YG 1(0,0,3)1.94-2.64-1.97-2.75lnYM 0 1(0,0,3) 1.94 -2.64 -1.97 -2.75lnYM 11(0,0,1) 1.97 -2.18 -1.97 -2.73lnYM 2 0(0,0,1) 1.97 -2.94 -1.96 -2.72B.协整检验(对lny 、ln Y 、ln Y 、ln Y 、ln Y)特征根迹统计量(p值)5%临界值λ-max统计量(p值)5%临界值原假设0.987433 125.7821(0.00)60.06141 70.02693(0.00)30.43961 0个协整向量0.809372 55.75515(0.0007)40.17493 26.51890(0.0236)24.15921 至少一个协整向量经济基本理论可以直接运用普通最小二乘法回归。
C.回归方程。
回归方程结果如下:重要反复试错,得出各个统计量之间的变动趋同性(相关系数和趋势图)、因果关系(数量方程)。
要注意各统计量之间滞后若干期数据之间的关系,工作量较大,要细心。
孝芳:可能需要做计量模型的节点在第三部分,即各个统计量之间的变动趋同性(相关系数和趋势图)、因果关系(数量方程)。
但是,不一定非做数量模型不可,发现统计规律(相关性)也是很好的。
如果做数量模型,那么,一定把握好逻辑通顺的因果关系,自己能够解释原因和结果,即明确设定解释变量和被解释变量,不能硬凑合。
同时,还要注意,一元模型一般是不可靠的,要考虑直接其他解释变量。
我们虚拟一下吧:假如,我们发现X/Y可能对I/Y有较为显著的解释关系,设前者为x1,后者为y,则有:y=f(x1),但是,这个模型不是很可靠的,因为社会经济中一个原因导致一个结果的是非常罕见的,一般都是多因一果。
因此,就必须考虑假如其他解释变量x2、x3等等,这样,模型的可绝系数才能比较高(可绝系数低的原因就是可能漏掉了重要的解释变量)。
模型做出来之后,可以只分析x1与y的关系,不管x2和x3的事儿,但模型必须涵盖这两个(或更多)解释变量。
其实,最为有意思的在第四部分,发现某种变动的前兆,并尝试解释。
抓紧做,别耽误了学报第二期印刷。
物质角度第一部分A消费率与对国货的内需率的趋势图、与投资率的趋势图、与对国货的外需率的趋势图如下B投资率与国内需求率的趋势图、对国货的外需率的趋势图、对国内的内需率的趋势图、居民消费率的趋势图如下:C净出口率与对国货的外需率的趋势图如下:D国内需求率与投资率的趋势图、与对国货的内需率的趋势图如下:E 对国货的内需率与居民消费率、对国货的外需率、投资率的趋势图如下:F 对国货的外需率与对国货的内需率、居民消费率、投资率、净出口率的趋势图如下:分析重要需求结构总的分析,从分析中可以看出来我国的需求结构失衡,我国主要靠投资和出口拉动经济增长,这是我国在经济发展过程中长期面临的一个重要问题。
因为总需求构成对于宏观经济政策的制定有着重要意义,对经济增长具有重大的拉动作用,而失衡的需求结构既会使得我国宏观经济运行暴露在外部冲击风险之下,也会降低经济运行的内在稳定性。
【来自文献11】 投资需求对经济的拉动作用在于它的两重功能:短期内投资需求是总需求的组成部分,投资增加使总产出增加;长期内投资的结果是资本存量的增加,即生产能力的增加,从而促进经济增长。
居民消费与政府消费之和组成国内最终消费。
消费对经济增长的拉动作用主要通过两个途径来实现:一是消费需求是最终需求,是总需求的重要组成部分,消费增加使总产出增加;二是消费(如教育和医疗保健等方面的支出)对人力资本的创造,以及政府提供的生产性公共产品,为长期经济增长提供生产要素,从而推动经济增长。
进出口对于弥补国内需求不足起着非常重要的作用,国际贸易被公认为是经济增长的引擎,因为全球化的资源流动主导着经济发展。
【来自文献6】货币角度可以从-11-13/7.html物质角度一:Y 与X/Y 的相关系数为0.18,y 与I/Y 的相关系数为0.51,y 与NX/Y 的相关系数为-0.20,y 与G/Y 的相关系数为0.19,y 与C/Y 的相关系数为-0.37,y 与YGI C ++的相关系数为0.42,y 与YMG I C -++的相关系数为-0.30。
X/Y 与I/Y 的相关系数为0.75,X/Y 与NX/Y 的相关系数为0.43,X/Y 与G/Y 的相关系数为0.1,X/Y 与C/Y 的相关系数为-0.65,X/Y 与YGI C ++的相关系数为0.52,X/Y 与YMG I C -++的相关系数为-0.6,I/Y 与NX/Y 的相关系数为-0.14,I/Y 与G/Y的相关系数为0.01,I/Y 与C/Y 相关系数为-0.48,I/Y 与YGI C ++相关系数为0.88,I/Y 与YM G I C -++相关系数为-0.47,NX/Y 与G/Y 的相关系数为0.16,NX/Y 与C/Y的相关系数为-0.24,NX/Y 与YGI C ++的相关系数为-0.25,NX/Y 与Y M G I C -++的相关系数为-0.19,G/Y 与C/Y 的相关系数为-0.07,G/Y 与YGI C ++的相关系数为0.14,G/Y 与Y M G I C -++的相关系数为0.23,C/Y 与YG I C ++的相关系数为-0.035,C/Y与Y M G I C -++的相关系数为0.96,YG I C ++与Y M G I C -++的相关系数为0.006。