下载文档原格式
自动控制系统校正方法介绍自动控制系统是指能够根据一定的规律或目标来自动调节和控制系统参数的一种系统。
在实际的应用中，自动控制系统往往会存在一定的误差或不稳定性，因此需要进行校正以提高系统的性能和稳定性。
下面将介绍几种常见的自动控制系统校正方法。
一、比例积分微分（PID）控制方法比例积分微分控制方法是一种基于系统误差的反馈控制方法。
该方法通过调节比例、积分和微分三个功能的权重来调节系统的动态响应和稳态误差。
具体来说，比例控制使得系统能够快速响应，积分控制消除系统的稳态误差，微分控制提高系统的稳定性。
通过合理的选择PID控制器的参数，可以有效地校正自动控制系统。
二、最小二乘法方法最小二乘法是一种通过最小化残差平方和来估计参数的数学方法。
在自动控制系统中，最小二乘法可以用于识别系统的模型参数。
通过采集系统的输入输出数据，然后利用最小二乘法进行拟合，可以得到最佳的模型参数。
这些参数可以用于校正系统，以提高控制系统的性能。
三、系统辨识方法系统辨识是通过选择合适的模型结构和估计参数来描述实际系统的过程。
系统辨识方法可以通过对系统的输入输出数据进行统计分析来估计系统的动态特性。
常见的系统辨识方法包括传递函数法、状态空间法、神经网络法等。
通过对系统进行辨识，可以得到系统的数学模型，并根据模型对系统进行校正。
四、自适应控制方法自适应控制是指根据系统的动态特性和状态变化来调整自动控制系统的控制参数。
自适应控制方法可以通过观察系统的输出和状态变量，来调整控制器的参数，以保持系统的稳定性和性能。
常见的自适应控制方法包括模型参考自适应控制、模型预测控制等。
通过自适应控制方法，可以实时地校正控制系统，并适应系统的动态变化。
总结来说，自动控制系统校正方法包括比例积分微分控制方法、最小二乘法方法、系统辨识方法和自适应控制方法等。
这些方法可以根据系统的需要选择合适的方式来进行校正，以提高自动控制系统的性能和稳定性。
在实际应用中，校正方法的选择应综合考虑系统的特性、校正精度和实施难度等因素。
工程系统校正方案怎么写一、前言工程系统校正是指在工程实施过程中对系统进行检查、调整和修正，以确保工程系统的正常运行和稳定性。
工程系统校正方案的编制是为了保证工程系统能够达到设计要求，并在系统正常运行期间具有高效率和低故障率。
本方案将对工程系统校正的目的、范围、方法、程序和注意事项进行详细阐述，以期通过科学的校正措施保障工程系统的安全稳定运行。
二、校正目的1. 确保工程系统能够按照设计要求正常运行，达到设定的性能指标；2. 保障工程系统能够在使用寿命内保持高效率、低故障率的运行状态；3. 增强工程系统的可靠性和安全性，减少系统故障和事故发生的可能性；4. 提高工程系统的能源利用效率，减少能源浪费，降低运行成本。
三、校正范围本方案适用于各类工程系统，包括但不限于建筑物电气系统、暖通空调系统、给排水系统、火灾报警系统、安防监控系统等。
针对各类工程系统的不同特点和运行要求，校正范围主要包括以下内容：1. 工程系统设备的检查、调整和测试；2. 系统运行参数的监测、校正和记录；3. 软件系统的更新、升级和优化。
四、校正方法1. 检查与测试校正前，应对工程系统进行全面的检查和测试，了解系统设备的运行状态、参数配置是否符合设计要求，软硬件是否存在异常。
对重要设备和系统部件的性能参数进行测试和记录。
2. 调整与优化根据检查和测试的结果，对系统设备进行必要的调整和优化，如调整设备的参数配置、优化控制策略、清理设备内部或更换易损件等，以保证设备在正常范围内运行。
3. 测试与验证对校正后的系统设备进行再次测试和验证，确保校正效果符合要求，系统能够正常运行和达到设计性能指标。
五、校正程序1. 制定校正计划根据工程系统的实际情况和校正要求，制定详细的校正计划，明确校正的范围、内容、时限和责任。
计划要求包括校正的时间安排、所需人员和物资配置、校正过程中的安全措施等。
2. 实施校正措施根据校正计划，对工程系统设备进行检查、调整和测试，进行设备参数的校正和优化，保证系统设备处于最佳运行状态。
系统校正的概念系统校正是指对系统的输出进行修正和改进的过程，以提高系统的准确性、可靠性和性能。
在计算机科学中，系统校正是指通过使用算法和技术来纠正和优化计算机系统的错误、偏差和噪声，以使系统输出更加准确和可靠。
系统校正可以应用于各种领域，包括自然语言处理、机器学习、计算机视觉和多媒体处理等。
在自然语言处理领域，系统校正的目标是改进自动语音识别（Automatic Speech Recognition，ASR）和机器翻译（Machine Translation，MT）等任务的性能。
自动语音识别系统通常存在误识别、漏识别和乱序等问题，而机器翻译系统可能会产生语法错误、歧义和不通顺的翻译。
通过系统校正，可以减少这些错误并提高系统的性能和可用性。
系统校正的方法可以分为两种：有监督学习和无监督学习。
有监督学习是指利用已标注的训练数据来训练系统校正模型，然后使用该模型对新的输入进行校正。
无监督学习则是在没有标注数据的情况下直接从数据中学习校正模型。
这两种方法各有优劣，具体选择哪种方法取决于具体的应用场景和数据情况。
在有监督学习中，常用的方法是使用统计模型或机器学习算法来训练校正模型。
统计模型，如隐马尔可夫模型（Hidden Markov Model，HMM）和条件随机场（Conditional Random Fields，CRF），可以对识别或翻译过程中的错误和偏差进行建模，并通过学习调整模型参数来校正系统的输出。
机器学习算法，如支持向量机（Support Vector Machines，SVM）和深度学习网络，可以通过训练大量的输入输出样本来学习模型的映射关系，从而实现系统校正。
无监督学习中的系统校正方法则主要依赖于无监督的统计建模和概率推断技术。
例如，可以使用自动编码器（Autoencoder）来学习输入数据的特征表示，然后使用这些特征来改善系统的输出。
也可以使用潜在语义分析（Latent Semantic Analysis，LSA）或主题模型（Topic Model）等方法来将输入数据映射到语义空间，从而更好地理解和校正系统的输出。
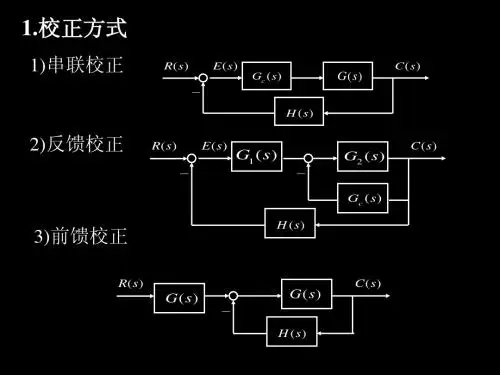
控制系统的校正（一）一、校正方式1、串联校正；2、反馈校正；3、对输入的前置校正；4、对干扰的前置校正。
二、校正设计的方法3．等效结构与等效传递函数方法主要是应用开环Bode 图。
基本做法是利用校正装置的Bode ，配合开环增益的调整，修改原系统的Bode 图，使得校正后的Bode 图符合性能指标的要求。
1．频率法2．根轨迹法利用校正装置的零、极点，使校正后的系统，根据闭环主导极点估算的时域性能指标满足要求。
将给定的结构（或传递函数）等效为已知的典型结构或典型的一、二阶系统，并进行对比分析，得出校正网络的参数。
三、串联校正1．超前校正（相位超前校正）2．滞后校正（相位滞后校正()111)(>++=a Ts aTss G c 超前校正装置的传递函数为L (ω)aT m 1=ω20lg G c (jωm )=10lg a 其中:11=tg ()()aT tg T （）−−−ϕωωω11sin 1m a a −−=+ϕ四、超前校正频率法超前校正频率法设计思路：利用超前校正装置提供的正相移，增大校正后系统的相稳定裕度。
因此，通常将校正后系统的截止频率取为：c m=ωω此时，超前装置提供的相移量为：11()sin 1m a a −−=+ϕω新的截止频率位于校正装置两个转折频率的几何中心，即：20lg ()10lg 0m G j a +=a T m 1=ω例1：单位负反馈系统的开环传递函数为)2()(+=s s Ks G 设计校正装置，使得系统的速度误差系数等于20,相稳定裕度。
45≥γ202)()(lim 0==⋅=→K s H s G s K s v 解K=40)15.0(20)(+=ωωωj j j G (1) 确定K 值调整增益后的开环频率特性为srad c /2.61=ω01004518)2.65.0(90180<=⨯−−=−tg γ11sin 1+−=−a a m ϕ(2) 计算原系统相稳定裕度14)(40211=+c c ωω截止频率满足1c ω计算相稳定裕度γ(3) 计算参数{ }a ()111)(>++=a Ts aTss G ca=3.26db 1.526.3lg 10=2020log() 5.12mm ωω=−⨯s rad m /5.8=ω5.81==a T m ω(4) 确定频率mω(5) 计算参数T 00015184511sin +−=+−−a a T =0.065011109.13421.0065.05.090)(−=+−−−=−−−c c c c tg tg tg ωωωωϕ加入校正装置后系统的开环传递函数为)1065.0)(15.0()121.0(20)()(+++=s s s s s G s G c (6) 验证001.45)(180=+=c ωϕγ满足性能指标要求。
自动控制原理第六章控制系统的校正控制系统的校正是为了保证系统的输出能够准确地跟随参考信号变化而进行的。
它是控制系统运行稳定、可靠的基础，也是实现系统优化性能的重要步骤。
本章主要讨论控制系统的校正方法和常见的校正技术。
一、校正方法1.引导校正：引导校正是通过给系统输入一系列特定的信号，观察系统的输出响应，从而确定系统的参数。
最常用的引导校正方法是阶跃响应法和频率扫描法。
阶跃响应法：即给系统输入一个阶跃信号，观察系统输出的响应曲线。
通过观察输出曲线的形状和响应时间，可以确定系统的参数，如增益、时间常数等。
频率扫描法：即给系统输入一个频率不断变化的信号，观察系统的频率响应曲线。
通过观察响应曲线的峰值、带宽等参数，可以确定系统的参数，如增益、阻尼比等。
2.通用校正：通用校正是利用已知的校准装置，通过对系统进行全面的测试和调整，使系统能够输出符合要求的信号。
通用校正的步骤通常包括系统的全面测试、参数的调整和校准装置的校准。
二、校正技术1.PID控制器的校正PID控制器是最常用的控制器之一，它由比例、积分和微分三个部分组成。
PID控制器的校正主要包括参数的选择和调整。
参数选择：比例参数决定控制系统的响应速度和稳定性，积分参数决定系统对稳态误差的响应能力，微分参数决定系统对突变干扰的响应能力。
选择合适的参数可以使系统具有较好的稳定性和性能。
参数调整：通过参数调整，可以进一步改善系统的性能。
常见的参数调整方法有经验法、试错法和优化算法等。
2.校正装置的使用校正装置是进行控制系统校正的重要工具，常见的校正装置有标准电压源、标准电阻箱、标准电流源等。
标准电压源：用于产生已知精度的参考电压，可以用来校正控制系统的电压测量装置。
标准电阻箱：用于产生已知精度的电阻，可以用来校正控制系统的电流测量装置。
标准电流源：用于产生已知精度的电流，可以用来校正控制系统的电流测量装置。
校正装置的使用可以提高系统的测量精度和控制精度，保证系统的稳定性和可靠性。
工程系统校正方案有哪些一、引言工程系统校正是指对于已经建造完成的工程系统进行调试、测试和优化，以确保系统的正常运行和高效性能。
工程系统包括了建筑物内的水电气设备、通风空调设备、照明系统等各种设备。
为了保证建筑物的正常运行和使用，需要对这些设备进行校正和优化。
本文将针对工程系统校正的相关内容进行详细的介绍，并在实际操作中提出一些可行的校正方案，以期对工程系统校正工作的实际操作提供一些帮助。
二、校正前的准备工作1. 准备校正的设备和工具：在进行工程系统校正之前，需要准备一些专业的测试仪器和工具，如电压表、电流表、压力表、温度计等。
这些设备和工具将用于对工程系统进行调试和测试。
2. 获取相关的资料和信息：在校正之前，需要对建筑物的设计图纸、安装图纸、设备运行手册等进行详细了解和熟悉。
这些资料和信息将对校正工作起到重要的指导作用。
3. 工程系统的检查和评估：在进行校正之前，需要对工程系统进行详细的检查和评估。
这包括对设备的状态、运行情况、故障情况等进行全面的了解。
三、校正方案的制定1. 根据工程系统的实际情况，确定校正的具体内容和范围。
校正的具体内容可以包括电气系统的电压电流测量、设备的功率消耗测试、通风系统的风速压力测试等。
2. 根据工程系统的实际情况，确定校正的时间和工作进程。
校正的时间可以根据建筑物的使用情况和设备的运行情况进行合理安排，以便最大限度地减少对建筑物的影响。
3. 根据工程系统的实际情况，确定校正的具体要求和标准。
校正的要求和标准可以根据建筑物的使用要求和设备的规定要求进行制定，以便确保校正工作的质量和效果。
四、校正方案的实施1. 按照校正方案的要求，对工程系统进行详细的检查和测试。
对于电气系统，可以通过测试仪器对电压、电流和功率进行测量，对设备的运行情况进行评估。
对于通风系统，可以通过测试仪器对风速、风压进行测量，对设备的运行情况进行评估。
2. 根据校正方案的要求，对工程系统进行详细的调试和优化。
控制系统的校正与调节方法一、引言控制系统的校正与调节方法是现代工程领域中重要的技术问题。
在制造和工业生产过程中，控制系统的准确性和性能稳定性对于提高生产效率和产品质量至关重要。
本文将介绍控制系统的校正与调节方法，以帮助读者更好地理解和应用控制系统技术。
二、控制系统的校正方法1. 传感器校正传感器是控制系统中的关键部件，其准确性和稳定性对整个系统的控制效果有着重要影响。
传感器校正是指通过对传感器进行实验或者理论推导，调整其输出信号以使之达到预期的准确性。
常见的传感器校正方法包括零点校正、放大倍数校正和线性度校正等。
2. 信号处理器的校正信号处理器用于处理从传感器获取的信号，将其转化为系统所需的控制信号。
为确保信号处理器的准确性和可靠性，有必要进行校正。
常见的信号处理器校正方法包括电压校准、频率校准和相位校准等。
三、控制系统的调节方法1. 反馈控制调节反馈控制调节是指根据系统输出信号与期望信号之间的差异，通过控制器对系统进行调节的方法。
该方法在工程领域被广泛应用，可以有效地改善系统的稳定性和动态性能。
常见的反馈控制调节方法包括比例控制、积分控制和微分控制等。
2. 前馈控制调节前馈控制调节是一种预先根据系统模型设计的控制器，通过输入信号的预测值来实现对系统的调节。
与反馈控制调节相比，前馈控制调节更快速、精确，适用于对系统动态特性要求较高的场景。
常见的前馈控制调节方法包括前馈增益调节和前馈补偿调节等。
3. 模糊控制调节模糊控制调节是一种利用模糊逻辑推理来实现对系统的调节的方法。
相较于传统的控制方法，模糊控制调节更适用于复杂、非线性的控制系统，能够提高系统的稳定性和鲁棒性。
常见的模糊控制调节方法包括模糊推理规则的设计和隶属度函数的确定等。
四、结论控制系统的校正与调节方法是实现高效、稳定控制的关键环节。
通过对传感器和信号处理器的校正，可以确保控制系统的准确性和可靠性。
同时，选择合适的调节方法，如反馈控制调节、前馈控制调节和模糊控制调节等，可根据系统需求来提高控制的性能指标。
·196· 第6章 线性系统的校正方法重点与难点 一、基本概念 1. 理想的频率特性系统开环频率特性与系统时域指标之间有一定的关系。
对于二阶系统而言，相位裕量γ、截止频率c ω与时域指标（超调量σ%、调节时间s t ）有确定性关系。
对高阶系统而言，γ，c ω都可以粗略估计高阶系统的响应特性。
相位裕量越大，系统阶跃响应的超调量σ%和调节时间s t 就越小；c ω也近似与s t 成反比关系。
因此，理想的频率特性应该有较大的相位裕量；希望响应快的系统就应该有大一点的c ω。
闭环系统（单位反馈）的频率特性有如下关系：⎪⎩⎪⎨⎧>>=<<≤= )( |)(20lg )( )1( )1|(| ||)(通常称为高频段通常称为低频段当有积分环节时c c j |G a a a A ωωωωωω (6.1) 式中)(ωj G 为开环频率特性。
因此，若希望系统有较强的抗高频干扰能力，c ω应该小，而且|)(|lg 20ωj G 要衰减快。
如果频率特性用渐近线方法描述，理想的频率特性应该在c ω处以－20dB/dec 斜率穿越0dB 线，才能获得较大的相位裕量。
综合上所述，理想的频率特性应有积分环节且开环增益大，以满足稳态误差的要求；在截止频率c ω的频域（通常称为中频段），应以－20dB/dec 的斜率穿越0dB 线，并占有足够宽的频带，以保证系统具备较大的相位裕量；在c ωω>>的高频段，频率特性应该尽快衰减，以消减噪声影响。
2. 系统的校正当系统频率特性不满足理想的频率特性指标（通常的指标体系为：闭环谐振峰值r M 、谐振频率r ω、带宽频率b ω或开环频率特性的相位裕量γ、截止频率c ω、开环增益K 、幅值裕量g H 等）时，需要引入校正网络，使新系统的频率特性满足要求。
设计校正网络参数通常用频率校正方法。
当希望系统的闭环极点达到要求时，需要加入某一校正网络以改变闭环极点。
通常采用根轨迹校正方法。
3. 校正方式·197·校正方式是指校正装置与被控对象的连接方式，通常有串联、反馈、前馈、干扰补偿、复合校正等方式。
以)(s G c 表示校正装置的传递函数，)(s G 表示被控对象的传递函数，可得以下几种校正连接。
串联校正方式如图6-1所示。
图6-1 串联校正反馈校正方式如图6-2所示。
图6-2 反馈校正干扰补偿校正方式如图6-3所示。
图6-3 干扰补偿复合校正方式如图6-4所示。
图6-4 复合校正·198· 4. 常用校正网络及其特性常用的校正网络及其特点如表6-1所示。
5. 频率响应校正方法（1）串联超前校正：利用超前网络的相位超前特性，正确地将截止频率置于超前网络交接频率1/)(aT 和T /1之间。
无源超前网络的设计步骤为：i. 根据稳态误差要求，确定开环增益K 。
ii. 利用已确定的开环增益K ，计算未校正系统的相位裕量。
iii. 根据截止频率cω''的要求，计算超前网络参数a 和T ，公式如下： ⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫-=''+=''=='''-=a a a L L a T m c m m c c m 21arctg )(lg 10)()(1ϕωγϕγωωω （6.2）式中T a m m ,,,ϕω为超前网络参数；)(cωγ''通常用估计方法给出，因此还需进行下一步。
iv. 验算已校正系统相位裕量和幅值裕量（有时没有幅值裕量要求）。
v. 确定超前网络的元件值。
（2）串联滞后校正：利用滞后网络的高频幅值衰减特性，使截止频率降低，从而使系统获得较大的相位裕量。
设计步骤如下：i. 根据稳态误差要求，确定开环增益K 。
ii. 利用已确定的开环增益，确定未校正系统的截止频率cω'、相位裕量γ和幅值裕量g h 。
iii. 选择不同的cω''，计算或查找相位裕量，根据相位裕量γ''要求，选择校正后系统的截止频率cω''。
iv. 确定滞后网络参数b 和T 。
v. 验算系统的幅值裕量和相位裕量。
计算公式为⎪⎪⎭⎪⎪⎬⎫''=='''+''+''=''ccc cbT L b ωωωϕωγγ1.010)(lg 20)()( (6.3)表6.1 常用的校正网络及其特点·199··226· （3）串联滞后－超前校正：利用超前部分提高相位裕量,利用滞后部分调整系统的稳态性能。
该网络具有滞后校正和超前校正的优点。
设计步骤如下：i ．根据稳态性能要求确定开环增益K 。
ii. 利用已确定出的开环增益K ，求出未校正系统的截止频率cω'、相位裕量γ及幅值裕量g h 。
iii. 选择未校正系统的对数幅频特性渐近线斜率从－20dB/dec 变为－40dB/dec 的交接频率，作为校正网络超前部分的交接频率b ω。
iv. 根据响应速度的要求，选择系统的截止频率cω''和校正网络的衰减因子a /1。
下式成立：0)lg(20)(lg 20=''+'''+-c b cT L a ωω (6.4) 式中 bb T ω1=v. 根据相位裕量要求，估算校正网络滞后部分的交接频率a ω。
vi. 验算相位裕量和幅值裕量。
vii. 选择网络元件值。
（4）三种串联校正方法的特点：串联超前校正可提高系统的截止频率和相位裕量，从而减小了阶跃响应的超调量和调节时间；串联滞后校正可以提高系统的相位裕量，降低系统的截止频率，从而使系统的阶跃响应超调量下降并提高了系统的抗干扰能力。
滞后－超前校正兼有两者的优点，既可提高系统的响应速度、降低超调量，又能抑制高频噪声。
（5）反馈校正：根据图6-2所示可知,反馈校正系统的开环传递函数为)()(1)()()(221s G s G s G s G s G c +⋅= （6.5）如果在对系统动态性能起主要影响的频率范围内，下列关系成立：1|)()(|2>>ωωj G j G c （6.6）那么 )(/)()(1s G s G s G c ≈这样，)(s G c 的设计就可参照串联校正的方法进行。
反馈校正可以消弱非线性影响、减小时间常数、降低参数变化的敏感性、抑制噪声等。
6. 根轨迹校正多数高阶系统具有一对共轭主导极点，其位置对系统动态性能起着决定性的影响。
·227·因此，可以把系统的性能指标要求转化成对系统希望主导极点的位置要求。
根轨迹校正实际上可按这些希望主导极点位置来确定校正装置中的参数，并称其为希望极点位置法。
（1）串联超前校正：如果原系统具有不理想的动态特性，且全部开环极点为实极点，则以采用单级超前网络进行校正。
设计步骤为：i. 根据系统的性能指标要求，确定希望闭环主导极点位置。
ii. 如果系统轨迹不通过该希望闭环主导极点，则不能用调整增益法来实现。
因此，需要按下式计算由超前网络产生的超前角c ϕ:ϕϕ-︒-=180c （6.7）式中∑∑==-∠--∠=m j ni i j p s z s 1111ϕiii. 确定超前网络的零极点位置。
iv. 验算性能指标要求。
（2）串联滞后校正：设计步骤为： i. 确定希望闭环主导极点位置。
ii. 由︒10夹角法确定滞后网络零点，并近似计算希望主导极点上的根轨迹增益。
iii. 根据稳态性能指标要求计算滞后网络参数。
iv. 根据相位条件验算希望主导极点。
7. 干扰补偿对于图6-3所示的干扰补偿系统，有01)()(1=+s G s G c8. 复合校正对于图6-4所示的复合校正系统，有)()()()]()()[()()(221s R s G s G s C s R s G s G s C c +-= （6.9）当取)(1)(2s G s G c =时，复合控制系统将实现误差全补偿。
当)(2s G 中的分母阶次大于分子阶次时，要考虑)(s G c 的可实现性问题。
二、基本要求（1）掌握校正网络频率特性及其作用。
（2）正确选择校正网络。
（3）重点掌握串联校正的设计方法，包括频率设计法和轨迹设计法。
（4）掌握反馈校正、复合校正设计方法。
（5）掌握指标验证方法。
·228· 三、重点与难点 1. 重点（1）正确理解控制系统校正的概念；明确系统校正的方式、校正的本质和校正装置的基本设计方法。
（2）正确理解串联校正的基本控制规律，及其控制作用的物理本质。
（3）掌握串联超前、串联滞后和滞后一超前校正的特点及其对系统的作用。
（4）掌握希望对数幅频特性曲线的绘制方法，能利用系统开环对数渐近幅频特性曲线，定性分析校正装置对原系统性能的影响。
（5）熟悉几种典型的有源及无源校正装置。
（6）掌握根轨迹校正方法。
2. 难点（1）根据性能指标确定选取的校正方案。
因为超前校正会使系统的截止频率c ω增大，因此，当未校正系统对数幅频特性在a c ωωω≤≤区间的斜率为－40dB/dec ，且c a ωω-足够大时，才可选择超前校正。
滞后校正实际上利用未校正系统的－20dB/dec 斜率的频率段。
因此当系统对c ω的要求不高，低频段－20dB/dec 斜率占有较宽的频带，且希望的c ω在此频带内时，可以选择滞后校正。
当对系统响应速度要求高，且系统在a c ωωω≤≤区间的－40dB/dec 斜率占有的频带c a ωω-较小时，宜采用滞后－超前校正。
（2）校正网络参数的确定。
① 串联超前校正网络参数的确定根据频率特性的渐近线方程，超前网络的参数可根据下式确定：⎪⎪⎪⎭⎪⎪⎪⎬⎫=''''=''-''≥=''=-=1|)(|1)(121a r c t gc ccG m c m m aT j G j a T a a ωωωγγϕωωϕ （6.10）式中 )(180)(c c G j G j ωωγ''∠+︒='' |)(|cj G ω''可用渐近线描述为 2)(|)(|ccKaj G ωω''≈'' （6.11） a K 为常数。
为了便于计算，取·229·︒+'-''=5()(cG m j ωγγϕ～)12︒ （6.12） 由于式（6.12）中对)(cG ωγ''的近似，相位裕量还需验算。
