新人教版八年级下数学第一次月考试题

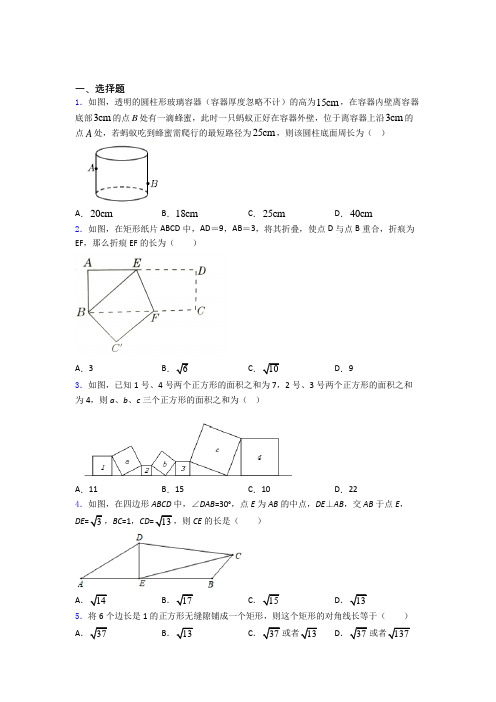
一、选择题1．如图，透明的圆柱形玻璃容器（容器厚度忽略不计）的高为15cm，在容器内壁离容器底部3cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在容器外壁，位于离容器上沿3cm的点A处，若蚂蚁吃到蜂蜜需爬行的最短路径为25cm，则该圆柱底面周长为（）A．20cm B．18cm C．25cm D．40cm2．如图，在矩形纸片ABCD中，AD＝9，AB＝3，将其折叠，使点D与点B重合，折痕为EF，那么折痕EF的长为（）A．3 B．6C．10D．93．如图，已知1号、4号两个正方形的面积之和为7，2号、3号两个正方形的面积之和为4，则a、b、c三个正方形的面积之和为（）A．11 B．15 C．10 D．224．如图，在四边形ABCD中，∠DAB=30°，点E为AB的中点，DE⊥AB，交AB于点E，DE=3，BC=1，CD=13，则CE的长是（）A14B17C15D135．将6个边长是1的正方形无缝隙铺成一个矩形，则这个矩形的对角线长等于（）A37B13C3713D371376．如图，OP ＝1，过点P 作PP 1⊥OP ，且PP 1＝1，得OP 1＝2；再过点P 1作P 1P 2⊥OP 1且P 1P 2＝1，得OP 2＝3；又过点P 2作P 2P 3⊥OP 2且P 2P 3＝1，得OP 3＝2……依此法继续作下去，得OP 2018的值为( )A ．2016B ．2017C ．2018D ．20197．在平面直角坐标系中，已知平行四边形ABCD 的点A （0，﹣2）、点B （3m ，4m +1）（m ≠﹣1），点C （6，2），则对角线BD 的最小值是（ ）A ．32B ．213C ．5D ．68．在Rt△ABC 中，∠C=90°，AC=3，BC=4，则点C 到AB 的距离是（ ）A ．34B ．35C ．45D ．1259．如图， 在ABC 中，CE 平分ACB ∠，CF 平分ABC 的外角ACD ∠，且EF //BC 交AC 于M ，若CM 4=，则22CE CF +的值为（ ）A ．8B ．16C ．32D ．6410．如图，在矩形ABCD 中，AB =8，BC =4，将矩形沿AC 折叠，点B 落在点B ′处，则重叠部分△AFC 的面积为（ ）A ．12B ．10C ．8D ．6二、填空题11．如图，AB ＝12，AB ⊥BC 于点B ， AB ⊥AD 于点A ，AD ＝5，BC ＝10，E 是CD 的中点，则AE 的长是____ ___．12．如图，Rt△ABC中，∠ACB＝90o，AC＝12，BC＝5，D是AB边上的动点，E 是AC边上的动点，则BE＋ED的最小值为．13．如图，正方体的底面边长分别为2cm和3cm，高为5cm．若一只蚂蚁从P点开始经过四个侧面爬行一圈到达Q点，则蚂蚁爬行的最短路径长为_____cm．14．已知x，y为一个直角三角形的两边的长，且（x﹣6）2=9，y=3，则该三角形的第三边长为_____．15．如图，在□ABCD中，AC与BD交于点O，且AB=3，BC=5．①线段OA的取值范围是______________；②若BD-AC=1，则AC•BD= _________．16．如图，直线l上有三个正方形a，b，c，若a，c的边长分别为5和12，则b的面积为_________________.17．如图，在矩形ABCD中，AD＞AB，将矩形ABCD折叠，使点C与点A重合，折痕为MN，连接CN．若△CDN的面积与△CMN的面积比为1：3，则22MNBM的值为______________．18．如图，在四边形ABCD 中，AD =4，CD =3，∠ABC =∠ACB =∠ADC =45°，则2________BD =．19．在ABC 中，12AB AC ==，30A ∠=︒，点E 是AB 中点，点D 在AC 上，32DE =，将ADE 沿着DE 翻折，点A 的对应点是点F ，直线EF 与AC 交于点G ，那么DGF △的面积=__________．20．如图，由两个直角三角形和三个正方形组成的图形，已知25AB = ，24AC = 其中阴影部分面积是_____________平方单位．三、解答题21．如图，在等腰直角三角形ABC 中，∠ACB =90°，AC=BC ，AD 平分∠BAC ，BD ⊥AD 于点D ，E 是AB 的中点，连接CE 交AD 于点F ，BD =3，求BF 的长．22．阅读与理解：折纸，常常能为证明一个命题提供思路和方法．例如，在ABC 中，AB AC >（如图），怎样证明C B ∠>∠呢？分析：把AC 沿A ∠的角平分线AD 翻折，因为AB AC >，所以，点C 落在AB 上的点C '处，即AC AC '=，据以上操作，易证明ACD AC D '△△≌，所以AC D C '∠=∠，又因为AC D B '∠>∠，所以C B ∠>∠．感悟与应用：（1）如图（a ），在ABC 中，90ACB ∠=︒，30B ∠=︒，CD 平分ACB ∠，试判断AC 和AD 、BC 之间的数量关系，并说明理由；（2）如图（b ），在四边形ABCD 中，AC 平分BAD ∠，16AC =，8AD =，12DC BC ==，①求证：180B D ∠+∠=︒；②求AB 的长．23．如图，△ACB 和△ECD 都是等腰直角三角形，∠ACB ＝∠ECD ＝90°，点D 在边AB 上，点E 在边AC 的左侧，连接AE ．（1）求证：AE ＝BD ；（2）试探究线段AD 、BD 与CD 之间的数量关系；（3）过点C 作CF ⊥DE 交AB 于点F ，若BD ：AF ＝1：22，CD ＝36+，求线段AB 的长．24．已知ABC ∆中，AB AC =.（1）如图1，在ADE ∆中，AD AE =，连接BD 、CE ，若DAE BAC ∠=∠，求证：BD CE =（2）如图2，在ADE ∆中，AD AE =，连接BE 、CE ，若60DAE BAC ∠=∠=，CE AD ⊥于点F ，4AE =，5EC =，求BE 的长；（3）如图3，在BCD ∆中，45CBD CDB ∠=∠=，连接AD ，若45CAB ∠=，求AD AB的值.25．如图，在△ABC 中，∠C ＝90°，把△ABC 沿直线DE 折叠，使△ADE 与△BDE 重合．(1)若∠A ＝35°，则∠CBD 的度数为________；(2)若AC ＝8，BC ＝6，求AD 的长；(3)当AB ＝m(m>0)，△ABC 的面积为m ＋1时，求△BCD 的周长．(用含m 的代数式表示)26．如图，己知Rt ABC ∆，90ACB ∠=︒，30BAC ∠=︒，斜边4AB =，ED 为AB 垂直平分线，且23DE =DB ，DA .（1）直接写出BC=__________，AC=__________；（2）求证：ABD∆是等边三角形；（3）如图，连接CD，作BF CD⊥，垂足为点F，直接写出BF的长；（4）P是直线AC上的一点，且13CP AC=，连接PE，直接写出PE的长.27．如图，点A是射线OE：y＝x（x≥0）上的一个动点，过点A作x轴的垂线，垂足为B，过点B作OA的平行线交∠AOB的平分线于点C．（1）若OA＝2，求点B的坐标；（2）如图2，过点C 作CG ⊥AB 于点G ，CH ⊥OE 于点H ，求证：CG ＝CH ．（3）①若点A 的坐标为（2，2），射线OC 与AB 交于点D ，在射线BC 上是否存在一点P 使得△ACP 与△BDC 全等，若存在，请求出点P 的坐标；若不存在，请说明理由．②在（3）①的条件下，在平面内另有三点P 1），P 2（2，），P 3（，2），请你判断也满足△ACP 与△BDC 全等的点是 ．（写出你认为正确的点）28．（知识背景）据我国古代《周髀算经》记载，公元前1120年商高对周公说，将一根直尺折成一个直角，两端连接得到一个直角三角形，如果勾是3，股是4，那么弦就等于5，后人概括为“勾三、股四、弦五”．像3、4、5这样为三边长能构成直角三角形的三个正整数，称为勾股数．（应用举例）观察3，4，5；5，12，13；7，24，25；…可以发现这些勾股数的勾都是奇数，且从3起就没有间断过，并且勾为3时，股14(91)2=-，弦15(91)2=+； 勾为5时，股112(251)2=-，弦113(251)2=+； 请仿照上面两组样例，用发现的规律填空：（1）如果勾为7，则股24＝ 弦25＝（2）如果勾用n （3n ≥，且n 为奇数）表示时，请用含有n 的式子表示股和弦，则股＝ ，弦＝ ．（解决问题）观察4，3，5；6，8，10；8，15，17；…根据应用举例获得的经验进行填空：（3）如果,,a b c 是符合同样规律的一组勾股数，2a m =（m 表示大于1的整数），则b = ，c = ，这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式． （4）请你利用柏拉图公式，补全下面两组勾股数（数据从小到大排列）第一组： 、24、 ：第二组： 、 、37．29．如图1，在正方形ABCD 中，点E ，F 分别是AC ，BC 上的点，且满足DE ⊥EF ，垂足为点E ，连接DF ．（1）求∠EDF= （填度数）；（2）延长DE 交AB 于点G ，连接FG ，如图2，猜想AG ，GF ，FC 三者的数量关系，并给出证明；（3）①若AB=6，G 是AB 的中点，求△BFG 的面积；②设AG=a ，CF=b ，△BFG 的面积记为S ，试确定S 与a ，b 的关系，并说明理由．30．（已知：如图1，矩形OACB的顶点A，B的坐标分别是（6，0）、（0，10），点D 是y轴上一点且坐标为（0，2），点P从点A出发以每秒1个单位长度的速度沿线段AC﹣CB方向运动，到达点B时运动停止．（1）设点P运动时间为t，△BPD的面积为S，求S与t之间的函数关系式；（2）当点P运动到线段CB上时（如图2），将矩形OACB沿OP折叠，顶点B恰好落在边AC上点B′位置，求此时点P坐标；（3）在点P运动过程中，是否存在△BPD为等腰三角形的情况？若存在，求出点P坐标；若不存在，请说明理由．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】将容器侧面展开，建立A关于EG的对称点A′，根据两点之间线段最短可知A′B的长度即为最短路径，由勾股定理求出A′D即圆柱底面周长的一半，由此即可解题．【详解】解：如图，将圆柱展开，EG为上底面圆周长的一半，作A 关于E 的对称点A '，连接A B '交EG 于F ，则蚂蚁吃到蜂蜜需爬行的最短路径为AF BF +的长，即 25cm AF BF A B '+==，延长BG ，过A '作A D BG '⊥于D ，3cm AE A E '==，153315cm BD BG DG BG AE ∴=+=+=-+=，Rt A DB '∴△中，由勾股定理得：2222251520cm A D A B BD ''=-=-=， ∴该圆柱底面周长为：20240cm ⨯=，故选D ．【点睛】本题考查了平面展开---最短路径问题，将图形展开，利用轴对称的性质和勾股定理进行计算是解题的关键．同时也考查了同学们的创造性思维能力．2．C解析：C【分析】做点F 做FH AD ⊥交AD 于点H ，因此要求出EF 的长，只要求出EH 和HF 即可；由折叠的性质可得BE=DE=9-AE ，在Rt ABE △中应用勾股定理求得AE 和BE ，同理在Rt BC F 'Rt ABE △中应用勾股定理求得BF ，在Rt EFH 中应用勾股定理即可求得EF ．【详解】过点F 做FH AD ⊥交AD 于点H ．∵四边形EFC B '是四边形EFCD 沿EF 折叠所得，∴ED=BE ，CF=C F '，3BC CD '==∵ED=BE ，DE=AD-AE=9-AE∴BE=9-AE∵Rt ABE △，AB=3，BE=9-AE∴()22293AE AE -=+∴AE=4∴DE=5∴9C F BC BF BF '=-=-∴Rt BC F '，3BC '=,9C F BF '=-∴()22293BF BF -+=∴BF=5，EH=1∵Rt EFH ，HF=3，EH=1∴EF ==故选：C ．【点睛】本题考查了翻折变换，矩形的性质，勾股定理等知识，解题的关键是学会利用参数构建方程解决问题． 3．B解析：B【分析】由直角三角形的勾股定理以及正方形的面积公式不难发现：a 的面积等于1号的面积加上2号的面积，b 的面积等于2号的面积加上3号的面积，c 的面积等于3号的面积加上4号的面积，据此可以求出三个的面积之和.【详解】利用勾股定理可得：12a S S S =+ ，23b S S S =+，34c S S S =+∴122334a b c S S S S S S S S S ++=+++++74415=++=故选B【点睛】本题主要考查勾股定理的应用，熟练掌握相关性质定理是解题关键.4．D解析：D【解析】【分析】连接BD ，作CF ⊥AB 于F ，由线段垂直平分线的性质得出BD=AD ，AE=BE ，得出∠DBE=∠DAB=30°，由直角三角形的性质得出BD=AD=2DE=DE=3，证出△BCD 是直角三角形，∠CBD=90°，得出∠BCF=30°，得出BF=12BC=12，求出EF=BE+BF=72，在Rt△CEF中，由勾股定理即可得出结果．【详解】解：连接BD，作CF⊥AB于F，如图所示：则∠BFC=90°，∵点E为AB的中点，DE⊥AB，∴BD=AD，AE=BE，∵∠DAB=30°，∴∠DBE=∠DAB=30°，BD=AD=2DE=233，∵BC2+BD2=12+（32=13=CD2，∴△BCD是直角三角形，∠CBD=90°，∴∠CBF=180°-30°-90°=60°，∴∠BCF=30°，∠BFC=90°，∴∠BCF=30°，∴BF=12BC=12，332，∴EF=BE+BF=72，在Rt△CEF中，由勾股定理得：227313 22⎛⎫⎛⎫+=⎪⎪ ⎪⎝⎭⎝⎭故选D．【点睛】本题考查了勾股定理、勾股定理的逆定理、线段垂直平分线的性质、等腰三角形的性质；熟练掌握勾股定理和逆定理是解题的关键．5．C解析：C【分析】如图1或图2所示，分类讨论，利用勾股定理可得结论．【详解】当如图1所示时，AB=2，BC=3，∴AC=2223=13；当如图2所示时，AB=1，BC=6，∴221+6=37故选C．【点睛】本题主要考查图形的拼接，数形结合，分类讨论是解答此题的关键．6．D解析：D【解析】【分析】由勾股定理求出各边，再观察结果的规律.【详解】∵OP=1，OP12OP23OP34=2，∴OP45…，OP20182019故选D【点睛】本题考查了勾股定理，读懂题目信息，理解定理并观察出被开方数比相应的序数大1是解题的关键．7．D解析：D【分析】先根据B（3m，4m+1），可知B在直线y=43x+1上，所以当BD⊥直线y=43x+1时，BD最小，找一等量关系列关于m的方程，作辅助线：过B作BH⊥x轴于H，则BH=4m+1，利用三角形相似得BH2=EH•FH，列等式求m的值，得BD的长即可．【详解】解：如图,∵点B(3m，4m+1)，∴令341m xm y=⎧⎨+=⎩，∴y=43x+1，∴B在直线y=43x+1上，∴当BD⊥直线y=43x+1时，BD最小，过B作BH⊥x轴于H，则BH=4m+1，∵BE在直线y=43x+1上，且点E在x轴上，∴E(−34，0)，G(0，1)∵F是AC的中点∵A(0，−2)，点C(6，2)，∴F(3，0)在Rt△BEF中，∵BH2=EH⋅FH，∴(4m+1)2=(3m+34)(3−3m)解得：m1=−14(舍)，m2=15，∴B(35，95)，∴2239(3)55⎛⎫-+ ⎪⎝⎭=6，则对角线BD的最小值是6；故选：D．【点睛】本题考查了平行四边形的性质，利用待定系数法求一次函数的解析式，三角形相似的判定，圆形与坐标特点，勾股定理等知识点.本题利用点B 的坐标确定其所在的直线的解析式是关键．8．D解析：D【解析】在Rt △ABC 中 ∠C=90°，AC=3，BC=4，根据勾股定理求得AB=5，设点C 到AB 的距离为h ，即可得12h×AB=12AC×BC ，即12h×5=12×3×4，解得h=125，故选D. 9．D解析：D【分析】根据角平分线的定义推出△ECF 为直角三角形，然后根据勾股定理求得CE 2+CF 2=EF 2．【详解】∵CE 平分∠ACB ，CF 平分∠ACD ，∴∠ACE=12∠ACB ，∠ACF=12∠ACD ，即∠ECF=12（∠ACB+∠ACD ）=90°， 又∵EF ∥BC ，CE 平分∠ACB ，CF 平分∠ACD ，∴∠ECB=∠MEC=∠ECM ，∠DCF=∠CFM=∠MCF ，∴CM=EM=MF=4，EF=8，由勾股定理可知CE 2+CF 2=EF 2=64．故选：D ．【点睛】此题考查角平分线的定义，直角三角形的判定，勾股定理的运用，解题关键在于掌握各性质定义.10．B解析：B【分析】已知AD 为CF 边上的高，要求AFC △的面积，求得FC 即可，求证AFD CFB '△≌△，得B F DF '=，设DF x =，则在Rt AFD △中，根据勾股定理求x ，于是得到CF CD DF =-，即可得到答案．【详解】解：由翻折变换的性质可知，AFD CFB '△≌△，'DF B F ∴=，设DF x =，则8AF CF x ==-，在Rt AFD △中，222AF DF AD =+，即222(8)4x x -=+，解得：3x =，835CF CD FD ∴=-=-=，1102AFC S AF BC ∴=⋅⋅=△． 故选：B ．【点睛】本题考查矩形的性质、折叠的性质、勾股定理等内容，根据折叠的性质得到AFD CFB '△≌△是解题的关键．二、填空题11．5【详解】解：如图，延长AE 交BC 于点F ，∵点E 是CD 的中点,∴DE=CE ，,∵AB ⊥BC ，AB ⊥AD,∴AD ∥BC,∴∠ADE=∠BCE 且DE=CE ，∠AED=∠CEF,∴△AED ≌△FEC （ASA ）,∴AD=FC=5，AE=EF,∴BF=BC-FC=5,∴在Rt △ABF 中，2213AF AB BF =+=,6.52AF AE == 故答案为：6.5． 12．【解析】试题分析：作点B 关于AC 的对称点B′，过B′点作B′D ⊥AB 于D ，交AC 于E ，连接AB′、BE ，则BE+ED=B′E+ED=B′D 的值最小．∵点B 关于AC 的对称点是B′，BC=5，∴B′C=5，BB′=10．∵Rt △ABC 中，∠ACB=90°，AC=12，BC=5，∴AB=22AC BC +=13，∵S △ABB′=12•AB•B′D=12•BB′•AC ，∴B′D=B 10121201313B AC AB '⋅⨯==,∴BE+ED= B′D=12013. 考点：轴对称-最短路线问题.13．55【解析】【分析】要求长方体中两点之间的最短路径，最直接的作法，就是将长方体展开，然后利用两点之间线段最短解答．【详解】展开图如图所示：由题意，在Rt △APQ 中，PD=10cm ，DQ=5cm ， ∴蚂蚁爬行的最短路径长2222105PD QD +=+5cm ），故答案为：5【点睛】本题考查了平面展开﹣最短路径问题，解答此类问题时要先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题．14．106232【解析】【详解】∵（x-6）2=9，∴x-6=±3，解得：x 1=9，x 2=3，∵x ，y 为一个直角三角形的两边的长，y=3，∴当x=3时，x 、y 都为直角三角形的直角边，则斜边为223332+=； 当x=9时，x 、y 都为直角三角形的直角边，则斜边为2293310+= ；当x=9时，x 为斜边、y 为直角边，则第三边为263922=-.故答案为：310，62或32.【点睛】本题主要考查了勾股定理的应用，正确分类讨论是解决问题的关键，解题时注意一定不要漏解．15．①1＜OA ＜4． ②672． 【解析】(1)由三角形边的性质5-3<2OA <5+3, 1＜OA ＜4.(2)过A 作AF BC ,F ⊥于过D 作DE BC ⊥于E,可知，ABF 全等DCE ,由题意知，22BD DE =+()2BC CE +=2DE +()24CE +， ()()222225AC DE BC CE DE CE ∴=+-=+-，2AC ∴+ 2BD=2DE +()()22245CE DE CE +++-=2(22)5018DE CE ++=+50=68，BD -AC =1，两边平方2AC ∴+ 2BD -2AC •BD =1， ∴AC •BD =672.16．169【解析】解：由于a 、b 、c 都是正方形，所以AC =CD ，∠ACD =90°；∵∠ACB +∠DCE =∠ACB +∠BAC =90°，即∠BAC =∠DCE ，∠ABC =∠CED =90°，AC =CD ，∴△ACB ≌△DCE ，∴AB =CE ，BC =DE ； 在Rt △ABC 中，由勾股定理得：AC 2=AB 2+BC 2=AB 2+DE 2，即S b =S a +S c =22512+=169． 故答案为：169．点睛：此题主要考查对全等三角形和勾股定理的综合运用，结合图形求解，对图形的理解能力要比较强．17．12【解析】如图，过点N 作NG ⊥BC 于点G ，连接CN ，根据轴对称的性质有：MA=MC ，NA=NC ，∠AMN=∠CMN.因为四边形ABCD 是矩形，所以AD ∥BC ，所以∠ANM=∠CMN.所以∠AMN=∠ANM，所以AM=AN.所以AM=AN=CM=CN.因为△CDN 的面积与△CMN 的面积比为1：3，所以DN:CM=1:3.设DN=x ，则CG=x ，AM=AN=CM=CN=3x ，由勾股定理可得NG=()22322x x x -=， 所以MN 2=()()22222312x x x x +-=，BM 2=()()222322x x x -=.所以222212MN x BM x==12. 枚本题应填12.点睛：矩形中的折叠问题，其本质是轴对称问题，根据轴对称的性质，找到对应的线段和角，也就找到了相等的线段和角，矩形中的折叠一般会伴随着等腰三角形(也就是基本图形“平行线+角平分线→等腰三角形”)，所以常常会结合等腰三角形，勾股定理来列方程求解. 18．41【解析】作AD′⊥AD ，AD′=AD ，连接CD′，DD ′，如图：∵∠BAC+∠CAD=∠DAD′+∠CAD ，即∠BAD=∠CAD′，在△BAD 与△CAD ′中，;BA CA BAD CAD AD AD ＝＝＝⎧⎪∠∠'⎨⎪⎩∴△BAD ≌△CAD′（SAS ）， ∴BD=CD′，∠DAD′=90°，由勾股定理得，∠D′DA+∠ADC=90°，由勾股定理得BD 2=41．故答案是：41．19．9或9【分析】通过计算E 到AC 的距离即EH 的长度为3，所以根据DE 的长度有两种情况：①当点D 在H 点上方时，②当点D 在H 点下方时，两种情况都是过点E 作EH AC ⊥交AC 于点E ，过点G 作GQ AB ⊥交AB 于点Q ，利用含30°的直角三角形的性质和勾股定理求出AH,DH 的长度，进而可求AD 的长度，然后利用角度之间的关系证明AG GE =，再利用等腰三角形的性质求出GQ 的长度，最后利用2DGF AED AEG SS S =-即可求解． 【详解】①当点D 在H 点上方时，过点E 作EH AC ⊥交AC 于点E ，过点G 作GQ AB ⊥交AB 于点Q ，12AB = ，点E 是AB 中点，162AE AB ∴== ． ∵EH AC ⊥，90AHE ∴∠=︒ ．30,6A AE ∠=︒=，132EH AE ∴== ， 22226333AH AE EH ∴=-=-=． 32DE =，2222(32)33DH DE EH ∴=-=-= ，DH EH ∴=，333AD AH DH =-=，45EDH ∴∠=︒，15AED EDH A ∴∠=∠-∠=︒ ．由折叠的性质可知，15DEF AED ∠=∠=︒，230AEG AED ∴∠=∠=︒ ，AEG A ∴∠=∠，AG GE ∴= ． 又GQ AE ⊥ ，132AQ AE ∴== ． 30A ∠=︒ ，12GQ AG ∴=． 222GQ AQ AG += ， 即2223(2)GQ GQ +=， 3GQ ∴= ．2DGF AED AEG S S S =- ，112(333)36363922DGF S ∴=⨯⨯-⨯-⨯⨯=-； ②当点D 在H 点下方时，过点E 作EH AC ⊥交AC 于点E ，过点G 作GQ AB ⊥交AB 于点Q ，12AB = ，点E 是AB 中点，162AE AB ∴== ． ∵EH AC ⊥，90AHE ∴∠=︒．30,6A AE ∠=︒= ，132EH AE ∴== ， 22226333AH AE EH ∴=-=-=．32DE =，2222(32)33DH DE EH ∴=-=-= ，DH EH ∴=，3AD AH DH =+=，45DEH ∴∠=︒ ，90105AED A DEH ∴∠=︒-∠+∠=︒ ．由折叠的性质可知，105DEF AED ∠=∠=︒，218030AEG AED ∴∠=∠-︒=︒ ，AEG A ∴∠=∠，AG GE ∴= ．又GQ AE ⊥ ，132AQ AE ∴== ． 30A ∠=︒，12GQ AG ∴= ． 222GQ AQ AG += ， 即2223(2)GQ GQ +=，GQ ∴= ．2DGF AED AEG S S S =- ，1123)36922DGF S ∴=⨯⨯⨯-⨯=，综上所述，DGF △的面积为9或9．故答案为：9或9．【点睛】本题主要考查折叠的性质，等腰三角形的判定及性质，等腰直角三角形的性质，勾股定理，含30°的直角三角形的性质，能够作出图形并分情况讨论是解题的关键． 20．49【分析】先计算出BC 的长，再由勾股定理求出阴影部分的面积即可.【详解】∵∠ACB=90︒，25AB = ，24AC =,∴22222252449BC AB AC =-=-=,∴阴影部分的面积=249BC =，故答案为：49.【点睛】此题考查勾股定理，能利用根据直角三角形计算得到所需的边长，题中根据勾股定理的图形得到阴影部分面积等于BC 的平方是解题的关键.三、解答题21．BF 的长为32【分析】先连接BF ，由E 为中点及AC=BC ，利用三线合一可得CE ⊥AB ，进而可证△AFE ≌△BFE ，再利用AD 为角平分线以及三角形外角定理，即可得到∠BFD 为45°，△BFD 为等腰直角三角形，利用勾股定理即可解得BF ．【详解】解：连接BF ．∵CA=CB ，E 为AB 中点∴AE=BE ，CE ⊥AB ，∠FEB=∠FEA=90°在Rt △FEB 与Rt △FEA 中， BE AE BEF AEF FE FE =⎧⎪∠=∠⎨⎪=⎩∴Rt △FEB ≌Rt △FEA又∵AD 平分∠BAC ，在等腰直角三角形ABC 中∠CAB=45°∴∠FBE=∠FAE=12∠CAB=22.5° 在△BFD 中，∠BFD=∠FBE+∠FAE=45°又∵BD ⊥AD ，∠D=90°∴△BFD 为等腰直角三角形，BD=FD=3∴222232BF BD FD BD =+==【点睛】本题主要考查等腰直角三角形的性质及判定、三角形全等的性质及判定、三角形外角、角平分线，解题关键在于熟练掌握等腰直角三角形的性质．22．（1）BC−AC ＝AD ；理由详见解析；（2）①详见解析；②AB=14【分析】（1）在CB 上截取CE ＝CA ，连接DE ，证△ACD ≌△ECD 得DE ＝DA ，∠A ＝∠CED ＝60°，据此∠CED＝2∠CBA，结合∠CED＝∠CBA＋∠BDE得出∠CBA＝∠BDE，即可得DE＝BE，进而得出答案；（2）①在AB上截取AM＝AD，连接CM，先证△ADC≌△AMC，得到∠D＝∠AMC，CD＝CM，结合CD＝BC知CM＝CB，据此得∠B＝∠CMB，根据∠CMB＋∠CMA＝180°可得；②设BN＝a，过点C作CN⊥AB于点N，由CB＝CM知BN＝MN＝a，CN2＝BC2−BN2＝AC2−AN2，可得关于a的方程，解之可得答案．【详解】解：（1）BC−AC＝AD．理由如下：如图（a），在CB上截取CE＝CA，连接DE，∵CD平分∠ACB，∴∠ACD＝∠ECD，又CD＝CD，∴△ACD≌△ECD（SAS），∴DE＝DA，∠A＝∠CED＝60°，∴∠CED＝2∠CBA，∵∠CED＝∠CBA＋∠BDE，∴∠CBA＝∠BDE，∴DE＝BE，∴AD＝BE，∵BE＝BC−CE＝BC−AC，∴BC−AC＝AD．（2）①如图（b），在AB上截取AM＝AD，连接CM，∵AC平分∠DAB，∴∠DAC＝∠MAC，∵AC＝AC，∴△ADC≌△AMC（SAS），∴∠D＝∠AMC，CD＝CM＝12，∵CD＝BC＝12，∴CM＝CB，∴∠B＝∠CMB，∵∠CMB＋∠CMA＝180°，∴∠B＋∠D＝180°；②设BN＝a，过点C 作CN ⊥AB 于点N ，∵CB ＝CM ＝12，∴BN ＝MN ＝a ，在Rt △BCN 中，2222212CN BC BN a --＝＝，在Rt △ACN 中，2222216(8)CN AC AN a --+＝＝， 则22221216(8)a a --+＝， 解得：a ＝3，即BN ＝MN ＝3，则AB ＝8+3+3=14，∴AB=14．【点睛】本题考查了四边形的综合题，以及全等三角形的判定与性质、勾股定理、等腰三角形的判定与性质；本题有一定难度，需要通过作辅助线证明三角形全等才能得出结果．23．（1）见解析；（2）BD 2+AD 2＝2CD 2；（3）AB ＝2+4．【分析】（1）根据等腰直角三角形的性质证明△ACE ≌△BCD 即可得到结论；（2）利用全等三角形的性质及勾股定理即可证得结论；（3）连接EF ，设BD ＝x ，利用（1）、（2）求出EF=3x ，再利用勾股定理求出x ，即可得到答案.【详解】（1）证明：∵△ACB 和△ECD 都是等腰直角三角形∴AC ＝BC ，EC ＝DC ，∠ACB ＝∠ECD ＝90°∴∠ACB ﹣∠ACD ＝∠ECD ﹣∠ACD∴∠ACE ＝∠BCD ，∴△ACE ≌△BCD （SAS ），∴AE ＝BD ．（2）解：由（1）得△ACE ≌△BCD ，∴∠CAE ＝∠CBD ，又∵△ABC 是等腰直角三角形，∴∠CAB ＝∠CBA ＝∠CAE ＝45°，∴∠EAD ＝90°，在Rt △ADE 中，AE 2+AD 2＝ED 2，且AE ＝BD ，∴BD 2+AD 2＝ED 2，∵ED ＝2CD ，∴BD 2+AD 2＝2CD 2，（3）解：连接EF ，设BD ＝x ，∵BD ：AF ＝1：2AF ＝2x ，∵△ECD 都是等腰直角三角形，CF ⊥DE ，∴DF ＝EF ，由 （1）、（2）可得，在Rt △FAE 中，EF 22AF AE +22(22)x x +3x ， ∵AE 2+AD 2＝2CD 2，∴222(223)2(36)x x x ++=，解得x ＝1，∴AB ＝2+4．【点睛】此题考查三角形全等的判定及性质，等腰直角三角形的性质，勾股定理.24．（1）详见解析；（241；（33【分析】 （1）证∠EAC=∠DAB.利用SAS 证△ACE ≌△ABD 可得；（2）连接BD ，证1302FEA AED ∠=∠=，证△ACE ≌△ABD 可得30FEA BDA ∠=∠=,CE=BD=5，利用勾股定理求解；（3）作CE 垂直于AC,且CE=AC,连接AE,则90,45ACE CAE ∠=∠=，利用勾股定理得AE 2AB =，3AB ，根据（1）思路得3AB .【详解】(1) 证明：∵∠DAE=∠BAC ，∴∠DAE+∠CAD=∠BAC+∠CAD ，即∠EAC=∠DAB.在△ACE 与△ABD 中，AD AE EAC BAB AC AB =⎧⎪∠=∠⎨⎪=⎩， ∴△ACE ≌△ABD(SAS)，∴BD CE =；(2)连接BD因为AD AE =， 60DAE BAC ∠=∠=，所以ADE ∆是等边三角形因为60DAE DEA EDA ∠=∠=∠=,ED=AD=AE=4因为CE AD ⊥ 所以1302FEA AED ∠=∠= 同(1)可知△ACE ≌△ABD(SAS)，所以30FEA BDA ∠=∠=,CE=BD=5所以90BDE BDA ADE ∠=∠+∠=所以BE=22225441BD DE +=+=(3)作CE 垂直于AC,且CE=AC,连接AE,则90,45ACE CAE ∠=∠=所以222AB AC AC +因为AB AC =所以AE 2=又因为45CAB ∠=所以90ABE ∠= 所以()222223BE AE AB AB AB AB =+=+= 因为45CBD CDB ∠=∠=所以BC=CD, 90BCD ∠=因为同(1)可得△ACD ≌△ECB(SAS)所以3AB所以33AD AB AB ==【点睛】考核知识点:等边三角形;勾股定理.构造全等三角形和直角三角形是关键.25．（1）∠CBD=20°；（2）AD=164；(3) △BCD的周长为m+2【分析】（1）根据折叠可得∠1=∠A=35°，根据三角形内角和定理可以计算出∠ABC=55°，进而得到∠CBD=20°；（2）根据折叠可得AD=DB，设CD=x，则AD=BD=8-x，再在Rt△CDB中利用勾股定理可得x2+62=（8-x）2，再解方程可得x的值，进而得到AD的长；（3）根据三角形ACB的面积可得11 2AC CB m=+，进而得到AC•BC=2m+2，再在Rt△CAB中，CA2+CB2=BA2，再把左边配成完全平方可得CA+CB的长，进而得到△BCD的周长．【详解】（1）∵把△ABC沿直线DE折叠，使△ADE与△BDE重合，∴∠1=∠A=35°，∵∠C=90°，∴∠ABC=180°-90°-35°=55°，∴∠2=55°-35°=20°，即∠CBD=20°；（2）∵把△ABC沿直线DE折叠，使△ADE与△BDE重合，∴AD=DB，设CD=x，则AD=BD=8-x，在Rt△CDB中，CD2+CB2=BD2，x2+62=（8-x）2，解得：x=74， AD=8-74=164； （3）∵△ABC 的面积为m+1， ∴12AC •BC=m+1， ∴AC •BC=2m+2， ∵在Rt △CAB 中，CA 2+CB 2=BA 2，∴CA 2+CB 2+2AC •BC=BA 2+2AC •BC ，∴（CA+BC ）2=m 2+4m+4=（m+2）2，∴CA+CB=m+2，∵AD=DB ，∴CD+DB+BC=m+2．即△BCD 的周长为m+2．【点睛】此题主要考查了图形的翻折变换，以及勾股定理，完全平方公式，关键是掌握勾股定理，以及折叠后哪些是对应角和对应线段．26．（1）2，2）证明见解析（3（4【分析】（1）根据含有30°角的直角三角形的性质可得BC=2，再由勾股定理即可求出AC 的长； （2）由ED 为AB 垂直平分线可得DB=DA ，在Rt △BDE 中，由勾股定理可得BD=4，可得BD=2BE ，故∠BDE 为60°，即可证明ABD ∆是等边三角形；（3）由（1）（2）可知，AC AD=4，进而可求得CD 的长，再由等积法可得BCD ACD ACBD S S S =+四边形，代入求解即可；（4）分点P 在线段AC 上和AC 的延长线上两种情况，过点E 作AC 的垂线交AC 于点Q ，构造Rt △PQE ，再根据勾股定理即可求解.【详解】（1）∵Rt ABC ∆，90ACB ∠=︒，30BAC ∠=︒，斜边4AB =，∴122BC AB ==，∴AC = （2）∵ED 为AB 垂直平分线，∴ADB=DA ，在Rt △BDE 中，∵122BE AE AB ===，DE =∴BD =，∴BD=2BE ，∴∠BDE 为60°，∴ABD ∆为等边三角形；（3））由（1）（2）可知，=23AC ，AD=4， ∴22=27CD AC AD =+，∵BCD ACD ACBD S SS =+四边形， ∴111()222BC AD AC AC AD BF CD +⨯=⨯+⨯， ∴221BF =； （4）分点P 在线段AC 上和AC 的延长线上两种情况，如图，过点E 作AC 的垂线交AC 于点Q ，∵AE=2，∠BAC=30°，∴EQ=1， ∵=23AC ，∴=3CQ QA =，①若点P 在线段AC 上， 则23=333PQ CQ CP =-=， ∴2223PE PQ EQ =+； ②若点P 在线段AC 的延长线上， 则2533333PQ CQ CP =+=， ∴22221=PE PQ EQ =+； 综上，PE 23221. 【点睛】 本题考查勾股定理及其应用、含30°的直角三角形的性质等，解题的关键一是能用等积法表示并求出BF 的长，二是对点P 的位置要分情况进行讨论.27．（1）（5，0）；（2）见解析；（3）①P （4，2），②满足△ACP 与△BDC 全等的点是P1、P2，P3．理由见解析【分析】（1）由题意可以假设A（a，a）（a＞0），根据AB2+OB2=OA2，构建方程即可解决问题；（2）由角平分线的性质定理证明CH=CF，CG=CF即可解决问题；（3）①如图3中，在BC的延长线上取点P，使得CP=DB，连接AP．只要证明△ACP≌△CDB（SAS），△ABP是等腰直角三角形即可解决问题；②根据SAS即可判断满足△ACP与△BDC全等的点是P1、P2，P3；【详解】解：（1）∵点A在射线y＝x（x≥0）上，故可以假设A（a，a）（a＞0），∵AB⊥x轴，∴AB＝OB＝a，即△ABO是等腰直角三角形，∴AB2+OB2＝OA2，∴a2+a2＝（52）2，解得a＝5，∴点B坐标为（5，0）．（2）如图2中，作CF⊥x轴于F．∵OC平分∠AOB，CH⊥OE，∴CH＝CF，∵△AOB是等腰直角三角形，∴∠AOB＝45°，∵BC∥OE，∴∠CBG＝∠AOB＝45°，得到BC平分∠ABF，∵CG⊥BA，CF⊥BF，∴CG＝CF，∴CG＝CH．（3）①如图3中，在BC的延长线上取点P，使得CP＝DB，连接AP．由（2）可知AC平分∠DAE，∴∠DAC＝12∠DAE＝12（180°﹣45°）＝67.5°，由OC平分∠AOB得到∠DOB＝12∠AOB＝22.5°，∴∠ADC＝∠ODB＝90°﹣22.5°＝67.5°，∴∠ADC＝∠DAC＝67.5°，∴AC＝DC，∠BDC＝∠OBD+∠DOB＝90°+22.5°＝112.5°，∠ACD＝180°﹣∠CAD﹣∠ADC＝180°﹣67.5°﹣67.5°＝45°，∠OCB＝45°﹣22.5°＝22.5°，∠ACP＝180°﹣∠ACD﹣∠OCB＝180°﹣45°﹣22.5°＝112.5°，在△ACP和△CDB中，AC ADACP DB CP DB=⎧⎪∠=∠⎨⎪=⎩，∴△ACP≌△CDB（SAS），∴∠CAP＝∠DCB＝22.5°，∴∠BAP＝∠CAP+∠DAC＝22.5°+67.5°＝90°，∴△ABP是等腰直角三角形，∴AP＝AB＝OB＝2，∴P（4，2）．②满足△ACP与△BDC全等的点是P1、P2，P3．理由：如图4中，由题意：AP 1＝BD ，AC ＝CD ，∠CAP 1＝∠CDB ，根据SAS 可得△CAP 1≌△CDB ； AP 2＝BD ，AC ＝CD ，∠CAP 2＝∠CDB ，根据SAS 可得△CAP 2≌△CDB ；AC ＝CD ，∠ACP 3＝∠BDC ，BD ＝CP 3根据SAS 可得△CAP 3≌△DCB ；故答案为P 1、P 2，P 3．【点睛】本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质、勾股定理、角平分线的性质定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．28．（1）1(491)2-；1(491)2+；（2）21(1)2n -；21(1)2n +；（3）21m -；21m +；（4）10；26； 12；35；【解析】【分析】（1）依据规律可得，如果勾为7，则股24=1(491)2-， 弦25=1(491)2+； （2）如果勾用n （n≥3，且n 为奇数）表示时，则股=21(1)2n -， 弦=21(1)2n +； （3）根据规律可得，如果a ，b ，c 是符合同样规律的一组勾股数，a=2m （m 表示大于1的整数），则b=m 2-1，c=m 2+1；（4）依据柏拉图公式，若m 2-1=24，则m=5，2m=10，m 2+1=26；若m 2+1=37，则m=6，2m=12，m 2-1=35．【详解】解：（1）依据规律可得，如果勾为7，则股24=1(491)2-，弦25=1(491)2+； 故答案为：1(491)2-；1(491)2+； （2）如果勾用n （n≥3，且n 为奇数）表示时，则股=21(1)2n -， 弦=21(1)2n +； 故答案为：21(1)2n -；21(1)2n +； （3）根据规律可得，如果a ，b ，c 是符合同样规律的一组勾股数，a=2m （m 表示大于1的整数），则b=m 2-1，c=m 2+1；故答案为：m 2-1，m 2+1；（4）依据柏拉图公式，若m 2-1=24，则m=5，2m=10，m 2+1=26；若m 2+1=37，则m=6，2m=12，m 2-1=35；故答案为：10、26；12、35．【点睛】此题主要考查了勾股数的定义，及勾股定理的逆定理：已知△ABC 的三边满足a 2+b 2=c 2，则△ABC 是直角三角形．29．(1)45°；(2)GF=AG+CF ，证明见解析；(3)①6； ②s ab =，理由见解析.【解析】【分析】（1）如图1中，连接BE ．利用全等三角形的性质证明EB=ED ，再利用等角对等边证明EB=EF 即可解决问题．（2）猜想：GF=AG+CF ．如图2中，将△CDF 绕点D 旋转90°，得△ADH ，证明△GDH ≌△GDF （SAS ）即可解决问题．（3）①设CF=x ，则AH=x ，BF=6-x ，GF=3+x ，利用勾股定理构建方程求出x 即可． ②设正方形边长为x ，利用勾股定理构建关系式，利用整体代入的思想解决问题即可．【详解】解：（1）如图1中，连接BE ．∵四边形ABCD 是正方形，∴CD=CB ，∠ECD=∠ECB=45°，∵EC=EC，∴△ECB≌△ECD（SAS），∴EB=ED，∠EBC=∠EDC，∵∠DEF=∠DCF=90°，∴∠EFC+∠EDC=180°，∵∠EFB+∠EFC=180°，∴∠EFB=∠EDC，∴∠EBF=∠EFB，∴EB=EF，∴DE=EF，∵∠DEF=90°，∴∠EDF=45°故答案为45°．（2）猜想：GF=AG+CF．如图2中，将△CDF绕点D旋转90°，得△ADH，∴∠CDF=∠ADH，DF=DH，CF=AH，∠DAH=∠DCF=90°，∵∠DAC=90°，∴∠DAC+∠DAH=180°，∴H、A、G三点共线，∴GH=AG+AH=AG+CF，∵∠EDF=45°，∴∠CDF+∠ADG=45°，∴∠ADH+∠ADG=45°∴∠GDH=∠EDF=45°又∵DG=DG∴△GDH≌△GDF（SAS）∴GH=GF，∴GF=AG+CF．（3）①设CF=x，则AH=x，BF=6-x，GF=3+x，则有（3+x）2=（6-x）2+32，解得x=2∴S△BFG=12•BF•BG=6．②设正方形边长为x，∵AG=a，CF=b，∴BF=x-b，BG=x-a，GF=a+b，则有（x-a）2+（x-b）2=（a+b）2，化简得到：x2-ax-bx=ab，∴S=12（x-a）（x-b）=12（x2-ax-bx+ab）=12×2ab=ab．【点睛】本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用参数构建方程解决问题，属于中考常考题型．30．（1）S=24(06)464(616)tt t<⎧⎨-+<<⎩（2）10,103⎛⎫⎪⎝⎭（3）存在，(6,6)或(6,10-，(6,2)【解析】【分析】（1）当P在AC段时，△BPD的底BD与高为固定值，求出此时面积；当P在BC段时，底边BD为固定值，用t表示出高，即可列出S与t的关系式；（2）当点B的对应点B′恰好落在AC边上时，设P（m，10），则PB=PB′=m，由勾股定理得m2=22+（6-m）2，即可求出此时P坐标；（3）存在，分别以BD，DP，BP为底边三种情况考虑，利用勾股定理及图形与坐标性质求出P坐标即可．【详解】解：（1）∵A，B的坐标分别是（6，0）、（0，10），∴OA=6，OB=10，当点P在线段AC上时，OD=2，BD=OB-OD=10-2=8，高为6，∴S=12×8×6=24；当点P在线段BC上时，BD=8，高为6+10-t=16-t，∴S=12×8×（16-t）=-4t+64；∴S与t之间的函数关系式为：240t6S4t64(6t16)<≤⎧=⎨-+<<⎩（）；（2）设P（m，10），则PB=PB′=m，如图1，∵OB′=OB=10，OA=6，∴AB′=22OB OA-＇=8，∴B′C=10-8=2，∵PC=6-m，∴m2=22+（6-m）2，解得m=10 3则此时点P的坐标是（103，10）；（3）存在，理由为：若△BDP为等腰三角形，分三种情况考虑：如图2，①当BD=BP1=OB-OD=10-2=8，在Rt△BCP1中，BP1=8，BC=6，根据勾股定理得：CP1228627-=∴AP1＝10−7，即P1（6，10-27②当BP2=DP2时，此时P2（6，6）；③当DB=DP3=8时，在Rt△DEP3中，DE=6，根据勾股定理得：P3228627-=，∴AP3=AE+EP3=7+2，即P3（6，27），综上，满足题意的P坐标为（6，6）或（6，10-276，7+2）．【点睛】本题是四边形综合题，考查了矩形的性质，坐标与图形性质，等腰三角形的性质，勾股定理等知识，注意分类讨论思想和方程思想的运用．。

人教版八年级第二学期 第一次月考数学试题含解析一、选择题1．对于所有实数a ，b ，下列等式总能成立的是（ ） A ．()2ba b a +=+ B ．22222(b a b )a +=+ C ．22b a b a +=+ D ．2(b)a b a +=+2．下列各式成立的是（ ） A ．2(3)3-=B ．633-=C ．222()33-=- D ．2332-=3．下列根式中，最简二次根式是（ ） A ．13B ．0.3C ．3D ．84．计算()21273632÷+⨯--的结果正确的是( ) A ．3B ．3C ．6D ．33-5．下列运算中，正确的是( ) A ．325+=B ．321-=C ．326⨯=D ．3322÷=6．若2()a b a b -=--则（ ） A ．0a b +=B ．0a b -=C ．0ab =D ．220a b +=7．下列二次根式中，是最简二次根式的是（ ）. A ．2xyB ．2ab C ．12D ．422x x y + 8．实数a ，b 在数轴上的位置如图所示，则化简﹣+b 的结果是（ ）A ．1B ．b+1C ．2aD ．1﹣2a9．下列计算正确的是（ ） A 366=± B ．422222=C ．83266= D a b ab =（a≥0，b≥0）10．若式子22(1)m m +-有意义，则实数m 的取值范围是（ ）A ．m ＞﹣2B ．m ＞﹣2且m ≠1C ．m ≥﹣2D ．m ≥﹣2且m ≠111．若a =，2b =+a b 的值为（ ）A ．12B ．14CD12．下列计算正确的是（ ）A =B ．2-= C ．22= D 3=二、填空题13．设12211112S =++，22211123S =++，32211134S =++，设...S =S=________________ (用含有n 的代数式表示，其中n 为正整数)． 14．已知x =，a 是x 的整数部分，b 是x 的小数部分，则a-b=_______ 15．下面是一个按某种规律排列的数阵：根据数阵排列的规律，第 5 行从左向右数第 3 个数是 ，第 n （n 3≥ 且 n 是整数）行从左向右数第 n 2- 个数是 （用含 n 的代数式表示）． 16．若实数x ，y ，m 满足等式()223x y m +-=m+4的算术平方根为________．17．已知实数m 、n 、p 满足等式，则p =__________．18．把19．函数y 中，自变量x 的取值范围是____________．20．1=-==++……=___________．三、解答题21．小明在解决问题：已知a2a 2－8a ＋1的值，他是这样分析与解答的：因为a＝2，所以a －2所以(a －2)2＝3，即a 2－4a ＋4＝3. 所以a 2－4a ＝－1.所以2a 2－8a ＋1＝2(a 2－4a)＋1＝2×(－1)＋1＝－1. 请你根据小明的分析过程，解决如下问题： (1)计算：= － . (2)… (3)若a，求4a 2－8a ＋1的值．【答案】 ，1；(2) 9；(3) 5 【分析】（11==；（2）根据例题可得：对每个式子的分子和分母中同时乘以与分母中的式子相乘符合平方差公式的根式，去掉分母，然后合并同类项二次根式即可求解； （3）首先化简a ，然后把所求的式子化成()2413a --代入求解即可. 【详解】(1)计算：1=； (2)原式)1...11019=++++==-=；(3)1a ===，则原式()()224213413a a a =-+-=--，当21a =+时，原式()24235=⨯-=.【点睛】本题考查了二次根式的化简求值，正确读懂例题，对根式进行化简是关键.22．阅读下列材料，然后解答下列问题：在进行代数式化简时，我们有时会碰上如53，231+这样的式子，其实我们还可以将其进一步化简： (一)553533333⨯==⨯； (二)2231)=3131(31)(31)-=-++-（； (三) 22231(3)1(31)(31)=3131313131--+-===-++++.以上这种化简的方法叫分母有理化． (1)请用不同的方法化简25+3： ①参照(二)式化简25+3＝__________. ②参照(三)式化简5+3＝_____________ (2)化简：++++315+37+599+97+.【答案】见解析. 【分析】（1）原式各项仿照题目中的分母有理化的方法计算即可得到结果； （2）原式各项分母有理化，计算即可. 【详解】 解:(1)①;②; (2)原式故答案为:(1)①;②【点睛】此题主要考查了二次根式的有理化，解答此题要认真阅读前面的分析，根据题目的要求选择合适的方法解题.23．像552)＝1a a ＝a (a ≥0)、b b ﹣1)＝b ﹣1(b ≥0)……两个含有二次根式的代数式相乘，积不含有二次根式，我们称这两个代数式互为有理化因552 +12﹣1，353﹣5因式．进行二次根式计算时，利用有理化因式，可以化去分母中的根号．请完成下列问题： (1)33；(2)2332+--； (3)2018201720172016的大小，并说明理由． 【答案】（123（2）32（3）＜ 【解析】分析：（13×3=1，确定互为有理化因式，由此计算即可； （2）确定分母的有理化因式为23与23+3232然后分母有理化后计算即可；（3201820172017201620182017与20172016，20182017+20172016+，然后比较即可. 详解：(1) 原式23333⋅23； （2）原式=2332+=223+ （3）根据题意，2018201720182017-=+2017201620172016=+，2018201720172016>2018201720172016<++，2018201720172016>点睛：此题是一个阅读题，认证读题，了解互为有理化因式的实际意义，以及特点，然后根据特点变形解题是关键.24．先化简，再求值：a+212a a -+，其中a ＝1007． 如图是小亮和小芳的解答过程．（1） 的解法是错误的；（2）错误的原因在于未能正确地运用二次根式的性质： ； （3）先化简，再求值：269a a -+a ＝﹣2018． 【答案】（1）小亮（22a （a ＜0）（3）2013. 【解析】试题分析：（12a ，判断出小亮的计算是错误的； （22a 的应用错误；（3）先根据配方法把被开方数配成完全平方，然后根据正确的性质化简，再代入计算即可. 试题解析：（1）小亮 （22a （a ＜0） （3）原式＝()23a -a+2（3-a ）＝6-a=6-（-2007）＝2013.25．先化简再求值：321943x y x y x x x x y ⎛- ⎝，其中340x y --=． 【答案】(25x x xy -3 【分析】先根据二次根式的混合运算顺序和运算法则化简原式，再利用非负数的性质得出x ，y 的值，继而将x 、y 的值代入计算可得答案． 【详解】解：321943x y x y x x x x y ⎛- ⎝ ()()24x xy x x xy =-(25x x xy =-∵ 340x y -- ∴ 3,4x y ==当3,4x y ==时原式(23=-==【点睛】本题主要考查了二次根式的化简求值，解题的关键是掌握非负数的性质和二次根式的混合运算顺序和法则．26．已知x y ==求下列各式的值： (1)22x xy y -+； (2).y xx y+ 【答案】(1) 72;(2)8. 【分析】计算出xy=12， （1）把x 2-xy+y 2变形为（x+y ）2-3xy ，然后利用整体代入的方法计算；（2）把原式变形为2()2x y xyxy+-，然后利用整体代入的方法计算.【详解】∵x =，y ==32∴xy=12, (1)22x xy y -+ =（x+y ）2-3xy,=2132-⨯ =72; (2)y x x y +=2212()22812x y xyxy-⨯+-==.【点睛】本题考查了二次根式的化简求值：二次根式的化简求值，一定要先化简再代入求值．二次根式运算的最后，注意结果要化到最简二次根式，二次根式的乘除运算要与加减运算区分，避免互相干扰．27．计算：（1；（2+2）2+2）．【答案】（1-2）【分析】（1）直接化简二次根式进而合并得出答案； （2）直接利用乘法公式计算得出答案． 【详解】解：（1）原式＝-（2）原式＝3434++-＝6+． 【点睛】本题考查了二次根式的运算，在进行二次根式运算时，可以运用乘法公式，运算率简化运算．28．已知x²+2xy+y²的值. 【答案】16 【解析】分析：（1）根据已知条件先计算出x+y=4，再利用完全平方公式得到x²+2xy+y²=（x+y ）²，然后利用整体代入的方法计算． 本题解析： ∵x² +2xy+y² =(x+y)²，∴当∴x²+2xy+y²=(x+y)²=(2−=16.29．已知长方形的长a =b =. (1)求长方形的周长；(2)求与长方形等面积的正方形的周长，并比较其与长方形周长的大小关系．【答案】（1）2）长方形的周长大. 【解析】试题分析：（1）代入周长计算公式解决问题；（2）求得长方形的面积，开方得出正方形的边长，进一步求得周长比较即可． 试题解析：(1)()11222223a b ⎛+=⨯=⨯⨯⨯=⨯= ⎝∴长方形的周长为 .(2)114.23=⨯⨯=正方形的面积也为4. 2.= 周长为：428.⨯=8.>∴长方形的周长大于正方形的周长．30．计算下列各题：（1（2）2-．【答案】（1）2）2-- 【分析】（1）根据二次根式的运算顺序和运算法则计算即可； （2）利用平方差、完全平方公式进行计算． 【详解】解：（1）原式==；（2）原式22(5=--+525=---2=--【点睛】本题考查二次根式的加减乘除混合运算，熟练掌握运算法则和乘法公式是关键．【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【详解】解：A 、错误，∵2=+a bB 、正确，因为a 2+b 2≥0a 2+b 2；CD=|a+b|，其结果a+b的符号不能确定．故选B．2．A解析：A【分析】根据各个选项中的式子，可以计算出正确的结果，从而可以解答本题．【详解】解：A3=，故A正确；B-不能合并，故B错误；C、22(3=，故C错误；D、=D错误；故选：A．【点睛】本题考查二次根式的混合运算，解答本题的关键是明确二次根式混合运算的计算方法．3．C解析：C【分析】根据最简二次根式的定义，可得答案．【详解】A、被开方数含分母，故选项A不符合题意；B、被开方数是小数，故选项B不符合题意；C、被开方数不含开的尽的因数，被开方数不含分母，故C符合题意；D、被开方数含开得尽的因数，故D错误不符合题意；故选：C．【点睛】本题考查了最简二次根式，被开方数不含开的尽的因数或因式，被开方数不含分母．4．A解析：A【分析】分别根据二次根式的除法和乘法法则以及二次根式的平方计算每一项，再合并即可．【详解】解：原式333=+=故选：A．【点睛】本题主要考查了二次根式的混合运算，属于基础题型，熟练掌握二次根式的乘除法则是解题的关键．解析：C【分析】根据二次根式的加、减、乘、除运算法则对各项进行计算即可得到结果．【详解】 A.3与2不是同类二次根式，不能合并，故此选项错误； B.3与2不是同类二次根式，不能合并，故此选项错误； C. 326⨯=，正确，故此选项符合题意； D 、632÷=，故此选项错误； 故选：C ．【点睛】此题主要考查了二次根式的混合运算，熟练掌握二次根式的运算法则是解答此题的关键． 6．C解析：C【分析】直接利用二次根式的性质 ，将已知等式左边化简，可以得到a 与b 中至少有一个为0，进而分析得出答案即可．【详解】解:∵ 2()a b a b -=--，∴a-b=-a-b ， 或b-a=-a-b∴a= -a ，或b=-b, ∴a=0,或b=0, ∴ab=0, ∴0ab =．故选：C ．【点睛】本题考查了二次根式的性质与化简，正确掌握二次根式的性质是解题的关键．7．A解析：A【详解】根据最简二次根式的意义，可知2xy 是最简二次根式，2ab =22ab ，1222=，422x x y +=x 22x y +，不是最简二次根式. 故选A.8．A解析：A【解析】﹣+b=111a a b b a a b b ---+=-+-+= ，故选A.解析：D6=，故A 不正确；根据二次根式的除法，可直接得到2=，故B 不正确；根据同类二次根式的性质，可知C 不正确；=（a≥0，b≥0）可知D 正确.故选：D 10．D解析：D【分析】根据二次根式有意义的条件即可求出答案．【详解】由题意可知：2010m m +≥⎧⎨-≠⎩， ∴m ≥﹣2且m ≠1，故选D ．【点睛】本题考查二次根式有意义的条件，解题的关键是熟练运用二次根式的条件.11．B解析：B【分析】将a 乘以 可化简为关于b 的式子, 从而得到a 和b 的关系, 继而能得出a b 的值【详解】解：4b a ==== 14a b ∴= 故选：B .【点睛】本题考查二次根式的乘除法，有一定难度，关键是在分母有理化时要观察b 的形式．12．C解析：C【分析】根据立方根、二次根式的加减乘除运算法则计算．【详解】A 、非同类二次根式，不能合并，故错误；B 、=C 、22=，正确；D故选C ．【点睛】本题考查二次根式、立方根的运算法则，熟练掌握基本法则是关键．二、填空题13．【分析】先根据题目中提供的三个式子，分别计算的值，用含n 的式子表示其规律，再计算S 的值即可．【详解】解：∵，∴；∵，∴；∵，∴；……∵，∴；∴．故答案为：【点睛】本题 解析：221n n n ++ 【分析】n 的式子表示其规律，再计算S 的值即可．【详解】解：∵1221191=124S =++311122===+-；∵222114912336S =++=7111116623===+=+-； ∵32211169134144S =++=1311111121234===+=+-； …… ∵()()()222222111111n n n S n n n n ++=++=++，()()2111111111n n n n n n n n ++===+=+-+++；∴...S =1111111112231n n =+-++-++-+…+ 111n n =+-+． 221n n n +=+ 故答案为：221n n n ++ 【点睛】本题为规律探究问题，难度较大，根据提供的式子发现规律，并表示规律是解题的关键，同时要注意对于式子()11111n n n n =-++的理解． 14．【分析】先把x 分母有理化求出x= ，求出a 、b 的值，再代入求出结果即可．【详解】∵∴∴∴【点睛】本题考查了分母有理化和估算无理数的大小的应用，解此题的关键是求a、b 的值．解析：6【分析】先把x 分母有理化求出2 ，求出a 、b 的值，再代入求出结果即可．【详解】2x === ∵23<<∴425<<∴4,242a b ==-=∴42)6a b -=-=【点睛】本题考查了分母有理化和估算无理数的大小的应用，解此题的关键是求a 、b 的值．15．；．【分析】根据被开方数是连续的自然数写出即可；根据每一行的最后一个数的被开方数是所在的行数乘比行数大1的数写出第（n-1）行的最后一个数，然后被开方数加上（n-2）即可求解．【详解】观察表【分析】根据被开方数是连续的自然数写出即可；根据每一行的最后一个数的被开方数是所在的行数乘比行数大1的数写出第（n-1）行的最后一个数，然后被开方数加上（n-2）即可求解．【详解】观察表格中的数据可得，第5行从左向右数第3=∵第（n-1，∴第n （n ≥3且n 是整数）行从左向右数第n-2个数是．．【点睛】本题是对数字变化规律的考查，观察出被开方数是连续自然数并且每一行的最后一个数的被开方数是所在的行数乘比行数大1的数是解题的关键．16．3【解析】【分析】先根据二次根式有意义的条件得出x+y 的值，再根据非负数的性质列出关于x ，y ，m 的方程组，求出m 的值，进而可得出结论．【详解】依题意得：，解得：x=1，y=1，m ＝5，∴3解析：3【解析】【分析】先根据二次根式有意义的条件得出x +y 的值，再根据非负数的性质列出关于x ，y ，m 的方程组，求出m 的值，进而可得出结论．【详解】依题意得：35302302x y m x y m x y +--=⎧⎪+-=⎨⎪+=⎩，解得：x =1，y =1，m ＝5，∴==3．故答案为3．【点睛】 本题考查了二次根式有意义得条件及非负数的性质，熟知二次根式具有非负性是解答此题的关键．17．5【解析】试题解析：由题可知，∴，∴，∴，①②得，，解方程组得，∴．故答案为：5.解析：5【解析】试题解析：由题可知3030m n m n -+≥⎧⎨--≥⎩， ∴3m n +=，0=， ∴35200m n p m n p +--=⎧⎨--=⎩①②， ①-②得2620m n +-=，31m n +=，解方程组331m n m n +=⎧⎨+=⎩得41m n =⎧⎨=-⎩， ∴4(1)5p m n =-=--=．故答案为：5.18．﹣【解析】解：通过有意义可以知道≤0，≤0，所以＝﹣＝﹣．故答案为：．点睛：此题主要考查了二次根式的性质应用，正确判断二次根式的整体符号是解题关键．解析：【解析】解：通过a ≤0，，所以故答案为：点睛：此题主要考查了二次根式的性质应用，正确判断二次根式的整体符号是解题关键．19．x≤4且x≠2【分析】根据被开方数是非负数、分母不能为零，可得答案．【详解】解：由y=，得4-x≥0且x-2≠0．解得x≤4且x≠2．【点睛】本题考查了函数自变量的取值范围，利用被开方解析：x≤4且x≠2【分析】根据被开方数是非负数、分母不能为零，可得答案．【详解】解：由，得4-x≥0且x-2≠0． 解得x≤4且x≠2．【点睛】本题考查了函数自变量的取值范围，利用被开方数是非负数、分母不能为零得出4-x≥0且x-2≠0是解题关键．【分析】先根据已知等式归纳类推出一般规律，再根据二次根式的加减法与乘法运算法则即可得．【详解】第1个等式为：，第2个等式为：，第3个等式为：，归纳类推得：第n 个等式为：（其中，解析：2018【分析】先根据已知等式归纳类推出一般规律，再根据二次根式的加减法与乘法运算法则即可得．【详解】第11=，第2=，第3=归纳类推得：第n 1=-n 为正整数），则2020++，2020=+，=， 20202=-，2018=，故答案为：2018．【点睛】本题考查了二次根式的加减法与乘法运算，依据已知等式，正确归纳出一般规律是解题关键．三、解答题21．无23．无24．无25．无26．无27．无28．无29．无30．无。

八年级数学月考试卷一、选择题（共10小题，每小题3分，满分30分）1、若有意义，则a 的取值范围是（ ）A ．任意实数B ．a ≥1C ．a ≤1 D.a ≥02、下列各式中①a ；②1+b ； ③2a ； ④32+a ； ⑤12-x ； ⑥122++x x 一定是二次根式的有（ ）个。

A . 1 个 B. 2个 C. 3个 D. 4个3、是整数，正整数n 的最小值是（ ）A ．4B ．3C ．2D ．04、如图，矩形ABCD 中，AB=3，AD=1，AB 在数轴上，若以点A 为圆心，对角线AC 的长为半径作弧交数轴的正半轴于M ，则点M 的坐标为（ ）A ．（2，0）B ．（）C ．（）D ．（） 5、 如图，透明的圆柱形容器（容器厚度忽略不计）的高为12cm ，底面周长为10cm ，在容器内壁离容器底部3 cm 的点B 处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿3 cm 的点A 处，则蚂蚁吃到饭粒需爬行的最短路径是（ ）A ．13cmB ．cmC ．cmD ．cm4题 5题 8题6、下列式子是最简二次根式的是（ ） A.41 B.30 C.3x D.a 277.、下列命题①如果a ，b ，c 为一组勾股数，那么a 4，b 4，c 4仍是勾股数；②如果直角三角形的两边是5、12，那么斜边必是13；③如果一个三角形的三边是12、25、21，那么此三角形必是直角三角形；④一个等腰直角三角形的三边是a ，b ，c （ab c >=），那么1:1:2::222=c b a 。

其中正确的是( ) A ．①② B ．①③ C ．①④ D ．②④8、如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A ，B ，C ，D 的边长分别是3，5，2，3，则最大正方形E 的面积是（ ）A ． 13B ． 26C ． 47D ． 949、如图，△ABC 中，△C=90°，AC=3，△B=30°，点P 是BC 边上的动点，则AP 长不可能是（ ）A.3.5 B ．4.2 C ．5.8 D.710、如图，将边长为8cm 的正方形ABCD 折叠，使点D 落在BC 边的中点E 处，点A 落在F 处，折痕为MN ，则线段CN 长是（ ）A ． 3cmB ． 4cmC ． 5cmD ． 6cm9题 10题 二、填空题（共5小题，每小题3分，满分15分）11、最简二次根式可以可以合并，则a 的值为_________ 12.、 计算：=_________．13、木工做一个长方形长方形的桌面，已知桌面的长为60cm ，宽为32cm ，对角线为68cm ，这个桌面_______(填“合格”或者“不合格”)14、在.△ABC 中，边AB=15，AC=13，高AD=12，则△ABC 的周长是________15、若实数c b a 、、在数轴的位置如图所示，则化简()=--+||2c b c a ____________三、解答题（共75分）16．（10分）计算（1）（﹣3）0﹣+|1﹣|+（2）．20082009(23)(23)+⋅-1(312248)233-+÷17．先化简，再求值：（）÷（﹣1），其中a=2﹣．（8分）18．（8分）已知x=+3，y=﹣3，求下列各式的值：（1）x2﹣2xy+y2（2）x2﹣y2．19、（12分）（1）已知55+的小数部分是a ，55-的整数部分是b ，求b a 5+的值。

人教版八年级数学第二学期 第一次月考检测测试卷含解析一、选择题1．如果0,0a b <<，且6a b -= ）A ．6B ．6-C ．6或6-D ．无法确定2．下列计算正确的为（ ）．A 5=-B =C ．2+=+D 2=3．下列二次根式中是最简二次根式的为（ ）A B C D 4．下列各式中，运算正确的是（ ）A ．=-=．2=D 2=-5．已知5x =-，则2101x x -+的值为（ ）A ．-B ．C ．2-D ．0 6．下列计算正确的是（ ）A =B 1-=C =D 6==7．设a b 21b a-的值为（ ）A 1+B 1+C 1D 18．关于代数式12a a ++，有以下几种说法， ①当3a =-时，则12a a ++的值为-4.②若12a a ++值为2，则a = ③若2a >-，则12a a ++存在最小值且最小值为0. 在上述说法中正确的是（ ） A ．①B ．①②C ．①③D ．①②③9．已知实数x ，y 满足（x y ）=2008，则3x 2-2y 2+3x -3y -2007的值为（ ）A ．-2008B ．2008C ．-1D ．110．下列说法中正确的是（ ）A ．25的值是±5B ．两个无理数的和仍是无理数C ．-3没有立方根.D ．22-a b 是最简二次根式.11．下列运算正确的是（ ） A ．235+= B ．()2228-=C ．112222÷=D ．()21313-=-12．化简（﹣3）2的结果是（ ） A ．±3B ．﹣3C ．3D ．9二、填空题13．已知412x =-，则()21142221x x x x -⎛⎫+⋅= ⎪-+-⎝⎭_________ 14．甲容器中装有浓度为a 的果汁40kg ，乙容器中装有浓度为b 的果汁90kg ，两个容器都倒出m kg ，把甲容器倒出的果汁混入乙容器，把乙容器倒出的果汁混入甲容器，混合后，两容器内的果汁浓度相同，则m 的值为_________．15．若()()22223310x y x y +++-+=，则222516x y +=______.16．方程14(1)(1)(2)(8)(9)x x x x x x ++⋅⋅⋅+=+++++的解是______．17．将1、2、3、6按右侧方式排列.若规定(m ，n )表示第m 排从左向右第n 个数，则(5，4)与(9，4)表示的两数之积是______.18．2，26，210，…，51若2的位置记为（2，3），7的位置记为（3，2），则这组数中最大数的位置记为______． 19．已知4a 2(3)|2|a a +--=_____．20．函数y ＝42xx --中，自变量x 的取值范围是____________． 三、解答题21．先阅读下列解答过程，然后再解答：2m n +,a b ，使a b m +=，ab n =，使得22)a b m +=a b n =22())m n a b a b a b ±=±=>743+743+7212+7,12m n ==，由于437,4312+=⨯=，即：22(4)(3)7+=，4312=27437212((43)23+=+=+=+。

人教版八年级第二学期 第一次月考数学试题含答案一、选择题1．下列运算中，正确的是 ( ) A ．53－23=3 B ．22×32=6 C ．33÷3=3D ．23＋32=552．下列式子中，属于最简二次根式的是（ ） A ．9B ．13C ．20D ．73．下列计算正确的是（ ） A ．2+3=5B ．8=42C ．32﹣2=3D ．23⋅=64．2的倒数是（ ） A ．2B ．22C ．2-D ．22-5．已知526x =-，则2101x x -+的值为（ ） A ．306-B ．106C ．1862--D ．06．若2()a b a b -=--则（ ） A ．0a b +=B ．0a b -=C ．0ab =D ．220a b +=7．下列式子一定是二次根式的是 ( ) A ．2a B ．－aC ．3aD ．a8．关于代数式12a a ++，有以下几种说法， ①当3a =-时，则12a a ++的值为-4. ②若12a a ++值为2，则3a =. ③若2a >-，则12a a ++存在最小值且最小值为0. 在上述说法中正确的是（ ） A ．① B ．①②C ．①③D ．①②③9．若a 、b 、c 为有理数，且等式成立，则2a ＋999b ＋1001c 的值是（ ）A ．1999B ．2000C ．2001D ．不能确定 10．2m +有意义，则实数m 的取值范围是（ ） A ．m ＞﹣2B ．m ＞﹣2且m ≠1C ．m ≥﹣2D ．m ≥﹣2且m ≠111．已知最简二次根式23a -与2a 是同类二次根式，则a 的值是（ ） A ．2B ．-1C ．3D ．-1或312．已知实数x 、y 满足222y x x =-+--，则yx 值是（ ）A ．﹣2B ．4C ．﹣4D ．无法确定二、填空题13．已知2215x 19x 2+--=，则2219x 215x -++=________． 14．定义：对非负实数x “四舍五入”到个位的值记为()f x z ， 即：当n 为非负整数时，如果1122n x n -<+≤，则()f x n =z ．如：(0)(0.48)0f f ==z z ，(0.64)(1.49)1f f ==z z ，(4)(3.68)4f f ==z z ，试解决下列问题：①(3)f =z __________；②2(33)f +=z __________； ③222222(11)(22)(22)(33)(33)(44)f f f f f f ++++⋅++⋅++⋅+z z z z z z22(20172017)(20182018)f f +=+⋅+z z __________．15．设12211112S =++，22211123S =++，32211134S =++，设12...n S S S S =+++，则S=________________ (用含有n 的代数式表示，其中n 为正整数)．16．222a a ++-1的最小值是______． 17．方程14(1)(1)(2)(8)(9)x x x x x x ++⋅⋅⋅+=+++++的解是______．18．已知20n 是整数，则正整数n 的最小值为___ 19．实数a 、b 在数轴上的位置如图所示，则化简()222a b a b -+-＝_____．20．4x -x 的取值范围是_____．三、解答题21．我国南宋时期有个著名的数学家秦九韶提出了一个利用三角形的三边求三角形的面积的公式，若三角形三边为a b c 、、，则此三角形的面积为：2222221122a b c S a b ⎛⎫+-=- ⎪⎝⎭同样古希腊有个几何学家海伦也提出了一个三角形面积公式：2S =2a b cp ++=（1）在ABC 中，若4AB =，5BC =，6AC =，用其中一个公式求ABC 的面积．（2）请证明：12S S【答案】（12） 证明见解析 【分析】（1）将4AB =，5BC =，6AC =代入1S = （2）对1S 和2S 分别平方，再进行整理化简得出2212S S =，即可得出12S S ．【详解】解：（1）将4AB =，5BC =，6AC =代入1S =得：S == （2）222222211[()]24a b a S c b +-=-=222222)1(22(4)a b c a b c ab ab +-+--+ =2222()2(21)4c a c a b b +⋅---⋅ =()(1()()16)c a b c a b a b c a b c +-++-++- 22()()()S p p a p b p c =---∵2a b cp ++=， ∴22()(2)(222)S a a b c a b c a b c a b c b c +++++++-+=-- =2222a b c b c a a c b a b c +++-+-+-⋅⋅⋅ =1()()()()16a b c b c a a c b a b c +++-+-+- ∴2212S S =∵10S >，20S >， ∴12S S ．【点睛】本题考查了二次根式的运算，解题的关键是理解题中给出的公式，灵活运用二次根式的运算性质进行运算．22．阅读材料，回答问题：两个含有二次根式的代数式相乘，如果它们的积不含有二次根式，我们就说这两个代数式a =，)111=11互为有理化因式．（1）1的有理化因式是；（2）这样，化简一个分母含有二次根式的式子时，采用分子、分母同乘以分母的有理化因式的方法就可以了，例如：==24====进行分母有理化．（3）利用所需知识判断：若a=，2b=ab，的关系是．（4）直接写结果：)1=．【答案】（1）1；（2）7-；（3）互为相反数；（4）2019【分析】（1）根据互为有理化因式的定义利用平方差公式即可得出；（2）原式分子分母同时乘以分母的有理化因式(2，化简即可；（3）将a=（4）化简第一个括号内的式子，里面的每一项进行分母有理化，然后利用平方差公式计算即可．【详解】解：（1）∵()()1111=，∴1的有理化因式是1；（22243743--==--（3）∵2a===，2b=-，∴a和b互为相反数；（4）)1 ++⨯=)11⨯=)11=20201-=2019，故原式的值为2019.【点睛】本题考查了互为有理化因式的定义及分母有理化的方法，并考查了利用分母有理化进行计算及探究相关式子的规律，本题属于中档题．23．计算：21)3)(3--【答案】.【解析】【分析】先运用完全平方公式、平方差公式进行化简，然后进行计算.【详解】解：原式22]-322]-4【点睛】本题主要考查了二次根式的化简；特别是灵活运用全平方公式、平方差公式是解答本题的关键.24．（112=3=4=；……写出④；⑤；（2）归纳与猜想．如果n 为正整数，用含n 的式子表示这个运算规律； （3）证明这个猜想．【答案】（12=55==；（2=3）证明见解析. 【解析】 【分析】(1)根据题目中的例子直接写出结果； (2)根据(1)中的特例，可以写出相应的猜想；(3)根据(2)中的猜想，对等号左边的式子进行化简，即可得到等号右边的式子，从而可以解答本题. 【详解】解：（1）由例子可得，④5=25，6，（2）如果n 为正整数，用含nn， （3）证明：∵n 是正整数，n．故答案为5=25 n；(3)证明见解析. 【点睛】本题考查了二次根式的混合运算、数字的变化类，解答本题的关键是明确题意，找出所求问题需要的条件.25．阅读下列材料，然后回答问题：1== . 以上这种化简过程叫做分母有理化.1===.（1）请用其中一种方法化简1511-；（2）化简：++++3+15+37+599+97.【答案】(1) 15＋11；(2) 311－1. 【分析】(1)运用了第二种方法求解，即将4转化为1511－；（2）先把每一个加数进行分母有理化，再找出规律，即后面的第二项可以和前面的第一项抵消，然后即可得出答案. 【详解】 （1）原式==；（2）原式=+++…=﹣1+﹣+﹣+…﹣=﹣1=3﹣1【点睛】本题主要考查了分母有理化，找准有理化的因式是解题的关键.26．2722322312-310 【分析】先根据二次根式的性质和平方差公式化简，然后再进行计算即可 【详解】 (2722322312=(223322323⎡⎤--⎢⎥⎣⎦=()3321223--310+． 310． 【点睛】本题主要考查了二次根式的性质、平方差公式，灵活运用二次根式的性质化简是解答本题的关键．27．先化简，再求值：221a a a -+，其中3【答案】2a-1，【分析】先根据二次根式的性质进行化简，再代入求值即可． 【详解】解：1a =-∴原式=1a a --=21a -当1a =-∴原式=(211-=1-【点睛】此题主要考查化简求值，正确理解二次根式的性质是解题关键．28．在一个边长为（cm 的正方形的内部挖去一个长为（）cm ，cm 的矩形，求剩余部分图形的面积．【答案】 【解析】试题分析：用大正方形的面积减去长方形的面积即可求出剩余部分的面积．试题解析：剩余部分的面积为：（2﹣（）=（）﹣（﹣）=（cm 2）． 考点：二次根式的应用29．计算：（1（2|a ﹣1|，其中1＜a 【答案】（1）1；（2）1 【分析】（1）根据二次根式的乘法法则计算；（2）由二次根式的非负性，a 的取值范围进行化简． 【详解】解：（1－1＝2－1＝1（2）∵1＜a ，a ﹣1＝2﹣a ＋a ﹣1＝1．本题考查二次根式的性质、二次根式的乘法法则，主要检验学生的计算能力．30．2020(1)- 【答案】1 【分析】先计算乘方，再化简二次根式求解即可． 【详解】2020(1)-=1 =1． 【点睛】本题考查了二次根式的混合运算，先把二次根式化为最简二次根式，再合并即可．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】根据二次根式的加减法对A 、D 进行判断；根据二次根式的乘法法则对B 进行判断；根据二次根式的除法法则对C 进行判断． 【详解】A 、A 选项错误；B 、×=12，所以B 选项错误；C 、3，所以C 选项正确；D 、，不能合并，所以D 选项错误； 故选：C ． 【点睛】本题考查了二次根式的混合运算，正确掌握运算法则是解题关键．2．D解析：D 【分析】根据直角二次根式满足的两个条件进行判断即可．被开方数中含能开得尽方的因数，不是最简二次根式，故选项A错误；=被开方数中含分母，不是最简二次根式，故选项B错误；3=被开方数中含能开得尽方的因数，不是最简二次根式，故选项C错误；是最简二次根式，故选项D正确.故选D．【点睛】本题考查的是最简二次根式的概念，满足（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式两个条件的二次根式是最简二次根式．3．D解析：D【解析】解：A A错误；B==，所以B错误；C．=C错误；D==D正确．故选D．4．B解析：B【分析】根据倒数的定义，即可得到答案.【详解】，；2故选：B.【点睛】本题考查了倒数的定义和化为最简二次根式，解题的关键是熟记倒数的定义进行解题. 5．D解析：D【分析】把x的值代入原式计算即可求出值．【详解】解：当时，原式=（）2-10×（）+1+1=0．故选：D ．【点睛】本题考查了二次根式的化简求值，熟练掌握运算法则是解题的关键．6．C解析：C【分析】直接利用二次根式的性质 ，将已知等式左边化简，可以得到a 与b 中至少有一个为0，进而分析得出答案即可．【详解】解:∵a b =--，∴a-b=-a-b ， 或b-a=-a-b∴a= -a ，或b=-b, ∴a=0,或b=0, ∴ab=0, ∴0ab =．故选：C ．【点睛】本题考查了二次根式的性质与化简，正确掌握二次根式的性质是解题的关键．7．A解析：A【分析】根据二次根式的定义，直接判断得结论．【详解】A A 正确；B 、0a <B 错误；C 是三次根式，故C 错误；D 、0a <D 错误；故选：A ．【点睛】0a ≥)是二次根式，注意二次根式的被开方数是非负数．8．C解析：C【分析】①将3a =-代入12a a ++计算验证即可；②根据题意12a a ++=2，解得a 的值即可作出判断；③若a ＞-2，则a+2＞0，则对12a a ++配方，利用偶次方的非负性可得答案． 【详解】 解：①当3a =-时， 1134232a a +=-+=-+-+． 故①正确； ②若12a a ++值为2， 则122a a +=+， ∴a 2+2a+1=2a+4，∴a 2=3，∴3a =±．故②错误；③若a ＞-2，则a+2＞0，∴12a a ++=1222a a ++-+ =2211(2)()2222a a a a ++-•+•++ =21(2)2a a +-+≥0． ∴若a ＞-2，则12a a ++存在最小值且最小值为0． 故③正确．综上，正确的有①③．故选：C ．【点睛】本题考查了分式的加减法、分式的值的计算及最值问题等知识点，熟练运用相关公式及运算法则是解题的关键．9．B解析：B【解析】因=，所以a =0，b =1，c =1，即可得2a ＋999b ＋1001c =999+1001=2000，故选B. 点睛：本题考查了二次根式的性质与化简，将复合二次根式根据完全平方公式化简并比较系数是解题的关键．10．D解析：D根据二次根式有意义的条件即可求出答案．【详解】由题意可知：2010mm+≥⎧⎨-≠⎩，∴m≥﹣2且m≠1，故选D．【点睛】本题考查二次根式有意义的条件，解题的关键是熟练运用二次根式的条件.11．C解析：C【分析】根据同类二次根式的性质即可求出答案．【详解】由题意可知：a2-3=2a∴解得：a=3或a=-1当a=-1时，该二次根式无意义，故a=3故选C．【点睛】本题考查二次根式的概念，解题的关键是熟练正确理解最简二次根式以及同类二次根式的概念.12．C解析：C【分析】依据二次根式中的被开方数是非负数求得x的值，然后可得到y的值，最后代入计算即可．【详解】∵实数x、y满足2y=，∴x＝2，y＝﹣2，∴yx＝22-⨯＝-4．故选：C．【点睛】本题主要考查的是二次根式有意义的条件，熟练掌握二次根式有意义的条件是解题的关键．二、填空题13．【解析】用换元法代替两个带根号的式子，得出m、n的关系式，解方程组求m、n的值即可．【详解】设m＝，n＝，那么m−n＝2①，m2＋n2＝()2＋()2＝34②．由①得，m＝2解析：13【解析】【分析】用换元法代替两个带根号的式子，得出m、n的关系式，解方程组求m、n的值即可．【详解】设m n那么m−n＝2①，m2＋n2＝2＋2＝34②．由①得，m＝2＋n③，将③代入②得：n2＋2n−15＝0，解得：n＝−5（舍去）或n＝3，因此可得出，m＝5，n＝3（m≥0，n≥0）．n＋2m＝13．【点睛】此题考查二次根式的减法，本题通过观察，根号里面未知数的系数为相反数，可通过换元法求解．14．3【解析】1、；2、根据题意，先推导出等于什么，（1）∵，∴，（2）再比较与的大小关系，①当n=0时，；②当为正整数时，∵，∴，∴，综合（1）、（2）可得：，解析：320172018【解析】1、(1.732)2z z f f ==；2、根据题意，先推导出f 等于什么，（1）∵2221142n n n n n ⎛⎫+<++=+ ⎪⎝⎭，12n <+，（2）12n -的大小关系，①当n=012n >-； ②当n 为正整数时，∵2212n n n ⎛⎫+-- ⎪⎝⎭1204n =->， ∴2212n n n ⎛⎫+>- ⎪⎝⎭，12n >-，综合（1）、（2）可得：1122n n -<+，∴f n =z ，∴3f =z ．3、∵f n =z ，∴(2017z f +111112233420172018=++++⨯⨯-⨯ 111111112233420172018=-+-+-++- 112018=-20172018=．故答案为（1）2；（2）3；（3）20172018. 点睛：（1）解第②小题的关键是应用“完全平方公式”和“作差的方法”分别证明到当n 为非负整数时，1122n n -<+，从而得到f n =z ；（2）解题③的要点是：当n 为正整数时，111(1)1n n n n =-++. 15．【分析】先根据题目中提供的三个式子，分别计算的值，用含n 的式子表示其规律，再计算S 的值即可．【详解】解：∵，∴；∵，∴；∵，∴；……∵，∴；∴．故答案为：【点睛】本题 解析：221n n n ++ 【分析】n 的式子表示其规律，再计算S 的值即可．【详解】解：∵1221191=124S =++311122===+-；∵222114912336S =++=7111116623===+=+-；∵32211169134144S =++=1311111121234===+=+-； ……∵()()()222222111111n n n S n n n n ++=++=++，()()2111111111n n n n n n n n ++===+=+-+++；∴...S =1111111112231n n =+-++-++-+…+ 111n n =+-+． 221n n n +=+ 故答案为：221n n n ++ 【点睛】本题为规律探究问题，难度较大，根据提供的式子发现规律，并表示规律是解题的关键，同时要注意对于式子()11111n n n n =-++的理解． 16．0【解析】【分析】先将化简为就能确定其最小值为1，再和1作差，即可求解。

人教版八年级第二学期第一次月考数学试题含答案一、选择题1．如果0,0a b <<，且6a b -=，则22a b -的值是（ ） A ．6 B ．6- C ．6或6- D ．无法确定 2．下列计算正确的是（ ） A ．=1212⨯ B ．4-3=1 C ．63=2÷ D ．8=2±3．下列根式是最简二次根式的是（ ）A ．4B ．21x +C ．12D ．40.54．下列各式计算正确的是（ ）A ．235+=B ．2222+=C ．236⨯=D ．1222= 5．下列计算结果正确的是（ ）A ．2+5=7B ．3223-=C ．2510⨯=D ．25105= 6．下列二次根式是最简二次根式的是( )A ．12B ．3C ．0.01D ．127．若ab ＜0，则代数式可化简为（ ） A ．a B ．a C ．﹣a D ．﹣a8．已知实数x ，y 满足（x 22008x -y 2-2008y ）=2008，则3x 2-2y 2+3x -3y -2007的值为（ ）A ．-2008B ．2008C ．-1D ．1 9．下列二次根式是最简二次根式的是（ ）A 0.1B 19C 8D 14410．2a a =-成立，那么a 的取值范围是（ ）A ．0a ≤B ．0a ≥C ．0a <D ．0a >11．已知m ＝12n ＝12223m n mn +- （ ） A ．±3B ．3C ．5D ．9 12．230x x +-=成立的x 的值为（ ） A ．-2 B ．3 C ．-2或3 D ．以上都不对二、填空题13．==________．14．已知函数1x f x x ，那么1f _____． 15．已知x =，a 是x 的整数部分，b 是x 的小数部分，则a-b=_______16．已知a ，b 是正整数，若有序数对（a ，b ）使得的值也是整数，则称（a ，b ）是的一个“理想数对”，如（1，4）使得=3，所以（1，4）是的一个“理想数对”．请写出其他所有的“理想数对”： __________．17．===据上述各等式反映的规律，请写出第5个等式：___________________________．18．已知x ，y 为实数，y 求5x +6y 的值________.19．n 的最小值为___20．已知2x =243x x --的值为_______．三、解答题21．计算：（1（2）)((222+-+．【答案】(1)【分析】（1）先化简二次根式，再合并同类二次根式即可；（2）根据平方差公式化简，再化简、合并同类二次根式即可.【详解】（1==（2）)((222+-+=2223--+ =5-4-3+2=022．解：设x222x=+，x=++2334x2=10∴x=10．0．【分析】根据题意给出的解法即可求出答案即可．【详解】设x两边平方得：x2=2+2+即x2=4+4+6，x2=14∴x=．0，∴x．【点睛】本题考查了二次根式的运算，解题的关键是正确理解题意给出的解法，本题属于中等题型．23．已知x=2，求代数式（7+x2+（2）x【答案】2【解析】试题分析：先求出x2，然后代入代数式，根据乘法公式和二次根式的性质，进行计算即可.试题解析：x2=（2）2=7﹣则原式=（7﹣+（2=49﹣24．计算（11)1)⨯； （2）【答案】（12+；（2）.【解析】分析：先将二次根式化为最简，然后再进行二次根式的乘法运算.详解：（1)11+；＝()31-2 ；（2）原式＝(22⨯,＝＝3⨯＝＝ 点睛：此题考查了二次根式的混合运算，熟练化简二次根式后，在加减的过程中，有同类二次根式的要合并；相乘的时候，被开方数简单的直接让被开方数相乘，再化简；较大的也可先化简，再相乘，灵活对待．25．计算下列各式：（1；（2【答案】（12 ；（2） 【分析】先根据二次根式的性质化简，再合并同类二次根式即可.【详解】（1）原式2=-2=；（2）原式==. 【点睛】本题考查了二次根式的加减，熟练掌握性质是解答本题的关键(0)(0)a aaa a≥⎧==⎨-<⎩，)0,0a b=≥≥=（a≥0，b>0）.26．计算（1（2）(()21-【答案】（1）；（2）24+【分析】（1）先将各二次根式化为最简二次根式，再进行合并即可得到答案；（2）原式运用平方差公式和完全平方公式把括号展开后，再合并同类二次根式即可得到答案．【详解】解：（1=2+=(2-+=2（2）(()21-=22(181)---=452181--+=24+．【点睛】此题主要考查了二次根式的混合运算，熟练掌握运算法则和运算顺序是解答此题的关键．27．一样的式子，其实我3====，1===；以上这种化简的步骤叫做分母有理化还可以用以下方法化简：221111===-=（12）化简：2n+++【答案】（1-2.【解析】试题分析：（12看出5-3，根据平方差公式分解因式，最后进进约分即可．（2）先每一个二次根式分母有理化，再分母不变，分子相加，最后合并即可．试题解析：（1）=====（2）原式=122n++++=12.考点：分母有理化．28．已知x²+2xy+y²的值.【答案】16【解析】分析：（1）根据已知条件先计算出x+y=4，再利用完全平方公式得到x²+2xy+y²=（x+y）²，然后利用整体代入的方法计算．本题解析：∵x² +2xy+y² =(x+y)²，∴当∴x²+2xy+y²=(x+y)²=(2−=16.29．计算：（1）()202131)()2---+ （2【答案】（1）12；（2）【分析】（1）按照负整数指数幂、0指数幂、乘方的运算法则计算即可；（2）根据二次根式的加减乘除运算法则计算即可．【详解】（1）解：原式＝ 9－1＋4＝12（2）【点睛】本题考查负整数指数幂、0指数幂、乘方以及二次根式的运算法则，熟练掌握二次根式的化简是关键．30．02020((1)π-．【答案】【分析】本题根据零次幂，最简二次根式，整数次幂的运算规则求解即可．【详解】原式11=-=【点睛】本题考查幂的运算与二次根式的综合，需牢记非零常数的零次幂为1，二次根式运算时需化为最简二次根式，其次注意计算仔细．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】=-a-(-b)=b-a=-6.故选B2．A解析：A【解析】2÷故选A.3．B解析：B【分析】可以根据最简二次根式的定义进行判断．【详解】A，原根式不是最简二次根式；B=，原根式不是最简二次根式；C2=⨯=D、=42故选B．【点睛】本题考查最简二次根式的定义，熟练掌握最简二次根式的定义及二次根式的化简方法是解题关键．4．C解析：C【分析】计算出各个选项中的正确结果，即可得到哪个选项是正确【详解】A错误；∵2+B错误；=，故选项C正确；=，故选项D错误.2故选C.【点睛】本题考查二次根式的混合运算，解题的关键是明确二次根式的混合运算的计算方法．5．C解析：C【分析】根据二次根式的加法、减法、乘法、分母有理化逐一进行计算判断即可．【详解】A不能合并，故A选项错误；B．-=B选项错误；C=D．22510555⨯==⨯，故D选项错误，故选C．【点睛】本题考查了二次根式的运算，分母有理化，熟练掌握各运算法则是解题的关键．6．B解析：B【分析】直接利用最简二次根式的定义分析得出答案．【详解】解：A、12=23，故此选项错误；B、3，是最简二次根式，故此选项正确；C、0.010.1=，故此选项错误；D、12=22，故此选项错误；故选：A．【点睛】此题主要考查了最简二次根式的定义，正确把握定义是解题关键．7．C解析：C【解析】【分析】二次根式有意义，就隐含条件b＜0，由ab＜0，先判断出a、b的符号，再进行化简即可．【详解】解：若ab＜0，且代数式有意义；故由b＞0，a＜0；则代数式故选：C．【点睛】本题主要考查二次根式的化简方法与运用：当a＞0时，，当a＜0时，，当a=0时，.8．D解析：D【解析】由（x22008x-y2-2008y）=2008，可知将方程中的x,y对换位置，关系式不变，那么说明x=y是方程的一个解由此可以解得，或者则3x 2-2y 2+3x -3y -2007=1，故选D.9．B解析：B【分析】判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．【详解】解：A 、被开方数含分母，故A 错误；B 、被开方数不含分母；被开方数不含能开得尽方的因数或因式，故B 正确；C 、被开方数含能开得尽方的因数，故C 错误；D 、被开方数含分母，故D 错误；故选B ．【点睛】本题考查最简二次根式的定义．根据最简二次根式的定义，最简二次根式必须满足两个条件：被开方数不含分母；被开方数不含能开得尽方的因数或因式．10．A解析：A【分析】由根号可知等号左边的式子为正，所以右边的式子也为正,所以可得答案.【详解】得-a≥0，所以a≤0，所以答案选择A 项.【点睛】本题考查了求解数的取值范围，等号两边的值相等是解答本题的关键.11．B解析：B【分析】由已知可得：2,(11m n mn +==+-=-，【详解】由已知可得：2,(11m n mn +==+-=-，原式3===故选B【点睛】考核知识点：二次根式运算.配方是关键. 12．B解析：B【分析】根据二次根式有意义的条件以及二次根式的乘法进行分析即可得答案.【详解】x 30-=，0=0=，∴x=-2或x=3，又∵2030x x +≥⎧⎨-≥⎩， ∴x=3，故选B.【点睛】本题考查了二次根式的乘法以及二次根式有意义的条件，熟练掌握相关知识是解题的关键.二、填空题13．3【解析】设，则 可化为：，∴，两边同时平方得：，即：，∴，解得：，∴.故答案为：.点睛：本题的解题要点是：设原式中的，从而使原式结构变得简单，这样应用二次根式的相关运算法则化简变形解析：【解析】设24x a -====两边同时平方得：128a a +=++4=，∴3216a =，解得：12a =，===故答案为： 点睛：本题的解题要点是：设原式中的24x a -=，从而使原式结构变得简单，这样应用二次根式的相关运算法则化简变形即可求得a的值，使问题得到解决.14．【分析】根据题意可知，代入原函数即可解答.【详解】因为函数，所以当时，．【点睛】本题主要考查了代数式求值问题，熟练掌握相关知识点以及二次根式的运算是解题关键.解析：2+【分析】根据题意可知1x=，代入原函数即可解答.【详解】因为函数1xf xx，所以当1x=时，211()2221f x．【点睛】本题主要考查了代数式求值问题，熟练掌握相关知识点以及二次根式的运算是解题关键. 15．【分析】先把x分母有理化求出x= ，求出a、b的值，再代入求出结果即可．【详解】∵∴∴∴【点睛】本题考查了分母有理化和估算无理数的大小的应用，解此题的关键是求a、b的值．解析：6【分析】先把x分母有理化求出2，求出a、b的值，再代入求出结果即可．【详解】2x===∵23<<∴425<<∴4,242a b ==-=∴42)6a b -=-=【点睛】本题考查了分母有理化和估算无理数的大小的应用，解此题的关键是求a 、b 的值．16．（1，1）、（4，1）、（4，4）、（9，36）、（16，16）、（36，9）【解析】试题解析：当a=1，=1，要使为整数，=1或时，分别为4和3，得出（1，4）和（1，1）是的“理想数对”，解析：（1，1）、（4，1）、（4，4）、（9，36）、（16，16）、（36，9）【解析】试题解析：当a =1，要使或12时，分别为4和3，得出（1，4）和（1，1）是的“理想数对”，当a =412，要使+或12时，分别为3和2，得出（4，1）和（4，4）是的“理想数对”，当a =913，要使16时，=1，得出（9，36）是的“理想数对”，当a =1614，要使14时，=1，得出（16，16）是的“理想数对”，当a =3616，要使13时，=1，得出（36，9）是的“理想数对”， 即其他所有的“理想数对”：（1，1）、（4，1）、（4，4）、（9，36）、（16，16）、（36，9）．故答案为：（1，1）、（4，1）、（4，4）、（9，36）、（16，16）、（36，9）．17．【解析】上述各式反映的规律是(n⩾1的整数),得到第5个等式为： (n⩾1的整数).故答案是： (n⩾1的整数).点睛:这是一道等式规律探寻题,此类题的一般推倒方法为:第一步.标序号;=【解析】上述各式反映的规律是=n⩾1的整数),得到第5==n⩾1的整数).=n⩾1的整数).点睛:这是一道等式规律探寻题,此类题的一般推倒方法为:第一步.标序号;第二步,找规律,分别比较等式中各部分与序号之间的关系,把其蕴含的规律用含序数的代数式表示出来;第三步,根据找出的规律得出第n个等式.18．-16【解析】试题分析：根据分式的有意义和二次根式有意义的条件，可知x2-9=0，且x-3≠0，解得x=-3，然后可代入得y=-，因此可得5x+6y=5×（-3）+6×（-）=-15-1=-16 解析：-16【解析】试题分析：根据分式的有意义和二次根式有意义的条件，可知x2-9=0，且x-3≠0，解得x=-3，然后可代入得y=-16，因此可得5x+6y=5×（-3）+6×（-16）=-15-1=-16.故答案为：-16.点睛：此题主要考查了分式的有意义和二次根式有意义，解题关键是利用二次根式的被开方数为非负数和分式的分母不为0，可列式求解.19．5【分析】因为是整数，且，则5n是完全平方数，满足条件的最小正整数n为5．【详解】∵，且是整数，∴是整数，即5n 是完全平方数；∴n 的最小正整数值为5．故答案为5．【点睛】主要考查了解析：5【分析】，则5n 是完全平方数，满足条件的最小正整数n 为5．【详解】∴是整数，即5n 是完全平方数；∴n 的最小正整数值为5．故答案为5．【点睛】主要考查了二次根式的定义，关键是根据乘除法法则和二次根式有意义的条件．二次根式有意义的条件是被开方数是非负数进行解答．20．-4【分析】把代入计算即可求解．【详解】解：当时，=-4故答案为：-4【点睛】本题考查了求代数式的值，二次根式混合运算，本题直接代入求值即可，能正确进行二次根式的混合运算是解题解析：-4【分析】把2x =243x x --计算即可求解．【详解】x=解：当2243--x x((2=---2423=--+4383=-4故答案为：-4【点睛】本题考查了求代数式的值，二次根式混合运算，本题直接代入求值即可，能正确进行二次根式的混合运算是解题关键．三、解答题21．无22．无23．无24．无25．无26．无27．无28．无29．无30．无。

一、选择题1．如图，在RtΔABC中，∠ACB＝90°，AC=9，BC=12，AD是∠BAC的平分线，若点P，Q 分别是AD和AC上的动点，则PC＋PQ的最小值是( )A．245B．365C．12 D．152．勾股定理是几何中的一个重要定理，在我国算书《网醉算经》中就有“若勾三，股四，则弦五”的记载．如图1，是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90°，AB=3，BC=5，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为( )A．121 B．110 C．100 D．903．已知三角形的三边长分别为a，b，c，且a+b=10，ab=18,c=8，则该三角形的形状是（）A．等腰三角形B．直角三角形C．钝角三角形D．等腰直角三角形4．如图，正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上的一动点，则DN+MN的最小值是（）A．8 B．9 C．10 D．125．下列结论中，矩形具有而菱形不一定具有的性质是（）A．内角和为360°B．对角线互相平分C．对角线相等D．对角线互相垂直6．下列各组线段能构成直角三角形的一组是（）A．30,40,60B．7,12,13C．6,8,10D．3,4,67．如图，西安路与南京路平行，并且与八一街垂直，曙光路与环城路垂直．如果小明站在南京路与八一街的交叉口，准备去书店，按图中的街道行走，最近的路程约为（）A ．200mB ．300mC ．400mD ．500m 8．以下列各组数为边长，能组成直角三角形的是（ ）A ．1，2，3B ．2，3，4C ．3，4，6D ．1，3，29．将一根 24cm 的筷子，置于底面直径为 15cm ，高 8cm 的装满水的无盖圆柱形水杯中，设筷子浸没在杯子里面的长度为 hcm ，则 h 的取值范围是（ ） A ．h≤15cm B ．h≥8cmC ．8cm≤h≤17cmD ．7cm≤h≤16cm10．已知三角形的两边分别为3、4，要使该三角形为直角三角形，则第三边的长为（ ） A ．5B ．7C ．5或7D ．3或4二、填空题11．如图，在矩形 ABCD 中，AB ＝10，BC ＝5，若点 M 、N 分别是线段 AC 、AB 上的两个动点，则 BM+MN 的最小值为_____________________．12．如图，RT ABC ，90ACB ∠=︒，6AC =，8BC =，将边AC 沿CE 翻折，使点A 落在AB 上的点D 处；再将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点B '处，两条折痕与斜边AB 分别交于点E 、F ，则B FC '△的面积为______．13．如图，等腰梯形ABCD 中，//AD BC ，1AB DC ==，BD 平分ABC ∠，BD CD ⊥，则AD BC +等于_________.14．如图，△ABC中，∠ABC＝45°，∠BCA＝30°，点D在BC上，点E在△ABC外，且AD＝AE＝CE，AD⊥AE，则ABBD的值为____________．15．Rt△ABC中，∠BAC=90°，AB=AC=2，以AC为一边．在△ABC外部作等腰直角三角形ACD，则线段BD的长为_____．16．如图，长方体纸箱的长、宽、高分别为50cm、30cm、60cm，一只蚂蚁从点A处沿着纸箱的表面爬到点B处.蚂蚁爬行的最短路程为_______cm.17．如图，直线l上有三个正方形a，b，c，若a，c的边长分别为5和12，则b的面积为_________________.18．如图，在矩形ABCD中，AD＞AB，将矩形ABCD折叠，使点C与点A重合，折痕为MN，连接CN．若△CDN的面积与△CMN的面积比为1：3，则22MNBM的值为______________．19．如图，在△ABC中，AB＝AC＝10，BC＝12，BD是高，则点BD的长为_____．20．在Rt ABC 中，90A ∠=︒，其中一个锐角为60︒，23BC =，点P 在直线AC 上（不与A ，C 两点重合），当30ABP ∠=︒时，CP 的长为__________．三、解答题21．如图，已知ABC ∆中，90B ∠=︒，8AB cm =，6BC cm =，P 、Q 是ABC ∆边上的两个动点，其中点P 从点A 开始沿A B →方向运动，且速度为每秒1cm ，点Q 从点B 开始沿B C →方向运动，且速度为每秒2cm ，它们同时出发，设出发的时间为t 秒．（1）当2t =秒时，求PQ 的长；（2）求出发时间为几秒时，PQB ∆是等腰三角形？（3）若Q 沿B C A →→方向运动，则当点Q 在边CA 上运动时，求能使BCQ ∆成为等腰三角形的运动时间．22．在等腰△ABC 与等腰△ADE 中，AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE ，且点D 、E 、C 三点在同一条直线上，连接BD ．（1）如图1，求证：△ADB ≌△AEC（2）如图2，当∠BAC ＝∠DAE ＝90°时，试猜想线段AD ，BD ，CD 之间的数量关系，并写出证明过程；（3）如图3，当∠BAC ＝∠DAE ＝120°时，请直接写出线段AD ，BD ，CD 之间的数量关系式为： （不写证明过程）23．如图1，在等腰直角三角形ABC 中，动点D 在直线AB （点A 与点B 重合除外）上时，以CD 为一腰在CD 上方作等腰直角三角形ECD ，且90ECD ∠=︒，连接AE ．（1）判断AE 与BD 的数量关系和位置关系；并说明理由．（2）如图2，若4BD =，P ，Q 两点在直线AB 上且5EP EQ ==，试求PQ 的长． （3）在第（2）小题的条件下，当点D 在线段AB 的延长线（或反向延长线）上时，判断PQ 的长是否为定值．分别画出图形，若是请直接写出PQ 的长；若不是请简单说明理由． 24．已知：如图，在ABC ∆中，90ACB ∠=，以点B 为圆心，BC 的长为半径画弧，交线段AB 于点D ，以点A 为圆心，AD 长为半径画弧，交线段AC 与点E . （1）根据题意用尺规作图补全图形（保留作图痕迹）； （2）设,BC m AC n ==①线段AD 的长度是方程2220x mx n +-=的一个根吗？并说明理由. ②若线段2AD EC =，求mn的值.25．已知ABC ∆中，90ACB ∠=︒，AC BC =，过顶点A 作射线AP .（1）当射线AP 在BAC ∠外部时，如图①，点D 在射线AP 上，连结CD 、BD ，已知21AD n =-，21AB n =+，2BD n =（1n >）.①试证明ABD ∆是直角三角形；②求线段CD 的长.（用含n 的代数式表示）（2）当射线AP 在BAC ∠内部时，如图②，过点B 作BD AP ⊥于点D ，连结CD ，请写出线段AD 、BD 、CD 的数量关系，并说明理由.26．定义：在△ABC 中，若BC ＝a ，AC ＝b ，AB ＝c ，若a ，b ，c 满足ac +a 2＝b 2，则称这个三角形为“类勾股三角形”，请根据以上定义解决下列问题：（1）命题“直角三角形都是类勾股三角形”是 命题（填“真”或“假”）；（2）如图1，若等腰三角形ABC 是“类勾股三角形”，其中AB ＝BC ，AC ＞AB ，请求∠A 的度数；（3）如图2，在△ABC 中，∠B ＝2∠A ，且∠C ＞∠A ．①当∠A ＝32°时，你能把这个三角形分成两个等腰三角形吗？若能，请在图2中画出分割线，并标注被分割后的两个等腰三角形的顶角的度数；若不能，请说明理由； ②请证明△ABC 为“类勾股三角形”．27．如图1, △ABC 和△CDE 均为等腰三角形，AC=BC, CD=CE, AC>CD, ∠ACB=∠DCE=a ，且点A 、D 、E 在同一直线上，连结BE.(1)求证: AD=BE.(2)如图2,若a=90°，CM ⊥AE 于E.若CM=7, BE=10, 试求AB 的长.(3)如图3,若a=120°, CM ⊥AE 于E, BN ⊥AE 于N, BN=a, CM=b,直接写出AE 的值(用a, b 的代数式表示).28．问题情境：综合实践活动课上，同学们围绕“已知三角形三边的长度，求三角形的面积”开展活动，启航小组同学想到借助正方形网格解决问题问题解决：图（1）、图（2）都是6×6的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，操作发现，启航小组同学在图（1）中画出△ABC ，其顶点A ，B ，C 都在格点上，同时构造长方形CDEF ，使它的顶点都在格点上，且它的边EF 经过点A ，ED 经过点B ．同学们借助此图求出了△ABC 的面积．（1）在图（1）中，△ABC 的三边长分别是AB ＝ ，BC ＝ ，AC ＝ ．△ABC 的面积是 ．（2）已知△PMN 中，PM ＝17，MN ＝25，NP ＝13．请你根据启航小组的思路，在图（2）中画出△PMN ，并直接写出△RMN 的面积 ．29．如图，在平面直角坐标系中，点O 是坐标原点，ABC ∆，ADE ∆，AFO ∆均为等边三角形，A 在y 轴正半轴上，点0()6,B -，点(6,0)C ，点D 在ABC ∆内部，点E 在ABC ∆的外部，32=AD ，30DOE ∠=︒，OF 与AB 交于点G ，连接DF ，DG ，DO ，OE .（1）求点A 的坐标；（2）判断DF 与OE 的数量关系，并说明理由； （3）直接写出ADG ∆的周长.30．已知：四边形ABCD 是菱形，AB ＝4，∠ABC ＝60°，有一足够大的含60°角的直角三角尺的60°角的顶点与菱形ABCD 的顶点A 重合，两边分别射线CB 、DC 相交于点E 、F ，且∠EAP ＝60°．（1）如图1，当点E 是线段CB 的中点时，请直接判断△AEF 的形状是 ． （2）如图2，当点E 是线段CB 上任意一点时（点E 不与B 、C 重合），求证：BE ＝CF ； （3）如图3，当点E 在线段CB 的延长线上，且∠EAB ＝15°时，求点F 到BC 的距离．【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】过点D 作DE ⊥AB 于点E ，过点E 作EQ ⊥AC 于点Q ，EQ 交AD 于点P ，连接CP ，此时PC+PQ=EQ 是最小值，根据勾股定理可求出AB 的长度，再根据EQ ⊥AC 、∠ACB=90°即可得出EQ ∥BC ，进而可得出AE EQAB BC=，代入数据即可得出EQ 的长度，此题得解. 【详解】解：如图所示，过点D 作DE ⊥AB 于点E ，过点E 作EQ ⊥AC 于点Q ，EQ 交AD 于点P ，连接CP ，此时PC+PQ=EQ 是最小值，在Rt △ABC 中，∠ACB=90°，AC=9，BC=12， ∴2215AB AC BC +=，∵AD 是∠BAC 的平分线， ∴∠CAD=∠EAD ，在△ACD 和△AED 中，90CAD EAD ACD AED AD AD ︒∠=∠⎧⎪∠=∠=⎨⎪=⎩，∴△ACD ≌△AED （AAS ）， ∴AE=AC=9．∵EQ ⊥AC ，∠ACB=90°， ∴EQ ∥BC ，AE EQAB BC ∴=， ∴91512EQ =， 653EQ ∴=. 故选B.本题考查了勾股定理、轴对称中的最短路线问题以及平行线的性质，找出点C 的对称点E ，及通过点E 找到点P 、Q 的位置是解题的关键．2．B解析：B 【分析】延长AB 交KF 于点O ，延长AC 交GM 于点P ，可得四边形AOLP 是正方形，然后求出正方形的边长，再求出矩形KLMJ 的长与宽，然后根据矩形的面积公式列式计算即可得解． 【详解】解：如图，延长AB 交KF 于点O ，延长AC 交GM 于点P ，则四边形OALP 是矩形．90CBF ∠=︒，90ABC OBF ∴∠+∠=︒，又直角ABC ∆中，90ABC ACB ∠+∠=︒，OBF ACB ∴∠=∠，在OBF ∆和ACB ∆中，BAC BOF ACB OBF BC BF ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()OBF ACB AAS ∴∆≅∆，AC OB =∴，同理：ACB PGC ∆≅∆，PC AB ∴=， OA AP ∴=，所以，矩形AOLP 是正方形， 边长347AO AB AC =+=+=，所以，3710KL =+=，4711LM =+=， 因此，矩形KLMJ 的面积为1011110⨯=， 故选B ．【点睛】本题考查了勾股定理的证明，作出辅助线构造出正方形是解题的关键．解析：B 【解析】 【分析】根据完全平方公式利用a+b=10，ab=18求出22a b +，即可得到三角形的形状. 【详解】∵a+b=10，ab=18，∴22a b +=（a+b ）2-2ab=100-36=64， ∵,c=8， ∴2c =64， ∴22a b +=2c ，∴该三角形是直角三角形， 故选：B. 【点睛】此题考查勾股定理的逆定理，完全平方公式，能够利用完全平方公式由已知条件求出22a b +是解题的关键.4．C解析：C 【解析】 【分析】要求DN ＋MN 的最小值，DN ，MN 不能直接求，可考虑通过作辅助线转化DN ，MN 的值，从而找出其最小值求解． 【详解】解：∵正方形是轴对称图形，点B 与点D 是关于直线AC 为对称轴的对称点，∴连接BN ，BD ，则直线AC 即为BD 的垂直平分线， ∴BN ＝ND ∴DN ＋MN ＝BN ＋MN 连接BM 交AC 于点P ， ∵点 N 为AC 上的动点， 由三角形两边和大于第三边， 知当点N 运动到点P 时， BN ＋MN ＝BP ＋PM ＝BM ， BN ＋MN 的最小值为BM 的长度， ∵四边形ABCD 为正方形，∴BC ＝CD ＝8，CM ＝8−2＝6，BCM ＝90°， ∴BM ＝＝10，∴DN ＋MN 的最小值是10．故选：C ．【点睛】此题考查正方形的性质和轴对称及勾股定理等知识的综合应用，解题的难点在于确定满足条件的点N 的位置：利用轴对称的方法．然后熟练运用勾股定理．5．C解析：C【分析】矩形与菱形相比，菱形的四条边相等、对角线互相垂直；矩形四个角是直角，对角线相等，由此结合选项即可得出答案．【详解】A 、菱形、矩形的内角和都为360°，故本选项错误；B 、对角互相平分，菱形、矩形都具有，故本选项错误；C 、对角线相等菱形不具有，而矩形具有，故本选项正确D 、对角线互相垂直，菱形具有而矩形不具有，故本选项错误，故选C ．【点睛】本题考查了菱形的性质及矩形的性质，熟练掌握矩形的性质与菱形的性质是解题的关键.6．C解析：C【分析】根据勾股定理的逆定理解答即可.【详解】A 、∵222304060+≠，∴该选项的三条线段不能构成直角三角形；B 、∵22271213+≠，∴该选项的三条线段不能构成直角三角形；C 、∵2226810+=，∴该选项的三条线段能构成直角三角形；D 、∵222346+≠，∴该选项的三条线段不能构成直角三角形；故选：C .【点睛】此题考查勾股定理的逆定理，掌握勾股定理的逆定理的计算法则及正确计算是解题的关键.7．D解析：D【分析】由于BC ∥AD ，那么有∠DAE=∠ACB ，由题意可知∠ABC=∠DEA=90°，BA=ED ，利用AAS 可证△ABC ≌△DEA ，于是AE=BC=300，再利用勾股定理可求AC ，即可求CE ，根据图可知从B 到E 的走法有两种，分别计算比较即可．【详解】解：如图所示，∵BC∥AD，∴∠DAE=∠ACB，又∵BC⊥AB，DE⊥AC，∴∠ABC=∠DEA=90°，又∵AB=DE=400m，∴△ABC≌△DEA，∴EA=BC=300m，在Rt△ABC中，22500AB BC m+=∴CE=AC-AE=200，从B到E有两种走法：①BA+AE=700m；②BC+CE=500m，∴最近的路程是500m．故选D．【点睛】本题考查了平行线的性质、全等三角形的判定和性质、勾股定理．解题的关键是证明△ABC≌△DEA，并能比较从B到E有两种走法．8．D解析：D【分析】根据勾股定理的逆定理，只要两边的平方和等于第三边的平方即可构成直角三角形．【详解】解：A、12+22=5≠32，故不符合题意；B、22+32=13≠42，故不符合题意；C、32+42=25≠62，故不符合题意；D、12+23=4=22，符合题意.故选D.【点睛】本题主要考查了勾股定理的逆定理，已知三条线段的长，判断是否能构成直角三角形的三边，简便的方法是：判断两个较小的数的平方和是否等于最大数的平方即可．9．C解析：C【分析】筷子浸没在水中的最短距离为水杯高度，最长距离如下图，是筷子斜卧于杯中时，利用勾股定理可求得.【详解】当筷子笔直竖立在杯中时，筷子浸没水中距离最短，为杯高=8cmAD是筷子，AB长是杯子直径，BC是杯子高，当筷子如下图斜卧于杯中时，浸没在水中的距离最长由题意得：AB=15cm，BC=8cm，△ABC是直角三角形∴在Rt△ABC中，根据勾股定理，AC=17cm∴8cm≤h≤17cm故选：C【点睛】本题考查勾股定理在实际生活中的应用，解题关键是将题干中生活实例抽象成数学模型，然后再利用相关知识求解.10．C解析：C【分析】根据勾股定理和分类讨论的方法可以求得第三边的长，从而可以解答本题．【详解】由题意可得，当3和42243+5，当斜边为422-7，43故选：C【点睛】本题考查勾股定理，解答本题的关键是明确题意，利用勾股定理和分类讨论的数学思想解答．二、填空题11．8【解析】如图作点B关于AC的对称点B′，连接B′A交DC于点E，则BM+MN的最小值等于的最小值作交于，则为所求；设,,由，，h+5=8，即BM+MN的最小值是8.点睛：本题主要是利用轴对称求最短路线，题中应用了勾股定理与用不同方式表示三角形的面积从而求出某条边上的高，利用轴对称得出M点与N点的位置是解题的关键．12．96 25【分析】将△B´CF的面积转化为求△BCF的面积，由折叠的性质可得CD＝AC＝6，∠ACE＝∠DCE，∠BCF＝∠B´CF，CE⊥AB，可证得△ECF是等腰直角三角形，EF＝CE，∠EFC＝45°，由等面积法可求CE的长，由勾股定理可求AE的长，进而求得BF的长，即可求解．【详解】根据折叠的性质可知，CD＝AC＝6，∠ACE＝∠DCE，∠BCF＝∠B´CF，CE⊥AB，∴∠DCE＋∠B´CF＝∠ACE＋∠BCF，∵∠ACB＝90°，∴∠ECF＝45°，且CE⊥AB，∴△ECF是等腰直角三角形，∴EF＝CE，∠EFC＝45°，∵S△ABC＝12AC•BC＝12AB•CE，∴AC•BC＝AB•CE，∵根据勾股定理求得AB＝10，∴CE＝245，∴EF ＝245，∵AE 185， ∴BF ＝AB−AE−EF ＝10－185－245＝85， ∴S △CBF ＝12×BF ×CE ＝12×85×245＝9625， ∴S △CB´F ＝9625， 故填：9625． 【点睛】此题主要考查了翻折变换，等腰三角形的判定和性质，勾股定理的应用等知识，根据折叠的性质求得相等的角是解决本题的关键．13．3【分析】由//AD BC ，BD 平分ABC ∠，易证得ABD ∆是等腰三角形，即可求得1AD AB ==，又由四边形ABCD 是等腰梯形，易证得2C DBC ∠=∠，然后由BD CD ⊥，根据直角三角形的两锐角互余，即可求得30DBC ∠=︒，则可求得BC 的值，继而求得AD BC +的值.【详解】解：∵//AD BC ，AB DC =，∴C ABC ∠=∠，ADB DBC ∠=∠，∵BD 平分ABC ∠，∴2ABC DBC ∠=∠，ABD DBC ∠=∠，∴ABD ADB ∠=∠，∴1AD AB ==，∴2C DBC ∠=∠，∵BD CD ⊥，∴90BDC ∠=︒，∵三角形内角和为180°，∴90DBC C ∠+∠=︒，∴260C DBC ∠=∠=︒，∴2212BC CD ==⨯=，∴123AD BC +=+=.故答案为：3．【点睛】本题主要考查对勾股定理，含30度角的直角三角形，等腰三角形的性质和判定，平行线的性质，等腰梯形的性质等知识点的理解和掌握，综合运用这些性质进行推理和计算是解此题的关键．14．62+ 【解析】 【分析】 过A 点作BC 的垂线，E 点作AC 的垂线，构造全等三角形，利用对应角相等计算得出∠DAM=15°，在AM 上截取AG=DG ，则∠DGM=30°，设DM=a,通过勾股定理可得到DG=AG=2a ，GM=3a,AM=BM=(32)a +，BD=(31)a +，AB=2(31)a +,代入计算即可.【详解】过A 点作AM ⊥BC 于M 点，过E 点EN ⊥AC 于N 点.∵∠BCA ＝30°，AE=EC∴AM=12AC ，AN=12AC ∴AM=AN又∵AD=AE∴R t∆ADM ≅ R t∆AEN (HL)∴∠DAM=∠EAN 又∵∠MAC=60°，AD ⊥AE∴∠DAM=∠EAN=15°在AM 上截取AG=DG ，则∠DGM=30°设DM=a,则 DG=AG=2a ，根据勾股定理得：GM=3a,∵∠ABC ＝45°∴AM=BM=(32)a +∴BD=(31)a +，AB=2(32)a +,∴()()6226231a AB BD a++==+ 故答案为：622+【点睛】本题主要考查等于三角形的性质、含30°角的直角三角形的性质，勾股定理等知识，关键是能根据已知条件构建全等三角形及构建等腰三角形将15°角转化为30°角，本题有较大难度.15．4或【分析】分三种情况讨论：①以A为直角顶点，向外作等腰直角三角形DAC；②以C为直角顶点，向外作等腰直角三角形ACD；③以AC为斜边，向外作等腰直角三角形ADC．分别画图，并求出BD．【详解】①以A为直角顶点，向外作等腰直角三角形DAC，如图1．∵∠DAC=90°，且AD=AC，∴BD=BA+AD=2+2=4；②以C为直角顶点，向外作等腰直角三角形ACD，如图2．连接BD，过点D作DE⊥BC，交BC的延长线于E．∵△ABC是等腰直角三角形，∠ACD=90°，∴∠DCE=45°．又∵DE⊥CE，∴∠DEC=90°，∴∠CDE=45°，∴CE=DE=2=在Rt△BAC中，BC==BD===③以AC为斜边，向外作等腰直角三角形ADC，如图3．∵∠ADC=90°，AD=DC，且AC=2，=∴AD=DC=AC sin45°=22又∵△ABC、△ADC是等腰直角三角形，∴∠ACB=∠ACD=45°，∴∠BCD=90°．又∵在Rt△ABC中，BC==∴BD==故BD的长等于4或25或10．故答案为4或25或10．【点睛】本题考查了等腰直角三角形的性质、勾股定理等知识．解题的关键是分情况考虑问题，16．100【解析】蚂蚁有三种爬法，就是把正视和俯视（或正视和侧视，或俯视和侧视）二个面展平成一个长方形，然后求其对角线：第一种情况：如图1，把我们所看到的前面和上面组成一个平面，则这个长方形的长和宽分别是90cm和50cm，则所走的最短线段AB==10cm；第二种情况：如图2，把我们看到的左面与上面组成一个长方形，则这个长方形的长和宽分别是110cm 和30cm ，所以走的最短线段AB==10cm ；第三种情况：如图3，把我们所看到的前面和右面组成一个长方形，则这个长方形的长和宽分别是80cm 和60cm ，所以走的最短线段AB==100cm ； 三种情况比较而言，第三种情况最短．故答案为100cm ．点睛：本题考查了立体图形中的最短路线问题；通常应把立体几何中的最短路线问题转化为平面几何中的求两点间距离的问题；注意长方体展开图形应分情况进行探讨． 17．169【解析】解：由于a 、b 、c 都是正方形，所以AC =CD ，∠ACD =90°；∵∠ACB +∠DCE =∠ACB +∠BAC =90°，即∠BAC =∠DCE ，∠ABC =∠CED =90°，AC =CD ，∴△ACB ≌△DCE ，∴AB =CE ，BC =DE ； 在Rt △ABC 中，由勾股定理得：AC 2=AB 2+BC 2=AB 2+DE 2，即S b =S a +S c =22512 =169． 故答案为：169．点睛：此题主要考查对全等三角形和勾股定理的综合运用，结合图形求解，对图形的理解能力要比较强．18．12【解析】如图，过点N 作NG ⊥BC 于点G ，连接CN ，根据轴对称的性质有：MA=MC ，NA=NC ，∠AMN=∠CMN.因为四边形ABCD 是矩形，所以AD ∥BC ，所以∠ANM=∠CMN.所以∠AMN=∠ANM，所以AM=AN.所以AM=AN=CM=CN.因为△CDN 的面积与△CMN 的面积比为1：3，所以DN:CM=1:3.设DN=x ，则CG=x ，AM=AN=CM=CN=3x ，由勾股定理可得()22322x x x -=， 所以MN 2=()()2222312x x x x +-=，BM 2=()()22232x x x -=.所以222212MN x BM x==12. 枚本题应填12.点睛：矩形中的折叠问题，其本质是轴对称问题，根据轴对称的性质，找到对应的线段和角，也就找到了相等的线段和角，矩形中的折叠一般会伴随着等腰三角形(也就是基本图形“平行线+角平分线→等腰三角形”)，所以常常会结合等腰三角形，勾股定理来列方程求解. 19．485【解析】 试题分析：根据等腰三角形的性质和勾股定理可知BC 边上的高为8，然后根据三角形的面积法可得111012822BD ⨯⨯=⨯⨯，解得BD=485. 20．232或4【分析】根据题意画出图形，分4种情况进行讨论，利用含30°角直角三角形与勾股定理解答．【详解】解：如图1：当∠C=60°时，∠ABC=30°，与∠ABP=30°矛盾；如图2：当∠C=60°时，∠ABC=30°，∵∠ABP=30°，∴∠CBP=60°，∴△PBC 是等边三角形， ∴23CP BC ==；如图3：当∠ABC=60°时，∠C=30°，∵∠ABP=30°，∴∠PBC=60°-30°=30°，∴PC=PB ， ∵23BC = ∴222213,(23)(3)32AB BC AC BC AB ===-=-=， 在Rt △APB 中，根据勾股定理222AP AB BP +=,即222()AC PC AB PC -+=, 即222(3)(3)PC PC -+=，解得2PC =，如图4：当∠ABC=60°时，∠C=30°，∵∠ABP=30°，∴∠PBC=60°+30°=90°，∴12BP PC = 在Rt △BCP 中，根据勾股定理222BP BC PC +=,即2221()(23)2PC PC +=,解得PC=4（已舍去负值）． 综上所述，CP 的长为232或4．故答案为：32或4．【点睛】本题考查含30°角直角三角形，等边三角形的性质和判定，勾股定理．理解直角三角形30°角所对边是斜边的一半，并能通过勾股定理去求另外一个直角边是解决此题的关键． 三、解答题21．（1）132）83；（3）5.5秒或6秒或6.6秒【分析】（1）根据点P 、Q 的运动速度求出AP ，再求出BP 和BQ ，用勾股定理求得PQ 即可； （2）由题意得出BQ BP =，即28t t =-，解方程即可；（3）当点Q 在边CA 上运动时，能使BCQ ∆成为等腰三角形的运动时间有三种情况： ①当CQ BQ =时（图1)，则C CBQ ∠=∠，可证明A ABQ ∠=∠，则BQ AQ =，则CQ AQ =，从而求得t ；②当CQ BC =时（图2)，则12BC CQ +=，易求得t ；③当BC BQ =时（图3)，过B 点作BE AC ⊥于点E ，则求出BE ，CE ，即可得出t ．【详解】（1）解：（1）224BQ cm =⨯=，8216BP AB AP cm =-=-⨯=，90B ∠=︒， 222246213()PQ BQ BP cm =+=+=； （2）解：根据题意得：BQ BP =，即28t t =-，解得：83t =； 即出发时间为83秒时，PQB ∆是等腰三角形； （3）解：分三种情况：①当CQ BQ =时，如图1所示：则C CBQ ∠=∠，90ABC ∠=︒， 90CBQ ABQ ∴∠+∠=︒，90A C ∠+∠=︒，A ABQ ∴∠=∠BQ AQ ∴=，5CQ AQ ∴==，11BC CQ ∴+=，112 5.5t ∴=÷=秒．②当CQ BC =时，如图2所示：则12BC CQ +=1226t ∴=÷=秒．③当BC BQ =时，如图3所示：过B点作BE AC⊥于点E，则684.8()10AB BCBE cmAC⨯===22 3.6CE BC BE cm∴=-=，27.2CQ CE cm∴==，13.2BC CQ cm∴+=，13.22 6.6t∴=÷=秒．由上可知，当t为5.5秒或6秒或6.6秒时，BCQ∆为等腰三角形．【点睛】本题考查了勾股定理、三角形的面积以及等腰三角形的判定和性质；本题有一定难度，注意分类讨论思想的应用．22．（1）见解析；（2）CD2AD+BD，理由见解析；（3）CD3+BD【分析】（1）由“SAS”可证△ADB≌△AEC；（2）由“SAS”可证△ADB≌△AEC，可得BD＝CE，由直角三角形的性质可得DE2AD，可得结论；（3）由△DAB≌△EAC，可知BD＝CE，由勾股定理可求DH＝32AD，由AD＝AE，AH⊥DE，推出DH＝HE，由CD＝DE+EC＝2DH+BD3AD+BD，即可解决问题；【详解】证明：（1）∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；（2）CD2AD+BD，理由如下：∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；∴BD＝CE，∵∠BAC＝90°，AD＝AE，∴DE2AD，∵CD＝DE+CE，∴CD＝2AD+BD；（3）作AH⊥CD于H．∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；∴BD＝CE，∵∠DAE＝120°，AD＝AE，∴∠ADH＝30°，∴AH＝12 AD，∴DH22AD AH32AD，∵AD＝AE，AH⊥DE，∴DH＝HE，∴CD＝DE+EC＝2DH+BD3+BD，故答案为：CD3+BD．【点睛】本题是结合了全等三角形的性质与判定，勾股定理等知识的综合问题，熟练掌握知识点，有简入难，层层推进是解答关键.23．（1）AE=BD且AE⊥BD；（2）6；（3）PQ为定值6，图形见解析【分析】（1）由“SAS”可证△ACE≌△BCD，可得AE=BD，∠EAC=∠DBC=45°，可得AE⊥BD；（2）由等腰三角形的性质可得PA=AQ，由勾股定理可求PA的长，即可求PQ的长；（3）分两种情况讨论，由“SAS”可证△ACE≌△BCD，可得AE=BD，∠EAC=∠DBC，可得AE⊥BD，由等腰三角形的性质可得PA=AQ，由勾股定理可求PA的长，即可求PQ的长．【详解】解：（1）AE=BD，AE⊥BD，理由如下：∵△ABC，△ECD都是等腰直角三角形，∴AC=BC，CE=CD，∠ACB=∠ECD=90°，∠ABC=∠CAB=45°，∴∠ACE=∠DCB，且AC=BC，CE=CD，∴△ACE≌△BCD（SAS）∴AE=BD，∠EAC=∠DBC=45°，∴∠EAC+∠CAB=90°，∴AE ⊥BD ；（2）∵PE=EQ ，AE ⊥BD ，∴PA=AQ ，∵EP=EQ=5，AE=BD=4，∴AQ=22=2516=3EQ AE --，∴PQ=2AQ=6；（3）如图3，若点D 在AB 的延长线上，∵△ABC ，△ECD 都是等腰直角三角形，∴AC=BC ，CE=CD ，∠ACB=∠ECD=90°，∠ABC=∠CAB=45°，∴∠ACE=∠DCB ，且AC=BC ，CE=CD ，∴△ACE ≌△BCD （SAS ）∴AE=BD ，∠CBD=∠CAE=135°，且∠CAB=45°，∴∠EAB=90°，∵PE=EQ ，AE ⊥BD ，∴PA=AQ ，∵EP=EQ=5，AE=BD=4，∴AQ=22=2516=3EQ AE --，∴PQ=2AQ=6；如图4，若点D 在BA 的延长线上，∵△ABC ，△ECD 都是等腰直角三角形，∴AC=BC ，CE=CD ，∠ACB=∠ECD=90°，∠ABC=∠CAB=45°，∴∠ACE=∠DCB ，且AC=BC ，CE=CD ，∴△ACE ≌△BCD （SAS ）∴AE=BD ，∠CBD=∠CAE=45°，且∠CAB=45°，∴∠EAB=90°，∵PE=EQ ，AE ⊥BD ，∴PA=AQ ，∵EP=EQ=5，AE=BD=4，∴AQ=22=2516=3EQ AE --，∴PQ=2AQ=6.【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，等腰三角形的性质，勾股定理等知识，证明AE ⊥BD 是本题的关键．24．（1）详见解析；（2）①线段AD 的长度是方程2220x mx n +-=的一个根，理由详见解析；②512m n = 【分析】（1）根据题意，利用尺规作图画出图形即可；（2）①根据勾股定理求出AD ，然后把AD 的值代入方程，即可得到答案； ②先得到出边长的关系，然后根据勾股定理，列出方程，解方程后得到答案.【详解】（1）解：作图，如图所示：（2）解：①线段AD 的长度是方程2220x mx n +-=的一个根.理由如下：依题意得， BD BC m ==，在Rt ABC 中，90ACB ∠=︒222BC AC AB ∴=+22AB m n =+22AD AB BD m n m ∴=-=+222AD m AD n ∴+-)()2222222m n m m m n m n =+++- 222222222222m n m m n m m m n m n =+-+++-0=；∴线段AD 的长度是方程22 20x mx n +-=的一个根②依题意得：,,AD AE BD BC AB AD BD ====2AD EC =2233AD AE AC n ∴=== 在RT ABC 中，90ACB ∠=222BC AC AB ∴+=22223m n n m ⎛⎫+=+ ⎪⎝⎭ 22224493m n n mn m +=++ 25493n mn = 512m n ∴= 【点睛】本题考查的是基本作图，勾股定理、一元二次方程的解法，掌握一元二次方程的求根公式、勾股定理是解题的关键．25．（1）①详见解析；（2）2CD =+-1n >）；（2）AD BD -=，理由详见解析.【分析】（1）①根据勾股定理的逆定理进行判断；②过点C 作CE ⊥CD 交DB 的延长线于点E ，利用同角的余角相等证明∠3=∠4，∠1=∠E ，进而证明△ACD ≌△BCE ，求出DE 的长，再利用勾股定理求解即可.（2）过点C 作CF ⊥CD 交BD 的延长线于点F ，先证∠ACD=∠BCF ，再证△ACD ≌△BCF ，得CD=CF ，AD=BF ，再利用勾股定理求解即可.【详解】（1）①∵()()()22222222212214AD BD n n n n n +=-+=-++()()22222211n n n =++=+ 又∵()2221AB n =+∴222AD BD AB +=∴△ABD 是直角三角形②如图①，过点C 作CE ⊥CD 交DB 的延长线于点E ，∵∠3+∠BCD=∠ACD=90°，∠4+∠BCD=∠DCE=90°∴∠3=∠4由①知△ABD 是直角三角形∴1290∠+∠=︒又∵290E ∠+∠=︒∴∠1=∠E在ACD ∆和BCE ∆中，A 34E AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ACD ≌△BCE∴CD CE =，AD BE =∴221DE BD BE BD AD n n =+=+=+-又∵CD CE =，90DCE ∠=︒ ∴由勾股定理得222DE CD DE CD =+=∴22CD =222222n n =+-（1n >） （2）AD 、BD 、CD 的数量关系为：2AD BD CD -=，理由如下：如图②，过点C 作CF ⊥CD 交BD 的延长线于点F ，∵∠ACD=90°+∠5，∠BCF=90°+∠5∴∠ACD=∠BCF∵BD ⊥AD∴∠ADB=90°∴∠6+∠7=90°∵∠ACB=90°∴∠9=∠8=90°又∵∠6=∠8∴∠7=∠9ACD ∆和BCF ∆中97AC BCACD BCF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ACD ≌△BCF∴CD=CF ，AD=BF又∵∠DCF=90° ∴由勾股定理得222DF CDCF CD =+=又DF=BF-BD=AD-BD∴2AD BD CD -=【点睛】本题考查的是三角形全等、勾股定理及其逆定理，掌握三角形全等的判定方法及勾股定理及其逆定理是关键.26．（1）假；（2）∠A ＝45°；（3）①不能，理由见解析，②见解析【分析】（1）先由直角三角形是类勾股三角形得出ab+a 2=c 2，再由勾股定理得a 2+b 2=c 2，即可判断出此直角三角形是等腰直角三角形；（2）由类勾股三角形的定义判断出此三角形是等腰直角三角形，即可得出结论； （3）①分三种情况，利用等腰三角形的性质即可得出结论；②先求出CD=CB=a ，AD=CD=a ，DB=AB-AD=c-a ，DG=BG=12（c-a ），AG=12（a+c ），两个直角三角形中利用勾股定理建立方程即可得出结论．【详解】解：（1）如图1，假设Rt △ABC 是类勾股三角形，∴ab +a 2＝c 2，在Rt △ABC 中，∠C ＝90°，根据勾股定理得，a 2+b 2＝c 2，∴ab +b 2＝a 2+b 2，∴ab＝a2，∴a＝b，∴△ABC是等腰直角三角形，∴等腰直角三角形是类勾股三角形，即：原命题是假命题，故答案为：假；（2）∵AB＝BC，AC＞AB，∴a＝c，b＞c，∵△ABC是类勾股三角形，∴ac+a2＝b2，∴c2+a2＝b2，∴△ABC是等腰直角三角形，∴∠A＝45°，（3）①在△ABC中，∠ABC＝2∠BAC，∠BAC＝32°，∴∠ABC＝64°，根据三角形的内角和定理得，∠ACB＝180°﹣∠BAC﹣∠ABC＝84°，∵把这个三角形分成两个等腰三角形，∴（Ⅰ）、当∠BCD＝∠BDC时，∵∠ABC＝64°，∴∠BCD＝∠BDC＝58°，∴∠ACD＝∠ACB﹣∠BCD＝84°﹣58°＝26°，∠ADC＝∠ABC+∠BCD＝122°∴△ACD不是等腰三角形，此种情况不成立；（Ⅱ）、当∠BCD＝∠ABC＝64°时，∴∠BDC＝52°，∴∠ACD＝20°，∠ADC＝128°，∴△ACD是等腰三角形，此种情况不成立；（Ⅲ）、当∠BDC＝∠ABC＝64°时，∴∠BCD＝52°，∴∠ACD＝∠ACB﹣BCD＝32°＝∠BAC，∴△ACD是等腰三角形，即：分割线和顶角标注如图2所示，Ⅱ、分∠ABC，同（Ⅰ）的方法，判断此种情况不成立；Ⅲ、分∠BAC，同（Ⅱ）的方法，判断此种情况不成立；②如图3，在AB边上取点D，连接CD，使∠ACD＝∠A图3作CG⊥AB于G，∴∠CDB＝∠ACD+∠A＝2∠A，∵∠B＝2∠A，∴∠CDB＝∠B，∴CD＝CB＝a，∵∠ACD＝∠A，∴AD＝CD＝a，∴DB＝AB﹣AD＝c﹣a，∵CG⊥AB，∴DG＝BG＝12（c﹣a），∴AG＝AD+DG＝a+12（c﹣a）＝12（a+c），在Rt△ACG中，CG2＝AC2﹣AG2＝b2﹣[12（c+a）]2，在Rt△BCG中，CG2＝BC2﹣BG2＝a2﹣[12（c﹣a）]2，∴b2﹣[12（a+c）]2＝a2﹣[12（c﹣a）]2，∴b2＝ac+a2，∴△ABC是“类勾股三角形”．【点睛】此题是三角形综合题，主要考查了等腰三角形的性质，勾股定理，新定义“类勾股三角形”，分类讨论的数学思想，解本题的关键是理解新定义．27．（1）见解析；（2）26；（3）33a+3【分析】（1）由∠ACB=∠DCE可得出∠ACD=∠BCE，再利用SAS判定△ACD≌△BCE，即可得到AD=BE；（2）由等腰直角三角形的性质可得CM=12DE，同（1）可证△ACD≌△BCE，得到AD=BE，然后可求AE的长，再判断∠AEB=90°，即可用勾股定理求出AB的长；。

人教版数学八年级（下）第一次月考测试卷（含答案）一．选择题（每小题3分，共30分）1．（3分）下列计算不正确的是（）A．B．C．D．＝2+32．（3分）下列根式中，属于最简二次根式的是（）A．B．C．D．3．（3分）有下列各组数：①3，4，5；②62，82，102；③0.5，1.2，1.3；④1，，．其中勾股数有（）A．1组B．2组C．3组D．4组4．（3分）下列条件中，不能判断一个三角形是直角三角形的是（）A．三个角的比为1：2：3B．三条边满足关系a2＝b2﹣c2C．三条边的比为1：2：3D．三个角满足关系∠B+∠C＝∠A5．（3分）如图，在3×3的网格中，每个小正方形的边长均为1，点A，B，C都在格点上，AD为△ABC的高，则AD的长为（）A．B．C．D．6．（3分）如图，在平面直角坐标系中，点P坐标为（﹣3，2），以点O为圆心，以OP的长为半径画弧，交x轴的负半轴于点A，则点A的横坐标介于（）A．﹣4和﹣3之间B．﹣5和﹣4之间C．3和4之间D．4和5之间7．（3分）国庆假期中，小华与同学去玩探宝游戏，按照探宝图，他们从门口A处出发先往东走8km，又往北走2km，遇到障碍后又往西走3km，再向北走到6km处往东拐，仅走了1km，就找到了宝藏，则门口A到藏宝点B的直线距离是（）A．20km B．14km C．11km D．10km8．（3分）如果一个三角形的三边长分别为、k、，则化简﹣|2k﹣5|的结果是（）A．﹣k﹣1B．k+1C．3k﹣11D．11﹣3k9．（3分）如图，是由四个全等的直角三角形拼成的“赵爽弦图”，得到正方形ABCD与正方形EFGH，连结DF．若S正方形ABCD＝5，EF＝BG，则DF的长为（）A．2B．C．3D．10．（3分）如图是一个按某种规律排列的数阵：根据数阵排列的规律，第n（n是整数，且n≥4）行从左向右数第（n﹣3）个数是（用含n的代数式表示）（）A．B．C．D．二．填空题（每小题3分，共15分）11．（3分）式子在实数范围内有意义，则实数x的取值范围是．12．（3分）α＝﹣的倒数是．13．（3分）在△ABC中，若AB＝AC＝5，BC＝6，则AC边上的高h＝．14．（3分）若关于x的一元一次不等式组无解，则a的取值范围是．15．（3分）如图，△ABC中，∠ACB＝90°，分别以AC、BC为斜边作等腰直角三角形S1、S2，以AB为边作正方形S．若S1与S2的面积和为9，则正方形S的边长等于．三．解答题（共9小题，共72分）16．（6分）计算：（1）；（2）．17．（6分）已知最简二次根式和可以合并，你能求出使有意义的x的取值范围吗？18．（6分）如图，有一个池塘，其底边长为10尺，一根芦苇AB生长在它的中央，高出水面部分BC为1尺．如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B 恰好碰到岸边的B'．请你计算这个池塘水的深度和这根芦苇的长度各是多少？19．（8分）如图，学校有一块三角形空地ABC，计划将这块三角形空地分割成四边形ABDE 和△EDC，分别摆放“秋海棠”和“天竺葵”两种不同的花卉，经测量，∠EDC＝90°，DC＝3，CE＝5，BD＝7，AB＝8，AE＝1，求四边形ABDE的面积．20．（8分）如图，在梯形纸片ABCD中，AD∥BC，∠A＝90°，∠C＝30°，折叠纸片使BC经过点D，点C落在点E处，BF是折痕，且BF＝CF＝8．求AB的长．21．（8分）定义：若两个二次根式a，b满足ab＝c，且c是有理数，则称a与b是关于c 的共轭（è）二次根式．问题解决：（1）若a与2是关于6的共轭二次根式，则a＝；（2）若4+与8﹣m是关于26的共轭二次根式，求m的值．22．（10分）实数a在数轴上的对应点A的位置如图所示，b＝|a﹣|+|2﹣a|．（1）求b的值；（2）已知b+2的小数部分是m，8﹣b的小数部分是n，求2m+2n+1的平方根．23．（11分）如图，△ABC中，∠ACB＝90°，AB＝10cm，BC＝6cm，若动点P从点A出发，以每秒1cm的速度沿折线A﹣C﹣B运动，设运动时间为t秒（t＞0）．（1）当点P在AB边的垂直平分线上时，求t的值；（2）当点P在∠BAC的平分线上时，求t的值．24．（12分）规律探索题：细心观察如图，认真分析各式，然后解答问题.；（S1是△OA1A2的面积）；；（S2是△OA2A3的面积）；；（S3是△OA3A4的面积）；…（1）请用含有n（n为正整数）的等式S n＝；（2）推算出OA10＝；（3）求出的值．参考答案一．选择题（每小题3分，共30分）1．D；2．C；3．A；4．C；5．D；6．A；7．D；8．D；9．B；10．C；二．填空题（每小题3分，共15分）11．x＞5；12．+；13．；14．a≥1；15．6；三．解答题（共9小题，共72分）16．（1）；（2）．；17．x≥2．；18．；19．四边形ABDE的面积为18．；20．6．；21．；22．（1）；（2）±．；23．；24．；.。

一、选择题1．如图，点A 的坐标是(2)2，，若点P 在x 轴上，且APO △是等腰三角形，则点P 的坐标不可能是（ ）A ．（2，0）B ．（4，0）C ．（－22，0）D ．（3，0）2．如图，等腰直角△ABC 中，∠C ＝90°，点F 是AB 边的中点，点D 、E 分别在AC 、BC 边上运动，且∠DFE ＝90°，连接DE 、DF 、EF ，在此运动变化过程中，下列结论：①图中全等的三角形只有两对；②△ABC 的面积是四边形CDFE 面积的2倍；③CD +CE ＝2FA ；④AD 2+BE 2＝DE 2．其中错误结论的个数有（ ）A ．1个B ．2个C ．3个D ．4个3．如图，四边形ABCD 中，AC ⊥BD 于O ，AB ＝3，BC ＝4，CD ＝5，则AD 的长为（ ）A ．1B ．32C ．4D ．234．在ABC 中，90C ∠=︒，30A ∠=︒，12AB =，则AC =（ ）A ．6B ．12C ．62D ．635．“折竹抵地”问题源自《九章算术》中，即：今有竹高一丈，末折抵地，去本四尺，问折者高几何？意思是：一根竹子，原高一丈，一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部4尺远(如图)，则折断后的竹子高度为多少尺？(1丈=10尺)( )A ．3B ．5C ．4.2D ．46．如图是甲、乙两张不同的矩形纸片，将它们分别沿着虚线剪开后，各自要拼一个与原来面积相等的正方形，则（）A．甲、乙都可以B．甲、乙都不可以C．甲不可以、乙可以D．甲可以、乙不可以7．如图，透明的圆柱形玻璃容器（容器厚度忽略不计）的高为16cm，在容器内壁离容器底部4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在容器外壁，位于离容器上沿4cm的点A处，若蚂蚁吃到蜂蜜需爬行的最短路径为20cm，则该圆柱底面周长为（）A．12cm B．14cm C．20cm D．24cm8．如图，已知AB是线段MN上的两点，MN＝12，MA＝3，MB＞3，以A为中心顺时针旋转点M，以点B为中心顺时针旋转点N，使M、N两点重合成一点C，构成△ABC，当△ABC为直角三角形时AB的长是（）A．3 B．5 C．4或5 D．3或519．如图，“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形，若直角三角形的两直角边长分别为5和3，则小正方形的面积为（）A．4 B．3 C．2 D．110．有下列的判断：①△ABC中，如果a2＋b2≠c2，那么△ABC不是直角三角形②△ABC中，如果a2－b2＝c2，那么△ABC是直角三角形③如果△ABC是直角三角形，那么a2＋b2＝c2以下说法正确的是（）A．①②B．②③C．①③D．②二、填空题11．如图，在四边形ABCD中，AB =AD，BC=DC，点E为AD边上一点，连接BD、CE，CE 与BD交于点F，且CE∥AB，若 A =60°，AB=4，CE=3，则BC的长为_______．CD=，12．如图，在四边形ABCD中，22AD=，3∠=∠=∠=︒，则BD的长为__________．45ABC ACB ADC13．如图，在Rt△ABC中，∠ACB＝90°，AB＝7.5cm，AC＝4.5cm，动点P从点B出发沿射线BC以2cm/s的速度移动，设运动的时间为t秒，当△ABP为等腰三角形时，t的取值为_____．14．已知Rt△ABC中，AC＝4，BC＝3，∠ACB＝90°，以AC为一边在Rt△ABC外部作等腰直角三角形ACD，则线段BD的长为_____．15．如图，在四边形ABCD中，AC平分∠BAD，BC=CD=10，AC=17，AD=9，则AB=_____.16．已知x，y为一个直角三角形的两边的长，且（x﹣6）2=9，y=3，则该三角形的第三边长为_____．17．在等腰Rt ABC △中，90C ∠=︒，2AC =，过点C 作直线l AB ，F 是l 上的一点，且AB AF =，则FC =__________．18．如图，在□ABCD 中，AC 与BD 交于点O ，且AB =3，BC =5．①线段OA 的取值范围是______________；②若BD -AC =1，则AC •BD = _________．19．如图，在△ABC 中，AB ＝AC ＝10，BC ＝12，BD 是高，则点BD 的长为_____．20．如图，把平面内一条数轴x 绕点O 逆时针旋转角θ（0°＜θ＜90°）得到另一条数轴y ，x 轴和y 轴构成一个平面斜坐标系．规定：已知点P 是平面斜坐标系中任意一点，过点P 作y 轴的平行线交x 轴于点A ，过点P 作x 轴的平行线交y 轴于点B ，若点A 在x 轴上对应的实数为a ，点B 在y 轴上对应的实数为b ，则称有序实数对（a ，b ）为点P 的斜坐标．在平面斜坐标系中，若θ＝45°，点P 的斜坐标为（1，22），点G 的斜坐标为（7，﹣22），连接PG ，则线段PG 的长度是_____．三、解答题21．如图，在△ABC 中，AB ＝30 cm ，BC ＝35 cm ，∠B ＝60°，有一动点M 自A 向B 以1 cm/s 的速度运动，动点N 自B 向C 以2 cm/s 的速度运动，若M ，N 同时分别从A ，B 出发．(1)经过多少秒，△BMN 为等边三角形；(2)经过多少秒，△BMN 为直角三角形．22．如图1，在△ABC 中，AB ＝AC ，∠BAC ＝90°，D 为AC 边上一动点，且不与点A 点C 重合，连接BD 并延长，在BD 延长线上取一点E ，使AE ＝AB ，连接CE ．（1）若∠AED ＝20°，则∠DEC ＝ 度；（2）若∠AED ＝a ，试探索∠AED 与∠AEC 有怎样的数量关系？并证明你的猜想； （3）如图2，过点A 作AF ⊥BE 于点F ，AF 的延长线与EC 的延长线交于点H ，求证：EH 2+CH 2＝2AE 2．23．如果一个三角形的两条边的和是第三边的两倍，则称这个三角形是“优三角形”，这两条边的比称为“优比”（若这两边不等，则优比为较大边与较小边的比），记为k . （1）命题：“等边三角形为优三角形，其优比为1”，是真命题还是假命题？（2）已知ABC 为优三角形，AB c =，AC b =，BC a =，①如图1，若90ACB ∠=︒，b a ≥，6b =，求a 的值.②如图2，若c b a ≥≥，求优比k 的取值范围.（3）已知ABC 是优三角形，且120ABC ∠=︒，4BC =，求ABC 的面积.24．我国古代数学家赵爽曾用图1证明了勾股定理，这个图形被称为“弦图”.2002年在北京召开的国际数学家大会(ICM 2002)的会标(图2)，其图案正是由“弦图”演变而来.“弦图”是由4个全等的直角三角形与一个小正方形组成，恰好拼成一个大正方形请你根据图1解答下列问题:(1)叙述勾股定理(用文字及符号语言叙述);(2)证明勾股定理;(3)若大正方形的面积是13,小正方形的面积是1,求()2a b +的值.25．如图，△ABC 中，90BAC ∠=︒，AB=AC ，P 是线段BC 上一点,且045BAP ︒<∠<︒.作点B 关于直线AP 的对称点D, 连结BD ，CD ，AD ．（1）补全图形.（2）设∠BAP 的大小为α.求∠ADC 的大小(用含α的代数式表示).（3）延长CD 与AP 交于点E,直接用等式表示线段BD 与DE 之间的数量关系.26．如图，在四边形ABCD 中，=AB AD ，=BC DC ，=60A ∠︒，点E 为AD 边上一点，连接CE ，BD . CE 与BD 交于点F ，且CE ∥AB .（1）求证:CED ADB ∠=∠；（2）若=8AB ，=6CE . 求BC 的长 .27．定义：在△ABC 中，若BC ＝a ，AC ＝b ，AB ＝c ，若a ，b ，c 满足ac +a 2＝b 2，则称这个三角形为“类勾股三角形”，请根据以上定义解决下列问题：（1）命题“直角三角形都是类勾股三角形”是命题（填“真”或“假”）；（2）如图1，若等腰三角形ABC是“类勾股三角形”，其中AB＝BC，AC＞AB，请求∠A的度数；（3）如图2，在△ABC中，∠B＝2∠A，且∠C＞∠A．①当∠A＝32°时，你能把这个三角形分成两个等腰三角形吗？若能，请在图2中画出分割线，并标注被分割后的两个等腰三角形的顶角的度数；若不能，请说明理由；②请证明△ABC为“类勾股三角形”．28．（1）如图1，在Rt△ABC和Rt△ADE中，AB＝AC，AD＝AE，且点D在BC边上滑动（点D不与点B，C重合），连接EC，①则线段BC，DC，EC之间满足的等量关系式为；②求证：BD2+CD2＝2AD2；（2）如图2，在四边形ABCD中，∠ABC＝∠ACB＝∠ADC＝45°．若BD＝9，CD＝3，求AD 的长．29．已知：四边形ABCD是菱形，AB＝4，∠ABC＝60°，有一足够大的含60°角的直角三角尺的60°角的顶点与菱形ABCD的顶点A重合，两边分别射线CB、DC相交于点E、F，且∠EAP＝60°．（1）如图1，当点E是线段CB的中点时，请直接判断△AEF的形状是．（2）如图2，当点E是线段CB上任意一点时（点E不与B、C重合），求证：BE＝CF；（3）如图3，当点E在线段CB的延长线上，且∠EAB＝15°时，求点F到BC的距离．30．菱形ABCD中，∠BAD＝60°，BD是对角线，点E、F分别是边AB、AD上两个点，且满足AE＝DF，连接BF与DE相交于点G．（1）如图1，求∠BGD的度数；（2）如图2，作CH⊥BG于H点，求证：2GH＝GB+DG；（3）在满足（2）的条件下，且点H在菱形内部，若GB＝6，CH＝43，求菱形ABCD的面积．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【详解】解：（1）当点P在x轴正半轴上，①以OA为腰时，∵A的坐标是（2，2），∴∠AOP=45°，OA=22，∴P的坐标是（4，0）或（22，0）；②以OA为底边时，∵点A的坐标是（2，2），∴当点P的坐标为：（2，0）时，OP=AP；（2）当点P在x轴负半轴上，③以OA为腰时，∵A的坐标是（2，2），∴OA= 22，∴OA=AP=22∴P的坐标是（-22，0）．故选D．2．B解析：B【分析】结论①错误，因为图中全等的三角形有3对；结论②正确，由全等三角形的性质可以判断；结论③错误，利用全等三角形和等腰直角三角形的性质可以判断；结论④正确，利用全等三角形的性质以及直角三角形的勾股定理进行判断．【详解】连接CF，交DE于点P，如下图所示结论①错误，理由如下：图中全等的三角形有3对，分别为△AFC≌△BFC，△AFD≌△CFE，△CFD≌△BFE．由等腰直角三角形的性质，可知FA=FC=FB，易得△AFC≌△BFC．∵FC⊥AB，FD⊥FE，∴∠AFD=∠CFE．∴△AFD≌△CFE（ASA）．同理可证：△CFD≌△BFE．结论②正确，理由如下：∵△AFD≌△CFE，∴S△AFD=S△CFE，∴S四边形CDFE=S△CFD+S△CFE=S△CFD+S△AFD=S△AFC=12S△ABC，即△ABC的面积等于四边形CDFE的面积的2倍．结论③错误，理由如下：∵△AFD≌△CFE，∴CE=AD，∴FA ．结论④正确，理由如下：∵△AFD ≌△CFE ，∴AD=CE ；∵△CFD ≌△BFE ，∴BE=CD ．在Rt △CDE 中，由勾股定理得：222CD CE DE +=，∴222AD BE DE += ．故选B ．【点睛】本题是几何综合题，考查了等腰直角三角形、全等三角形和勾股定理等重要几何知识点，综合性比较强．解决这个问题的关键在于利用全等三角形的性质．3．B解析：B【分析】设OA ＝a ，OB ＝b ，OC ＝c ，OD ＝d ，根据勾股定理求出a 2+b 2＝AB 2＝9，c 2+b 2＝BC 2＝16，c 2+d 2＝CD 2＝25，即可证得a 2+d 2＝18，由此得到答案.【详解】设OA ＝a ，OB ＝b ，OC ＝c ，OD ＝d ，由勾股定理得，a 2+b 2＝AB 2＝9，c 2+b 2＝BC 2＝16，c 2+d 2＝CD 2＝25，则a 2+b 2+c 2+b 2+c 2+d 2＝50，∴a 2+d 2+2（b 2+c 2）＝50，∴a 2+d 2＝50﹣16×2＝18，∴AD ==故选：B ．【点睛】此题考查勾股定理的运用，根据题中的已知条件得到直角三角形，再利用勾股定理求出未知的边长，解题中注意直角边与斜边.4．D解析：D【分析】根据直角三角形的性质求出BC ，根据勾股定理计算，得到答案．【详解】解：∵∠C=90°，∠A=30°，∴BC=12AB=6，由勾股定理得，= 故选：D ．本题考查的是直角三角形的性质、勾股定理，掌握在直角三角形中，30°角所对的直角边等于斜边的一半是解题的关键．5．C解析：C【分析】根据题意结合勾股定理得出折断处离地面的长度即可．【详解】解：设折断处离地面的高度OA是x尺，根据题意可得：x2+42=（10-x）2，解得：x=4.2，答：折断处离地面的高度OA是4.2尺．故选C．【点睛】此题主要考查了勾股定理的应用，根据题意正确应用勾股定理是解题关键．6．A解析：A【解析】试题分析：剪拼如下图：乙考点：剪拼，面积不变性，二次方根7．D解析：D【分析】将容器侧面展开，建立A关于EG的对称点A′，根据两点之间线段最短可知A′B的长度即为所求．【详解】解：如图：将圆柱展开，EG为上底面圆周长的一半，作A关于E的对称点A'，连接A'B交EG于F，则蚂蚁吃到蜂蜜需爬行的最短路径为AF+BF 的长，即AF+BF=A'B=20cm，延长BG，过A'作A'D⊥BG于D，∵AE=A'E=DG=4cm，∴BD=16cm，Rt△A'DB中，由勾股定理得：22-=cm201612∴则该圆柱底面周长为24cm．故选：D．【点睛】本题考查了平面展开---最短路径问题，将图形展开，利用轴对称的性质和勾股定理进行计算是解题的关键．同时也考查了同学们的创造性思维能力．8．C解析：C【分析】设AB＝x，则BC＝9－x，根据三角形两边之和大于第三边，得到x的取值范围，再利用分类讨论思想，根据勾股定理列方程，计算解答．【详解】解：∵在△ABC中，AC＝AM＝3，设AB＝x，BC＝9－x，由三角形两边之和大于第三边得：3939x x x x +-⎧⎨+-⎩＞＞， 解得3＜x ＜6，①AC 为斜边，则32＝x 2＋（9－x ）2，即x 2－9x ＋36＝0，方程无解，即AC 为斜边不成立，②若AB 为斜边，则x 2＝（9－x ）2＋32，解得x ＝5，满足3＜x ＜6，③若BC 为斜边，则（9－x ）2＝32＋x 2，解得x ＝4，满足3＜x ＜6，∴x ＝5或x ＝4；故选C ．【点睛】本题考查三角形的三边关系，勾股定理等，分类讨论和方程思想是解答的关键．9．A解析：A【分析】根据直角三角形的两直角边长分别为5和3，可计算出正方形的边长，从而得出正方形的面积.【详解】解：3和5为两条直角边长时，小正方形的边长=5-3=2，∴小正方形的面积22=4；综上所述：小正方形的面积为4；故答案选A ．【点睛】本题考查了勾股定理及其应用，正确表示出直角三角形的面积是解题的关键． 10．D解析：D【分析】欲判断三角形是否为直角三角形，这里给出三边的长，需要验证两小边的平方和等于最长边的平方即可．【详解】①c 不一定是斜边，故错误；②正确；③若△ABC 是直角三角形，c 不是斜边，则a 2＋b 2≠c 2，故错误，所以正确的只有②，故选D.【点睛】本题考查了勾股定理以及勾股定理的逆定理，熟练掌握勾股定理以及勾股定理的逆定理的内容是解题的关键.二、填空题11．7【分析】连接AC交BD于点O，由题意可证AC垂直平分BD，△ABD是等边三角形，可得∠BAO＝∠DAO＝30°，AB＝AD＝BD，BO＝OD，通过证明△EDF是等边三角形，可得DE＝EF＝DF，由勾股定理可求OC，BC的长．【详解】连接AC，交BD于点O，∵AB＝AD，BC＝DC，∠A＝60°，∴AC垂直平分BD，△ABD是等边三角形，∴∠BAO＝∠DAO＝30°，AB＝AD＝BD＝4，BO＝OD＝2，∵CE∥AB，∴∠BAO＝∠ACE＝30°，∠CED＝∠BAD＝60°，∴∠DAO＝∠ACE＝30°，∴AE＝CE＝3，∴DE＝AD−AE＝1，∵∠CED＝∠ADB＝60°，∴△EDF是等边三角形，∴DE＝EF＝DF＝1，∴CF＝CE−EF＝2，OF＝OD−DF＝1，22OC CF OF3∴-=22∴BC=OB+OC=77【点睛】本题考查了等边三角形的性质和判定，勾股定理，熟练运用等边三角形的判定是本题的关键．12．5【分析】作AD′⊥AD，AD′=AD构建等腰直角三角形，根据SAS求证△BAD≌△CAD′，证得BD=CD′，∠DAD′=90°，然后在Rt△AD′D和Rt△CD′D应用勾股定理即可求解．【详解】作AD ′⊥AD ，AD′=AD ，连接CD′，DD′，如图：∵∠BAC+∠CAD=∠DAD′+∠CAD ，∴∠BAD=∠CAD′，在△BAD 与△CAD′中，{BA CABAD CAD AD AD =∠=∠=''，∴△BAD ≌△CAD′（SAS ），∴BD=CD′，∠DAD′=90°，由勾股定理得22()4AD AD +='，∵∠D′DA+∠ADC=90°，∴由勾股定理得22(')5DC DD +=，∴BD=CD′=5故答案为5．【点睛】本题考查了全等三角形的判定与性质，勾股定理，等腰直角三角形，正确引出辅助线构造等腰直角三角形是本题的关键．13．75或6或94 【分析】当△ABP 为等腰三角形时，分三种情况：①当AB ＝BP 时；②当AB ＝AP 时；③当BP ＝AP 时，分别求出BP 的长度，继而可求得t 值．【详解】在Rt △ABC 中，BC 2＝AB 2﹣AC 2＝7.52﹣4.52＝36，∴BC ＝6（cm ）；①当AB ＝BP ＝7.5cm 时，如图1，t ＝7.52＝3.75（秒）；②当AB＝AP＝7.5cm时，如图2，BP＝2BC＝12cm，t＝6（秒）；③当BP＝AP时，如图3，AP＝BP＝2tcm，CP＝（4.5﹣2t）cm，AC＝4.5cm，在Rt△ACP中，AP2＝AC2+CP2，所以4t2＝4.52+（4.5﹣2t）2，解得：t＝94，综上所述：当△ABP为等腰三角形时，t＝3.75或t＝6或t＝94．故答案为：3.75或6或94．【点睛】此题是等腰三角形与动点问题，考查等腰三角形的性质，勾股定理，解题中应根据每两条边相等分情况来解答，不要漏解.14．72965【分析】分三种情形讨论：（1）如图1中，以点C所在顶点为直角时；（2）如图2中，以点D所在顶点为直角时；（3）如图3中，以点A所在顶点为直角时．【详解】（1）如图1中，以点C所在顶点为直角时．∵AC=CD=4，BC=3，∴BD=CD+BC=7；（2）如图2中，以点D所在顶点为直角时，作DE⊥BC与E，连接BD．在Rt△BDE中DE=2，BE=5，∴BD2229DE BE+（3）如图3中，以点A所在顶点为直角时，作DE⊥BC于E，在Rt△BDE中，DE=4．BE=7，∴BD2265DE BE+故答案为：72965【点睛】本题考查了勾股定理、等腰直角三角形等知识，解题的关键是学会用分类讨论的思想思考问题．15．21【分析】在AB 上截取AE=AD ，连接CE ，过点C 作CF ⊥AB 于点F ，先证明△ADC ≌△AEC ，得出AE=AD=9，CE=CD=BC ＝10的长度，再设EF=BF=x ，在Rt △CFB 和Rt △CFA 中，由勾股定理求出x ，再根据AB=AE+EF+FB 求得AB 的长度．【详解】如图所示，在AB 上截取AE=AD ，连接CE ，过点C 作CF ⊥AB 于点F ，∵AC 平分∠BAD ，∴∠DAC=∠EAC ．在△AEC 和△ADC 中，AE AD DAC EACAC AC ⎧⎪∠∠⎨⎪⎩＝＝＝∴△ADC ≌△AEC （SAS ），∴AE=AD=9，CE=CD=BC =10，又∵CF ⊥AB ，∴EF=BF ，设EF=BF=x ．∵在Rt △CFB 中，∠CFB=90°，∴CF 2=CB 2-BF 2=102-x 2，∵在Rt △CFA 中，∠CFA=90°，∴CF 2=AC 2-AF 2=172-（9+x ）2，即102-x 2=172-（9+x ）2，∴x=6，∴AB=AE+EF+FB=9+6+6=21，∴AB 的长为21．故答案是：21.【点睛】考查全等三角形的判定和性质、勾股定理和一元二次方程等知识，解题的关键是作辅助线，构造全等三角形，再运用用方程的思想解决问题．16．310，62或32【解析】【详解】∵（x-6）2=9，∴x-6=±3，解得：x 1=9，x 2=3，∵x ，y 为一个直角三角形的两边的长，y=3，∴当x=3时，x 、y 都为直角三角形的直角边，则斜边为223332+=；当x=9时，x 、y 都为直角三角形的直角边，则斜边为2293310+= ；当x=9时，x 为斜边、y 为直角边，则第三边为263922=-.故答案为：310，62或32.【点睛】本题主要考查了勾股定理的应用，正确分类讨论是解决问题的关键，解题时注意一定不要漏解．17．31+或31-【解析】如图，l AB ，2AC =，作AD l ⊥于点D ，∴1AD =，∵222AF AB ==⋅=，且F 有2个， ∴2212213DF DF ==-=，∵1DC AD ==， ∴1113CF CD DF =+=+， 2231CF DF CD =-=-．点睛：本题考查了勾股定理的运用，通过添加辅助线，可将问题转化到直角三角形中，利用勾股定理解答，考查了学生的空间想象能力．18．①1＜OA ＜4． ②672． 【解析】(1)由三角形边的性质5-3<2OA <5+3,1＜OA ＜4.(2)过A 作AF BC ,F ⊥于过D 作DE BC ⊥于E,可知，ABF 全等DCE ,由题意知，22BD DE =+()2BC CE +=2DE +()24CE +， ()()222225AC DE BC CE DE CE ∴=+-=+-，2AC ∴+ 2BD=2DE +()()22245CE DE CE +++-=2(22)5018DE CE ++=+50=68，BD -AC =1，两边平方2AC ∴+ 2BD -2AC •BD =1， ∴AC •BD =672.19．485【解析】试题分析：根据等腰三角形的性质和勾股定理可知BC 边上的高为8，然后根据三角形的面积法可得111012822BD ⨯⨯=⨯⨯，解得BD=485. 20．5【分析】如图，作PA ∥y 轴交X 轴于A ，PH ⊥x 轴于H ．GM ∥y 轴交x 轴于M ，连接PG 交x 轴于N ，先证明△ANP ≌△MNG （AAS ），再根据勾股定理求出PN 的值，即可得到线段PG 的长度．【详解】如图，作PA∥y轴交X轴于A，PH⊥x轴于H．GM∥y轴交x轴于M，连接PG交x轴于N．∵P（1，2），G（7．﹣2），∴OA＝1，PA＝GM＝2，OM＝7，AM＝6，∵PA∥GM，∴∠PAN＝∠GMN，∵∠ANP＝∠MNG，∴△ANP≌△MNG（AAS），∴AN＝MN＝3，PN＝NG，∵∠PAH＝45°，∴PH＝AH＝2，∴HN＝1，∴2222215PN PH NH=+=+=∴PG＝2PN＝5．故答案为5【点睛】本题考查了全等三角形的综合问题，掌握全等三角形的性质以及判定定理、勾股定理是解题的关键．三、解答题21．(1) 出发10s后，△BMN为等边三角形；(2)出发6s或15s后，△BMN为直角三角形．【分析】（1）设时间为x，表示出AM=x、BN=2x、BM=30-x，根据等边三角形的判定列出方程，解之可得；（2）分两种情况：①∠BNM=90°时，即可知∠BMN=30°，依据BN=12BM列方程求解可得；②∠BMN=90°时，知∠BNM=30°，依据BM=12BN列方程求解可得．【详解】解(1)设经过x秒，△BMN为等边三角形，则AM＝x，BN＝2x，∴BM＝AB－AM＝30－x，根据题意得30－x＝2x，解得x＝10，答：经过10秒，△BMN为等边三角形；(2)经过x秒，△BMN是直角三角形，①当∠BNM＝90°时，∵∠B＝60°，∴∠BMN＝30°，∴BN＝12BM，即2x＝12(30－x)，解得x＝6；②当∠BMN＝90°时，∵∠B＝60°，∴∠BNM＝30°，∴BM＝12BN，即30－x＝12×2x，解得x＝15，答：经过6秒或15秒，△BMN是直角三角形．【点睛】本题考查勾股定理的逆定理，等边三角形的判定.22．（1）45度；（2）∠AEC﹣∠AED＝45°，理由见解析；（3）见解析【分析】（1）由等腰三角形的性质可求∠BAE＝140°，可得∠CAE＝50°，由等腰三角形的性质可得∠AEC＝∠ACE＝65°，即可求解；（2）由等腰三角形的性质可求∠BAE＝180°﹣2α，可得∠CAE＝90°﹣2α，由等腰三角形的性质可得∠AEC＝∠ACE＝45°+α，可得结论；（3）如图，过点C作CG⊥AH于G，由等腰直角三角形的性质可得EH EF，CH＝CG，由“AAS”可证△AFB≌△CGA，可得AF＝CG，由勾股定理可得结论．【详解】解：（1）∵AB＝AC，AE＝AB，∴AB＝AC＝AE，∴∠ABE＝∠AEB，∠ACE＝∠AEC，∵∠AED＝20°，∴∠ABE＝∠AED＝20°，∴∠BAE＝140°，且∠BAC＝90°∴∠CAE＝50°，∵∠CAE+∠ACE+∠AEC＝180°，且∠ACE＝∠AEC，∴∠AEC＝∠ACE＝65°，∴∠DEC＝∠AEC﹣∠AED＝45°，故答案为：45；（2）猜想：∠AEC﹣∠AED＝45°，理由如下：∵∠AED＝∠ABE＝α，∴∠BAE＝180°﹣2α，∴∠CAE＝∠BAE﹣∠BAC＝90°﹣2α，∵∠CAE+∠ACE+∠AEC＝180°，且∠ACE＝∠AEC，∴∠AEC＝45°+α，∴∠AEC﹣∠AED＝45°；（3）如图，过点C作CG⊥AH于G，∵∠AEC﹣∠AED＝45°，∴∠FEH＝45°，∵AH⊥BE，∴∠FHE＝∠FEH＝45°，∴EF＝FH，且∠EFH＝90°，∴EH2EF，∵∠FHE＝45°，CG⊥FH，∴∠GCH＝∠FHE＝45°，∴GC＝GH，∴CH2CG，∵∠BAC＝∠CGA＝90°，∴∠BAF+∠CAG＝90°，∠CAG+∠ACG＝90°，∴∠BAF＝∠ACG，且AB＝AC，∠AFB＝∠AGC，∴△AFB≌△CGA（AAS）∴AF＝CG，∴CH2AF，∵在Rt△AEF中，AE2＝AF2+EF2，2AF）2+2EF）2＝2AE2，∴EH2+CH2＝2AE2．【点睛】本题是综合了等腰直角三角形的性质，全等三角形的性质与判定的动点问题，三个问题由易到难，在熟练掌握各个相关知识的基础上找到问题之间的内部联系，层层推进去解答是关键.23．（1）该命题是真命题，理由见解析；（2）①a 的值为92；②k 的取值范围为13k ≤<；（3）ABC ∆． 【分析】 （1）根据等边三角形的性质、优三角形和优比的定义即可判断；（2）①先利用勾股定理求出c 的值，再根据优三角形的定义列出,,a b c 的等式，然后求解即可；②类似①分三种情况分析，再根据三角形的三边关系定理得出每种情况下,,a b c 之间的关系，然后根据优比的定义求解即可；（3）如图（见解析），设BD x =，先利用直角三角形的性质、勾股定理求出AC 、AB 的长及ABC ∆面积的表达式，再类似（2），根据优三角形的定义分三种情况分别列出等式，然后解出x 的值，即可得出ABC ∆的面积．【详解】（1）该命题是真命题，理由如下：设等边三角形的三边边长为a则其中两条边的和为2a ，恰好是第三边a 的2倍，满足优三角形的定义，即等边三角形为优三角形又因该两条边相等，则这两条边的比为1，即其优比为1故该命题是真命题；（2）①90,6CB b A ∠=︒=c ∴=根据优三角形的定义，分以下三种情况：当2a b c +=时，6a +=，整理得24360a a -+=，此方程没有实数根当2a c b +=时，12a =，解得92a =当2b c a +=时，62a =，解得86a =>，不符题意，舍去综上，a 的值为92； ②由题意得：,,a b c 均为正数 根据优三角形的定义，分以下三种情况：（c b a ≥≥）当2a b c +=时，则1b k a=≥由三角形的三边关系定理得b a c a b -<<+ 则2a b b a a b +-<<+，解得3b a <，即3b k a=< 故此时k 的取值范围为13k ≤< 当2a c b +=时，则1c k a =≥ 由三角形的三边关系定理得c a b a c -<<+ 则2a c c a a c +-<<+，解得3c a <，即3c k a=< 故此时k 的取值范围为13k ≤< 当2b c a +=时，则1c k b =≥ 由三角形的三边关系定理得c b a b c -<<+ 则2b c c b b c +-<<+，解得3c b <，即3c k b=< 故此时k 的取值范围为13k ≤<综上，k 的取值范围为13k ≤<；（3）如图，过点A 作AD BC ⊥，则180********ABC ABD ∠=︒-︒∠-==︒︒ 设BD x =22,AB BD x AD ∴====AC ===11422ABC S BC AD ∆=⋅=⨯= ABC ∆是优三角形，分以下三种情况：当2AC BC AB +=时，即44x =，解得103x =则1033ABC S ∆===当2AC AB BC +=时，即28x =，解得65x =则655ABC S ∆===当2BC AB AC +=时，即42x +=，整理得234120x x ++=，此方程没有实数根综上，ABC ∆．【点睛】本题考查了等边三角形的性质、直角三角形的性质、勾股定理、三角形的三边关系定理等知识点，理解题中的新定义，正确分多种情况讨论是解题关键．24．（1）见解析；（2）证明见解析；（3）25.【分析】（1）直接叙述勾股定理的内容，并用字母表明三边关系；（2）利用大正方形面积、小正方形面积和4个直角三角形的面积和之间的关系列式整理即可证明；（3）将原式利用完全平方公式展开，由勾股定理的内容可得出()2a b +为大正方形面积和4个直角三角形的面积和，根据已知条件即可求得.【详解】解：（1）勾股定理：直角三角形两直角边的平方和等于斜边的平方．在直角三角形中，两条直角边分别为 a 、b ，斜边为 c ，a 2+b 2= c 2．（2）∵ S 大正方形=c 2，S 小正方形=(b-a)2，4 S Rt △=4×12ab=2ab ， ∴ c 2=2ab+(b-a)2=2ab+b 2-2ab+a 2=a 2+b 2，即 a 2+b 2= c 2．（3）∵ 4 S Rt △= S 大正方形- S 小正方形=13-1=12,∴ 2ab=12.∴ (a+b)2= a 2+b 2+2ab=c 2+2ab=13+12=25.【点睛】本题考查勾股定理的内容及勾股定理的几何验证，利用等面积法证明勾股定理及运用勾股定理是解答此题的关键.25．（1）见解析；（2）∠ADC=45α︒+；（3）2BD DE =【分析】（1）根据题意画出图形即可；（2）根据对称的性质，等腰三角形的性质及角与角之间的和差关系进行计算即可； （3）画出图形，结合（2）的结论证明△BED 为等腰直角三角形，从而得出结论.【详解】解：（1）如图所示；（2）∵点B 与点D 关于直线AP 对称，∠BAP=α，∴∠PAD=α，AB=AD ，∵90BAC ∠=︒，∴902DAC α∠=︒-，又∵AB=AC ，∴AD=AC ，∴∠ADC=1[180(902)]2α⨯︒-︒-=45α︒+； （3）如图，连接BE ，由（2）知：∠ADC=45α︒+，∵∠ADC=∠AED+∠EAD ，且∠EAD=α，∴∠AED=45°，∵点B 与点D 关于直线AP 对称，即AP 垂直平分BD ，∴∠AED=∠AEB=45°，BE=DE ，∴∠BED=90°，∴△BED 是等腰直角三角形，∴22222BD BE DE DE =+=，∴2BD DE =.【点睛】本题考查了轴对称的性质，等腰三角形的性质，勾股定理等知识，明确角与角之间的关系，学会添加常用辅助线构造直角三角形是解题的关键.26．（1）见解析；（2）27BC =.【分析】（1）由等边三角形的判定定理可得△ABD 为等边三角形，又由平行进行角度间的转化可得出结论.（2）连接AC 交BD 于点O ，由题意可证AC 垂直平分BD ，△ABD 是等边三角形，可得∠BAO=∠DAO=30°，AB=AD=BD=8，BO=OD=4，通过证明△EDF 是等边三角形，可得DE=EF=DF=2，由勾股定理可求OC ，BC 的长．【详解】（1）证明：∵AB AD =，=60A ∠︒，∴△ABD 是等边三角形.∴60ADB ∠=︒.∵CE ∥AB ，∴60CED A ∠=∠=︒.∴CED ADB ∠=∠.（2）解：连接AC 交BD 于点O ，∵AB AD =，BC DC =，∴AC 垂直平分BD .∴30BAO DAO ∠=∠=︒.∵△ABD 是等边三角形，8AB =∴8AD BD AB ===，∴4BO OD ==.∵CE ∥AB ，∴ACE BAO ∠=∠.∴6AE CE ==, 2DE AD AE =-=.∵60CED ADB ∠=∠=︒.∴60EFD ∠=︒.∴△EDF 是等边三角形.∴2EF DF DE ===,∴4CF CE EF =-=,2OF OD DF =-=.在Rt △COF 中， ∴2223OC CF OF =-=.在Rt △BOC 中，∴22224(23)27BC BO OC =+=+=. 【点睛】本题考查了等边三角形的性质和判定，勾股定理，熟练运用等边三角形的判定是本题的关键．27．（1）假；（2）∠A ＝45°；（3）①不能，理由见解析，②见解析【分析】（1）先由直角三角形是类勾股三角形得出ab+a 2=c 2，再由勾股定理得a 2+b 2=c 2，即可判断出此直角三角形是等腰直角三角形；（2）由类勾股三角形的定义判断出此三角形是等腰直角三角形，即可得出结论； （3）①分三种情况，利用等腰三角形的性质即可得出结论；②先求出CD=CB=a ，AD=CD=a ，DB=AB-AD=c-a ，DG=BG=12（c-a ），AG=12（a+c ），两个直角三角形中利用勾股定理建立方程即可得出结论．【详解】解：（1）如图1，假设Rt △ABC 是类勾股三角形，∴ab +a 2＝c 2，在Rt △ABC 中，∠C ＝90°，根据勾股定理得，a 2+b 2＝c 2，∴ab +b 2＝a 2+b 2，∴ab ＝a 2，∴a ＝b ，∴△ABC是等腰直角三角形，∴等腰直角三角形是类勾股三角形，即：原命题是假命题，故答案为：假；（2）∵AB＝BC，AC＞AB，∴a＝c，b＞c，∵△ABC是类勾股三角形，∴ac+a2＝b2，∴c2+a2＝b2，∴△ABC是等腰直角三角形，∴∠A＝45°，（3）①在△ABC中，∠ABC＝2∠BAC，∠BAC＝32°，∴∠ABC＝64°，根据三角形的内角和定理得，∠ACB＝180°﹣∠BAC﹣∠ABC＝84°，∵把这个三角形分成两个等腰三角形，∴（Ⅰ）、当∠BCD＝∠BDC时，∵∠ABC＝64°，∴∠BCD＝∠BDC＝58°，∴∠ACD＝∠ACB﹣∠BCD＝84°﹣58°＝26°，∠ADC＝∠ABC+∠BCD＝122°∴△ACD不是等腰三角形，此种情况不成立；（Ⅱ）、当∠BCD＝∠ABC＝64°时，∴∠BDC＝52°，∴∠ACD＝20°，∠ADC＝128°，∴△ACD是等腰三角形，此种情况不成立；（Ⅲ）、当∠BDC＝∠ABC＝64°时，∴∠BCD＝52°，∴∠ACD＝∠ACB﹣BCD＝32°＝∠BAC，∴△ACD是等腰三角形，即：分割线和顶角标注如图2所示，Ⅱ、分∠ABC，同（Ⅰ）的方法，判断此种情况不成立；Ⅲ、分∠BAC，同（Ⅱ）的方法，判断此种情况不成立；②如图3，在AB边上取点D，连接CD，使∠ACD＝∠A图3作CG⊥AB于G，∴∠CDB＝∠ACD+∠A＝2∠A，∵∠B＝2∠A，∴∠CDB＝∠B，∴CD＝CB＝a，∵∠ACD＝∠A，∴AD＝CD＝a，∴DB＝AB﹣AD＝c﹣a，∵CG⊥AB，∴DG＝BG＝12（c﹣a），∴AG＝AD+DG＝a+12（c﹣a）＝12（a+c），在Rt△ACG中，CG2＝AC2﹣AG2＝b2﹣[12（c+a）]2，在Rt△BCG中，CG2＝BC2﹣BG2＝a2﹣[12（c﹣a）]2，∴b2﹣[12（a+c）]2＝a2﹣[12（c﹣a）]2，∴b2＝ac+a2，∴△ABC是“类勾股三角形”．【点睛】此题是三角形综合题，主要考查了等腰三角形的性质，勾股定理，新定义“类勾股三角形”，分类讨论的数学思想，解本题的关键是理解新定义．28．（1）①BC＝DC+EC，理由见解析；②证明见解析；（2）6.【解析】【分析】(1)证明△BAD≌△CAE，根据全等三角形的性质解答;(2)根据全等三角形的性质得到BD＝CE，∠ACE＝∠B，得到∠DCE＝90°，根据勾股定理计算即可;(3)作AE⊥AD，使AE＝AD，连接CE，DE，证明△BAD≌△CAE，得到BD＝CE＝9，根据勾股定理计算即可.【详解】（1）①解：BC＝DC+EC，理由如下：∵∠BAC＝∠DAE＝90°，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，在△BAD和△CAE中，，∴△BAD≌△CAE（SAS），∴BD＝EC，∴BC＝DC+BD＝DC+EC，；故答案为：BC＝DC+EC；②证明：∵Rt△ABC中，AB＝AC，∴∠B＝∠ACB＝45°，由（1）得，△BAD≌△CAE，∴BD＝CE，∠ACE＝∠B＝45°，∴∠DCE＝∠ACB+∠ACE＝90°，∴CE2+CD2＝ED2，在Rt△ADE中，AD2+AE2＝ED2，又AD＝AE，∴BD2+CD2＝2AD2；（2）解：作AE⊥AD，使AE＝AD，连接CE，DE，如图2所示：∵∠BAC+∠CAD＝∠DAE+∠CAD，即∠BAD＝∠CAE，在△BAD与△CAE中，，∴△BAD≌△CAE（SAS），∴BD＝CE＝9，∵∠ADC＝45°，∠EDA＝45°，∴∠EDC＝90°，∴DE＝＝＝6，∵∠DAE＝90°，∴AD＝AE＝DE＝6．【点睛】本題是四边形综合题目，考查的是全等三角形的判定和性质、等直角三角形的性质、勾股定理、直角三角形的判定等知识:本题综合性强，熟练掌握等腰直角三角形的性质，证明三角形全等是解题的关键.29．（1）△AEF是等边三角形，理由见解析；（2）见解析；（3）点F到BC的距离为3﹣．【解析】【分析】（1）连接AC，证明△ABC是等边三角形，得出AC＝AB，再证明△BAE≌△DAF，得出AE ＝AF，即可得出结论；（2）连接AC，同（1）得：△ABC是等边三角形，得出∠BAC＝∠ACB＝60°，AB＝AC，再证明△BAE≌△CAF，即可得出结论；（3）同（1）得：△ABC和△ACD是等边三角形，得出AB＝AC，∠BAC＝∠ACB＝∠ACD＝60°，证明△BAE≌△CAF，得出BE＝CF，AE＝AF，证出△AEF是等边三角形，得出∠AEF ＝60°，证出∠AEB＝45°，得出∠CEF＝∠AEF﹣∠AEB＝15°，作FH⊥BC于H，在△CEF 内部作∠EFG＝∠CEF＝15°，则GE＝GF，∠FGH＝30°，由直角三角形的性质得出FG＝2FH，GH＝FH，CF＝2CH，FH＝CH，设CH＝x，则BE＝CF＝2x，FH＝x，GE＝GF＝2FH＝2x，GH＝FH＝3x，得出EH＝4+x＝2x+3x，解得：x＝﹣1，求出FH＝x ＝3﹣即可．【详解】（1）解：△AEF是等边三角形，理由如下：连接AC，如图1所示：∵四边形ABCD是菱形，∴AB＝BC＝AD，∠B＝∠D，∵∠ABC＝60°，∴∠BAD＝120°，△ABC是等边三角形，∴AC＝AB，∵点E是线段CB的中点，∴AE⊥BC，∴∠BAE＝30°，∵∠EAF＝60°，∴∠DAF＝120°﹣30°﹣60°＝30°＝∠BAE，在△BAE和△DAF中，，∴△BAE≌△DAF（ASA），。