阿氏圆作法及应用

动点最值-阿氏圆
阿氏圆经常有两种考法，第一种：给出一动一定并且动点轨迹为圆，求另一定点；第二种：给出2定点一动点，求动点的轨迹。

一、阿氏圆定义
到两定点A、B的距离比值为定值k（k≠1）的动点的轨迹为一个圆。

且这个圆的直径为线段AB的内分点和外分点（按k进行分）组成的线段。

二、阿氏圆证明
由角分线定理2（角平分线其对边所成的两条线段与这个角的两邻边对应成比例）+定角定弦可证明，另外角分线定理2可由等面积法证明。

三、解题步骤
①判断阿氏圆：所求是否为形如PA+kPB最值；
②根据角分线定理找出另一定点，并做好辅助线；
③通过相似三角形证明是否符合阿氏圆定理；
④求最值：“一箭穿心”模型（通过三角形三边关系可证），动点到圆心的距离+半径为最大值，动点到圆心的距离-半径为最小值。

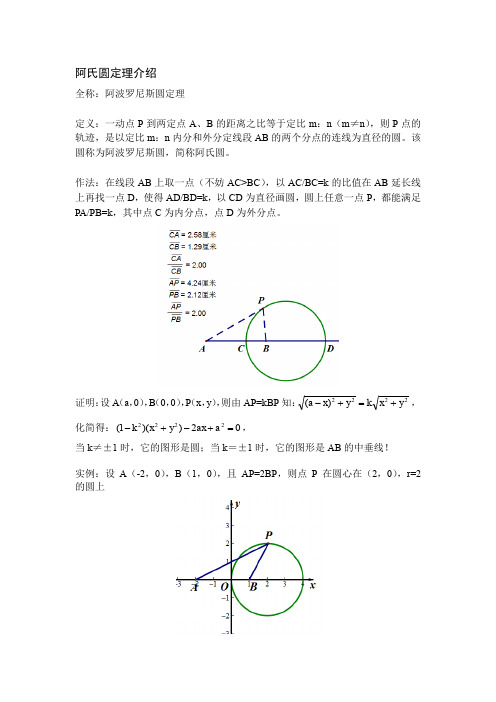
阿氏圆定理介绍
全称：阿波罗尼斯圆定理
定义：一动点P 到两定点A 、B 的距离之比等于定比m ：n （m ≠n ），则P 点的轨迹，是以定比m ：n 内分和外分定线段AB 的两个分点的连线为直径的圆。

该圆称为阿波罗尼斯圆，简称阿氏圆。

作法：在线段AB 上取一点（不妨AC>BC ），以AC/BC=k 的比值在AB 延长线上再找一点D ，使得AD/BD=k ，以CD 为直径画圆，圆上任意一点P ，都能满足PA/PB=k ，其中点C 为内分点，点D 为外分点。

证明：设A （a ，0），B （0，0），P （x ，y ），则由AP=kBP 知：2222)(y x k y x a +=+-，化简得：02))(1(2222=+-+-a ax y x k ，
当k ≠±1时，它的图形是圆；当k ＝±1时，它的图形是AB 的中垂线！
实例：设A （-2，0），B （1，0），且AP=2BP ，则点P 在圆心在（2，0），r=2的圆上
应用：可知阿氏圆上任意一点P 到点A 和点B 的距离比都是定值k ，那么在证明过程中可以用这个原理，就是说如果我们知道了圆上一点到直径上两定点的距离比，那么我们就可以知道圆上另一点到两定点的距离比。

实战：
对于PB 22的转化，就是找到另外一个定点E ，使得：2
2 PB PE ，且这个定点在OB 直线上，圆O 即为阿氏圆！
点拨：遇到两点一圆转化线段*k 时，当系数k 不为1时，可以利用阿氏圆进行转化！
整理：长沙huyoo
来源：网络。

阿氏圆公式
阿氏圆公式是描述圆的一种数学公式，它由法国数学家欧仁·阿氏于1841年提出。

阿氏圆公式的形式为x^2+y^2+Dx+Ey+F=0，其中D、E、F是常数。

这个公式描述了平面上所有的圆，包括半径为0的圆（即点），以及不存在的圆（例如D、E、F不满足特定条件时）。

阿氏圆公式的推导相对简单，可以通过几何方法或代数方法得到。

几何方法包括使用平移和旋转变换，将一般的圆转化为标准方程的圆，即x^2+y^2=r^2。

代数方法则采用完全平方的方法将一般的圆方程转化为标准方程。

在应用阿氏圆公式时，我们可以根据已知的圆心坐标和半径，求解出D、E、F的值，从而得到对应的阿氏圆方程。

反之，如果已知了阿氏圆方程，我们可以通过配方的方法，提取出圆心坐标和半径的信息。

阿氏圆公式的应用非常广泛。

在几何学中，我们经常需要求解两个圆的交点、切线方程等问题，阿氏圆公式可以帮助我们解决这些问题。

在工程学中，阿氏圆公式可以用于描述圆形物体的特征，如轮胎、齿轮等。

在计算机图形学中，阿氏圆公式可以用于绘制圆形，进行图形的变换和裁剪等操作。

除了阿氏圆公式，还有其他描述圆的公式，如一般方程、极坐标方程、参数方程等。

每种方程都有其特点和应用范围，在具体问题中
选择适合的公式进行求解是十分重要的。

阿氏圆公式是描述圆的一种常用数学工具，它可以帮助我们解决各种与圆有关的问题。

了解和掌握阿氏圆公式的应用，可以提高我们的数学建模和问题求解能力。

同时，我们还需要深入理解圆的性质和特点，才能更好地应用阿氏圆公式解决实际问题。

阿氏圆几何画板作法及应用我们知道，到两定点F 1、F 2的距离之和为定值（大于F 1F 2）的点M 的轨迹为椭圆，而距离之差为定值（小于F 1F 2）的点M 的轨迹为双曲线，那么圆是否有相类似的结论呢答案是肯定的，事实上满足到两定点F 1、F 2的距离之比为定值t(t>0且t ≠1)点M 的轨迹为圆，这个结论是阿波罗尼(Apollonius ，约前260～前190)发现的，所以往往称为阿波罗尼圆。

但圆的这一性质比较“隐晦”，为帮助学生直观理解需要我们创设“所见即所得”的教学情境，本文以几何画板为例谈谈在画板环境中阿波罗尼圆的构造方式，并与读者分享画板中自定义工具功能的实现与应用。

一、阿波罗尼圆的画板实现 1.几何构造法实现阿波罗尼圆步骤1、构造一直线上两点F 1、F 2，新建参数t ，其初值赋为2； 记为比步骤2、度量计算1tt +并标值，双击点F 1标记为中心，选中F 2按标记比值缩放得到点P ；标记为步骤3、度量计算1tt --+并比值，双击点F 1标记为中心，选中F 2图1按标记比值缩放得到点得到点Q ；步骤4、构造线段PQ 并构造线段PQ 的中点C ，以C 为圆心以P 为圆上一点构造圆C 。

试试效果如何取圆C 上任意一点M 构造线段MF 1、MF 2，并先后选中两线段度量比值，拖动点M 会发现比值不变并且与参数t 值恒相等（如图1所示）。

2.解析构造法实现阿波罗尼圆 步骤1、在x 轴上任取两点F 1、F 2，度量其横坐标将标签分别设为x 1、x 2，新建参数t 初值赋为3；步骤2、计算121x tx t++令，在弹出窗口中选择“绘制”按纽得到点P ；步骤3、计算121x tx t--，重复步骤2可得到点Q ； 步骤4、同方法一，以PQ 为直径构造圆C 。

我们也可仿照方法一验证效果（如图2所示）。

3.实现方法构造详解及比较从以上构造过程我们可以发现，确实阿波罗尼圆关键在图2于找到圆与直线F 1F 2的交点P 、Q （因为圆C 以PQ 为直径）。

初中数学最值一阿氏圆模型初中数学中的最值问题是数学中的重要问题之一。

数学教学中经常涉及到最大值和最小值的求解，而阿氏圆模型是解决这类问题的一种方法。

阿氏圆模型是一种简便的方法，可以用来解决初中数学中的最值问题。

它可以帮助我们更好地理解和解决这类问题。

下面我将通过详细的论述来介绍阿氏圆模型的原理和应用。

首先，我们来看最大值问题。

最大值是一组数中的最大数，我们要找出这个最大值。

在阿氏圆模型中，我们可以通过绘制一个圆形来表示一组数。

圆的半径表示这组数中的最大值。

圆心表示这组数的平均值。

通过观察圆的大小和位置，我们可以快速确定最大值。

例如，给定一组数{3，5，7，9}，我们可以计算它们的平均值为6。

然后，我们绘制一个以6为圆心的圆，然后找到圆上的最大值。

在这种情况下，最大值为9。

我们可以通过阿氏圆模型很容易地找到最大值。

接下来我们来看最小值问题。

最小值是一组数中的最小数，我们要找出这个最小值。

阿氏圆模型同样可以用来解决这类问题。

与最大值问题类似，我们也是通过绘制一个圆形来表示一组数。

圆的半径表示这组数中的最小值。

圆心代表平均值。

通过观察圆的大小和位置，我们可以迅速确定最小值。

例如，给定一组数{2，4，6，8}，我们计算它们的平均值为5。

然后，我们可以绘制以5为圆心的圆，并找到圆上的最小值。

在这种情况下，最小值为2。

阿氏圆模型同样帮助我们很容易地找到最小值。

阿氏圆模型不仅可以用来解决最大值和最小值问题，还可以扩展到其他数学问题中。

例如，我们可以用阿氏圆模型来求一组数的平均值。

通过将这组数放在一个圆的周围，我们可以找到圆心的位置，这个位置就是这组数的平均值。

这使得求平均值变得非常简单。

此外，阿氏圆模型还可以用来解决其他问题，如中位数、众数等统计问题。

阿氏圆模型在初中数学中的应用非常广泛，通过它我们可以更好地理解和解决各种数学问题。

总结起来，阿氏圆模型是一种在初中数学中解决最值问题的简便方法。

它通过绘制一个圆形来表示一组数，圆心代表平均值，圆的半径代表最大值或最小值。

中考必考的阿氏圆原理应用什么是阿氏圆原理阿氏圆原理是由法国数学家阿氏发现的一种几何学原理。

根据阿氏圆原理，对于平面上一个确定的圆，通过圆上任意三个非共线点，都可以确定这个圆。

这个原理在实际生活中有着广泛的应用，特别是在中学数学中的几何部分经常被考察。

阿氏圆原理的重要性阿氏圆原理在中学数学中被广泛应用，不仅在解题中起到了重要的作用，而且在培养学生的几何思维和逻辑推理能力方面也是非常重要的。

因此，掌握阿氏圆原理的应用是中学数学学习中必不可少的一部分。

阿氏圆原理的应用范围阿氏圆原理的应用范围广泛，下面列举几个常见的应用：1.圆心和半径已知，求圆上任意一点的坐标2.通过圆上三点的坐标求圆心坐标和半径3.平面上两条切线交点的连线与圆心连线垂直4.求过已知点的切线方程5.求两条切线的交点坐标案例分析：通过圆上三点的坐标求圆心坐标和半径假设有一个平面上的圆O，已知圆上的三个点A(x1, y1)、B(x2, y2)、C(x3, y3)，现在要求解这个圆的圆心坐标和半径。

根据阿氏圆原理，我们可以采用以下步骤来求解：1.求取点A和B之间的中垂线的方程，设中垂线的方程为L1。

2.求取点B和C之间的中垂线的方程，设中垂线的方程为L2。

3.求解L1和L2的交点坐标，即为圆心坐标。

4.计算圆心坐标和点A、B、C之间的距离，即为圆的半径。

通过以上步骤，我们可以利用阿氏圆原理求解出圆的圆心坐标和半径。

小结阿氏圆原理作为中学数学中的重要部分，在中考中经常被考察。

掌握了阿氏圆原理的应用，可以帮助我们解决一些与圆相关的几何题目。

在学习过程中，我们不仅要理解阿氏圆原理的概念，还要掌握它的具体应用方法，并运用到实际的解题中去。

通过不断的练习和实践，我们能够提高我们的几何思维和解题能力。

以上就是中考必考的阿氏圆原理应用的文档内容，简单介绍了阿氏圆原理的定义和重要性，列举了其常见的应用范围，并以通过圆上三点的坐标求圆心坐标和半径为例进行了分析。

专题15动点最值之阿氏圆模型背景故事：“阿氏圆”又称为“阿波罗尼斯圆”，如下图，已知A 、B 两点，点P 满足PA ：PB=k （k≠1），则满足条件的所有的点P 的轨迹构成的图形为圆．这个轨迹最早由古希腊数学家阿波罗尼斯发现，故称“阿氏圆”.模型建立：当点P 在一个以O 为圆心，r 为半径的圆上运动时，如图所示：易证：△BOP ∽△POA，，∴对于圆上任意一点P 都有.对于任意一个圆，任意一个k 的值，我们可以在任意一条直径所在直线上，在同侧适当的位置选取A 、B点，则需【技巧总结】计算PA k PB 的最小值时，利用两边成比例且夹角相等构造母子型相似三角形问题：在圆上找一点P 使得PA k PB 的值最小，解决步骤具体如下：①如图，将系数不为1的线段两端点与圆心相连即OP ，OB ②计算出这两条线段的长度比OPk OB③在OB 上取一点C ，使得OC k OP ，即构造△POM ∽△BOP ，则PCk PB，PC k PB ④则=PA k PB PA PC AC ，当A 、P 、C 三点共线时可得最小值例1.如图，在Rt △ABC 中，∠ACB ＝90°，CB ＝7，AC ＝9，以C 为圆心、3为半径作⊙C ，P 为⊙C 上一动点，连接AP 、BP ，则13AP ＋BP 的最小值为（）A ．7B ．C ．4D ．【答案】B【详解】如图，在CA 上截取CM ，使得CM ＝1，连接PM ，PC ，BM ．∵PC ＝3，CM ＝1，CA ＝9，∴PC 2＝CM •CA ，∴PC CMCA CP，∵∠PCM ＝∠ACP ，∴△PCM ∽△ACP ，∴13PM PC PA AC ，∴PM 13 PA ，∴13AP +BP ＝PM +PB ，∵PM +PB ≥BM ，在Rt △BCM 中，∵∠BCM ＝90°，CM ＝1，BC ＝7，∴BM ，∴13AP +BP ∴13AP +BP 的最小值为．故选：B ．例2.在ABC 中，AB =9，BC =8，∠ABC =60°，⊙A 的半径为6，P 是A 上一动点，连接PB ，PC ，则32PC PB 的最小值_____________73PB PC 的最小值_______【答案】21【详解】①连接AP ，在AB 上取点Q ，使AQ =4，连接CQ ，∵⊙A 的半径为6，即AP =6，∴23AB AP ，又6923AP AB ，且PAQ BAP ，∴APQ ABP ∽，∴23PQ AP P AB B ，∴23PQ BP ，∴ 232333PC PB PC BP PC PQ，当P C Q 、、三点共线时，PC PQ 的值最小，最小值为CQ 的长，过C 作CI ⊥AB 于I ，∴90CIB CIQ ，在Rt △CIB 中，∵60CBI ，BC =8，sin CI CBI BC，∴CI∴4BI ，9441QI AB AQ BI ，在Rt △CIQ 中，7CQ ，∴32PC PB 的最小值为 321PC PQ ；故答案为：21；②连接AP ，由①得：在Rt △CIA 中，AC在AC 上取点G ，使AG ，连接PG ，BG ，∴73673AG AP ，∵67373AP AC ，∴P P AC A AG A ，且GAP PAC ，∴AGP APC ∽，∴73GP AG A P P C，∴73GP PC，∴73PB PB GP ，当G P B 、、三点共线时，PB GP 的值最小，最小值为BG 的长，过G 作GH ⊥AB 于H ，∴90GHA GHB ，在Rt △CIA 中，sin C CI AI ACRt △GAH 中，sin GH GAH AG∴GH ，∴18073AH，180********BH AB AH ，在Rt △GHB中，73BG ，∴73PB PC的最小值为73．故答案为：73．例题3.如图，已知正方ABCD 的边长为6，圆B 的半径为3，点P 是圆B 上的一个动点，则12PD PC 的最大值为_______．AB CDP【解析】当P 点运动到BC 边上时，此时PC=3，根据题意要求构造12PC ，在BC 上取M 使得此时PM=32，则在点P 运动的任意时刻，均有PM=12PC ，从而将问题转化为求PD-PM的最大值．连接PD ，对于△PDM ，PD-PM ＜DM ，故当D 、M 、P 共线时，PD-PM=DM 为最大值152．【变式训练1】如图，已知菱形ABCD 的边长为4，60B ，B 的半径为2，P 为B 上一动点，则12PD PC 的最小值_______．PC PD 的最小值_______3【详解】①如图，在BC 上取一点G ，使得BG =1，连接PB 、PG 、GD ，作DF ⊥BC 交BC 延长线于F ．∵221PB BG ，422BC PB ，∴PB BC BG PB ，∵PBG PBC ，∴PBG CBP ，∴12PG BG PC PB ，∴12PG PC ，∴12PD PC DP PG，∵DP PG DG ，∴当D 、P 、G 共线时，PD +12PC 的值最小，最小值为DG ，在Rt △CDF 中，∠DCF =60°，CD =4，∴DF =CD •sin CF =2，在Rt △GDF 中，DG ；②如图，连接BD ，在BD 上取一点M ，使得BM 连接PB 、PM 、MC ，过M 作MN ⊥BC 于N ．∵四边形ABCD 是菱形，且60ABC ，∴AC ⊥BD ，∠AOB =90 ，∠ABO =∠CBO =12∠ABC =30 ，∴AO =12AB =2，BO ∴BD =2BO =∴326BM PB ，6PB BD，∴BM PB PB BD ∠MBP =∠PBD ，∴△MBP ~△PBD ，∴PM PB PD BD∴PM ，∴PC PC PM MC ，∴当M 、P 、C 共线时，PC 的值最小，最小值为CM ，在Rt △BMN 中，∠CBO =30 ，BM ∴MN =12BM BN 12 ，∴CN =4-1722，∴MC，∴PC 的最小值为1113．【变式训练2】如图，正方形ABCD 的边长为4，圆B 的半径为2，点P 是圆B 上一动点，则的最小值为，的最大值为.【答案】最小值为5，最大值为5【解析】在BC 上取一点G ，使得BG ＝1，连接PG 、DG ，如图所示：∵∠PBG＝∠PBC，∴△PBG∽△CBP，，∴，在△PDG中，DP＋PG≥DG，∴当D、G、P共线时，；当点P在DG的延长线时，DG，最大值为5.【变式训练3】如图，在平面直角坐标系中，点A（4，0），B（4，4），点P在半径为2的圆O上运动，则的最小值是.【答案】5【解析】取点K（1，0），连接OP、PK、BK，如图所示：∵OP ＝2，OA ＝4，OK ＝1，∵∠POK ＝∠AOP ，∴△POK ∽△AOP ，在△PBK 中，，的最小值为BK 的长，∵B （4，4），K （1，0），，∴的最小值为5.【变式训练4】如图，菱形ABCD 的边长为2，锐角大小为60 ，A 与BC 相切于点E ，在A上任取一点P ，则2PB PD的最小值为___________．【答案】2．【详解】解：在AD 上截取AH =1.5，连接PH 、AE ，过点B 作BF ⊥DA 延长线，垂足为F ，∵AB =2，∠ABC =60°，∴BE =AF =1，AE =BF ，∴3AP AD AH AP，∵∠PAD =∠PAH ，∴△ADP ∽△APH ，∴3DP AD PH AP，∴PH ，当B 、P 、H 共线时，PB 的最小，最小值为BH 长，BH课后训练1.如图，矩形ABCD 中，4,2AB AD ，以B 为圆心，以BC 为半径画圆交边AB 于点E ，点P 是弧CE 上的一个动点，连结,PD PA ，则12AP DP 的最小值为（）A BC D 【答案】C【详解】解：如图，连接BP ，取BE 的中点G ，连接PG ，∵2AD BC BP ，4AB ，∴2142BP BA ，∵G 是BE 的中点，∴12BG BP ，∴BP BGBA BP，∵PBG ABP ，∴BPG BAP ，∴12PG BP AP BA ，∴12PG AP ，则12AP DP PG DP ，当P 、D 、G 三点共线时，取最小值，即DG 长，DG C ．2.如图，在平面直角坐标系中，A （2，0）、B （0，2）、C （4，0）、D （3，2），P 是△AOB 外部的第一象限内一动点，且∠BPA ＝135º，则2PD ＋PC 的最小值是.【解析】依题意可得OA＝OB＝2，∠BPA＝135º，∴点P的轨迹是以原点为圆心，OA长为半径的圆O上的劣弧AB，构造圆O，连接OP，在OC上截取OE＝1，连接PE、ED，过点D作DF⊥OC于点F，如图所示：∠POC＝∠EOP，∴△POC∽△EOP，，，，当E、P、D三点共线时，PD＋PE的值最小，最小值为DE的值，∵DF⊥OC于点F，则DF＝2，EF＝2，的最小值为2DE.3.如图，在Rt ABC中，∠C=90°，CA=3，CB=4．C 的半径为2，点P是C 上一动点，则12AP BP的最小值______________23PB PA的最小值_______【详解】①在BC 上取点D ，使CD =14BC =1，连接AD ，PD ，PC ，由题意知：PC =2，∵12DC PC PC BC ，∠PCD =∠BCP ，∴PDC BPC ∽，∴12PD PB ，且12PA PB PA PD AD，∴AD∴2PA PB ；②在AC 上取点E ，使CE =43，连接PE ，BE ，PC ，∵42323CE PC ，23PC AC ，∴23CE PC PC AC ，且∠PCE =∠ACP ，∴PEC APC ∽，∴23PE PC PA AC ，∴23PE PA ，∴23PB PA PB PE BE ，∴BE ∴23 PB PA 的最小值为3，故答案为：3．4.如图，半圆的半径为1，AB 为直径，AC 、BD 为切线，AC ＝1，BD ＝2，点P 为弧AB上一动点，求的最小值.【答案】【解析】当A、P、D三点共线时，的值最小.连接PB、CO，AD与CO相交于点M，如图所示：∵AB＝BD＝2,BD是⊙O的切线,∴∠ABD＝90º,∠BAD＝∠D＝45º,∵AB是⊙O直径,∴∠APB＝90º,∴∠PAB＝∠PBA＝45º,∴PA＝PB,PO⊥AB,∵AC是⊙O的切线,∴AC⊥AB,∴AC∥PO,∠CAO＝90º∵AC＝PO＝1,∴四边形AOPC是平行四边形,而OA＝OP,∠CAO＝90º,∴四边形AOPC是正方形,PC＋PD＝PM＋PD＝DM,∵DM⊥OC,∴由"垂线段最短"可知此时＋PD的值最小，最小值为.5.（1）如图1，在△ABC中，AB＝AC，BD是AC边上的中线，请用尺规作图做出AB边上的中线CE，并证明BD＝CE：（2）如图2，已知点P是边长为6的正方形ABCD内部一动点，PA＝3，求PC+PD的最小值；（3）如图3，在矩形ABCD中，AB＝18，BC＝25，点M是矩形内部一动点，MA＝15，当MC+MD最小时，画出点M的位置，并求出MC+MD的最小值．【解答】解：（1）如图1中，作线段AB的垂直平分线MN交AB于点E，连接EC．线段EC即为所求；∵AB＝AC，AE＝EC，AD＝CD，∴AE＝AD，∵AB＝AC，∠A＝∠A，AD＝AE，∴△BAD≌△CAE（SAS），∴BD＝CE．（2）如图2中，在AD上截取AE，使得AE＝．∵PA2＝9，AE•AD＝×6＝9，∴PA2＝AE•AD，∴＝，∵∠PAE＝∠DAP，∴△PAE∽△DAP，∴＝＝，∴PE＝PD，∴PC+PD＝PC+PE，∵PC+PE≥EC，∴PC+PD的最小值为EC的长，在Rt△CDE中，∵∠CDE＝90°，CD＝6，DE＝，∴EC＝＝，∴PC+PD的最小值为．（3）如图3中，如图2中，在AD上截取AE，使得AE＝9．∵MA2＝225，AE•AD＝9×25＝225，∴MA2＝AE•AE，∴＝，∵∠MAE＝∠DAM，∴△MAE∽△DAM，∴＝＝＝，∴ME＝MD，∴MC+MD＝MC+ME，∵MC+ME≥EC，∴MC+MD的最小值为EC的长，在Rt△CDE中，∵∠CDE＝90°，CD＝18，DE＝16，∴EC＝＝2，∴MC+MD的最小值为2．6.如图1，抛物线y＝ax2＋（a＋3）x＋3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．（1）求a的值和直线AB的函数表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，若＝，求m的值；（3）如图2，在（2）条件下，将线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜90°），连接E′A、E′B，求E’A＋E’B的最小值．【解答】（1）；（2）m＝2；（3）【解析】（1）令y＝0，则ax2＋（a＋3）x＋3＝0，∴（x＋1）（ax＋3）＝0，∴x＝﹣1或，∵抛物线y＝ax2＋（a＋3）x＋3（a≠0）与x轴交于点A（4，0），∴＝4，∴a．∵A（4，0），B（0，3），设直线AB解析式为y＝kx＋b，则，解得，∴直线AB解析式．（2）如图1中，∵PM⊥AB，PE⊥OA，∴∠PMN＝∠AEN，∵∠PNM＝∠ANE，∴△PNM∽△ANE，∵NE∥OB，∴AN（4﹣m），∵抛物线解析式为，∴PN＝﹣（）＝，，解得m＝2．（3）如图2中，在y轴上取一点M′使得OM′＝，连接AM′，在AM′上取一点E′使得OE′＝OE．∵OE′＝2，OM′•OB×3＝4，∴OE′2＝OM′•OB，，∵∠BOE′＝∠M′OE′，∴△M′OE′∽△E′OB，，∴M′E′＝BE′，∴AE BE′＝AE′＋E′M′＝AM′，此时AE′＋BE′最小（两点间线段最短，A、M′、E′共线时），最小值＝AM′＝．。

第17篇 阿氏圆在保护中的应用百度文库是这样说的：阿波罗尼斯（Apollonius ）圆，简称阿氏圆。

在平面上给定相异两点A 、B ，设P 点在同一平面上且满足PA/PB=λ，当λ>0且λ≠1时，P 点的轨迹是个圆，这个圆我们称作阿波罗尼斯圆。

这个结论称作阿波罗尼斯轨迹定理。

我再把“阿波罗尼斯轨迹定理”说通俗点：一动点P 到两定点A 、B 的距离之比PA/PB=λ为一常数，P 的轨迹为圆。

λ=1时，为A 与B 连线的垂直平分线（无穷大圆）；λ≠1时，λ与1/λ是一对镜象圆，镜象轴为垂直平分线。

A Bλ=1λ<11/λ>1我们在拟定继电器的动作特性时，往往在某一复平面上表示。

这样阿氏圆又可以表示为：B A -=-ρλρ，ρ 为复变量，其余常数。

这也太像我们的比幅式动作方程了，因此才想到它。

应用1）全相振荡测量阻抗的轨迹ZS Z ’EMEN全相振荡，又假设系统电势的幅值之比不变N M E E λ=，λ为常数。

N M E E λ=→I Z U I Z U S '-=+λ→Z Z Z Z S'-=+λ应用2）方向继电器正向故障：故障点在正向，避开正向，据反向阻抗有I Z U S ∆-=∆ 或0=∆+∆I Z U S（1） 反向故障：故障点在反向，避开反向，据正向阻抗有I Z U ∆'=∆ 或0=∆'-∆I Z U （2）显然，将（2）式为动作量、（1）式为制作量是一个理想的动作特性 ||||I Z U I Z U S∆+∆>∆'-∆或||||S Z Z Z Z +∆>'-∆ （3）应用3）差动继电器 NM N M I I I I ->+35.0λ→ρλρ ->+35.01Re分析ρ在复平面：区外故障，1-=ρ ；单电源区内故障，0=ρ 。

因此，我们可以假设ρ 的动作特性为红线所示的区域ρλρ ->+35.01或NM N M I I I I ->+35.0λ。

高中阿氏圆例题
（最新版）
目录
1.阿氏圆的定义与性质
2.阿氏圆的构造方法
3.阿氏圆的性质与应用
4.阿氏圆的例题解析
正文
一、阿氏圆的定义与性质
阿氏圆，又称为圆的外接圆或外接圆，是指一个三角形的外接圆。

阿氏圆具有以下性质：
1.阿氏圆的圆心是三角形三顶点所在直线的垂直平分线的交点。

2.阿氏圆的半径等于三角形面积除以半周长。

二、阿氏圆的构造方法
构造阿氏圆的方法有多种，常见的有以下两种：
1.以三角形的三个顶点为圆心，以三角形三边的垂直平分线为半径，分别作圆。

这三个圆相交于一点，该点即为阿氏圆的圆心。

2.作三角形的三边的垂直平分线，将垂直平分线相交于一点，该点即为阿氏圆的圆心。

然后以圆心到三角形三顶点的距离为半径，作圆。

三、阿氏圆的性质与应用
阿氏圆在解决一些与三角形相关的数学问题时具有重要作用，例如：
1.判断三角形是否为直角三角形。

若阿氏圆的圆心与三角形某一顶点重合，则该三角形为直角三角形。

2.求解三角形的面积。

通过阿氏圆的半径可以求得三角形的面积。

3.求解三角形的半周长。

通过阿氏圆的半径可以求得三角形的半周长。

四、阿氏圆的例题解析
例题：已知三角形 ABC 的三边长分别为 a、b、c，求三角形 ABC 的面积。

解：首先构造三角形 ABC 的阿氏圆，然后求得阿氏圆的半径。

根据
阿氏圆的性质，半径 r 等于三角形面积 S 除以半周长 p，即 r = S / p。