滚动训练三(5~6)
- 格式:docx
- 大小:241.23 KB
- 文档页数:10
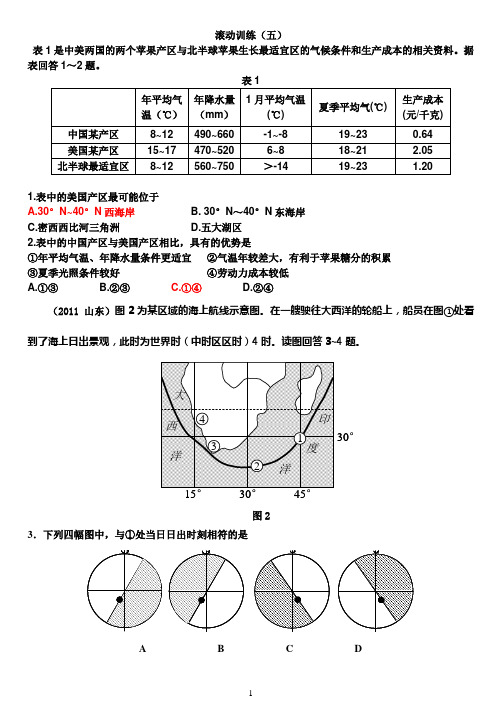
滚动训练(五)表1是中美两国的两个苹果产区与北半球苹果生长最适宜区的气候条件和生产成本的相关资料。
据表回答1~2题。
表1年平均气温(℃) 年降水量(mm ) 1月平均气温(℃) 夏季平均气(℃)生产成本(元/千克) 中国某产区 8~12 490~660 -1~-8 19~23 0.64 美国某产区 15~17 470~520 6~8 18~21 2.05 北半球最适宜区8~12560~750>-1419~231.201.表中的美国产区最可能位于 A.30°N~40°N 西海岸 B. 30°N ~40°N 东海岸 C.密西西比河三角洲 D.五大湖区2.表中的中国产区与美国产区相比,具有的优势是①年平均气温、年降水量条件更适宜 ②气温年较差大,有利于苹果糖分的积累 ③夏季光照条件较好 ④劳动力成本较低 A.①③ B.②③ C.①④ D.②④(2011 山东)图2为某区域的海上航线示意图。
在一艘驶往大西洋的轮船上,船员在图①处看到了海上日出景观,此时为世界时(中时区区时)4时。
读图回答3~4题。
1234大西洋印度洋15°30°45°30°图23.下列四幅图中,与①处当日日出时刻相符的是A B C D (注:阴影部分表示夜半球,●表示①处位置)4.下列叙述正确的是A .①处该船逆水航行B .②处风平浪静C .③地河流正值丰水期D .④地森林密布图3为我国东部地区甲、乙两城市三 个年份的常住人口密度分布图,图中楼高表示2000年城市商务楼相对高度。
读图回答7~8题。
20001000020000300004000050000600000MN3060距市中心距离(km )常住人口密度(人/k m 2)年1990年1982年楼高200050001000015000200002500030000350000年1990年1982年楼高常住人口密度(人/k m 2)PQ51015距市中心距离(km )甲城市 乙城市图35.下列说法正确的是A .1982~2000年,两城市的市中心人口密度变化特征相同B .1982~2000年,两城市的市中心人口密度变化特征不同C .2000年甲城市的人口规模比乙城市的小D .2000年乙城市的服务范围比甲城市的小6.关于2000年两城市功能区分布的推断,最有可能的是①甲城市的中心商务区位于M 处 ②乙城市的中心商务区位于P 处 ③甲城市的卫星城位于N 处 ④乙城市的卫星城位于Q 处 A .①② B .②③ C .①④ D .③④参考答案(五)1-2 A C3. 【答案】C。

趣味“课课练”1260例第一部分:滚动类练习 (4)一、初级:直体左右滚动 (5)(一)绑手侧滚动(自由人) (5)(二)单臂侧滚动(独臂人) (6)(三)直体直臂圆周侧滚动(旋转木马) (7)(四)有人帮助侧滚动(烙煎饼) (9)(五)固定下肢侧滚动(分身术) (10)(六)无手侧滚动(钟摆运动) (11)(七)单腿抱膝侧滚动(独轮车) (12)(八)抱球交叉腿侧滚动(婴儿翻身) (13)(九)多层弧形垫上侧滚动(木头下山) (14)(十)双手抱头屈膝侧滚动(抱头好窜) (15)(十一)团身抱球侧滚动(怀璧滚动) (17)(十二)屈肘屈膝侧滚动(鸡蛋侧滚) (18)(十三)纵叉侧滚动(小小变身) (19)(十四)跨栏步侧滚动(单轴运动) (21)(十五)仰俯卧撑交替侧滚动(螺旋桨) (21)(十六)双人拉手同侧滚动(并驾齐驱) (23)(十七)双人侧滚动(双龟摇摆) (24)(十八)双人抱脚侧滚动(同抱佛脚) (25)(十九)多人拉手侧滚动(同心协力) (26)(二十)多人抱脚侧滚动(同舟共济) (27)二、中级:团身前后滚动 (27)(一)分腿蹲前滚翻(变形青蛙) (28)(二)单手前滚翻(一手遮天) (28)(三)单脚前滚翻(金鸡独翻) (30)(四)多层弧形垫上前滚翻(刺猬下山) (31)(五)在绳网上前滚翻(蜘蛛侠) (32)(六)弓步后滚翻(后仰看天) (32)(六)弓步后滚翻(后仰看天) (33)(七)后滚翻靠墙倒立(后滚登墙) (33)(八)夹物后滚翻(滚翻运输) (34)(九)手膝着地前滚翻(乌龟翻身) (36)(十)分腿坐后滚翻(四仰八叉) (37)(十一)高处跳下前滚翻(小小跑酷) (38)(十二)扑球单肩前滚翻(足球守门) (39)(十三)抢球单肩前滚翻(橄榄球战) (40)(十四)双杠悬垂滚翻(杠间滚翻) (41)(十五)单杠骑撑前回环(杠上回环) (42)(十六)双人拉手连环后滚翻(连环滚翻) (43)(十七)双人持球前滚翻(双人戏球) (44)(十八)双人推手后滚翻(掌滚之间) (46)(十九)多人不抱腿前滚翻(拉手滚翻) (47)(二十)多人持棍前滚翻(龙卷风) (48)三、高级:生活状态下的滚动 (49)(一)趴球滚动(大象翻身) (49)(二)躲物滚动(小心触电) (50)(三)移垫滚动(滚石过河) (51)(四)绊倒滚动(自救行动) (52)(五)躲悬物滚动(枪林弹雨) (53)(六)持筋滚动(渔人撒网) (54)(七)字母滚动(创意滚动) (54)(八)背人摔跤滚动(罗汉摔跤) (56)(九)冰上滚动(冰上芭蕾) (57)(十)滚翻接球(排球防守) (59)第一部分:滚动类练习滚动是锻炼价值和安全性都极高的体育锻炼形式,很受学生的喜爱。

单元知识滚动练Unit 4 复习强化Ⅰ.单词拼写1.He felt the rough surface of the rock cutting into his knees.2.He can’t decide which candidate he should vote in the next election.3.The club has created an exciting atmosphere for gaming and recreation(娱乐).4.The young couple were busy filling their new house with some furniture(家具).5.It is natural that one might question the motives(动机) of some politicians.6.Our manager ordered us to have a thorough cleaning that weekend.7.The young man is genuine,so you can rely on him to help you out.8.The woman entered the room and put a blanket(毯子) over the little baby.Ⅱ.单句语法填空9.Strengthening our emotional endurance(endure) is vital for a happy life.10.As a qualified(qualify) new employee,he was highly thought of in the company. 11.I’m afraid that I can’t finish the work assigned(assign) to me within three days. 12.The little boy burst into tears when he found his favorite toy crushed(crush).13.The old man was so kind that he adopted the child abandoned(abandon) by his parents. 14.To be honest,I’m not sure whether the results have any practical application(apply).15.Fortunately(fortunate),the two boys were saved by the local villagers.Unit 5 巩固落实Ⅲ.单词拼写16.The present situation is complicated(复杂的),so you’d better leave here.17.The farmers had to depend on the barren(贫瘠的) field in the past.18.The girl spent much time polishing the article before handing it in.19.If your son fails in the contest,you’d better comfort him in time.20.They were working hard in order not to miss the deadline(最后期限).21.When she turned around,she saw her mother’s blank(没表情的) eyes.22.The fact is that the woman has been awaiting her husband all the time.23.It is better for you to talk about that matter when he is in a good mood.Ⅳ.单句语法填空24.Our monitor is sympathetic(sympathy) and he often helps the poor classmates. 25.After the accident,she left the city with a sorrowful(sorrow) heart.26.Having read the text many times,he found it really hard to recite(recite).27.The leader will pay a visit to a team made(make) up of over 200 people.28.They turned to one another with the same expression of comprehension(comprehend) and relief.29.It was cruel of the general to put some innocent(innocence) soldiers into prison.30.There is a large variation(vary) in the amount of sleep people feel happy with.Ⅴ.完成句子31.He was the first person to question racial prejudice in this town.他是这个镇上第一个对种族偏见提出质疑的人。

考案[十七] 模块滚动训练周测卷(十四)散文阅读+诗歌阅读+名句默写+语言文字运用+写作一、现代文阅读Ⅱ(本题共4小题,18分)(2023·肥城一中开学摸底检测)阅读下面的文字,完成1~4题。
放火者萧红从五月一号那天起,重庆就动了,在这个月份里,我们要纪念好几个日子,所以街上有多少人在游行,他们还准备着在夜里火炬游行。
街上的人带着民族的信心,排成大队行列沉静地走着。
五三的中午,日本飞机二十六架飞到重庆的上空,在人口最稠密的街道上投下燃烧弹和炸弹,那一天就有三条街起了带着硫磺气的火焰。
五四的那天,日本飞机又带了多量的炸弹,投到他们上次没有完全毁掉的街上和上次没可能毁掉的街道上。
大火的十天以后,那些断墙之下,瓦砾堆中仍冒着烟。
人们走在街上用手帕掩着鼻子或者挂着口罩,因为有一种奇怪的气味满街散布着。
那怪味并不十分浓厚,但随时都觉得吸得到。
似乎每人都用过于细微的嗅觉存心嗅到那说不出的气味似的,就在十天以后发掘的人们,还在深厚的灰烬里寻出尸体来。
断墙笔直的站着,在一群瓦砾当中,只有它那么高而又那么完整。
设法拆掉它,拉倒它,但它站得非常坚强。
断牌坊就站着这断墙,很远就可以听到几十人在喊着,好像拉着帆船的纤绳,又像抬着重物。
“唉呀……喔呵……唉呀……喔呵……”……街道是哑默的,一切店铺关了门,在黑大的门扇上贴着白帖或红帖,上面坐着一个苍白着脸色的恐吓的人,用水盆子在洗刷着弄脏了的胶皮鞋、汗背心……毛巾之类,这东西是从火中抢救出来的。
被炸过了的街道,飞尘卷着白沫扫着稀少的行人,行人挂着口罩,或用帕子掩着鼻子。
街是哑然的,许多人生存的街毁掉了,生活秩序被破坏了,饭馆关起了门。
大瓦砾场一个接着一个,前边是一群人在拉着断墙,这使人一看上去就要低了头。
无论你心胸怎样宽大,但你的心不能不跳,因为那摆在你面前的是荒凉的,是横遭不测的,千百个母亲和小孩子是吼叫着的,哭号着的,他们嫩弱的生命在火里边挣扎着,生命和火在斗争。

滚动训练(三)滚动训练(三)一、选择题1.已知等比数列{a n}的前3项的和等于首项的3倍,则该等比数列的公比为()A.-2B.1C.-2或1D.2或-1答案 C解析由题设条件,可得a1+a1q+a1q2=3a1,所以q2+q-2=0,所以q=1或q=-2,故选C.2.设△ABC的内角A,B,C的对边分别为a,b,c.若a=2,c=23,cos A=32且b<c,则b等于()A. 3B.2C.2 2D.3答案 B解析由余弦定理a2=b2+c2-2bc cos A,得4=b2+12-2×b×23×32,即b2-6b+8=0,∴bA. 3B.7C.19D.13-6 3答案 B解析 在△ABC 中,由余弦定理得BC 2=AB 2+AC 2-2AB ·AC cos 60°,解得BC =3,所以AC 2=AB 2+BC 2,故BC ⊥AB ,在Rt △BCD 中,CD =BD 2-BC 2=12-3=3,在△ACD 中,由余弦定理得AD 2=AC 2+CD 2-2AC ·CD cos 60°=7,所以AD =7.5.△ABC 的三个内角所对的边分别为a ,b ,c ,a sin A sin B +b cos 2A =2a ,则b a 等于( ) A.2 3 B.2 2 C. 2 D. 3答案 C解析 ∵a sin A sin B +b cos 2A =2a , ∴sin 2A sin B +sin B cos 2A =2sin A ,∴sin B (sin 2A +cos 2A )=2sin A ,∴sin B sin A =2,即b a = 2. 6.已知等差数列{a n }的前n 项和为S n ,若a 10+a 11=10,则ln S 20ln 110等于( ) A.1 B.2 C.-1 D.-2答案 D解析 在等差数列{a n }中,S 20=(a 1+a 20)×202=10(a 1+a 20)=10(a 10+a 11)=100,所以ln S 20ln 110=ln 100ln 10-1=-ln 100ln 10=-2ln 10ln 10=-2.故选D.7.对于正项数列{a n },定义G n =a 1+2a 2+3a 3+…+na n n为数列{a n }的“匀称”值.已知数列{a n }的“匀称”值为G n =n +2,则该数列中的a 10等于( )A.2 3B.45C.1D.2110答案 D解析 因为G n =a 1+2a 2+3a 3+…+na n n, 数列{a n }的“匀称”值为G n =n +2,所以a 1+2a 2+3a 3+…+na n =n (n +2),① 所以n ≥2时,a 1+2a 2+3a 3+…+(n -1)a n -1=(n -1)(n +1),②①-②得na n =2n +1,所以a n =2n +1n ,n ≥2;当n =1时,a 1=G 1=3满足上式,所以a n =2n +1n ,故a 10=2110. 二、填空题8.已知数列{a n },a n =b n +m (b <0,n ∈N +),满足a 1=2,a 2=4,则a 3= .答案 2解析 ∵a 1=2,a 2=4,∴⎩⎪⎨⎪⎧ b <0,b +m =2,b 2+m =4,∴⎩⎨⎧b =-1,m =3. 即a n =(-1)n +3,∴a 3=2.9.在△ABC 中,角A ,B ,C 分别对应的边为a ,b ,c .已知cos A =35,cos B =513,b =3,则c = .答案 145解析 在△ABC 中,∵cos A =35>0, 又∵A ∈(0,π),∴sin A =45. ∵cos B =513>0,又∵B ∈(0,π),∴sin B =1213. ∴sin C =sin[π-(A +B )]=sin(A +B )=sin A cosB +cos A sin B =45×513+35×1213=5665.由正弦定理,知b sin B =c sin C, ∴c =b sin C sin B =3×56651213=145. 10.等比数列{a n }中,a 4=2,a 5=4,则数列{lg a n }的通项公式为 . 答案 lg a n =(n -3)lg 2,n ∈N +解析 ∵a 5=a 4q ,∴q =2,∴a 1=a 4q 3=14, ∴a n =14·2n -1=2n -3,∴lg a n =(n -3)lg 2,n ∈N +. 11.等差数列{a n }中,公差d ≠0,a 22=a 1a 4,若a 1,a 3,12nk k k a a a ,,,,成等比数列,则k n = . 答案 3n +1解析 由题意得(a 1+d )2=a 1(a 1+3d ), ∴a 1=d ,∴a n =na 1,∴q =a 3a 1=3a 1a 1=3.∵13k a a =k 1a 13a 1=k 13=3, ∴k 1=9,∴nk a =a 1·3n +1=k n a 1, ∴k n =3n +1.三、解答题12.在等差数列{a n }中,a 3=4,a 7=8.(1)求数列{a n }的通项公式a n ;(2)令b n =a n 2n -1,求数列{b n }的前n 项和T n . 解 (1)因为d =a 7-a 37-3=1,所以a n =a 3+(n -3)d =n +1,n ∈N +.(2)b n =a n 2n -1=n +12n -1, T n =b 1+b 2+…+b n =2+32+422+…+n +12n -1,① 12T n =22+322+…+n 2n -1+n +12n ,②由①-②得12T n =2+12+122+…+12n -1-n +12n =⎝⎛⎭⎪⎫1+12+122+…+12n -1+1-n +12n =1-12n 1-12+1-n +12n =2⎝ ⎛⎭⎪⎪⎫1-12n +1-n +12n =3-n +32n ,所以T n =6-n +32n -1. 13.设数列{a n }的前n 项和为S n ,若对于任意的正整数n 都有S n =2a n -3n .(1)设b n =a n +3,求证:数列{b n }是等比数列;(2)求出{a n }的通项公式;(3)求数列{na n }的前n 项和T n .(1)证明 因为S n =2a n -3n ,对于任意的正整数都成立,所以S n +1=2a n +1-3n -3, 两式相减,得a n +1=2a n +1-2a n -3, 即a n +1+3=2(a n +3),所以b n +1=2b n . 所以数列{b n }是以2为公比的等比数列.(2)解由已知条件,得S1=2a1-3,a1=3.所以首项b1=a1+3=6,公比q=2,即b n=6·2n -1.所以a n=6·2n-1-3=3·2n-3,n∈N+.(3)解因为na n=3×n·2n-3n,所以T n=3(1·2+2·22+3·23+…+n·2n)-3(1+2+3+…+n),2T n=3(1·22+2·23+3·24+…+n·2n+1)-6(1+2+3+…+n),所以-T n=3(2+22+23+…+2n-n·2n+1)+3(1+2+3+…+n)=3×2(2n-1)2-1-6n·2n+3n(n+1)2,故T n=(6n-6)·2n+6-3n(n+1)2.四、探究与拓展14.在等比数列{a n}中,a1+a2+…+a6=10,1a1+1a 2+…+1a 6=5,则a 1·a 2·…·a 6等于( ) A.2 B.8 C.12 D.18答案 B解析 由a 1+a 2+…+a 6=10,得a 1(1-q 6)1-q=10, 由1a 1+1a 2+…+1a 6=5,得1a 1⎝ ⎛⎭⎪⎪⎫1-1q 61-1q=5, ∴a 21q 5=2,∴a 1·a 2·…·a 6=a 61q 1+2+…+5=(a 21q 5)3=23=8.15.已知数列{a n }的前n 项和S n =1+λa n ,其中λ≠0.(1)证明{a n }是等比数列,并求其通项公式;(2)若S 5=3132,求λ. 解 (1)由题意,得a 1=S 1=1+λa 1,故λ≠1,a 1=11-λ,a 1≠0.由S n =1+λa n ,S n +1=1+λa n +1,得a n +1=λa n +1-λa n ,即a n +1(λ-1)=λa n .由a 1≠0,λ≠0且λ≠1,得a n ≠0,所以a n +1a n=λλ-1. 因此{a n }是首项为11-λ,公比为λλ-1的等比数列, 于是a n =11-λ⎝ ⎛⎭⎪⎫λλ-1n -1. (2)由(1)得S n =1-⎝ ⎛⎭⎪⎫λλ-1n .由S 5=3132, 得1-⎝ ⎛⎭⎪⎫λλ-15=3132,即⎝ ⎛⎭⎪⎫λλ-15=132,解得λ=-1.。

2022-2023学年七年级地理下册单元考点梳理分层卷(商务星球版)阶段滚动分层卷【范围:第六、七章】(B卷·真题重组卷)一、选择题(本大题共25小题,每小题2分,共50分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.(2022·黑龙江绥化·统考中考真题)受地形的影响,亚洲的大河多发源于中部山地、高原,呈放射状流向()A.加勒比海B.挪威海C.周边海洋D.白海2.(2022·广西贵港·统考中考真题)亚洲河流众多,大多发源于中部,呈放射状流向四周,由此判断亚洲的地势特征是()A.中部高,四周低B.西高东低C.西北高,东南低D.北高南低(2021·山东济南·统考中考真题)水稻被称为“亚洲粮食”,下图是亚洲水稻主要种植区分布示意图。
据此完成下面3-4小题。
3.亚洲水稻主要种植区分布在()A.河流上游地区B.亚洲东部和南部C.温带大陆内部D.热带雨林气候区4.亚洲水稻主要种植区种植水稻的优势条件是()①地形复杂多样,地势起伏大②热量充足,降水丰沛③多长河,河流呈放射状分布④人口稠密,劳动力丰富A.①②B.②③C.②④D.①④(2022·辽宁葫芦岛·统考中考真题)东南亚地区有丰富的旅游资源,成为中国人出境旅游的热点地区之一。
据此完成下面5-6小题。
5.近些年,许多中国人出境旅游选择了东南亚。
对其理由的叙述完全正确的一组是()①热带海岛风光旖旎②距离我国较近③发达国家较多④语言沟通障碍小A.①②③B.①②④C.①③④D.②③④6.游客可以在东南亚地区欣赏到的景观是()A.吴哥窟B.埃菲尔铁塔C.白金汉宫D.罗马古斗兽场(2022·湖北·统考中考真题)2021年12月3日,中老铁路全线通车运营。
该铁路全长1035公里。
总投资约505.4亿元,线路北起昆明,终点为老挝首都万象。
据此完成下面小题。
人教版八年级上册滚动训练(六)[范围:第六章第1节~第2节](162)1.随着人们环保意识的日益提高,节水型洁具逐渐进入百姓家庭。
所谓节水型洁具,是指每冲洗一次的耗水量在6L以内的洁具。
某家庭新安装了一套耗水量为5L的节水型洁具,而原有的洁具每次耗水量为9L。
问:(1)1000kg的水可供这套节水型洁具冲洗多少次?(2)该家庭每月节约用水多少千克?(设平均每天使用10次,每月以30天计)2.感受身边的物理——质量为1.5kg的物体最可能是()A.一个乒乓球B.一只母鸡C.一张桌子D.一头牛3.天平的每一个砝码都有一定的质量,它们的质量在下述情况下会发生改变的是()A.生锈了B.放在月球上C.掉在干净的水泥地上D.气温升高4.体温计示数升高时,对于体温计里的水银,下列物理量不变的是()A.体积B.质量C.密度D.温度5.用托盘天平称量物体的质量时,将被测物体和砝码放错了位置,若天平平衡时,左盘上放着100g和20g的砝码各一个,游码的读数为4g,则物体的质量是()A.124gB.118gC.122gD.116g6.某同学在使用托盘天平称量前,天平的指针不在分度盘的中央,稍微向右偏。
用此天平称物体的质量,测量值与物体的实际质量相比()A.相等B.偏小C.偏大D.都有可能7.世界上密度最小的固体“气凝胶”是人类在探索新材料中取得的重要成果,该物质的坚固耐用程度不亚于钢材,且能承受1400℃的高温,而密度只有3kg/m3。
一架用钢材(ρ钢=7.9×103kg/m3)制成的质量约160t的大型飞机,如果用“气凝胶”做成,其质量相当于()A.一片鸡毛的质量B.一只鸡蛋的质量C.一个成年人的质量D.一台大卡车的质量8.规格相同的瓶装了不同的液体,放在横梁已平衡的天平上横梁仍平衡,如图所示,则()A.甲瓶液体质量较大B.乙瓶液体质量较大C.乙瓶液体密度较大D.两瓶液体密度相等9.分别由不同物质a、b、c组成的三个实心体,它们的体积和质量关系如图所示,由图可知下列说法中正确的是()A.a物质的密度最大B.b物质的密度是1×103kg/m3C.c物质的密度是a的两倍D.a、b、c的密度与它们的质量、体积有关10.一个瓶子能盛1kg水,可用该瓶子盛1kg下列哪种液体(已知ρ水银>ρ水>ρ植物油>ρ酒精>ρ汽油)()A.酒精B.汽油C.植物油D.水银11.一个质量为0.25kg的玻璃瓶,盛满水时称得质量是1.5kg,若盛满某液体时称得质量是1.75kg,那么这种液体的密度是()A.1.0×103kg/m3B.1.16×103kg/m3C.1.75×103kg/m3D.1.2×103kg/m312.单位及单位换算:海洋中一头蓝鲸的质量约为120t=kg;某位八年级男同学的质量约为6×104;我们教室中地板所用的大理石密度约为2.7×103。
考案[七] 模块滚动训练周测卷(六)论述类文本阅读+诗歌阅读+名句默写+语言文字运用+写作一、现代文阅读Ⅰ(本题共5小题,17分)(2023·三湘创新发展联合调研)阅读下面的文字,完成1~5题。
材料一:古典文学是中华文化的上游,而古典文学的载体——文言文,是根底,是骨架。
不读文言文,几千年的中华文化,包括文学,我们很难吸收,很难理解。
先秦时代是中国文言文形成并逐渐成型的重要时期。
那个时代的文言文虽然离所谓“今古文”还较有距离,但已经为后来文学的发展奠定了基础,为汉代华丽的赋体、魏晋风骨、唐诗宋词做了铺垫。
应该说,从先秦开始,中华绚烂的文化便和文言文紧密地结合在了一起。
所以说,不熟读古文,就不会见识到中文能美到什么程度,也不会领悟古人的造诣能抵达怎样的深度和高度。
学习古文可以提高一个人的人格修养。
文以载道,经典古文是中国优秀传统文化最好的载体。
处世为人的哲学,修身、齐家、治国、平天下的道理都蕴含其中。
背诵和学习这些经典古文,对我们的眼界、志气、品格修养的提高大有帮助。
有很多人对学习古诗文有误解,认为学了这些诗文也不能吃,也不能喝,甚至想到是不是还要回到古代那样的生活,我必须告诉各位,其实这是一种功利思想在作怪。
当然,读了古诗文,的确可能不能马上看到什么成效,获得什么收益。
但是,学习古诗文一个最大的好处在于能涵养一个人的心性并为之奠定坚实的文化底蕴。
而最重要的是,这样一种文化熏陶正是我们作为一个现代人与自己的先人进行对话的基本途径。
现代著名文史学家顾随先生曾经说过:“学古诗文的目的是为了做一个现代人。
”一个人学习了古诗文,能够爱生活、有情趣、平等待人、学会宽容,而且可以获得阅读体验和精神感悟,这无疑是最大的收获。
一个现代中国人,没有对自己民族的传统文化的继承和发扬,从严格意义上讲,尤其从文化意义上来说,不能算作一个真正的现代人。
(摘编自张胜强《古诗文学习的现代意义》) 材料二:古人说“仓廪实而知礼节”,当人们吃饱穿暖,自然就会有更高的精神追求。
滚动训练三(§1~§3)一、选择题1.假设抛物线y 2=x 上一点P 到准线的间隔 等于它到顶点的间隔 ,那么点P 的坐标为( ) A.⎝⎛⎭⎫14,±24 B.⎝⎛⎭⎫18,±24 C.⎝⎛⎭⎫14,24 D.⎝⎛⎭⎫18,24 考点 抛物线的标准方程题点 求抛物线方程答案 B解析 由题意知,点P 到焦点F 的间隔 等于它到顶点O 的间隔 ,因此点P 在线段OF 的垂直平分线上,而F ⎝⎛⎭⎫14,0,所以点P 的横坐标为18,代入抛物线方程得y =±24,故点P 的坐标为⎝⎛⎭⎫18,±24,应选B. 2.抛物线y 2=4x 的焦点到双曲线x 2-y 23=1的渐近线的间隔 是( ) A.12B.32 C .1D.3考点 抛物线的简单性质题点 抛物线与其他曲线结合有关问题答案 B解析 抛物线y 2=4x 的焦点F (1,0),双曲线x 2-y 23=1的渐近线方程是y =±3x , 即3x ±y =0,所以所求间隔 为|3±0|(3)2+(±1)2=32,应选B. 3.设双曲线的一个焦点为F ,虚轴的一个端点为B ,假如直线FB 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( ) A. 2B.3C.1+32D.1+52答案 D解析 不妨设双曲线方程为x 2a 2-y 2b 2=1(a >0,b >0),那么可令F (c,0),B (0,b ),直线FB :bx +cy -bc =0与渐近线y =b a x 垂直,所以-b c ·b a=-1,即b 2=ac ,所以c 2-a 2=ac ,即e 2-e -1=0,所以e =1+52或e =1-52(舍去). 4.一条直线过点⎝⎛⎭⎫14,0,且与抛物线y 2=x 交于A ,B 两点.假设|AB |=4,那么弦AB 的中点到直线x +12=0的间隔 等于( ) A.74B .2 C.94D .4考点 抛物线的焦点弦问题题点 与焦点弦有关的其他问题答案 C解析 ∵抛物线方程为y 2=x ,∴其焦点坐标为⎝⎛⎭⎫14,0,准线方程为x =-14, ∴直线AB 过抛物线焦点,∴由抛物线的定义知,弦AB 的中点到直线x =-14的间隔 为2, ∴弦AB 的中点到直线x +12=0的间隔 等于2+14=94. 5.抛物线C 的顶点为原点,焦点在x 轴上,直线y =x 与抛物线C 交于A ,B 两点,假设P (2,2)为AB 的中点,那么抛物线C 的方程为( )A .y 2=4xB .y 2=-4xC .x 2=4yD .y 2=8x 考点 直线与抛物线的位置关系题点 直线与抛物线相交弦中点问题答案 A解析 依题意可设抛物线方程为y 2=2px (p >0),设A (x 1,y 1),B (x 2,y 2),那么y 2-y 1x 2-x 1=1,∵P (2,2)为AB 的中点,∴y 1+y 2=4,由⎩⎪⎨⎪⎧y 21=2px 1,y 22=2px 2, 得(y 2+y 1)(y 2-y 1)=2p (x 2-x 1),∴2p =(y 2+y 1)y 2-y 1x 2-x 1=4, ∴抛物线C 的方程为y 2=4x .6.假设双曲线与椭圆x 216+y 264=1有一样的焦点,它的一条渐近线方程为y =-x ,那么双曲线的方程为( )A .y 2-x 2=96B .y 2-x 2=160C .y 2-x 2=80D .y 2-x 2=24考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题答案 D解析 设双曲线方程为x 2-y 2=λ(λ≠0),因为双曲线与椭圆有一样的焦点,且焦点为(0,±43),所以λ<0,且-2λ=(43)2,得λ=-24.应选D.7.椭圆y 225+x 29=1与双曲线y 215-x 2=1有公共点P ,那么P 与双曲线两焦点连线构成的三角形的面积为( )A .4B .55C .5D .3 考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题答案 D解析 由得椭圆与双曲线具有共同的焦点F 1(0,4)和F 2(0,-4),不妨设|PF 1|>|PF 2|, 由椭圆与双曲线的定义可得 ⎩⎪⎨⎪⎧|PF 1|+|PF 2|=10,|PF 1|-|PF 2|=215,所以|PF 1|=5+15,|PF 2|=5-15.在△PF 1F 2中,由余弦定理,得cos ∠F 1PF 2=|PF 1|2+|PF 2|2-|F 1F 2|22|PF 1|·|PF 2|=(5+15)2+(5-15)2-822×(5+15)×(5-15)=45, 且∠F 1PF 2是三角形的内角,于是sin ∠F 1PF 2=35. 因此△PF 1F 2的面积S =12|PF 1|·|PF 2|sin ∠F 1PF 2=12×(5+15)×(5-15)×35=3. 8.一动圆与直线x =-1相切且始终过点(1,0),动圆的圆心的轨迹为曲线C ,那么曲线C 上的一点到直线x =-1的间隔 与到直线x +y +4=0的间隔 和的最小值为( )A. 2B.522C.423D.722考点 抛物线的定义题点 由抛物线定义求最值答案 B解析 由题意知动圆的圆心轨迹为以F (1,0)为焦点,直线x =-1为准线的抛物线,其方程为y 2=4x ,设抛物线上的一点P ,点P 到直线x =-1的间隔 为d 1,到直线x +y +4=0的间隔 为d 2, 由抛物线的定义知,d 1=|PF |,所以d 1+d 2=|PF |+d 2,|PF |+d 2的最小值为点F 到直线x +y +4=0的间隔 |1+4|2=522.应选B. 二、填空题9.双曲线x 2m -y 2n=1(mn ≠0)的离心率为2,有一个焦点与抛物线y 2=4x 的焦点重合,那么mn 的值为________.考点 抛物线的简单性质题点 抛物线与其他曲线结合有关问题答案 316 解析 抛物线y 2=4x 的焦点坐标为(1,0),那么双曲线的焦距为2,那么有⎩⎪⎨⎪⎧m +n =1,1m =4, 解得⎩⎨⎧ m =14,n =34,∴mn =316. 10.双曲线x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线与抛物线y 2=2px (p >0)的准线分别交于A ,B 两点,O 为坐标原点.假设双曲线的离心率为2,△AOB 的面积为3,那么p =________. 考点 抛物线的简单性质题点 抛物线与其他曲线结合有关问题答案 2解析 双曲线的离心率e =c a =a 2+b 2a =2, 解得b a =3,联立⎩⎨⎧ y =-b a x ,x =-p 2,得y =bp 2a, 所以S △OAB =p 2×bp 2a =3, 将b a=3代入解得p =2. 11.抛物线y 2=8x ,过动点M (a,0),且斜率为1的直线l 与抛物线交于不同的两点A ,B ,假设|AB |≤8,那么实数a 的取值范围是________.考点 直线与抛物线的位置关系题点 直线与抛物线相交时的其他问题答案 (-2,-1]解析 将l 的方程y =x -a 代入y 2=8x ,得x 2-2(a +4)x +a 2=0,那么Δ=4(a +4)2-4a 2>0,∴a >-2.设A (x 1,y 1),B (x 2,y 2),那么x 1+x 2=2(a +4),x 1x 2=a 2,∴|AB |=2[(x 1+x 2)2-4x 1x 2]=64(a +2)≤8,即a +2≤1.又a >-2,∴-2<a ≤-1.三、解答题12.双曲线的一条渐近线为x +3y =0,且与椭圆x 2+4y 2=64有一样的焦距,求双曲线的标准方程.解 椭圆方程为x 264+y 216=1,可知椭圆的焦距为8 3. ①当双曲线的焦点在x 轴上时,设双曲线方程为x 2a 2-y 2b 2=1 (a >0,b >0), ∴⎩⎪⎨⎪⎧a 2+b 2=48,b a =33,解得⎩⎪⎨⎪⎧ a 2=36,b 2=12. ∴双曲线的标准方程为x 236-y 212=1. ②当双曲线的焦点在y 轴上时, 设双曲线方程为y 2a 2-x 2b2=1 (a >0,b >0), ∴⎩⎪⎨⎪⎧ a 2+b 2=48,a b =33, 解得⎩⎪⎨⎪⎧a 2=12,b 2=36. ∴双曲线的标准方程为y 212-x 236=1. 由①②可知,双曲线的标准方程为 x 236-y 212=1或y 212-x 236=1. 13.斜率为k 的直线l 经过抛物线y =14x 2的焦点F ,且与抛物线相交于A ,B 两点,假设线段|AB |的长为8.(1)求抛物线的焦点F 的坐标和准线方程;(2)求直线的斜率k .考点 抛物线的焦点弦问题题点 与焦点弦有关的其他问题解 (1)化y =14x 2为标准方程x 2=4y ,由此,可知抛物线的焦点F 的坐标为(0,1),准线方程为y =-1.(2)设A (x 1,y 1),B (x 2,y 2),由抛物线的定义知|AF |=y 1+1,|BF |=y 2+1,于是|AB |=y 1+y 2+2,又|AB |=8,所以y 1+y 2=6,由(1)得,抛物线的焦点为(0,1),所以直线l 的方程为y =kx +1,所以kx 1+1+kx 2+1=6,k (x 1+x 2)=4,由直线l 的方程与抛物线方程联立得kx +1=x 24, 即x 2-4kx -4=0,Δ=16k 2+16>0,所以x 1+x 2=4k ,代入k (x 1+x 2)=4,得k 2=1,k =±1.四、探究与拓展14.假设抛物线y 2=x 上两点A (x 1,y 1),B (x 2,y 2)关于直线y =x +b 对称,且y 1y 2=-1,那么实数b 的值为( )A .-3B .3C .2D .-2 考点 直线与抛物线的位置关系题点 直线与抛物线相交时的其他问题答案 D解析 由题意知,y 1-y 2x 1-x 2=-1, ∴y 1-y 2y 21-y 22=-1,那么y 1+y 2=-1,∵y 1y 2=-1,∴x 1+x 2=y 21+y 22=(y 1+y 2)2-2y 1y 2=3, ∴两点A (x 1,y 1),B (x 2,y 2)中点坐标为⎝⎛⎭⎫32,-12,代入y =x +b ,可得b =-2. 15.如图,△AOB 的一个顶点为抛物线y 2=2x 的顶点O ,A ,B 两点都在抛物线上,且∠AOB =90°,(1)证明:直线AB 必过一定点;(2)求△AOB 面积的最小值.考点 直线与抛物线的位置关系题点 直线与抛物线相交时的其他问题(1)证明 设OA 所在直线的方程为y =kx (k ≠0),那么直线OB 的方程为y =-1kx , 由⎩⎪⎨⎪⎧ y =kx ,y 2=2x ,解得⎩⎪⎨⎪⎧ x =0,y =0或⎩⎨⎧ x =2k 2,y =2k ,即A 点的坐标为⎝⎛⎭⎫2k 2,2k . 同样由⎩⎪⎨⎪⎧y =-1k x ,y 2=2x ,解得B 点的坐标为(2k 2,-2k ). 所以AB 所在直线的方程为y +2k =2k +2k 2k 2-2k 2(x -2k 2), 化简并整理,得⎝⎛⎭⎫1k -k y =x -2.不管实数k 取任何不等于0的实数,当x =2时,恒有y =0.故直线过定点P (2,0).(2)解 由于AB 所在直线过定点P (2,0),所以可设AB 所在直线的方程为x =my +2,A (x 1,y 1),B (x 2,y 2). 由⎩⎪⎨⎪⎧ x =my +2,y 2=2x ,消去x 并整理, 得y 2-2my -4=0,Δ=4m 2+16>0.所以y 1+y 2=2m ,y 1y 2=-4.于是|y 1-y 2|=(y 1-y 2)2 =(y 1+y 2)2-4y 1y 2=4m 2+16 =2m 2+4.S△AOB=12×|OP|×(|y1|+|y2|)=12|OP|·|y1-y2|=12×2×2m2+4=2m2+4.所以当m=0时,△AOB的面积获得最小值4.。
滚动训练三(§5~§6)一、选择题1.下列命题正确的是()A.两两相交的三条直线可确定一个平面B.两个平面与第三个平面所成的角都相等,则这两个平面一定平行C.过平面外一点的直线与这个平面只能相交或平行D.和两条异面直线都相交的两条直线一定是异面直线考点异面直线的判定题点异面直线的判定答案 C解析对于A,两两相交的三条直线可确定一个平面或三个平面,故A错误;对于B,两个平面与第三个平面所成的角都相等,则这两个平面平行或相交,故B错误;对于C,过平面外一点的直线一定在平面外,且直线与这个平面相交或平行,故C正确;对于D,和两条异面直线都相交的两条直线是异面直线或共面直线,故D错误.故选C.2.设X,Y,Z是空间不同的直线或平面,对下面四种情形,使“X⊥Z且Y⊥Z⇒X∥Y”为真命题的是()①X,Y,Z是直线;②X,Y是直线,Z是平面;③Z是直线,X,Y是平面;④X,Y,Z是平面.A.①②B.①③C.③④D.②③考点线、面平行、垂直的综合应用题点平行与垂直的判定答案 D解析对于①,X,Y,Z是直线,“X⊥Z且Y⊥Z⇒X∥Y”是假命题,如正方体共顶点的三条棱;对于②,X,Y是直线,Z是平面,“X⊥Z且Y⊥Z⇒X∥Y”是真命题,根据线面垂直的性质定理可知正确;对于③,Z是直线,X,Y是平面,“X⊥Z且Y⊥Z⇒X∥Y”是真命题,根据垂直于同一直线的两个平面平行,故正确;对于④,X ,Y ,Z 是平面,“X ⊥Z 且Y ⊥Z ⇒X ∥Y ”是假命题,如正方体共顶点的三个面.故选D.3.已知m ,n 表示两条不同的直线,α,β表示两个不同的平面,则下列说法正确的是( ) A .若m α,α⊥β,则m ⊥βB .若mα,n α,m ∥β,n ∥β,则α∥βC .若α⊥β,m ⊥β,则m ∥αD .若m ⊥α,m ∥β,则α⊥β 考点 线、面平行、垂直的综合应用 题点 平行与垂直的判定 答案 D解析 由m ,n 表示两条不同的直线,α,β表示两个不同的平面知,在A 中,若m α,α⊥β,则m 与β相交、平行或m β,故A 错误; 在B 中,若m α,n α,m ∥β,n ∥β,则α与β相交或平行,故B 错;在C 中,若α⊥β,m ⊥β,则m ∥α或mα,故C 错误;在D 中,若m ⊥α,m ∥β,则由面面垂直的判定定理得α⊥β,故D 正确. 4.正四棱锥P -ABCD 的底面积为3,体积为22,E 为侧棱PC 的中点,则P A 与BE 所成的角为( )A .30°B .60°C .45°D .90° 考点 异面直线所成的角 题点 求异面直线所成的角 答案 B解析 过顶点作垂线,交底面于正方形对角线的交点O ,连接OE ,∵正四棱锥P -ABCD 的底面积为3,体积为22, ∴PO =22,AB =3,AC =6,P A =2,OB =62,∵OE 与P A 在同一平面且是△P AC 的中位线, ∴OE ∥P A 且OE =12P A ,∴∠OEB 即为P A 与BE 所成的角,OE =22, 在Rt △OEB 中,tan ∠OEB =OBOE=3, ∴∠OEB =60°. 故选B.5.如图,ABCD -A 1B 1C 1D 1为正方体,下面结论:①BD ∥平面CB 1D 1;②AC 1⊥BD ;③AC 1⊥平面CB 1D 1;④直线B 1D 1与BC 所成的角为45°.其中正确结论的个数为( )A .4B .3C .2D .1考点 线、面平行、垂直的综合应用 题点 平行与垂直的判定 答案 A解析 在①中,由正方体的性质,得BD ∥B 1D 1, 又BD 平面CB 1D 1,B 1D 1平面CB 1D 1, ∴BD ∥平面CB 1D 1,故①正确;在②中,由正方体的性质得AC ⊥BD ,CC 1⊥BD , 又AC ∩CC 1=C ,AC ,CC 1平面ACC 1,∴BD ⊥平面ACC 1, ∴AC 1⊥BD ,故②正确;在③中,由正方体的性质得BD ∥B 1D 1, 由②知,AC 1⊥BD ,∴AC 1⊥B 1D 1, 同理可证AC 1⊥CB 1,∴AC1⊥平面CB1D1内的两条相交直线,∴AC1⊥平面CB1D1,故③正确;在④中,异面直线B1D1与BC所成的角就是直线BC与BD所成的角,故∠CBD为异面直线B1D1与BC所成的角,在等腰直角△BCD中,∠CBD=45°,故直线B1D1与BC所成的角为45°,故④正确.故选A.6.如图所示,已知六棱锥P ABCDEF的底面是正六边形,P A⊥平面ABC,P A=2AB,则下列结论正确的是()A.PB⊥ADB.平面P AB⊥平面PBCC.直线BC∥平面P AED.直线PD与平面ABC所成的角为45°考点线、面平行、垂直的综合应用题点平行与垂直的判定答案 D解析∵P A⊥平面ABC,∴∠ADP是直线PD与平面ABC所成的角.∵六边形ABCDEF是正六边形,∴AD=2AB,即tan∠ADP=P AAD=2AB2AB=1,∴直线PD与平面ABC所成的角为45°,故选D.7.在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为矩形,AB=2BC,E是CD上一点,若AE ⊥平面PBD ,则CEED的值为( )A.32B.52C .3D .4 考点 线、面平行、垂直的综合应用 题点 平行与垂直的计算与探索性问题 答案 C解析 ∵PD ⊥底面ABCD ,AE 底面ABCD , ∴PD ⊥AE ,当AE ⊥BD 时,AE ⊥平面PBD ,此时△ABD ∽△DAE , 则AB AD =AD DE, ∵AB =2BC , ∴DE =14AB =14DC ,∴CEED=3. 故选C.8.边长为2的正三角形ABC 中,D ,E ,M 分别是AB ,AC ,BC 的中点,N 为DE 的中点,将△ADE 沿DE 折起至△A ′DE 的位置,使A ′M =62.设MC 的中点为Q ,A ′B 的中点为P ,给出下列四个结论:①A ′N ⊥平面BCED ;②NQ ∥平面A ′EC ;③DE ⊥平面A ′MN ;④平面PMN ∥平面A ′EC . 以上结论正确的是( ) A .①②④ B .②③④ C .①②③D .①③④考点 线、面平行、垂直的综合应用 题点 平行与垂直的判定 答案 C解析 由题意可知MN 与CE 在同一平面内且不平行,所以MN 与CE 一定有交点,即平面PMN 与平面A ′EC 有交线,④错误,故选C.二、填空题9.二面角α-l-β为60°,异面直线a,b分别垂直于α,β,则a与b所成角的大小是________.考点空间角题点空间角的综合应用答案60°解析过直线a上一点作b的平行线b′,则根据二面角的定义和线面垂直的性质可知,a与b′的夹角为60°,所以a与b所成角的大小是60°.10.如图,两个正方形ABCD和ADEF所在平面互相垂直,设M,N分别是BD和AE的中点,那么①AD⊥MN;②MN∥平面CDE;③MN∥CE;④MN,CE异面,其中正确结论的序号是________.考点线、面平行、垂直的综合应用题点平行与垂直的判定答案①②③解析∵两个正方形ABCD和ADEF所在平面互相垂直,设M,N分别是BD和AE的中点,取AD的中点G,连接MG,NG,易得AD⊥平面MNG,进而得到AD⊥MN,故①正确;连接AC,CE,根据三角形中位线定理,可得MN∥CE,由线面平行的判定定理,可得②MN∥平面CDE及③MN∥CE正确,④MN,CE异面错误.11.我们将一个四面体四个面中直角三角形的个数定义为此四面体的直度,在四面体ABCD中,AD ⊥平面ABC ,AC ⊥BC ,则四面体ABCD 的直度为________. 考点 空间中的垂直问题 题点 空间中的垂直问题 答案 4解析 ∵在四面体ABCD 中,AD ⊥平面ABC , ∴AD ⊥AB ,AD ⊥AC ,AD ⊥BC , ∵AC ⊥BC ,AC ∩AD =A , ∴BC ⊥平面ACD ,∴BC ⊥CD ,∴四面体ABCD 的四个面均为直角三角形, ∴四面体ABCD 的直度为4. 三、解答题12.如图,已知△ABC 是正三角形,EA ,CD 都垂直于平面ABC ,且EA =AB =2a ,DC =a ,F 是BE 的中点,求证:(1)FD ∥平面ABC ; (2)AF ⊥平面EDB .考点 线、面平行、垂直的综合应用 题点 平行、垂直综合问题的证明 证明 取AB 的中点M ,连接FM ,MC .(1)∵F ,M 分别是BE ,BA 的中点, ∴FM ∥EA ,FM =12EA =a .∵EA ,CD 都垂直于平面ABC ,∴CD∥EA,∴CD∥FM.又∵DC=a,∴FM=DC,∴四边形FMCD是平行四边形,∴FD∥MC.∵FD⊈平面ABC,MC平面ABC,∴FD∥平面ABC.(2)∵M是AB的中点,△ABC是正三角形,∴CM⊥AB.又∵AE⊥平面ABC,CM平面ABC,∴CM⊥AE,又∵AB∩AE=A,AB,AE平面EAB,∴CM⊥平面EAB,又AF平面EAB,∴CM⊥AF.又∵CM∥FD,∴FD⊥AF.∵F是BE的中点,EA=AB,∴AF⊥BE.又∵FD∩BE=F,FD,BE平面EDB,∴AF⊥平面EDB.13.如图所示,已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,求证:PQ∥平面CBE.考点 直线与平面平行的判定 题点 直线与平面平行的证明证明 作PM ∥AB 交BE 于点M ,作QN ∥AB 交BC 于点N ,连接MN ,则PM ∥QN ,∴PM AB =EP EA ,QN CD =BQBD .∵AP =DQ ,∴EP =BQ .又∵AB =CD ,EA =BD ,∴PM =QN . ∴四边形PMNQ 是平行四边形,∴PQ ∥MN .∵PQ ⊈平面CBE ,MN 平面CBE ,∴PQ ∥平面CBE . 四、探究与拓展14.已知m ,n 是两条不重合的直线,a ,b 分别垂直于两个不重合的平面α,β,有以下四个命题:①若m ⊥a ,n ∥b ,且α⊥β,则m ∥n ;②若m ∥a ,n ∥b ,且α⊥β,则m ⊥n ;③若m ∥a ,n ⊥b 且α∥β,则m ⊥n ;④若m ⊥a ,n ⊥b ,且α∥β,则m ∥n .其中真命题的序号是________. 考点 线、面平行、垂直的综合应用 题点 平行与垂直的判定 答案 ②③解析 ①中m ,n 不一定平行,还可能相交或异面;④中m ,n 不一定平行,还可能异面或相交.15.如图所示,P A ⊥矩形ABCD 所在的平面,M ,N 分别是AB ,PC 的中点.(1)求证:MN ∥平面P AD ; (2)求证:MN ⊥CD ;(3)若∠PDA =45°,求证:MN ⊥平面PCD .证明 (1)如图所示,取PD 的中点E ,连接AE ,EN ,则有EN ∥CD ,EN =12CD ,又AM ∥CD ,AM =12CD ,∴EN ∥AM ,且EN =AM . ∴四边形AMNE 是平行四边形, ∴MN ∥AE .∵AE 平面P AD ,MN 平面P AD , ∴MN ∥平面P AD .(2)∵P A ⊥平面ABCD ,∴P A ⊥AB .又AD ⊥AB ,P A ∩AD =A ,P A ,AD 平面P AD , ∴AB ⊥平面P AD . 又∵AE 平面P AD , ∴AB ⊥AE ,又AE ∥MN , ∴AB ⊥MN ,又CD ∥AB , ∴MN ⊥CD .(3)∵P A ⊥平面ABCD ,∴P A ⊥AD . 又∠PDA =45°,E 是PD 的中点, ∴AE ⊥PD ,即MN ⊥PD .又MN ⊥CD ,CD ∩PD =D ,CD ,PD 平面PCD , ∴MN ⊥平面PCD .。