几何不变体系

几何不变体系原则几何不变体系原则是几何学的一个基本概念，用来描述物体在变化中保持几何形态和关系的性质。

它可以用来解释许多物理和数学中的问题，也是很多科学和工程领域的基础概念。

本文将详细介绍几何不变体系原则的基本概念和应用。

几何不变体系原则指的是在空间中一个对象的几何性质在变换之后保持不变。

这种不变性可以通过旋转、平移和缩放等操作来实现。

几何不变性的基本思想是，一个物体的形状和位置可以通过一系列几何变换来描述，并且这些变换不会改变物体的几何性质。

换句话说，无论如何改变一个物体的形状和位置，其几何关系都会保持不变。

几何不变体系原则的应用非常广泛。

在数学中，它被用来推导和证明几何定理。

在物理中，它被用来描述物体运动和相互作用的几何性质。

在计算机图形学中，它被用来实现图像的变换和处理。

在工程中，它被用来设计和分析各种结构和系统。

1.形状不变性：几何不变体系原则的最基本特点是对象的形状在几何变换之后保持不变。

例如，一个正方形经过旋转和缩放后仍然是一个正方形，只是大小和位置可能发生了变化。

这种形状不变性是几何不变体系原则的核心概念。

2.位置不变性：几何不变体系原则还要求对象的位置在几何变换之后保持不变。

例如，一个圆经过平移和旋转后仍然在原来的位置上，只是方向和位置可能发生了变化。

这种位置不变性是几何不变体系原则的另一个重要特点。

3.比例不变性：几何不变体系原则还要求对象的比例在几何变换之后保持不变。

例如，一个矩形经过缩放和旋转后仍然是一个矩形，只是长度和宽度可能发生了变化。

这种比例不变性是几何不变体系原则的另一个关键特点。

几何不变体系原则的应用可以通过各种几何变换来实现。

最常见的几何变换包括旋转、平移和缩放。

旋转是指将一个对象绕一个固定的点旋转一定角度，使对象的形状和位置发生变化。

平移是指将一个对象沿着一个固定的方向移动一定距离，使对象的位置发生变化但形状不变。

缩放是指将一个对象按照一个比例因子改变其尺寸，使对象的大小发生变化但形状和位置不变。

几何不变体系的组成规则包括几何不变体系是理解自然界和计算机图形学的重要工具，它用以描述不同的对象的几何特征的抽象，其中的对象可以是几何图形也可以是多维数据集。

下面介绍一下几何不变体系的组成规则：第一，几何不变体系是由不变性函数强加在几何形状上的。

不变性函数是用来表示不同尺度的不变性特征的函数，它可以包括质心不变性、形状不变性、大小不变性、方向不变性、对称不变性和角度不变性等特性。

这些不变性函数确保不同尺度的几何形状始终保持某些不变的特征，因此能够有效的描述几何图形的不变性。

第二，几何不变体系的组成规则还包括特征提取器。

特征提取器是用来提取不变性特征的函数，它可以包括边界跟踪提取器、最小二乘曲线提取器、三维孔洞提取器、绘图提取器、平面提取器、多边形提取器、点云提取器等。

第三，几何不变体系的组成规则还包括匹配器。

匹配器是一种用来判断两个几何形状之间是否存在相似度的函数，它可以使用不同的算法，如 Hausdorff距离法、K-means聚类算法、SIFT（Scale Invariant Feature Transform）特征检测算法等，来计算两个几何形状之间的相似度。

第四，几何不变体系的组成规则还包括识别器。

识别器是一种用来将几何形状识别为精确的实例的函数，它使用匹配器计算出的相似度作为输入，根据输入的几何形状的特征来识别对应的实例，从而可以准确的将几何形状识别出来。

以上就是几何不变体系的组成规则，它包括不变性函数、特征提取器、匹配器和识别器四部分。

不变性函数用于提取几何图形的不变性特征，特征提取器用于提取不变性特征，匹配器用于判断两个几何形状之间的相似度，而识别器用于将几何形状识别为精确的实例。

这样，几何不变体系的组成规则既能描述几何形状的不变性，又能够准确的识别几何图形，从而有效的捕捉几何形状的精细特征，为计算机图形学的研究提供了一种有效的手段。

几何不变体系的简单组成规则
几何不变体系是指一类具有几何性质不变的变换组合，其组成规则可以简化为以下几点：
1. 平移不变性：任何平移对几何体的性质不产生变化。

平移是指将几何体的每个点沿着同一方向移动相同距离而保持原始形状不变。

2. 旋转不变性：任何旋转对几何体的性质不产生变化。

旋转是指将几何体绕着一个固定的点旋转一定角度而保持原始形状不变。

3. 缩放不变性：任何等比例的缩放对几何体的性质不产生变化。

缩放是指将几何体的每个点按照相同比例放大或缩小而保持原始形状不变。

4. 对合不变性：任何对合操作下几何体的性质不产生变化。

对合是指对几何体的两个操作进行反向操作，如顺时针旋转和逆时针旋转。

5. 反射不变性：任何对称操作不改变几何体的性质。

反射是指将几何体沿着一个对称轴折叠而保持原始形状不变。

根据这些规则，可以构建一系列几何变换操作，通过不同的变换组合来产生不同的几何不变体系。

这些简单的规则可以用来描述和理解许多几何问题和模式。

几何不变体系的基本组成规则
几何不变体系是一种表征物体或几何空间重要特征的一般化空间变换方式，包括轴对称、对称翻转、镜像反转和旋转等。

它是建立在几何变换理论上，为不同对象提供了统一
的描述，它可以将一系列具有相同几何形状的物体（诸如多胞体、细胞、植物、微生物等）联系起来，比如可以将相同的多面体定义成同一个物体的不同形状，以及把特定的空间位
置变换为另一个不同的空间位置。

也就是说，几何不变体系可以将某些特定物体的形状改
变而构建出几何变换模型。

首先，几何变换的结果（简称目标）必须与被变换的研究对象（简称源）具有相同的
几何形状和空间位置，即几何形状保持不变。

其次，在不同的空间轴上，几何变换的向量必须与原向量相同，以保持目标图形的方
向一致性。

此外，一个几何变换是旋转不变的，遵循“几何变换后，所有物体子集之间的距离和
角度不变”的原则。

最后，几何变换是完全对称的，它会最大限度地保持目标图形与源图形之间的相似程度。

以上是几何不变体系的基本组成规则。

几何变换是用来表达一个物体的一般几何空间
变换方式，在许多领域都有重要的应用，比如计算机图形学、数学建模、生物学、地理学中。

几何变换的基本规则提供了一个统一的框架，为特定的对象或空间位置提供了统一的
描述，有助于提高计算机模型的准确性和精确性，同时还为微量模型的研究奠定基础。

几何不变体系的两刚片规则1.引言1.1 概述几何不变体系是一种在几何学中应用的重要概念。

它指的是在特定条件下，某些物体或者形状的一些关键性质在变换过程中保持不变的情况。

通过研究几何不变体系，我们能够深入理解形状和物体变换的规律，从而探索出更多的相关性质和应用。

在本篇长文中，我们将关注两刚片规则这一几何不变体系，并详细讨论其相关性质和应用。

两刚片规则是在刚性变换下保持不变的几何体系。

所谓刚性变换，指的是保持形状和大小不变的平移、旋转和镜像等变换方式。

而两刚片规则，则是在进行刚性变换后，两个刚片之间的相对位置和角度保持不变。

本文将系统地介绍两刚片规则的定义、性质和证明过程，并通过一系列实例和应用案例来解释其实际意义和应用价值。

我们将探讨两刚片规则在几何学、机械工程、建筑设计等领域的应用，以及如何利用这一规则进行问题的求解和优化。

了解和掌握两刚片规则对于我们深入理解刚体变换和几何形状的变化具有重要意义。

通过运用两刚片规则，我们可以更加精准地描述和分析物体的运动和形变，为相关领域的研究和应用提供有效的工具和方法。

本文将为读者提供一个全面的概述和指导，帮助读者更好地理解和应用两刚片规则。

1.2 文章结构文章结构：本文主要包含三个部分：引言、正文和结论。

引言部分主要对文章的背景和意义进行概述，介绍几何不变体系的研究背景及其在实际应用中的重要性。

同时，该部分还会描述文章的整体结构，以帮助读者了解文章的组成部分和内容安排。

正文部分是文章的核心部分，包含两个要点。

第一个要点将详细介绍几何不变体系的概念和基本原理，并探讨其在实际问题中的应用。

通过具体的例子和分析，阐述几何不变体系在解决问题时的有效性和可行性。

第二个要点将扩展和深化第一个要点的内容，进一步阐述几何不变体系的两刚片规则。

详细解释两个刚片规则的定义和作用，并结合实际案例进行说明。

通过对两刚片规则的深入讨论，读者可以更好地理解几何不变体系的运作机制和优势所在。

几何不变体系的简单组成规则1. 引言几何不变体系是一种研究几何对象不随变换而改变的性质和规则的数学体系。

在这个体系中，我们通过定义一些基本的变换和一些不变量来描述几何对象的性质。

本文将介绍几何不变体系的简单组成规则，包括基本变换、不变量的定义和应用。

2. 基本变换在几何不变体系中，我们定义了一些基本的变换，这些变换可以改变几何对象的位置、形状和方向。

以下是几个常见的基本变换：2.1 平移变换平移变换是将几何对象沿着指定的方向移动一定的距离，而不改变其形状和方向。

平移变换可以用一个向量来表示，向量的大小和方向表示移动的距离和方向。

2.2 旋转变换旋转变换是将几何对象围绕某个点旋转一定的角度，而不改变其形状和大小。

旋转变换可以用一个角度来表示，角度的正负和大小表示旋转的方向和角度。

2.3 缩放变换缩放变换是将几何对象按照比例因子在各个方向上进行放大或缩小，而不改变其形状和方向。

缩放变换可以用一个比例因子来表示，比例因子大于1表示放大，小于1表示缩小。

2.4 对称变换对称变换是将几何对象围绕某个轴或点进行镜像对称，而不改变其形状和方向。

对称变换可以用一个轴或点来表示，轴表示沿着轴进行镜像对称，点表示围绕点进行镜像对称。

3. 不变量的定义在几何不变体系中，不变量是指在变换下保持不变的性质或规则。

不变量是描述几何对象的重要特征，可以用来判断几何对象是否相似或相等。

以下是几个常见的不变量：3.1 长度长度是指两点之间的距离，是一个几何对象的基本属性。

在平移变换下，长度保持不变。

3.2 角度角度是指两条线段之间的夹角，是一个几何对象的重要特征。

在旋转变换下，角度保持不变。

3.3 面积面积是指一个几何对象所占据的平面区域的大小，是一个几何对象的重要特征。

在缩放变换下，面积按比例因子的平方改变。

3.4 对称性对称性是指一个几何对象具有的镜像对称或旋转对称的性质。

在对称变换下，对称性保持不变。

4. 不变量的应用不变量在几何不变体系中有广泛的应用，可以用来解决各种几何问题。

几何不变体系的三个基本组成规则
几何不变体系（Geometric Invariance System）指的是一种几何性质在变换下保持不变的规则或原则。

在数学中，有三个基本组成规则构成了几何不变体系，它们是：
尺度不变性（Scale Invariance）：
尺度不变性指的是几何形状在尺度变换下保持不变。

当进行等比例缩放时，形状的大小会改变，但其相似性质保持不变。

这意味着图形的所有尺寸会按照相同的比例进行缩放。

例如，将一幅图形按照2：1的比例放大，无论是边长、角度还是形状的比例关系都保持不变。

旋转不变性（Rotation Invariance）：
旋转不变性表明几何形状在旋转变换下保持不变。

无论将几何图形以何种角度旋转，其性质不随着旋转而改变。

在平面几何中，若一幅图形经过旋转后能够重合于原始图形，则它具有旋转不变性。

平移不变性（Translation Invariance）：
平移不变性表示几何图形在平移变换下保持不变。

这意味着将图形在平面上沿着某个方向移动，但形状和大小保持不变。

换句话说，图形的位置改变，但其形状和性质不受影响。

这三个基本组成规则构成了几何不变体系的核心，使得我们能够在变换下保持对几何形状性质的观察和研究，无论是缩放、旋转还是平移，形状的性质都保持恒定。

请简述几何不变体系的俩刚片规则。

一致性是指在一种几何形状变换中，它保持不变的特性，即对象的相对长度和形状保持不变。

例如，当平行线移动时，它的相对距离仍然保持不变。

因此，一致性是指形状变换的可比性，它使得基本形状保持不变。

另一个规则是对称性，即形状变换的可对称性。

对称性的意思是，其中的几何形状变换可以通过旋转、缩放或移动来反转形状，但是它保持原来的形状。

例如，圆形可以旋转180度，但其形状仍然保持不变。

因此，对称性指几何变换中任何形状的可逆变换，它们可以与原始形状保持相同。

几何不变体系的这两个主要规则为几何学提供了基本的结构，使它能够更准确地表达形状变换的规律性。

通过一致性和对称性的规律，几何可以更自然地描述几何形状变换的规律，而不需要像以往那样依赖于实际形状的绘制。

几何不变体系的这两个规则也使得几何学更容易地与其他领域
的学科相结合，从而给出几何中变换规律的精确描述。

比如，几何不变体系可以用来帮助计算机科学家研究图形学，以有效地描述几何形状的变换。

另外，它还可以应用到物理学和化学等领域中，帮助科学家更好地了解宇宙中构成物质的变化规律。

总之，几何不变体系以其两个主要规则一致性和对称性，为几何学提供了一个基本的结构，以帮助科学家们准确描述几何形状变换中的规律性，并且可以将其应用到其他学科中，以更好地了解宇宙的结
构和变化规律。

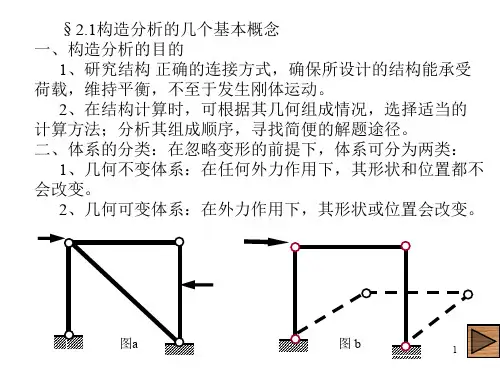
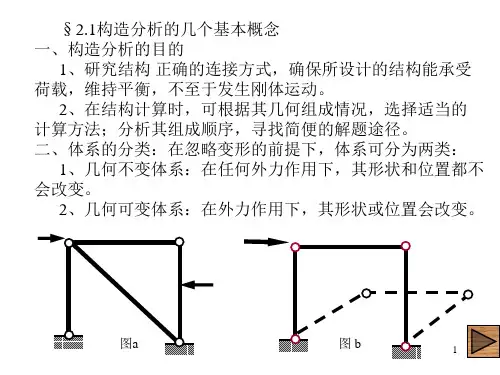
［几何可变体系与几何不变体系］几何可变体系——在任意荷载的作用下，即使不考虑材料的应变，它的形状和位置也是可以改变的。

几何不变体系——如果不考虑材料的应变，它的形状和位置是不能改变的。

［机动分析的目的］（1）判断体系是否可变；（2）研究不变体系的基体组成规律；（3）确定结构的静定次数；（4）进行组成分析，选择简单的计算次序。

［自由度与刚片］物体在运动时决定其位置的几何参变数称为自由度。

几何形状不变的平面体称为刚片。

一个刚片在平面内运动有三个自由度；一个点在平面内运动有两个自由度；一个点在空间内运动有三个自由度；一个刚体在空间内运动有六个自由度。

［约束］减少自由度的装置称为约束。

［约束的影响］（1）支座约束可动铰支座相当于一个约束，减少一个自由度；固定铰支座相当于两个约束，减少两个自由度；固定端支座相当于三个约束，减少三个自由度；定向支座相当于两个约束，减少两个自由度。

（2）链杆两刚片加一链杆约束，减少一个自由度。

（3）铰结点单铰：两刚片加一单铰结点约束，减少两个自由度。

复铰：个刚片在同一点用铰连接，相当于个单铰的约束。

（4）刚结点单刚结点：两刚片加一刚结点约束，减少三个自由度。

复刚结点：个刚片在同一点用刚结点连接，相当于个单刚结点的约束。

［结构体系自由度的计算公式］（1）一般公式各部件自由度总和－全部约束数为结构体系自由度。

（2）平面杆件体系自由度的计算公式式中为刚片个数；为单刚结点个数；为单铰结点个数；为链杆个数；为支座约束个数，如果为自由体，即无支座约束，则。

（3）平面桁架自由度的计算公式式中为结点个数；为链杆个数；为支座约束个数，如果为自由体，即无支座约束，则。

［自由度与几何不变性的关系］体系为几何不变的必要条件是自由度等于或小于零，此条件并非充分条件。

如果，则体系为几何可变体系；如果或，则不能确定。

几何不变体系的简单组成规则1.平移：平移是最基本的几何变换之一，它将图形的每个点都沿着相同方向和距离移动。

在几何不变体系中，平移被定义为一个不变操作，即它不会改变图形的任何性质。

2.旋转：旋转是将图形围绕一个固定点旋转一定角度的变换。

在几何不变体系中，旋转也是一个不变操作，即它保持图形的性质不变。

旋转可以通过矩阵运算或使用复数表示来描述。

3.缩放：缩放是通过改变图形的大小来进行的几何变换。

在几何不变体系中，缩放也是一个不变操作。

缩放可以被定义为一个矩阵运算，其中图形的每个顶点都乘以一个比例因子。

4.对称：对称是通过翻转图形的一部分来进行的几何变换。

在几何不变体系中，对称也是一个不变操作。

对称可以沿着一个直线或一个点进行。

5.直线和圆：直线和圆是几何不变体系中最基本的图形元素。

直线可以通过两个点确定，而圆可以通过一个点和一个距离确定。

在几何不变体系中，直线和圆的性质是不变的，即它们保持不变。

6.平行：平行是直线之间没有交点的关系。

在几何不变体系中，平行性质是不变的，即无论如何进行几何变换，平行直线仍然保持平行。

7.垂直：垂直是直线之间成90度角的关系。

在几何不变体系中，垂直性质也是不变的，即无论如何进行几何变换，垂直直线仍然保持垂直。

8.角度：角度描述了两条线之间的旋转关系。

在几何不变体系中，角度保持不变，即无论如何进行几何变换，两条线之间的角度不会改变。

9.面积和体积：面积和体积描述了图形和物体的大小。

在几何不变体系中，面积和体积也是不变的，即无论如何进行几何变换，图形和物体的面积和体积保持不变。

10.拓扑性质：拓扑性质描述了空间中点、线、面之间的连接关系。

在几何不变体系中，拓扑性质是不变的，即无论如何进行几何变换，点、线、面之间的连接关系保持不变。

总结起来，几何不变体系由一系列的组成规则组成，例如平移、旋转、缩放、对称等操作，以及基本的几何图形元素如直线、圆等，以及几何性质如平行、垂直、角度、面积和体积、拓扑性质等。

请简述几何不变体系的两刚片规则
几何不变体系的两刚片规则是关于刚片运动的基本法则。

这两个规则分别是刚片的点转动规则和平面运动规则。

1. 点转动规则：刚片上的任意一点，其运动轨迹是一个固定的圆。

这个圆称为该点的转动圆，其圆心位于刚片上的固定点，称为转动中心。

无论刚片做何种位移和姿态变化，处于同一点的转动圆轨迹半径始终不变，相对于转动中心的角速度也始终相等。

2. 平面运动规则：刚片上的所有点都在平面内运动。

无论刚片做何种位移和姿态变化，刚片上的任意一点始终保持在一个平面内运动。

这个平面称为刚片的运动平面。

这两个规则是几何不变体系的基础，用于描述刚片的运动和姿态变化。

无论刚片的形状如何复杂，只要满足这两个基本规则，就可以应用几何不变体系进行分析和计算。

名词解释几何不变体系
几何不变体系是结构力学中的基本概念，它描述了在力的作用下不发生刚体位移或转动的体系。

这种体系的稳定性和安全性在建筑、桥梁等工程领域中具有至关重要的作用。

几何不变体系通过合理配置杆件和节点，能够有效地抵抗外部载荷的作用，维持结构的稳定性。

在几何不变体系中，各个杆件通过节点连接，形成一个整体的结构。

这些杆件可以是直线、曲线、梁、柱等，而节点则起到连接和传递力的作用。

根据杆件和节点的不同特性，几何不变体系可以分为无多余约束的几何不变体系和有多余约束的几何不变体系。

无多余约束的几何不变体系是指体系中所有的约束都是必要的，没有多余的约束；有多余约束的几何不变体系则是指体系中存在一些多余的约束，这些约束在某些情况下可以用来平衡外部载荷或提供稳定性。

节点的类型也会影响几何不变体系的性能。

节点可以分为刚性节点、柔性节点和半刚性节点等类型。

刚性节点是指连接处不能发生相对位移或转动的节点；柔性节点则是指连接处可以发生相对位移或转动的节点；半刚性节点则是指节点的刚度介于刚性和柔性之间，可以发生一定程度的相对位移或转动。

综上所述，几何不变体系是结构工程中的重要概念，它能够确保结构的稳定性和安全性。

通过合理的结构布置和节点连接方式，以及深入理解几何不变体系的组成和特性，可以更好地应用几何不变体系，从而设计出更加稳定、安全的结构。