09组合变形习题
- 格式:doc
- 大小:1.06 MB
- 文档页数:9

材料力学组合变形习题L1AL101ADB (3)偏心压缩时,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点 到形心之距离e和中性轴到形心距离d之间的关系有四种答案:(A ) e=d; (B ) e>d;(C ) e越小,d越大; (D ) e越大,d越小。
正确答案是______。
答案(C )1BL102ADB (3)三种受压杆件如图。
设杆1、杆2和杆3中的最大压应力(绝对值)分别用 max1σ、max 2σ和max3σ表示,现有下列四种答案:(A )max1σ=max 2σ=max3σ; (B )max1σ>max 2σ=max3σ;(C )max 2σ>max1σ=max3σ; (D )max 2σ<max1σ=max3σ。
正确答案是______。
答案(C )1BL103ADD (1)在图示杆件中,最大压应力发生在截面上的哪一点,现有四种答案:(A )A点; (B )B点; (C )C点; (D )D点。
正确答案是______。
答案(C )1AL104ADC (2)一空心立柱,横截面外边界为正方形, 内边界为等边三角形(二图形形心重 合)。
当立柱受沿图示a-a线的压力时,此立柱变形形态有四种答案:(A )斜弯曲与中心压缩组合; (B )平面弯曲与中心压缩组合;(C )斜弯曲; (D )平面弯曲。
正确答案是______。
答案(B )1BL105ADC (2)铸铁构件受力如图所示,其危险点的位置有四种答案:(A )①点; (B )②点; (C )③点; (D )④点。
正确答案是______。
答案(D )1BL106ADC (2)图示矩形截面拉杆中间开一深度为h/2的缺口,与不开口的拉杆相比,开口处的最大应力的增大倍数有四种答案:(A )2倍; (B )4倍; (C )8倍; (D )16倍。
正确答案是______。
答案(C )1BL107ADB (3)三种受压杆件如图,设杆1、杆2和杆3中的最大压应力(绝对值)分别用 max1σ、max 2σ和max3σ表示,它们之间的关系有四种答案:(A )max1σ<max 2σ<max3σ; (B )max1σ<max 2σ=max3σ;(C )max1σ<max3σ<max 2σ; (D )max1σ=max3σ<max 2σ。
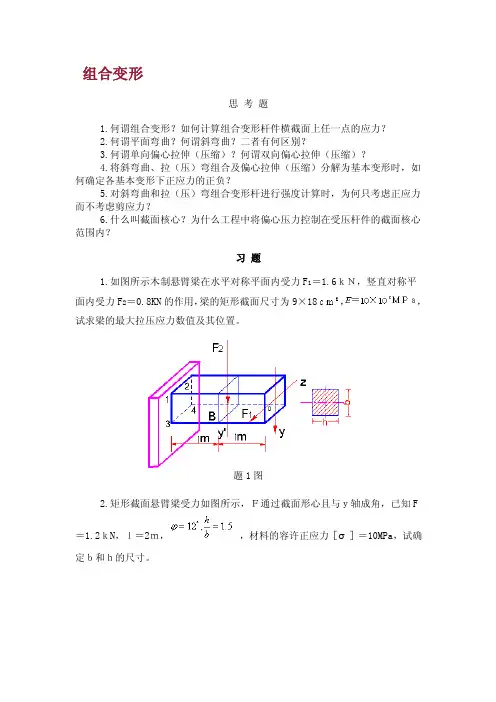
组合变形思考题1.何谓组合变形?如何计算组合变形杆件横截面上任一点的应力?2.何谓平面弯曲?何谓斜弯曲?二者有何区别?3.何谓单向偏心拉伸(压缩)?何谓双向偏心拉伸(压缩)?4.将斜弯曲、拉(压)弯组合及偏心拉伸(压缩)分解为基本变形时,如何确定各基本变形下正应力的正负?5.对斜弯曲和拉(压)弯组合变形杆进行强度计算时,为何只考虑正应力而不考虑剪应力?6.什么叫截面核心?为什么工程中将偏心压力控制在受压杆件的截面核心范围内?习题1.如图所示木制悬臂梁在水平对称平面内受力F1=1.6kN,竖直对称平面内受力F2=0.8KN的作用,梁的矩形截面尺寸为9×18,,试求梁的最大拉压应力数值及其位置。
题1图2.矩形截面悬臂梁受力如图所示,F通过截面形心且与y轴成角,已知F =1.2kN,l=2m,,材料的容许正应力[σ]=10MPa,试确定b和h的尺寸。
题2图3.承受均布荷载作用的矩形截面简支梁如图所示,q与y轴成角且通过形心,已知l=4m,b=10cm,h=15cm,材料的容许应力[σ]=10MPa,试求梁能承受的最大分布荷载。
题3图4.如图所示斜梁横截面为正方形,a=10cm,F=3kN作用在梁纵向对称平面内且为铅垂方向,试求斜梁最大拉压应力大小及其位置。
题4图5.柱截面为正方形,边长为a,顶端受轴向压力F作用,在右侧中部挖一个槽(如图),槽深。
求开槽前后柱内的最大压应力值。
题5图6.砖墙及其基础截面如图,设在1m长的墙上有偏心力F=40kN的作用,试求截面1-1和2-2上的应力分布图。
题6图7.矩形截面偏心受拉木杆,偏心力F=160kN,e=5cm,[σ]=10MPa,矩形截面宽度b=16cm,试确定木杆的截面高度h。
题7图8.一混凝土重力坝,坝高H=30m,底宽B=19m,受水压力和自重作用。
已知坝前水深H=30m,坝体材料容重,许用应力[]=10MPa,坝体底面不允许出现拉应力,试校核该截面正应力强度。
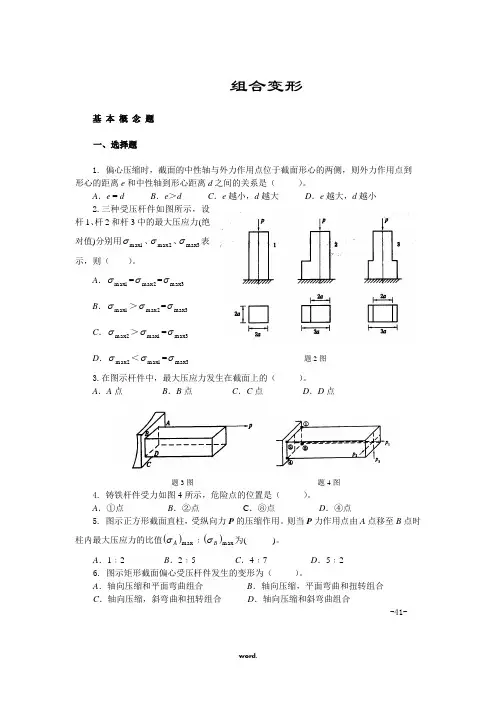
组合变形基 本 概 念 题一、选择题1. 偏心压缩时,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点到 形心的距离e 和中性轴到形心距离d 之间的关系是( )。
A .e = dB .e >dC .e 越小,d 越大D .e 越大,d 越小2.三种受压杆件如图所示,设杆1、杆2和杆3中的最大压应力(绝对值)分别用1max σ、2max σ、3max σ表示,则( )。
A .1max σ=2max σ=3max σB .1max σ>2max σ=3max σC .2max σ>1max σ=3max σD .2max σ<1max σ=3max σ 题2图3.在图示杆件中,最大压应力发生在截面上的( )。
A .A 点B .B 点C .C 点D .D 点题3图 题4图4. 铸铁杆件受力如图4所示,危险点的位置是( )。
A .①点B .②点C .⑧点D .④点5. 图示正方形截面直柱,受纵向力P 的压缩作用。
则当P 力作用点由A 点移至B 点时柱内最大压应力的比值()max A σ﹕()max B σ为( )。
A .1﹕2B .2﹕5C .4﹕7D .5﹕26. 图示矩形截面偏心受压杆件发生的变形为( )。
A .轴向压缩和平面弯曲组合B .轴向压缩,平面弯曲和扭转组合C .轴向压缩,斜弯曲和扭转组合D .轴向压缩和斜弯曲组合-41-题5图 题6图 7. 图所示悬臂梁的横截面为等边角钢,外力P 垂直于梁轴,其作用线与形心轴y 垂直,那么该梁所发生的变形是( )。
A .平面弯曲B .扭转和斜弯曲C .斜弯曲D .两个相互垂直平面(xoy 平面和xoz 平面)内的平面弯曲题7图 8. 图示正方形截面杆受弯扭组合变形,在进行强度计算时,其任一截面的危险点位置有四种答案,正确的是( )。
A .截面形心B .竖边中点A 点C .横边中点B 点D .横截面的角点D 点题8图 题9图9. 图示正方形截面钢杆,受弯扭组合作用,若已知危险截面上弯矩为M ,扭矩为T ,截面上A 点具有最大弯曲正应力σ和最大剪应力τ,其抗弯截面模量为W 。

工程力学第10章组合变形学习目标(1)了解组合变形的概念及其强度问题的分析方法;(2)掌握斜弯曲、拉伸(压缩)与弯曲和偏心压缩的应力及强度计算。
10.1 组合变形的概念例如,烟囱的变形,除自重W引起的轴向压缩外,还有水平风力引起的弯曲变形,同时产生两种基本变形,如图10-1(a)所示。
又如图10-1(b)所示,设有吊车的厂房柱子,作用在柱子牛腿上的荷载F,它们合力的作用线偏离柱子轴线,平移到轴线后同时附加力偶。
此时,柱子既产生压缩变形又产生弯曲变形。
再如图10-1(c)所示的曲拐轴,在力F作用下,AB 段同时产生弯曲变形和扭转变形。
10.1 组合变形的概念图10-110.1 组合变形的概念上述这些构件的变形,都是两种或两种以上的基本变形的组合,称为组合变形。
研究组合变形问题依据的是叠加原理,进行强度计算的步骤如下:(1)将所作用的荷载分解或简化为几个只引起一种基本变形的荷载分量。
(2)分别计算各个荷载分量所引起的应力。
(3)根据叠加原理,将所求得的应力相应叠加,即得到原来荷载共同作用下构件所产生的应力。
(4)判断危险点的位置,建立强度条件。
10.2例如图10-2(a)所示的横截面为矩形的悬臂梁,外力F作用在梁的对称平面内,此类弯曲称为平面弯曲。
斜弯曲与平面弯曲不同,如图10-2(b)所示同样的矩形截面梁,外力F的作用线通过横截面的形心而不与截面的对称轴重合,此梁弯曲后的挠曲线不再位于梁的纵向对称面内,这类弯曲称为斜弯曲。
斜弯曲是两个平面弯曲的组合,本节将讨论斜弯曲时的正应力及其强度计算。
10.2图10-210.210.2.1 正应力计算斜弯曲时,梁的横截面上同时存在正应力和切应力,但因切应力值很小,一般不予考虑。
下面结合图10-3(a)所示的矩形截面梁说明斜弯曲时正应力的计算方法。
图10-310.2.1 正应力计算10.2.1.1 外力的分解由图10-3(a)可知:10.2.1.2 内力的计算如图10-3(b)所示,距右端为a 的横截面上由F y 、F z 引起的弯曲矩分别是:10.2 10.2.1 正应力计算10.2.1.3 应力的计算由M z 和M y (即F y 和F z )在该截面引起K 点的正应力分别为:F y 和F z 共同作用下K 点的正应力为:10.210-110.210.2.1 正应力计算10.2.1.3 应力的计算通过以上分析过程,我们可以将组合变形问题计算的思路归纳为“先分后合”,具体如下:10.210.2.2 正应力强度条件同平面弯曲一样,斜弯曲梁的正应力强度条件仍为:10-2即危险截面上危险点的最大正应力不能超过材料的许用应力[σ]。
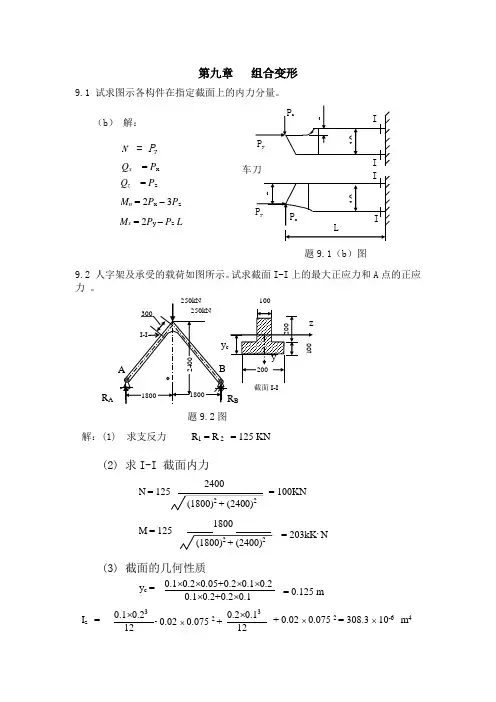
第九章组合变形9.1 试求图示各构件在指定截面上的内力分量。
9.2 人字架及承受的载荷如图所示。
试求截面I-I上的最大正应力和A点的正应力9.3 图示起重架的最大起吊重量(包括行走小车等)为P = 40kN ,横梁AC 由两根No.18槽钢组成,材料为A3钢,许用应力[σ] = 120 MPa 。
试校核横梁的强度。
9.7 图示短柱受载荷P 和H 的作用,试求固定端截面上角点A 、B 、C 及D 的正应力,并确定其中性轴的位置。
9.14 图为操纵装置水平杆,截面为空心圆形,内径d = 24 mm,外径D = 30 mm。
材料为A3钢,[σ] = 100 MPa。
控制片受力P1= 600 N。
试用第三强度理论校核杆的强度。
9.17图示皮带轮传动轴,传递功率N = 7kW,转速n =200r/min。
皮带轮重量Q = 1.8kN。
左端齿轮上啮合力Pn与齿轮节圆切线的夹角(压力角)为200。
轴的材料为A5钢,其许用应力[σ] = 80 MPa。
试分别在忽略和考虑皮带轮重量的两种情况下,按第三强度理论估算轴的直径。
9.19 飞机起落架的折轴为管状截面,内径d =70 mm ,外径D = 80 mm 。
材料的许用应力[σ] = 100 MPa ,试按第三强度理论校核折轴的强度。
若P = 1 kN ,Q = 4 kN 。
9.24 端截面密封的曲管的外径为100mm ,壁厚t = 5mm ,内压p = 8MPa 。
集中力P = 3kN 。
A 、B 两点在管的外表面上,一为截面垂直直径的端点,一为水平直径的端点。
试确定两点的应力状态。
解:在内压p 作用下,B 点应力状态分别如图9.24a ,b 所示。
σp1 = pD/(2t) = 8⨯100/(2⨯5) = 80 MPa, σp2 = pD/(4t) = 40 MPa 在集中力P 作用下,曲管受弯扭组合变形,A 点和B 点应力状态分别如图9.24c ,d 所示。


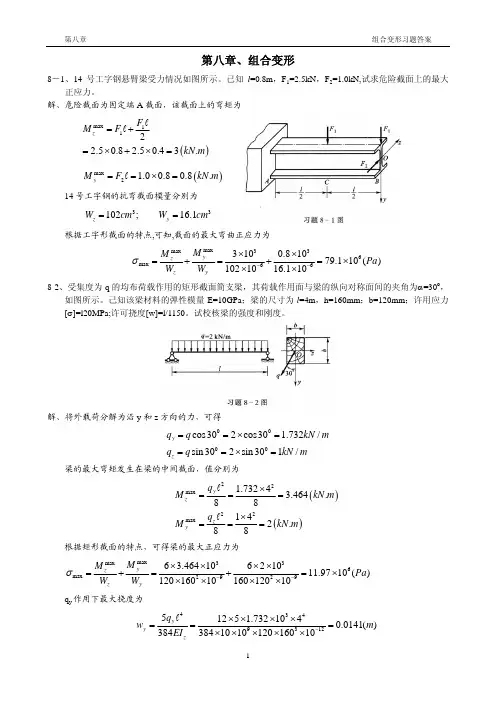

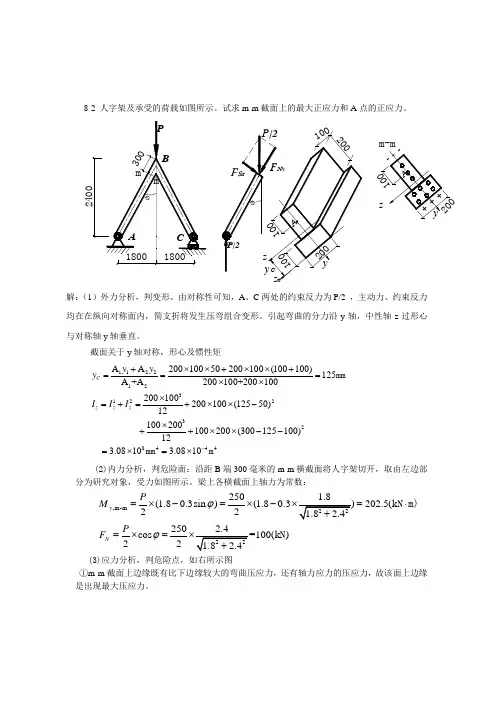
8-2 人字架及承受的荷载如图所示。
试求m-m 截面上的最大正应力和A 点的正应力。
m解:(1)外力分析,判变形。
由对称性可知,A 、C 两处的约束反力为P/2 ,主动力、约束反力均在在纵向对称面内,简支折将发生压弯组合变形。
引起弯曲的分力沿y 轴,中性轴z 过形心与对称轴y 轴垂直。
截面关于y 轴对称,形心及惯性矩1122123122328444A A 20010050200100(100100)125A +A 200100+200100200100200100(12550)12100200100200(300125100)123.0810 3.0810C z zzy y y I I I -+⨯⨯+⨯⨯+===⨯⨯⨯=+=+⨯⨯-⨯++⨯⨯--=⨯=⨯mmmm m(2)内力分析,判危险面:沿距B 端300毫米的m-m 横截面将人字架切开,取由左边部分为研究对象,受力如图所示。
梁上各横截面上轴力为常数:,m-m 250(1.80.3sin )(1.80.3202.5(k 22250cos =100(k )22y N P M P F ϕϕ=⨯-=⨯-=⋅=⨯=N m)N(3)应力分析,判危险点,如右所示图①m-m 截面上边缘既有比下边缘较大的弯曲压应力,还有轴力应力的压应力,故该面上边缘是出现最大压应力。
m mmax33410010202.510(0.30.125)(Pa) 2.5115.06MPa 117.56MPa 2(0.20.1) 3.0810N zF M y A I σ---=+⋅-⨯⨯=-⨯-=--=-⨯⨯⨯上② A 点是压缩区的点,故m m33410010202.510(0.30.1250.1)(Pa) 2.549.31MPa 51.83MPa 2(0.20.1) 3.0810N a a zF M y A I σ--=+⋅-⨯⨯=-⨯--=--=-⨯⨯⨯注意:最大拉应力出现在下边缘m mmax33410010202.5100.125(Pa) 2.582.18MPa 79.68MPa2(0.20.1) 3.0810N zF M y A I σ---=+⋅-⨯⨯=+⨯=-+=⨯⨯⨯下8-3 图示起重机的最大起吊重量为W=35kN ,横梁AC 由两根NO.18槽钢组成。
组合变形一、判断题1.斜弯曲区别与平面弯曲的基本特征是斜弯曲问题中荷载是沿斜向作用的。
( )2.斜弯曲时,横截面的中性轴是通过截面形心的一条直线。
( )3.梁发生斜弯曲变形时,挠曲线不在外力作用面内。
( )4.正方形杆受力如图1所示,A点的正应力为拉应力。
( )图 15. 上图中,梁的最大拉应力发生在B点。
( )6. 图2所示简支斜梁,在C处承受铅垂力F的作用,该梁的AC段发生压弯组合变形,CB段发生弯曲变形。
( )图 27.拉(压)与弯曲组合变形中,若不计横截面上的剪力则各点的应力状态为单轴应力。
( )8.工字形截面梁在图3所示荷载作用下,截面m--m上的正应力如图3(C)所示。
( )图 39. 矩形截面的截面核心形状是矩形。
( )10.截面核心与截面的形状与尺寸及外力的大小有关。
( )11.杆件受偏心压缩时,外力作用点离横截面的形心越近,其中性轴离横截面的形心越远。
( )12.计算组合变形的基本原理是叠加原理。
()二、选择题1.截面核心的形状与()有关。
A、外力的大小B、构件的受力情况C、构件的截面形状D、截面的形心2.圆截面梁受力如图4所示,此梁发生弯曲是()图 4A、斜弯曲B、纯弯曲C、弯扭组合D、平面弯曲三、计算题1.矩形截面悬臂梁受力F1=F,F2=2F,截面宽为b,高h=2b,试计算梁内的最大拉应力,并在图中指明它的位置。
图 52.图6所示简支梁AB上受力F=20KN,跨度L=2.5m,横截面为矩形,其高h=100mm,宽b=60mm,若已知α=30°,材料的许用应力[σ]=80Mpa,试校核梁的强度。
3.如图7所示挡土墙,承受土压力F=30KN,墙高H=3m,厚0.75m,许用压应力[σ]ˉ=1 Mpa,许用拉应力[σ]﹢=0.1 Mpa,墙的单位体积重量为,试校核挡土墙的强度。
图 6 图 74.一圆直杆受偏心压力作用,其偏心矩e=20mm,杆的直径d=70mm,许用应力[σ]=120Mpa,试求此杆容许承受的偏心压力F之值。
第六章直梁弯曲弯曲变形是杆件比较常见的基本变形形式。
通常把以发生弯曲变形为主的杆件称为梁。
本章主要讨论直梁的平面弯曲问题,内容包括:弯曲概念和静定梁的力学简图;弯曲内力及内力图;弯曲应力和强度计算;弯曲变形和刚度计算。
其中,梁的内力分析和画弯矩图是本章的重点。
第一节平面弯曲的概念和力学简图一、弯曲概念和受力特点当杆件受到垂直于杆轴的外力作用或在纵向平面内受到力偶作用(图6-1)时,杆轴由直线弯成曲线,这种在外力作用下其轴线变成了一条曲线。
这种形式的变形称为弯曲变形。
工程上通常把以弯曲变形为主的杆件称为梁。
图 6-1 弯曲变形是工程中最常见的一种基本变形。
例如房屋建筑中的楼面梁和阳台挑梁,受到楼面荷载和梁自重的作用,将发生弯曲变形,如图6-2所示。
一些杆件在荷载作用下不仅发生弯曲变形,还发生扭转等变形,当讨论其弯曲变形时,仍然把这些杆件看做梁。
图6-2工程实际中常见到的直梁,其横截面大多有一根纵向对称轴,如图6-3所示。
梁的无数个横截面的纵向对称轴构成了梁的纵向对称平面,如图6-4所示。
图 6-3 图6-4若梁上的所有外力(包括力偶)作用在梁的纵向对称平面内,梁的轴线将在其纵向对称平面内弯成一条平面曲线,梁的这种弯曲称为平面弯曲,它是最常见、最基本的弯曲变形。
本章主要讨论直梁的平面弯曲变形。
从以上工程实例中可以得出,直梁平面弯曲的受力与变形特点是:外力作用于梁的纵向对称平面内,梁的轴线在此纵向对称面内弯成一条平面曲线。
二、梁的受力简图为了便于分析和计算直梁平面弯曲时的强度和刚度,需建立梁的力学简图。
梁的力学简图(力学模型)包括梁的简化、荷载的简化和支座的简化。
1、梁的简化由前述平面弯曲的概念可知,载荷作用在梁的纵向对称平面内,梁的轴线弯成一条平面曲线。
因此,无论梁的外形尺寸如何复杂,用梁的轴线来代替梁可以使问题得到简化。
例如,图6-1a和图6-2a所示的火车轮轴和桥式起重机大梁,可分别用梁的轴线AB代替梁进行简化(图6-1b和图6-2b)。
组合变形练习题一、选择1、应用叠加原理旳前提条件是:。
A:线弹性构件;B:小变形杆件;C:线弹性、小变形杆件;D:线弹性、小变形、直杆;2、平板上边切h/5,在下边相应切去h/5,平板旳强度。
A:减少一半; B:减少不到一半;C:不变; D:提高了;3、AB杆旳A处靠在光滑旳墙上,B端铰支,在自重作用下发生变形,AB杆发生变形。
A:平面弯曲B:斜弯;C:拉弯组合; D:压弯组合;4、简支梁受力如图:梁上。
A:AC段发生弯曲变形、CB段发生拉弯组合变形B:AC段发生压弯组合变形、CB段发生弯曲变形C:两段只发生弯曲变形D:AC段发生压弯组合、CB段发生拉弯组合变形5、图示中铸铁制成旳压力机立柱旳截面中,最合理旳是。
6、矩形截面悬臂梁受力如图,P2作用在梁旳中间截面处,悬臂梁根部截面上旳最大应力为: 。
A:σmax=(My2+M z2)1/2/WﻩﻩﻩB:σmax=M y/W y+MZ/WZC:σmax=P1/A+P2/A ﻩﻩﻩD:σmax=P1/W y+P2/W z7、塑性材料制成旳圆截面杆件上承受轴向拉力、弯矩和扭矩旳联合伙用,其强度条件是。
A:σr3=N/A+M/W≤|σ| B:σr3=N/A+(M2+T2)1/2/W≤|σ|C:σr3=[(N/A+M/W)2+(T/W)2]1/2≤|σ|D:σr3=[(N/A)2+(M/W)2+(T/W)2]1/2≤|σ|8、方形截面等直杆,抗弯模量为W,承受弯矩M,扭矩T,A点处正应力为σ,剪应力为τ,材料为一般碳钢,其强度条件为: 。
A:σ≤|σ|, τ≤|τ| ;B: (M2+T2)1/2/W≤|σ| ;C:(M2+0.75T2)1/2/W≤|σ|; D:(σ2+4τ2)1/2≤|σ| ;9、圆轴受力如图。
该轴旳变形为:A:AC段发生扭转变形,CB段发生弯曲变形B:AC段发生扭转变形,CB段发生弯扭组合变形C:AC段发生弯扭组合变形,CB段发生弯曲变形D:AC、CB均发生弯扭组合变形二、填空1、图示构造中,m-m面发生变形。