第九章组合变形
- 格式:ppt
- 大小:422.50 KB
- 文档页数:16



材料力学 804一、参考教材:《材料力学I、II》,第四版,高等教育出版社,单辉祖编著。
二、课程内容的基本要求:第一章:绪论第二章:轴向拉压应力第三章:轴向拉压变形第四章:扭转第五章:弯曲内力第六章:弯曲应力第七章:弯曲变形第八章:应力分析和强度理论第九章:组合变形第十章:压杆稳定第十一章:能量方法第十二章:动载荷第十三章:应力分析的实验方法三、应该掌握的内容和重点内容第一章绪论材料力学的任务、基本概念,变形体的基本假设,杆件变形的基本形式。
第二章轴向拉压应力1、轴向拉(压)的概念、内力、截面法、轴力的计算和轴力图的画法。
2、轴向拉(压)杆件横截面及斜截面上的应力计算;许用应力;强度条件及应用。
3、材料在拉伸、压缩时的机械性能。
4、剪切面、挤压面的概念及其判定;剪应力和挤压的公式及其计算。
重点:1、轴力及轴力图的画法。
2、拉(压)应力及强度计算。
3、材料的主要性能。
第三章轴向拉压变形1、轴向拉(压)杆件的变形,纵向变形、弹性模量、抗拉刚度、横向变形、泊松比等概念;虎克定律及其应用。
2、桁架节点位移计算。
3、简单静不定问题的计算。
重点:1、轴向拉(压)变形计算。
2、静不定问题的分析和计算。
第四章扭转1、外力扭矩的计算,扭矩、扭矩图。
2、圆轴扭转时横截面上的应力分布和计算;强度条件及其应用。
3、圆轴扭转时变形和刚度计算;材料的扭转破坏实验。
4、扭转静不定问题的计算。
重点:1、圆轴扭转应力和强度计算。
2、圆轴扭转变形和刚度计算。
3、简单扭转静不定的计算。
第五章弯曲内力1、平面弯曲、剪力、弯矩的概念。
2、剪力方程、弯矩方程的列法;剪力图与弯矩图的画法。
3、利用微分关系画剪力图和弯矩图。
重点:剪力图与弯矩图的画法。
第六章弯曲应力1、纯弯曲的概念和平面假设;平面图形的几何性质。
2、弯曲正应力公式及应用;弯曲剪应力计算。
3、弯曲强度计算;提高梁的强度的主要措施。
重点:弯曲正应力分析与强度计算。
第七章弯曲变形1、挠度、转角及其关系;挠曲线微分方程式;积分法、叠加法求梁的变形。
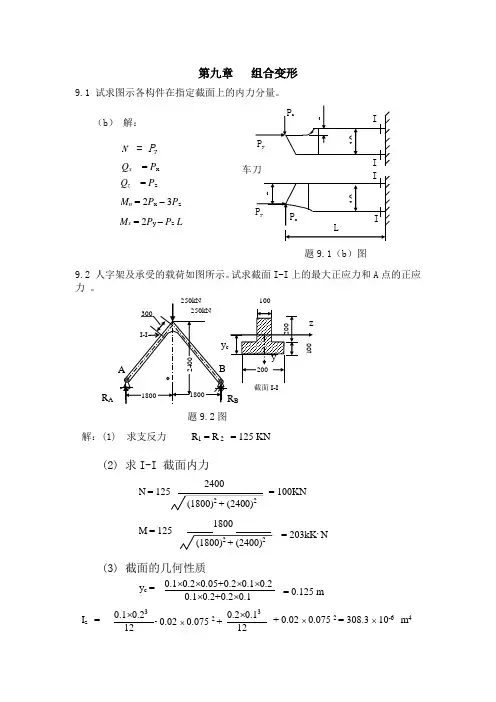
第九章组合变形9.1 试求图示各构件在指定截面上的内力分量。
9.2 人字架及承受的载荷如图所示。
试求截面I-I上的最大正应力和A点的正应力9.3 图示起重架的最大起吊重量(包括行走小车等)为P = 40kN ,横梁AC 由两根No.18槽钢组成,材料为A3钢,许用应力[σ] = 120 MPa 。
试校核横梁的强度。
9.7 图示短柱受载荷P 和H 的作用,试求固定端截面上角点A 、B 、C 及D 的正应力,并确定其中性轴的位置。
9.14 图为操纵装置水平杆,截面为空心圆形,内径d = 24 mm,外径D = 30 mm。
材料为A3钢,[σ] = 100 MPa。
控制片受力P1= 600 N。
试用第三强度理论校核杆的强度。
9.17图示皮带轮传动轴,传递功率N = 7kW,转速n =200r/min。
皮带轮重量Q = 1.8kN。
左端齿轮上啮合力Pn与齿轮节圆切线的夹角(压力角)为200。
轴的材料为A5钢,其许用应力[σ] = 80 MPa。
试分别在忽略和考虑皮带轮重量的两种情况下,按第三强度理论估算轴的直径。
9.19 飞机起落架的折轴为管状截面,内径d =70 mm ,外径D = 80 mm 。
材料的许用应力[σ] = 100 MPa ,试按第三强度理论校核折轴的强度。
若P = 1 kN ,Q = 4 kN 。
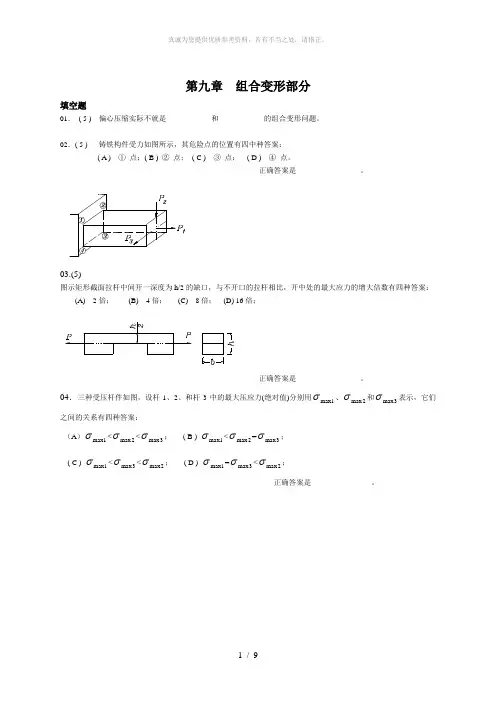
9.24 端截面密封的曲管的外径为100mm ,壁厚t = 5mm ,内压p = 8MPa 。
集中力P = 3kN 。
A 、B 两点在管的外表面上,一为截面垂直直径的端点,一为水平直径的端点。
试确定两点的应力状态。
解:在内压p 作用下,B 点应力状态分别如图9.24a ,b 所示。
σp1 = pD/(2t) = 8⨯100/(2⨯5) = 80 MPa, σp2 = pD/(4t) = 40 MPa 在集中力P 作用下,曲管受弯扭组合变形,A 点和B 点应力状态分别如图9.24c ,d 所示。


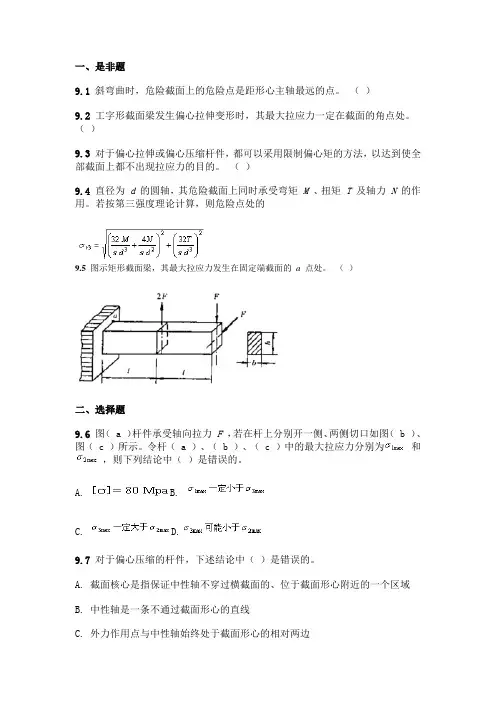
一、是非题9.1 斜弯曲时,危险截面上的危险点是距形心主轴最远的点。
()9.2 工字形截面梁发生偏心拉伸变形时,其最大拉应力一定在截面的角点处。
()9.3 对于偏心拉伸或偏心压缩杆件,都可以采用限制偏心矩的方法,以达到使全部截面上都不出现拉应力的目的。
()9.4 直径为d 的圆轴,其危险截面上同时承受弯矩M 、扭矩T 及轴力N 的作用。
若按第三强度理论计算,则危险点处的9.5 图示矩形截面梁,其最大拉应力发生在固定端截面的a 点处。
()二、选择题9.6 图( a )杆件承受轴向拉力F ,若在杆上分别开一侧、两侧切口如图( b )、图( c )所示。
令杆( a )、( b )、( c )中的最大拉应力分别为和,则下列结论中()是错误的。
A. B.C. D.9.7 对于偏心压缩的杆件,下述结论中()是错误的。
A. 截面核心是指保证中性轴不穿过横截面的、位于截面形心附近的一个区域B. 中性轴是一条不通过截面形心的直线C. 外力作用点与中性轴始终处于截面形心的相对两边D. 截面核心与截面的形状、尺寸及载荷大小有关三. 计算题9.8材料为灰铸铁HT 15-33的压力机框架如图所示。
许用拉应力为,许用压应力为,试校核该框架立柱的强度。
9.9图示皮带轮传动轴,传递功率N =7kW ,转速n =200 r/min 。
皮带轮重量Q =1.8 kN 。
左端齿轮上啮合力与齿轮节圆切线的夹角(压力角)为。
轴的材料为A5钢,其许用应力。
试分别在忽略和考虑皮带轮重量的两种情况下,按第三强度理论估算轴的直径。
答案9.1 × 9.2 √ 9.3 × 9.4 √ 9.5 √ 9.6 C 9.7 D9.8解:9.9解:。


第一章绪论1.土木工程中,各种建筑物在施工和使用阶段所承受的所有外力统称为荷载。
建筑物中承受荷载并且传递荷载的空间骨架称为结构,而任何结构都是由构件所组成的。
为保证构件在荷载作用下的正常工作,必须使它同时满足三方面的力学要求,即强度、刚度和稳定性的要求:(1) 构件抵抗破坏的能力称为强度(strength)。
对构件的设计应保证它在规定的荷载作用下能够正常工作而不会发生破坏(2) 构件抵抗变形的能力称为刚度(stiffness)。
构件的变形必须要限制在一定的限度内,构件刚度不满足要求同样也不能正常工作。
(3) 构件在受到荷载作用时在原有形状下的平衡应保证为稳定的平衡,这就是对构件的稳定性(stability)要求。
但是在材料力学中,构件的变形不能忽略不计,因此我们把构件作为可变形体来研究,称它们为可变形固体(deformable solid)。
在对可变形固体材料制成的构件进行强度、刚度和稳定性研究时,为抽象出某种理想的力学模型,通常根据其主要性质做出一定的假设,同时忽略一些次要因素,然后进行理论分析。
在材料力学中,通常对可变形固体作如下基本假设:(1) 连续性假设(continuity assumption)。
这一假设认为,构件的材料在变形后仍然保持连续性,在其整个体积内都毫无空隙地充满了物质,忽略了体积内空隙对材料力学性质的影响。
(2) 均匀性假设(homogenization assumption)。
这一假设认为,构件的材料各部分的力学性能是相同的。
从任意一点取出的单元体,都具有与整体同样的力学性能。
(3) 各向同性假设(isotropy assumption)。
这一假设认为,构件的材料在各个方向的力学性能是相同的。
如工程上常用的金属材料,虽然从它们的晶粒来说,其力学性能并不一样;但从宏观上看,各个方向的力学性能接近相同。
有些材料沿各方向的力学性能并不相同,像这样的材料称之为各向异性材料,如木材等。
第九章 组合变形授课学时:8学时主要内容:拉弯、斜弯曲和弯扭组合变形的强度和变形的校核和计算。
§9–1 概 述1.定义在复杂外载荷作用下,构件的变形会包含几种简单变形,当几种变形所对应的应力属同一量级时,不能忽略之,这类构件的变形称为组合变形。
2.组合变形形式两个平面弯曲的组合;拉伸或压缩与弯曲的组合;扭转与弯曲。
3.组合变形的研究方法 —— 叠加原理 对于线弹性状态的构件,将其组合变形分解为基本变形,考虑在每一种基本变形下的应力和变形,然后进行叠加。
4.解题步骤外力分析:外力向形心简化并沿主惯性轴分解内力分析:求出每个外力分量对应的内力方程和内力图,确定危险面。
应力分析:画危险面应力分布图,叠加,建立危险点的强度条件。
§9–2拉(压)弯组合例 起重机的最大吊重kN P 12=,[]2/100m kN =σ。
试为横梁AB 选择适用的工字钢。
解:(1)受力分析由0=∑AM得kN T y 18=,kN T T y x 245.12==(2)作AB 的弯矩图和剪力图,确定C(3)确定工字钢型号按弯曲强度确定工字钢的抗弯截面系数[]363120101001012cm MW =⨯⨯=≥σ查表取3141cm W =的16号工字钢,其横截面积为21.26cm 。
在C 左侧的下边缘压应力最大,需要进行校核。
+=MPaMPa W M A N 1003.94101411012104.2610246343max max <=⨯⨯+⨯⨯=+=--σ固所选工字钢为合适。
§9–3斜弯曲1.斜弯曲概念:梁的横向力不与横截面对称轴或形心主惯性轴重合,这时杆件将在形心主惯性平面内发生弯曲,变形后的轴线与外力不在同一纵向平面内,2.解题方法1)分解:将外载沿横截面的两个形心主轴分解,于是得到两个正交的平面弯曲。
2)叠加:对两个平面弯曲进行研究;然后将计算结果叠加起来。
例 矩形截面悬臂梁,求根部的最大应力和梁端部的位移。