诊断试验四格表资料分析
- 格式:pdf
- 大小:387.10 KB
- 文档页数:7

定性资料常用的统计学方法一、χ2检验χ2检验(chi-square test)是一种主要用于分析分类变量数据的假设检验方法,该方法主要目的是推断两个或多个总体率或构成比之间有无差别。
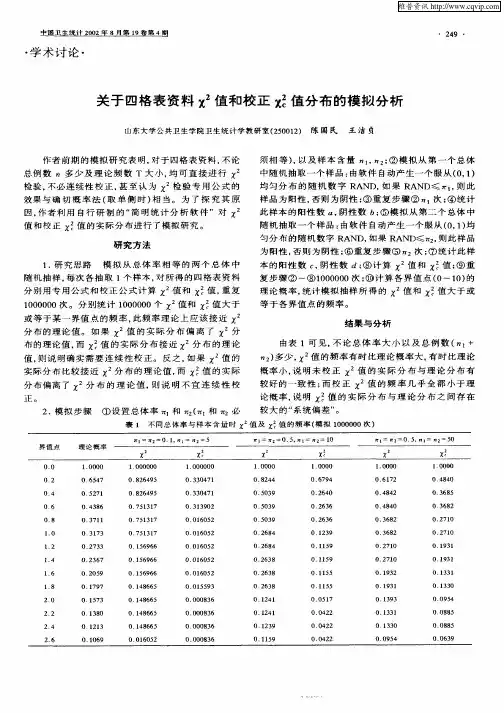
(一)四格表资料的χ2检验例17:为了解吲达帕胺片治疗原发性高血压的疗效,将70名高血压患者随机分为两组,试验组用吲达帕胺片加辅助治疗,对照组用安慰剂加辅助治疗,观察结果见表4 -5-1,试分析吲达帕胺片治疗原发性高血压的有效性。
表4 -5-1 两种疗法治疗原发性高血压的疗效1.四格表χ2检验的原理:对于四格表资料,χ2检验的基本公式为:式中,A为实际频数(actual frequency),T为理论频数(theoreticalfrequency)。
理论频数T根据检验假设H0:π1=π2确定,其中π1和π2分别为两组的总体率。
计算理论频数T的公式为:式中Tij 为第i行第j列的理论频数,ni+和n+j分别为相应行与列的周边合计数,n为总例数。
现以例17为例说明χ2检验的步骤:(1)建立检验假设并确定检验水准。
H0:π1=π2,即试验组与对照组的总体有效率相等H1:π1≠π2,即试验组与对照组的总体有效率不等α=0.05(2)计算检验统计量。
按式(4 -5-2)计算T11,然后利用四格表的各行列的合计数计算T12、T21和T22,即T11=(44×41)/70=25.77,T12=44-25.77=18.23T21=41-25.77=15.23,T22=26-15.23=10.77按式(4 -5-3)计算χ2值(3)确定P值,作出推断结论。
以ν=1查χ2分布界值表,得P<0.005。
按α=0.05水准,拒绝H,接受H1,可以认为两组治疗原发性高血压的总体有效率不等,即可以认为吲达帕胺片治疗原发性高血压优于对照组。
2.四格表资料χ2检验的专用公式:在对两样本率比较时,当总例数n≥40且所有格子的T≥5时,可用χ2检验的通用公式(4 -5-1)。

配对四格表资料卡方检验的公式选用条件配对四格表资料卡方检验的公式选用条件引言•配对四格表资料卡方检验是统计学中常用的分析方法之一,用于判断两个变量之间是否存在关联关系。
•在进行配对四格表资料卡方检验时,正确选用公式是至关重要的。
公式选用条件1.样本数据满足独立性:在进行配对四格表资料卡方检验时,需要保证样本数据中的观测值之间相互独立,即每个观测值的出现与其他观测值的出现无关。
2.样本数据满足随机性:样本数据需要能够代表总体的特点,即样本选择要随机进行,以减小抽样偏差对检验结果的影响。
3.样本数据满足预期频数要求:进行配对四格表资料卡方检验时,需要确保每个分类下的观测值的预期频数大于等于5,以保证卡方检验的准确性。
4.样本数据满足分类独立性:进行配对四格表资料卡方检验时,需要确保变量的分类是相互独立的,即不出现因两个变量分类方法不同而导致的观测值分类重叠的情况。
公式推导•配对四格表资料卡方检验的公式选用条件主要基于卡方检验的原理进行推导。
•卡方检验是通过比较观测频数与预期频数之间的差异来判断两个变量之间的关系。
•在配对四格表资料卡方检验中,需要计算卡方值,并基于卡方值进行假设检验。
结论•在进行配对四格表资料卡方检验时,应遵守公式选用条件,确保样本数据的独立性、随机性、预期频数要求和分类独立性。
•正确选用公式可以提高卡方检验的准确性,从而更好地判断两个变量是否存在关联关系。
参考文献•[1] Agresti, A. (2002). Categorical data analysis (2nd ed.). Wiley-Interscience.公式选用条件的解释1.样本数据满足独立性:–独立性是指样本数据中的观测值之间相互独立,即每个观测值的出现与其他观测值的出现无关。
–例如,在研究两种药物治疗效果时,如果每个患者的数据只与自己所接受的药物有关,而不受其他患者的影响,那么就满足了独立性的条件。
2.样本数据满足随机性:–随机性是指样本数据能够代表总体的特点,即样本选择要随机进行,以减小抽样偏差对检验结果的影响。

利用Excel对IVD二分类临床试验数据进行统计分析的方法举例中国器审20200416临床试验资料中常出现人工数据统计错误的问题,现有临床试验数据通常使用Excel进行数据的汇总及展示,合理利用Excel工具,可有效减少该类错误。
Excel作为一个表格工具,除了具有数据记录、筛选等常用的功能外,还有单元格引用及公式等用于统计分析的功能。
可将这些功能在临床试验数据表格内部直接进行运算,对临床试验结果进行分析统计。
下面以二分类指标的临床试验数据为例进行简要介绍。
一、数据转换本文以申报试剂对临床诊断结果的灵敏度、特异度为例。
临床试验数据表通常包括受试者(样本)编号、年龄、性别、样本类型、临床诊断结果、考核试剂检测结果等数据列。
为了利于后期统计分析,首先进行数据的转换。
在Excel中,数据表中的临床诊断结果、考核试剂检测结果无论以“确诊/排除”或“+/-”的方式进行表示,均以文本格式进行记录。
在进行条件判断时需要使用半角引号,并且无法进行运算,因此推荐将其转换为“0/1”的数字格式。
下面以对“临床诊断”数据进行转换为例。
通过数据筛选可以看出,临床诊断中以“确诊”和“排除”进行表示。
需将确诊转换为“1”,将排除转换为“0”。
在数据表格右侧加入“临床诊断”转换列,在与数据首行对应的单元格写如下公式:=IF(E2="确诊",1,0)所引用单元格(E2)可以通过点击的方式自动写入。
按“回车”之后,可以看到数据表格显示的为“1”,即“确诊”。
同理我们将考核试剂检测结果进行“0/1”转换。
通过筛选功能可以看出考核试剂检测结果以“+/-”进行表示。
在诊断转换结果列右侧加入“考核试剂检测结果”转换列,在与数据首行对应的单元格写如公式“=IF(F2="+",1,0)”,将考核试剂检测结果转换为“0/1”表示。
二、四格表判定四格表分别用a、b、c、d表示四种检测结果与临床诊断结果之间的关系。




诊断试剂的统计学分析对于定性试剂,主要是1、阳性符合率、阴性符合率、总体符合率及其95%(或99%)的置信区间。
2、行四格表卡方或kappa检验以验证两种试剂定性结果的一致性。
做完这些统计应该是足够了。
这些在IVDstatistics中都有体现。
这里探讨几个统计技术方面的话题:1、95%的可信区间:目前有好几种算法:可参见程序和帮助文件:个人感觉最常用的是二项分布法,这个算法应该是最准确的算法,但只能用程序算;另外用比较多的Wald法(点估计,近似正态分布法?),这个算法最简单,但准确度较低。
2、配对卡方检验(McNemar)在国内的教科书中,都是用传统的公式,b+c<40时用校正公式。
但在不同的程序中,并不相同,SPSS只采用精确概率法,MedCalc在<25时用精确概率法,而在>25时用校正的公式,而SAS好象只用传统的公式计算。
这里我无法认定用哪种算法好,但应都有道理,不能认定为错。
我想可能理论上精确概率法最好,但只能用程序算,另外对于很大的数据,可能出现无法计算的情况。
3、一致性检验这是指导原则中的必选项之一。
然而在一般的教科书中,只对Kappa系数计算进行了说明,对于其95%的可信区间和非0检验提的很少。
统计上Kappa系数不只应用于配对的四格表,对于半定量的有序数据同样适用,反过来可认为四格表是有序数据的最简单的特例。
在这里要注意的事Kappa的标准误有两个,分别用于可信区间和非0检验,计算公式不同,SPSS 和MedCalc都没能同时给出计算值,另有限的几篇中文期刊文章竟然不少用错了。
关于这两个Se的计算公式在程序的帮助里可以找到,Se(K)用于计算可信区间,Se0(K)用于非0的检验。
定量试剂的临床统计:1、以上指导原则均指出要进行回归分析,即计算回归方程y=a+bx,相关系数(R)或R2;从统计学角度,对方程进行检验,即a,b的检测,得出直线相关关系是否成立。



诊断试验四格表资料分析
例:ECG诊断心梗发生的结果
分析目的:
分析试验结果与真实情况(金标准)的吻合程度。
金标准是指当前公认的诊断疾病最可靠的标准方法,可正确区分“有病”或“无病”。
数据如用通用符号表示:
分析指标:
1.检测患病率(prevalence):是指被检测的全部对象中,检测出来的患者的比例。
即:检测患
病率 = (a+b)/(a+b+c+d)
2.实际患病率(prevalence):是指被检测的全部对象中,真正患者的比例。
患病率对被评价的
诊断试验,也称为验前概率,而预测值属于验后概率。
即:实际患病率 = (a+c)/( a+b+c+d) 3.敏感性:敏感性就是指由金标准确诊有病组内所检测出阳性病例数的比率(%)。
即本实验诊
断的真阳性率。
其敏感性越高,漏诊的机会就越少。
即:敏感性= a/( a+c)
4.特异性:是指由金标准确诊为无病组内所检测出阴性人数的比率(%),即本诊断实验的真阴
性率。
特异性越高,发生误诊的机会就越少。
即:特异性= d/(b+d)
5.诊断准确率:是指临床诊断检测出的真阳性和真阴性例数之和,占总检测人数的比例,即称
本临床实验诊断的准确性。
即:准确性= (a+d)/ (a+b+c+d)
6.阳性似然比(positive likelihood ratio):阳性似然比是指临床诊断检测出的真阳性率与
假阳性率之间的比值,即阳性似然比=敏感性/(1-特异性)。
可用以描述诊断试验阳性时,患病与不患病的机会比。
提示正确判断为阳性的可能性是错误判断为阳性的可能性的倍数。
阳性似然比数值越大,提示能够确诊患有该病的可能性越大。
它不受患病率影响,比起敏感度和特异度更为稳定。
阳性似然比=敏感性/(1-特异性)= (a/(a+c))/(b/ (b+d))
7.阴性似然比(negative liklihoodratio):阴性似然比是指临床实验诊断检测出的假阴性率
与真阴性率之比值,此值越小,说明该诊断方法越好。
可用以描述诊断试验阴性时,患病与不患病的机会比。
阴性似然比提示错误判断为阴性的可能性是正确判断为阴性的可能性的倍数。
阴性似然比数值越小,提示能够否定患有该病的可能性越大。
阴性似然比=(1-敏感性)/特异性= (c/(a+c))/(d/(b+d))
8.诊断比值比(OR):阳性似然比与阴性似然比的比值。
数值越大,表明诊断试验区分患者与
非患者的能力越大。
诊断比值比=(a/(a+c)/(b/(b+d))/(c/(a+c)/(d/(b+d))) = (ab)/(cd) 9.诊断所需检测数(NND):真阳性率(敏感度)与假阳性率(1-特异度)的差的倒数。
诊断所需
检测数(NND)=1/(a/(a+c)- b/(b+d))
10.Yuden 指数:Yuden 指数 = 敏感性+特异性-1= a/(a+c)+d/(b+d)-1
11.阳性预测值(postivepredictive value):又称预测阳性结果的正确率,是指待评价的诊断试
验结果判为阳性例数中,真正患某病的例数所占的比例。
即:阳性预测值=真阳性/(真阳性+假阳性)= a/ (a+b)
12.阴性预测值(negative predictive value):又称预测阴性结果的正确率,是指临床诊断实验
检测出的全部阴性例数中,真正没有患本病的例数所占的比例。
即:阴性预测值=真阴性/(真阴性+假阴性)= d/(c+d)
详细公式见后面附件
例:输入界面:
注:一组数据可以输入于四格表中,多组数据可以按a b c d顺序输入到下表。
输出结果:
计算公式
Totals m1=a+c m2=b+d N=n1+n2
Define:
The 100(1-α)% confidence interval is defined as:
For Specificity,
Define:
The 100(1-α)% confidence interval is defined as:
For Positive Predictive Value (PPV),
Define:
The 100(1-α)% confidence interval is defined as:
For Negative Predictive Value (NPV), Define:
The 100(1-α)% confidence interval is defined as:
For Pre-test probability,
For Likelihood Ratio Positive (LR+), Define:
The 100(1-α)% confidence interval is defined as:
For Positive Post-test probability,
Define
For Likelihood Ratio Negative (LR-),
Define:
The 100(1-α)% confidence interval is defined as:
For Negative Post-test probability,
Define
Notation:
100(1-α)% confidence interval: We are 100(1-α)% sure the true value of the parameter is included in the confidence interval
: The z-value for standard normal distribution with left-tail probability
Example
Suppose
Disease No disease Totals
a=20 b=180 n1=200 Test Outcome
Positive
Test Outcome
c=10 d=1820 n2=1830 Negative
Totals m1=30 m2=2000 N=2030
Then the Sensitivity is 0.66667 and the corresponding 95% C.I. ((1-α) =0.95) is (0.49798, 0.83535).
The Specificity is 0.91 and the 95% C.I. is (0.89746, 0.92254).
The Positive Predictive Value (PPV) is 0.1 and the 95% C.I. is (0.05842, 0.14158).
The Negative Predictive Value (NPV) is 0.99454 and the 95% C.I. is (0.99116, 0.99791). The Pre-Test Probability is 0.01478.
The Likelihood Ratio Positive (LR+) is 7.40741 and the 95% C.I. is (5.54896, 9.88828). The Positive Post-Test Probability is 0.1.
The Likelihood Ratio Negative (LR-) is 0.3663 and the 95% C.I. is (0.22079, 0.60771). The Negative Post-Test Probability is 0.00546.。