第2章 缩聚和逐步聚合
- 格式:doc
- 大小:233.00 KB
- 文档页数:7

第二章缩聚及其他逐步聚合反应一、学习要求1、了解线形缩聚的单体种类及类型,掌握官能团及官能度的概念,等物质的量的概念。
2、熟悉线形缩聚的机理和特点,熟悉在密闭体系与开放体系中聚合度与平衡常数和残留小分子的关系,熟悉线形缩聚中出现的副反应。
3、掌握官能团等活性概念,了解线形缩聚动力学,自催化聚酯化动力学及外加酸聚酯化动力学,平衡缩聚动力学。
4、掌握线形缩聚产物聚合度的影响因素及控制方法,了解反应程度和平衡常数对聚合度的影响;了解等物质的量对聚合度的影响;掌握摩尔系数的计算,聚合度与反应程度、摩尔系数的关系,了解线形缩聚物的分子量分布。
5、掌握体型缩聚的形成条件,凝胶化现象与凝胶点,Carothers方程的理论基础及方程式,等物质的量及非等物质的量条件下的体系平均官能度的计算,了解Flory统计法估算体系凝胶点的方法。
6、掌握缩聚反应的实施方法,了解聚酯、聚酰胺的制备原理及过程,了解酚醛树脂、尿醛树脂及三聚氰胺甲醛树脂的制备原理及过程。
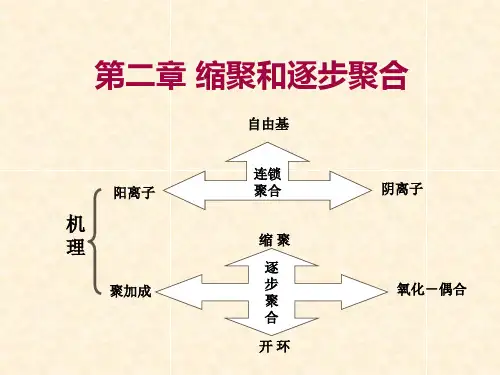
二、学时学时聚合反应从机理上可分为逐步聚合反应和连锁聚合反应两大类型。
在高分子化学和高分子合成工业中,逐步聚合反应占有重要地位。
其中包括人们熟知的涤纶、尼龙、酚醛树脂及脲醛树脂等高分子材料。
近年来,逐步聚合反应的研究在理论上和实际应用上都有了新的发展,一些高强度、高模量、耐老化及抗高温等综合性能优异的高分子材料不断问世。
逐步聚合反应中最重要是缩合聚合,简称缩聚。
本章着重讨论缩聚反应,并介绍其他常用的逐步聚合反应。
2.1 聚合反应类型及特点逐步聚合反应包括缩聚反应、逐步加成聚合,一些环状化合物的开环聚合、Diels—Alder 加成反应(狄尔斯-阿尔德反应是一种有机反应(具体而言是一种环加成反应)。
共轭双烯与取代烯烃(一般称为亲双烯体)反应生成取代环己烯。
即使新形成的环之中的一些原子不是碳原子,这个反应也可以继续进行。
一些狄尔斯-阿尔德反应是可逆的,这样的环分解反应叫做逆狄尔斯-阿尔德反应(retro-Diels–Alder)。

56弗洛里小传弗洛里小传((Paul J. Flory )(1910-1985)1910年6月19日生于伊利诺伊州斯特灵日生于伊利诺伊州斯特灵;;1934年在俄亥俄州州立大学获物理化学博士学位博士学位,,后任职于杜邦公司后任职于杜邦公司,,进行高分子基础理论研究分子基础理论研究;;1948年在康奈尔大学任教授年在康奈尔大学任教授;;1953年当选为美国科学院院士年当选为美国科学院院士;;1957年任梅隆科学研究所执行所长年任梅隆科学研究所执行所长;;1961年任斯坦福大学化学系教授年任斯坦福大学化学系教授;;1974年获诺贝尔化学奖年获诺贝尔化学奖。
1975年退休年退休;;1985年9月9日逝世日逝世。
在高分子物理化学方面的贡献,几乎遍及各个领域几乎遍及各个领域。
既是实验家又是理论家是实验家又是理论家,,是高分子科学理论的主要开拓者和奠基人之一和奠基人之一。
著有著有《《高分子化学原理子化学原理》》和《长链分子的统计力学的统计力学》》等。
线形缩聚反应的统计学假设官能团等活性反应程度p,则的百分数,它表示聚合反应到达时刻t 时,参加反应的COOH的百分数1-p就是时刻t 时一个给定的COOH 还没参加反应的几率57聚酰胺化反应的过程分子式存在的结构单元数反应了的COOH数10213243x x-158591、x-聚体的数量分布函数问题:从聚合的混合物中从聚合的混合物中,,随机选择一个分子随机选择一个分子,,恰好含有x 个结构单元(x-聚体聚体))的几率是多少的几率是多少??aAb 型则:x-1个COOH 连续反应掉的几率:p x-11个COOH 未反应掉的几率未反应掉的几率::1-pP(x)=p x-1(1-p)a-A-A-A-A-A-A ┅A-A-bp p p p p p pp x-11-p60共有N 个分子个分子,,x-聚体的数目为N x 反应产生的水被脱除反应产生的水被脱除,,则COOH 的总数总是等于分子总数NP(x)=p x-1(1 -p)N x /N =p x-1(1 -p)N x =Np x-1(1 -p)N(COOH)=N =N 0(1-p )N x =N 0p x-1(1-p)22-4161•此式是线型缩聚反应产物分子量的数量分布函数•在任何反应程度p 时单体时单体((x=1)总是有最大的存在几率•随反应程度的提高随反应程度的提高,,其分布变宽其分布变宽,,平均分子量增大N x =N 0p x-1 (1-p)22-4162N x =N 0p x-1 (1-p)2所示的数量分布曲线关系不同反应程度下线性缩聚物分子量的数量分布曲线1. p=0.9600;2. p=0.9875;3. p=0.995063线形缩聚产物的分子量分布函数可完全参照自由基聚合中推导的函数式来表达函数式来表达。






第二章 计算题1、通过碱滴定法和红外光谱法,同时测得21.3 g 聚己二酰己二胺试样中含有2.50⨯10-3mol 羧基。
根据这一数据,计算得数均分子量为8520。
计算时需作什么假定?如何通过实验来确定的可靠性?如该假定不可靠,怎样由实验来测定正确的值?解:∑∑=ii nNm M ,g m i 3.21=∑,852010*5.23.213==-n M ,310*5.2=∑i N 上述计算时需假设:聚己二酰己二胺由二元胺和二元酸反应制得,每个大分子链平均只含一个羧基,且羧基数和胺基数相等。
可以通过测定大分子链端基的COOH 和NH 2摩尔数以及大分子的摩尔数来验证假设的可靠性,如果大分子的摩尔数等于COOH 和NH 2的一半时,就可假定此假设的可靠性。
用气相渗透压法可较准确地测定数均分子量,得到大分子的摩尔数。
碱滴定法测得羧基基团数、红外光谱法测得羟基基团数2、羟基酸HO-(CH 2)4-COOH 进行线形缩聚,测得产物的质均分子量为18,400 g/mol -1,试计算:a. 羧基已经酯化的百分比 b. 数均聚合度 c. 结构单元数n X解:已知100,184000==M M w根据ppX M M X w w w -+==110和得:p=0.989,故已酯化羧基百分数为98.9%。
9251,1=+=n nw M P M M51.9210092510===M M X n n3、等摩尔己二胺和己二酸进行缩聚,反应程度p 为0.500、0.800、0.900、0.950、0.980、0.990、0.995,试求数均聚合度n X 、DP 和数均分子量n M ,并作n X -p 关系图。
4、等摩尔二元醇和二元酸经外加酸催化缩聚,试证明从开始到进行缩聚,反应程度p 为0.500、0.800、0.900、0.950、0.980、0.990、0.995,试求数均聚合度n X 、DP 和数均分子量n M ,并作n X -p 关系图。
解:在外加酸催化的聚酯合成反应中存在10+'=t c k X nP=0.98时, 50=n X , 所需反应时间0149c k t '=; P=0.99时, 100=n X , 所需反应时间0199c k t '=。
所以,t 2大约是t 1的两倍,故由0.98到0.99所需的时间相近。
5、由1mol 丁二醇和1mol 己二酸合成数均分子量为5000的聚酯,a. 两基团数完全相等,忽略端基对数均分子量的影响,求终止缩聚的反应程度P ;b. 在缩聚过程中,如果有5mmol 的丁二醇脱水成乙烯而损失,求达到同样反应程度时的数均分子量;c. 如何补偿丁二醇脱水损失,才能获得同一数均分子量的缩聚物?d. 假定原始混合物中羧基的总浓度为2mol ,其中1.0%为醋酸,无其它因素影响两基团数比,求获得同一数均聚合度时所需的反应程度。
解:a. —[CO(CH 2)4COO(CH 2)4O]— M 0=(112+88)/2=100,5010050000===M M X n n 由9800.011=⇒-=P PX n b. r=Na/Nb=2×(1-0.005) /(2×1)=0.995445310053.4453.449800.0995.02995.01995.012110=⨯=⨯==⨯⨯-++=-++=M X M rP r r X n n n c. 可排除小分子以提高P 或者补加单体来补偿丁二醇的脱水损失。
d. 依题意,醋酸羧基为2×1.0%=0.02mol 己二酸单体为(2-0.02)÷2=0.99mol ∴9900.102.0199.022=+++=f根据fP X n -=22代入数据9900.12253.44⨯-=P解得P =0.98256、(略)7、(略)8、等摩尔的乙二醇和对苯二甲酸在280℃下封管内进行缩聚,平衡常数K=4,求最终n X 。
另在排除副产物水的条件下缩聚,欲得100=n X ,问体系中残留水分有多少?解:3111=+=-=K pX nLm ol n n Kpn KpX w w wn /10*4100114-==≈=-=9、等摩尔二元醇和二元酸缩聚,另加醋酸1.5%,p=0.995或0.999时聚酯的聚合度多少?解:假设二元醇与二元酸的摩尔数各为1mol ,则醋酸的摩尔数为0.015mol 。
N a =2mol ,N b =2mol ,015.0'=b N mol985.0015.0*2222,=+=+=bb a N N N r当p=0.995时,88.79995.0*985.0*2985.01985.01211=-++=-++=rp r r X n当p=0.999时,98.116999.0*985.0*2985.01985.01211=-++=-++=rp r r X n10、尼龙1010是根据1010盐中过量的癸二酸来控制分子量,如果要求分子量为20000,问1010盐的酸值应该是多少?(以mg KOH/g 计)解:尼龙1010重复单元的分子量为338,则其结构单元的平均分子量M=16934.11816920000==n X假设反应程度p=1,983.0,11211=-+=-++=r rrrp r r X n尼龙1010盐的结构为:NH 3+(CH 2)NH 3OOC (CH 2)8COO -,分子量为374。
由于癸二酸过量,假设Na (癸二胺)=1,N b (癸二酸)=1.0/0.983=1.0173,则 酸值)1010/(18.53742*56*)10173.1(*2*)(*)(1010盐g mgKOH M N KOH M N N a a b =-=-=11、己内酰胺在封管内进行开环聚合。
按1 mol 己内酰胺计,加有水0.0205mol 、醋酸0.0205mol ,测得产物的端羧基为19.8 mmol ,端氨基2.3mmol 。
从端基数据,计算数均分子量。
解:NH(CH 2)5CO +H 2O ————HO-CO (CH 2)5NH-H└-------┘0.0205-0.0023 0.0023NH(CH 2)5CO +CH 3COOH ————HO-CO (CH 2)5NH-COCH3 └-------┘0.0205-0.0175 0.0198-0.0023 M=1132.57620198.00175.0*430023.0*10198.0*17113*1=+++==∑in n m M 12、等摩尔己二胺和己二酸缩合,p=0.99和0.995,试画出数量分布曲线和质量分布曲线,并计算数均聚合度和重均聚合度,比较两者分子量分布分布的宽度。
解:x -聚体的数量分布函数为)1(1P P NN x x-=- x -聚体的重量分布函数为21)1(P xP WW x x-=-99.1199111001199.0==-+==-==n ww n X X P PX PX P 时995.13991120011995.0==-+==-==n ww n X X P PX PX P 时W x / W ×103xN x / N ×103反应程度高的,分子量分布要宽一些。
13、邻苯二甲酸酐与甘油或季戊四醇缩聚,两种基团数相等,试求:a. 平均官能度 b. 按Carothers 法求凝胶点 c. 按统计法求凝胶点解:a 、平均官能度: 1)甘油:4.2233*22*3=++=f2)季戊四醇:67.2121*42*2=++=fb 、 Carothers 法: 1)甘油:833.04.222===fp c 2)季戊四醇:749.067.222===f p c c 、Flory 统计法: 1)甘油:1,1,703.0)2([12/1===-+=ρρr f r r p c2)季戊四醇:1,1,577.0)2([12/1===-+=ρρr f r r p c14、分别按Carothers法和Flory统计法计算下列混合物的凝胶点:a. 邻苯二甲酸酐和甘油的摩尔比为1.50:0.9815、用乙二胺或二亚乙基三胺使1000g环氧树脂(环氧值为0.2)固化,固化剂按化学计量计算,再多加10%,问两种固化剂的用量使多少?解:环氧树脂f=2,乙二胺f=4,二次乙基三胺f=5乙二胺用量(1000/100)×0.2×(1/4)×(1+10%)=0.55mol 重量=0.55×60=33g二次乙基三胺用量(1000/100)×0.2×(1/5)×(1+10%)=0.44mol 重量=0.44×103=45.32g16、AA、BB、A3混合体系进行缩聚,NA0=NB0=3.0,A3中A基团数占混合物中A 总数(ρ)的10%,试求p=0.970时的n X以及n X= 200时的p。
解:N A0=N B0=3.0,A3中A基团数占混合物中A总数(ρ)的10%,则A3中A基团数为0.3mol,A3的分子数为0.1 mol。
N A2=1.35mol;N A3=0.1mol;N B2=1.5mol034.21.035.15.133=+++=++++=C B A C C B B A A N N N f N f N f N ffp X n -=22当p=0.970时,74034.2*97.022=-=nX200=n X 时,p fp X n 034.22222-=-=p=0.97317、2.5mol 邻苯二甲酸酐、1mol 乙二醇、1mol 丙三醇体系进行缩聚,为控制凝胶点需要,在聚合过程中定期测量树脂的熔点、酸值(mgKOH/g 试样)、溶解性能。
试计算反应至多少酸值时会出现凝胶。
解:已知按Carothers 方程计算:按Flory 方程计算以P 0=0.9计,起始反应羧基摩尔数为2.5×2×0.9=4.5,剩余羧基摩尔数为0.5,体系总重为524g ,每克树脂含羧基摩尔数为0.5/524=9.6×10-4mol/g ,酸值为9.5×10-4×56.1×103=53.52(mg KOH )。
以P 0=0.7906可作相似的计算。
实际凝胶点时的酸值在这两者之间。
18、制备醇酸树脂的配方为1.21mol 季戊四醇、0.50mol 邻苯二甲酸酐、0.49mol 丙三羧酸[C3H5(COOH )3],问能否不产生凝胶而反应完全?解:根据配方可知醇过量。
245.249.05.021.1)3*49.02*5.0(*2=++++=f89.02==fp c ,所以必须控制反应程度小于0.89过不会产生凝胶。