当前位置：文档之家 › 第二章角动量分解

第二章角动量分解

  • 格式：ppt
  • 大小：4.15 MB
  • 文档页数：84

下载文档原格式

  / 84

合集下载

Ch3.4(角动量定理和角动量守恒定律)

Ch3.4(角动量定理和角动量守恒定律)


分量式
M
M
x
yF z zF y
zF x xF z
y
M z xF y yF x
3) 作用于质点上所有力矩的矢量和，等于合力的力矩。

i
M
i
r F1 r F 2 r F n
r ( F1 F 2 F n ) r F M
1 p1
m
v1
m
2
B p2
r sin
r1
r2
L 2 r2 p 2 sin 2 mr 2 v 2 sin 2 mv 2 OD
O
讨论：
① 作直线运动的质点， r 和 p 可能逐点变化，但 d r sin 保持不变。
② 对不同参考点的角动量一般不同。 ③ 若 p m v 不变，则：L1 L 2 ，即匀速直线运动 的质点对同一参考点的角动量守恒 L C 。
一、角动量 （一）质点的角动量 1. 定义：某一质点，动量 对 O 点的径矢为 r ，则它 对 O 点的角动量(动量矩)为 注意：
x
P
z
L
p sin
O
r sin
r
y
p
m

p cos
（1）大小： L rp sin mrv sin 方向： 用右手螺旋定则确定。 （2）相对性 ① 对不同的参考系，矢径不同，动 量不同，角动量也不同。 ② 参考点不同， 矢径不同，角动量也不同。
L L1 L 2 L n r1 p 1 r2 p 2 rn p n

2-5角动量 角动量守恒定律

2-5角动量 角动量守恒定律


例：一个人站在转台（质量为M，半径为R）的边
缘，质量为m ，当人沿转台边缘行走一周时，人和转台
相对地面各转过了多少角度？
解：取人和转台为一系统，对整个系统而言，M 0
系统的角动量守恒。
取地面为参照系，人相对地面转动的角速度为 1，
转台相对地面转动的角速度为 2 ，人相对转台转动的
角速度为 。
(mR2 )1
12 v0
7l
由角动量定理
M dL d(I) dI
dt dt
dt
即
mgr cos d ( 1 ml2 mr2 ) 2mr dr
dt 12
dt
考虑到 t
dr g cost 7lg cos(12v0 t)
dt 2
24 v0
7l
§2.5角动量 角动量守恒定律 第2章 运动定律与力学中的守恒定律
§2.5角动量 角动量守恒定律 第2章 运动定律与力学中的守恒定律
2.5.L2 质r点的p角动量定dp理
F,
dL ?
dL
d
(r
dt
p)
r dp
dt
dr
p
dt
dr v,
dt
v p 0
dt dL
dt r dp
r
F
dt
dt
dt
M
dL
作用于质点的合力对参考点 O 的力矩 ，等于质点对该点 O 的角
得 LdL m2 gR3 cosd
L LdL m2gR3
cosd
0
0
L mR 3 2 (2g sin )1 2
L mR 2
( 2g sin )1 2
R
§2.5角动量 角动量守恒定律 第2章 运动定律与力学中的守恒定律
动力学3-角动量

动力学3-角动量


例7 一小球沿竖直的光滑圆轨道由静止开始下滑.求 小球在B点时对环心的角动量和角速度.
解:力矩分析 M mgR cos
用角动量定理： M dL dt
O

R
A
dL mgR cos dt
又 L mR 2 mR 2 d dt
B
mg
LdL m 2 gR3 cos d
dL d mvl cos mgl sin dt dt
d g sin dt v cos
gl sin 2 2 v cos

g l cos
而
d v l sin dt
gl v sin cos
由此解得
19
§3.6 质点系的角动量、角动量定理
1、质点系的角动量（对同一动的开普勒第二定律 例:行星相对太阳的矢径在单位时间内扫过的面积(面 积速度)是常量
解:
行星在太阳作用 下沿椭圆轨道运 动。
径矢扫过的面积等 于图中阴影面积
L
v

m
r
r
面积速度
行星受力方向与矢径在一条直线（中心力），故角动量守恒。


有
令 定义为力 力矩的大小 对固定点O的力矩
M
r
o
F

称力臂
质点角动量定理的微分形式：
若力矩作用一段有限时间，则有质点角动量定理的积分形式：
称冲量矩，它反映在一段时间内力矩的时 间积累作用。
——质点角动量定理的积分形式
例1：自由下落质点的角动量(对 A 点,对 O 点) o （1）对 A 点的角动量 任意时刻 t， 有
c ri '
mi
由 ri rc ri ' 得 vi vc vi '
动量与角动量

动量与角动量

2mv 2 0.58 6.26 2 F 3.82 10 N t 0.019
例2：质量为m的质点做圆锥摆运动，质点的速 率为v，圆半径为R。圆锥母线与轴线之间的夹 角为 ，计算质点所受的拉力在一周内的冲量。

演示
逆风行舟
F进 风
F风对帆
F横
1 1 2
帆
Δ
2
F帆对风 Δ
×
i c i
x 质心位置是质点位置 以质量为权重的平均值。
二、几种系统的质心 ● 两质点系统 m1
·r
z
C
1
×
m2 r2
·
m1 r1 = m2 r2
● 连续体
dm ×C rc m y
r
0
r dm rC m
xdm xC m
x
……
●均匀杆、圆盘圆环、球，质心为其几何中心。 ●“小”线度物体的质心和重心是重合的。 求挖掉小圆盘后系统的质心坐标。 [例6]如图示， 解： 由对称性分析，质心C应在x轴上。 y 令 为圆盘的面密度， 均质圆盘 R
L r p
·
于是有
dL M dt
质点角动量定理 （微分形式）
或
d L M dt
积分

t2 M t1
d t L2 L1
质点角动量定理 （积分形式）

t2 M t1
d t 称冲量矩 ——力矩对时间的积累作用。
力矩的量纲是ML2T-2，单位是N.m
可认为动量近似守恒。
6、动量守恒定律是比牛顿定律更普遍、更基本 的定律，它在宏观和微观领域均适用。 7、用守恒定律作题，应注意分析过程、系统和 条件。
例4：一个有1/4圆弧滑槽的大物体的质量为M， 停在光滑的水平面上，另一质量为m的小物体自 圆弧顶端由静止下滑。求当小物体m滑到底时， 大物体M在水平面上移动的距离。
角动量

角动量

中L，摆r球.L相m是对v一支个点可O以的绕角z动轴量为
旋转的矢量.将其分解两个分量
Lz , L,其大小分别为
Lz mvl sin
L mvl cos
L
O Lz
L
l
v
显然，Lz不变，而 L随时间改变.如图,有
L L L mvl cos
mg
（１）
10
另一方面，作用于摆球的外力有张力和重力，张力对支点O 无力矩，而重力矩的方向与圆周半径垂直，其大小为
M mgl sin
（２）
在式①两边都除以 ，t并取 t极限，0 利用角动量
定理及式②，得
dL mvl cos d mgl sin
dt
dt
d g sin dt v cos （３）
而 v l sin d
dt
由此解得
（４）
v sin gl cos
（３）和（４）
v2
gl sin2
cos
g l cos
20
例 太阳质量 M，行星椭圆轨道半长轴 A、半短轴 B。
行星的轨道运动周期 T，导出开普勒第三定律。
2
B
C
m
v1
A v2
M1
选择长轴的两点：近日点 1 和远日点 2， 速度与径矢垂直的唯一的两点。
21
机械能守恒 角动量守恒
1 2
mv12
G
Mm AC
1 2
mv22
G
Mm AC
1 2
(
A
C)mv1
角动量
为什么要定义角动量？ 有心运动中的守恒量，开普勒第二定律
（一）角动量和力矩 （二）质点系角动量定理 （三）质心系的角动量定理
2
动量与角动量分解课件

动量与角动量分解课件


转动定律
力矩等于角动量的变化率。
角动量守恒定律的数学表达式
dL/dt = ΣM(t) = 0，其中dL/dt表示角动量的变化率，ΣM(t) 表示在某一时刻作用于系统的所有力矩的矢量和。
角动量守恒定律的应用实例
01
02
03
天体运动
行星绕太阳旋转、卫星绕 行星旋转等天体运动遵循 角动量守恒定律。
陀螺仪
动量守恒定律的应用实例
总结词
动量守恒定律在日常生活和科技领域中有着广泛的应用。
详细描述
在日常生活和科技领域中，动量守恒定律的应用非常广泛。例如，在航天工程中，火箭通过反作用力 推进，遵守动量守恒定律；在车辆工程中，安全气囊的设计和碰撞实验也需要考虑动量守恒定律；在 体育运动中，例如棒球、篮球等，动量守恒定律也起着重要的作用。
03
动量守恒定律
动量守恒定律的表述总Fra bibliotek词动量守恒定律的表述是系统不受外力或所受外力的矢量和为零时，系统总动量保 持不变。
详细描述
动量守恒定律是经典力学中的一个基本定律，它表述的是在一个封闭系统中，如 果没有外力作用或者外力的矢量和为零，那么系统的总动量将保持不变。也就是 说，系统的初始动量将等于未来的任何时刻的动量。
在量子力学中的应用
描述粒子状态
在量子力学中，动量和角动量是 描述粒子状态的重要物理量，可 以用来分析粒子的波函数和能量
等。
确定粒子相互作用
通过动量和角动量守恒定律，可 以确定粒子之间的相互作用力和 扭矩，从而分析系统的量子态。
解决实际问题
在量子力学中，动量和角动量广 泛应用于解决实际问题，如原子 和分子结构、核结构和凝聚态物
VS
详细描述
角动量定义为转动惯量I与角速度ω的乘 积，即L=Iω。转动惯量是描述物体转动 惯性大小的量，与物体的质量分布和旋转 轴的位置有关。角速度是描述物体旋转快 慢的物理量，其方向沿旋转轴。在计算时， 应注意角动量的矢量性，即需要同时考虑 转动惯量和角速度的大小和方向。
角动量 角动量定理

角动量 角动量定理


d M (r P) dt
定义： L r P ——角动量
——角动量定理
第2章 运动定律与力学中的守恒定律
2–5 角动量 角动量定理
3
作用在质点上的力矩等于质点角动量对时间的变化率。 此即质点对固定点的角动量定理。

t
t0
Mdt L L0

t
t0
Mdt
叫冲量矩
1
1
第2章 运动定律与力学中的守恒定律
2–5 角动量 角动量定理 用绳系一质量为m小球使之在光滑的桌面上作圆周运动，球的速率
12
vo ，半径为ro 。问：当缓慢拉下绳的另一端，圆的半径变为 r 时 ，小球的速率v是多少？
解：因为通过转轴的合力矩为零，所以小球的角动量 守恒
Z
vo
ro
L
mr o vo mr v
ro v vo r
F
第2章 运动定律与力学中的守恒定律
2–5 角动量 角动量定理
13
判断：匀速圆周运动的质点受到向心力的作用，所 以其角动量一定守恒。
L
mv
F
r
L
O
r
mv
F
O’
第2章 运动定律与力学中的守恒定律
2–5 角动量 角动量定理
14
角动量守恒的情况: 匀速直线运动。 (1) 力 F等于零； (2) 力 F的作用线与通过固定点，即 r =0。 (3) 力 F 的作用线与矢径 r 共线即(sin=0)。
角动量
1. L r P
L 的方向符合右手法则.
L m vrsin
第2章 运动定律与力学中的守恒定律
第2章刚体力学分解

第2章刚体力学分解

1 Rmv ( MR 2 mR 2 ) 2

mv 1 ( M m )R 2
R
M
O
损失的动能为:
1 1 2 Ek 0 Ek mv ( J圆柱 mR 2 ) 2 2 2
mM v2 2 M 4m
课堂练习
3. 如图，求
解:
1 mgh mv 2 2
1 1 1 2 2 2 mgh mv J MR 2 '2 2 2 2 3
J
v r
v 'R
2 1 1 J 1 2 v 1 1 J 2 2 2 2 mgh mv 2 v MR ( m M ) v 2 2 r2 2 3 R2 2 2 r2 3
v
mi
vi
转动惯量 J ( mi ri2 )
i
转动动能
1 2 Ek J 2
1 2 E k mv 2
二、转动惯量

O
ri
m1
J
2 ( m r ii) i
2 r dm
m2
mi
vi
r1
o
r2
dl
质量为线分布 质量为面分布
dm
dS
dV 质量为体分布
转动惯量以下三个因素决定： 刚体的质量、质量的分布、转轴的位置
例2. 一根长为l、质量为m的均匀细直棒，其一端有一 固定的光滑水平轴，因而可以在竖直平面内转动。最 初棒静止在水平位置，求它由此下摆角时的角加速度 和角速度。
解：棒下摆 时，重力矩为
1 M mgl cos 2 转动定律M = J 得
O

1 M 2 mgl cos 3 g cos 1 J 2l ml 2 3
大学物理角动量PPT精选文档

大学物理角动量PPT精选文档


解 设盘对地的角速度为
体系初态角动量 [12mR 21m0(12R)2]o
o
末态盘的角动量 1 mR 2
2
R/2
V 人 地 V 人 盘 V 盘地 v
R 2
21
[12m2R1m0(12R)2]o12 mR 2 1m0(R2v)R2
o
2v 21R
o
(2) 欲使盘静止，可令
o
2v 0 21R
R/2
质量为m、长度为L的细直棒，通过质心 C且垂直于棒的轴
I 1 mL2 12
3
上次内容回顾
均质圆盘(m,R)绕中心轴转动时，
I 1 mR2 2
刚体对任一转轴的转动惯量I等于刚体通过质心的 平行轴的转动惯量Ic加上刚体的总质量M乘以两平行 轴间距离d的平方，即
I=Ic+Md2
4
上次内容回顾
LI
M dL dt
l
mg
讨论: (1)当=0时，=3g/2l， =0 ； (2)当=90°时， =0，=(3g/l)1/2。
11
例题5 一质量为m、半径为R的匀质圆盘绕通过盘 心且垂直于盘面的光滑轴正以o的角速度转动。现将 盘置于粗糙的水平桌面上，圆盘与桌面间的摩擦系数 为µ，求圆盘经转几圈将停下来？
I 1 mR 2 2
计算出来摩 擦力矩是关键
o
dr r
M0Rrgm R22rdr
2 3
mgR
12
M0Rrgm R22rdr
2 3
mgR
I 1 mR 2 2
于是得M4g
I 3R
o
dr r
又由2-o2=2，所以停下来前转过的圈数为
N 22o2 136o2R g 13
角动量和角动量守恒

角动量和角动量守恒


dv dω at = = r = rα dt dt 2 v 2 an = = rω r
dθ ω= dt
v
dS
r dθ P
O 匀变速定轴转动
dS v= dt dv at = dt
v = v0 + at 1 2 S = v0t + at 2
2 v2 − v0 = 2aS
dω α= dt
ω = ω0 +αt
i
v r v L = L轨道 + L 旋 自
轨道角动量 例,地球绕太阳转 . 地球绕太阳转 电子绕原子核转 自旋角动量 也叫固有角动量 也叫固有角动量
v rc
5.2.2、质点系的角动量定理 、
v v dLi = Mi dt
分离出系统; 分离出系统
j
i
j
'
代表系统内的质点 代表系统外的质点 j 代表系统内的质点, j'代表系统外的质点. v v v v dL = M = ∑M + ∑M dt
质点系角动量
选原点 O 质心在 c
C质心 质心
n v v v v L = ∑Li = ∑(r × mvi ) i
5.2.1、 5.2.1、质点系角动量
i =1
v v v' v [( c 以上两式先后代入前式 L = ∑ r + r ) × m vi ] i i i v v v v v v v v v ∑[ri '×mvc ] = [∑mri ']×vc = rc ×∑mivi + ∑ri '×mi (vc + vi ' ) i i i i i i v' ∑mri v v' v = r × mv + [r '×mv ] + [r '×mv '] v v v v v v i ∑i ii i c =M i ×vc = Mrc ×vc = 0 c ∑ i i ∑ i i i i M
角动量

角动量

m1 x1 m2 x2 xC m1 m2

y
y2 yC y1
m2
C
m1
x1 xC x2
解 根据质心的位置坐标式可知
; yC m1 y1 m2 y2 m1 m2
O
x
可以证明，该质点系的质心C位于两质点的连线上，且质 心到各质点的距离与质点的质量成反比。
由质心的位置可得 比较此两式还可知
24
3. 角动量守恒定律 若 M 0，则 L r mv 常矢量
如果对于某一固定点O，质点所受的合力矩为零，则此质点对该 定点的角动量保持不变。 讨论
时， ，质点的角动量守恒。 当合力 0 F M 0

力的作用线始终通过一固定点（力心）， 对力心的力矩为零。
o
r
r
m

p
p
o
* 质点对某参考点的角动量反映质点绕该参考点旋
转运动的强弱。 *必须指明参考点，角动量才有实际意义。
16
讨论

L rpsin mv rsin 角动量的方向： 位矢 r 和动量mv 的矢积方向。 质点绕圆心作圆周运动时 L m r v
人相对于湖岸移动的距离为s
m
xC xC
l
m1l sb m1 m2
3m
12
一、角动量 问题：将一绕通过质心的固定轴转动的圆 盘视为一个质点系，系统总动量为多少？
p总 MvC 0
C M
Байду номын сангаас
由于该系统质心速度为零，所以，系统总动量为零， 系统有机械运动，总动量却为零？
3.9 质心

(m1 , r1 ,v1 ) ,(m2 , r2 ,v 2 )

3动量与角动量

第三章 动量与角动量牛顿定律是瞬时的规律。

但在有些问题中，如：碰撞（宏观）、散射（微观）…我们往往只关心过程中力的效果，即只关心始末态间的关系，对过程的细节不感兴趣；而有些问题我们甚至尚弄不清楚过程的细节。

作为一个过程，我们关心的是力对时间和空间的积累效应。

⎩⎨⎧⇒⇒角动量转动动量平动冲量矩，改变冲量，改变 力在空间上的积累 ⇒作功，改变动能§1 冲量，动量，质点动量定理定义：力的冲量 ⎰=21d t t t F I质点动量 vm p =由 tp t m F d d d )v d( == 有 p t F Id d d == ─ 动量定理(微分形式)12d 21p p t F I t t-==⎰ ─ 动量定理（积分形式）平均冲力 tp t t t F F t t ∆∆=-=⎰1221d [例]已知：一篮球质量m = 0.58kg ，从h = 2.0m 的高度下落，到达地面后，以同样速率反弹，接触地面时间t ∆= 0.019s 。

求：篮球对地面的平均冲力球对地F解：篮球到达地面的速率为：m/s 26.6280.922v =⨯⨯==gh ，篮球接触地面前后动量改变（大小）为： v 2m p =∆由动量定理有：v 2m p t F =∆=∆⋅地对球由牛顿第三定律有：力在时间 上的积累υ1υ2Δυ风 F F地对球球对地F F =N1082.3019.026.658.02v 22⨯=⨯⨯=∆=t m 逆风行舟的原理如下图所示：§2 质点系动量定理对于质点系，设：i F为第i 个质点受的合外力，ij f为第i 个质点受第j 个质点的内力。

对第i 个质点： i i j ij i p t f Fd d =+∑≠）（对质点系： ∑∑∑=+≠i ii i j ij i p t f F d d (）由牛顿第三定律有： ∑∑=≠iij ij f 0令 P p F F ii i i==∑∑ ，外 则 P t F d d =外 或 tPF d d=外──质点系动量定理（微分形式）积分得 1221d P P t F t t-=⋅⎰外──质点系动量定理（积分形式）质点系动量定理处理问题可避开内力，较方便。

大学物理-角动量守恒定律 PPT


dt 12
dt
考虑到 t
dr g cost 7lg cos(12v0 t)
dt 2
24 v0
7l
37
例6 一杂技演员M由距水平跷板高为h 处 自由下落到跷板的一端A，并把跷板另一端 的演员N弹了起来．问演员N可弹起多高?
M
h
N
C
A
B
l/2
l
38
设跷板是匀质的，长度为l，质量为m'，
6mv0
(M 3m)l
v0 m
31
例3 摩擦离合器 飞轮1：J1、 w1 摩擦轮2： J2 静止，两轮沿轴向结合，结合后两轮达到 的共同角速度。 解：两轮对共同转轴的角动量守恒
21
试与下例的齿轮啮合过程比较。
32
例4 两圆盘形齿轮半径r1 、 r2 ，对通过盘心
垂轮直以于0 盘转面动转，轴然的后转两动轮惯正量交为啮J1合、，J2求，啮开合始后1
点o的矢径为 r ，动量为 p ，如下图。在计算其
角动量时，注意有两个特点：
(1) o点到 p 方向的垂直距离 r sin 不变;
(2) L 方向不变;
p2
假如 p 的大小也不变， 显然L 的大小不变。这表
明，自由质点对任意参考 点的角动量保持不变。
p1
1 r1

2
r2
r sin o
5
1.5.2 质点角动量定理
必须指明是对哪个点而言的
注意两点：
(1) 质点的角动量是相对某一参考点而言的，因此
对不同的参考点，角动量 L 不同;
(2) L 的大小在0~ rp 之间变化，如果把动量分解
为径向分量 pcos 和横向分量 psin ，则仅横

角动量

周运动。小球所需的向心力由系在小球上并通过一竖直管的轻绳所提供。当往 下拉绳, 使小球作圆周运动的半径变为 r2 时, 试问此时小球的速度为多大及拉 力所作的功。
己 知 : r1 v1 r2 求 : v2 A
解 : 重 力 和 板 的 反 作 用 力平 相 衡, 只 受 绳 的 有 心 力 作 用 M 0 角动量守恒 : r1 m v1 r2 m v 2 r1v1 r2 v 2 v2
角动量定理、角动量守恒定律
本课时教学基本要求
1、掌握质点和质点系的角动量、力矩等概念，会计算相 应的角动量和力矩。
2、理解质点和质点系的角动量原理及角动量守恒定律， 并能求解质点作平面运动时相应的力学问题。
3、熟练掌握三大守恒定律的综合应用。
2015-4-12
质点动力学
角动量——与物体转动相联系的守恒量
2015-4-12
质点动力学
【例题】如图所示，有一劲度系数为 k的弹簧， 将m2和墙壁连 接，m2静止在光滑水平面上。质量为 m1的小车自高为 h的斜面 上由静止开始沿轨道下滑，并与 m2相撞，撞后合在一起运动。 求弹簧所受的最大压力。
全过程可分为三个阶段来处理： 1.小车 m1由静止开始下滑到与 m2碰撞前，机械能守恒定律； 2. m1与 m2作完全非弹性碰撞，动量守恒定律； 3. m1与 m2压缩弹簧过程，机械能守恒定律。
r2
r1 v1 r2
( r1 ＞ r2
v 2 ＞ v1 )
r2
r2 A F dr Fn dr r1 r1 r2

r1
2 v2 1 m dr m (vr ) 2 3 dr r r r1
r
m (v1 r1 ) 2

第 2 章 角动量 角动量守恒定律解剖


L
行星绕恒星的转动： ——轨道在一平面内！
因为 F 与 r 共线： L = c
即：mvrsin = c
dr
mvrsinα = m rsinα
dt
= 2m
1 r dr sinα
2
= 2m dS
dt
dt
dS = c dt
v α dr
r Fm
dr α
r
例：如图，光滑的水平面上一绳子长L=2m，一端固定于O 点，另一端系一质量m=0.5kg的物体。初始物体位于A 点，OA间距d=0.5m，绳处于松驰状态。现使物体以 初速vA=4m/s垂直于OA向右滑动，随后物体到达B点， 此时其速度方向与绳垂直，求此时物体速度的大小vB。
dt dt
dt
dr p = v p = 0 dt
即恒有：r dp d(r p) dt dt
卫星
r p = L ——角动量
——描述转动状态
M = dL ——转动定律
地球
+
dt
•力矩的大小
M = rF
M = r Fsinθ
力矩的方向：由 r F 确定，满足右手规则。
L = rp
力矩的单位：N ·m
M
=
rF
=
rm
d2r dt2
=
mr [-ω2 (acosωt
i
+ bsinωt
j
)]
= -mω2r r = 0
接上题：求质点对o的 L、M 。
ML
解：由力矩与角动量的定义，有：
L
=
r p
=
(r
+ r0 ) m
d(r + r0 ) dt
dr

角动量定理及角动量守恒定律

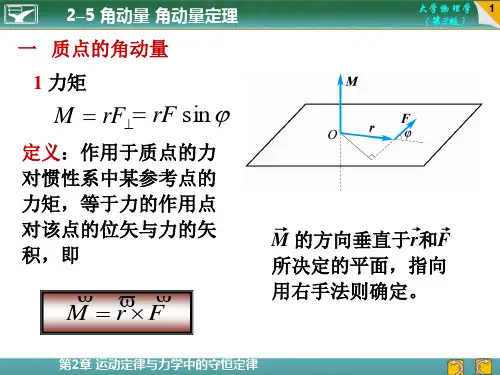
角动量定理及角动量守恒定律一、力对点的力矩：如图所示,定义力F对O 点的力矩为： F r M ⨯=大小为: θsin Fr M ＝力矩的方向：力矩是矢量，其方向可用右手螺旋法则来判断：把右手拇指伸直,其余四指弯曲，弯曲的方向由矢径通过小于1800的角度转向力的方向时,拇指指向的方向就是力矩的方向.二、力对转轴的力矩:力对O 点的力矩在通过O 点的轴上的投影称为力对转轴的力矩。

1）力与轴平行，则0=M;2）刚体所受的外力F 在垂直于转轴的平面内，转轴和力的作用线之间的距离d 称为力对转轴的力臂。

力的大小与力臂的乘积，称为力F对转轴的力矩,用M表示。

力矩的大小为： Fd M ＝或： θsin Fr M ＝其中θ是F 与r的夹角.3）若力F不在垂直与转轴的平面内,则可把该力分解为两个力,一个与转轴平行的分力1F，一个在垂直与转轴平面内的分力2F ，只有分力2F 才对刚体的转动状态有影响.对于定轴转动，力矩M 的方向只有两个，沿转轴方向或沿转轴方向反方向，可以化为标量形式，用正负表示其方向.三、合力矩对于每个分力的力矩之和。

合力 ∑=i F F合外力矩 ∑∑∑=⨯=⨯=⨯i i i M F r F r F r M＝即 ∑i M M＝四、质点的角动量定理及角动量守恒定律在讨论质点运动时，我们用动量来描述机械运动的状态，并讨论了在机械运动过程中所遵循的动量守恒定律。

同样，在讨论质点相对于空间某一定点的运动时，我们也可以用角动量来描述物体的运动状态。

角动量是一个很重要的概念，在转动问题中，它所起的作用和(线）动量所起的作用相类似。

在研究力对质点作用时,考虑力对时间的累积作用引出动量定理，从而得到动量守恒定律；考虑力对空间的累积作用时,引出动能定理，从而得到机械能守恒定律和能量守恒定律。

至于力矩对时间的累积作用，可得出角动量定理和角动量守恒定律；而力矩对空间的累积作用，则可得出刚体的转动动能定理，这是下一节的内容.本节主要讨论的是绕定轴转动的刚体的角动量定理和角动量守恒定律，在这之前先讨论质点对给定点的角动量定理和角动量守恒定律。

角动量


二、刚体的转动定律
d M iz I I dt i 1
n
刚体绕定轴转动时，它的角加速度与作用于刚 体上的合外力矩成正比，与刚体对转轴的转动惯量 成反比。 刚体定轴转动的转动定律
刚体转动定律可由牛顿第二定律直接导出
dF df adm
dF 和 df为合外力和合内力
dm dV
2
2rdr l
3
Z
O
dJ r dm 2lr dr
I dI
R 0
R
m 1 2 I mR R 2 l 2
1 4 2lr dr R l 2
3
可见，转动惯量与l无关。所以，实心圆柱对其轴的 转动惯量也是mR2/2。
—— 质点的角动量守恒定律。
§2.6 刚体的定轴转动
一、质点系的角动量定理
1、质点系对固定点的角动量定理
对由n个质点组成的质点系中第i个质点，有：
n1 d ri ( Fi外 f ji ) (ri mi vi ) dt j 1
质点i受力
对i求和有：
n
n n 1 d n ri Fi外 r f ji (ri mi vi ) dt i 1 i 1 i 1 j 1
dL d ( mv ) dr d ( mv ) dr r mv F v dt dt dt dt dt dL v mv 0 r F M r F v mv dt dL 角动量定理的微分形式 M dt
分解为作用在质量元dm上的 切向力和法向力：
Z
dF df a dm
dFn df n an dm
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

o
x
dx
x
解： 如图，距O点为x，长为dx的质元dm m 的质量 dm dx
其所受阻力矩
M xdmg
l dM x(dm g) mg L 1
l
x

0
xdx
2
mgL
o
dx x
三、质点角动量守恒定律
若外力对某个固定点O的力矩为零时，即 M 0 ， 则对同一固定点O的角动量不变，即 L L0
【补充例】质点的圆周运动 （对圆心的）角动量：
L
m
v
【补充例】 行星在绕太阳公转时的椭圆轨 道运动对定点（太阳）的角动量： L
大小： L mvr sin
L r p m(r v)
voBiblioteka rθ方向：垂直于轨道平面
【补充例】 一质量为m、长为L的均匀细棒， 可在水平桌面上绕通过其一端的竖直固定轴转 动，已知细棒与桌面的摩擦因素为 ,求棒转动 时受到的摩擦力矩的大小。
2.何时M 为零？ a. F 0 b.力的作用线与轴相交 c.受到有心力作用
注意：
3.如果力 F 的方向始终指向一个固定点，则该力就称为
有心力，该固定点称为这个力的力心。 受到有心力作用的物体，相对于力心，其所受力矩为零。
【补充例】一质量为m的质点沿着一条空间曲线运 动，该曲线在直角坐标下的矢径为：
r a cost i b sint j
其中a、b、 皆为常数，求该质点对原点的角动量。
d r 解： v a sin t i b cos t j d r v dt a sin t i b cos tj
§2.3 角动量定理
力矩是通过分析引起转动状态改变的原因而引入的。 本部分通过研究力矩的时间累积效应，引进冲量矩的 概念，建立刻画与力矩的作用效果有关的质点运动 状态的另一描述量—角动量，推导出质点角动量定 理，并将之推广到质点系的一般情形，并考虑了重 要的力矩的时间累计效应为零这一特殊情形。作为 力学基本定理的总结，本部分扼要介绍对称性与守 恒律的问题。 本 §2.3 .1 质点角动量定理与角动量守恒定律 部 §2.3 .2 质点角动量定理与角动量守恒定律 分 内 §2.4 对称性与守恒定律 容
§2.3.1 质点的角动量定理 一、力矩 M 力对参考点O的力矩：
z
r
M r F
为力的作用点的位置矢量
x
O
r

P
F
y
方向由右手螺旋规则确定。
力矩大小：
M Fr sin
在直角坐标系中
r xi yj zk
F Fxi Fy j Fz k
2
M r F
L r mv
P x
1 2 L r m v b i gt j mgtj bmgtk 2
方向垂直于纸面向里
o r L r (mv) mr v (r v) 大小：L mvr sin mvr 方向：
d A B dA dB B A dt dt dt


r F M
v mv r F
dL M dt
质点对固定点O的角动量定理 在惯性参考系中，质点对固定参考点的角 动量在任意时刻的时间变化率等于质点在 该时刻所受合外力对该点的力矩。
二、质点的角动量、角动量定理 在惯性参考系中，一质点 的角动量 L
z
L r p r mv
p
r
为质点的位置矢量
方向由右手螺旋规则确定
大小： L pr sin 由矢量微商法则
x
O
r

P
y
得
dL dr d p pr dt dt dt
z
i j k j k i k i j
M r F x
k
i
j
P
x
i j y Fy k z Fz
O
y
( yFz zFy )i
M xi M y j M z k
Fx
( zFx xFz ) j ( xFy yFx )k
L (4i 3 j ) 6mj 24m k (Z轴正方向)
解：分析 L r mv, r 4i 3 j
0
x
思考：该时刻质点受到的对0点
利用
的力矩的大小和方向？
M r F
【补充例】 t=0时，质量为m的质点由 P点自由下落。 问：1. 在任意t时刻，质点所受的对原点O的力矩? 2.在任意t时刻，质点对原点O的角动量。 O b 解: 在任意t时刻 F mgj 1 2 r xi yj bi gt j v gt j 2 y 1 2 M r F ( bi gt j ) mgj bmg k
dt
L r mv
2 2 mab k mab cos t k mab sin t k
【补充例】质量为 m 的质点，某时刻的位置如图， y 速度为 v 6 j 受力为 F 2 j （4，3） 求：该时刻质点对 0点的角动量 L ？ （SI）
定义冲量矩：

tb
ta
b Mdt dL Lb La
a
角动量定理的另一形式 在惯性参考系中，质点所受合外力在其任一运动过程 中对任一固定点的冲量矩等于质点对该点的角动量在 该过程中的增量。
1. r 为物体相对于指定参考点的位矢，所以求物体所受 的力矩时必须先指明参考点，相对于不同的参考点，对 应的位矢 r 不同。物体所受的力矩不同。