大学文科数学——极限

大一上文科高数知识点总结1. 函数与极限1.1 数列和函数的极限1.2 无穷小与无穷大1.3 连续性与间断点1.4 极限运算法则2. 导数与微分2.1 导数的定义与性质2.2 基本微分公式2.3 高阶导数2.4 隐函数与参数方程的导数3. 微分中值定理与应用3.1 罗尔定理与拉格朗日中值定理3.2 柯西中值定理与洛必达法则3.3 泰勒展开与泰勒公式3.4 极值与最优化问题4. 积分与区间4.1 定积分与不定积分的定义4.2 牛顿—莱布尼茨公式4.3 反常积分4.4 曲线的弧长与平面图形的面积5. 微分方程5.1 微分方程的基本概念5.2 一阶常微分方程5.3 分离变量法与线性微分方程 5.4 高阶线性微分方程6. 无穷级数6.1 数项级数的概念6.2 收敛级数与发散级数6.3 正项级数的审敛法6.4 幂级数与幂级数展开7. 多元函数的极限、偏导数与全微分 7.1 多元函数的极限与连续性7.2 偏导数与全微分的定义7.3 多元函数的极值与条件极值7.4 隐函数的偏导数与全微分8. 多元函数的积分8.1 二重积分的概念与性质8.2 二重积分的计算8.3 三重积分的概念与性质8.4 三重积分的计算9. 空间解析几何9.1 点、直线与平面的位置关系9.2 球面与曲面方程9.3 曲线与曲面的切线与法线9.4 空间直角坐标系与柱面、锥面以上是大一上文科高数的主要知识点总结。

通过学习这些内容，你将对数学的基本思维方式和理论基础有更深入的了解，并为进一步学习更高级的数学课程打下坚实的基础。

记得不仅要理解概念和理论，还要多做练习题，提升自己的解题能力和应用能力。

祝你在数学学习中取得好成绩！。

高等数学基础概念——极限学院：印刷工程系专业：包装技术与设计班级：15包装2班姓名：卢慧学号：150703217一、摘要高等数学极限理论是高等数学教学环节中的重要内容，是学习高等数学、线性代数以及复变函数等大学数学科目的基础科目，极限概念是微积分中最基本的概念，极限思想是数学中极为重要的思想。

下面主要介绍了高等数学中的数列与函数极限的概念、运算法则以及求解方法进行简析。

文章最后，介绍了数学极限思想的发展简史，并对其日后的发展趋势进行展望。

二、关键词高等数学，数列极限，函数极限，运算法则三、正文(一)极限的概念极限概念是由某些实际问题的精确破解而产生的，是用以描述变量在一定的变化过程中的终极状态的一个概念。

比如物理中的瞬时速度的问题。

我们知道速度可以用位移差与时间差的比值表示，若时间差趋于零，则此比值就是某时刻的瞬时速度，这就产生了一个问题：趋于无限小的时间差与位移差求比值，就是0÷0，这有意义吗（这个意义是指“分析”意义，因为几何意义颇为直观，就是该点斜率）？这也迫使人们去为此开发出合乎理性的解释，极限的思想呼之欲出在数学领域中“极限”是用来描述变量在一定的变化过程中的极限状态的。

粗略地讲，在高等数学中，极限一直是一个重要内容，并以各种形式出现而贯穿全部内容。

（二）数列极限首先介绍刘徽的"割圆术",设有一半径为1的圆，在只知道直边形的面积计算方法的情况下，要计算其面积。

为此，他先作圆的内接正六边形，其面积记为A1，再作内接正十二边形，其面积记为A2，内接二十四边形的面积记为A3，如此将边数加倍，当n无限增大时，An无限接近于圆面积，他计算到3072=6*2的9次方边形，利用不等式An+1<A<An+2[(An+1)-An](n=1，2，3....)得到圆周率=3927/1250约等于3.1416。

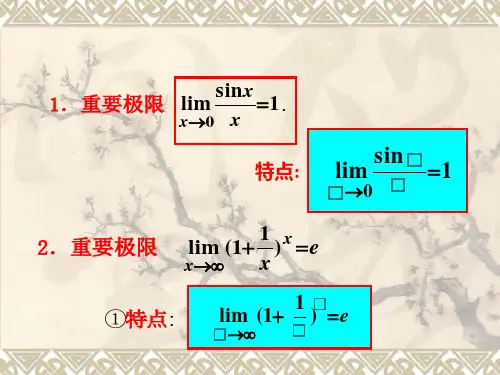
数列极限标准定义：对数列{xn}，若存在常数a，对于任意ε>0，总存在正整数N，使得当n>N时，|xn-a|<ε成立，那么称a是数列{xn}的极限。

第一章微积分的基础问题——集合、实数、极限学而不思则罔，思而不学则殆-----孔子《论语²为政》历史使人聪明，诗歌使人机智，数学使人精细，哲学使人深邃，道德使人严肃，逻辑与修辞使人善辩。

-----培根本章简介在中学，我们学习过集合、实数和简单的极限以及微积分知识，这为进一步学习高等数学奠定了一定的基础．然而，学习微积分为什么要学习集合、实数和极限，它们之间有什么关系，这涉及到所谓的数学基础问题，即数学的可靠性问题．本章将粗略介绍微积分的基础问题，使文科学生对数学有较深入的了解，同时对中学学过的实数和极限知识作一些引申，而集合的具体知识不再述及。

（一）学习目的和要求本章的目的是介绍集合、实数和极限。

要求了解集合、实数与极限在微积分中的作用。

了解我国数学家祖冲之在我国古代数学中所作出的杰出贡献。

（二）课程内容1．极限、实数与集合在微积分中的作用2．实数系的建立及邻域的概念实数系的演变及性质、刻画极限的邻域概念。

3．变量无限变化的数学模型——极限从分形几何中Koch雪花的周长谈起——数列极限、函数极限、无穷小量、极限的四则运算。

4．我国古代伟大数学家——祖冲之（三）重点和难点本章重点：集合、实数与极限在微积分中的作用、邻域的概念。

本章难点：极限概念及其在微积分中的作用。

（四）课程要求1.了解：集合、实数与极限在微积分中的作用，我国数学家祖冲之在我国古代数学中所作出的杰出贡献。

2.理解：函数极限、无穷小量。

3.掌握：极限的四则运算法则。

§1极限、实数与集合在微积分中的作用提出问题数学史中有所谓的第二次数学危机，它与微积分有什么关系呢？现在来开始研究这一问题。

学习过程（1）第二次数学危机概说17 世纪上半叶笛卡儿（法）创建解析几何之后，变量便进入了数学．随之，牛顿（英）和莱布尼茨（德）集众多数学家之大成，各自独立地发明了微积分，被誉为数学史上划时代的里程碑．微积分诞生不久，便在许多学科中得到广泛有效的应用．然而初期的微积分在逻辑上存在着矛盾．粗略地讲，牛顿、莱布尼茨的导数概念是建立在所谓的“无穷小”理论之上的，他们所谓的无穷小，时而是零时而又不是零，这违背了逻辑学中的排中律．正因此，不少学者对微积分的可靠性产生了怀疑，并且一些思想保守的人物借此提出非难，特别是代表守旧势力的英国红衣大主教贝克莱，从维护宗教神学的利益出发，亟力反对蕴含运动变化这一新潮思想的微积分．数学界、哲学界、宗教界的许多人围绕微积分的逻辑基础问题展开了激烈的争论，被数学史界称为第二次数学危机．（2）微积分的理论基础是什么？微积分在长达两个世纪的自身理论完善过程中，法国数学家柯西和德国数学家魏尔斯特拉斯先后建立了极限理论，从而摒弃牛顿、莱布尼茨的含混不清的“无穷小”概念，而代之以“以零为极限的变量为无穷小量”的明确定义，从而解决了微积分的逻辑基础问题，也就消除了第二次数学危机．可见极限是微积分的理论基础．（3）极限的理论基础是什么？极限是微积分的理论基础，然而极限作为运算不总是通行无阻的，例如在有理数范围内就可能行不通．譬如，由的不足近似值构成的有理数序列1， 1．4， 1．41， 1．414， 1．4142，…若在有理数范围内来考察，就不存在极限．但在实数范围内来考察，它的极限就是．可见实数是极限的理论基础，进而可知实数是微积分的基础．（4）实数的理论基础是什么？在19世纪，数学家们认识到实数的可靠性来源于自然数.于是自然数便成了实数的基础，进而自然数成了微积分的基础．（5）自然数的基础是什么？数学家们对数学基础的研究并未到自然数为止．19世纪末，又认识到自然数可由德国数学家康托儿提出的集合来定义，于是微积分的可靠性就取决于集合论的可靠性．因而集合又成了微积分的基础．而微积分又是现代数学的基础知识，于是几乎全部数学都可以建立在集合基础之上．可见集合是整个数学大厦的基石．（6）数学发展的动力是什么？通过前面的介绍，我们体会到，对微积分基础的研究大大推动了微积分的完善和发展，体现了数学发展动力的一个方面，即由数学自身矛盾运动产生的内部力量．还应认识到数学发展动力的另一个方面，即由人类社会实践所产生的外部力量．17世纪资本主义生产力的发展正是推动微积分产生和发展的外部力量．（7）检验数学可靠性的标准是什么？关于数学的可靠性问题，我们固然应该根据数学科学的特点追求数学的逻辑可靠性，但最终还要符合实践可靠性，即数学的可靠性尚需接受社会实践的检验.小结微积分的理论基础如下图所示.集合自然数实数极限微积分作业思考题微积分的基础是什么？§2 实数系的建立及邻域概念提出问题实数既然是极限的基础，那么，实数具有什么性质呢？在实数范围内又是如何实现极限的呢？学习过程由微积分的基础可知，微积分所涉及的数仅限于实数，本节将简述实数的演变及刻画极限的邻域概念.2.1 实数系的演变及性质（略，有兴趣的学生可参阅教材）（1）为什么要先介绍邻域概念？微积分的理论基础是极限，而极限的理论基础是实数.要在实数范围内用极限解决微积本身的问题，就要借助于邻域概念.（2）如何从几何直观抽象出邻域概念？观察图1.1，在点x0附近的数轴上，有一个开区间（x0－δx0+δ）（δ＞0），其内凝聚着无穷多个连绵不断的点，当δ变小时，开区间（x0－δx0+δ）便会变小，其内仍然凝聚着无穷多个连绵不断的点，由点与实数的一一对应，以及实数的连续性可知，当δ越来越小时，开区间也会越来越小，但其内仍有无穷多个连绵不断的点，这就表明落在（x0－δx0+δ）内的变数x便会与x0越来越接近.显然这样的开区间便可作为刻划变量x无限接近于常数x0的一种工具，这一工具便称为x0的δ领域.由此可抽象出领域概念.定义与点x0距离小于δ（＞0）的全体实数的集合称为点x0的δ领域，记作U（x0，δ），x0称为邻域的中心，δ称为邻域的半径（图1.1）.显然点x0的δ领域可用集合记号表示为｛x｜｜x-x｜＜δ﹜，或用区间表示为（x0－δ，x0+δ）.如果点x0的δ邻域U（x0，δ）不包括点x0，则称为点x的去心邻域（图1.2）,记作U°（x0，δ），也可用集合记号表示为｛x｜0＜｜x- x｜＜δ.例用邻域符号和区间符号表示不等式（ε＞0）所确定的x的范围，并描绘在数轴上.解由得，即.所以它表示以点为中心、以为半径的邻域，用邻域符号表示为U（）.由得，所以用区间符号表示为（，）.数轴表示略.小结实数最重要的性质是连续性，正是由于这一性质，极限才得以通行无阻，而邻域是极限在实数范围内得以实行的工具。

第二章 微积分的直接基础——极限§2.1 从阿基里斯追赶乌龟谈起——数列的极限 一个实际问题:如可用渐近的方程法求圆的面积？设有一圆, 首先作内接正四边形, 它的面积记为A 1；再作内接正八边形, 它的面积记为A 2；再作内接正十六边形, 它的面积记为A 3；如此下去, 每次边数加倍, 一般把内接正8×2n -1边形的面积记为A n . 这样就得到一系列内接正多边形的面积: A 1, A 2, A 3, ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ , A n , ⋅ ⋅ ⋅设想n 无限增大（记为n →∞, 读作n 趋于穷大）, 即内接正多边形的边数无限增加, 在这个过程中, 内接正多边形无限接近于圆, 同时A n 也无限接近于某一确定的数值, 这个确定的数值就理解为圆的面积. 这个确定的数值在数学上称为上面有次序的数（数列） A 1, A 2, A 3, ⋅ ⋅ ⋅ , A n , ⋅ ⋅ ⋅当n →∞时的极限.数列的概念:如果按照某一法则, 使得对任何一个正整数n 有一个确定的数x n , 则得到一列有次序的数x 1, x 2, x 3, ⋅ ⋅ ⋅ , x n , ⋅ ⋅ ⋅这一列有次序的数就叫做数列, 记为{x n }, 其中第n 项x n 叫做数列的一般项. 数列的例子: {1+n n }: 21, 32, 43, ⋅ ⋅ ⋅ ,1+n n⋅ ⋅ ⋅; {2n}: 2, 4, 8, ⋅ ⋅ ⋅ , 2n, ⋅ ⋅ ⋅; {n 21}: 21, 41, 81, ⋅ ⋅ ⋅ , n 21, ⋅ ⋅ ⋅ ; {(-1)n +1}: 1, -1, 1, ⋅ ⋅ ⋅ , (-1)n +1, ⋅ ⋅ ⋅ ; {nn n 1)1(--+}: 2,21, 34, ⋅ ⋅ ⋅ , n n n 1)1(--+, ⋅ ⋅ ⋅ .它们的一般项依次为1+n n , 2n , n 21, (-1)n +1, n n n 1)1(--+.数列的几何意义:数列{x n }可以看作数轴上的一个动点, 它依次取数轴上的点x 1, x 2, x 3, ⋅ ⋅ ⋅ , x n , ⋅ ⋅ ⋅.数列与函数:数列{x n }可以看作自变量为正整数n 的函数: x n =f (n ),它的定义域是全体正整数. 数列的极限:数列的极限的通俗定义:对于数列{x n }, 如果当n 无限增大时, 数列的一般项x n 无限地接近于某一确定的数值a , 则称常数a 是数列{x n }的极限, 或称数列{x n }收敛a . 记为a x n n =∞→lim . 如果数列没有极限, 就说数列是发散的.例如11l i m =+∞→n n n ,021lim =∞→nn , 1)1(lim 1=-+-∞→nn n n ; 而{2n }, { (-1)n +1}, 是发散的.对无限接近的刻划:x n 无限接近于a 等价于|x n -a |无限接近于0,极限的精确定义:定义 如果数列{x n }与常a 有下列关系:对于任意给定的正数ε (不论它多么小), 总存在正整数N , 使得对于n >N 时的一切x n , 不等式|x n -a |<ε都成立, 则称常数a 是数列{x n }的极限, 或者称数列{x n }收敛于a , 记为 a x n n =∞→lim 或x n →a (n →∞).如果数列没有极限, 就说数列是发散的.a x n n =∞→l i m ⇔∀ε >0, ∃N ∈N +, 当n >N 时, 有|x n -a |<ε .数列极限的几何解释: 例题: 例1. 证明1)1(lim 1=-+-∞→nn n n .分析: |x n -1|=nn n n 1|1)1(|1=--+-. 对于∀ε >0, 要使|x n -1|<ε , 只要ε<n1, 即ε1>n .证明: 因为∀ε >0, ∃]1[ε=N ∈N +, 当n >N 时, 有|x n -1|=ε<=--+-nn n n 1|1)1(|1, 所以1)1(lim1=-+-∞→nn n n .例2. 证明0)1()1(lim 2=+-∞→n nn .分析: |x n -0||0)1()1(|2-+-=n n 11)1(12+<+=n n .对于∀ε >0, 要使|x n -0|<ε , 只要ε<+11n , 即11->εn .证明: 因为∀ε >0, ∃]11[-=εN ∈N +, 当n >N 时, 有|x n -0|=ε<+<+=-+-11)1(1|0)1()1(|22n n n n ,所以0)1()1(lim2=+-∞→n nn .例3. 设|q |<1, 证明等比数列 1, q , q 2, ⋅ ⋅ ⋅ , q n -1, ⋅ ⋅ ⋅的极限是0.分析: 对于任意给定的ε >0, 要使 |x n -0|=| q n -1-0|=|q | n -1<ε ,只要n >log |q |ε +1就可以了, 故可取N =[log |q |ε +1]。

课程名称：大学文科数学授课班级：XX级XX班授课时间：2课时教学目标：1. 理解极限的概念，掌握极限的计算方法。

2. 能够运用极限解决实际问题。

3. 培养学生的逻辑思维能力、分析问题和解决问题的能力。

教学重点：1. 极限的概念。

2. 极限的计算方法。

教学难点：1. 极限概念的理解。

2. 极限计算中的复杂性。

教学过程：第一课时一、导入1. 回顾初等数学中的极限概念，引导学生思考极限在现实生活中的应用。

2. 引出本节课的主题——大学文科数学中的极限。

二、新课讲解1. 极限的概念：- 介绍极限的定义，包括数列极限和函数极限。

- 通过实例讲解极限的概念，如函数在一点处的极限、数列的极限等。

- 强调极限在数学中的重要性，以及它在其他学科中的应用。

2. 极限的计算方法：- 讲解直接计算法、夹逼法、洛必达法则等极限计算方法。

- 通过实例演示这些方法的运用，使学生掌握计算技巧。

三、课堂练习1. 学生独立完成课后习题，巩固所学知识。

2. 教师巡视指导，解答学生在练习中遇到的问题。

四、课堂小结1. 总结本节课的重点内容，强调极限的概念和计算方法。

2. 引导学生思考极限在实际问题中的应用。

第二课时一、复习1. 复习上一节课的内容，检查学生对极限概念和计算方法的掌握情况。

2. 学生分享自己在练习中的心得体会。

二、深化讲解1. 讲解极限计算中的难点问题，如分段函数的极限、无穷小量与无穷大量等。

2. 通过实例讲解如何处理这些难点问题。

三、课堂练习1. 学生完成课后习题，进一步巩固所学知识。

2. 教师巡视指导，解答学生在练习中遇到的问题。

四、课堂小结1. 总结本节课的重点内容，强调极限在数学和其他学科中的应用。

2. 鼓励学生在生活中发现极限的应用，提高数学素养。

教学反思：1. 本节课通过实例讲解，使学生更好地理解极限的概念和计算方法。

2. 在课堂练习中，教师应关注学生的个体差异，给予个别指导。

3. 鼓励学生在生活中发现极限的应用，提高数学素养。