整式的乘除专题复习

整式的乘除期末总复习【知识点幂的基本运算】【方法点拨】掌握幂的基本运算是解题关键．同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加．a m•a n=a m+n（m，n是正整数）幂的乘方法则：底数不变，指数相乘．（a m）n=a mn（m，n是正整数）积的乘方法则：把每一个因式分别乘方，再把所得的幂相乘．（ab）n=a n b n（n是正整数）同底数幂的除法法则：底数不变，指数相减．a m÷a n=a m-n（a≠0，m，n是正整数，m＞n）【考点3巧用幂的运算进行简便运算】方法：化异指为同指，底数凑整，得结果【例3】（2020春•宁远县期中）计算（−512）2019×（225）2020的结果是（）A．−512B．−125C．512D．﹣2020【变式3-1】（2020春•市中区校级期中）计算：0.1252020×（﹣8）2021＝．【变式3-2】（2020春•沙坪坝区校级月考）计算82×42021×（﹣0.25）2019的值等于．【变式3-3】（2019春•城关区校级期中）计算：（23）2014×1.52012×（﹣1）2014【考点4幂的逆运算】方法：逆用公式，配已知，代整体，求出值【例4】（2019秋•岳麓区校级月考）解答下列问题（1）已知2x＝a，2y＝b，求2x+y的值；（2）已知3m＝5，3n＝2，求33m+2n+1的值；（3）若3x+4y﹣3＝0，求27x•81y的值．【变式4-1】（2020春•江阴市期中）（1）已知m+4n﹣3＝0，求2m•16n的值．（2）已知n为正整数，且x2n＝4，求（x3n）2﹣2（x2）2n的值．【变式4-2】（2019春•邗江区校级月考）（1）若4a+3b＝3，求92a•27b．（2）已知3×9m×27m＝321，求m的值【变式4-3】（2020•河北模拟）若a m＝a n（a＞0且a≠1，m、n是正整数），则m＝n．利用上面结论解决下面的问题：（1）如果2÷8x•16x＝25，求x的值；（2）如果2x+2+2x+1＝24，求x的值；（3）若x＝5m﹣3，y＝4﹣25m，用含x的代数式表示y．【考点5巧用幂的运算进行大小比较】方法：1、化异底为同底，比较指数大小；2、化异指为同指，比较底数大小。

01 Chapter单项式多项式单项式与多项式的定义0102整式运算的基本法则单项式与单项式相乘，把他们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。

单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，再把所得的积相加。

多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加。

平方差公式：两数和乘两数差，等于两数平方差。

完全平方公式：首平方又末平方，二倍首末在中央；和的平方加再加，先减后加差平方。

整式的乘除运算规则02 Chapter多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加。

例如，$(x+y)(x-y)=x^2-y^2+xy-xy=x^2-y^2$。

多项式乘多项式详细描述总结词详细描述掌握除法法则，能熟练进行整式除法运算。

详细描述整式除法需遵循一定的法则，学生需了解并掌握这些法则，如单项式除以单项式时，把系数、同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同他的指数一起作为商的一个因式等。

03 Chapter符号错误运算顺序幂的运算性质030201易错点的总结复杂运算在整式的乘除运算中，符号的变化经常容易让人困惑。

解决办法是注意观察符号的变化规律，并理解其意义。

符号变化分配律应用难点解析及解决办法例题1$(x + y)^{2} \cdot (x - y)^{3} \div (x^{2} - y^{2})^{2}$解答$(x + y)^{2} \cdot (x - y)^{3} \div (x^{2} - y^{2})^{2} = (x^{2} + 2xy + y^{2}) \cdot (x^{3} - 3x^{2}y + 3xy^{2} - y^{3}) \div (x^{4} - 2x^{2}y^{2} + y^{4}) = x^{5} - 3x^{4}y + 3x^{3}y^{2} - x^{2}y^{3} \div x^{4} - 2x^{2}y^{2} + y^{4} = x - 3xy + 3y^{2} - y^{3}$$(3a + 5b)^{2}(7a + 9b)^{3} \div (4a^{2} + 6ab + 7b^{2})^{2}$例题2$(3a + 5b)^{2}(7a + 9b)^{3} \div (4a^{2} + 6ab + 7b^{2})^{2} = (9a^{2} + 30ab + 25b^{2})(7a^{3} + 27a^{2}b + 81ab^{2} + 9b^{3}) \div (16a^{4} + 48a^{3}b + 56a^{2}b^{2} + 6ab^{3} + 7b^{4}) = (63a^{5} + 810a^{4}b + 1890a^{3}b^{2} + 1575a^{2}b^{3} + 675ab^{4} + 175b^{5}) \div (16a^{4} + 48a^{3}b + 56a^{2}b^{2} + 6ab^{3} + 7b^{4}) = (4.5a + b)^{5}$解答04 Chapter与因式分解的交叉运用与方程的交叉运用与分式的交叉运用与其他数学知识的交叉运用实际生活中的整式乘除问题面积计算路程计算建立数学模型解决实际问题数学建模与解决实际问题05 Chapter题目解析$(3x + 5y)^{2}$解析此题考查的是完全平方公式，即$(a + b)^{2} = a^{2} + 2ab + b^{2}$。

专题1.5 整式的乘除全章五类必考压轴题【北师大版】1．已知4x =a,2y =b,8z =ab ，那么x ，y ，z 满足的等量关系是（ ）A ．2x +y =zB ．xy =3zC ．2x +y =3zD ．2xy =z 2．已知100a =20，1000b =50，则a +32b−32的值是（ ）A ．0B ．52C ．3D ．923．若x ，y 均为实数，43x =2021,47y =2021，则x y xy =_______．4．我们知道下面的结论，若a m =a n (a >0，且a ≠1)，则m =n ，利用这个结论解决下列问题：设2m =3，2n =6，2p =24，现给出m ，n ，p 三者之间的三个关系式：①m +p =2n +1，②p +n =2m +4，③m 2−mp +3n =0，其中正确的是___________．（填编号）5．比较下列各题中幂的大小：（1）已知a =8131,b =2741,c =961，比较a 、b 、c 的大小关系;（2）比较255,344,533,622这4个数的大小关系;（3）已知P =999999,Q =119990，比较P 、Q 的大小关系;（4）(−2)234_______5100（填“>”“<”或“=”）.6．由幂的运算法则逆向思维可以得到a m +n =a m ⋅a n ，a mn =(a m )n ，a m b m =(ab)m ，在解题过程中，根据算式的结构特征，逆向运用幂的运算法则，常可化繁为简，化难为易，使问题巧妙获解，收到事半功倍的效果．请解决以下问题：(1)计算：52020×(15)2018；(2)若3×9m ×27m =311，求m 的值；(3)比较大小：a =255，b =344，c =533，d =622，请确定a ，b ，c ，d 的大小关系．7．阅读以下材料：对数的创始人是苏格兰数学家纳皮尔（J．Napier，1550年-1617年），纳皮尔发明对数是在指数概念建立之前，直到18世纪瑞士数学家欧拉（Euler，1707年-1783年）才发现指数与对数之间的联系．对数的定义：一般地，若a x=N(a＞0,a≠1)，则x叫做以a为底N的对数，记作x=log a N．比如指数式24=16可以转化为4=log216，对数式2=log525可以转化为52=25．我们根据对数的定义可得到对数的一个性质：log(M·N)=log a M+log a N(a＞0,a≠1,M＞0,N＞0)．理由如下：设log a M=m，log a N=n，所以M=a m，N=a n，所以MN=a m a n=a m+n，由对数的定义得m+n=log a(M+N)，又因为m+n=log a M+log a N，所以log a(MN)=log a M+log a N．解决以下问题：（1）将指数53=125转化为对数式：．=log a M-log a N(a＞0,a≠1,M＞0,N＞0)（2）仿照上面的材料，试证明：log a MN（3）拓展运用：计算log32+log318-log34=．1．关于x的三次三项式A=5x3−6x2+10=a(x−1)3+b(x−1)2+c(x−1)+d（其中a，b，c，d均为常数），关于x的二次三项式B=x2+ex+f（e，f均为非零常数），下列说法中正确的个数有（ ）①当A+B为关于x的三次三项式时，则f=−10；②当多项式A与B的乘积中不含x⁴项时，则e=6；③a+b+c=9；A．0个B．1个C．2个D．3个2．已知(x2−ax2+bx+2)(2x2−3x+5)的展开式中不含三次项和四次项，则展开式中二次项和一次项的系数之和为______．3．若x2+2−3x+q的积中不含x项与x3项，(1)求p、q的值；(2)求代数式−2p2q2+(3pq)3+p2022q2024的值．4．（1）试说明代数式(s−2t)(s+2t+1)+4t t s、t的值取值有无关系；（2）已知多项式ax−b与2x2−x+2的乘积展开式中不含x的一次项，且常数项为−4，试求a b的值；（3）已知二次三项式2x2+3x−k有一个因式是(2x−5)，求另一个因式以及k的值．5．给出如下定义：我们把有序实数对a，b，c叫做关于x的二次多项式ax2+bx+c的附属系数对，把关于x的二次多项式ax2+bx+c叫做有序实数对a，b，c的附属多项式．(1)关于x的二次多项式3x2+2x−1的附属系数对为_________；(2)有序实数对2，a，1的附属多项式与有序实数对1，−2，4的附属多项式的差中不含一次项，求a的值．1．若一个只含a字母的多项式的项数是偶数，用该多项式去乘(a+1)，若该多项式的项数是奇数，则用该多项式去乘(a−1)，称这为第一次操作；若第一次操作后所得多项式的项数是偶数，用该多项式去乘(a+1)，若该多项式的项数是奇数，则用该多项式去乘(a−1)称这为第二此操作，以此类推．①将多项式(a2−1)以上述方式进行2次操作后所得多项式项数是5；②将多项式(a2+2a)以上述方式进行3次操作后，多项式的所有系数和为0；③将多项式(a2+2a+1)以上述方式进行4次操作后，当a=2时，所得多项式的值为243；④将多项式(a−1)以上述方式进行n次操作后所得多项式为(a−1)(a+1)n−1；四个结论错误的有（）A．0B．1C．2D．32．我国宋代数学家杨辉所著《详解九章算法》中记载了用如图所示的三角形解释了二项式的乘方展开式中的系数规律，我们把这种数字三角形叫做“杨辉三角”，请你利用杨辉三角，计算(a+b)6的展开式中，从左起第四项是____________．(a+b)0=1 (1)(a+b)1=a+b (11)(a+b)2=a2+2ab+b2 (121)(a+b)3=a3+3a2b+3ab2+b3 (1331)(a+b)4=a4+4a3b+6a2b2+4ab3+b4··146413．观察下列各式及其展开式：(a+b)2=a2+2ab+b2，(a+b)3=a3+3a2b+3ab2+b3，(a+b)4=a4+4a3b+6a2b2+4ab3+b4，(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5，⋯⋯请你猜想(2x−1)8的展开式中含x2项的系数是（）A．224B．180C．112D．484．阅读下列材料，完成相应任务．杨辉三角，是二项式系数在三角形中的一种几何排列．在欧洲，这个表叫做“帕斯卡三角形”．帕斯卡是在1654年发现这一规律的，比杨辉迟393年，比贾宪迟600年．杨辉三角是我国古代数学的杰出研究成果之一，他把二项式乘方展开式系数图形化，如下图所示：(a+b)1=a+b(a+b)2=a2+2ab+b2(a+b)3=a3+3a2b+3ab2+b2(a+b)4=a4+4a3b+6a2b2+4ab3+b4…完成下列任务：(1)写出(a+b)5的展开式．(2)计算：75+5×74×(−6)+10×73×(−6)2+10×72×(−6)3+5×7×(−6)4+(−6)5．5．观察下列各式：(x−1)(x+1)=x2−1(x−1)(x2+x+1)=x3−1(x−1)(x3+x2+x+1)=x4−1(1)根据以上规律，则(x−1)(x6+x5+x4+x3+x3+x+1)=___________．(2)你能否由此归纳出一般规律(x−1)(x n+x n−1+⋯+x+1)=___________．(3)根据以上规律求32022+32021+32020+⋯+32+3+1的值．6．（1）计算并观察下列各式：第1个：(a−b )(a +b )= ；第2个：(a−b )(a 2+ab +b 2)= ；第3个：(a−b )(a 3+a 2b +ab 2+b 3)= ；……这些等式反映出多项式乘法的某种运算规律．（2）猜想：若n 为大于1的正整数，则(a−b )(a n−1+a n−2b +a n−3b 2+⋯+a 2b n−3+ab n−2+b n−1)= ；（3）利用（2）的猜想计算：2n−1+2n−2+2n−3+⋯+23+2+1= ．（4）拓广与应用：3n−1+3n−2+3n−3+⋯+33+3+1= ．1．已知：(x +y )2=12，(x−y )2=4，则x 2+3xy +y 2的值为_____．2．已知1b −1a =8−c ab ，ab +bc +2b +c 2+25=0，则b a 的值为______．3．已知a ，b ，c 满足：a 2+2b =7，b 2−2c =−1，c 2−6a =−17，则13a +b +3c 的值等于______．4．已知a−b =4时，多项式ab +c 2的值为−4，则ab a 2b 2c 2的值为( )A ．−1B ．−12C ．−13D ．05．已知有理数a ，b ，c 满足a−b +c−3=0，a 2+b 2+c 2−3=0，则a 3+b 3+c 3−2022=（ ）A ．−2019B ．−2020C ．−2021D ．−20226．已知a =2020m +2021n +2020，b =2020m +2021n +2021，c =2020m +2021n +2022，那么a 2+b 2+c 2−ab−bc−ca 的值为（ ）A ．1B ．3C ．6D ．10107．已知：x +y =5，xy =3．求：①x 2+5xy +y 2；②x 4+y 4．8．阅读下列材料，完成后面的任务．完全平方公式的变形及其应用我们知道，完全平方公式有：(a+b)2=a2+2ab+b2；(a−b)2=a2−2ab+b2．在解题过程中，根据题意，若将公式进行变形，则可以达到快速求解的目的，其变形主要有下列几种情形：①a2+b2=(a+b)2−2ab；②a2+b2=(a−b)2+2ab；③a2+b2a+b)2+(a−b)2；④ab a+b)2−(a−b)2．根据上述公式的变形，可以迅速地解决相关问题．例如：已知x+y=3，x−y=1，求x2+y2的值．×(32+12)=5．解：x2+y2x+y)2+(x−y)2=12任务：(1)已知x+y=5，x−y=3，则xy=______．(2)已知x+y=7，x2+y2=25，求(x−y)2的值．1．数学活动课上，老师准备了图1中三种不同大小的正方形与长方形，拼成了一个如图2所示的正方形．(1)请用两种不同的方法表示图2中阴影部分的面积和．方法1：_________；方法2：__________．(2)请你直接写出三个代数式：(a+b)2，a2+b2，ab之间的等量关系．(3)根据（2）题中的等量关系，解决如下问题：①已知m+n=5，m2+n2=20，求mn和(m−n)2的值．②已知(x−2021)2+(x−2023)2=34，求(x−2022)2的值．2．两个边长分别为a和b的正方形如图放置（图①），其未叠合部分（阴影）面积为S1；若再在图①中大正方形的右下角摆放一个边长为b的小正方形（如图②），两个小正方形叠合部分（阴影）面积为S2．（1）用含a、b的代数式分别表示S1、S2；（2）若a−b=8，ab=13，求S1+S2的值；（3）用a、b的代数式表示S3；并当S1+S2=34时，求出图③中阴影部分的面积S3．3．阅读理解，解答下列问题：利用平面图形中面积的等量关系可以得到某些数学公式．（1）例如，根据下图①，我们可以得到两数和的平方公式：（a＋b）2＝a2＋2ab＋b2根据图②能得到的数学公式是__________．（2）如图③，请写出（a＋b）、（a﹣b）、ab之间的等量关系是__________（3）利用（2）的结论，解决问题：已知x＋y＝8，xy＝2，求（x﹣y）2的值．（4）根据图④，写出一个等式：__________．（5）小明同学用图⑤中x张边长为a的正方形，y张边长为b的正方形，z张宽、长分别为a、b的长方形纸片，用这些纸片恰好拼出一个面积为（3a＋b）（a＋3b）长方形，请画出图形，并指出x＋y＋z的值．类似地，利用立体图形中体积的等量关系也可以得到某些数学公式．（6）根据图⑥，写出一个等式：___________．4．（1）【知识生成】我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式．例如：从边长为a的正方形中剪掉一个边长为b的正方形如图1，然后将剩余部分拼成一个长方形如图2．图1中阴影部分面积为__________，图2中阴影部分面积为__________，请写出这个乘法公式__________．（2）【知识应用】应用（1）中的公式，完成下面任务：若m是不为0的有理数，已知P=(m2+2m+1) (m2−2m+1)，Q=(m2+m+1)(m2−m+1)，比较P、Q大小．（3）【知识迁移】事实上，通过计算几何图形的体积也可以表示一些代数恒等式，图3表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体，请你根据图3中图形的变化关系，写出一个代数恒等式：____________________．5．若x满足(7−x)(x−4)=2，求(x−7)2+(4−x)2的值：解：设7−x=a, x−4=b，则(7−x)(x−4)=ab=2，a+b=(7−x)+(x−4)=3所以(x−7)2+(4−x)2=(7−x)2+(x−4)2=a2+b2=(a+b)2−2ab=32−2×2=5请仿照上面的方法求解下面的问题（1）若x满足(8−x)(x−3)=3，求(8−x)2+(x−3)2的值；（2）已知正方形ABCD的边长为x，E，F分别是AD，DC上的点，且AE=2，CF=5，长方形EMFD的面积是28，分别以MF、DF为边作正方形，求阴影部分的面积．6．对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式，例如图1可以得到(a+b)2=a2+2ab+b2，请解答下列问题（1）写出图2中所表示的数学等式（2）根据整式乘法的运算法则，通过计算验证上述等式；（3）利用（1）中得到的结论，解决下面的问题：若a+b+c=10,ab+ac+bc=35，则a2+b2+c2=（4）小明同学用图3中x张边长为a的正方形，y张边长为b的正方形z张边长分别为a,b的长方形纸片拼出一个面积为(5a+7b)(9a+4b)长方形，则x+y+z=7．问题发现：若x满足（9﹣x）（x﹣4）＝2，求（9﹣x）2+（x﹣4）2的值．小明在解决该问题时，采用了以下解法：解：设（9﹣x）＝a，（x﹣4）＝b，则ab＝（9﹣x）（x﹣4）＝ ，a+b＝（9﹣x）+（x﹣4）＝ ．所以（9﹣x）2+（x﹣4）2＝a2+b2＝（a+b）2﹣2ab＝ ．(1)请补全小明的解法；(2)已知（30﹣x）（x﹣20）＝﹣10，则（30﹣x）2+（x﹣20）2的值为 ．类比研究(3)若x满足（2023﹣x）2+（x﹣2021）2＝2022，求（2023﹣x）（x﹣2021）的值．拓伸延伸(4)如图，正方形ABCD的边长为x，AE＝1，CG＝3，长方形EFGD的面积是10，分别以DE、DG为边长作正方形MEDQ和NGDH，PQDH是长方形，求图中阴影部分的面积为 （结果必须是一个具体数值）．。

整式的乘除复习考点1、幂的有关运算①=⋅nm a a （m 、n 都是正整数）②=n m a )( （m 、n 都是正整数） ③=n ab )( （n 是正整数） ④=÷n m a a （a ≠0，m 、n 都是正整数，且m>n ）⑤=0a （a ≠0）⑥=-p a （a ≠0，p 是正整数）幂的四种运算：1、同底数幂的乘法：⑴语言叙述：同底数幂相乘，底数不变，指数相加；⑵字母表示：a m ·a n = a m+n ；(m ，n 都是整数) ； ⑶逆运用：a m+n = a m ·a n2、幂的乘方：⑴语言叙述：幂的乘方，底数不变，指数相乘；⑵字母表示：(a m ) n = a mn ；(m ，n 都是整数)； ⑶逆运用：a mn =(a m )n =(a n )m ；3、积的乘方：⑴语言叙述：积的乘方，等于每个因式乘方的积；⑵字母表示：(ab)n = a n b n ；(n 是整数)； ⑶逆运用：a n b n = (a b)n ；4、同底数幂的除法：⑴语言叙述：同底数幂相除，底数不变，指数相减；⑵字母表示：a m ÷a n = a m-n ；(a ≠0，m 、n 都是整数)； ⑶逆运用：a m-n = a m ÷a n⑷零指数与负指数： 01a =(a ≠0)； 1p p a a-=(a ≠0)； 例：在下列运算中，计算正确的是（ ） （A ）326a a a ⋅=（B ）235()a a = （C ）824a a a ÷=（D ）2224()ab a b = 练习： 1、()()103x x -⨯-=________.2、()()()32101036a a a a -÷-÷-÷ = 。

3、23132--⎛⎫-+ ⎪⎝⎭ = 。

4、322(3)---⨯- = 。

5、下列运算中正确的是（ ）A ．336x y x =；B ．235()m m =；C ．22122xx-=； D ．633()()a a a -÷-=- 6、计算()8p m n a a a ⋅÷的结果是（ ） A 、8mnp a - B 、()8m n p a ++ C 、8mp np a +- D 、8mn p a +-7、下列计算中，正确的有（ ）①325a a a ⋅= ②()()()4222ab ab ab ab ÷= ③()322a a a a ÷÷= ④()752a a a -÷=。

整式的乘除知识点及题型复习整式的乘除是初中数学中的重要内容，它不仅是后续学习分式、二次根式等知识的基础，还在实际生活中有着广泛的应用。

接下来，我们就对整式的乘除的知识点及常见题型进行一次全面的复习。

一、整式乘法的知识点1、同底数幂的乘法同底数幂相乘，底数不变，指数相加。

即：＄a^m×a^n ＝a^｛m+n}＄（＄m$、＄n$都是正整数）例如：＄2^3×2^4 ＝ 2^｛3+4} ＝ 2^7$2、幂的乘方幂的乘方，底数不变，指数相乘。

即：＄（a^m)＾n ＝ a^｛mn}＄（＄m$、＄n$都是正整数）比如：＄（3^2)＾3 ＝ 3^｛2×3} ＝ 3^6$3、积的乘方积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘。

即：＄（ab)＾n ＝ a^n b^n$（＄n$为正整数）例如：＄（2×3)＾2 ＝ 2^2×3^2 ＝ 36$4、单项式乘以单项式系数与系数相乘，同底数幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。

比如：＄3x^2y × 5xy^2 ＝（3×5)×（x^2×x)×（y×y^2) ＝ 15x^3y^3$5、单项式乘以多项式用单项式去乘多项式的每一项，再把所得的积相加。

即：＄m(a ＋b ＋ c) ＝ ma ＋ mb ＋ mc$例如：＄2x(x ＋ 2y 3z) ＝ 2x^2 ＋ 4xy 6xz$6、多项式乘以多项式先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。

即：＄（a ＋ b)（m ＋ n) ＝ am ＋ an ＋ bm ＋ bn$比如：＄（x ＋ 2)（x 3) ＝ x^2 3x ＋ 2x 6 ＝ x^2 x 6$二、整式除法的知识点1、同底数幂的除法同底数幂相除，底数不变，指数相减。

即：＄a^m÷a^n ＝ a^｛m n}＄（＄a≠0$，＄m$、＄n$都是正整数，且$m ＞ n$）例如：＄6^5÷6^3 ＝ 6^｛5 3} ＝ 6^2$2、单项式除以单项式系数与系数相除，同底数幂分别相除，对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式。

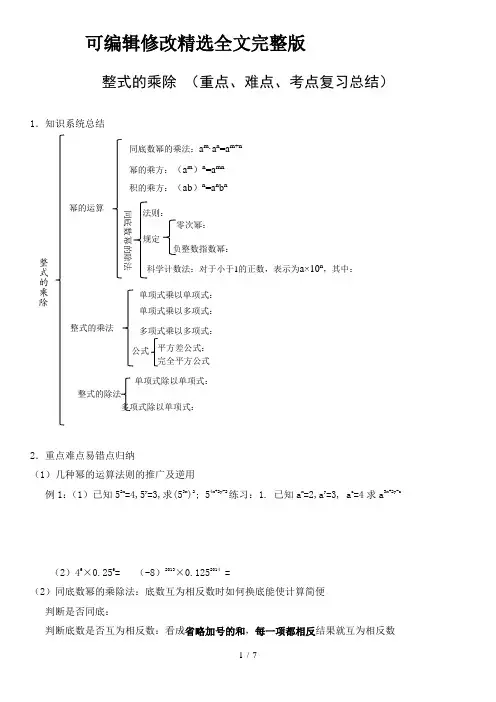
可编辑修改精选全文完整版整式的乘除（重点、难点、考点复习总结）1．知识系统总结2．重点难点易错点归纳（1）几种幂的运算法则的推广及逆用例1：（1）已知52x=4,5y=3,求(53x)2; 54x+2y-2练习：1. 已知a x=2,a y=3, a z=4求a3x+2y-z（2）46×0.256= （-8）2013×0.1252014 =（2）同底数幂的乘除法：底数互为相反数时如何换底能使计算简便判断是否同底：判断底数是否互为相反数：看成省略加号的和，每一项都相反结果就互为相反数换底常用的两种变形：例2：（1）-x7÷（-x）5·（-x）2 (2)(2a-b)7·（-b+2a）5÷（b-2a）8（3）区分积的乘方与幂的乘方例3：计算（1）（x3）2 (2) (-x3）2 (3)（-2x3）2（4）-（2x3）2（4）比较法：逆用幂的乘方的运算性质求字母的值（或者解复杂的、字母含指数的方程）例4：（1）如果2×8n×16n=28n ,求n的值（2）如果（9n）2=316，求n的值（3）3x=,求x的值（4）（-2）x= -,求x的值（5）利用乘方比较数的大小指数比较法：833，1625, 3219底数比较法：355,444,533乘方比较法：a2=5,b3=12，a>0,b>0,比较a,b的大小比较840与6320的大小（6）分类讨论思想例6：是否存在有理数a，使（│a│-3）a =1成立，若存在，求出a的值，若不存在，请说明理由整式的乘法（1）计算法则明确单项式乘以单项式、单项式乘以多项式、多项式乘以多项式的计算法则，尤其注意符号的问题，结果一定要是最简形式。

单项式乘以多项式、多项式乘以多项式最终都是要转化为单项式乘以单项式，通过省略加号的和巧妙简化符号问题。

【例1】计算：（1）(-3x2y)(-xz4)(-2y3zt) (2)-5x n y n+2(3x n+2y-2x n y n-1+y n) （3）（-x+2）(x3-x2)练一练：先化简再求值：[xy(x2-3y)+3xy2](-2xy)+x3y2(2x-y),其中x=-0.25,y=4(2)利用整式的乘法求字母的值①指数类问题：②系数类问题：【例2】已知-2x3m+1y2n与7x m-6y-3-n的积与x4y是同【例3】在x2+ax+b与2x2-3x-1的积中，x3项项，求m与n的值的系数为—5，x2项的系数为-6，求a,b的值（3）新定义题【例4】现规定一种新运算：a*b=ab+a-b，其中a,b为有理数，则（a*b）+[(b-a)*b]=练一练：现规定一种新运算：a※b=ab+a-b，其中a,b为有理数，计算：[（m+n）※n]+[(n-m)※n] 课后提升：1.（-0.7×104）×（0.4×103）×（-10）=2.若（2x-3）（5-2x）=ax2+bx+c,则a= ,b=3.若（-2x+a）(x-1)的结果不含x的一次项，则a=4.计算：(1)（-5x-6y+z）(3x-6y) (2)-2xy(x2-3y2)- 4xy(2x2+y2)平方差公式（1）公式：（a+b）(a-b)=a2-b2注意：公式中的a,b既可以是具体的数字，也可以是单项式或多项式，只要不是单独的数字或字母，写成平方的差时都要加括号公式的验证：根据面积的不同表达方式是验证整式乘法公式常用的方法(2)平方差公式的不同变化形式【例1】计算下列各式：（1）（-5x+2y）(-2y-5x)= （2）（2a-1）(2a+1)(4a2+1)=（3）20132-2012×2014 =练一练：1、（2y-x-3z）(-x-2y-3z)=2、99×101×10001=3、 3×（22+1）×（24+1）×（28+1）×…×（232+1）+1=（3）平方差公式的逆用【例2】∣x+y-3∣+(x-y+5)2=0,求3x2-3y2的值练一练：已知实数a,b满足a+b=2，a-b=5，求（a+b）3（a-b）3的值.课后提升：1.已知下列式子：①（x-y）（-x-y）；②（-x+y）(x-y)；③（-x-y）（x+y）；④（x-y）（y-x）.其中能利用平方差公式计算的是2.(-a-3)( )=9-a23.如果a2-2k=(a-0.5)（a+0.5），那么k=4.为了美化城市，经统一规划，将一正方形的南北方向增加3米，东西方向缩短3米，将改造后的长方形草坪面积与原来的正方形草坪面积相比（）A.增加6平方米B.增加9平方米C.减少9平方米D.保持不变5.解方程：（3x+4）（3x-4）=9（x-2）26.计算：（2+1）×（22+1）×（24+1）×…×（22014+1）完全平方公式（1）公式：（a±b）2=a2±2ab +b2首平方，尾平方，2倍乘积放中央，同号加，异号减注意：公式中的a,b既可以是具体的数字，也可以是单项式或多项式【例1】计算下列各式：（2x-5y）2 = (-mn+1)2 =(-t2-2)2=（2）完全平方公式的推广应用①直接推广②间接推广【例2】计算（a-2b+3c)2【例3】已知x+y+z=10,xy+xz+yz=8,求x2+y2+z2的值（3）利用完全平方公式求字母的值【例4】两数和的平方的结果是x2+(a-1)x+25,则a的值是（）A.-9B.1C.9或-11D.-9或11（4）利用完全平方公式进行简化计算【例5】计算：（1）1992 （2）3.012（5）完全平方公式的变形应用【例6】（1）已知m+n=7,mn=10,求8m2+8n2的值（2）已知（x+y）2=16,(x-y)2=4,求xy的值课后提升：1.下列展开结果是2mn-m2-n2的式子是（）A.（m+n）2B.(-m+n)2C.-(m-n)2D.-(m+n)22.(x+2y-z)2=3.若∣x+y-7∣+(xy-6)2=0,则3x2+3y2=4.若代数式x2+3x+2可以表示为 (x-1)2+a（x-1）+b的形式，则a+b的值是5.计算：（2x-y）2（2x+y）2整式的除法（1）计算法则整式乘法的逆运算，可以互相验证。