当前位置：文档之家 › 运筹学模拟卷2运筹学胡运权清华大学出版社

运筹学模拟卷2运筹学胡运权清华大学出版社

  • 格式：doc
  • 大小：48.50 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

运筹学教程（第二版）（胡运权）课后答案（清华大学出版社）

运筹学教程（第二版）（胡运权）课后答案（清华大学出版社）

运筹学教程（第⼆版）（胡运权）课后答案（清华⼤学出版社）运筹学教程（第⼆版）习题解答第⼀章习题解答运筹学教程1.1 ⽤图解法求解下列线性规划问题。

并指出问题具有惟⼀最优解、⽆穷多最优解、⽆界解还是⽆可⾏解。

1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5 x 1 + 6 x 2≤ 82 5 ≤ x ? 1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3) 1 2 x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 21 2 ? ≥ 12 2 1 ? x , x ≥ 0 .? ?2 x 1 + x 2 ≤ 2st ?3x + 4 x (2) max Z = 3x 1 + 2 x 2x , x ≥ 0 1 2该问题⽆解≥ 12 2 1 ? ? 2 x 1 + x 2 ≤ 2st .?3 x +4 x ( 2 ) max Z = 3 x 1 + 2 x 2第⼀章习题解答3 2 1x = 1, x = 1, Z = 3是⼀个最优解⽆穷多最优解，1 2x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 2该问题有⽆界解1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5x 1 + 6 x 2第⼀章习题解答唯⼀最优解， x 1 = 10, x 2 = 6, Z = 16 ≤ 82 5 ≤ x ?1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3)第⼀章习题解答运筹学教程1.2 将下述线性规划问题化成标准形式。

运筹学清华大学出版社胡运权着课后答案

运筹学清华大学出版社胡运权着课后答案

�12 x1 � 3 x2 � 6 x3 � 3 x4 � 9
(1)
st
��8 ��3
x1 x1
� �
x2 x6
� 4 x3 �0
�
2 x5
� 10
�� x j � 0�, j � 1,� ,6�
min Z � 5 x1 � 2 x2 � 3 x3 � 2 x4
� x1 � 2 x2 � 3 x3 � 4 x4 � 7
运筹学教程�第二版� 习题解答
运筹学教程
1.1 用图解法求解下列线性规划问题。并指出问 题具有惟一最优解、无穷多最优解、无界解还是无可 行解。
min Z � 2 x1 � 3 x2 � 4 x1 � 6 x2 � 6
(1) st .�� 2 x1 � 2 x2 � 4 �� x1 , x2 � 0
Z
0
0.5
2
0
5
0
0
1
1
5
2/5
0
11/5
0
43/5
page 10 6 January 2011
School of Management
运筹学教程
1.4 分别用图解法和单纯形法求解下述线性规划 问题�并对照指出单纯形表中的各基可行解对应图解 法中可行域的哪一顶点。
max Z � 10 x1 � 5 x2 �3 x1 � 4 x2 � 9
max Z � x1 � x2 �6 x1 � 10 x2 � 120 (3) st.�� 5 � x1 � 10 �� 5 � x2 � 8
max Z � 3x1 � 2 x2 �2 x1 � x2 � 2
(2) st.��3x1 � 4 x2 � 12 �� x1, x2 � 0

《运筹学》胡运权清华版-2-02单纯形算法的矩阵表示

《运筹学》胡运权清华版-2-02单纯形算法的矩阵表示

?
-1 -2 1/2 1/2
-1/2 1/2
解：
cj CB 0 0 0 XB x4 x5 b 60 10 2 x1 3 1 1 2 -1 x2 1 -1 1 -1 1 x3 1 2 -1 1 0 x4 1 0 0 0 0 x5 0 1 0 0 0 x6 0 0 1 0
.............................................................
1. 两者的最优值相同 z w 17 / 2 2. 从任一个问题的最优表，可以直接 找到另一个问题的最优解，对应关系 原问题决策变量 原问题松弛变量
对偶问题剩余变量 对偶问题决策变量
例2、用单纯形表求解 x1 LP问题所得最优表如下， 4 x1 试直接写出对偶问题最 优解。 x1 , x2
单纯形法的矩阵描述
一、初始单纯形表 线性规划问题：
标准型：
max
z CX
max
z CX 0 X S
AX b s.t. X 0
初始单纯形表
AX I X S b s.t. X , XS 0
C 0
基系数
0
基列
XS
常数列
b
X
A
XS
I
cj- zj
C
0
二、迭代后的单纯形表（当前可行基——B）
结论：当采用单纯形法求得原问题的一个 最优解的时候，检验行上同时得到对偶问 题的一个可行解，且两者具有相同的目标 值。利用对偶性质，可以证明这个对偶问 题的解也为最优解。
例、以求解下面LP问题以及它的对偶问题过程为 例，验证前述结论
原 问 题
max z 2 x1 x 2 s.t. 5 x 2 15 6 x1 2 x 2 24 x1 x 2 5 x1, x 2 0 min w 15 y 24 y 5 y s.t 6y y 2 5y 2y y 1 y ,y ,y 0

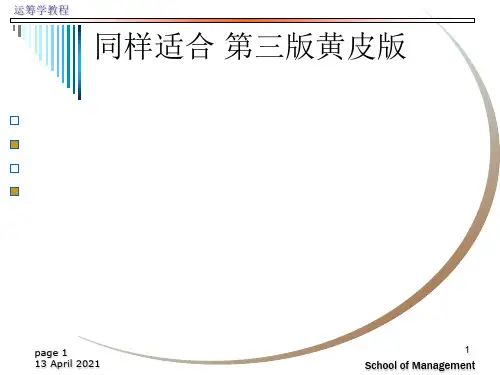
清华大学《运筹学教程》胡运权主编课后习题答案

清华大学《运筹学教程》胡运权主编课后习题答案

该题是唯一最优解：
29
17
x1 5 , x2 5 , x3 1, x4 0, Z 5
page 21 13 April 2021
21
School of Management
运筹学教程
第一章习题解答
max Z 10x1 15x2 12x3
5x1 3x2 x3 9
(4)
st
5x1 2x1
(2)
st
x1 x2 x3 4 2x1 x2 x3 6
x1 0, x2 0, x3无约束
page 6 13 April 2021
6
School of Management
运筹学教程
第一章习题解答
min Z 3x1 4x2 2x3 5x4
4x1 x2 2x3 x4 2
17
School of Management
运筹学教程
第一章习题解答
解：下界对应的模型如下（ c,b取小，a取大）
max Z x1 4x2
st.43xx1165xx22
8 10
x1, x2 0
最优值（下界）为：6.4
page 18 13 April 2021
18
School of Management
运筹学教程
第一章习题解答
1.2 将下述线性规划问题化成标准形式。
min Z 3x1 4x2 2x3 5x4
4x1 x2 2x3 x4 2
(1)
st
x12x1x23xx23
2x4 x3
14 x4
. 2
x1, x2 , x3 0, x4无约束
min Z 2x1 2x2 3x3
st
8x1 3x1

(完整word版)运筹学(胡运权)第五版课后答案,运筹作业

(完整word版)运筹学(胡运权)第五版课后答案,运筹作业

47页1.1b羅蕿用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解薅47页1。

1d蒂无界解（b）衿1.2蕿约束方程的系数矩阵A=1234莇2112蚄P1P2P3P4,运筹作业肀最优解A=（01/220）T和(0011）T页13题肆49膃设Xij为第i月租j个月的面积羄minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13+6000x23+7300x 14螁s.t.聿x11+x12+x13+x14≥15膃x12+x13+x14+x21+x22+x23≥10膀x13+x14+x22+x23+x31+x32≥20艿x14+x23+x32+x41≥12袇Xij≥0芃用excel求解为：薁用LINDO求解：羁LPOPTIMUMFOUNDATSTEP3薆OBJECTIVEFUNCTIONVALUE 蚇1)118400.0羂VARIABLEVALUEREDUCEDCOST 荿Z0.0000001。

000000虿X113.0000000。

000000螇X210。

0000002800。

000000莃X318。

0000000.000000肁X410.0000001100。

000000莈X120.0000001700.000000袆X220.0000001700。

000000螄X320.0000000。

000000蕿X130.000000400.000000膇X230。

0000001500。

000000袆X1412.0000000.000000袁ROWSLACKORSURPLUSDUALPRICES芁2)0。

000000—2800。

000000羆3）2.0000000.000000羆4)0。

000000—2800.000000节5）0。

000000-1700.000000蝿NO。

ITERATIONS=3罿答若使所费租借费用最小，需第一个月租一个月租期300平方米，租四个月租期1200平方米，第三个月租一个月租期800平方米,页14题肆50蚃设a1，a2，a3,a4,a5分别为在A1，A2，B1，B2，B3加工的Ⅰ产品数量，b1，b2，b3分别为在A1，A2，B1加工的Ⅱ产品数量,c1为在A2，B2上加工的Ⅲ产品数量。

《运筹学》胡运权-第4版-第二章--线性规划的对偶理论及灵敏度分析

《运筹学》胡运权-第4版-第二章--线性规划的对偶理论及灵敏度分析

y1, y2 , y3 0
LP1和LP2两个线性规划问题，通常称LP1为原问题， LP2为前者的对偶问题。
m Z c a 1 x 1 x c 2 x 2 c n x n
对 偶 问 题
s.t.
a1 1 a2 1
am1
a1 2 a2 2
am2
a1n x1 b1
a2n
x2
生的线性规划问题，称为其“对偶”
问题。
对
对偶问题是对原问题从另一角度进
偶
行的描述，其最优解与原问题的最 优解有着密切的联系，在求得一个
原
线性规划最优解的同时也就得到对 偶线性规划的最优解，反之亦然。
理
对偶理论就是研究线性规划及其对 偶问题的理论，是线性规划理论的
重要内容之一。
问 题 的 导 出
例2-1
项目
y2 1/4 y3 1/2
cj-zj 变量
对偶问题变量
y1
y2
y3
-5/4
1
0
15/2
0
1
15/2
0
0
原问题松弛变量
x3
x4
x5
原问题松弛变量
x3
x4
x5
1 5/4 -15/2
0
1/4
-1/2
0 -1/4
3/2
0 1/4
1/2
对偶问题变量
y1
y2
y3
对偶问题剩余变量
y4
y5
-1/4
1/4
1/2
-3/2
问
m a x z 2 x 1 x 2 0 x 3 0 x 4 0 x 5 对偶变量
题 的
5x2 x3 15

《运筹学》胡运权清华版-2-01对偶问题

对偶问题往往具有非线性、非凸性和大规模等特性 ，求解难度较大，需要发展高效的求解算法。
应用场景限制
对偶问题在某些应用场景中可能存在限制， 需要探索更广泛的应用领域和场景。
对偶问题的未来发展方向
交叉学科融合
对偶问题将与数学、物理、工程等多个学科交叉融合，形成新的 研究领域和方向。
算法优化与并行计算
针对大规模对偶问题的求解，将发展更高效的算法和并行计算技 术，提高求解效率。
应用领域拓展
02
对偶问题在优化、机器学习、大数据等领域的应用将进一步深
化，推动相关领域的发展。
算法创新
03
针对对偶问题的求解算法将不断创新，提高求解效率，满足大
规模复杂问题的求解需求。
对偶问题的研究难点与挑战
理论证明
对偶理论中的一些基本定理和性质仍需进一 步证明和完善，以增强其数学严谨性。
求解难度
求解动态规划对偶问题的方法包括状态转移方程、最优子结构、备忘录法等。这些方法可以帮助我们找 到最优解，并避免重复计算。
在求解动态规划对偶问题时，需要注意对偶问题的最优解并不一定对应原问题的最优解，因此需要对解 进行验证和调整。
博弈论对偶问题的求解方法
01
博弈论是研究多个决策者之间 决策问题的学科，而博弈论对 偶问题则是将原问题转化为求 最大值的问题。
题
非线性规划对偶问题是将原非线 性规划问题的目标函数和约束条 件转换为对偶形式后得到的新问 题。
对偶问题的重要性
理论意义
对偶问题在运筹学理论中具有重要的 地位，它揭示了原问题与对偶问题之 间的内在联系，有助于深入理解运筹 学的基本原理。
应用价值
在实际应用中，对偶问题可以用于求 解原问题的近似解或启发式解，提高 求解效率，尤其在处理大规模优化问 题时具有显著的优势。

线性规划对偶问题__运筹学__胡运权__清华大学出版社


6 互补松弛性
20
1 单纯形法的矩阵描述
max z CX AX b
A, I B, N
C CB,CN
X
XB XN
X 0
max z CX 0X s AX IX s b X 0, X s 0
max z CB X B CN X N BX B NX N b X B 0, X N 0
4
2、 换个角度审视生产计划问题
例 要求制定一个生产计划方案，在劳动力和原材料可能供应的
范围内，使得产品的总利润最大 。
MaxZ 2x1 3x2 3x3
s.t.xx11
x2 x3 3 4x2 7x3
9
x1, x2 , x3 0
它的对偶问题就是一个价格系统，使在平衡了劳动力和原材料 的直接成本后，所确定的价格系统最具有竞争力：
设 y1, y2, y3 分别为设备A、B、C的每台时的租金。为了叙述方便，这里把租金定义为扣 除 原成 利本润后50的元利，润即。y1作 2为y出2 租50者，来否说则，就把不生出产租单还位是用产于品生所产需各产设品备以的获台利时5各0元总；租同金样不把应低于
生产一单位产品所需各设备的台时的总租金也不应当低于原利润100元， 即 y1 y2 y3 100 ，否则这些设备台时就不出租，还是用于生产 产品以获利100元。但对于租用者来说，他要 求在满足上述要求的前提下，也就是在出租者愿意出租的前提下尽量要求全部设备台时的总 租金越低越好，即min 300 y1 400 y2 250 y3 ，这样我们得到了该问题的数学模型：
y1, y2 , , ym 0
这两个式子之间的变换关系称为“对称
形式的对偶关系”。
8
（2）对称形式的对偶关系的矩阵描述

清华大学《运筹学教程》胡运权主编课后习题答案(第一章)


2)c=0
3)c>0
d<0 d=0 d>0
0
c 3 d 4
A1点 A1点 A3点
A2A3线段
3 c 5 4 d 2
c 5 d 2 c 5 d 2
c 3 d 4
A2点
A1A2线段 A1点
l.6 考虑下述线性规划问题：
max Z c1 x1 c2 x2 a11 x1 a12 x2 b1 st .a21 x1 a22 x2 b2 x1 , x2 0
-1
x2
0
x3
0
x4
-M
x5
-M
x6
CB
xB
x5
x6
x4
i
-M -M 0
3 6 4
[3] 4 1
1 3 2
0 -1 0
0 0 1
1 0 0
0 1 0 0
1 3/2 4 3 6/5 9/5
cj zj
7M-4
1 2 3 1 0 0 0
4M-1
1/3 [5/3] 5/3
5M/3+1/3
-M
0 -1 0 -M
0
0 0 1 0
0
1/3 -4/3 -1/3
-7M/3+4/3
-4 -M 0
x1
0
1 0 0
x6
x4
cj zj
cj
x6
是否基 可行解
Z
(x1,x2,x3)
(x1,x2,x4) (x1,x2,x5) (x1,x2,x6)
0
0 0 7/4
61/3
10 3 -4
-7/6
0 0 0

清华大学《运筹学教程》胡运权主编课后习题答案


0
0
0 -1/5 2/5 0
1
0 3/5 -1/5 0
0
x3
1
0
0
1
1
1 -1
cj zj
0
0
0 -1/5 -M+7/5 -M
由于上表中所有检验数都小于等于零(且非基变量检验数都 小于0)，因此已经得到唯一最优解，最优解为：
X * 25 ,9 /5 ,1 ,0 ,0 ,0 T
方法二：两阶段法
第一阶段：
4x1 x2 2x3 x4 2
(1)
stx12x1x23xx23
2x4 14 x3 x4
. 2
x1, x2, x3 0, x4无约束
minZ 2x1 2x2 3x3
(2)
st
x1 x2 x3 4 2x1 x2 x3 6
x1 0, x2 0, x3无约束
minZ 3x1 4x2 2x3 5x4
7
4 -1
1
1/3 0
0 [5/3] -1
0
5/3 0
0
5/3
-1
0 -1 -1
i
x4
x5
x6
0
10
1
0
0 1 3/2
1
00
4
0
00
0 1/3 0 3
0 -4/3 1 6/5 1 -1/3 0 9/5 0 -7/3 0
cj
0
CB
xB
b
x1
0
x1 3/5
1
0
x 2 6/5
0
0
x4
1
0
cj zj
0
4x1 x2 2x3 x41 x42 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

运筹学模拟2
3分，共5题，总计15分）
1.线性规划问题中可行域的顶点与线性规划问题的（）对应。

A 可行解
B 基本解
C 基本可行解
D 不能确定
2．在对偶理论中下列说法正确的是：（）
A 原问题任一可行解的目标函数值是其对偶问题目标函数值的上界。

B 对偶问题任一可行解的目标函数值是其原问题目标函数的下界。

C 如原问题有可行解且目标函数值无界，则其对偶问题无可行解
D 若原问题有可行解而其对偶问题无可行解，则原问题目标函数值有界。

3．资源的影子价格实际上是一种机会成本。

在纯市场经济条件下，当市场价格低于影子价格时，这种资源应该：（）
A买进
B卖出
C不买进也不卖出
D不能确定
4．关于整数线性规划问题与它的松弛问题之间的关系说法不正确的是：（）A整数线性规划问题的可行域是它的松弛问题可行域的子集。

B若松弛问题无可行解，则整数线性规划问题也无可行解
C松弛问题的最优解是整数线性规划问题的最优解的一个下界。

D若松弛问题的最优解的各个分量都是整数，则它也是整数线性规划的最优解
5．一个人的效用曲线反映了他对风险的态度。

对实际收入的增加的反应比较迟钝的是（） A 保守型 B 中间型 C 冒险型 D 无法确定
2分，共5题，总计10分）
1．如果一个线性规划问题有可行解，那么它一定有最优解。

（）
2．若线性规划的原问题和对偶问题都有最优解，则它们最优解一定相等。

（）
y>0,说明在最优生产计划中，
3．已知在线性规划的对偶问题的最优解中，对偶变量
i
第i种资源已经完全用尽。

（）
4．因为运输问题是一种特殊的线性规划模型，因而求其解也可能出现下列4种情况：有唯一最优解，有无穷最优解，无界解，无可行解。

（）
5．对于一个动态规划问题，应用顺推法和逆推法可能会得到不同的最优解。

（）
A，B，C三种类型的设备。

生产甲，乙两种产品，每件产品在生产中
问题（1
（2）确定出最优的生产计划。

A1，A2，A3将物品运往四个销地甲，乙，丙，丁各产地的产量和各销地的销量，还有各产地运往各销地每件物品的运费如表所示。

问应该如何调运，
4万元，可向A，B，C三个项目投资，已知各项目不同投资额的
八、70盒；另一组内
装黑球，有30盒，现从这100盒中任取一盒，让你猜，如果这个盒内装是白球，猜对得500分，猜错罚150分，如果这个盒内装的是黑球，猜对得1000分，猜错罚200分。

为了得分最
一批钢筋，需要长度为3米的90根，长度4米60根，已知所用的下料钢筋每根长10米，问如何下料，可使所用原料最省？（只建数学模型）。