(T1 T2 )/ 2
T1
(T1 T2 )/ 2 dT dQ T T2 Cp C p ln 1 T1 T T 2T1
S ( S1 S10 ) (S 2 S 20 ) C p ln
•当T1
2 1 2 2
T1 T2
4T1T2
2
T2 时,存在不等式
可得
dV/V = dT/T- dp/p
dT dV R T V
dT dp T p
dS CV ,m
dS C p ,m
可得
T p S S 0 C p ,m ln R ln T0 p0
§5.3 熵与熵增加原理
理想气体熵的公式
T p S S 0 C p ,m ln R ln T0 p0
这就是说,积分
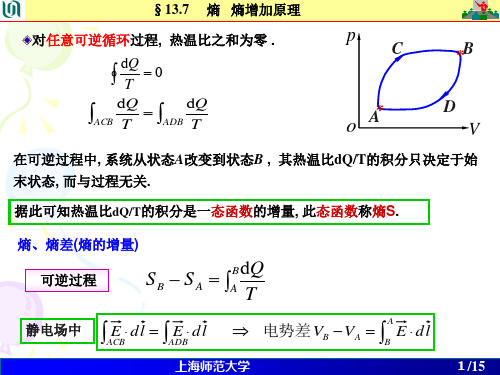
仅与处于相同初末态的 dQ / T 的数值 有关,而与路径无关。 这个结论对任意选定的初末两态(均为平 衡态)都能成立。 在第一定律中也曾指出, 功和热量都与变化路径有关,它们都 不与系统状态有一一对应关系,因而都不 是态函数。
§5.3 熵与熵增加原理
b
a
dQ / T
b b dQ dQ dQ a ( A) T a ( B ) T a ( E ) T 上式可见, dQ / T 可逆变化 仅与初末状 态有关,与所选变化路径无关, 说明dQ / T 是一个态函数的微分量, 我们把 b dQ Sb S a a可逆 T •这个态函数称为熵,以符号 S 表示。 它满足如下关系: b
§5.3 熵与熵增加原理
Qd S 0S T
(四)以熵来表示热容 既然可逆过程中T dS = 可以用熵来表示CV 及 Cp .