饱和软土的经验型蠕变模型

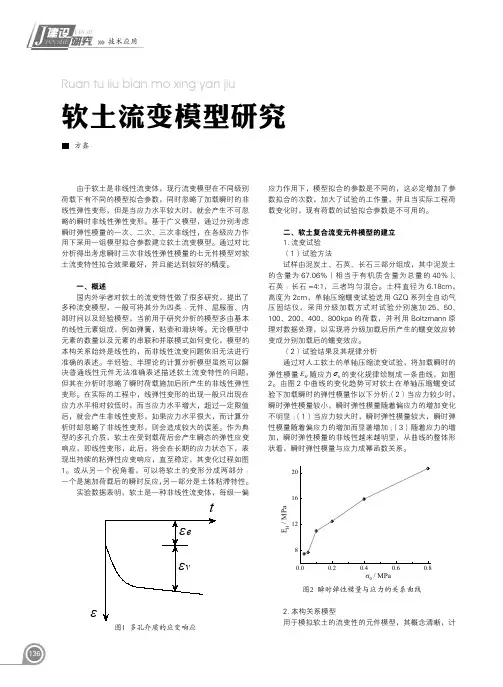
软土结构性流变力学模型的研究关超【摘要】以粉质软粘土为研究对象进行室内蠕变实验,对比分析土体结构性变化对流变特性的影响.提出土体结构性影响系数的概念.根据试验数据确定应力效果参数与应力水平的关系式,进而建立了软土的结构性宏观流变力学模型,描述了软土结构改变后的流变规律.【期刊名称】《辽宁省交通高等专科学校学报》【年(卷),期】2010(012)005【总页数】4页(P7-9,18)【关键词】流变;结构性影响系数;力学模型;结构性【作者】关超【作者单位】辽宁省交通高等专科学校,辽宁沈阳110122【正文语种】中文【中图分类】TU4331 引言随着道路建设高速发展，软土地基路段的路基沉降问题一直困扰工程界。

越来越多的工程实例表明，造成沉降过大的原因之一是因为软土不仅仅具有弹塑性，还具有粘滞性，即流变性，是一种粘弹塑性土体，其本构关系模型应把时间考虑进去，成为应力、应变和时间三者之间的力学模型。

此外，近年来的研究发现，软土的应力应变关系等性质随土结构性的变化而发生变化，但是关于结构性对软土流变性质的影响尚未得到解决。

因此有必要研究结构性变化对软土流变特性的影响，比较天然原状软土与重塑后软土在流变特性中的差异，建立反应结构性影响的宏观流变力学模型，才能准确把握软土的流变性质，从本质上认识软土变形规律，进而准确估算工后沉降。

2 蠕变实验及实验数据实验以粉质软粘土为研究对象，土样的物理力学性质指标如表1所示。

三轴剪切蠕变实验设备由普通应变式三轴剪力仪经改装而成，实验设备如图1所示。

直剪蠕变实验设备由普通应变式直剪仪经改装而成，实验设备如图2所示。

为显示结构性变化对流变力学性质的影响，采用重塑的方法进行土样制备，破坏天然原状土的原始结构，分别进行原状土和重塑土的平行实验。

重塑土的各项实验条件与原状土相同，这样便于进行力学性质比较分析。

由原状土样的蠕变实验曲线可以得出原状土应力应变等时曲线，如图3所示。

由重塑土的蠕变实验曲线可得出重塑土应力应变等时曲线，如图4所示。

第３３卷第３期烟台大学学报（自然科学与工程版）Ｖｏｌ．３３Ｎｏ．３２０２０年７月ＪｏｕｒｎａｌｏｆＹａｎｔａｉＵｎｉｖｅｒｓｉｔｙ（ＮａｔｕｒａｌＳｃｉｅｎｃｅａｎｄＥｎｇｉｎｅｅｒｉｎｇＥｄｉｔｉｏｎ）Ｊｕｌ．２０２０ 文章编号：１００４８８２０（２０２０）０３０３５４０６ｄｏｉ：１０．１３９５１／ｊ．ｃｎｋｉ．３７１２１３／ｎ．１９１２０９ 收稿日期：２０１９１２０９ 基金项目：国家自然科学基金资助项目（４１６０２２８４）；烟台大学研究生科技创新基金资助项目（ＹＤＺＤ２００６）． 通信作者：徐进（ｊｉｎｘｕ１０３１＠１６３．ｃｏｍ），副教授，博士，主要从事岩土工程方面的教学与科研工作．含水层饱和砂土蠕变试验及流变模型辨识研究杨伟涛，徐　进，王少伟（烟台大学土木工程学院，山东烟台２６４００５）摘要：利用高压固结仪和梯度加载方法，对地面沉降地区的含水层砂土进行了室内蠕变试验，分别得到了多级荷载下应力－应变长期关系曲线与应力－应变等时曲线．试验结果表明：与弱透水层的黏性土一样，含水层砂性土也具有典型的蠕变特征，而且这种蠕变性与应力水平有关，在双对数坐标系中表现出明显的线性特点．在此基础上，利用Ｍａｔｌａｂ编写了计算程序，对试验数据进行了参数反演和模型识别，获得了能够反映含水层砂土蠕变特性的最优黏弹性流变模型．关键词：地面沉降；含水层；饱和砂性土；蠕变试验；流变模型中图分类号：ＴＵ４４１ 文献标志码：Ａ 含水层抽水引起地下水位降低，导致含水层土体骨架承受的有效应力增加，致使含水层固结压密，弱透水层释水变形，从而引起地面沉降，抽水引起的地面沉降包括含水层变形和弱透水层变形两部分［１］．传统观念认为在地面沉降中含水层砂土的贡献可以忽略不计，地面沉降主要是由弱透水层的压缩变形引起，而且弱透水层黏性土的蠕变是导致地面沉降长期发展的主要原因［２－５］．然而，近些年对于地面沉降的进一步研究发现，当含水层厚度较大时，地面沉降中砂性土的变形也占有一定的比例，甚至与弱透水层变形量相当［６－９］．同时，由于颗粒重组和颗粒破碎等机理，砂土也具有蠕变变形特征［１０］．因此，通过试验找出合适的流变模型来描述含水层砂土的蠕变特性，对于地面沉降长期变形的精确预测具有重要的理论意义．目前多采用经验流变模型和理论流变模型来描述土体的流变性［７，１０］．经验模型主要是在蠕变，应力松弛和恒应变率这些拟合试验结果的基础上得到［１０］．近年来，随着对土体流变特性的不断深入研究，各种经验模型在一些地区的含水层土体蠕变研究中得到了很好的应用．王艳芳等［１１］利用室内改装的应力控制式三轴仪对河北唐山京唐港饱和砂土进行排水蠕变特性研究，发现在应力水平不超过０ ８的情况下，Ｍｅｓｒｉ经验模型对该地区砂土的蠕变规律拟合效果较好．王非等［１２］利用常州和上海的地面沉降实测数据验证了用Ｓｉｎｇｈ经验模型计算含水层变形的有效性．经验模型容易求取、应用方便，但是由于缺乏物理意义，普适性较差，也不便于数值应用［１０，１３］．理论流变模型借助力学元件来模拟土体的弹性和黏性变形，概念直观，物理意义明确，可以直接代入数值计算用于地面沉降预测［１３－１４］．施小清等［６］对常州含水层饱和砂性土进行单轴压缩试验，从Ｍｅｒｃｈａｎｔ体、Ｂｕｒｇｅｒｓ体２个流变模型中识别出Ｂｕｒ ｇｅｒｓ体能够更好地描述该地区含水层砂土的流变性．杨奇等［１５］用三单元Ｍｅｒｃｈａｎｔ体和四单元Ｓｃｈｉｆｆｍａｎ体较好地描述了桩底砂土层的蠕变变形特性．孙晓涵等［１６］运用自行研制的高压固结仪，选取了西　第３期杨伟涛，等：含水层饱和砂土蠕变试验及流变模型辨识研究安市含水层具有代表性的中细砂样进行研究，提出了适合于西安地区含水层蠕变特性的广义Ｋｅｌｖｉｎ体．不同地区土体流变特性迥异，流变本构模型又形式多样．因此，除了参数反演，流变本构模型本身的反演问题（即如何根据实测资料辨识出最佳的流变模型）也同样重要［１４］．目前关于砂土流变特性的研究中，多是基于给定的一种或２种流变模型进行参数反演，从更广泛的流变模型中识别筛选出最优模型的相关研究仍然较少［１５－１８］．为此，本文选取长三角地面沉降区饱和砂性土进行单轴压缩试验，验证了砂性土具有蠕变特征并基于试验现象与结果，从Ｍｅｒｃｈａｎｔ体、开尔文体（Ｋ）、广义开尔文体（Ｈ－Ｋ）、Ｂｕｒｇｅｒｓ体、饱依丁－汤姆逊体（Ｈ－Ｍ）５个能表征衰减蠕变的流变模型中识别出最优的理论流变模型，以便能够更好地描述含水层饱和砂性土的流变特性，为后续的地面沉降理论计算和数值分析做参考．１　单轴蠕变试验土样是选自长三角地面沉降区的饱和砂性土，利用环刀进行取样，试样高２０ｃｍ，面积为３０ｃｍ２，各项物理指标如表１所示．通过单轴高压固结仪，对试样进行室内高压固结试验，采用梯度加载法，加载比为３．设置了２组试验，如图１所示，分别在图中左右２台仪器中进行试验，通过２组试验的数据对比确保试验操作流程没有出现失误而导致数据失真．每级荷载施加后数据的读取按照１ｍｉｎ、１０ｍｉｎ、１５ｍｉｎ、２０ｍｉｎ、３０ｍｉｎ、４５ｍｉｎ、１ｈ、２ｈ、４ｈ、８ｈ、１２ｈ、２３ｈ、１ｄ、２ｄ（后期每隔一天读取一次）的时间间隔直至变形稳定，当变形量小于０００５ｍｍ／ｄ时视为变形稳定．起始压力和最大压力分别为５０ｋＰａ和３２００ｋＰａ，试验过程中温度始终保持在（２３±３）℃．表１　饱和砂土的各项物理力学性质指标Ｔａｂ．１　Ｐｈｙｓｉｃａｌａｎｄｍｅｃｈａｎｉｃａｌｐｒｏｐｅｒｔｉｅｓｏｆｓａｔｕｒａｔｅｄｓａｎｄ含水量ｗ／％重度／（ｋＮ·ｍ－３）孔隙比ｅ土粒比重压缩系数凝聚力ｃ／ｋＰａ内摩擦角／（°）粒度组成／％２～０ ５０ ５～０ ２５０ ２５～０ ０７５０ ０７５～０ ００５２３１９ １０ ７３６２ ６９０ １３４３５ ９１７ ０４６ ６２２ ５１３９图１　分级荷载下蠕变试验Ｆｉｇ．１　Ｃｒｅｅｐｔｅｓｔｕｎｄｅｒｇｒａｄｅｄｌｏａｄｓ２　试验结果与分析通过２组试验数据对比发现其变形值近乎一致，表明试验未出现不当操作．选其中一组试样，该试样各级荷载作用下的蠕变曲线如图２所示，从图中可以发现蠕变曲线具有明显的阶段性．第一阶段为衰减蠕变过程，即加载初期变形随着时间的增加而增加，但相同时间增量内变形增量逐渐减小，最终变形趋向于与荷载有关的某个定值［１９－２０］．第二阶段即在加载后期变形继续增加，但变形速率基本保持不变，这是由于在室内高压固结试验中，试样受到了来自环刀的侧向约束，在轴向应力下土样不断被挤压密实，强度也因此不断提高，故没有出现因变形快速增加而导致试样被破坏的现象［１９］．烟台大学学报（自然科学与工程版）第３３卷　的透水性极强，固结沉降完成快，导致瞬时沉降与固结沉降已分不开．因此，前２种沉降完成的快，在后期变形中主要是次固结沉降即蠕变变形，所以该转折点所对应的时间可以看成是固结完成的时间［２１－２２］．!"#$%&'(#(('((('#((&(((&#((%(((%#(()*+,)-./0./0./0./0./0$$(./0&11(./0图４　应力应变等时曲线Ｆｉｇ．４　Ｓｔｒｅｓｓ ｓｔｒａｉｎｉｓｏｃｈｒｏｎｏｕｓｃｕｒｖｅｓ３　流变模型由试验现象和前面的分析可以看出，长三角地面沉降区饱和砂性土在高压应力下变形复杂，且同样具有蠕变特性．为了对该地区饱和砂性土的流变特性进行分析以及对地面沉降加以预测，需要在试验的基础上找出应力、应变和时间三者之间关系的数学表达式，即流变模型．所谓理论流变模型就是把砂土看作均质连续体，通过“虎克体”和“牛顿体”等基本元件的组合来模拟土体的复杂变形［１４，２３］．３ １　模型的选择由试验可以看出该地区饱和砂性土在轴向应力的作用下，其变形为包括瞬时沉降、固结沉降和次固结沉降的衰减蠕变．因此在流变模型中必须要具有虎克弹簧来模拟土体在应力作用下所发生的瞬时沉降，且该虎克弹簧应与其他元件串联；其次为了模拟衰减蠕变的特征，流变模型中还应当具有牛顿黏壶．不同模型所含有的元件种类虽然相同，但其所具有的元件个数和组合方式却是各异的，考虑到各地区土体物理力学性质的差异性，流变本构模型本身的反演问题（即如何根据实测资料辨识出最佳的流变模型）显得尤为重要．为此，本文找出了目前常用的５个能表征衰减蠕变的流变模型（Ｍｅｒｃｈａｎｔ体、开尔文体（Ｋ）、广义开尔文体（Ｈ－Ｋ）、Ｂｕｒｇｅｒｓ体、饱依丁－汤姆逊体（Ｈ－Ｍ）），并将其蠕变公式和结构模型列于表２．３ ２　模型的识别根据试验结果，采用Ｂｏｌｔｚｍａｎｎ叠加原理将分级加载下的应力应变曲线转换为不同荷载下的蠕变曲线［１４］．利用最小二乘法原则，结合各模型的蠕变公式建立目标函数见式（１），式中向量槇ε（ｔｉ）是试验测得的土体蠕变变形量，各流变模型公式中的σ０和ｔ都是已知常量．采用软件Ｍａｔｌａｂ编写反演分析程序，利用该程序对目标函数进行迭代求得各流变模型中的未知参数，反演结果列于表３．Ｑ＝∑［槇ε（ｔｉ）－ε（ｔｉ）］２，（１）求得未知参数之后，在相同的时间向量下，由各模型的蠕变公式求出土体的蠕变变形理论值，并将其与试验测得的蠕变变形量绘制在同一个双对数坐标系中．其中理论值用实线代替，试验真实值用散点代替，如图５．３ ３　结果分析根据数理统计，当相关系数Ｒ在０ ４～０ ６之间时两变量为中等程度相关，在０ ６～０ ８之间时为强相关，在０ ８～１ ０之间时为极强相关．由表３中的相关系数可知，５个模型的相关系数均大于０ ５，即本文列出的５个流变模型对于该地区饱和砂性土变形的拟合在一定程度上都是可行的，也证明了饱和砂性土的流变性．６５３　第３期杨伟涛，等：含水层饱和砂土蠕变试验及流变模型辨识研究表２　常见流变模型的蠕变公式Ｔａｂ．２　Ｃｒｅｅｐｆｏｒｍｕｌａｆｏｒｃｏｍｍｏｎｒｈｅｏｌｏｇｉｃａｌｍｏｄｅｌｓ模型名称蠕变公式结构模型开尔文体（Ｋ体）ε＝σ０Ｅ１１－ｅ－Ｅ１ｔη１()ｔ广义开尔文体（Ｈ－Ｋ体）ε＝σ０Ｅ０＋σ０Ｅ１×１－ｅ－Ｅ１η１()ｔ＋σ０Ｅ２×１－ｅ－Ｅ２η２()ｔＢｕｒｇｅｒｓ体ε＝σ０１Ｅ０＋ｔη２＋１Ｅ１１－ｅ－Ｅ１η１()[]ｔ鲍依丁－汤姆逊体（Ｈ－Ｍ）ε＝σ０Ｅ０１－Ｅ１Ｅ１＋Ｅ０ｅ－Ｅ１Ｅ０（Ｅ１＋Ｅ０）η１()ｔ表３　参数反演结果Ｔａｂ．３　Ｐａｒａｍｅｔｅｒｉｎｖｅｒｓｉｏｎｒｅｓｕｌｔｓ模型名称σ０／ＭＰａＥ０／ＭＰａＥ１／ＭＰａＥ２／ＭＰａη１／（ＭＰａ·ｄ）η２／（ＭＰａ·ｄ）ＲＭｅｒｃｈａｎｔ体０ ０５１２ ６６５０５ ３４４４０ ００１９０ ６４５２０ ２１５ ８１９０１６ ５７４３０ ００６００ ５２６７０ ８４１ ７１６９４０ ７２３６０ ０１２００ ５４２５３ ２７６ １２４９１９３ １３９５０ ０７９７０ ５１８１开尔文体（Ｋ体）０ ０５３ ７５８８０ ００１１０ ６４５２０ ２８ ０９４２０ ００２１０ ５２６７０ ８２０ ６０６１０ ００４７０ ５４２５３ ２５４ ６１４００ ０１２８０ ５１８１广义开尔文体（Ｈ－Ｋ体）０ ０５７ ６３１８８ １８５２０ ００２７１８ ６９５５１８ ４８４２０ ９０３００ ２１５ ７３８４１８ １２５６０ ００４９７４ ２０９５４５ ９５８４０ ９７１３０ ８３５ ０７５７５４ ５５６６０ ０１２２１９６ ９２９１１４８ ０１９９０ ９３１３３ ２１０９ １８３８１２２ ６９３６０ ０１５６５０８ ６３５８１７７ ９５４８０ ９４９８Ｂｕｒｇｅｒｓ体０ ０５７ ４３７４８ １１３８０ ００３１４６ ７９６７０ ８８５２０ ２１３ ５７５６２１ ３３６１０ ００７１１９２ １８５５０ ８８７９０ ８３５ ７１４０５３ ４５９００ ０１１０３１８ ９４３３０ ７８４３３ ２８０ ２１８８ ４０ １１９９８ ６０ ８７２１鲍依丁－汤姆逊体（Ｈ－Ｍ）０ ０５３ ３９０１０ ４９４１０ ５９７９０ ８０１９０ ２８ ０９３２４ ５５７７０ ００１３０ ５２６７０ ８２０ ６０５０９ ０２３７０ ００２４０ ５４２５３ ２５４ ６１２６１３ ０１５６０ ００５６０ ５１８１７５３烟台大学学报（自然科学与工程版）第３３卷　! $%!"#$ $&.*/01234*56%!8%!&#$ 8&.9/'()%!"#""!"#"!"#!!8%!"*+ 8&'"()*+""()*,""()*-+""()*.3/,-.()%!"#""!"#"!"#!!8%!&*+ 8&'"()*+""()*,""()*-+""()*.%/:;2<12=%!8%!&*+ 8&.1//01>234%图５　模型计算结果与试验数据对比Ｆｉｇ．５　Ｔｈｅｃｏｍｐａｒｉｓｏｎｂｅｔｗｅｅｎｔｈｅｃａｌｃｕｌａｔｅｄｒｅｓｕｌｔｓｏｆｍｏｄｅｌｓａｎｄｔｅｓｔｄａｔａ 对各流变模型在不同应力下的相关系数求平均值，结果见表４．可以看出广义开尔文体和Ｂｕｒｇｅｒｓ体的平均相关系数均大于０ ８，都属于极强相关，从表３各级应力下的相关系数也可以发现两者均能很好地对试验土样的蠕变特性进行拟合．其中广义开尔文体是五单元模型，Ｂｕｒｇｅｒｓ体是四单元模型，相比较而言广义开尔文体参数更多，但其拟合精度更高，相关系数高出Ｂｕｒｇｅｒｓ体９ ５％．表４　各模型的平均相关系数Ｔａｂ．４　Ａｖｅｒａｇｅｃｏｒｒｅｌａｔｉｏｎｃｏｅｆｆｉｃｉｅｎｔｏｆｅａｃｈｍｏｄｅｌ平均相关系数Ｍｅｒｃｈａｎｔ体开尔文体广义开尔文体Ｂｕｒｇｅｒｓ体鲍依丁－汤姆逊体珔Ｒ０ ５５８１０ ５５８１０ ９３８９０ ８５７４０ ５９７３ 从表３各模型参数的反演结果发现，同一模型的各参数和应力水平有关，随着应力的增加其反演结果也随之增加．如果假设模型一旦给定，其中参数值也应为定值．因为当应力增加时，为了保持模量不变，应变也应当增加相应的倍数．但是，土体是具有三相特性的典型非线性体，且当土体被压密挤实到一定程度之后，其孔隙比也将缩减到一定程度，同时伴随内部土体颗粒的滑移调整和颗粒破碎导致的级配改变．因此，为了更好地描述土体的这种非线性特点，可以采用一些非线性元件（如非线性弹簧）来组合模型，使得各参数（如弹簧的模量Ｅ）随应力的变化而不同［６］．４　结　论（１）试验结果表明，瞬时加载下饱和砂性土的变形是具有明显阶段性的衰减蠕变，其应力应变等时曲线也显示饱和砂性土的变形同样具有流变性．在地面沉降计算分析中，应该同时考虑弱透水层黏性土和含水层砂土流变性带来的变形滞后效应．（２）从常用的５个流变模型中识别出最佳模型．结果表明，广义开尔文体和Ｂｕｒｇｅｒｓ体都能对长三角地面沉降区饱和砂性土的蠕变趋势加以描述．其中广义开尔文体的平均拟合相关系数高出Ｂｕｒ ｇｅｒｓ体９ ５％，精度更高，是描述该地区饱和砂性土流变特性的最优模型；但Ｂｕｒｇｅｒｓ体所含参数少于广义开尔文体，相比较而言应用更方便．（３）由于所选的流变模型由线性元件组合而成，本文中同一模型在不同应力下所反演出的参数不同，不能用某一级应力下反演出的参数来描述其他荷载下的流变规律．为了更好地模拟土体这种非８５３　第３期杨伟涛，等：含水层饱和砂土蠕变试验及流变模型辨识研究线性材料，有必要对模型进行改进，采用非线性元件，使得模型参数随着应力变化而改变，这方面仍有待开展进一步的理论和试验研究．参考文献：［１］　罗东娜，曾婕，王旭东．抽注水作用下含水层砂土变形特征试验［Ｊ］．南京工业大学学报（自然科学版），２０１３，３５（３）：１１－１５．［２］　ＯＲＴＥＧＡ ＧＵＥＲＲＥＲＯＡ，ＲＵＤＯＬＰＨＤＬ，ＣＨＥＲＲＹＪＡ．Ａｎａｌｙｓｉｓｏｆｌｏｎｇ ｔｅｒｍｌａｎｄｓｕｂｓｉｄｅｎｃｅｎｅａｒＭｅｘｉｃｏＣｉｔｙ：Ｆｉｅｌｄｉｎｖｅｓｔｉｇａｔｉｏｎｓａｎｄｐｒｅｄｉｃｔｉｖｅｍｏｄｅｌｉｎｇ［Ｊ］．ＷａｔｅｒＲｅ ｓｏｕｒｃｅｓＲｅｓｅａｒｃｈ，１９９９，３５（１１）：３３２７－３３４１．［３］　ＢＵＤＨＵＭ，ＡＤＩＹＡＭＡＮＩ．Ｔｈｅｉｎｆｌｕｅｎｃｅｏｆｃｌａｙｚｏｎｅｓｏｎｌａｎｄｓｕｂｓｉｄｅｎｃｅｆｒｏｍｇｒｏｕｎｄｗａｔｅｒｐｕｍｐｉｎｇ［Ｊ］．ＧｒｏｕｎｄＷａ ｔｅｒ，２０１３，５１（１）：５１－５７．［４］　ＸＵＹＳ，ＳＨＥＮＳＬ，ＣＡＩＺＹ，ｅｔａｌ．Ｔｈｅｓｔａｔｅｏｆｌａｎｄｓｕｂｓｉｄｅｎｃｅａｎｄｐｒｅｄｉｃｔｉｏｎａｐｐｒｏａｃｈｅｓｄｕｅｔｏｇｒａｕｎｄｗａｔｅｒｗｉｔｈｄ ｖａｗａｌｉｎＣｈｉｎａ［Ｊ］．ＮａｔｕｒａｌＨａｚａｒｄｓ，２００８：４５（１）：１２３－１３５．［５］　ＧＡＬＬＯＷＡＹＤＬ，ＪＯＮＥＳＤＲ，ＩＮＧＥＢＲＩＴＳＥＮＳＥ．ＬａｎｄＳｕｂｓｉｄｅｎｃｅｉｎｔｈｅＵｎｉｔｅｄＳｔａｔｅｓ［Ｍ］．Ｒｅｓｔｏｎ：ＵＳＧｅｏｌｏｇ ｉｃａｌＳｕｒｖｅｙ，１９９９．［６］　施小清，薛禹群，吴吉春，等．饱和砂性土流变模型的试验研究［Ｊ］．工程地质学报，２００７，１５（２）：２１２－２１６．［７］　张云，薛禹群，施小清，等．饱和砂性土非线性蠕变模型试验研究［Ｊ］．岩土力学，２００５，２６（１２）：１８６９－１８７３［８］　张云，薛禹群，吴吉春，等．上海砂土蠕变变形特征的试验研究［Ｊ］．岩土力学，２００９，３０（５）：１２２６－１２３０，１２１６．［９］　施小清，薛禹群，吴吉春，等．常州地区含水层系统土层压缩变形特征研究［Ｊ］．水文地质工程地质，２００６，３３（３）：１－６．［１０］　温亚楠，朱鸿鹄，张诚诚，等．砂土蠕变特性研究现状及展望［Ｊ］．工程地质学报，２０１５：２９４－３０１．［１１］　王艳芳，蔡燕燕，蔡正银．饱和砂土蠕变特性实验［Ｊ］．华侨大学学报（自然科学版），２０１７，３８（１）：３１－３７．［１２］　王非，缪林昌．抽水地面沉降中含水层长期变形特性研究［Ｊ］．岩石力学与工程学报，２０１１，３０（Ｓ１）：３１３５－３１４０．［１３］　路德春，苗金波，林庆涛，等．土的三维弹黏塑性应力路径本构模型［Ｊ］．岩石力学与工程学报，２０１８，３７（Ｓ１）：３６３３－３６４４．［１４］　孙钧．岩土材料流变及其工程应用［Ｍ］．北京：中国建筑工业出版社，１９９９．［１５］　杨奇，冷伍明，聂如松，等．砂土蠕变特性试验研究［Ｊ］．岩石力学与工程学报，２０１４，３３（Ｓ２）：４２８２－４２８６．［１６］　孙晓涵，崔向美．高应力下西安含水层砂土蠕变特性的试验研究［Ｊ］．南水北调与水利科技，２０１５，１３（６）：１１３３－１１３７．［１７］　李明霞．地下水控采条件下上海地面沉降特征研究［Ｄ］．南京：南京大学，２０１４．［１８］　李帅．高氯盐细砂土流变模型的试验研究［Ｄ］．兰州：兰州交通大学，２０１５．［１９］　王惠敏，张云，何佳佳．单向压缩状态下饱和砂性土蠕变特性试验研究［Ｊ］．地下空间与工程学报，２００９，５（Ｓ２）：１５８０－１５８４．［２０］　汤斌．软土固结蠕变耦合特性的试验研究与理论分析［Ｄ］．武汉：武汉大学，２００４．［２１］　赵明华．基础工程－下－土力学与基础工程［Ｍ］．武汉：武汉理工大学出版社，２０１８．［２２］　张云，薛禹群，吴吉春，等．饱和黏性土蠕变变形试验研究［Ｊ］．岩土力学，２０１１，３２（３）：６７２－６７６，６８３［２３］　范广勤．岩土工程流变力学［Ｍ］．北京：中国建筑出版社，１９９９．ＣｒｅｅｐＥｘｐｅｒｉｍｅｎｔａｌＳｔｕｄｙｏｎＡｑｕｉｆｅｒＳａｔｕｒａｔｅｄＳａｎｄｙＳｏｉｌａｎｄＲｈｅｏｌｏｇｉｃａｌＭｏｄｅｌＩｄｅｎｔｉｆｉｃａｔｉｏｎＹＡＮＧＷｅｉ ｔａｏ，ＸＵＪｉｎ，ＷＡＮＧＳｈａｏ ｗｅｉ（ＳｃｈｏｏｌｏｆＣｉｖｉｌＥｎｇｉｎｅｅｒｉｎｇ，ＹａｎｔａｉＵｎｉｖｅｒｓｉｔｙ，Ｙａｎｔａｉ２６４００５，Ｃｈｉｎａ）Ａｂｓｔｒａｃｔ：Ｔｈｅｌａｂｏｒａｔｏｒｙｃｒｅｅｐｔｅｓｔｓｏｆａｑｕｉｆｅｒｓａｎｄ，ｗｈｉｃｈｉｓｓａｍｐｌｅｄｆｒｏｍｌａｎｄｓｕｂｓｉｄｅｎｃｅａｒｅａ，ａｒｅｃｏｎｄｕｃｔｅｄｂｙｕｓｉｎｇｈｉｇｈ ｐｒｅｓｓｕｒｅｃｏｎｓｏｌｉｄａｔｉｏｎａｐｐａｒａｔｕｓａｎｄｇｒａｄｉｅｎｔｌｏａｄｉｎｇｍｅｔｈｏｄ，ｔｈｅｎｔｈｅｌｏｎｇ ｔｅｒｍｓｔｒｅｓｓ ｓｔｒａｉｎｒｅｌａ ｔｉｏｎｓｈｉｐｃｕｒｖｅｓａｎｄｉｓｏｃｈｒｏｎｏｕｓｓｔｒｅｓｓ ｓｔｒａｉｎｃｕｒｖｅｓｕｎｄｅｒｍｕｌｔｉ ｌｅｖｅｌｌｏａｄａｒｅｏｂｔａｉｎｅｄｒｅｓｐｅｃｔｉｖｅｌｙ．Ｔｈｅｅｘｐｅｒｉ ｍｅｎｔｒｅｓｕｌｔｓｄｅｍｏｎｓｔｒａｔｅｔｈａｔ，ｌｉｋｅｔｈｅｃｌａｙｅｙｓｏｉｌｆｒｏｍｗｅａｋ ｐｅｒｍｅａｂｉｌｉｔｙｌａｙｅｒｓ，ａｑｕｉｆｅｒｓａｎｄａｌｓｏｓｈｏｗｓｔｈｅｔｙｐｉ ｃａｌｃｒｅｅｐｃｈａｒａｃｔｅｒｉｓｔｉｃｗｈｉｃｈｉｓｒｅｌａｔｅｄｔｏｓｔｒｅｓｓｌｅｖｅｌｗｉｔｈｏｂｖｉｏｕｓｌｉｎｅａｒｉｔｙｉｎａｄｏｕｂｌｅｌｏｇａｒｉｔｈｍｉｃｃｏｏｒｄｉｎａｔｅ．Ｂａｓｅｄｏｎｔｈｅｅｘｐｅｒｉｍｅｎｔａｌｒｅｓｕｌｔｓ，ｔｈｅｐａｒａｍｅｔｅｒｓｉｎｖｅｒｓｉｏｎａｎｄｍｏｄｅｌｉｄｅｎｔｉｆｉｃａｔｉｏｎｏｎｔｈｅｔｅｓｔｄａｔａａｒｅｃａｒｒｉｅｄｏｕｔｂｙａｃｏｍｐｕｔａｔｉｏｎｐｒｏｇｒａｍｄｅｖｅｌｏｐｅｄｗｉｔｈＭａｔｌａｂ，ａｎｄｔｈｅｏｐｔｉｍａｌｖｉｓｃｏｅｌａｓｔｉｃｒｈｅｏｌｏｇｉｃａｌｍｏｄｅｌｗｈｉｃｈｃａｎｄｅｓｃｒｉｂｅｔｈｅｃｒｅｅｐｃｈａｒａｃｔｅｒｉｓｔｉｃｏｆａｑｕｉｆｅｒｓａｎｄｉｓｉｄｅｎｔｉｆｉｅｄ．Ｋｅｙｗｏｒｄｓ：ｌａｎｄｓｕｂｓｉｄｅｎｃｅ；ａｑｕｉｆｅｒ；ｓａｔｕｒａｔｅｄｓａｎｄｙｓｏｉｌ；ｃｒｅｅｐｔｅｓｔ；ｒｈｅｏｌｏｇｉｃａｌｍｏｄｅｌ（责任编辑　苏晓东）９５３。

第27卷 第9期 岩 土 工 程 学 报 Vol.27 No.9 2005年 9月 Chinese Journal of Geotechnical Engineering Sep., 2005 饱和软粘土的循环蠕变特性朱登峰1，黄宏伟1，殷建华2（1.同济大学 地下建筑与工程系，上海 200092；2.香港理工大学 土木及结构工程学系，香港 中国）摘 要：本文介绍对上海淤泥质饱和粘土在长期循环荷载作用下的变形特性的试验研究结果。

考虑到土的各向异性性质，在三轴试验中，在K0固结条件下把土试样恢复到天然的K0应力状态，然后进行排水及不排水单向循环加载蠕变试验。

从试验结果可以观察到一些重要的现象：（1）当循环轴向应力小于初始固结压力的50％时，饱和粘土的循环蠕变可分成三个阶段；（2）循环应变可分成不可逆的累积应变与可逆应变两部分，可逆应变的大小与循环应力幅值近似成线性关系；（3）孔压增长较为滞后，不排水试样孔压增长稳定时其值约为应力幅值50％，而排水试样的残余孔压约为应力幅值的20％。

关键词：饱和粘土；循环荷载；蠕变，K0固结中图分类号：TU 435 文献标识码：A 文章编号：1000–4548(2005)09–1060–05作者简介：朱登峰(1975–)，男，博士生，研究方向是循环荷载作用下软土理论研究及其工程应用。

Cyclic creep behavior of saturated soft clayZHU Deng-feng1, HUANG Hong-wei1, YIN Jian-hua2(1. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China; 2. Department of Civil and Structure Engineering,The Hong Kong Polytechnic University, Hong Kong, China)Abstract: A study on the deformation behavior of a saturated soft clay under cyclic loading was presented. Considering the intrinsic anisotropy of the soil, a soil specimen was initially restored to the in-situ stress state under K0 consolidation in a triaxial cell, and then the specimen was sheared in the same triaxial cell under axial cyclic loading and tested in a drained or undrained creep condition. The test results showed that: (a) The cyclic creep process of the saturated clays could be divided into three stages if the cyclic axial stress was less than 50% of the initial confining pressure. (b) The cyclic strain could be divided into two parts, that is, a irreversible accumulated strain and a reversible strain. The magnitude of the there was approximately a linear relation between the reversible strain and the amplitude of the cyclic stress. (c) The increase of excess pore water pressure initially lagged behind that of stress. The stable excess pore pressure was about 50% of the stress amplitude for a undrained specimen, however the residual excess pore water pressure was approximately 20% of stress amplitude for a drained specimen.Key words: saturated clay; cyclic loading; creep; K0 consolidation0 前 言软土的循环荷载效应研究开始于20世纪50年代。

饱和砂土蠕变特性实验王艳芳;蔡燕燕;蔡正银【摘要】为证实和进一步了解砂土蠕变规律，利用室内改装的应力控制式三轴仪研究饱和砂土排水蠕变特性．实验结果表明：砂土蠕变受围压和密实度的影响较大，低围压下，砂样更易发生剪胀；密实砂蠕变变形量明显比中密砂小，密实砂比中密砂更易剪胀；侧向减载条件比轴向加载更易剪胀；在应力水平不超过0．8的情况下，Mesri蠕变模型对砂土蠕变规律拟合效果较好．%In order to verify and investigate further the sandy soil creep properties,the stress-controlled triax-ial apparatuses are used to study the drainage creep of saturated sand.The result shows that the creep of satu-rated sand is significantly affected by confining pressure and dense degree.Under low confining pressure,the sample shear dilatancy occurs easily.The creep deformation of dense sand is significantly smaller than the de-formation of middle dense sand,the dense sand shear dilatancy occurs more frequently by comparison with middle dense sand.When the stress level is less than0 .8 ,the Mesri creep model is fitted well for sandy soil creep.【期刊名称】《华侨大学学报（自然科学版）》【年(卷),期】2017(038)001【总页数】7页(P31-37)【关键词】砂土;排水蠕变特性;剪胀;密实度;Mesri蠕变【作者】王艳芳;蔡燕燕;蔡正银【作者单位】南京大学金陵学院，江苏南京 210093;华侨大学福建省隧道与城市地下空间工程技术研究中心，福建厦门 361021;南京水利科学研究院岩土工程研究所，江苏南京 210014【正文语种】中文【中图分类】TU447随着国民经济建设的发展，百年大计工程项目越来越多，对工程建设中地基和构筑物的长期稳定和变形问题提出了新的更高要求.不仅粘土的蠕变效应给工程项目的长期稳定和变形带来不利影响，无粘性土如坝体堆石料、砂土的蠕变[1-6]也对越来越多工程项目造成了不可忽视的影响.文献[7-13]通过室内实验和现场进行实测研究，发现长期开采地下水引起的地面沉降问题与砂土层压缩变形有密切关系，抽水或回灌引起水位升降导致砂层发生的变形并非弹性变形，而与时间存在一定关系，具有蠕变特性.对于软土，其蠕变多受含水量、土的结构、粘粒含量、有机质、应力历史、应力路径等主要因素影响[14-18]；对于软岩，其蠕变多受温度、湿度、应力路径等主要因素影响[19-22]；对于砂土，其蠕变多受土颗粒大小、形状、级配、密实度等因素影响[23-25].本文通过三轴试验研究饱和粉细砂的蠕变规律.1.1 试验方案王艳芳[26]通过对已建河北唐山京唐港10万t级遮帘桩板桩码头工程进行长期原位观测，发现泊位工程的前墙、遮帘桩、后锚定墙的侧向变形均存在时间效应，其原因为板桩结构两侧砂层蠕变位移.为此，文中取该区域一定数量粉细砂进行轴向加载和侧向减载条件下的三轴排水蠕变试验.砂样基本物理力学参数，如表1所示.表1中：γ为天然重度；Gs为土粒密度；ω为水的质量分数；Cq为粉细砂在固结快剪条件下的粘聚力；φq为内摩擦角；下标q表示的固结快剪条件.粉细砂的颗粒级配试验曲线，如图1所示.图1中；η为小于某直径的百分含量；d为试样直径.试验仪器采用改装后的应力控制式三轴仪，尺寸为d=39.1 mm，H=80 mm.实验有如下5个步骤.步骤1 制样.砂样直接在仪器基座上制备，称取相对密度(Dr)为60%，75%的粉细砂，并分3等份，分层击实.步骤2 饱和.分初始饱和与反压饱和两步进行.初始饱和历时约1 h，测定孔隙应力系数(B)值大于0.8即可.接下来，反压饱和后B值须大于0.95才可进入下一步骤. 步骤3 等向固结.施加围压σ3使试样完成等向固结，砂样稳定固结时间约2 h，并记录等向固结时间内体变管读数，进行试样尺寸修正.步骤4 不等向固结.以围压50 kPa为例，按k0=0.45，缓慢增加轴压至111 kPa，并静止.待试样完成k0固结，试样在24 h内轴向变形小于0.01 mm，视为完成不等向.固结此时体变管读数和轴向百分表读数，将其作为试样固结产生的初始体变、初始轴变值.步骤5 排水蠕变实验.砂样蠕变试验加载方案,如表2所示.每级荷载施加后，一天内多次记录百分表读数及体变管读数.当连续1天土样轴向变形小于0.01 mm时，认为蠕变变形已稳定，可继续施加下一级加载，或结束试验[27].1.2 试验结果分析按照Boltzmann叠加原理，将各级围压作用下分级加载方式转化为分别加载方式的蠕变曲线，则砂样在轴向加载及侧向减载条件下，剪应变和体应变随时间的变化曲线，如图2～5所示.图2～5中：εs为剪应力；εv为体积应力；S为偏应力比，S=q/qf=(σ1-σ3)/(σ1-σ3)f.由图2～5可知以下5点结论.1) 实验未设定体积蠕变稳定标准，单从剪应变随时间变化曲线可看出：砂土的蠕变变形随着应力水平的增大而变大，没有出现等速蠕变和加速蠕变，为衰减蠕变. 2) 当没有剪胀时，体积变形较易稳定，一旦发生剪胀现象，体应变较难稳定.图2(f)表现为剪缩，图4(f)先剪缩后剪胀，其他组砂样体变均为剪胀.说明低围压条件下，砂样更易发生剪胀，且密实砂比中密砂更易剪胀.3) 侧向减载条件下，砂样更易发生剪胀(图3，5).侧向减载条件下，所有砂样均为剪胀，说明应力路径会影响土体体积蠕变规律，且围压越低，剪胀效应越明显.4) 密实度对砂样蠕变变形影响较大.密实砂蠕变量明显比中密砂小，即便是高偏应力水平下，在土样未破坏之前，密实砂的变形值仅为2%～4%(图4，5).进一步增大偏应力值，砂样只会剪坏，而不会像中密砂突变稳定后，还能进一步发生蠕变变形(图3(c)).5) 砂土存在蠕变，砂土有良好渗透性，荷载作用很难引起超静孔压，几乎不存在次固结效应，其蠕变特性受围压和相对密实度的影响较大.因此，砂土蠕变机制细观上表现为在恒定荷载下，土颗粒位置的重新调整或部分破碎，宏观上表现为变形随时间而变化，即蠕变.2.1 Mesri模型基于蠕变试验结果，每级荷载下的总应变可分为瞬时应变及与时间有关的蠕应变两部分.蠕应变与应力、时间有关，一般可假设为式(1)中：f1和f2分别为应力和时间的函数.对于应力函数f1,Mesri借鉴Konder提出的应力-应变双曲线型方程[28-29]，即式(2)中：S为偏应力比；Su为不排水剪切强度，Su=(1/2)(σ1-σ3)f.对于排水试验，可以用Su=(1/2)(σ1-σ3)f代替.对于时间函数，Mesri模型选用了幂次函数作为应变-时间关系，即将式(2)，(3)相结合，得到Mesri模型，也即Mesri蠕变模型方程，其表达式为由式(4)知，蠕变速率的公式为Mesri模型共有等4个参数需要确定[30].2.2 模型参数的求取根据ln εa-ln t关系，直线段位置选取参考时间t1=100 min(因100 min之前，ln εa-ln t直线关系不明显)，并取此时的应变为初始蠕应变.根据不同应力水平下的ln εa-ln t，拟合直线关系的斜率，求取平均值,即为λ值.将式(2)作移项变换，有选取各级应力水平下参考时间t1=100 min时的轴向应变值，作ε1/S-ε1关系图，对关系曲线作直线拟合，则直线截距和斜率分别为参数，(Rf)1的值.据上述参数求取思路，当σ3=250 kPa时，中密和密实砂模型参数，如表3所示.2.3 Mesri模型适应性将表3中参数代入式(4)，拟合出砂土蠕变试验曲线如图6，7所示.图6,7中：εa为轴向应变;σ3=250 kPa.由图6,7可知：在应力水平不超过0.8的情况下，Mesri 模型对砂土蠕变规律拟合效果较好，基本不受土样的密实程度、加卸载应力路径的的影响.在高应力水平下，拟合效果不佳的原因有两个方面.一方面,在各级偏应力水平下，Mesri模型参数λ取ln εa～ln t拟合直线斜率的平均值，另一方面是经验模型本身精度所致.Mesri模型建议采用幂函数描述应变-时间关系曲线，幂函数拟合的曲线特点是缓慢地不断增长.曲线初期较陡，后期增加缓慢，导致其与试验曲线本身发展趋势的不完全吻合.而实际上λ是随着偏应力水平的变化而变化，相同围压、不同偏应力水平下的λ值相差也比较大.为此，建议可进一步修正Mesri蠕变法则，并将其与弹塑性模型相结合，建立起考虑砂土蠕变特性的弹粘塑性模型.考虑砂土蠕变规律与土体密实程度有关，尤其建议加入与密实度状态相关的参量，描述砂土蠕变规律.1) 不论是轴向加载还是侧向减载蠕变，砂土变形规律基本一致，均证实了砂土存在蠕变.砂土蠕变特性受围压和相对密实度的影响较大，其蠕变变形随着应力水平的增大而变大.土样未破坏前，不管应力水平的高低，砂土的蠕变规律均为衰减型，没有出现等速蠕变和加速蠕变.2) 试样体积应变明显小于剪应变，且低围压条件下，砂样易发生剪胀；密实砂比中密砂更易剪胀；侧向减载条件下，土体更易发生剪胀.当没有发生剪胀时，体积变形较容易稳定，一旦发生剪胀现象，体应变较难稳定.3) 密实砂蠕变变形量明显比中密砂小.即便是高偏应力水平下，在土样未破坏之前，密实砂的变形值仅为2%～4%.进一步增大偏应力值，砂样只会剪坏，而不会像中密砂突变稳定后，还能进一步发生蠕变变形，故砂土蠕变特性必须考虑密实度对其蠕变规律的影响，且必须考虑体积剪胀效应的影响.4) 依据Mesri经验蠕变模型，在应力水平不超过0.8的情况下，Mesri模型对砂土蠕变规律拟合效果较好，基本不受土样的密实程度、加卸载应力路径的的影响.对粉细砂或砂土而言，建议加入考虑与密实度状态相关的参量，以建立新的蠕变法则来描述其蠕变规律.【相关文献】[1] BJERRUM L.Engineering geology of Norwegian normally consolidated marine clays as related to the settlement of buildings[J].Geotechnique,1967,17(2):81-118.[2] 王者超,乔丽苹.土蠕变性质及其模型研究综述与讨论[J].岩土力学，2011,32(8):2251-2259.[3] 杨超,汪稔,孟庆山.软土三轴剪切蠕变试验研究及模型分析[J].岩土力学,2012,33(增刊1):105-111.[4] 卢萍珍,曾静,盛谦.软黏土蠕变试验及其经验模型研究[J].岩土力学,2008,29(4):1041-1045.[5] 程展林,丁红顺.堆石料蠕变特性试验研究[J].岩土工程学报,2004,26(4):473-476.[6] DIPRISCO C,IMPOSIMATO S.Time dependent mechanical behaviour of loosesands[J].Mechanics of Cohesive-frictional Materials,1996,1(1):45-73.[7] SHI Xiaoqing,WU Jichun,YE Shujun,et al.Regional land subsidence simulation in Su-Xi-Chang area and Shanghai City[J].China Engineering Geology，2008，100(1/2):27-42.[8] 孙晓涵.西安地面沉降与砂土蠕变关系初探[D].西安:长安大学，2011：35-40.[9] 王非,缪林昌.抽水地面沉降中含水层长期变形特性研究[J].岩石力学与工程学报,2011,30(增刊1):3135-3140.[10] WANG Fei,MIAO Linchang,ZHANG Yajun.A simplified method to predictcreep behavior of the Yangtze River sand[J].Bulletin of Engineering Geology and the Environment,2012,71(2):317-324.[11] BURLAND J B,BURBRIDGE M C.Settlements of foundations on sand andgravel[J].Proceedings of the Institution of Civil Engineers,1985,78(6):1325-1381.[12] 冷伍明,杨奇,聂如松，等.高速铁路桥梁桩基工后沉降组合预测研究[J].岩土力学,2011,32(11):3341-3348.[13] 杨奇,冷伍明,聂如松，等.砂土蠕变特性试验研究[J].岩石力学与工程学报,2014,33(增刊2):4282-4286.[14] 陈晓平,朱鸿鹄,张芳枝.软土变形时效特性的试验研究[J].岩石力学与工程学报,2005,24(12):2142-2148.[15] 朱鸿鹄,陈晓平,程小俊,等.考虑排水条件的软土蠕变特性及模型研究[J].岩土力学，2006，27(5):694-698.[16] 袁杰,房营光,谷任国,等.流变物质含量及其分布对软土蠕变特性影响的试验研究[J].岩石力学与工程学报,2014,33(增刊1):2924-2929.[17] 谷任国,房营光.有机质和黏土矿物对软土流变性质影响的对比试验研究[J].华南理工大学学报(自然科学版),2008,36(10):31-36.[18] 杨爱武,闫澍旺,杜东菊.结构性吹填软土蠕变模型研究[J].岩土力学，2012,33(11):3213-3219.[19] 杨春和,白世伟,吴益民.应力水平及加载路径对盐岩时效的影响[J].岩石力学与工程学报,2000,19(3):270-275.[20] 张向东,傅强.泥岩三轴蠕变实验研究[J].应用力学学报,2012,29(2):154-159.[21] 高小平,杨春和,吴文,等.盐岩蠕变特性温度效应的实验研究[J].岩石力学与工程学报,2005,24(12):2054-2059.[22] 谌文武,原鹏博,刘小伟.分级加载条件下红层软岩蠕变特性试验研究[J].岩石力学与工程学报,2009,28(增刊1):3075-3080.[23] 胡桂衔,房营光,袁杰.砂性土的蠕变性质影响试验研究[J].工程勘察,2012(12):8-11.[24] 张云，薛禹群，施小清，等.饱和砂性土非线性蠕变模型试验研究[J].岩土力学,2005,26(12):1869-1873.[25] 张云,薛禹群,吴吉，等.上海砂土蠕变变形特征的试验研究[J].岩土力学,2009,30(5):1226-1231.[26] 王艳芳.饱和土蠕变特性试验及计算模型研究[D].南京:南京水利科学研究院,2012:131-135.[27] 王艳芳,蔡正银,周治刚,等.k0固结条件下淤泥土排水蠕变特性研究[J].岩土力学,2015,36(8):2243- 2248.[28] 李军世,孙钧.上海淤泥质粘土的Mesri蠕变模型[J].土木工程学报,2001,34(6):74-79.[29] MESRI G,REBERS-CORDERO E,SHIELDS D R,et al.Shear stress-strain-time behavior of clays[J].Geotechnique,1981,31(4):537-552.[30] 赖小玲,叶为民,王世梅.滑坡滑带土非饱和蠕变特性试验研究[J].岩土工程学报,2012,34(2):286-292.。

非饱和土蠕变力学特性试验及经验模型研究魏建柄; 刘卫斌【期刊名称】《《水文地质工程地质》》【年(卷),期】2019(046)006【总页数】8页(P67-73,82)【关键词】非饱和土; 蠕变; 经验模型; 基质吸力; 初始切线模量【作者】魏建柄; 刘卫斌【作者单位】陕西铁道工程勘察有限公司陕西西安710043【正文语种】中文【中图分类】TU411.5; TU411.7蠕变特性是土力学中的核心内容之一，与基坑工程、边坡工程等长期稳定性紧密关联[1-3]。

非饱和土是一种包含固、液、气的三相土，相比饱和土而言，非饱和土蠕变特性更为复杂。

在库岸边坡中，由于降雨入渗及库水位的变化，土体在饱和及非饱和状态之间转化，土体具备非饱和特性，其蠕变变形逐渐累积，对库岸边坡的长期稳定性造成潜在威胁[4-5]。

现对于非饱和土蠕变特性的研究已有一定的进展，李滨锷[6]针对非饱和堆积土，进行压缩蠕变状态下的土-水特征曲线试验，以此建立非饱和土固-液-气三相耦合模型；李晓宁等[7]研究地基土的非饱和蠕变特性，发现含水率的增加会引起回弹变形和压缩蠕变变形，前者变形大于后者；王新刚等[8]进行了基质吸力控制条件下的非饱和黄土蠕变试验，研究表明基质吸力越小，蠕变曲线达到稳定所需的时间越长，且当应力水平较低时，黄土的变形较小，具有一定程度的可恢复性；李冬等[9]研究了应变率对非饱和土变形和强度影响，将屈服应力表示为应变率的函数，从而推导一维条件下非饱和土的增量方程，以此描述非饱和土随时间变化的长期变形行为。

目前关于土体蠕变模型的研究已取得一定成果，现有蠕变模型主要分为经验模型和元件模型，其中经验模型因其针对性、灵活性强而得到广泛应用。

比较典型的经验模型有Singh-Mitchell模型和Mesri模型[10-11]。

Singh-Mitchell模型的应力-应变关系采用指数函数来描述，而Mesri模型采用双曲线函数来描述，两者的应变-时间关系都采用幂函数来描述[12]。