高三数学专题讲义册一学生版

高中数学复习讲义一、代数1.1 一元一次方程1.2 一元二次方程1.3 平面直角坐标系1.4 解析几何与向量1.5 指数与对数1.6 三角函数与三角恒等变换1.7 数列与数学归纳法二、几何2.1 平面与立体几何基本概念2.2 直线与角2.3 三角形与三角形的性质2.4 四边形与四边形的性质2.5 圆与圆的性质2.6 空间几何与立体几何三、概率与统计3.1 随机事件与概率的计算3.2 组合与排列3.3 抽样与统计四、数学思想方法4.1 推理与证明4.2 逻辑与谬误4.3 数学建模与解题策略五、应用题本讲义将针对高中数学涵盖的主要内容进行复习总结，旨在帮助大家全面复习数学知识，掌握解题方法和技巧，为高考做好充分准备。

一、代数1.1 一元一次方程一元一次方程是数学中最基础的方程形式之一，解一元一次方程需要掌握方程的基本性质和求解方法。

我们将重点讲解常见的一元一次方程类型，并提供解题思路和方法。

掌握一元一次方程的求解技巧对于解决实际问题具有重要意义。

1.2 一元二次方程一元二次方程在高中数学中起着重要的作用，解一元二次方程需要掌握配方法、因式分解法以及求根公式等知识点。

我们将介绍一元二次方程的基本概念和解法，并通过大量例题帮助大家提高解题能力。

1.3 平面直角坐标系平面直角坐标系是研究平面几何和解析几何的基础，了解坐标系的性质和坐标变换的规律对于解决几何问题至关重要。

我们将详细介绍直角坐标系的相关概念和性质，并结合实例进行讲解，帮助大家掌握平面直角坐标系的应用。

1.4 解析几何与向量解析几何是将代数与几何相结合的重要数学分支，研究空间中点、直线、平面等几何对象的解析表达和性质。

向量是解析几何中的重要工具，学习向量的表示方法和运算规律有助于解决几何问题。

我们将讲解解析几何基本概念和向量的数学性质，并通过练习题提高大家的解题能力。

1.5 指数与对数指数和对数是高中数学中重要的数学工具和运算方法，涉及到数学表达式的简化、方程的求解等。

二项式定理进门测判断下列结论是否正确(请在括号中打“√”或“×”)(1)C k n a n－k b k是二项展开式的第k项．()(2)二项展开式中，系数最大的项为中间一项或中间两项．()(3)(a＋b)n的展开式中某一项的二项式系数与a，b无关．()(4)在(1－x)9的展开式中系数最大的项是第五、第六两项．()(5)若(3x－1)7＝a7x7＋a6x6＋…＋a1x＋a0，则a7＋a6＋…＋a1的值为128.()作业检查无第2课时阶段训练题型一二项展开式命题点1求二项展开式中的特定项或指定项的系数例1(1)(2x＋x)5的展开式中，x3的系数是______________．(用数字填写答案)(2)(x 2＋x ＋y )5的展开式中，x 5y 2的系数为( ) A ．10 B ．20 C ．30D ．60命题点2 已知二项展开式某项的系数求参数例2 (1)(a ＋x )(1＋x )4的展开式中x 的奇数次幂项的系数之和为32，则a ＝____________. (2)若⎝⎛⎭⎫ax 2＋1x 5的展开式中x 5的系数为－80，则实数a ＝________. (1)(x －y )(x ＋y )8的展开式中x 2y 7的系数为________．(用数字填写答案)(2)(x ＋a )10的展开式中，x 7的系数为15，则a ＝________.(用数字填写答案) 题型二 二项式系数的和或各项系数的和的问题 例3 在(2x －3y )10的展开式中，求： (1)二项式系数的和； (2)各项系数的和；(3)奇数项的二项式系数和与偶数项的二项式系数和； (4)奇数项系数和与偶数项系数和； (5)x 的奇次项系数和与x 的偶次项系数和．(1)设m 为正整数，(x ＋y )2m 展开式的二项式系数的最大值为a ，(x ＋y )2m＋1展开式的二项式系数的最大值为b ，若13a ＝7b ，则m 等于( ) A ．5 B ．6 C ．7 D ．8(2)若(1－2x )2 016＝a 0＋a 1x ＋a 2x 2＋…＋a 2 016x 2 016，则a 12＋a 222＋…＋a 2 01622 016的结果是多少？题型三 二项式定理的应用例4 (1)设a ∈Z 且0≤a ＜13，若512 012＋a 能被13整除，则a 等于( ) A ．0 B ．1 C ．11 D ．12(2)1.028的近似值是________．(精确到小数点后三位)(1)1－90C 110＋902C 210－903C 310＋…＋(－1)k 90k C k 10＋…＋9010C 1010除以88的余数是( )A ．－1B ．1C ．－87D ．871．二项式定理二项式定理(a ＋b )n ＝C 0n a n ＋C 1n a n －1b 1＋…＋C k na n －k b k ＋…＋C n n b n (n ∈N *)二项展开式的通项公式T k ＋1＝C k n an －k b k，它表示第k ＋1项 二项式系数二项展开式中各项的系数C k n(k ∈{0,1,2，…，n })2.二项式系数的性质(1)C 0n ＝1，C n n＝1. C m n ＋1＝C m －1n＋C mn . (2)C m n ＝C n －mn.(3)n 是偶数时，12n T+项的二项式系数最大；n 是奇数时，12n T+与112n T++T 项的二项式系数相等且最大．(4)C 0n ＋C 1n ＋C 2n ＋…＋C n n＝2n . 阶段重难点梳理【知识拓展】二项展开式形式上的特点(1)项数为n ＋1.(2)各项的次数都等于二项式的幂指数n，即a与b的指数的和为n.(3)字母a按降幂排列，从第一项开始，次数由n逐项减1直到零；字母b按升幂排列，从第一项起，次数由零逐项增1直到n.(4)二项式的系数从C0n，C1n，一直到C n－1n，C n n.典例(1)若(x－3x)n展开式的各项系数绝对值之和为1 024，则展开式中含x项的系数为________．(2)已知(x－m)7＝a0＋a1x＋a2x2＋…＋a7x7的展开式中x4的系数是－35，则a1＋a2＋…＋a7＝________. 1．(x－y)n的二项展开式中，第m项的系数是()A．C m n B．C m＋1nC．C m－1n D．(－1)m－1C m－1n2．设i为虚数单位，则(x＋i)6的展开式中含x4的项为() A．－15x4B．15x4C．－20i x4D．20i x43．使(3x＋1x x)n(n∈N*)的展开式中含有常数项的最小的n值为() A．4 B．5 C．6 D．7重点题型训练4．在(x 2－3x )n的展开式中，只有第5项的二项式系数最大，则展开式中常数项是________．1．在x 2(1＋x )6的展开式中，含x 4项的系数为( ) A ．30 B ．20 C ．15 D ．102．已知⎝⎛⎭⎫x －ax 5的展开式中含32x 的项的系数为30，则a 等于( )A. 3 B ．－ 3 C ．6 D ．－63．(4x －2－x )6(x ∈R )展开式中的常数项是( ) A ．－20 B ．－15 C ．15D ．204．已知(1＋x )n 的展开式中第4项与第8项的二项式系数相等，则奇数项的二项式系数和为( ) A ．29 B ．210 C ．211 D ．2125．若在(x ＋1)4(ax －1)的展开式中，x 4的系数为15，则a 的值为( ) A ．－4 B.52 C ．4 D.726．若(1＋x )＋(1＋x )2＋…＋(1＋x )n ＝a 0＋a 1(1－x )＋a 2(1－x )2＋…＋a n (1－x )n ，则a 0－a 1＋a 2－a 3＋…＋(－1)n a n 等于( ) A.34(3n －1) B.34(3n －2) 作业布置C.32(3n －2) D.32(3n －1) 7．若(x ＋a )2(1x －1)5的展开式中常数项为－1，则a 的值为( )A ．1B ．9C ．－1或－9D ．1或98．在(1－2x )6的展开式中，x 2的系数为________．(用数字作答) 9．⎝⎛⎭⎫x 2－1x 8的展开式中x 7的系数为________．(用数字作答) 10．在(2－x )6的展开式中，含x 3的二项式系数为________，系数为________．(均用数字作答) 11．若将函数f (x )＝x 5表示为f (x )＝a 0＋a 1(1＋x )＋a 2(1＋x )2＋…＋a 5(1＋x )5，其中a 0，a 1，a 2，…，a 5为实数，则a 3＝________.12．已知(1－2x )7＝a 0＋a 1x ＋a 2x 2＋…＋a 7x 7. 求：(1)a 1＋a 2＋…＋a 7； (2)a 1＋a 3＋a 5＋a 7； (3)a 0＋a 2＋a 4＋a 6； (4)|a 0|＋|a 1|＋|a 2|＋…＋|a 7|.13．求证：1＋2＋22＋…＋25n －1(n ∈N *)能被31整除．*14.若(x ＋412x)n 展开式中前三项的系数成等差数列，求：(1)展开式中所有x 的有理项； (2)展开式中系数最大的项．二项式定理判断下列结论是否正确(请在括号中打“√”或“×”)(1)C k n an －k b k是二项展开式的第k 项．( × ) (2)二项展开式中，系数最大的项为中间一项或中间两项．( × ) (3)(a ＋b )n 的展开式中某一项的二项式系数与a ，b 无关．( √ ) (4)在(1－x )9的展开式中系数最大的项是第五、第六两项．( × )(5)若(3x －1)7＝a 7x 7＋a 6x 6＋…＋a 1x ＋a 0，则a 7＋a 6＋…＋a 1的值为128.( × )题型一 二项展开式命题点1 求二项展开式中的特定项或指定项的系数阶段训练进门测例1 (1)(2x ＋x )5的展开式中，x 3的系数是______________．(用数字填写答案) (2)(x 2＋x ＋y )5的展开式中，x 5y 2的系数为( ) A ．10 B ．20 C ．30D ．60答案 (1)10 (2)C解析 (1)(2x ＋x )5展开式的通项公式T k ＋1＝C k 5(2x )5－k ·(x )k ＝C k 525－k52kx-，k ∈{0,1,2,3,4,5}，令5－k 2＝3，解得k ＝4，得T 5＝C 4525－445-2x＝10x 3，∴x 3的系数是10.(2)方法一 利用二项展开式的通项公式求解． (x 2＋x ＋y )5＝[(x 2＋x )＋y ]5，含y 2的项为T 3＝C 25(x 2＋x )3·y 2. 其中(x 2＋x )3中含x 5的项为C 13x 4·x ＝C 13x 5. 所以x 5y 2的系数为C 25C 13＝30.故选C.方法二 利用组合知识求解．(x 2＋x ＋y )5为5个x 2＋x ＋y 之积，其中有两个取y ，两个取x 2，一个取x 即可，所以x 5y 2的系数为C 25C 23＝30.故选C. 命题点2 已知二项展开式某项的系数求参数例2 (1)(a ＋x )(1＋x )4的展开式中x 的奇数次幂项的系数之和为32，则a ＝____________. (2)若⎝⎛⎭⎫ax 2＋1x 5的展开式中x 5的系数为－80，则实数a ＝________. 答案 (1)3 (2)－2解析 (1)设(a ＋x )(1＋x )4＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋a 4x 4＋a 5x 5，令x ＝1，得16(a ＋1)＝a 0＋a 1＋a 2＋a 3＋a 4＋a 5，① 令x ＝－1，得0＝a 0－a 1＋a 2－a 3＋a 4－a 5.② ①－②，得16(a ＋1)＝2(a 1＋a 3＋a 5)，即展开式中x 的奇数次幂的系数之和为a 1＋a 3＋a 5＝8(a ＋1)，所以8(a ＋1)＝32，解得a ＝3.(2)∵T k ＋1＝C k 5(ax 2)5－k⎝⎛⎭⎫1x k ＝a 5－k C k 55102k x －，∴10－52k ＝5，解得k ＝2，∴a 3C 25＝－80，解得a ＝－2. 思维升华 求二项展开式中的特定项，一般是利用通项公式进行，化简通项公式后，令字母的指数符合要求(求常数项时，指数为零；求有理项时，指数为整数等)，解出项数k ＋1，代回通项公式即可．(1)(x －y )(x ＋y )8的展开式中x 2y 7的系数为________．(用数字填写答案)(2)(x ＋a )10的展开式中，x 7的系数为15，则a ＝________.(用数字填写答案) 答案 (1)－20 (2)12解析 (1)x 2y 7＝x ·(xy 7)，其系数为C 78， x 2y 7＝y ·(x 2y 6)，其系数为－C 68，∴x 2y 7的系数为C 78－C 68＝8－28＝－20.(2)设通项为T k ＋1＝C k 10x10－k a k ，令10－k ＝7， ∴k ＝3，∴x 7的系数为C 310a 3＝15， ∴a 3＝18，∴a ＝12.题型二 二项式系数的和或各项系数的和的问题例3 在(2x －3y )10的展开式中，求： (1)二项式系数的和； (2)各项系数的和；(3)奇数项的二项式系数和与偶数项的二项式系数和； (4)奇数项系数和与偶数项系数和； (5)x 的奇次项系数和与x 的偶次项系数和．解 设(2x －3y )10＝a 0x 10＋a 1x 9y ＋a 2x 8y 2＋…＋a 10y 10，(*)各项系数的和为a 0＋a 1＋…＋a 10，奇数项系数和为a 0＋a 2＋…＋a 10，偶数项系数和为a 1＋a 3＋a 5＋…＋a 9，x 的奇次项系数和为a 1＋a 3＋a 5＋…＋a 9，x 的偶次项系数和为a 0＋a 2＋a 4＋…＋a 10. 由于(*)是恒等式，故可用“赋值法”求出相关的系数和．(1)二项式系数的和为C 010＋C 110＋…＋C 1010＝210.(2)令x ＝y ＝1，各项系数和为(2－3)10＝(－1)10＝1.(3)奇数项的二项式系数和为C 010＋C 210＋…＋C 1010＝29，偶数项的二项式系数和为C 110＋C 310＋…＋C 910＝29.(4)令x ＝y ＝1，得到a 0＋a 1＋a 2＋…＋a 10＝1，① 令x ＝1，y ＝－1(或x ＝－1，y ＝1)， 得a 0－a 1＋a 2－a 3＋…＋a 10＝510，② ①＋②得2(a 0＋a 2＋…＋a 10)＝1＋510， ∴奇数项系数和为1＋5102；①－②得2(a 1＋a 3＋…＋a 9)＝1－510，∴偶数项系数和为1－5102.(5)x 的奇次项系数和为a 1＋a 3＋a 5＋…＋a 9＝1－5102；x 的偶次项系数和为a 0＋a 2＋a 4＋…＋a 10＝1＋5102.思维升华 (1)“赋值法”普遍适用于恒等式，是一种重要的方法，对形如(ax ＋b )n ，(ax 2＋bx ＋c )m (a ，b ∈R )的式子求其展开式的各项系数之和，常用赋值法，只需令x ＝1即可；对形如(ax ＋by )n (a ，b ∈R )的式子求其展开式各项系数之和，只需令x ＝y ＝1即可．(2)若f (x )＝a 0＋a 1x ＋a 2x 2＋…＋a n x n ，则f (x )展开式中各项系数之和为f (1)，奇数项系数之和为a 0＋a 2＋a 4＋…＝f (1)＋f (－1)2，偶数项系数之和为a 1＋a 3＋a 5＋…＝f (1)－f (－1)2.(1)设m 为正整数，(x ＋y )2m 展开式的二项式系数的最大值为a ，(x ＋y )2m＋1展开式的二项式系数的最大值为b ，若13a ＝7b ，则m 等于( ) A ．5 B ．6 C ．7 D ．8 答案 B解析 由题意得a ＝C m 2m ，b ＝C m ＋12m ＋1，∴13C m 2m ＝7C m ＋12m ＋1，∴13·(2m )！m ！·m ！＝7·(2m ＋1)！m ！·(m ＋1)！， ∴7(2m ＋1)m ＋1＝13，解得m ＝6，经检验符合题意，故选B.(2)若(1－2x )2 016＝a 0＋a 1x ＋a 2x 2＋…＋a 2 016x 2 016，则a 12＋a 222＋…＋a 2 01622 016的结果是多少？解 当x ＝0时，左边＝1，右边＝a 0，∴a 0＝1.当x ＝12时，左边＝0，右边＝a 0＋a 12＋a 222＋…＋a 2 01622 016，∴0＝1＋a 12＋a 222＋…＋a 2 01622 016.即a 12＋a 222＋…＋a 2 01622 016＝－1.题型三 二项式定理的应用例4 (1)设a ∈Z 且0≤a ＜13，若512 012＋a 能被13整除，则a 等于( ) A ．0 B ．1 C ．11 D ．12(2)1.028的近似值是________．(精确到小数点后三位) 答案 (1)D (2)1.172解析 (1)512 012＋a ＝(52－1)2 012＋a ＝C 02 012·522 012－C 12 012·522 011＋…＋C 2 0112 012×52·(－1)2 011＋C 2 0122 012·(－1)2 012＋a ，∵C 02 012·522 012－C 12 012·522 011＋…＋C 2 0112 012×52·(－1)2 011能被13整除且512 012＋a 能被13整除， ∴C 2 0122 012·(－1)2 012＋a ＝1＋a 也能被13整除，因此a 的值为12. (2)1.028＝(1＋0.02)8≈C 08＋C 18·0.02＋C 28·0.022＋C 38·0.023≈1.172.思维升华 (1)整除问题和求近似值是二项式定理中两类常见的应用问题，整除问题中要关注展开式的最后几项，而求近似值则应关注展开式的前几项．(2)二项式定理的应用基本思路是正用或逆用二项式定理，注意选择合适的形式．(1)1－90C 110＋902C 210－903C 310＋…＋(－1)k 90k C k 10＋…＋9010C 1010除以88的余数是( )A ．－1B ．1C ．－87D ．87 答案 B解析 1－90C 110＋902C 210－903C 310＋…＋(－1)k 90k C k 10＋…＋9010C 1010＝(1－90)10＝8910＝(88＋1)10＝8810＋C 110889＋…＋C 91088＋1，∵前10项均能被88整除，∴余数是1.(2)已知2n ＋2·3n ＋5n －a 能被25整除，求正整数a 的最小值． 解 原式＝4·6n ＋5n －a ＝4(5＋1)n ＋5n －a＝4(C 0n 5n ＋C 1n 5n －1＋…＋C n －2n 52＋C n －1n 5＋C n n)＋5n －a ＝4(C 0n 5n ＋C 1n 5n －1＋…＋C n －2n52)＋25n ＋4－a ， 显然正整数a 的最小值为4.1．二项式定理二项式定理(a ＋b )n ＝C 0n a n ＋C 1n a n －1b 1＋…＋C kna n －k b k ＋…＋C n n b n (n ∈N *)二项展开式的通项公式T k ＋1＝C k n an －k b k ，它表示第k ＋1项 二项式系数二项展开式中各项的系数C k n (k ∈{0,1,2，…，n })第3课时阶段重难点梳理2.二项式系数的性质(1)C 0n ＝1，C n n＝1. C m n ＋1＝C m －1n＋C m n . (2)C m n ＝C n －mn.(3)n 是偶数时，12n T+项的二项式系数最大；n 是奇数时，12n T+与112n T++T 项的二项式系数相等且最大．(4)C 0n ＋C 1n ＋C 2n ＋…＋C n n＝2n . 【知识拓展】二项展开式形式上的特点 (1)项数为n ＋1.(2)各项的次数都等于二项式的幂指数n ，即a 与b 的指数的和为n .(3)字母a 按降幂排列，从第一项开始，次数由n 逐项减1直到零；字母b 按升幂排列，从第一项起，次数由零逐项增1直到n .(4)二项式的系数从C 0n ，C 1n ，一直到C n －1n ，C n n .典例 (1)若(x －3x )n 展开式的各项系数绝对值之和为1 024，则展开式中含x 项的系数为________．(2)已知(x －m )7＝a 0＋a 1x ＋a 2x 2＋…＋a 7x 7的展开式中x 4的系数是－35，则a 1＋a 2＋…＋a 7＝________. 错解展示解析 (1)(x ＋3x)n 展开式中，令x ＝1可得4n ＝1 024，∴n ＝5，重点题型训练∴(x －3x )n 展开式的通项T k ＋1＝(－3)k ·C k 5·532kx -，令5－3k2＝1，得k ＝1.故展开式中含x 项的系数为C 15＝5.(2)a 1＋a 2＋…＋a 7＝C 17＋C 27＋…＋C 77＝27－1.答案 (1)5 (2)27－1 现场纠错解析 (1)在(x ＋3x)n 的展开式中，令x ＝1，可得(x －3x )n 展开式的各项系数绝对值之和为4n ＝22n ＝1 024＝210，∴n ＝5.故(x －3x )5展开式的通项为T k ＋1＝(－3)k ·C k 5·532kx -，令5－3k2＝1，得k ＝1，故展开式中含x 项的系数为－15. (2)∵(x －m )7＝a 0＋a 1x ＋a 2x 2＋…＋a 7x 7， 令x ＝0，∴a 0＝(－m )7.又∵展开式中x 4的系数是－35，∴C 37·(－m )3＝－35， ∴m ＝1.∴a 0＝(－m )7＝－1.在(x －m )7＝a 0＋a 1x ＋a 2x 2＋…＋a 7x 7中， 令x ＝1，得0＝－1＋a 1＋a 2＋…＋a 7， 即a 1＋a 2＋a 3＋…＋a 7＝1. 答案 (1)－15 (2)1纠错心得 和二项展开式有关的问题，要分清所求的是展开式中项的系数还是二项式系数，是系数和还是二项式系数的和.1．(x －y )n 的二项展开式中，第m 项的系数是( ) A ．C m nB ．C m ＋1nC ．C m －1nD ．(－1)m －1C m －1n答案 D解析 (x －y )n 展开式中第m 项的系数为C m －1n(－1)m －1. 2．设i 为虚数单位，则(x ＋i)6的展开式中含x 4的项为( ) A ．－15x 4 B ．15x 4 C ．－20i x 4 D ．20i x 4答案 A解析 由题可知，含x 4的项为C 26x 4i 2＝－15x 4.故选A.3．使(3x ＋1x x )n (n ∈N *)的展开式中含有常数项的最小的n 值为( )A ．4B ．5C ．6D ．7 答案 B解析 (3x ＋1x x)n的展开式中的第k ＋1项为C k n()323k n kx x-－＝C k n 3n －k·52k xn-.若展开式中含常数项，则存在n ∈N *，k ∈N ，使n －52k ＝0.故最小的n 值为5.4．在(x 2－3x )n的展开式中，只有第5项的二项式系数最大，则展开式中常数项是________．答案 7解析 由题意知n2＋1＝5，解得n ＝8，(x 2－3x )8的展开式的通项T k ＋1＝C k 8(x 2)8－k (－3x)k ＝(－1)k 2k －8C k 848-3k x，令8－4k3＝0，得k ＝6，则展开式中的常数项为(－1)626－8C 68＝7.1．在x 2(1＋x )6的展开式中，含x 4项的系数为( ) A ．30 B ．20 C ．15 D ．10 答案 C解析 因为(1＋x )6的展开式的第k ＋1项为T k ＋1＝C k 6x k ，x 2(1＋x )6的展开式中含x 4的项为C 26x 4＝15x 4，所以系数为15.2．已知⎝⎛⎭⎫x －ax 5的展开式中含32x 的项的系数为30，则a 等于( )A. 3 B ．－ 3 C ．6 D ．－6 答案 D作业布置解析 ⎝⎛⎭⎫x －a x 5的展开式通项T k ＋1＝C k 552k x -(－1)k a k ·2k x -＝(－1)k a k C k 552k x-，令52－k ＝32，则k ＝1，∴T 2＝－a C 1532x ，∴－a C 15＝30，∴a ＝－6，故选D. 3．(4x －2－x )6(x ∈R )展开式中的常数项是( ) A ．－20 B ．－15 C ．15 D ．20答案 C解析 设展开式中的常数项是第k ＋1项，则T k ＋1＝C k 6·(4x )6－k ·(－2－x )k ＝C k 6·(－1)k ·212x －2kx·2－kx＝C k 6·(－1)k ·212x－3kx，∵12x －3kx ＝0恒成立，∴k ＝4， ∴T 5＝C 46·(－1)4＝15. 4．已知(1＋x )n 的展开式中第4项与第8项的二项式系数相等，则奇数项的二项式系数和为( ) A ．29 B ．210 C ．211 D ．212 答案 A解析 由题意，C 3n ＝C 7n ，解得n ＝10，则奇数项的二项式系数和为2n －1＝29.故选A. 5．若在(x ＋1)4(ax －1)的展开式中，x 4的系数为15，则a 的值为( ) A ．－4 B.52 C ．4 D.72答案 C解析 ∵(x ＋1)4(ax －1)＝(x 4＋4x 3＋6x 2＋4x ＋1)(ax －1)，∴x 4的系数为4a －1＝15，∴a ＝4. 6．若(1＋x )＋(1＋x )2＋…＋(1＋x )n ＝a 0＋a 1(1－x )＋a 2(1－x )2＋…＋a n (1－x )n ，则a 0－a 1＋a 2－a 3＋…＋(－1)n a n 等于( )A.34(3n －1) B.34(3n －2) C.32(3n －2) D.32(3n －1) 答案 D解析 在展开式中，令x ＝2，得3＋32＋33＋…＋3n ＝a 0－a 1＋a 2－a 3＋…＋(－1)n a n ， 即a 0－a 1＋a 2－a 3＋…＋(－1)na n ＝3(1－3n )1－3＝32(3n －1)． 7．若(x ＋a )2(1x －1)5的展开式中常数项为－1，则a 的值为( )A ．1B ．9C ．－1或－9D ．1或9答案 D解析 由于(x ＋a )2＝x 2＋2ax ＋a 2，而(1x －1)5的展开式通项为T k ＋1＝(－1)k C k 5·x k －5，其中k ＝0,1,2，…，5.于是(1x －1)5的展开式中x －2的系数为(－1)3C 35＝－10，x －1项的系数为(－1)4C 45＝5，常数项为－1，因此(x ＋a )2(1x －1)5的展开式中常数项为1×(－10)＋2a ×5＋a 2×(－1)＝－a 2＋10a －10，依题意－a 2＋10a －10＝－1，解得a 2－10a ＋9＝0，即a ＝1或a ＝9. 8．在(1－2x )6的展开式中，x 2的系数为________．(用数字作答) 答案 60解析 展开式的通项T k ＋1＝C k 6·16－k ·(－2x )k ＝C k 6(－2)k ·x k .令k ＝2，得T 3＝C 26·4x 2＝60x 2，即x 2的系数为60.9．⎝⎛⎭⎫x 2－1x 8的展开式中x 7的系数为________．(用数字作答)答案 －56解析 ⎝⎛⎭⎫x 2－1x 8的通项T k ＋1＝C k 8(x 2)8－k ⎝⎛⎭⎫－1x k ＝(－1)k C k 8x 16－3k ，当16－3k ＝7时，k ＝3，则x 7的系数为(－1)3C 38＝－56.10．在(2－x )6的展开式中，含x 3的二项式系数为________，系数为________．(均用数字作答) 答案 20 －160解析 (2－x )6展开式的通项T k ＋1＝C k 626－k (－x )k ， 令k ＝3，∴含x 3的二项式系数为C 36＝20，系数为C 36×23×(－1)3＝－160.11．若将函数f (x )＝x 5表示为f (x )＝a 0＋a 1(1＋x )＋a 2(1＋x )2＋…＋a 5(1＋x )5，其中a 0，a 1，a 2，…，a 5为实数，则a 3＝________.答案 10解析 f (x )＝x 5＝(1＋x －1)5，它的通项为T k ＋1＝C k 5(1＋x )5－k ·(－1)k ， T 3＝C 25(1＋x )3(－1)2＝10(1＋x )3，∴a 3＝10.12．已知(1－2x )7＝a 0＋a 1x ＋a 2x 2＋…＋a 7x 7.求：(1)a 1＋a 2＋…＋a 7；(2)a 1＋a 3＋a 5＋a 7；(3)a 0＋a 2＋a 4＋a 6；(4)|a 0|＋|a 1|＋|a 2|＋…＋|a 7|.解 令x ＝1，则a 0＋a 1＋a 2＋a 3＋a 4＋a 5＋a 6＋a 7＝－1.①令x ＝－1，则a 0－a 1＋a 2－a 3＋a 4－a 5＋a 6－a 7＝37.②(1)∵a 0＝C 07＝1，∴a 1＋a 2＋a 3＋…＋a 7＝－2.(2)(①－②)÷2，得a 1＋a 3＋a 5＋a 7＝－1－372＝－1 094.(3)(①＋②)÷2，得a 0＋a 2＋a 4＋a 6＝－1＋372＝1 093.(4)方法一 ∵(1－2x )7展开式中，a 0、a 2、a 4、a 6大于零，而a 1、a 3、a 5、a 7小于零， ∴|a 0|＋|a 1|＋|a 2|＋…＋|a 7|＝(a 0＋a 2＋a 4＋a 6)－(a 1＋a 3＋a 5＋a 7)＝1 093－(－1 094)＝2 187. 方法二 |a 0|＋|a 1|＋|a 2|＋…＋|a 7|，即(1＋2x )7展开式中各项的系数和，令x ＝1， ∴|a 0|＋|a 1|＋|a 2|＋…＋|a 7|＝37＝2 187.13．求证：1＋2＋22＋…＋25n －1(n ∈N *)能被31整除． 证明 ∵1＋2＋22＋…＋25n －1＝25n －12－1＝25n －1＝32n －1＝(31＋1)n －1＝C 0n ×31n ＋C 1n ×31n －1＋…＋C n －1n ×31＋C n n －1 ＝31(C 0n ×31n －1＋C 1n ×31n －2＋…＋C n －1n )，显然C 0n ×31n －1＋C 1n ×31n －2＋…＋C n －1n 为整数， ∴原式能被31整除．*14.若(x)n 展开式中前三项的系数成等差数列，求：(1)展开式中所有x 的有理项；(2)展开式中系数最大的项．解 易求得展开式前三项的系数为1，12C 1n ，14C 2n .据题意得2×12C 1n ＝1＋14C 2n ⇒n ＝8.(1)设展开式中的有理项为T k ＋1， 由T k ＋1＝C k 8(x )8－k)k ＝(12)k C k 81634kx -，∴k 为4的倍数，又0≤k ≤8，∴k ＝0,4,8.故有理项为T 1＝(12)0C 0816304x -⨯＝x 4，T 5＝(12)4C 4816344x -⨯＝358x ，T 9＝(12)8C 8816384x -⨯＝1256x 2.(2)设展开式中T k ＋1项的系数最大，则⎩⎨⎧ (12)k C k 8≥(12)k ＋1C k ＋18，(12)k C k 8≥(12)k －1C k －18⇒k＝2或k ＝3. 故展开式中系数最大的项为T 3＝(12)2C 2816324x -⨯＝752x ，T 4＝(12)3C 3816334x -⨯＝774x .。

第74讲存在性问题的探究知识梳理题型一：存在点使向量数量积为定值例1．（2024·甘肃天水·高二天水市第一中学校考期末）已知椭圆E 的中心在原点，焦点在x轴上，椭圆的左顶点坐标为()，离心率为e =()1求椭圆E 的方程；()2过点()1,0作直线l 交E 于P 、Q 两点，试问：在x 轴上是否存在一个定点M ，使MP MQ ⋅为定值？若存在，求出这个定点M 的坐标；若不存在，请说明理由．例2．（2024·山西大同·高二统考期末）已知椭圆22221(0)x y a b a b+=>>的一个焦点与抛物线2y =的焦点F 重合，且椭圆短轴的两个端点与F 构成正三角形.(1)求椭圆的方程；(2)若过点(1,0)的直线l 与椭圆交于不同两点P Q 、，试问在x 轴上是否存在定点(m,0)E ，使PE QE ⋅ 恒为定值?若存在，求出E 的坐标及定值；若不存在，请说明理由.例3．（2024·重庆渝北·高二重庆市松树桥中学校校考阶段练习）已知椭圆C 的中心在坐标原点，焦点在x 轴上，其左、右焦点分别为1F ，2F ，短轴长为点P 在椭圆C 上，且满足12PF F ∆的周长为6.（I ）求椭圆C 的方程；（Ⅱ）过点(1,0)-的直线l 与椭圆C 相交于A ，B 两点，试问在x 轴上是否存在一定点M ，使得MA MB ⋅ 恒为定值？若存在，求出该点M 的坐标；若不存在，请说明理由.变式1．（2024·全国·高三专题练习）已知椭圆2222:1(0)x y C a b a b +=>>的离心率为2，椭圆经过点1,2A ⎛- ⎝⎭.（1）求椭圆C 的方程；（2）过点(1,0)作直线l 交C 于,M N 两点，试问：在x 轴上是否存在一个定点P ，使PM PN⋅ 为定值？若存在，求出这个定点P 的坐标；若不存在，请说明理由.变式2．（2024·辽宁锦州·统考模拟预测）已知12F F ､为双曲线2222:1(0,0)x y E a b a b-=>>的左、右焦点，E M 为E 上一点，且212MF MF -=.(1)求E 的方程；(2)设点M 在坐标轴上，直线l 与E 交于异于M 的A B ､两点，且点M 在以线段AB 为直径的圆上，过M 作MC AB ⊥，垂足为C ，是否存在点D ，使得CD 为定值？若存在，求出点D 的坐标；若不存在，请说明理由.变式3．（2024·山西大同·统考模拟预测）已知椭圆()22122:10x y C a b a b +=>>的离心率为2，且直线y x b =+是抛物线22:4C y x =的一条切线．(1)求椭圆1C 的方程；(2)过点10,3S ⎛⎫- ⎪⎝⎭的动直线L 交椭圆1C 于,A B 两点，试问：在直角坐标平面上是否存在一个定点T ，使得以AB 为直径的圆恒过定点T ？若存在，求出T 的坐标；若不存在，请说明理由．变式4．（2024·江苏扬州·统考模拟预测）已知椭圆2222:1(0)x y C a b a b+=>>的左顶点为A ，过右焦点F 且平行于y 轴的弦3PQ AF ==．(1)求APQ △的内心坐标；(2)是否存在定点D ，使过点D 的直线l 交C 于,M N ，交PQ 于点R ，且满足MR ND MD RN ⋅=⋅ 若存在，求出该定点坐标，若不存在，请说明理由．题型二：存在点使斜率之和或之积为定值例4．（2024·山东泰安·统考模拟预测）已知为O 坐标原点，()()()()2,0,0,1,0,1,2,1A B C D -，,,01OE OA DF DA λλλ==<≤ ，CE 和BF 交点为P .(1)求点P 的轨迹G ；(2)直线(0)=+≠y x m m 和曲线G 交与M N ，两点，试判断是否存在定点Q 使14MQ NQ k k =？如果存在，求出Q 点坐标，不存在请说明理由.例5．（2024·重庆渝中·高三重庆巴蜀中学校考阶段练习）已知点()2,0A -，()2,0B ，(),P x y 是异于A ，B 的动点，AP k ，BP k 分别是直线AP ，BP 的斜率，且满足34AP BP k k ⋅=-.(1)求动点P 的轨迹方程；(2)在线段AB 上是否存在定点E ，使得过点E 的直线交P 的轨迹于M ，N 两点，且对直线4x =上任意一点Q ，都有直线QM ，QE ，QN 的斜率成等差数列.若存在，求出定点E ，若不存在，请说明理由.例6．（2024·吉林·吉林省实验校考模拟预测）以双曲线2222:1(0,0)x y C a b a b-=>>的右焦点F 为圆心作圆，与C 的一条渐近线相切于点4,33Q ⎛ ⎝⎭(1)求C 的方程.(2)在x 轴上是否存在定点M ，过点M 任意作一条不与坐标轴垂直的直线l ，当l 与C 交于,A B 两点时，直线,AF BF 的斜率之和为定值？若存在，求出M 点的坐标，若不存在，说明理由.变式5．（2024·湖北荆州·高二荆州中学校考阶段练习）已知圆C 方程为228(62)610(,0)x y mx m y m m R m +--+++=∈≠，椭圆中心在原点，焦点在x 轴上.（1）证明圆C 恒过一定点M ，并求此定点M 的坐标；（2）判断直线4330x y +-=与圆C 的位置关系，并证明你的结论；（3）当2m =时，圆C 与椭圆的左准线相切，且椭圆过（1）中的点M ，求此时椭圆方程；在x 轴上是否存在两定点A ，B 使得对椭圆上任意一点Q （异于长轴端点），直线QA ，QB 的斜率之积为定值？若存在，求出A ，B 坐标；若不存在，请说明理由.变式6．（2024·河北·高三校联考阶段练习）已知椭圆C ：()222210x y a b a b+=>>的左、右焦点分别为1F ，2F ，焦距为2，实轴长为4.（1）求椭圆C 的方程；（2）设过点1F 不与x 轴重合的直线l 与椭圆C 相交于E ，D 两点，试问在x 轴上是否存在一个点M ，使得直线ME ，MD 的斜率之积恒为定值？若存在，求出该定值及点M 的坐标；若不存在，请说明理由.变式7．（2024·吉林长春·高三长春外国语学校校考开学考试）已知椭圆()2222:10x y C a b a b+=>>的离心率为12，1F 、2F 分别是椭圆的左、右焦点，P 是椭圆上一点，且12PF F △的周长是6.（1）求椭圆C 的方程；（2）设直线l 经过椭圆的右焦点2F 且与C 交于不同的两点M ，N ，试问：在x 轴上是否存在点Q ，使得直线QM 与直线QN 的斜率的和为定值？若存在，请求出点Q 的坐标；若不存在，请说明理由.变式8．（2024·全国·高三专题练习）设椭圆222210)x y C a b a b +=：（＞＞的离心率是2，过点()0,1P 的动直线L 于椭圆相交于,A B 两点，当直线L 平行于x 轴时，直线L 被椭圆C 截得弦长为（Ⅰ）求E 的方程；（Ⅱ）在y 上是否存在与点P 不同的定点Q ，使得直线AQ 和BQ 的倾斜角互补？若存在，求Q 的坐标；若不存在，说明理由．题型三：存在点使两角度相等例7．（2024·新疆阿勒泰·统考三模）已知椭圆2212:1(1)x C y a a+=>的左右焦点分别为12F F 、，,A B 分别为椭圆1C 的上，下顶点，2F 到直线1AF (1)求椭圆1C 的方程；(2)直线0x x =与椭圆1C 交于不同的两点,C D ，直线,AC AD 分别交x 轴于,P Q 两点．问：y 轴上是否存在点R ，使得π2∠+∠=ORP ORQ ？若存在，求出点R 的坐标；若不存在，请说明理由．例8．（2024·全国·高三专题练习）已知椭圆:C ()222210x y a b a b+=>>经过点()2,0A -且两个焦点及短轴两顶点围成四边形的面积为4.(1)求椭圆C 的方程和离心率；(2)设P ，Q 为椭圆C 上不同的两个点，直线AP 与y 轴交于点E ，直线AQ 与y 轴交于点F ，且P 、O 、Q 三点共线.其中O 为坐标原点.问：x 轴上是否存在点M ，使得AME EFM ∠=∠？若存在，求点M 的坐标，若不存在，说明理由.例9．（2024·四川绵阳·模拟预测）已知点A 是圆()22:116C x y -+=上的任意一点，点()1,0F -，线段AF 的垂直平分线交AC 于点P ．(1)求动点P 的轨迹E 的方程；(2)若过点()3,0G 且斜率不为O 的直线l 交（1）中轨迹E 于M 、N 两点，O 为坐标原点，点()2,0B ．问：x 轴上是否存在定点T ，使得MTO NTB ∠=∠恒成立．若存在，请求出点T 的坐标，若不存在，请说明理由．变式9．（2024·陕西西安·陕西师大附中校考模拟预测）已知椭圆222:1(0)3x y C a a +=>经过点31,2-（，过点)T 的直线交该椭圆于P ，Q 两点.(1)求OPQ △面积的最大值，并求此时直线PQ 的方程；(2)若直线PQ 与x 轴不垂直，在x 轴上是否存在点(),0S s 使得PST QST ∠=∠恒成立？若存在，求出s 的值；若不存在，说明理由.变式10．（2024·四川成都·高三四川省成都市新都一中校联考开学考试）已知椭圆()2222:10x y C a b a b +=>>过点1,2⎛⎫ ⎪ ⎪⎝⎭(1)求椭圆C 的方程；(2)若过点()3,0P 的直线l 交椭圆C 于,A B 两点，x 轴上是否存在点Q 使得πPQA PQB ∠+∠=，若存在，求出点Q 的坐标；若不存在，请说明理由．变式11．（2024·河南信阳·高三信阳高中校考阶段练习）在平面直角坐标系xOy 中，动点M到点()2,0D 的距离等于点M 到直线1x =倍，记动点M 的轨迹为曲线C .(1)求曲线C 的方程；(2)已知直线l ：()122y x t t =+≥与曲线C 交于,A B 两点，问曲线C 上是否存在两点,P Q 满足90APB AQB ∠=∠=︒，若存在，请求出两点坐标，不存在，请说明理由.题型四：存在点使等式恒成立例10．（2024·福建漳州·统考模拟预测）已知R 是圆M ：(228x y +=上的动点，点)N，直线NR 与圆M 的另一个交点为S ，点L 在直线MR 上，MS NL ∥，动点L 的轨迹为曲线C .(1)求曲线C 的方程；(2)若过点()2,0P -的直线l 与曲线C 相交于A ，B 两点，且A ，B 都在x 轴上方，问：在x 轴上是否存在定点Q ，使得QAB 的内心在一条定直线上?请你给出结论并证明.例11．（2024·全国·高三专题练习）已知椭圆2222:1(0)x y a b a bΓ+=>>的左、右焦点分别为12,F F ，过点()0,B b 且与直线2BF 垂直的直线交x 轴负半轴于D ，且12220F F F D += ．(1)求椭圆Γ的离心率；(2)若过B 、D 、2F 三点的圆恰好与直线:60l x -=相切，求椭圆Γ的方程；(3)设2a =．过椭圆Γ右焦点2F 且不与坐标轴垂直的直线l 与椭圆Γ交于P 、Q 两点，点M 是点P 关于x 轴的对称点，在x 轴上是否存在一个定点N ，使得M 、Q 、N 三点共线？若存在，求出点N 的坐标；若不存在，说明理由．例12．（2024·福建福州·福州三中校考模拟预测）如图，双曲线的中心在原点，焦点到渐近A 、B ．曲线C 是以双曲线的实轴为长轴，虚轴为短轴，且离心率为12的椭圆，设P 在第一象限且在双曲线上，直线BP 交椭圆于点M ，直线AP 与椭圆交于另一点N ．(1)求椭圆及双曲线的标准方程；(2)设MN 与x 轴交于点T ，是否存在点P 使得4P T x x =(其中P x ，T x 为点P ，T 的横坐标)，若存在，求出P 点的坐标，若不存在，请说明理由．变式12．（2024·福建福州·福州四中校考模拟预测）已知在平面直角坐标系xOy 中，椭圆22:143x y E +=的左顶点和右焦点分别为,A F ，动点P 满足2219||||22PA PF +=，记动点P 的轨迹为曲线C .(1)求C 的方程；(2)设点Q 在E 上，过Q 作C 的两条切线，分别与y 轴相交于,M N 两点.是否存在点Q ，使得MN 等于E 的短轴长？若存在，求点Q 的坐标；若不存在，请说明理由.变式13．（2024·甘肃定西·统考模拟预测）已知点M 到点30,2F ⎛⎫ ⎪⎝⎭的距离比它到直线l ：=2y -的距离小12，记动点M 的轨迹为E .(1)求E 的方程；(2)若过点F 的直线交E 于()11,A x y ，()22,B x y 两点，则在x 轴的正半轴上是否存在点P ，使得PA ，PB 分别交E 于另外两点C ，D ，且3AB CD = ？若存在，请求出P 点坐标，若不存在，请说明理由.变式14．（2024·北京海淀·中关村中学校考三模）已知椭圆2222:1(0)x y E a b a b +=>>的焦距为2，长轴长为4.(1)求椭圆E 的方程及离心率；(2)过点()3,0M -且与x 轴不重合的直线l 与椭圆E 交于不同的两点B 、C ，点B 关于x 轴的对称点为B '.问：平面内是否存在定点P ，使得B '恒在直线PC 上？若存在，求出点P 的坐标；若不存在，说明理由.题型五：存在点使线段关系式为定值例13．（2024·全国·高三专题练习）椭圆E 经过两点2⎛⎫ ⎪ ⎪⎝⎭，22⎫⎪⎪⎝⎭，过点P 的动直线l 与椭圆相交于A ，B 两点．(1)求椭圆E 的方程；(2)若椭圆E 的右焦点是P ，其右准线与x 轴交于点Q ，直线AQ 的斜率为1k ，直线BQ 的斜率为2k ，求证：120k k +=；(3)设点(,0)P t 是椭圆E 的长轴上某一点（不为长轴顶点及坐标原点），是否存在与点P 不同的定点Q ，使得QA PAQB PB =恒成立？只需写出点Q 的坐标，无需证明．例14．（2024·福建宁德·校考模拟预测）已知双曲线C 与双曲线221123y x -=有相同的渐近线，且过点1)A -.(1)求双曲线C 的标准方程；(2)已知点(2,0)D ，E ，F 是双曲线C 上不同于D 的两点，且·0DE DF = ，DG EF ⊥于点G ，证明:存在定点H ，使GH 为定值.例15．（2024·四川成都·高三校考阶段练习）已知椭圆C ：()222210x y a b a b+=>>的离心率为12，过椭圆右焦点F 的直线l 与椭圆交于A ，B 两点，当直线l 与x 轴垂直时，3AB =．(1)求椭圆C 的标准方程；(2)当直线l 的斜率为k ()0k ≠时，在x 轴上是否存在一点P （异于点F ），使x 轴上任意一点到直线PA 与到直线PB 的距离相等？若存在，求P 点坐标；若不存在，请说明理由．变式15．（2024·陕西安康·陕西省安康中学校考模拟预测）已知椭圆E 的中心为坐标原点，对称轴为坐标轴，且过点()2,0A ，2B ⎛⎫ ⎪ ⎪⎝⎭.直线x t =（不经过点B ）与椭圆E 交于,M N 两点，()1,0Q ，直线MQ 与椭圆E 交于另一点C ，点P 满足0QP NC ⋅= ，且P 在直线NC 上.(1)求E 的方程；(2)证明：直线NC 过定点，且存在另一个定点R ，使PR 为定值.变式16．（2024·湖南衡阳·高三衡阳市八中校考阶段练习）已知双曲线()2222:10,0x y C a b a b-=>>的右焦点，右顶点分别为F ，A ，()0,B b ，1AF =，点M 在线段AB 上，且满足BM MA =，直线OM 的斜率为1，O 为坐标原点.(1)求双曲线C 的方程.(2)过点F 的直线l 与双曲线C 的右支相交于P ，Q 两点，在x 轴上是否存在与F 不同的定点E ，使得EP FQ EQ FP ⋅=⋅恒成立？若存在，求出点E 的坐标；若不存在，请说明理由.变式17．（2024·河北秦皇岛·校联考模拟预测）如图，椭圆2222:1(0)x y C a b a b+=>>的左、右顶点分别为A ，B ．左、右焦点分别为1F ，2F ，离心率为2，点M 在椭圆C 上．(1)求椭圆C 的方程；(2)已知P ，Q 是椭圆C 上两动点，记直线AP 的斜率为1k ，直线BQ 的斜率为2k ，122k k =．过点B 作直线PQ 的垂线，垂足为H ．问：在平面内是否存在定点T ，使得TH 为定值，若存在，求出点T 的坐标；若不存在，试说明理由．变式18．（2024·四川遂宁·高三射洪中学校考阶段练习）在平面直角坐标系xOy 中，设点P 的轨迹为曲线C .①过点()1,0F 的动圆恒与y 轴相切，FP 为该圆的直径；②点P 到()1,0F 的距离比P 到y 轴的距离大1.在①和②中选择一个作为条件:(1)选择条件：求曲线C 的方程；(2)在x 轴正半轴上是否存在一点M ，当过点M 的直线l 与抛物线C 交于Q R ，两点时，11MQ MR+为定值？若存在，求出点M 的坐标，若不存在，请说明理由.变式19．（2024·四川成都·高三树德中学校考开学考试）已知椭圆()2222:10x y C a b a b+=>>的离心率为e =()1,e ．P 为椭圆C 在第一象限内部分上的一点．(1)若(),0A a ，()0,B b ，求ABP 面积的最大值；(2)是否存在点P ，使得过点P 作圆()22:11M x y ++=的两条切线，分别交y 轴于D ，E 两点，且3DE =．若存在，点求出P 的坐标；若不存在，说明理由。

第80讲阿基米德三角形知识梳理如图所示，AB 为抛物线22(0)x py p =>的弦，11(,)A x y ，22(,)B x y ，分别过,A B 作的抛物线的切线交于点P ，称PAB △为阿基米德三角形，弦AB为阿基米德三角形的底边．1、阿基米德三角形底边上的中线平行于抛物线的轴．2、若阿基米德三角形的底边即弦AB 过抛物线内定点()00 C x y ，，则另一顶点P 的轨迹为一条直线．3、若直线l 与抛物线没有公共点，以l 上的点为顶点的阿基米德三角形的底边过定点．4、底边长为a 的阿基米德三角形的面积的最大值为38a p．5、若阿基米德三角形的底边过焦点，则顶点Q 的轨迹为准线，且阿基米德三角形的面积的最小值为2p ．6、点P 的坐标为1212,22x x x x p ⎛⎫+ ⎪⎝⎭；7、底边AB 所在的直线方程为()121220; x x x py x x +--=8、PAB △的面积为3128PAB x x S p-=．9、若点P 的坐标为()00,x y ，则底边AB 的直线方程为()000x x p y y -+=．10、如图1，若E 为抛物线弧AB 上的动点，点E 处的切线与PA ，PB 分别交于点C ，D ，则||||||||||||AC CE PD CP ED DB ==.11、若E 为抛物线弧AB 上的动点，抛物线在点E 处的切线与阿基米德三角形PAB △的边PA ，PB 分别交于点C ，D ，则2EABPCDS S = ．12、抛物线和它的一条弦所围成的面积，等于以此弦为底边的阿基米德三角形面积的23．图1必考题型全归纳题型一：定点问题例1．（2024·山西太原·高二山西大附中校考期末）已知点()0,1A -，()0,1B ，动点P 满足PB AB PA BA =⋅．记点P 的轨迹为曲线C ．（1）求C 的方程；（2）设D 为直线=2y -上的动点，过D 作C 的两条切线，切点分别是E ，F ．证明：直线EF 过定点．例2．（2024·陕西西安·西安市大明宫中学校考模拟预测）已知动圆M 恒过定点10,8F ⎛⎫⎪⎝⎭，圆心M 到直线14y =-的距离为1,8d d MF =+．(1)求M 点的轨迹C 的方程；(2)过直线1y x =-上的动点Q 作C 的两条切线12,l l ，切点分别为,A B ，证明：直线AB 恒过定点．例3．（2024·全国·高二专题练习）已知平面曲线C 满足：它上面任意一定到10,2⎛⎫⎪⎝⎭的距离比到直线32y =-的距离小1.(1)求曲线C 的方程；(2)D 为直线12y =-上的动点，过点D 作曲线C 的两条切线，切点分别为A B ､，证明：直线AB 过定点；(3)在（2）的条件下，以50,2E ⎛⎫⎪⎝⎭为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求四边形ADBE 的面积.变式1．（2024·陕西·校联考三模）已知直线l 与抛物线2:2(0)C x py p =>交于A ，B 两点，且OA OB ⊥，OD AB ⊥，D 为垂足，点D 的坐标为(1,1)．(1)求C 的方程；(2)若点E 是直线4y x =-上的动点，过点E 作抛物线C 的两条切线EP ，EQ ，其中P ，Q 为切点，试证明直线PQ 恒过一定点，并求出该定点的坐标．变式2．（2024·安徽·高二合肥市第八中学校联考开学考试）抛物线的弦与在弦两端点处的切线所围成的三角形被称为“阿基米德三角形”．对于抛物线C ：2y ax =给出如下三个条件：①焦点为10,2F ⎛⎫⎪⎝⎭；②准线为12y =-；③与直线210y -=相交所得弦长为2．(1)从以上三个条件中选择一个，求抛物线C 的方程；(2)已知ABQ 是（1）中抛物线的“阿基米德三角形”，点Q 是抛物线C 在弦AB 两端点处的两条切线的交点，若点Q 恰在此抛物线的准线上，试判断直线AB 是否过定点？如果是，求出定点坐标；如果不是，请说明理由．变式3．（2024·湖北武汉·高二武汉市第四十九中学校考阶段练习）已知抛物线2:C y ax =（a 是常数）过点(2,2)P -，动点1,2D t ⎛⎫- ⎪⎝⎭，过D 作C 的两条切线，切点分别为A ，B ．(1)求抛物线C 的焦点坐标和准线方程；(2)当1t =时，求直线AB 的方程；(3)证明：直线AB 过定点．变式4．（2024·全国·高三专题练习）已知动点P 在x 轴及其上方，且点P 到点(0,1)F 的距离比到x 轴的距离大1.（1）求点P 的轨迹C 的方程；（2）若点Q 是直线4y x =-上任意一点，过点Q 作点P 的轨迹C 的两切线QA ､QB ，其中A ､B 为切点，试证明直线AB 恒过一定点，并求出该点的坐标.题型二：交点的轨迹问题例4．（2024·全国·高三专题练习）已知抛物线C 的顶点为原点，其焦点()0,F c (0)c >到直线:20l x y --=．(1)求抛物线C 的方程；(2)设点0(P x ，0)y 为直线l 上一动点，过点P 作抛物线C 的两条切线PA ，PB ，其中A ，B 为切点，求直线AB 的方程，并证明直线AB 过定点Q ；(3)过（2）中的点Q 的直线m 交抛物线C 于A ，B 两点，过点A ，B 分别作抛物线C 的切线1l ，2l ，求1l ，2l 交点M 满足的轨迹方程．例5．（2024·全国·高三专题练习）已知抛物线2:4C x y =的焦点为F ，过点F 作直线l 交抛物线C 于A 、B 两点；椭圆E 的中心在原点，焦点在x 轴上，点F 是它的一个顶点，且其离心率2e =．(1)求椭圆E 的方程；(2)经过A 、B 两点分别作抛物线C 的切线1l 、2l ，切线1l 与2l 相交于点M ．证明：点M 定在直线1y =-上；(3)椭圆E 上是否存在一点M '，经过点M '作抛物线C 的两条切线M A ''、(M B A '''、B '为切点），使得直线A B ''过点F ？若存在，求出切线M A ''、M B ''的方程；若不存在，试说明理由．例6．（2024·全国·高三专题练习）已知动点Q 在x 轴上方，且到定点()0,1F 距离比到x 轴的距离大1.（1）求动点Q 的轨迹C 的方程；（2）过点()1,1P 的直线l 与曲线C 交于A ，B 两点，点A ，B 分别异于原点O ，在曲线C 的A ，B 两点处的切线分别为1l ，2l ，且1l 与2l 交于点M ，求证：M 在定直线上.变式5．（2024·全国·高三专题练习）已知动点P 与定点(1,0)F 的距离和它到定直线:4l x =的距离之比为12，记P 的轨迹为曲线C ．(1)求曲线C 的方程；(2)过点(4,0)M 的直线与曲线C 交于,A B 两点，,R Q 分别为曲线C 与x 轴的两个交点，直线,AR BQ 交于点N ，求证:点N 在定直线上．变式6．（2024·全国·高三专题练习）已知点F 为抛物线2:2(0)C x py p =>的焦点，点M 、N 在抛物线上，且M 、N 、F 三点共线.若圆22:(2)(3)16P x y -+-=的直径为MN .（1）求抛物线C 的标准方程；（2）过点F 的直线l 与抛物线交于点A ，B ，分别过A 、B 两点作抛物线C 的切线1l ，2l ，证明直线1l ，2l 的交点在定直线上，并求出该直线.变式7．（2024·全国·高三专题练习）下面是某同学在学段总结中对圆锥曲线切线问题的总结和探索，现邀请你一起合作学习，请你思考后，将答案补充完整．(1)圆222:O x y r +=上点()00,M x y 处的切线方程为．理由如下：．(2)椭圆22221(0)x y a b a b+=>>上一点()00,x y 处的切线方程为；(3)(,)P m n 是椭圆22:13x L y +=外一点，过点P 作椭圆的两条切线，切点分别为A ，B ，如图，则直线AB 的方程是．这是因为在()11,A x y ，()22,B x y 两点处，椭圆L 的切线方程为1113x x y y +=和2213x x y y +=．两切线都过P 点，所以得到了1113x m y n +=和2213x my n +=，由这两个“同构方程”得到了直线AB 的方程；(4)问题（3）中两切线PA ，PB 斜率都存在时，设它们方程的统一表达式为()y n k x m -=-，由22()33y n k x m x y -=-⎧⎨+=⎩，得222(13)6()3()30k x k n km x n km ++-+--=，化简得Δ0=，得222(3)210m x mnk n -++-=．若PA PB ⊥，则由这个方程可知P 点一定在一个圆上，这个圆的方程为．（5）抛物线22(0)y px p =>上一点()00,x y 处的切线方程为00()y y p x x =+；（6）抛物线2:4C x y =，过焦点F 的直线l 与抛物线相交于A ，B 两点，分别过点A ，B 作抛物线的两条切线1l 和2l ，设()11,A x y ，()22,B x y ，则直线1l 的方程为112()x x y y =+．直线2l 的方程为222()x x y y =+，设1l 和2l 相交于点M ．则①点M 在以线段AB 为直径的圆上；②点M 在抛物线C 的准线上．题型三：切线垂直问题例7．（2024·全国·高三专题练习）已知抛物线C 的方程为24x y =，过点P 作抛物线C 的两条切线，切点分别为,A B .（1）若点P 坐标为()0,1-，求切线,PA PB 的方程；（2）若点P 是抛物线C 的准线上的任意一点，求证：切线PA 和PB 互相垂直.例8．（2024·全国·高三专题练习）已知抛物线C 的方程为24x y =，点P 是抛物线C 的准线上的任意一点，过点P 作抛物线C 的两条切线，切点分别为,A B ，点M 是AB 的中点.（1）求证：切线PA 和PB 互相垂直；（2）求证：直线PM 与y 轴平行；（3）求PAB 面积的最小值.例9．（2024·全国·高三专题练习）已知中心在原点的椭圆1Γ和抛物线2Γ有相同的焦点(1,0)，椭圆1Γ的离心率为12，抛物线2Γ的顶点为原点.(1)求椭圆1Γ和抛物线2Γ的方程；(2)设点P 为抛物线2Γ准线上的任意一点，过点P 作抛物线2Γ的两条切线PA ，PB ，其中,A B 为切点.设直线PA ，PB 的斜率分别为1k ，2k ，求证：12k k 为定值.变式8．（2024·全国·高三专题练习）已知中心在原点的椭圆1C 和抛物线2C 有相同的焦点()1,0，椭圆1C 过点31,2G ⎛⎫⎪⎝⎭，抛物线2C 的顶点为原点．()1求椭圆1C 和抛物线2C 的方程；()2设点P 为抛物线2C 准线上的任意一点，过点P 作抛物线2C 的两条切线PA ，PB ，其中A ，B 为切点．①设直线PA ，PB 的斜率分别为1k ，2k ，求证：12k k 为定值；②若直线AB 交椭圆1C 于C ，D 两点，PAB S ，PCD S 分别是PAB ，PCD 的面积，试问：PABPCDS S 是否有最小值？若有，求出最小值；若没有，请说明理由．变式9．（2024·全国·高三专题练习）抛物级22(0)x py p =>的焦点F 到直线2py =-的距离为2.（1）求抛物线的方程；（2）设直线1y kx =+交抛物线于()11,A x y ，()22,B x y 两点，分别过A ，B 两点作抛物线的两条切线，两切线的交点为P ，求证：PF AB ⊥.变式10．（2024·河南驻马店·校考模拟预测）已知抛物线E ：()220x py p =>的焦点为F ，点P 在E 上，直线l ：20x y --=与E 相离．若P 到直线l 的距离为d ，且PF d +的最小值为2．过E 上两点,A B 分别作E 的两条切线，若这两条切线的交点M 恰好在直线l 上．（1）求E 的方程；（2）设线段AB 中点的纵坐标为n ，求证：当n 取得最小值时，MA MB ⊥．题型四：面积问题例10．（2024·全国·高三专题练习）已知抛物线C 的方程为()220x py p =>，点3,2A x ⎛⎫ ⎪⎝⎭是抛物线上的一点，且到抛物线焦点的距离为2．（1）求抛物线的方程；（2）点Q 为直线12y =-上的动点，过点Q 作抛物线C 的两条切线，切点分别为D ，E ，求QDE △面积的最小值．例11．（2024·全国·高三专题练习）已知抛物线22x py =上一点()0,1M x 到其焦点F 的距离为2．（1）求抛物线的方程；（2）如图，过直线:2l y =-上一点A 作抛物线的两条切线AP ，AQ ，切点分别为P ，Q ，且直线PQ 与y 轴交于点N ．设直线AP ，AQ 与x 轴的交点分别为B ，C ，求四边形ABNC 面积的最小值．例12．（2024·全国·高三专题练习）已知抛物线2:2(0)C x py p =>的焦点到原点的距离等于直线:440l x y --=的斜率.（1）求抛物线C 的方程及准线方程；（2）点P 是直线l 上的动点，过点P 作抛物线C 的两条切线，切点分别为A ，B ，求PAB 面积的最小值.变式11．（2024·全国·高三专题练习）如图，已知抛物线2:2(0)C y px p =>上的点R 的横坐标为1，焦点为F ，且||2RF =，过点(4,0)P -作抛物线C 的两条切线，切点分别为A 、B ，D 为线段PA 上的动点，过D 作抛物线的切线，切点为E （异于点A ，B ），且直线DE 交线段PB 于点H .(1)求抛物线C 的方程；(2)（i ）求证：||||AD BH +为定值；（ii ）设EAD ，EBH △的面积分别为12S S ，，求12133S S S =+的最小值.变式12．（2024·全国·高三专题练习）已知点A （﹣4，4）、B （4，4），直线AM 与BM 相交于点M ，且直线AM 的斜率与直线BM 的斜率之差为﹣2，点M 的轨迹为曲线C ．（1）求曲线C 的轨迹方程；（2）Q 为直线y=﹣1上的动点，过Q 作曲线C 的切线，切点分别为D 、E ，求△QDE 的面积S 的最小值．变式13．（2024·河南开封·河南省兰考县第一高级中学校考模拟预测）已知点()F ，平面上的动点S 到F 的距离是S 40+=的距离的2倍，记点S 的轨迹为曲线C ．(1)求曲线C 的方程；(2)过直线:2l y =上的动点()(),22P s s >向曲线C 作两条切线1l ，2l ，1l 交x 轴于M ，交y 轴于N ，2l 交x 轴于T ，交y 轴于Q ，记PNQ V 的面积为1S ，PMT △的面积为2S ，求12S S ⋅的最小值．题型五：外接圆问题例13．（2024·全国·高三专题练习）已知P 是抛物线C ：2134y x =-的顶点，A ，B 是C 上的两个动点，且4PA PB ⋅=- ．（1）试判断直线AB 是否经过某一个定点？若是，求这个定点的坐标；若不是，说明理由；（2）设点M 是PAB 的外接圆圆心，求点M 的轨迹方程．例14．（2024·高二单元测试）已知点P 是抛物线21:34C y x =-的顶点，A ，B 是C 上的两个动点，且4PA PB ⋅=- .（1）判断点()0,1D 是否在直线AB 上？说明理由；（2）设点M 是△PAB 的外接圆的圆心，点M 到x 轴的距离为d ，点()1,0N ，求MN d -的最大值.例15．（2024·全国·高三专题练习）已知点P 是抛物线21:34C y x =-的顶点，A ，B 是C 上的两个动点，且4PA PB ⋅=- .（1）判断点()0,1D -是否在直线AB 上？说明理由；（2）设点M 是△PAB 的外接圆的圆心，求点M 的轨迹方程.题型六：最值问题例16．（2024·全国·高三专题练习）如图已知()2,P t -是直线2x =-上的动点，过点P 作抛物线24y x =的两条切线，切点分别为,A B ，与y 轴分别交于,C D.（1）求证：直线AB 过定点，并求出该定点；（2）设直线AB 与x 轴相交于点Q ，记,A B 两点到直线PQ 的距离分别为12,d d ；求当12AB d d +取最大值时PCD 的面积.例17．（2024·湖南·高三校联考阶段练习）在直角坐标系xoy 中，已知抛物线()2:20C x py p =>，P 为直线1y x =-上的动点，过点P 作抛物线C 的两条切线，切点分别为,A B ，当P 在y 轴上时，OA OB ⊥.(1)求抛物线C 的方程；(2)求点O 到直线AB 距离的最大值.例18．（2024·辽宁沈阳·校联考二模）从抛物线的焦点发出的光经过抛物线反射后，光线都平行于抛物线的轴，根据光路的可逆性，平行于抛物线的轴射向抛物线后的反射光线都会汇聚到抛物线的焦点处，这一性质被广泛应用在生产生活中．如图，已知抛物线()2:21C x py p =>，从点()4,9发出的平行于y 轴的光线照射到抛物线上的D 点，经过抛物线两次反射后，反射光线由G 点射出，经过点()1,5-．(1)求抛物线C 的方程；(2)已知圆()22:34M x y +-=，在抛物线C 上任取一点E ，过点E 向圆M 作两条切线EA 和EB ，切点分别为A 、B ，求EA EB ⋅ 的取值范围．变式14．（2024·贵州·高三校联考阶段练习）已知抛物线()2:20C x py p =>上的点()02,y 到其焦点F 的距离为2.(1)求抛物线C 的方程；(2)已知点D 在直线l ：=3y -上，过点D 作抛物线C 的两条切线，切点分别为,A B ，直线AB 与直线l 交于点M ，过抛物线C 的焦点F 作直线AB 的垂线交直线l 于点N ，当MN 最小时，求ABMN 的值.变式15．（2024·黑龙江大庆·高二大庆实验中学校考阶段练习）已知抛物线2:4C y x =，点P 为直线2x =-上的任意一点，过点P 作抛物线C 的两条切线，切点分别为A ，B ，则点()0,1M 到直线AB 的距离的最大值为（）A ．1B ．4C ．5D题型七：角度相等问题例19．设抛物线2:C y x =的焦点为F ，动点P 在直线:20l x y --=上运动，过P 作抛物线C 的两条切线PA 、PB ，且与抛物线C 分别相切于A 、B 两点.（1）求△APB 的重心G 的轨迹方程.（2）证明∠PFA=∠PFB ．例20．（2024·全国·高三专题练习）已知F ，F '分别是椭圆221:171617C x y +=的上、下焦点，直线1l 过点F '且垂直于椭圆长轴，动直线2l 垂直1l 于点G ，线段GF 的垂直平分线交2l 于点H ，点H 的轨迹为2C .(1)求轨迹2C 的方程；(2)若动点P 在直线:20l x y --=上运动，且过点P 作轨迹2C 的两条切线PA 、PB ，切点为A 、B ，试猜想PFA ∠与PFB ∠的大小关系，并证明你的结论的正确性.例21．（2024·江苏南通·高三统考阶段练习）在平面直角坐标系xOy中，已知圆22=>交于点M，N（异于原点O），MN恰为该圆的+-=与抛物线2:2(0)C x py pG x y:(1)1直径，过点E（0，2）作直线交抛物线于A，B两点，过A，B两点分别作抛物线C的切线交于点P．(1)求证：点P的纵坐标为定值；∠=∠．(2)若F是抛物线C的焦点，证明：PFA PFBy x=的焦点为F，动点P 变式16．（2024·全国·高三专题练习）如图所示，设抛物线C：2x y--=上运动，过P作抛物线C的两条切线PA，PB，切点分别为A，B，在直线l：20求证：AFB BFP∠=∠.变式17．（2024·全国·高三专题练习）在平面直角坐标系xOy中，已知点E(0，2)，以OE为直径的圆与抛物线C∶x2=2py(p>0)交于点M，N(异于原点O)，MN恰为该圆的直径，过点E作直线交抛物线与A，B两点，过A，B两点分别作拋物线C的切线交于点P.（1）求证∶点P的纵坐标为定值；（2）若F是抛物线C的焦点，证明∶∠PFA=∠PFB。

随机事件的概率进门测判断下列结论是否正确(请在括号中打“√”或“×”)(1)事件发生频率与概率是相同的．()(2)随机事件和随机试验是一回事．()(3)在大量重复试验中，概率是频率的稳定值．()(4)两个事件的和事件是指两个事件都得发生．()(5)对立事件一定是互斥事件，互斥事件不一定是对立事件．()(6)两互斥事件的概率和为1. ( )阶段训练题型一事件关系的判断例1(1)从1,2,3，…，7这7个数中任取两个数，其中：①恰有一个是偶数和恰有一个是奇数；②至少有一个是奇数和两个都是奇数；③至少有一个是奇数和两个都是偶数；④至少有一个是奇数和至少有一个是偶数．上述事件中，是对立事件的是()A．①B．②④C．③D．①③(2)设条件甲：“事件A与事件B是对立事件”，结论乙：“概率满足P(A)＋P(B)＝1”，则甲是乙的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件(3)在5张电话卡中，有3张移动卡和2张联通卡，从中任取2张，若事件“2张全是移动卡”的概率是310，那么概率是710的事件是()A．至多有一张移动卡B．恰有一张移动卡C．都不是移动卡D．至少有一张移动卡从装有两个白球和两个黄球的口袋中任取2个球，以下给出了四组事件：①至少有1个白球与至少有1个黄球；②至少有1个黄球与都是黄球；③恰有1个白球与恰有1个黄球；④恰有1个白球与都是黄球．其中互斥而不对立的事件共有()A．0组B．1组C．2组D．3组题型二随机事件的频率与概率例2某险种的基本保费为a(单位：元)，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：(1)记A为事件：“一续保人本年度的保费不高于基本保费”，求P(A)的估计值；(2)记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”，求P(B)的估计值；(3)求续保人本年度的平均保费的估计值．某超市随机选取1 000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买.(1)估计顾客同时购买乙和丙的概率；(2)估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；(3)如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？题型三互斥事件、对立事件的概率命题点1 互斥事件的概率例3 袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率是13，得到黑球或黄球的概率是512，得到黄球或绿球的概率也是512，试求得到黑球、黄球和绿球的概率各是多少？命题点2 对立事件的概率例4 某商场有奖销售中，购满100元商品得1张奖券，多购多得.1 000张奖券为一个开奖单位，设特等奖1个，一等奖10个，二等奖50个．设1张奖券中特等奖，一等奖，二等奖的事件分别为A ，B ，C ，求：(1)P (A )，P (B )，P (C )； (2)1张奖券的中奖概率；(3)1张奖券不中特等奖且不中一等奖的概率．经统计，在某储蓄所一个营业窗口等候的人数相应的概率如下：求：(1)至多2人排队等候的概率；(2)至少3人排队等候的概率．1．概率和频率(1)在相同的条件S 下重复n 次试验，观察某一事件A 是否出现，称n 次试验中事件A 出现的次数n A 为事件A 出现的频数，称事件A 出现的比例f n (A )＝n An为事件A 出现的频率．(2)对于给定的随机事件A ，在相同条件下，随着试验次数的增加，事件A 发生的频率会在某个常数附近摆动并趋于稳定，我们可以用这个常数来刻画随机事件A 发生的可能性大小，并把这个常数称为随机事件A 的概率，记作P (A )． 2．事件的关系与运算定义符号表示包含关系如果事件A 发生，则事件B 一定发生，这时称事件B 包含事件A (或称事件A 包含于事件B )B ⊇A (或A ⊆B ) 相等关系若B ⊇A 且A ⊇BA ＝B 并事件(和事件)若某事件发生当且仅当事件A 发生或事件B 发生，称此事件为事件A 与事件B 的并事件(或和事件)A ∪B (或A ＋B )交事件 若某事件发生当且仅当事件A 发生且事件B 发生，则称此事件为事件A 与事件B 的交事件(或A ∩B (或AB )阶段重难点梳理(积事件)积事件)若A∩B为不可能事件(A∩B＝∅)，那么称事件A互斥事件A∩B＝∅与事件B互斥若A∩B为不可能事件，A∪B为必然事件，那P(A)＋P(B)＝1 对立事件么称事件A与事件B互为对立事件3.概率的几个基本性质(1)概率的取值范围：0≤P(A)≤1.(2)必然事件的概率P(E)＝1.(3)不可能事件的概率P(F)＝0.(4)概率的加法公式如果事件A与事件B互斥，则P(A∪B)＝P(A)＋P(B)．(5)对立事件的概率若事件A与事件B互为对立事件，则P(A)＝1－P(B)．【知识拓展】互斥事件与对立事件的区别与联系互斥事件与对立事件都是两个事件的关系，互斥事件是不可能同时发生的两个事件，而对立事件除要求这两个事件不同时发生外，还要求二者之一必须有一个发生，因此，对立事件是互斥事件的特殊情况，而互斥事件未必是对立事件．重点题型训练典例 某超市为了了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示.已知这100位顾客中一次购物量超过8件的顾客占55%. (1)确定x ，y 的值，并估计顾客一次购物的结算时间的平均值；(2)求一位顾客一次购物的结算时间不超过．．．2分钟的概率．(将频率视为概率)1．从{1,2,3,4,5}中随机选取一个数a ，从{1,2,3}中随机选取一个数b ，则b >a 的概率是( ) A.45 B.35 C.25 D.152．将一枚硬币向上抛掷10次，其中“正面向上恰有5次”是( ) A ．必然事件B ．随机事件C ．不可能事件D ．无法确定3．某射手在一次射击中，射中10环，9环，8环的概率分别为0.2,0.3,0.1，则此射手在一次射击中不超过8环的概率为( ) A ．0.5 B ．0.3 C ．0.6 D ．0.94．袋中装有9个白球，2个红球，从中任取3个球，则①恰有1个红球和全是白球；②至少有1个红球和全是白球；③至少有1个红球和至少有2个白球；④至少有1个白球和至少有1个红球．在上述事件中，是对立事件的为________．1．甲、乙两人下棋，两人下成和棋的概率是12，甲获胜的概率是13，则甲不输的概率为( )A.56 B.25 C.16D.132．袋中装有3个白球，4个黑球，从中任取3个球，则①恰有1个白球和全是白球；②至少有1个白球和全是黑球；③至少有1个白球和至少有2个白球；④至少有1个白球和至少有1个黑球． 在上述事件中，是对立事件的为( ) A ．① B ．② C ．③ D ．④3．从一箱产品中随机地抽取一件，设事件A ＝{抽到一等品}，事件B ＝{抽到二等品}，事件C ＝{抽到三等品}，且已知P (A )＝0.65，P (B )＝0.2，P (C )＝0.1，则事件“抽到的产品不是一等品”的概率作业布置为()A．0.7 B．0.65 C．0.35 D．0.54．有一个游戏，其规则是甲、乙、丙、丁四个人从同一地点随机地向东、南、西、北四个方向前进，每人一个方向．事件“甲向南”与事件“乙向南”是()A．互斥但非对立事件B．对立事件C．相互独立事件D．以上都不对5．从一篮子鸡蛋中任取1个，如果其重量小于30克的概率为0.3，重量在[30,40]克的概率为0.5，那么重量不小于30克的概率为()A．0.8 B．0.5 C．0.7 D．0.36．从存放的号码分别为1,2,3，…，10的卡片的盒子中，有放回地取100次，每次取一张卡片并记下号码，统计结果如下：则取到号码为奇数的卡片的频率是()A．0.53 B．0.5 C．0.47 D．0.377．在200件产品中，有192件一级品，8件二级品，则下列事件：①在这200件产品中任意选出9件，全部是一级品；②在这200件产品中任意选出9件，全部是二级品；③在这200件产品中任意选出9件，不全是二级品．其中________是必然事件；________是不可能事件；________是随机事件．8．若随机事件A，B互斥，A，B发生的概率均不等于0，且P(A)＝2－a，P(B)＝4a－5，则实数a 的取值范围是________________．9．在5张卡片上分别写有数字1,2,3,4,5，然后将它们混合，再任意排列成一行，则得到的数能被2或5整除的概率是________．10．一个口袋内装有大小相同的红球，白球和黑球，从中摸出一个球，摸出红球或白球的概率为0.58，摸出红球或黑球的概率为0.62，那么摸出红球的概率为________．11．某保险公司利用简单随机抽样方法，对投保车辆进行抽样，样本车辆中每辆车的赔付结果统计如下：(1)若每辆车的投保金额均为2 800元，估计赔付金额大于投保金额的概率；(2)在样本车辆中，车主是新司机的占10%，在赔付金额为4 000元的样本车辆中，车主是新司机的占20%，估计在已投保车辆中，新司机获赔金额为4 000元的概率．12．国家射击队的队员为在射击世锦赛上取得优异成绩，正在加紧备战，经过近期训练，某队员射击一次命中7～10环的概率如下表所示：求该射击队员射击一次：(1)射中9环或10环的概率；(2)命中不足8环的概率．*13.一盒中装有12个球，其中5个红球，4个黑球，2个白球，1个绿球．从中随机取出1球，求：(1)取出1球是红球或黑球的概率；(2)取出1球是红球或黑球或白球的概率．随机事件的概率进门测判断下列结论是否正确(请在括号中打“√”或“×”)(1)事件发生频率与概率是相同的．(×)(2)随机事件和随机试验是一回事．(×)(3)在大量重复试验中，概率是频率的稳定值．(√)(4)两个事件的和事件是指两个事件都得发生．(×)(5)对立事件一定是互斥事件，互斥事件不一定是对立事件．(√)(6)两互斥事件的概率和为1.(×)阶段训练题型一事件关系的判断例1(1)从1,2,3，…，7这7个数中任取两个数，其中：①恰有一个是偶数和恰有一个是奇数；②至少有一个是奇数和两个都是奇数； ③至少有一个是奇数和两个都是偶数； ④至少有一个是奇数和至少有一个是偶数． 上述事件中，是对立事件的是( ) A ．① B ．②④ C ．③ D ．①③(2)设条件甲：“事件A 与事件B 是对立事件”，结论乙：“概率满足P (A )＋P (B )＝1”，则甲是乙的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件(3)在5张电话卡中，有3张移动卡和2张联通卡，从中任取2张，若事件“2张全是移动卡”的概率是310，那么概率是710的事件是( )A ．至多有一张移动卡B ．恰有一张移动卡C ．都不是移动卡D ．至少有一张移动卡答案 (1)C (2)A (3)A解析 (1)③中“至少有一个是奇数”即“两个奇数或一奇一偶”，而从1～7中任取两个数根据取到数的奇偶性可认为共有三个事件：“两个都是奇数”、“一奇一偶”、“两个都是偶数”，故“至少有一个是奇数”与“两个都是偶数”是对立事件，易知其余都不是对立事件．(2)若事件A 与事件B 是对立事件，则A ∪B 为必然事件，再由概率的加法公式得P (A )＋P (B )＝1.设掷一枚硬币3次，事件A ：“至少出现一次正面”，事件B ：“3次出现正面”，则P (A )＝78，P (B )＝18，满足P (A )＋P (B )＝1，但A ，B 不是对立事件． (3)至多有一张移动卡包含“一张移动卡，一张联通卡”，“两张全是联通卡”两个事件，它是“2张全是移动卡”的对立事件．思维升华(1)准确把握互斥事件与对立事件的概念①互斥事件是不可能同时发生的事件，但可以同时不发生．②对立事件是特殊的互斥事件，特殊在对立的两个事件不可能都不发生，即有且仅有一个发生．(2)判别互斥、对立事件的方法判别互斥事件、对立事件一般用定义判断，不可能同时发生的两个事件为互斥事件；两个事件，若有且仅有一个发生，则这两事件为对立事件，对立事件一定是互斥事件．从装有两个白球和两个黄球的口袋中任取2个球，以下给出了四组事件：①至少有1个白球与至少有1个黄球；②至少有1个黄球与都是黄球；③恰有1个白球与恰有1个黄球；④恰有1个白球与都是黄球．其中互斥而不对立的事件共有()A．0组B．1组C．2组D．3组答案 B解析①中“至少有1个白球”与“至少有1个黄球”可以同时发生，如恰好1个白球和1个黄球，①中的两个事件不是互斥事件．②中“至少有1个黄球”说明可以是1个白球和1个黄球或2个黄球，则两个事件不互斥．③中“恰有1个白球”与“恰有1个黄球”，都是指有1个白球和1个黄球，因此两个事件是同一事件．④中两事件不能同时发生，也可能都不发生，因此两事件是互斥事件，但不是对立事件，故选B.题型二随机事件的频率与概率例2 某险种的基本保费为a (单位：元)，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：(1)记A 为事件：“一续保人本年度的保费不高于基本保费”，求P (A )的估计值；(2)记B 为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”，求P (B )的估计值；(3)求续保人本年度的平均保费的估计值．解 (1)事件A 发生当且仅当一年内出险次数小于2.由所给数据知，一年内出险次数小于2的频率为60＋50200＝0.55，故P (A )的估计值为0.55. (2)事件B 发生当且仅当一年内出险次数大于1且小于4.由所给数据知，一年内出险次数大于1且小于4的频率为30＋30200＝0.3，故P (B )的估计值为0.3.(3)由所给数据得调查的200名续保人的平均保费为0.85a×0.30＋a×0.25＋1.25a×0.15＋1.5a×0.15＋1.75a×0.10＋2a×0.05＝1.192 5a.因此，续保人本年度平均保费的估计值为1.192 5a.思维升华(1)概率与频率的关系频率反映了一个随机事件出现的频繁程度，频率是随机的，而概率是一个确定的值，通常用概率来反映随机事件发生的可能性的大小，有时也用频率作为随机事件概率的估计值．(2)随机事件概率的求法利用概率的统计定义求事件的概率，即通过大量的重复试验，事件发生的频率会逐渐趋近于某一个常数，这个常数就是概率．某超市随机选取1 000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买.(1)估计顾客同时购买乙和丙的概率；(2)估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；(3)如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？ 解 (1)从统计表可以看出，在这1 000位顾客中有200位顾客同时购买了乙和丙， 所以顾客同时购买乙和丙的概率可以估计为2001 000＝0.2.(2)从统计表可以看出，在这1 000位顾客中，有100位顾客同时购买了甲、丙、丁，另有200位顾客同时购买了甲、乙、丙，其他顾客最多购买了2种商品．所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为100＋2001 000＝0.3.(3)与(1)同理，可得：顾客同时购买甲和乙的概率可以估计为2001 000＝0.2，顾客同时购买甲和丙的概率可以估计为100＋200＋3001 000＝0.6，顾客同时购买甲和丁的概率可以估计为1001 000＝0.1.所以，如果顾客购买了甲，则该顾客同时购买丙的可能性最大． 题型三 互斥事件、对立事件的概率 命题点1 互斥事件的概率例3 袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率是13，得到黑球或黄球的概率是512，得到黄球或绿球的概率也是512，试求得到黑球、黄球和绿球的概率各是多少？解 方法一 从袋中选取一个球，记事件“摸到红球”“摸到黑球”“摸到黄球”“摸到绿球”分别为A ，B ，C ，D ，则有P (A )＝13，P (B ∪C )＝P (B )＋P (C )＝512，P (C ∪D )＝P (C )＋P (D )＝512，P (B ∪C ∪D )＝P (B )＋P (C )＋P (D )＝1－P (A )＝1－13＝23，解得P (B )＝14，P (C )＝16，P (D )＝14，因此得到黑球、黄球、绿球的概率分别是14，16，14.方法二 设红球有n 个，则n 12＝13，所以n ＝4，即红球有4个． 又得到黑球或黄球的概率是512，所以黑球和黄球共5个． 又总球数是12，所以绿球有12－4－5＝3(个)．又得到黄球或绿球的概率也是512，所以黄球和绿球共5个，而绿球有3个，所以黄球有5－3＝2(个)．所以黑球有12－4－3－2＝3(个)． 因此得到黑球、黄球、绿球的概率分别是 312＝14，212＝16，312＝14. 命题点2 对立事件的概率例4 某商场有奖销售中，购满100元商品得1张奖券，多购多得.1 000张奖券为一个开奖单位，设特等奖1个，一等奖10个，二等奖50个．设1张奖券中特等奖，一等奖，二等奖的事件分别为A ，B ，C ，求：(1)P (A )，P (B )，P (C )；(2)1张奖券的中奖概率；(3)1张奖券不中特等奖且不中一等奖的概率． 解 (1)P (A )＝11 000，P (B )＝101 000＝1100， P (C )＝501 000＝120.故事件A ，B ，C 的概率分别为11 000，1100，120. (2)1张奖券中奖包含中特等奖，一等奖，二等奖． 设“1张奖券中奖”这个事件为M ，则M ＝A ∪B ∪C . ∵A ，B ，C 两两互斥，∴P (M )＝P (A ∪B ∪C )＝P (A )＋P (B )＋P (C ) ＝1＋10＋501 000＝611 000.故1张奖券的中奖概率为611 000.(3)设“1张奖券不中特等奖且不中一等奖”为事件N ，则事件N 与“1张奖券中特等奖或中一等奖”为对立事件，∴P (N )＝1－P (A ∪B )＝1－⎝⎛⎭⎫11 000＋1100＝9891 000. 故1张奖券不中特等奖且不中一等奖的概率为9891 000.思维升华 求复杂事件的概率的两种方法求概率的关键是分清所求事件是由哪些事件组成的，求解时通常有两种方法： (1)将所求事件转化成几个彼此互斥的事件的和事件，利用概率加法公式求解概率；(2)若将一个较复杂的事件转化为几个互斥事件的和事件时，需要分类太多，而其对立面的分类较少，可考虑利用对立事件的概率公式，即“正难则反”．它常用来求“至少”或“至多”型事件的概率．经统计，在某储蓄所一个营业窗口等候的人数相应的概率如下：排队人数012345人及5人以上概率0.10.160.30.30.10.04求：(1)至多2人排队等候的概率；(2)至少3人排队等候的概率．解记“无人排队等候”为事件A，“1人排队等候”为事件B，“2人排队等候”为事件C，“3人排队等候”为事件D，“4人排队等候”为事件E，“5人及5人以上排队等候”为事件F，则事件A、B、C、D、E、F彼此互斥．(1)记“至多2人排队等候”为事件G，则G＝A＋B＋C，所以P(G)＝P(A＋B＋C)＝P(A)＋P(B)＋P(C)＝0.1＋0.16＋0.3＝0.56.(2)方法一记“至少3人排队等候”为事件H，则H＝D＋E＋F，所以P(H)＝P(D＋E＋F)＝P(D)＋P(E)＋P(F)＝0.3＋0.1＋0.04＝0.44.方法二记“至少3人排队等候”为事件H，则其对立事件为事件G，所以P(H)＝1－P(G)＝0.44.1．概率和频率(1)在相同的条件S 下重复n 次试验，观察某一事件A 是否出现，称n 次试验中事件A 出现的次数n A 为事件A 出现的频数，称事件A 出现的比例f n (A )＝n An为事件A 出现的频率．(2)对于给定的随机事件A ，在相同条件下，随着试验次数的增加，事件A 发生的频率会在某个常数附近摆动并趋于稳定，我们可以用这个常数来刻画随机事件A 发生的可能性大小，并把这个常数称为随机事件A 的概率，记作P (A )． 2．事件的关系与运算若A∩B为不可能事件，A∪B为必然事件，那对立事件P(A)＋P(B)＝1么称事件A与事件B互为对立事件3.概率的几个基本性质(1)概率的取值范围：0≤P(A)≤1.(2)必然事件的概率P(E)＝1.(3)不可能事件的概率P(F)＝0.(4)概率的加法公式如果事件A与事件B互斥，则P(A∪B)＝P(A)＋P(B)．(5)对立事件的概率若事件A与事件B互为对立事件，则P(A)＝1－P(B)．【知识拓展】互斥事件与对立事件的区别与联系互斥事件与对立事件都是两个事件的关系，互斥事件是不可能同时发生的两个事件，而对立事件除要求这两个事件不同时发生外，还要求二者之一必须有一个发生，因此，对立事件是互斥事件的特殊情况，而互斥事件未必是对立事件．重点题型训练典例某超市为了了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示.已知这100位顾客中一次购物量超过8件的顾客占55%.(1)确定x，y的值，并估计顾客一次购物的结算时间的平均值；(2)求一位顾客一次购物的结算时间不超过．．．2分钟的概率．(将频率视为概率)思想方法指导若某一事件包含的基本事件多，而它的对立事件包含的基本事件少，则可用“正难则反”思想求解．规范解答解(1)由已知得25＋y＋10＝55，x＋30＝45，所以x＝15，y＝20.[2分]该超市所有顾客一次购物的结算时间组成一个总体，所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本，顾客一次购物的结算时间的平均值可用样本平均数估计，其估计值为1×15＋1.5×30＋2×25＋2.5×20＋3×10100＝1.9(分钟)．[7分](2)记A为事件“一位顾客一次购物的结算时间不超过2分钟”，A1，A2分别表示事件“该顾客一次购物的结算时间为2.5分钟”，“该顾客一次购物的结算时间为3分钟”，将频率视为概率得P(A1)＝20100＝15，P(A2)＝10100＝110.[10分]P(A)＝1－P(A1)－P(A2)＝1－15－110＝710.[12分]故一位顾客一次购物的结算时间不超过2分钟的概率为710.[15分]1．从{1,2,3,4,5}中随机选取一个数a ，从{1,2,3}中随机选取一个数b ，则b >a 的概率是( ) A.45 B.35 C.25 D.15 答案 D解析 基本事件的个数有5×3＝15，其中满足b >a 的有3种，所以b >a 的概率为315＝15.2．将一枚硬币向上抛掷10次，其中“正面向上恰有5次”是( ) A ．必然事件 B ．随机事件 C ．不可能事件 D ．无法确定答案 B解析 抛掷10次硬币正面向上的次数可能为0～10，都有可能发生，正面向上5次是随机事件． 3．某射手在一次射击中，射中10环，9环，8环的概率分别为0.2,0.3,0.1，则此射手在一次射击中不超过8环的概率为( ) A ．0.5 B ．0.3 C ．0.6 D ．0.9 答案 A解析 依题设知，此射手在一次射击中不超过8环的概率为1－(0.2＋0.3)＝0.5.4．袋中装有9个白球，2个红球，从中任取3个球，则①恰有1个红球和全是白球；②至少有1个红球和全是白球；③至少有1个红球和至少有2个白球；④至少有1个白球和至少有1个红球．在上述事件中，是对立事件的为________． 答案 ②解析 ①是互斥不对立的事件，②是对立事件，③④不是互斥事件.1．甲、乙两人下棋，两人下成和棋的概率是12，甲获胜的概率是13，则甲不输的概率为( )A.56 B.25 C.16 D.13答案 A解析 事件“甲不输”包含“和棋”和“甲获胜”这两个互斥事件，所以甲不输的概率为12＋13＝56.2．袋中装有3个白球，4个黑球，从中任取3个球，则①恰有1个白球和全是白球；②至少有1个白球和全是黑球；③至少有1个白球和至少有2个白球；④至少有1个白球和至少有1个黑球． 在上述事件中，是对立事件的为( ) A ．① B ．② C ．③ D ．④ 答案 B解析 至少有1个白球和全是黑球不同时发生，且一定有一个发生． ∴②中两事件是对立事件．3．从一箱产品中随机地抽取一件，设事件A ＝{抽到一等品}，事件B ＝{抽到二等品}，事件C ＝{抽到三等品}，且已知P (A )＝0.65，P (B )＝0.2，P (C )＝0.1，则事件“抽到的产品不是一等品”的概率为( )A ．0.7B ．0.65C ．0.35D ．0.5作业布置答案 C解析∵“抽到的产品不是一等品”与事件A是对立事件，∴所求概率P＝1－P(A)＝0.35.4．有一个游戏，其规则是甲、乙、丙、丁四个人从同一地点随机地向东、南、西、北四个方向前进，每人一个方向．事件“甲向南”与事件“乙向南”是()A．互斥但非对立事件B．对立事件C．相互独立事件D．以上都不对答案 A解析由于每人一个方向，故“甲向南”意味着“乙向南”是不可能的，故是互斥事件，但不是对立事件，故选A.5．从一篮子鸡蛋中任取1个，如果其重量小于30克的概率为0.3，重量在[30,40]克的概率为0.5，那么重量不小于30克的概率为()A．0.8 B．0.5 C．0.7 D．0.3答案 C解析由互斥事件概率公式知重量大于40克的概率为1－0.3－0.5＝0.2，又∵0.5＋0.2＝0.7，∴重量不小于30克的概率为0.7.6．从存放的号码分别为1,2,3，…，10的卡片的盒子中，有放回地取100次，每次取一张卡片并记下号码，统计结果如下：则取到号码为奇数的卡片的频率是( ) A ．0.53 B ．0.5 C ．0.47 D ．0.37 答案 A解析 取到号码为奇数的卡片的次数为13＋5＋6＋18＋11＝53，则所求的频率为53100＝0.53.故选A.7．在200件产品中，有192件一级品，8件二级品，则下列事件： ①在这200件产品中任意选出9件，全部是一级品； ②在这200件产品中任意选出9件，全部是二级品； ③在这200件产品中任意选出9件，不全是二级品．其中________是必然事件；________是不可能事件；________是随机事件． 答案 ③ ② ①8．若随机事件A ，B 互斥，A ，B 发生的概率均不等于0，且P (A )＝2－a ，P (B )＝4a －5，则实数a 的取值范围是________________． 答案 (54，43]解析 由题意可知⎩⎪⎨⎪⎧0<P (A )<1，0<P (B )<1，P (A )＋P (B )≤1⇒⎩⎪⎨⎪⎧0<2－a <1，0<4a －5<13a －3≤1，⇒⎩⎪⎨⎪⎧1<a <2，54<a <32，a ≤43⇒54<a ≤43. 9．在5张卡片上分别写有数字1,2,3,4,5，然后将它们混合，再任意排列成一行，则得到的数能被2或5整除的概率是________． 答案 35解析个位数字共有5种情况，只有当个位数字取2,4,5时，得到的数才能被2或5整除，所以概率为3 5.10．一个口袋内装有大小相同的红球，白球和黑球，从中摸出一个球，摸出红球或白球的概率为0.58，摸出红球或黑球的概率为0.62，那么摸出红球的概率为________．答案0.2解析记事件A，B，C分别是摸出红球，白球和黑球，则A，B，C互为互斥事件且P(A＋B)＝0.58，P(A＋C)＝0.62，所以P(C)＝1－P(A＋B)＝0.42，P(B)＝1－P(A＋C)＝0.38，P(A)＝1－P(C)－P(B)＝1－0.38－0.42＝0.2.11．某保险公司利用简单随机抽样方法，对投保车辆进行抽样，样本车辆中每辆车的赔付结果统计如下：(1)若每辆车的投保金额均为2 800元，估计赔付金额大于投保金额的概率；(2)在样本车辆中，车主是新司机的占10%，在赔付金额为4 000元的样本车辆中，车主是新司机的占20%，估计在已投保车辆中，新司机获赔金额为4 000元的概率．解(1)设A表示事件“赔付金额为3 000元”，B表示事件“赔付金额为4 000元”，以频率估计概率得P(A)＝1501 000＝0.15，P(B)＝1201 000＝0.12.由于投保金额为2 800元，赔付金额大于投保金额对应的情形是赔付金额为3 000元和4 000元，所以其概率为P(A)＋P(B)＝0.15＋0.12＝0.27.。

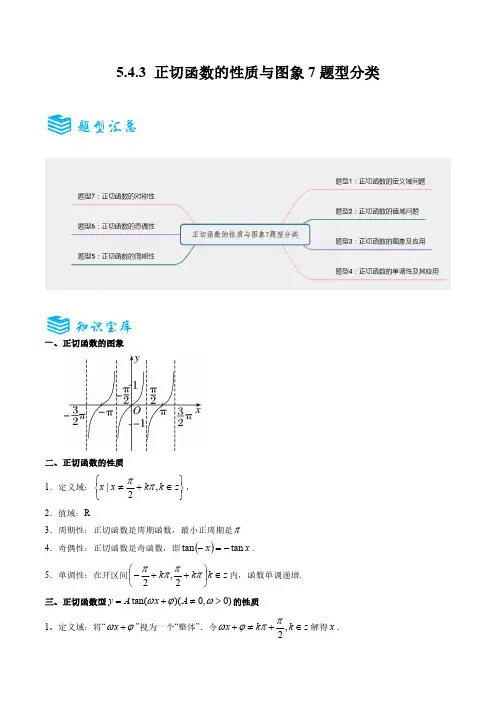
5.4.3 正切函数的性质与图象7题型分类一、正切函数的图象二、正切函数的性质1．定义域：⎭⎬⎫⎩⎨⎧∈+≠z k k x x ,2|ππ，2．值域：R3．周期性：正切函数是周期函数，最小正周期是π4．奇偶性：正切函数是奇函数，即()x x tan tan -=-．5．单调性：在开区间z k k k ∈⎪⎭⎫⎝⎛++-ππππ2,2内，函数单调递增三、正切函数型tan()(0,0)y A x A ωϕω=+≠>的性质1、定义域：将“x ωϕ+”视为一个“整体”．令,2x k k z πωϕπ+≠+∈解得x ．2、值域：(),-¥+¥3、单调区间：（1）把“x ωϕ+”视为一个“整体”；（2）0(0)A A ><时，函数单调性与tan (,)2y x x k k z ππ=≠+∈的相同（反）；（3）解不等式，得出x 范围．4、周期：T πω=（一）正切函数的定义域、值域问题(1)求正切函数定义域的方法①求与正切函数有关的函数的定义域时，除了求函数定义域的一般要求外，还要保证正切函数y ＝tan x 有意义，即x ≠π2＋k π，k ∈Z.②求正切型函数y ＝A tan (ωx ＋φ)(A ≠0，ω＞0)的定义域时，要将“ωx ＋φ”视为一个“整体”．令ωx ＋φ≠k π＋π2，k ∈Z ，解得x . (2)求正切函数值域的方法①对于y ＝Atan (ωx ＋φ)的值域，可以把ωx ＋φ看成整体，结合图象，利用单调性求值域．②对于与y ＝tan x 相关的二次函数，可以把tan x 看成整体，利用配方法求值域（二）正切函数的图象问题熟练掌握正切函数的图象和性质是解决与正切函数有关的综合问题的关键，需注意的是正切曲线是被相互平行的直线x ＝π2＋k π，k ∈Z 隔开的无穷多支形状相同的曲线组成的．　题型3：正切函数的图象及应用3-1．（2024高一上·宁夏银川·期末）函数()2tan f x x x =×（11x -<<）的图象可能是（ ）A ．B ．C ．D ．3-2．（2024高二下·浙江丽水·期中）函数3()3tan f x x x =-在ππ,22⎛⎫- ⎪⎝⎭的图象大致为（ ）A ．B ．C ．D ．3-3．（2024高一上·全国·课后作业）画出函数|tan |y x =的图象．(1)根据图象判断其定义域、值域、单调区间、奇偶性、周期性；(2)求不等式|tan |1x £的解集．3-4．（2024高一上·广东·期末）若函数tan()(0)y x ϕϕ=-³的图象与直线πx =没有交点，则ϕ的最小值为（ ）A ．0B ．π4C ．π2D ．π3-5．（2024高一·全国·课堂例题）观察正切函数曲线，写出满足下列条件的x 的集合．(1)满足tan 0x =的集合．(2)满足tan 0x <的集合．(3)满足tan 0x >的集合．（三）正切函数的单调性及其应用(1)运用正切函数单调性比较大小的方法①运用函数的周期性或诱导公式将角化到同一单调区间内．②运用单调性比较大小关系．(2)求函数y ＝tan(ωx ＋φ)的单调区间的方法y ＝tan(ωx ＋φ)(ω>0)的单调区间的求法是把ωx ＋φ看成一个整体，解－π2＋k π<ωx ＋φ<π2＋k π，k ∈Z 即可．当ω<0时，先用诱导公式把ω化为正值再求单调区间．题型4：正切函数的单调性及其应用4-1．（2024高一下·全国·单元测试）函数tan 36y x π⎛⎫=-+ ⎪⎝⎭的单调区间是（ ）A ．πππ,π()33k k k ⎡⎤-+∈⎢⎥⎣⎦Z B ．2,()99k k k ππ⎛⎫π-π+∈ ⎪⎝⎭Z C ．2,()3939k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z D ．2,()3939k k k ππππ⎛⎫-+∈⎪⎝⎭Z 4-2．（2024高一·全国·课后作业）已知函数tan y x ω=在,22ππ⎛⎫- ⎪⎝⎭上是严格减函数，则实数ω的取值范围是 ．4-3．（2024高一·全国·课堂例题）函数πtan 34y x ⎛⎫=-+ ⎪⎝⎭的单调递减区间为．4-4．（2024高三·全国·专题练习） π3tan 64x y ⎛⎫=- ⎪⎝⎭的单调递减区间为 .4-5．（2024·湖南长沙·模拟预测）已知函数π()tan()(0)3f x A x ωω=+>，若f x （）在区间ππ2⎛⎫⎪⎝⎭，内单调递减，（四）正切函数的奇偶性与周期性与正切函数有关的函数的周期性、奇偶性问题的解决策略(1)一般地，函数y＝A tan(ωx＋φ)的最小正周期为T＝π|ω|，常常利用此公式来求周期．(2)判断函数的奇偶性要先求函数的定义域，判断其是否关于原点对称，若不对称，则该函数无奇偶性；若对称，再判断f(－x)与f(x)的关系．A ．cos y x=B ．sin y x =C ．sin2y x =D ．tan2y x=6-4．（2024高一上·全国·课后作业）已知()tansin 42xf x a b x =-+（其中a b 、为常数且0ab ≠），如果()35f =，则2010()3f π-的值为（ ）A ．3-B ．3C ．5-D ．56-5．（2024高三上·陕西·阶段练习）已知函数()5tan 3f x x x =+-，且()2f m -=-，则()f m =（ ）A ．4-B ．1-C ．1D ．46-6．（2024高一下·山东潍坊·期中）已知()2023sin 2024tan 1f x x x =+-，()()()()()21012f f f f f -+-+++=.（五）正切函数的对称性正切曲线的对称中心为(k π2，0)(k ∈Z)，解关于对称中心的题目时需要把整个三角函数看成一个整体，从整体性入手求出具体范围．题型7：正切函数的对称性7-1．（2024高一下·辽宁铁岭·阶段练习）函数1π()3tan 23f x x ⎛⎫=+ ⎪⎝⎭的图象的对称中心为.7-2．（2024高一下·辽宁·阶段练习）已知函数()()()sin 0,0πf x x ωϕωϕ=+><<的最小正周期为2π3，其图像的一个对称中心的坐标为π,04⎛⎫⎪⎝⎭，则曲线()()tan g x x ωϕ=+的对称中心坐标为（ ）A ．ππ,0312k ⎛⎫- ⎪⎝⎭，k ∈ZB ．ππ,0612k ⎛⎫- ⎪⎝⎭，k ∈ZC ．ππ,0312k ⎛⎫+ ⎪⎝⎭，k ∈ZD ．ππ,0612k ⎛⎫+ ⎪⎝⎭，k ∈Z7-3．（2024·江苏扬州·模拟预测）以点π,0()2k k ⎛⎫∈ ⎪⎝⎭Z 为对称中心的函数是（ ）．A ．sin y x =B ．cos y x =C ．tan y x=D ．|tan |y x =一、单选题1．（2024高一上·福建漳州·期末）函数ππ()tan 23f x x ⎛⎫=+ ⎪⎝⎭的单调区间是（ ）A ．512,2(Z)33k k k ⎛⎫-++∈ ⎪⎝⎭B ．512,2(Z)33k k k ⎡⎤-++∈⎢⎥⎣⎦C ．514,4(Z)33k k k ⎛⎫-++∈ ⎪⎝⎭D ．514,4(Z)33k k k ⎡⎤-++∈⎢⎥⎣⎦2．（2024高一下·内蒙古包头·期末）函数πtan 23y x ⎛⎫=- ⎪⎝⎭的定义域是（ ）A ．5ππ,Z 122k x x k ⎧⎫≠+∈⎨⎬⎩⎭B ．5ππ,Z 12x x k k ⎧⎫≠+∈⎨⎬⎩⎭C ．ππ,Z 32k x x k ⎧⎫≠+∈⎨⎬⎩⎭D ．ππ,Z 3x x k k ⎧⎫≠+∈⎨⎬⎩⎭3．（2024高三上·山西晋中·阶段练习）函数()πtan 2xf x =的最小正周期是（ ）A ．2πB ．4πC ．2D ．44．（2024高二下·湖南·学业考试）函数tan y x =在一个周期内的大致图象是（ ）A ．B ．C ．D ．5．（2024·河南·模拟预测）已知函数()f x 对任意x ∈R 都有()()2=-+f x f x ，且函数()1f x +的图象关于()1,0-对称，当[]1,1x ∈-时，()tan =f x x .则下列结论正确的是（ ）A ．函数()y f x =的图象关于点()(),0k k ∈Z 对称B ．函数()y f x =的图象关于直线()2x k k =∈Z 对称C ．函数()y f x =的最小正周期为2D ．当[]2,3x ∈时，()()tan 2f x x =-6．（2024高一下·北京·期中）函数()tan sin tan sin f x x x x x =--+-|在区间（π2，3π2）内的图象是（ ）A ．B ．C ．D ．7．（2024高一·全国·课后作业）下列各式中正确的是（ ）A ．tan1tan 2>-B ．tan 735tan 800°>°C ．5π4πtantan 77>D ．9ππtantan 87>8．（2024高一下·河南平顶山·阶段练习）函数()πtan 27f x x ⎛⎫=- ⎪⎝⎭图象的对称中心可能是( )A ．π,07⎛⎫⎪⎝⎭B ．π,07⎛⎫- ⎪⎝⎭C ．π,014⎛⎫ ⎪⎝⎭D ．π,014⎛⎫- ⎪⎝⎭9．（2024高一下·上海·课后作业）已知函数tan y x ω=在,22ππ⎛⎫- ⎪⎝⎭内是减函数，则ω的取值范围为（ ）A ．()2,0-B ．[)1,0-C ．(]0,1D ．[]1,210．（2024·河南郑州·模拟预测）已知函数()π2sin 2πZ 3=πtan πZ3x x k k f x x x k k ⎧≠+∈ïï⎨ï=+∈ï⎩，，，，，若方程()f x =在()0m ，上恰有5个不同实根，则m 的取值范围是（ ）A ．7463⎛⎤⎥⎝⎦ππ，B ．71936⎛⎤ ⎥⎝⎦ππ，C ．51336⎛⎤ ⎥⎝⎦ππ，D ．13763⎛⎤⎥⎝⎦ππ，11．（2024高三·全国·对口高考）已知定义在R 上的奇函数()f x 满足()()2f x f x +=，且当()0,1x ∈时，()t πan 2f x x=，则()f x 在[0,5]上的零点个数是（ ）A ．3B ．4C ．5D ．612．（2024高二下·湖南·阶段练习）若π0,3q ⎛⎫∈ ⎪⎝⎭，则2tan q + ）A ．B 2+C 52D 13．（2024·宁夏银川·模拟预测）若π()tan3n f n =，（*n ∈N ），则(1)(2)(2023)f f f ++×××+=（ ）A ．BC ．0D ．-14．（2024高一下·河北衡水·阶段练习）函数()π26f x x m ⎛⎫=-- ⎪⎝⎭在π,12n ⎡⎤-⎢⎥⎣⎦上的最大值为3，最小值为1-，则mn =（ ）A ．π6B ．π3C ．π6-D ．π3-15．（2024·湖北武汉·模拟预测）函数()()πtan 0,2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的图像如图所示，图中阴影部分的面积为6π，则2023π3f ⎛⎫= ⎪⎝⎭（ ）A ．B ．CD 二、多选题16．（2024高一上·吉林长春·阶段练习）已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭，则下列说法错误的是（ ）A ．()f x 的最小正周期为π2B ．()f x 的定义域为ππ,3x x k k ⎧⎫≠+∈⎨⎬⎩⎭Z C ．ππ44f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭D ．()f x 在ππ,32⎛⎫⎪⎝⎭上单调递减17．（2024高一下·辽宁大连·阶段练习）已知函数()tan 2f x x =，则下列说法正确的是（ ）A ．函数()f x 是奇函数B ．函数()f x 的最小正周期是πC ．函数()f x 在ππ(,)44-上单调递增D ．函数()f x 图象的对称中心是π(,0)(Z)4k k ∈18．（2024高三上·山东·开学考试）已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭，则下列说法正确的是（ ）A ．()f x 的最小正周期为π2B ．()f x 在ππ,63⎛⎫⎪⎝⎭上单调递减C ．π3π510f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭D ．()f x 的定义域为ππ,Z 3x x k k ⎧⎫≠+∈⎨⎬⎩⎭19．（2024高一下·四川成都·期中）已知函数()ππtan 23f x x ⎛⎫=+ ⎪⎝⎭，则下列描述中正确的是（ ）．A ．函数()f x 的图象关于点1,03⎛⎫- ⎪⎝⎭成中心对称B ．函数()f x 的最小正周期为2C ．函数()f x 的单调增区间为514,433k k ⎛⎫-++ ⎪⎝⎭，k ∈ZD ．函数()f x 的图象没有对称轴20．（2024高三上·吉林长春·阶段练习）已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭，则（ ）A ．π2f ⎛⎫= ⎪⎝⎭B ．()f x 的最小正周期为πC ．把()f x 向左平移π6可以得到函数()tan 2g x x =D ．()f x 在π,06⎛⎫- ⎪⎝⎭上单调递增21．（2024高一下·辽宁沈阳·期中）已知函数()πtan 4f x x ⎛⎫=+ ⎪⎝⎭，则下列叙述中，正确的是（ ）A ．函数()f x 的图象关于点0π4,⎛⎫⎪⎝⎭-对称B ．函数()f x 在ππ,44⎛⎫- ⎪⎝⎭上单调递增C ．函数()f x 的图象关于直线π2x =对称D ．函数()y f x =是偶函数22．（2024高一下·安徽芜湖·期中）下列坐标所表示的点是函数πtan 26y x ⎛⎫=- ⎪⎝⎭的图像的对称中心的是（ ）A ．π,012⎛⎫ ⎪⎝⎭B ．π,06⎛⎫ ⎪⎝⎭C ．5π,012⎛⎫- ⎪⎝⎭D ．π,03⎛⎫ ⎪⎝⎭23．（2024高一下·全国·单元测试）下列说法中正确的是（ ）A ．对于定义在实数R 上的函数()f x 中满足()()2f x f x +=，则函数()f x 是以2为周期的函数B ．函数()πtan 3f x x ⎛⎫=+ ⎪⎝⎭的单调递增区间为5πππ,π66k k ⎛⎫-++ ⎪⎝⎭，Zk ∈C ．函数()πsin 2f x x ⎛⎫=+ ⎪⎝⎭为奇函数D ．角a的终边上一点坐标为(-，则cos a =24．（2024高一下·广东佛山·阶段练习）已知函数()π7tan 23f x x ⎛⎫=+ ⎪⎝⎭，则（ ）A．π6f ⎛⎫=- ⎪⎝⎭B ．π6f x ⎛⎫- ⎪⎝⎭为奇函数C ．()f x 图象的对称中心为()ππ,0Z 68k k ⎛⎫-+∈ ⎪⎝⎭D ．()f x 的定义域为ππ,Z 122k xx k ⎧⎫≠+∈⎨⎬⎩⎭∣三、填空题25．（2024高一下·辽宁锦州·期中）()tan sin 1f x x x =++，若()22f =，则()2f -= ．26．（2024高一下·广东阳江·期末）已知πtan 4a ⎛⎫+= ⎪⎝⎭a = ．27．（2024高一下·上海徐汇·期中）函数2()tan tan 2,,44f x x x x ππ⎡⎤=+-∈-⎢⎥⎣⎦的值域是28．（2024高二上·广西崇左·开学考试）若函数πtan 23y x k ⎛⎫=-+ ⎪⎝⎭，π0,6x ⎛⎫∈ ⎪⎝⎭的图象都在x 轴上方，则实数k 的取值范围为 .29．（2024高一下·上海·课后作业）函数2tan 2tan ,,64⎡⎤=+∈-⎢⎥⎣⎦y x x x ππ的值域为．30．（2024高一·全国·课后作业）若函数()tan f x x =在区间ππ,32a a ⎛⎫- ⎪⎝⎭上是增函数，则实数a 的取值范围是 ．31．（2024高一·上海·专题练习）函数2tan 4tan 1y x x =+-的值域为32．（2024高一下·上海静安·期中）函数ππtan 63y x ⎛⎫=+ ⎪⎝⎭的定义域是．33．（2024高一下·湖北·期中）已知函数()πππ,222ππtan ,22a x x x f x x x ⎧+£-³ïï=⎨ï-<<ï⎩或，若函数()3π2y f f x ⎡⎤=-⎣⎦有5个零点，则实数a 的取值范围是 ．34．（2024高一下·全国·课后作业）已知函数tan y x ω=-在ππ,22⎛⎫- ⎪⎝⎭内是减函数，则ω的取值范围是 ．35．（2024高一上·江苏徐州·期末）已知函数()()tan 4f x nx n π⎛⎫=-∈ ⎪⎝⎭Z 在区间3,88ππ⎛⎫ ⎪⎝⎭上是减函数，则n 的取值集合为 .（用列举法表示）36．（2024·全国·模拟预测）若函数tan 4y x πω⎛⎫=+ ⎪⎝⎭在,33ππ⎡⎤-⎢⎥⎣⎦上单调递减，且在,33ππ⎡⎤-⎢⎥⎣⎦上的最大值为ω=.37．（2024高一下·上海浦东新·期中）若函数tan()y x ω=在,44ππ⎡⎤-⎢⎥⎣⎦上为严格减函数，则实数ω的取值范围是 ．四、解答题38．（2024高一·全国·课后作业）已知()tan 23f x x π⎛⎫=+ ⎪⎝⎭.（1）求()f x 的最小正周期；（2）若()f x ϕ+是奇函数，则ϕ应满足什么条件？并求出满足||2ϕπ<的ϕ值.39．（2024高一下·辽宁抚顺·期中）已知函数()()π2tan 08f x x ωω⎛⎫=+> ⎪⎝⎭的最小正周期为π2，(1)求()f x 图象的对称中心；(2)求不等式()2f x >-在5π3π,1616⎛⎫- ⎪⎝⎭上的解集．40．（2024高一·全国·课堂例题）画出函数1π2tan 24y x ⎛⎫=- ⎪⎝⎭在[0,2π] x ∈上的简图．41．（2024高一下·江西抚州·阶段练习）设函数()()πtan 0,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭，已知函数()y f x =的图象与x 轴相邻两个交点的距离为π2，且图象关于点π,08M ⎛⎫- ⎪⎝⎭对称.(1)求()f x 的单调区间；(2)求不等式()1f x -££的解集.42．（2024高一·全国·课后作业）已知函数()y f x =，其中()()tan f x A x ωϕ=+，（0ω>，π2ϕ<），()y f x =的部分图像如下图．(1)求A ，ω，ϕ的值；(2)求()y f x =的单调增区间，43．（2024高一下·上海·课后作业）已知函数()()0xf x πωω=>．（1）当4ω=时，求()f x 的最小正周期及单调区间；（2）若()3f x …在,34x ππ⎡⎤∈-⎢⎥⎣⎦上恒成立，求ω的取值范围．44．（2024高一·全国·课后作业）已知函数π()tan 3f x x ω⎛⎫=+ ⎪⎝⎭，0ω>．(1)若2ω=，求()f x 的最小正周期与函数图像的对称中心；(2)若()f x 在[]0,π上是严格增函数，求ω的取值范围；(3)若方程()f x =在[],a b 上至少存在2022个根，且b －a 的最小值不小于2022，求ω的取值范围．45．（2024高一下·上海虹口·期末）已知函数()πtan 3f x x ω⎛⎫=+ ⎪⎝⎭，其中0ω>.(1)若2ω=，求函数()f x 的最小正周期以及函数图象的对称中心；(2)若()f x 在闭区间[]0,π上是严格增函数，求正实数ω的取值范围.。

(2)已知集合A＝{0，m，m2－3m＋2}，且2∈A，则实数m的值为
A.2
√B.3
C.0
D.－2
因为集合A＝{0，m，m2－3m＋2}，且2∈A， 则m＝2或m2－3m＋2＝2，解得m∈{0,2,3}. 当m＝0时，集合A中的元素不满足互异性； 当m＝2时，m2－3m＋2＝0，集合A中的元素不满足互异性； 当m＝3时，A＝{0,3,2}，符合题意.综上所述，m＝3.
知识梳理
3.集合的基本运算
表示 运算
集合语言
并集 _{_x_|x_∈__A_，__或__x_∈__B_}_
交集 _{_x_|x_∈__A_，__且__x_∈__B_}_
补集 _{_x_|x_∈__U__，__且__x∉_A__}_
图形语言
记法 _A__∪__B_ _A__∩__B_
_∁_U_A_
常用结论
例5 (多选)群论是代数学的分支学科，在抽象代数中具有重要地位，且 群论的研究方法也对抽象代数的其他分支有重要影响，例如一元五次及 以上的方程没有根式解就可以用群论知识证明.群的概念则是群论中最基 本的概念之一，其定义如下：设G是一个非空集合，“·”是G上的一个代 数运算，即对所有的a，b∈G，有a·b∈G，如果G的运算还满足：①∀a， b，c∈G，有(a·b)·c＝a·(b·c)；②∃e∈G，使得∀a∈G，有e·a＝a·e＝a； ③∀a∈G，∃b∈G，使a·b＝b·a＝e，则称G关于“·”构成一个群.
1.若集合A有n(n≥1)个元素，则集合A有2n个子集，2n－1个真子集. 2.空集是任何集合的子集，是任何非空集合的真子集. 3.A∩B＝A⇔A⊆B，A∪B＝A⇔B⊆A. 4.∁U(A∩B)＝(∁UA)∪(∁UB)，∁U(A∪B)＝(∁UA)∩(∁UB).

第85讲计数原理知识梳理知识点1、分类加法计数原理完成一件事，有n 类办法，在第1类办法中有1m 种不同的办法，在第2类办法中有2m 种不同的方法，…，在第n 类办法中有n m 种不同的方法，那么完成这件事共有：12n N m m m =+++ 种不同的方法．知识点2、分步乘法计数原理完成一件事，需要分成n 个步骤，做第1步有1m 种不同的方法，做第2步有2m 种不同的方法，…，做第n 步有n m 种不同的方法，那么完成这件事共有：12n N m m m =⋅⋅⋅ 种不同的方法．注意：两个原理及其区别分类加法计数原理和“分类”有关，如果完成某件事情有n 类办法，这n 类办法之间是互斥的，那么求完成这件事情的方法总数时，就用分类加法计数原理．分步乘法计数原理和“分步”有关，是针对“分步完成”的问题．如果完成某件事情有n 个步骤，而且这几个步骤缺一不可，且互不影响（独立），当且仅当依次完成这n 个步骤后，这件事情才算完成，那么求完成这件事情的方法总数时，就用分步乘法计数原理．当然，在解决实际问题时，并不一定是单一应用分类计数原理或分步计数原理，有时可能同时用到两个计数原理．即分类时，每类的方法可能运用分步完成；而分步后，每步的方法数可能会采取分类的思想求方法数．对于同一问题，我们可以从不同的角度去处理，从而得到不同的解法（但方法数相同），这也是检验排列组合问题的很好方法．知识点3、两个计数原理的综合应用如果完成一件事的各种方法是相互独立的，那么计算完成这件事的方法数时，使用分类计数原理．如果完成一件事的各个步骤是相互联系的，即各个步骤都必须完成，这件事才告完成，那么计算完成这件事的方法数时，使用分步计数原理．必考题型全归纳题型一：分类加法计数原理的应用例1．（2024·全国·高三专题练习）如果一条直线与一个平面垂直，那么称此直线与平面构成一个“正交线面对”.在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是（）A．48B．18C．24D．36例2．（2024·四川成都·双流中学校考模拟预测）如图，小黑圆表示网络的结点，结点之间的连线表示它们有网线相连．连线上标注的数字表示该段网线单位时间内可以通过的最大信息量．现从结点A向结点B传递信息（）A．26B．24C．20D．19例3．（2024·江苏镇江·高三扬中市第二高级中学校考阶段练习）定义：“各位数字之和为7的四位数叫好运数”，比如1006，2203，则所有好运数的个数为（）A．82B．83C．84D．85变式1．（2024·全国·高三专题练习）从1，2，3，4，5，6中选取4个数字，组成各个数位上的数字既不全相同，也不两两互异的四位数，记四位数中各个数位上的数字从左往右依次≤≤≤，则满足条件的四位数的个数为.为a，b，c，d，且要求a b c d变式2．（2024·全国·高三专题练习）已知直线方程0Ax By +=，若从0、1、2、3、5、7这六个数中每次取两个不同的数分别作为A 、B 的值，则0Ax By +=可表示条不同的直线．变式3．（2024·辽宁·高三校联考开学考试）某迷宫隧道猫爬架如图所示，B ，C 为一个长方体的两个顶点，A ，B 是边长为3米的大正方形的两个顶点，且大正方形由完全相同的9小正方形拼成.若小猫从A 点沿着图中的线段爬到B 点，再从B 点沿着长方体的棱爬到C 点，则小猫从A 点爬到C 点可以选择的最短路径共有条.【解题方法总结】分类标准的选择（1）应抓住题目中的关键词、关键元素、关键位置．根据题目特点恰当选择一个分类标准．（2）分类时应注意完成这件事情的任何一种方法必须属于某一类，并且分别属于不同种类的两种方法是不同的方法，不能重复，但也不能有遗漏．题型二：分步乘法计数原理的应用例4．（2024·广东深圳·高三校考阶段练习）甲、乙、丙3个公司承包6项不同的工程，甲承包1项，乙承包2项，丙承包3项，则共有种承包方式（用数字作答）.例5．（2024·全国·高三专题练习）若一个三位数同时满足：①各数位的数字互不相同；②任意两个数位的数字之和不等于9，则这样的三位数共有个．(结果用数字作答)例6．（2024·安徽亳州·高三蒙城第一中学校考阶段练习）将3名男生，2名女生排成一排，要求男生甲必须站在中间，2名女生必须相邻的排法种数有（）A ．4种B ．8种C ．12种D ．48种变式4．（2024·四川成都·高三统考开学考试）“数独九宫格”原创者是18世纪的瑞士数学家欧拉，它的游戏规则很简单，将1到9这九个自然数填到如图所示的小九宫格的9个空格里，每个空格填一个数，且9个空格的数字各不相同，若中间空格已填数字5，且只填第二行和第二列，并要求第二行从左至右及第二列从上至下所填的数字都是从小到大排列的，则不同的填法种数为（）A．72B．108C．144D．196变式5．（2024·全国·高三专题练习）三棱柱各面所在平面将空间分成不同部分的个数为（）A．18B．21C．24D．27变式6．（2024·河北石家庄·高三校联考期中）临近春节，某校书法爱好小组书写了若干副春联，准备赠送给四户孤寡老人．春联分为长联和短联两种，无论是长联或短联，内容均不相同．经过调查，四户老人各户需要1副长联，其中乙户老人需要1副短联，其余三户各要2副短联．书法爱好小组按要求选出11副春联，则不同的赠送方法种数为（）A．15120B．7560C．12520D．12160变式7．（2024·北京东城·高三北京市广渠门中学校考开学考试）鱼缸里有8条热带鱼和2条冷水鱼，为避免热带鱼咬死冷水鱼，现在把鱼缸出孔打开，让鱼随机游出，每次只能游出1条，直至2条冷水鱼全部游出就关闭出孔，若恰好第3条鱼游出后就关闭了出孔，则不同游出方案的种数为（）A．16B．32C．36D．48变式8．（2024·湖南·高三临澧县第一中学校联考开学考试）在如图所示的表格中填写1，2，3三个数字，要求每一行、每一列均有这3个数字，则不同的填法种数为（）．A．6B．9C．12D．18变式9．（2024·黑龙江佳木斯·高三校考开学考试）甲、乙分别从4门不同课程中选修1门，且2人选修的课程不同，则不同的选法有（）种．A．6B．8C．12D．16变式10．（2024·陕西西安·西安市第三十八中学校考模拟预测）从六人（含甲）中选四人完成四项不同的工作（含翻译），则甲被选且甲不参加翻译工作的不同选法共有（）A．120种B．150种C．180种D．210种变式11．（2024·贵州黔东南·凯里一中校考模拟预测）某足球比赛有A，B，C，D，E，F，G，H，J共9支球队，其中A，B，C为第一档球队，D，E，F为第二档球队，G，H，J为第三档球队，现将上述9支球队分成3个小组，每个小组3支球队，若同一档位的球队不能出现在同一个小组中，则不同的分组方法有（）A．27种B．36种C．72种D．144种【解题方法总结】利用分步乘法计数原理解题的策略（1）明确题目中的“完成这件事”是什么，确定完成这件事需要几个步骤，且每步都是独立的．（2）将这件事划分成几个步骤来完成，各步骤之间有一定的连续性，只有当所有步骤都完成了，整个事件才算完成．题型三：两个计数原理的综合应用例7．（2024·全国·高三专题练习）第31届世界大学生夏季运动会于6月26日至7月7日在成都举办，现在从6男4女共10名青年志愿者中，选出3男2女共5名志愿者，安排到编号为1、2、3、4、5的5个赛场，每个赛场只有一名志愿者，其中女志愿者甲不能安排在编号为1、2的赛场，编号为2的赛场必须安排女志愿者，那么不同安排方案有（）A．1440种B．2352种C．2880种D．3960种例8．（2024·江苏南京·高三校联考阶段练习）从2位男生，3位女生中安排3人到三个场馆做志愿者，每个场馆各1人，且至少有1位男生入选，则不同安排方法有（）种A．16B．36C．54D．96例9．（2024·上海黄浦·高三上海市敬业中学校考开学考试）三位同学参加跳高、跳远、铅球项目的比赛，若每人只选择一个项目，则同一个项目最多只有2人参赛的情况共有种．变式12．（2024·广东·高三河源市河源中学校联考阶段练习）现有5名同学从北京、上海、深圳三个路线中选择一个路线进行研学活动，每个路线至少1人，至多2人，其中甲同学不选深圳路线，则不同的路线选择方法共有种．（用数字作答）变式13．（2024·浙江·高三舟山中学校联考开学考试）杭州亚运会举办在即，主办方开始对志愿者进行分配．已知射箭场馆共需要6名志愿者，其中3名会说韩语，3名会说日语．目前可供选择的志愿者中有4人只会韩语，5人只会日语，另外还有1人既会韩语又会日语，则不同的选人方案共有种．（用数字作答）．变式14．（2024·江苏扬州·高三仪征中学校考阶段练习）已知如图所示的电路中，每个开关都有闭合、不闭合两种可能，因此5个开关共有52种可能，在这52种可能中，电路从P到Q接通的情况有种．变式15．（2024·湖北·高三校联考开学考试）从5男3女共8名学生中选出组长1人，副组长1人，普通组员3人组成5人志愿组，要求志愿组中至少有3名男生，且组长和副组长性别不同，则共有种不同的选法.（用数字作答）变式16．（2024·湖北·高三校联考阶段练习）有两个家庭共8人暑假到新疆结伴旅游（每个家庭包括一对夫妻和两个孩子），他们在乌鲁木齐租了两辆不同的汽车进行自驾游，每辆汽车乘坐4人，要求每对夫妻乘坐同一辆汽车，且该车上至少有一个该夫妻自己的孩子，则满足条件的不同乘车方案种数为.变式17．（2024·福建福州·高三统考开学考试）“二十四节气”是中国古代劳动人民伟大的智慧结晶，其划分如图所示．小明打算在网上搜集一些与二十四节气有关的古诗．他准备在春季的6个节气与夏季的6个节气中共选出3个节气，若春季的节气和夏季的节气各至少选出1个，则小明选取节气的不同情况的种数是（）A．90B．180C．270D．360【解题方法总结】利用两个计数原理解题时的三个注意点（1）当题目无从下手时，可考虑要完成的这件事是什么，即怎样做才算完成这件事．（2）分类时，标准要明确，做到不重不漏，有时要恰当画出示意图或树状图．（3）对于复杂问题，一般是先分类再分步。

第84讲成对数据的统计分析知识梳理知识点一、变量间的相关关系1、变量之间的相关关系当自变量取值一定时，因变量的取值带有一定的随机性，则这两个变量之间的关系叫相关关系．由于相关关系的不确定性，在寻找变量之间相关关系的过程中，统计发挥着非常重要的作用．我们可以通过收集大量的数据，在对数据进行统计分析的基础上，发现其中的规律，对它们的关系作出判断．注意：相关关系与函数关系是不同的，相关关系是一种非确定的关系，函数关系是一种确定的关系，而且函数关系是一种因果关系，但相关关系不一定是因果关系，也可能是伴随关系．2、散点图将样本中的n 个数据点(,)(1,2,,)i i x y i n =⋅⋅⋅描在平面直角坐标系中，所得图形叫做散点图．根据散点图中点的分布可以直观地判断两个变量之间的关系．（1）如果散点图中的点散布在从左下角到右上角的区域内，对于两个变量的这种相关关系，我们将它称为正相关，如图（1）所示；（2）如果散点图中的点散布在从左上角到右下角的区域内，对于两个变量的这种相关关系，我们将它称为负相关，如图（2）所示．3、相关系数若相应于变量x 的取值i x ，变量y 的观测值为(1)i y i n ≤≤，则变量x 与y的相关系数()nnii iixx y y x ynx yr ---==∑∑通常用r 来衡量x 与y 之间的线性关系的强弱，r 的范围为11r -≤≤．（1）当0r >时，表示两个变量正相关；当0r <时，表示两个变量负相关．（2）r 越接近1，表示两个变量的线性相关性越强；r 越接近0，表示两个变量间几乎不存在线性相关关系．当||1r =时，所有数据点都在一条直线上．（3）通常当0.75r >时，认为两个变量具有很强的线性相关关系．知识点二、线性回归1、线性回归线性回归是研究不具备确定的函数关系的两个变量之间的关系（相关关系）的方法．对于一组具有线性相关关系的数据（x 1，y 1），（x 2，y 2），…，（x n ，y n ），其回归方程y bx a =+ 的求法为1122211()()nni i i ii i nni i i i x x y y x ynx yb x x x nxa y bx====⎧---⎪⎪==⎪⎨--⎪⎪=-⎪⎩∑∑∑∑ 其中，11n i i x x n ==∑，11ni i y y n ==∑，（x ，y ）称为样本点的中心．2、残差分析对于预报变量y ，通过观测得到的数据称为观测值i y ，通过回归方程得到的 y 称为预测值，观测值减去预测值等于残差，ˆi e称为相应于点(,)i i x y 的残差，即有ˆi e =ˆi i y y -．残差是随机误差的估计结果，通过对残差的分析可以判断模型刻画数据的效果以及判断原始数据中是否存在可疑数据等，这方面工作称为残差分析．（1）残差图通过残差分析，残差点()ˆ,i i x e比较均匀地落在水平的带状区域中，说明选用的模型比较合适，其中这样的带状区域的宽度越窄，说明模型拟合精确度越高；反之，不合适．（2）通过残差平方和21ˆ()ni i i Q y y==-∑分析，如果残差平方和越小，则说明选用的模型的拟合效果越好；反之，不合适．（3）相关指数用相关指数来刻画回归的效果，其计算公式是：22121ˆ()1()nii i n ii yyR yy ==-=--∑∑．2R 越接近于1，说明残差的平方和越小，也表示回归的效果越好．知识点三、非线性回归解答非线性拟合问题，要先根据散点图选择合适的函数类型，设出回归方程，通过换元将陌生的非线性回归方程化归转化为我们熟悉的线性回归方程．求出样本数据换元后的值，然后根据线性回归方程的计算方法计算变换后的线性回归方程系数，还原后即可求出非线性回归方程，再利用回归方程进行预报预测，注意计算要细心，避免计算错误．1、建立非线性回归模型的基本步骤：（1）确定研究对象，明确哪个是解释变量，哪个是预报变量；（2）画出确定好的解释变量和预报变量的散点图，观察它们之间的关系（是否存在非线性关系）；（3）由经验确定非线性回归方程的类型（如我们观察到数据呈非线性关系，一般选用反比例函数、二次函数、指数函数、对数函数、幂函数模型等）；（4）通过换元，将非线性回归方程模型转化为线性回归方程模型；（5）按照公式计算线性回归方程中的参数（如最小二乘法），得到线性回归方程；（6）消去新元，得到非线性回归方程；（7）得出结果后分析残差图是否有异常．若存在异常，则检查数据是否有误，或模型是否合适等．知识点四、独立性检验1、分类变量和列联表（1）分类变量：变量的不同“值”表示个体所属的不同类别，像这样的变量称为分类变量．（2）列联表：①定义：列出的两个分类变量的频数表称为列联表．②2×2列联表．一般地，假设有两个分类变量X 和Y ，它们的取值分别为{1x ，2x }和{1y ，2y }，其样本频数列联表（称为2×2列联表）为1y 2y 总计1x aba b2x cd c d+总计a c+b d+n a b c d=+++从22⨯列表中，依据a a b +与cc d+的值可直观得出结论：两个变量是否有关系．2、等高条形图（1）等高条形图和表格相比，更能直观地反映出两个分类变量间是否相互影响，常用等高条形图表示列联表数据的频率特征．（2）观察等高条形图发现a a b +与cc d+相差很大，就判断两个分类变量之间有关系．3、独立性检验计算随机变量22()()()()()n ad bc a b c d a c b d χ-=++++利用2χ的取值推断分类变量X 和Y 是否独立的方法称为χ2独立性检验．α0．100．050．0100．0050．001x α2．7063．8416．6357．87910．828【解题方法总结】常见的非线性回归模型（1）指数函数型x y ca =（0a >且1a ≠，0c >）两边取自然对数，()ln ln x y ca =，即ln ln ln y c x a =+，令ln y yx x '=⎧⎨'=⎩，原方程变为ln ln y c x a ''=+，然后按线性回归模型求出ln a ，ln c ．（2）对数函数型ln y b x a=+令ln y y x x'=⎧⎨'=⎩，原方程变为y bx a ''=+，然后按线性回归模型求出b ，a ．（3）幂函数型ny ax =两边取常用对数，()lg lg n y ax =，即lg lg lg y n x a =+，令lg lg y y x x'=⎧⎨'=⎩，原方程变为lg y nx a ''=+，然后按线性回归模型求出n ，lg a ．（4）二次函数型2y bx a=+令2y y x x'=⎧⎨'=⎩，原方程变为y bx a ''=+，然后按线性回归模型求出b ，a ．（5）反比例函数型b y a x=+型令1y y x x '=⎧⎪⎨'=⎪⎩，原方程变为y bx a ''=+，然后按线性回归模型求出b ，a ．必考题型全归纳题型一：变量间的相关关系例1．（2024·河北·高三校联考期末）下列四幅残差分析图中，与一元线性回归模型拟合精度最高的是（）A ．B．C．D ．例2．（2024·天津蓟州·高三校考开学考试）对两个变量x ，y 进行线性相关检验，得线性相关系数10.8995r =，对两个变量u ，v 进行线性相关检验，得线性相关系数20.9568r =-，则下列判断正确的是（）A ．变量x 与y 正相关，变量u 与v 负相关，变量x 与y 的线性相关性较强B ．变量x 与y 负相关，变量u 与v 正相关，变量x 与y 的线性相关性较强C ．变量x 与y 正相关，变量u 与v 负相关，变量u 与v 的线性相关性较强D ．变量x 与y 负相关，变量u 与v 正相关，变量u 与v 的线性相关性较强例3．（2024·宁夏吴忠·高三盐池高级中学校考阶段练习）在如图所示的散点图中，若去掉点P，则下列说法正确的是（）A．样本相关系数r变大B．变量x与变量y的相关程度变弱C．变量x与变量y呈正相关D．变量x与变量y的相关程度变强变式1．（2024·四川成都·高三统考阶段练习）已知建筑地基沉降预测对于保证施工安全，实现信息化监控有着重要意义．某工程师建立了四个函数模型来模拟建筑地基沉降随时间的变化趋势，并用相关指数、误差平方和、均方根值三个指标来衡量拟合效果．相关指数越接近1表明模型的拟合效果越好，误差平方和越小表明误差越小，均方根值越小越好．依此判断下面指标对应的模型拟合效果最好的是（）A．相关指数误差平方和均方根值0.9498.4910.499B．相关指数误差平方和均方根值0.933 4.1790.436C．相关指数误差平方和均方根值0.997 1.7010.141D．相关指数误差平方和均方根值0.997 2.8990.326变式2．（2024·高三课时练习）甲、乙、丙、丁四位同学各自对，A，B两变量的线性相关性做试验，并用回归分析方法分别求得相关系数r与残差平方和m如下表:甲乙丙丁r0.820.780.690.85m106115124103则能体现A，B两变量有更强的线性相关性的是（）A．甲B．乙C．丙D．丁变式3．（2024·河北石家庄·统考三模）观察下列四幅残差图，满足一元线性回归模型中对随机误差的假定的是（）A．B．C．D．变式4．（2024·全国·高三专题练习）甲、乙、丙、丁四位同学分别对一组变量进行线性相关试验，并分别计算出相关系数r，则线性相关程度最高的是（）甲乙丙丁r0.870.910.580.83A．甲B．乙C．丙D．丁变式5．（2024·全国·高三专题练习）给出下列有关线性回归分析的四个命题：x y；①线性回归直线未必过样本数据点的中心()②回归直线就是散点图中经过样本数据点最多的那条直线；r 时，两个变量正相关；③当相关系数0④如果两个变量的相关性越强，则相关系数r就越接近于1.其中真命题的个数为（）A．1B．2C．3D．4【解题方法总结】判定两个变量相关性的方法（1）画散点图：点的分布从左下角到右上角，两个变量正相关；点的分布从左上角到右下角，两个变量负相关．（2）样本相关系数：当r >0时，正相关；当r <0时，负相关；|r |越接近于1，相关性越强．（3）经验回归方程：当ˆ>0b时，正相关；当ˆ<0b 时，负相关．题型二：一元线性回归模型例4．（2024·天津蓟州·高三校考开学考试）为研究某种细菌在特定环境下，随时间变化的繁殖情况，得到如下实验数据：天数(x 天)3456繁殖个数(y 千个)2.5344.5由最小二乘法得y 与x 的线性回归方程为 0.7y x a=+，则当7x =时，繁殖个数y 的预测值为（）A ．4.9B ．5.25C ．5.95D ．6.15例5．（2024·湖南长沙·高三长郡中学校联考阶段练习）某社区为了丰富退休人员的业余文化生活，自2018年以来，始终坚持开展“悦读小屋读书活动”.下表是对2018年以来近5年该社区退休人员的年人均借阅量的数据统计：年份20182019202020212022年份代码x 12345年人均借阅量y （册）1y 2y 162228（参考数据：5190i i y ==∑）通过分析散点图的特征后，年人均借阅量y 关于年份代码x 的回归分析模型为 5y x m =+，则2024年的年人均借阅量约为（）A ．31B ．32C ．33D ．34例6．（2024·辽宁·辽宁实验中学校考模拟预测）已知x ，y 的对应值如下表所示：x2468y 11m +21m +33m +11若y 与x 线性相关，且回归直线方程为 1.60.6y x =+，则m =（）A ．2B ．3C ．4D ．5变式6．（2024·广西南宁·南宁二中校联考模拟预测）某单位在当地定点帮扶某村种植一种草莓，并把这种原本露天种植的草莓搬到了大棚里，获得了很好的经济效益．根据资料显示，产出的草莓的箱数x （单位：箱）与成本y （单位：千元）的关系如下：x 102030406080y1y 2y 3y 4y 5y 6y (1)根据散点图可以认为x 与y 之间存在线性相关关系，请用最小二乘法求出线性回归方程ˆˆˆybx a =+（ˆa ，ˆb 用分数表示）(2)某农户种植的草莓主要以300元/箱的价格给当地大型商超供货，多余的草莓全部以200元/箱的价格销售给当地小商贩．据统计，往年1月份当地大型商超草莓的需求量为50箱、100箱、150箱、200箱的概率分别为110，15，12，15，根据回归方程以及往年商超草莓的需求情况进行预测，求今年1月份农户草莓的种植量为200箱时所获得的利润情况．（最后结果精确到个位）附：()()61790i i i x x y y =--=∑，6154i i y ==∑，在线性回归直线方程ˆˆˆybx a =+中()()()121ˆniii nii x x y y bx x ==--=-∑∑，ˆˆay bx =-．变式7．（2024·江西·高三统考开学考试）某新能源汽车销售部对今年1月至7月的销售量进行统计与分析，因不慎丢失一些数据，现整理出如下统计表与一些分析数据：月份1月2月3月4月5月6月7月月份代号x1234567销售量y （单位：万辆）15.6m ns37.739.644.5其中31.2y =.(1)若m ，n ，s 成递增的等差数列，求从7个月的销售量中任取1个，月销售量不高于27万辆的概率；(2)若()721670.48i i y y =-=∑，x 与y 的样本相关系数0.99r =，求y 关于x 的线性回归方程ˆˆˆybx a =+，并预测今年8月份的销售量（ˆb 精确到0.1）.附：相关系数()()niix x y y r --=∑ˆˆˆybx a =+中斜率和截距的最小二乘估计公式分别为()()()121ˆniii niix x y y bx x ==--=-∑∑，ˆˆay bx =-.2.65≈25.89≈.变式8．（2024·四川成都·高三石室中学校考开学考试）已知某绿豆新品种发芽的适宜温度在6~22℃℃之间，一农学实验室研究人员为研究温度x （℃）与绿豆新品种发芽数y （颗）之间的关系，每组选取了成熟种子50颗，分别在对应的8~14℃℃的温度环境下进行实验，得到如下散点图：其中24y =，71()()70i i i x x y y =--=∑，721()=176i i y y =-∑．(1)运用相关系数进行分析说明，是否可以用线性回归模型拟合y 与x 的关系？(2)求出 y 关于 x 的线性回归方程y bx a =+$$$，并预测在19℃的温度下，种子的发芽的颗数．参考公式：相关系数()()niix x y y r --=∑y bx a =+$$$，其中121((niii nii x x y y bx x ==--=-∑∑ ，a y bx =-$$8.77≈．变式9．（2024·安徽亳州·蒙城第一中学校联考模拟预测）为调查某地区植被覆盖面积x （单位：公顷）和野生动物数量y 的关系，某研究小组将该地区等面积花分为400个区块，从中随机抽取40个区块，得到样本数据(),i i x y （1,2,,40i = ），部分数据如下：x … 2.7 3.6 3.2 3.9…y…50.663.752.154.3…经计算得：401160==∑i i x ，4012400==∑i i y ，()4021160=-=∑i i x x ，()()4011280=--=∑i i i x x y y .(1)利用最小二乘估计建立y 关于x 的线性回归方程；(2)该小组又利用这组数据建立了x 关于y 的线性回归方程，并把这两条拟合直线画在同一坐标系xOy 下，横坐标x ，纵坐标y 的意义与植被覆盖面积x 和野生动物数量y 一致.设前者与后者的斜率分别为1k ，2k ，比较1k ，2k 的大小关系，并证明.附：y 关于x 的回归方程 y abx =+ 中，斜率和截距的最小二乘估计公式分别为：1221ˆni ii nii x y nx ybxnx==-⋅=-∑∑，a y bx =-$$，ni ix y nx yr -=∑【解题方法总结】求经验回归方程的步骤题型三：非线性回归例7．（2024·湖南·校联考模拟预测）若需要刻画预报变量w 和解释变量x 的相关关系，且从已知数据中知道预报变量w 随着解释变量x 的增大而减小，并且随着解释变量x 的增大，预报变量w 大致趋于一个确定的值，为拟合w 和x 之间的关系，应使用以下回归方程中的（0b >，e 为自然对数的底数）（）A ．w bx a=+B ．ln w b x a=-+C ．w a=-D ．e xw b a-=+例8．（2024·全国·高三专题练习）云计算是信息技术发展的集中体现，近年来，我国云计算市场规模持续增长.已知某科技公司2018年至2022年云计算市场规模数据，且市场规模y与年份代码x 的关系可以用模型21e c xy c =（其中e 为自然对数的底数）拟合，设ln z y =，得到数据统计表如下：年份2018年2019年2020年2021年2022年年份代码x12345云计算市场规模y /千万元7.4112036.666.7ln z y=22.433.64由上表可得经验回归方程0.52z x a =+，则2025年该科技公司云计算市场规模y 的估计值为（）A ． 5.08e B ． 5.6e C ． 6.12e D ． 6.5e例9．（多选题）（2024·福建厦门·厦门一中校考三模）在对具有相关关系的两个变量进行回归分析时，若两个变量不呈线性相关关系，可以建立含两个待定参数的非线性模型，并引入中间变量将其转化为线性关系，再利用最小二乘法进行线性回归分析.下列选项为四个同学根据自己所得数据的散点图建立的非线性模型，且散点图的样本点均位于第一象限，则其中可以根据上述方法进行回归分析的模型有（）A ．212y c x c x=+B ．12x c y x c +=+C ．()12ln y c x c =++D ．21x c y c e+=变式10．（2024·全国·高三专题练习）已知变量的关系可以用模型e mx y k =拟合，设ln z y =，其变换后得到一组数据如下．由上表可得线性回归方程3z x a =+，则k =（）x 12345z2451014A ．3e -B ．2e -C ．2e D ．3e 变式11．（2024·全国·高三专题练习）某校课外学习小组研究某作物种子的发芽率y 和温度x （单位：C ）的关系，由实验数据得到如图所示的散点图.由此散点图判断，最适宜作为发芽率y 和温度x 的回归方程类型的是（）A ．y a bx =+B ．()20y a bx b =+>C ．e xy a b =+D ．ln y a b x=+变式12．（2024·全国·高二专题练习）兰溪杨梅从5月15日起开始陆续上市，据调查统计，得到杨梅销售价格（单位：Q 元/千克）与上市时间t （单位：天）的数据如下表所示：时间t /（单位：天）102070销售价格Q （单位：元/千克）10050100根据上表数据，从下列函数模型中选取一个描述杨梅销售价格Q 与上市时间t 的变化关系：2,,,log t b Q at b Q at bt c Q a b Q a t =+=++=⋅=⋅.利用你选取的函数模型，在以下四个日期中，杨梅销售价格最低的日期为（）A ．6月5日B ．6月15日C ．6月25日D ．7月5日变式13．（2024·四川泸州·高三四川省泸县第四中学校考开学考试）抗体药物的研发是生物技术制药领域的一个重要组成部分，抗体药物的摄入量与体内抗体数量的关系成为研究抗体药物的一个重要方面.某研究团队收集了10组抗体药物的摄入量与体内抗体数量的数据，并对这些数据作了初步处理，得到了如图所示的散点图及一些统计量的值，抗体药物摄入量为x （单位：mg ），体内抗体数量为y （单位：AU/mL ）.101i ii t z=∑101ii t=∑101ii z=∑1021ii t=∑29.2121634.4(1)根据经验，我们选择d y cx =作为体内抗体数量y 关于抗体药物摄入量x 的回归方程，将d y cx =两边取对数，得ln ln ln y c d x =+，可以看出ln x 与ln y 具有线性相关关系，试根据参考数据建立y 关于x 的回归方程，并预测抗体药物摄入量为25mg 时，体内抗体数量y 的值；(2)经技术改造后，该抗体药物的有效率z 大幅提高，经试验统计得z 服从正态分布()20.48,0.03N :，那这种抗体药物的有效率z 超过0.54的概率约为多少？附：①对于一组数据()(),1,2,,10i i u v i =L ，其回归直线 vu a β=+ 的斜率和截距的最小二乘估计分别为µ1221ni i i nii u v nuvunuβ==-=-∑∑， av u β=- ；②若随机变量()2~,Z N μσ，则有()0.6826P Z μσμσ-<<+≈，(22)0.9544P Z μσμσ-<<+≈，(33)0.9974P Z μσμσ-<<+≈；③取e 2.7≈.变式14．（2024·江西赣州·高三校考阶段练习）为了研究某种细菌随天数x 变化的繁殖个数y ，收集数据如下：天数x 123456繁殖个数y612254995190(1)在图中作出繁殖个数y 关于天数x 变化的散点图，并由散点图判断ˆˆy bxa =+（ ˆ,ab 为常数）与 21e ˆc xc y =（ 12,c c 为常数，且 120,0c c >≠）哪一个适宜作为繁殖个数y 关于天数x 变化的回归方程类型？（给出判断即可，不必说明理由）(2)对于非线性回归方程 21e ˆc xc y =（ 12,c c 为常数，且 120,0c c >≠），令ln z y =，可以得到繁殖个数的对数z 关于天数x 具有线性关系及一些统计量的值．xyz()621ii x x =-∑()()61ii i xx y y =--∑()()61ii i xx z z =--∑3.5062.83 3.5317.50596.5712.09（ⅰ）证明：“对于非线性．．．回归方程 21e ˆc x c y =，令ln z y =，可以得到繁殖个数的对数z 关于天数x 具有线性．．关系（即ˆˆˆ,ˆˆ,z x βαβα=+为常数）”；（ⅱ）根据（ⅰ）的判断结果及表中数据，建立y 关于x 的回归方程（系数保留2位小数）．附：对于一组数据()()()1122,,,,,,n n u v u v u v ，其回归直线方程ˆˆˆvu βα=+的斜率和截距的最小二乘估计分别为()()()121ˆˆˆ,niii nii u u v v v u u u βαβ==--==--∑∑．变式15．（2024·重庆沙坪坝·高三重庆八中校考阶段练习）在正常生产条件下，根据经验，可以认为化肥的有效利用率近似服从正态分布2(0.54,0.02)N ，而化肥施肥量因农作物的种类不同每亩也存在差异.(1)假设生产条件正常，记X 表示化肥的有效利用率，求(0.56)PX ≥；(2)课题组为研究每亩化肥施用量与某农作物亩产量之间的关系，收集了10组数据，并对这些数据作了初步处理，得到了如图所示的散点图及一些统计量的值.其中每亩化肥施用量为x （单位：公斤），粮食亩产量为y （单位：百公斤）参考数据：101i ii x y =∑101ii x =∑101ii y =∑1021ii x=∑101ii i t z =∑101ii t =∑101ii z =∑1021ii t=∑65091.552.51478.630.5151546.5ln i i t x =，ln (1i zi y i ==，2，⋯，10).（i ）根据散点图判断，y a bx =+与d y cx =，哪一个适宜作为该农作物亩产量y 关于每亩化肥施用量x 的回归方程（给出判断即可，不必说明理由）；（ii ）根据（i ）的判断结果及表中数据，建立y 关于x 的回归方程；并预测每亩化肥施用量为27公斤时，粮食亩产量y 的值.(e 2.7)≈附：①对于一组数据(,)(1i i u v i =，2，3，⋯，)n ，其回归直线ˆˆˆvu βα=+的斜率和截距的最小二乘估计分别为121ˆni i i nii u v nuvunu β==-=-∑∑，ˆˆˆv u αβ=-；②若随机变量2(,)X N μσ ，则()0.6827P X μσμσ-<<+≈，(22)0.9545P X μσμσ-<<+≈.变式16．（2024·重庆·高三校联考开学考试）某公司为了解年研发资金投入量x （单位:亿元）对年销售额y （单位:亿元）的影响.对公司近12年的年研发资金投入量xi 和年销售额yi 的数据，进行了对比分析，建立了两个模型:①2ˆˆy x αβ=+，②ˆˆe x t y λ+=$，其中α，β，λ，t 均为常数，e 为自然对数的底数，并得到一些统计量的值.令()2,,l 1n ,2,3,,12i i i i x i u v y =⋅⋅⋅==，经计算得如下数据:xy()1221i i x x =-∑()1221i i y y=-∑uv20667724604.20()1221ii uu=-∑()()121iii u u y y =--∑()1221ii v v =-∑()()121iii x x v v =--∑312502153.0814(1)请从相关系数的角度，分析哪一个模型拟合程度更好?(2)（ⅰ）根据分析及表中数据，建立y 关于x 的回归方程;（ⅱ）若下一年销售额y 需达到90亿元，预测下一年的研发资金投入量x 是多少亿元?附:①相关系数()()niix x y y r --=∑ˆˆy abx =+$中公式分别为()()()1122211ˆˆˆ，n niii ii i nniii i x x y y x y nx ybay b x x x xnx====---⋅===-⋅--∑∑∑∑;②参考数据： 4.499830849.4868,e 90=⨯≈≈.变式17．（2024·江苏镇江·江苏省镇江中学校考三模）经观测，长江中某鱼类的产卵数y 与温度x 有关，现将收集到的温度i x 和产卵数()1,2,,10i y i = 的10组观测数据作了初步处理，得到如图的散点图及一些统计量表.101ii x=∑101ii t=∑101ii y=∑101ii z=∑()1021ii x x =-∑36054.5136044384()1021ii tt=-∑()()101ii i tt y y =--∑()()101iii x x zz =--∑()()101iii x x y y =--∑3588326430表中1011ln ,10i i i ii t z y z z ====∑(1)根据散点图判断，,y a bx y n =+=+21e c xy c =哪一个适宜作为y 与x 之间的回归方程模型并求出y 关于x 回归方程；（给出判断即可，不必说明理由）(2)某兴趣小组抽取两批鱼卵，已知第一批中共有6个鱼卵，其中“死卵”有2个；第二批中共有8个鱼卵，其中“死卵”有3个．现随机挑选一批，然后从该批次中随机取出2个鱼卵，求取出“死卵”个数的分布列及数学期望.附：对于一组数据()()()1122,,,,,n n u v u v u v ，其回归直线v u αβ=+的斜率和截距的最小二乘估计分别为()()()121,niii nii u u v v v u u u βαβ==--==--∑∑.变式18．（2024·广西南宁·南宁三中校考一模）数据显示中国车载音乐已步入快速发展期，随着车载音乐的商业化模式进一步完善，市场将持续扩大，下表为2018－2022年中国车载音乐市场规模（单位：十亿元），其中年份2018—2022对应的代码分别为1-5．年份代码x12345车载音乐市场规模y2.83.97.312.017.0(1)由上表数据知，可用指数函数模型x y a b =⋅拟合y 与x 的关系，请建立y 关于x 的回归方程；(2)根据上述数据求得y 关于x 的回归方程后，预测2024年的中国车载音乐市场规模．参考数据：v51i ii x v=∑0.524e 0.472e 71.61.9433.82 1.7 1.626.84其中ln i i v y =，5115i i v v ==∑．参考公式：对于一组数据()11,u v ，()22,u v ，L ，(),n n u v 其回归直线ˆˆˆv u αβ=+的斜率和截距的最小二乘法估计公式分别为 121ni ii ni i u v nu vu nuβ==-⋅=-∑∑，ˆˆv u αβ=-．变式19．（2024·安徽合肥·合肥市第八中学校考模拟预测）当前移动网络已融入社会生活的方方面面，深刻改变了人们的沟通､交流乃至整个生活方式.4G 网络虽然解决了人与人随时随地通信的问题，但随着移动互联网快速发展，其已难以满足未来移动数据流量暴涨的需求，而5G 作为一种新型移动通信网络，不但可以解决人与人的通信问题，而且还可以为用户提供增强现实､虚拟现实､超高清（3D ）视频等更加身临其境的极致业务体验，更重要的是还可以解决人与物､物与物的通信问题，从而满足移动医疗､车联网､智能家居､工业控制､环境监测等物联网应用需求，为更好的满足消费者对5G 网络的需求，中国电信在某地区推出了六款不同价位的流量套餐，每款套餐的月资费x （单位：元）与购买人数y （单位：万人）的数据如下表：套餐A B C D E F 月资费x （元）384858687888购买人数y （万人）16.818.820.722.424.025.5对数据作初步的处理，相关统计量的值如下表：61iii v ω=∑61ii v=∑61ii ω=∑621ii v=∑75.324.618.3101.4其中ln ,ln i i i i v x y ω==，且绘图发现，散点()(),16i i v i ω≤≤集中在一条直线附近.(1)根据所给数据，求出y 关于x 的回归方程；(2)已知流量套餐受关注度通过指标()36x T x y +=来测定，当()8568,7e 5e T x ⎛⎫∈ ⎪⎝⎭时相应的流量套餐受大众的欢迎程度更高，被指定为“主打套餐”.现有一家四口从这六款套餐中，购买不同的四款各自使用.记四人中使用“主打套督”的人数为X ，求随机变量X 的分布列和期望.附：对于一组数据()()()1122,,,,,,n n v v v ωωω ，其回归方程bv a ω=+的斜率和截距的最小二乘估计值分别为()()()121ˆˆ,niii ni i v v ba bvv v ωωω==-⋅-==--∑∑.【解题方法总结】换元法变成一元线性回归模型题型四：列联表与独立性检验例10．（2024·广东佛山·华南师大附中南海实验高中校考模拟预测）四川省将从2022年秋季入学的高一年级学生开始实行高考综合改革，高考采用“3+1+2”模式，其中“1”为首选科目，即物理与历史二选一.某校为了解学生的首选意愿，对部分高一学生进行了抽样调查，制作出如下两个等高条形图，根据条形图信息，下列结论正确的是（）A ．样本中选择物理意愿的男生人数少于选择历史意愿的女生人数B ．样本中女生选择历史意愿的人数多于男生选择历史意愿的人数C ．样本中选择物理学科的人数较多D ．样本中男生人数少于女生人数例11．（2024·全国·高三专题练习）在新高考改革中，浙江省新高考实行的是7选3的33+模式，即语数外三门为必考科目，然后从物理、化学、生物、政治、历史、地理、技术（含信息技术和通用技术）7门课中选考3门.某校高二学生选课情况如下列联表一和列联表二（单位:人）选物理不选物理总计男生340110450女生140210350总计480320800表一选生物不选生物总计男生150300450女生150200350总计300500800表二试根据小概率值0.005α=的独立性检验，分析物理和生物选课与性别是否有关（）附:()222.n ad bc n a b c d P x a b c d a c b d αχαχ-==+++=≥++++（），（）（）（）（）α0.150.100.050.0250.010.0050.001ax 2.0722.7063.8415.0246.6357.87910.828A ．选物理与性别有关，选生物与性别有关B ．选物理与性别无关，选生物与性别有关C ．选物理与性别有关，选生物与性别无关D ．选物理与性别无关，选生物与性别无关例12．（2024·全国·高三专题练习）通过随机询问相同数量的不同性别大学生在购买食物时是否看营养说明，得知有16的男大学生“不看”，有13的女大学生“不看”，若有99%的把握认为性别与是否看营养说明之间有关，则调查的总人数可能为（）A ．150B ．170C ．240D ．175变式20．（2024·全国·高三专题练习）针对时下的“短视频热”，某高校团委对学生性别和喜欢短视频是否有关联进行了一次调查，其中被调查的男生､女生人数均为()*5m m ∈N 人，男生中喜欢短视频的人数占男生人数的45，女生中喜欢短视频的人数占女生人数的35.零假设为0H ：喜欢短视频和性别相互独立.若依据0.05α=的独立性检验认为喜欢短视频和性别不独立，则m 的最小值为（）附：()()()()()22n ad bc a b c d a c b d χ-=++++，附表：α0.050.01x α3.841 6.635A ．7B ．8C ．9D ．10变式21．（2024·全国·高三专题练习）在一次联考后，某校对甲、乙两个文科班的数学考试成绩进行分析，规定：大于或等于120分为优秀，120分以下为非优秀，统计成绩后，得到如下2×2列联表：优秀非优秀合计甲班人数50乙班人数20。

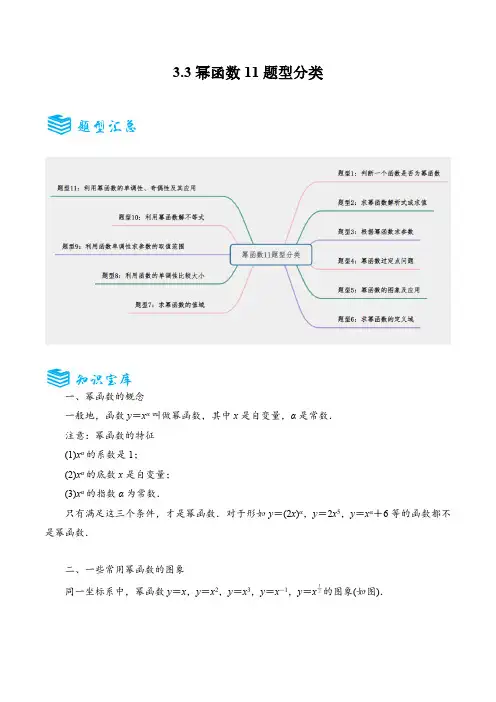
3.3幂函数11题型分类一、幂函数的概念一般地，函数y＝xα叫做幂函数，其中x是自变量，α是常数．注意：幂函数的特征(1)xα的系数是1；(2)xα的底数x是自变量；(3)xα的指数α为常数．只有满足这三个条件，才是幂函数．对于形如y＝(2x)α，y＝2x5，y＝xα＋6等的函数都不是幂函数．二、一些常用幂函数的图象同一坐标系中，幂函数y＝x，y＝x2，y＝x3，y＝x－1，y＝x的图象(如图)．三、一些常用幂函数的性质函数特征性质y＝x y＝x2y＝x3y ＝x y＝x－1定义域R R R[0，＋∞){x|x≠0}值域R[0，＋∞)R[0，＋∞){y|y≠0}奇偶性奇函数偶函数奇函数非奇非偶函数奇函数在[0，＋∞)上单调递增在(0，＋∞)上单调递减单调性在(－∞，＋∞)上单调递增在(－∞，0]上单调递减在(－∞，＋∞)上单调递增在[0，＋∞)上单调递增在(－∞，0)上单调递减注意：幂函数的性质(1)所有的幂函数在(0，＋∞)上都有定义，并且图象都过点(1,1)；(2)如果α＞0，那么幂函数的图象过原点，并且在区间[0，＋∞)上单调递增；(3)如果α＜0，那么幂函数的图象在区间(0，＋∞)上单调递减，在第一象限内，当x从右边趋向于原点时，图象在y轴右方无限接近y轴，当x从原点趋向于＋∞时，图象在x轴上方无限接近x轴；(4)在(1，＋∞)上，随幂指数的逐渐增大，图象越来越靠近y轴．（一）幂函数的概念判断一个函数是否为幂函数的方法判断一个函数是否为幂函数的依据是该函数是否为y＝xα(α为常数)的形式，即函数的解析式为一个幂的形式，且需满足：(1)指数为常数；(2)底数为自变量；(3)系数为1.C ．3D ．132-4．（2024·浙江·模拟预测）已知()f x 是幂函数，且满足：①()()f x f x -=；②()f x 在()0,+¥上单调递增，请写出符合上述条件的一个函数()f x =.2-5．（2024高一上·安徽合肥·期末）已知幂函数()f x x a = (α是常数)的图象经过点()2,4，那么f (−2)=（ ）A ．4B ．-4C ．14D ．-14题型3：根据幂函数求参数3-1．（24-25高一上·上海·单元测试）函数()12122m y m m x -=+-是幂函数，则m =．3-2．（2024高一上·湖北孝感·阶段练习）函数()2227y k k x =--是幂函数，则实数k 的值是（ ）A ．4k =B ．2k =-C ．4k =或2k =-D ．4k ¹且2k ¹-3-3．（2024高一下·上海杨浦·开学考试）已知幂函数()()22325m m f x m m x--=+-×的图像不经过原点，则实数m =.（二）幂函数的图象及应用依据图象高低判断幂指数大小，相关结论为：在(0,1]上，指数越大，幂函数图象越靠近x 轴(简记为指大图低)；在[1，＋∞)上，指数越大，幂函数图象越远离x 轴(简记为指大图高)．题型4：幂函数过定点问题4-1．（2024高一上·广东东莞·期中）函数()2y x a a =-为常数的图象过定点．4-2．（2024高一上·上海浦东新·阶段练习）幂函数a y x =的图象不可能在第四象限，但所有图象过定点，定点坐标为.题型5：幂函数的图象及应用5-1．（2024·新疆阿勒泰·三模）已知函数则函数2,0,()()()1,0,x xf xg x f xxxì³ï==-í<ïî，则函数()g x的图象大致是（）A．B．C．D．5-2．（2024·全国·模拟预测）函数()11 3x xf xx --=的图象大致为（）A．B．C．D．5-3．（2024高三·全国·对口高考）已知幂函数p qy x=（,p q ZÎ且p与q互质）的图像如图所示，则（）A ．p 、q 均为奇数且0p q<B ．p 为奇数，q 为偶数且0p q <C ．p 为奇数，q 为偶数且0p q>D ．p 为偶数，q 为奇数且0p q<5-4．（2024高一上·福建泉州·期中）已知幂函数()()2231mm f x m m x+-=--，其图像与坐标轴无交点，则实数m的值为 ．5-5．（2024高一上·黑龙江哈尔滨·期末）若点()4,2P 在幂函数()f x 的图象上，则()f x 的图象大致是（ ）A ．B ．C ．D ．5-6．（2024高三·全国·对口高考）给定一组函数解析式：①34y x =；②23y x =；③32y x -=；④23y x -=；⑤32y x =；⑥13y x -=；⑦13y x =．如图所示一组函数图象．图象对应的解析式号码顺序正确的是（ ）A ．⑥③④②⑦①⑤B ．⑥④②③⑦①⑤C ．⑥④③②⑦①⑤D ．⑥④③②⑦⑤①（三）求幂函数的定义域和值域幂函数的定义域和值域要根据解析式来确定，要保证解析式有意义，值域要在定义域范围内求解.幂函数的定义域由幂指数a 确定：①当幂指数取正整数时，定义域为R ；②当幂指数取零或负整数时，定义域为(一∞,0) U (0,+∞)；③当幂指数取分数时，可以先化成根式(在第四章会学到)，再根据根式的要求求定义域.题型6：求幂函数的定义域6-1．（2024高一·全国·课后作业）若幂函数()f x 的图象经过点(25,5)，求()f x 的定义域.6-2．（2024·上海杨浦·一模）函数()12f x x -=的定义域为．6-3．（2024高一上·浙江·期末）已知幂函数3y x a a =-，则此函数的定义域为．题型7：求幂函数的值域（四）利用幂函数的性质比较大小（1）比较幂大小的三种常用方法:(2)利用幂函数单调性比较大小时要注意的问题:比较大小的两个实数必须在同一函数的同一个单调区间内,否则无法比较大小.（五）幂函数的性质综合应用利用幂函数解不等式的步骤利用幂函数解不等式，实质是已知两个函数值的大小，判断自变量的大小，常与幂函数的单调性、奇偶性等综合命题．求解步骤如下：(1)确定可以利用的幂函数；(2)借助相应的幂函数的单调性，将不等式的大小关系，转化为自变量的大小关系；(3)解不等式(组)求参数范围，注意分类讨论思想的应用．题型10：利用幂函数解不等式10-1．（2024高三上·四川遂宁·阶段练习）若12()f x x =，则不等式()(816)f x f x >-的解集是（ ）A ．162,7éö÷êëøB ．(]0,2C ．16(,)7-¥D ．[2,+∞)10-2．（2024高一上·安徽·期中）已知幂函数()f x 的图象经过点1,93æöç÷èø，且()()12f a f +<，则a 的取值范围为（ ）A ．(),1-¥B ．()1,+¥C ．()3,1-D ．()(),31,-¥-+¥U 10-3．（2024高三上·四川绵阳·阶段练习）“1122(1)(32)a a +<-”是“223a -<<”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件10-4．（2024高一上·上海浦东新·期中）不等式()()3355252x x --+<-的解集为 ．10-5．（2024高一上·江苏盐城·阶段练习）函数12()f x x -=，则不等式(21)(1)f x f x ->+的解集为．题型11：利用幂函数的单调性、奇偶性及其应用11-1．（2024高一下·黑龙江齐齐哈尔·开学考试）已知幂函数()()22322mm f x x m ,m --+=-<<ÎΖ在区间()0,¥+上单调递增.请从如下2个条件：①对任意的x ÎR ，都有()()f x f x -=；②对任意的x ÎR ，都有()()0f x f x -+=中任选1个作为已知条件，求解下列问题.(1)求()f x 的解析式；(2)在（1）问的条件下，当[]3,3x Î-时，求()f x 的值域.（注：如果选择多个条件分别解答，按第一个解答计分.）11-2．（2024高一·全国·课后作业）已知函数：①2y x -=，②43y x =，③35y x =，④45y x -=，既是偶函数，又在(,0)-¥上为增函数的是．11-3．（2024高一上·上海杨浦·期末）已知112,1,,,1,2,322a ìüÎ---íýîþ，若幂函数()f x x a =奇函数，且在()0,¥+上为严格减函数，则a =.11-4．（2024高一上·安徽马鞍山·期中）已知幂函数()()()2157R m f x m m xm --=-+Î为奇函数.(1)求12f æöç÷èø的值；(2)若()()21f a f a +>，求实数a 的取值范围.一、单选题1．（2024高一上·四川成都·期末）函数()f x ）A ．B ．C ．D ．2．（2024高一上·青海西宁·期末）已知点()3,2a 在幂函数()()1b f x a x =-的图象上，则（ ）A ．()1f x x-=B ．()122f x x =C ．()3f x x=D ．()13f x x =3．（2024高一上·内蒙古包头·期末）已知幂函数()f x 的图象过点(，则12f æöç÷èø等于（ ）A B C D ．144．（2024·海南·模拟预测）已知()()25mf x m m x =+-为幂函数，则（ ）．A ．()f x 在(),0-¥上单调递增B ．()f x 在(),0-¥上单调递减C ．()f x 在()0,¥+上单调递增D ．()f x 在()0,¥+上单调递减5．（2024高三下·上海浦东新·阶段练习）设R m Î，若幂函数221m m y x -+=定义域为R ，且其图像关于y 轴成轴对称，则m 的值可以为（ ）A ．1B ．4C ．7D ．106．（2024高二下·陕西咸阳·期末）现有下列函数：①3y x =；②12xy æö=ç÷èø；③24y x =；④51y x =+；⑤()21y x =-；⑥y x =；⑦(1)x y a a =>，其中幂函数的个数为（ ）A ．1B ．2C ．3D ．47．（2024高一·全国·课后作业）已知幂函数()2133m y m m x +=-+的图像关于y 轴对称，则m 等于（ ）A ．1B ．2C ．1或2D ．38．（2024高三上·上海浦东新·阶段练习）如图所示是函数mn y x =（,m n 均为正整数且,m n 互质）的图象，则（ ）A ．,m n 是奇数且1mn<B ．m 是偶数，n 是奇数，且1m n<C ．m 是偶数，n 是奇数，且1m n>D ．,m n 是奇数，且1m n>9．（24-25高二下·福建莆田·期中）如图所示，图中的曲线是幂函数n y x =在第一象限的图象，已知n 取2±，12±四个值，则相应于1C ，2C ，3C ，4C 的n 依次为（ ）A ．2-，12-，12，2B ．2，12，12-，2-C ．12-，2-，2，12D ．2，12，2-，12-10．（2024高一上·安徽·期末）若幂函数()()224122m m f x m m x-+=--在区间()0,¥+上单调递减，则m =（ ）A ．3B ．1C ．1-或3D ．1或3-11．（2024高一上·重庆九龙坡·期末）已知111333332,,555a b c -æöæöæö===ç÷ç÷ç÷èøèøèø，则,,a b c 的大小关系为（ ）A ．a b c <<B ．b c a <<C ．c a b <<D ．a c b<<12．（2024高一·全国·课后作业）已知()21f x x =，若01a b <<<，则下列各式中正确的是（ ）A ．()()11f a f b f f a b æöæö<<<ç÷ç÷èøèøB ．()()11f f f b f a a b æöæö<<<ç÷ç÷èøèøC ．()()11f a f b f f b a æöæö<<<ç÷ç÷èøèøD ．()()11f f a f f b a b æöæö<<<ç÷ç÷èøèø13．（2024高一下·辽宁本溪·阶段练习）若幂函数()()224122m m f x m m x-+=--在区间()0,¥+上单调递增，则m =（ ）A ．1-B ．3C ．1-或3D ．1或3-14．（2024高一上·浙江杭州·期末）已知幂函数()()22222n nf x n n x-=+-×在()0,¥+上是减函数，则n 的值为（ ）A ．3-B ．1C ．3D ．1或3-15．（2024高一上·江西萍乡·期末）已知幂函数()f x 的图像过点()64,4，则()8f 的值为（ ）A ．2B ．3C ．4D ．516．（2024高一上·云南德宏·期末）下列函数既是幂函数又是奇函数的是（ ）A ．y =B ．21y x =C ．22y x =D ．1y x x=+17．（2024高一上·全国·课后作业）如图，下列3个幂函数的图象，则其图象对应的函数可能是（ ）A ．①1y x -=，②12y x =，③13y x =B ．①1y x -=，②13y x =，③12y x =C ．①13y x =，②12y x =，③1y x-=D ．①13y x =，②1y x -=，③12y x =18．（2024高一下·内蒙古呼和浩特·开学考试）已知幂函数()y f x =的图象过()4,32点，则()2f =（ ）．A ．B ．4C ．D ．8二、多选题19．（2024高一下·山西忻州·开学考试）已知幂函数()()23m x m x f =-的图象过点12,4æöç÷èø，则（ ）A ．()f x 是偶函数B ．()f x 是奇函数C ．()f x 在(),0-¥上为减函数D ．()f x 在()0,¥+上为减函数20．（2024高一上·宁夏银川·期末）幂函数()()211m f x m m x --=+-，m ∈N ∗，则下列结论正确的是（ ）A ．1m =B ．函数()f x 是偶函数C ．()()23f f -<D ．函数()f x 的值域为()0,¥+21．（2024高一上·重庆长寿·期末）下列函数既是幂函数，又在(),0-¥上单调递减的是（ ）A ．y x =-B ．2y x -=C ．1y x -=D ．2y x =22．（2024高一上·云南红河·期末）已知幂函数()f x 的图象经过点(8,，则下列说法正确的是（ ）A ．函数()f x 为增函数B ．函数()f x 为偶函数C ．当4x ³时，()2f x ³D ．当120x x <<时，()()121222f x f x x x f ++æö<ç÷èø三、填空题23．（2024高一·全国·课后作业）幂函数()()2732351t t f x t t x+-=-+是偶函数，且在(0,)+¥上为增函数，则函数解析式为 ．24．（2024高一上·宁夏吴忠·期中）若()f x 是幂函数，且()124f =，则13f æö=ç÷èø25．（2024高一下·江苏南京·阶段练习）请写出一个满足条件①和②的幂函数()f x ，条件：①()f x 是偶函数；②()f x 为()0,¥+上的减函数．则()f x =．26．（2024高一上·广东肇庆·期中）已知幂函数()f x 的图象过点()3,3和()m,2，则实数m ＝ .27．（2024高一·全国·课后作业）幂函数()21N nn y x n ++=Î的图像一定经过第象限28．（2024高一上·江苏徐州·阶段练习）若幂函数()f x 过点()42，，则满足不等式()()21f a f a ->-的实数a 的取值范围是．29．（2024高一上·陕西咸阳·期末）已知幂函数()()222m f x m m x =--满足()()23f f <，则m = .30．（2024·宁夏银川·二模）已知函数()()22221m m f x m m x--=--是幂函数，且为偶函数，则实数m = ．31．（2024高一上·辽宁·期末）已知幂函数()()231m f x m m x =++在第一象限单调递减，则()f m = .32．（2024高三上·河南许昌·期末）已知函数()()21m f x m m x =+-是幂函数，且在()0,¥+上是增函数，则实数m 的值为 ．33．（2024高三下·上海杨浦·阶段练习）已知幂函数()y f x =的图像过点(9,3)，则(2)f 的值为．34．（2024高一上·江西赣州·期中）幂函数f (x )=(m 2−2m−2)x 2m−1在()0,¥+上为减函数，则m 的值为 .35．（2024高三下·上海·阶段练习）已知函数()13f x x =，则关于t 的表达式()()222210f t t f t -+-<的解集为 .36．（2024高一上·全国·课后作业）已知幂函数1101 ()f x x æö=ç÷èø，若f (a−1)<f (8−2a )，则a 的取值范围是.37．（2024高一上·浙江宁波·期中）已知幂函数()f x 过点，则满足(2)(1)f a f a ->-的实数a 的取值范围是 ．38．（2024高二下·陕西宝鸡·期末）幂函数()()226633m m f x m m x-+=-+在()0,¥+上单调递减，则m 的值为 ．四、解答题39．（2024高一上·四川眉山·期末）已知幂函数()y f x =的图象经过点1,22æöç÷èø．(1)求()f x 的解析式，并指明函数()f x 的定义域；(2)设函数()()g x x f x =+，用单调性的定义证明()g x 在()1,+¥单调递增．40．（2024高一·全国·课后作业）比较下列各组数的大小：(1)()32--，()32.5--；(2)788--，7819æö-ç÷èø；(3)3412æöç÷èø，3415æöç÷èø，1412æöç÷èø．41．（2024高一·全国·课后作业）求不等式()()2233131x x ->+的解.42．（2024高三·全国·课后作业）已知幂函数()223mm f x x --=（m 为正整数）的图像关于y 轴对称，且在()0,¥+上是严格减函数，求满足()()33132mma a --+>-的实数a 的取值范围．43．（2024高一上·福建龙岩·期末）已知幂函数()21()2910m f x m m x -=-+为偶函数，()()(R)kg x f x k x =+Î．(1)若(2)5g =，求k ；(2)已知2k £，若关于x 的不等式21()02g x k ->在[1,)+¥上恒成立，求k 的取值范围．44．（2024高一下·四川广安·阶段练习）已知幂函数()()()215R m f x m m x m +=+-Î在()0,¥+上单调递增．(1)求m 的值及函数()f x 的解析式；(2)若函数()21g x ax a =+-在[]0,2上的最大值为3，求实数a 的值．45．（2024高一上·辽宁辽阳·期末）已知幂函数()()25af x a a x =+-为奇函数．(1)求()f x 的解析式；(2)若正数,m n 满足31250m n a ++=，若不等式91b m n+³恒成立．求b 的最大值．46．（2024高一上·山东枣庄·期末）已知幂函数()()215m f x m m x -=--的图像关于y 轴对称.(1)求m 的值;(2)若函数()()g x f x =-()g x 的单调递增区间.。

立体几何中向量方法1、判断下列结论是否正确(请在括号中打“√”或“×”) (1)平面的单位法向量是唯一确定的．( ) (2)若两平面的法向量平行，则两平面平行．( ) (3)若两直线的方向向量不平行，则两直线不平行．( )(4)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角．( )(5)两异面直线夹角的范围是(0，π2]，直线与平面所成角的范围是[0，π2]，二面角的范围是[0，π]．( )(6)若二面角α－a －β的两个半平面α，β的法向量n 1，n 2所成角为θ，则二面角α－a －β的大小是π－θ.( )2、已知A (1,0,0)，B (0,1,0)，C (0,0,1)，则下列向量是平面ABC 法向量的是( ) A ．(－1,1,1)B ．(1，－1,1)C ．(－33，－33，－33) D ．(33，33，－33) 3、如图，在空间直角坐标系中有直三棱柱ABC －A 1B 1C 1，CA ＝CC 1＝2CB ，则直线BC 1与直线AB 1所成角的余弦值为( ) A.55 B.53 C.56D.544、设u ，v 分别是平面α，β的法向量，u ＝(－2,2,5)，当v ＝(3，－2,2)时，α与β的位置关系为________；当v ＝(4，－4，－10)时，α与β的位置关系为________．5、如图所示，在正方体ABCD －A 1B 1C 1D 1中，O 是底面正方形ABCD 的中心，M 是D 1D 的中点，N 是A 1B 1的中点，则直线ON ，AM 的位置关系是________． 题型一 利用空间向量证明平行问题例1如图所示，平面P AD ⊥平面ABCD ，ABCD 为正方形，△P AD 是直角三角形，且P A ＝AD ＝2，E ，F ，G 分别是线段P A ，PD ，CD 的中点．求证：PB ∥平面EFG . 引申探究本例中条件不变，证明平面EFG ∥平面PBC . 【同步练习】1、正方体ABCD －A 1B 1C 1D 1中，M ，N 分别是C 1C ，B 1C 1的中点．求证：MN ∥平面A 1BD . 题型二 利用空间向量证明垂直问题例2 如图，在多面体ABC －A 1B 1C 1中，四边形A 1ABB 1是正方形，AB ＝AC ，BC ＝2AB ，B 1C 1綊12BC ，二面角A 1－AB －C 是直二面角．求证： (1)A 1B 1⊥平面AA 1C ； (2)AB 1∥平面A 1C 1C . 【同步练习】1、如图，在四棱锥P －ABCD 中，底面ABCD 是边长为a 的正方形，侧面P AD ⊥底面ABCD ，且P A ＝PD ＝22AD ，设E ，F 分别为PC ，BD 的中点． (1)求证：EF ∥平面P AD ； (2)求证：平面P AB ⊥平面PDC .1．直线的方向向量与平面的法向量的确定(1)直线的方向向量：在直线上任取一非零向量作为它的方向向量．(2)平面的法向量可利用方程组求出：设a ，b 是平面α内两不共线向量，n 为平面α的法向量，则求法向量的方程组为⎩⎪⎨⎪⎧n ·a ＝0，n ·b ＝0. 2．用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ，与平面α共面的两个不共线向量v 1和v 2，则l ∥α或l ⊂α⇔存在两个实数x ，y ，使v ＝x v 1＋y v 2.(3)设直线l 的方向向量为v ，平面α的法向量为u ，则l ∥α或l ⊂α⇔v ⊥u . (4)设平面α和β的法向量分别为u 1，u 2，则α∥β⇔u 1∥u 2. 3．用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2＝0. (2)设直线l 的方向向量为v ，平面α的法向量为u ，则l ⊥α⇔v ∥u . (3)设平面α和β的法向量分别为u 1和u 2，则α⊥β⇔u 1⊥u 2⇔u 1·u 2＝0. 4．两条异面直线所成角的求法设a ，b 分别是两异面直线l 1，l 2的方向向量，则l 1与l 2所成的角θa 与b 的夹角β范围(0，π2][0，π]求法cos θ＝|a ·b ||a ||b |cos β＝a ·b|a ||b |5.设直线l 的方向向量为a ，平面α的法向量为n ，直线l 与平面α所成的角为θ，a 与n 的夹角为β，则sin θ＝|cos β|＝|a ·n ||a ||n |. 6．求二面角的大小(1)如图①，AB ，CD 分别是二面角α－l －β的两个面内与棱l 垂直的直线，则二面角的大小θ＝〈AB →，CD →〉．(2)如图②③，n 1，n 2分别是二面角α－l －β的两个半平面α，β的法向量，则二面角的大小θ满足|cos θ|＝|cos 〈n 1，n 2〉|，二面角的平面角大小是向量n 1与n 2的夹角(或其补角)．题型三 利用空间向量求空间角命题点1 求直线和平面所成的角例3 如图1，在Rt △ACB 中，∠C ＝90°，BC ＝3，AC ＝6，D ，E 分别是AC ，AB 上的点，且DE ∥BC ，DE ＝2，将△ADE 沿DE 折起到△A 1DE 的位置，使A 1C ⊥CD ，如图2. (1)求证：A 1C ⊥平面BCDE ；(2)若M 是A 1D 上的点，试确定点M 的位置，使得直线CM 与平面A 1BE 所成角的正弦值为51428.命题点2 求二面角例4 已知点E ，F 分别在正方体ABCD －A 1B 1C 1D 1的棱BB 1，CC 1上，且B 1E ＝2EB ，CF ＝2FC 1，则平面AEF 与平面ABCD 所成的二面角的正切值为________． 【同步练习】1、如图，四棱锥P-ABCD 中，P A ⊥底面ABCD ，AD ∥BC ，AB ＝AD ＝AC ＝3，P A ＝BC ＝4，M 为线段AD 上一点，AM ＝2MD ，N 为PC 的中点． (1)证明MN ∥平面P AB ；(2)求直线AN 与平面PMN 所成角的正弦值．2、如图1所示，正△ABC 的边长为4，CD 是AB 边上的高，E ，F 分别是AC 和BC 边的中点，现将△ABC 沿CD 翻折成直二面角A －DC －B ，如图2所示． (1)试判断直线AB 与平面DEF 的位置关系，并说明理由； (2)求二面角E －DF －C 的余弦值；(3)在线段BC 上是否存在一点P ，使AP ⊥DE ？证明你的结论． 一、证明垂直问题的方法重点题型训练(1)利用已知的线面垂直关系构建空间直角坐标系，准确写出相关点的坐标，从而将几何证明转化为向量运算．其中灵活建系是解题的关键．(2)其一证明直线与直线垂直，只需要证明两条直线的方向向量垂直；其二证明线面垂直，只需证明直线的方向向量与平面内不共线的两个向量垂直即可，当然 ，也可证直线的方向向量与平面的法向量平行；其三证明面面垂直：①证明两平面的法向量互相垂直；②利用面面垂直的判定定理，只要能证明一个平面内的一条直线的方向向量为另一个平面的法向量即可． 二、利用向量法求空间角的方法(1)先求出直线的方向向量和平面的法向量，将求空间角转化为求两个向量的夹角．(2)利用数量积求向量的夹角，然后根据和所求角的关系得到空间角，但要注意所求角的大小． 1．若平面α，β的法向量分别是n 1＝(2，－3,5)，n 2＝(－3,1，－4)，则( ) A ．α∥βB ．α⊥βC ．α，β相交但不垂直D ．以上答案均不正确2．已知平面α内有一点M (1，－1,2)，平面α的一个法向量为n ＝(6，－3,6)，则下列点P 中，在平面α内的是( ) A ．P (2,3,3) B ．P (－2,0,1) C ．P (－4,4,0)D ．P (3，－3,4)3．若AB →＝λCD →＋μCE →，则直线AB 与平面CDE 的位置关系是( ) A ．相交 B ．平行C ．在平面内D ．平行或在平面内4．设u ＝(－2,2，t )，v ＝(6，－4,4)分别是平面α，β的法向量．若α⊥β，则t 等于( ) A ．3 B ．4 C ．5 D ．65．如图所示，在正方体ABCD －A 1B 1C 1D 1中，棱长为a ，M ，N 分别为A 1B 和AC 上的点，A 1M ＝AN ＝2a3，则MN 与平面BB 1C 1C 的位置关系是( )A ．斜交B ．平行C ．垂直D ．MN 在平面BB 1C 1C 内6．在正方体ABCD －A 1B 1C 1D 1中，点E 为BB 1的中点，则平面A 1ED 与平面ABCD 所成的锐二面角的余弦值为( ) A.12 B.23 C.33 D.227．已知平面α内的三点A (0，0，1)，B (0,1,0)，C (1,0,0)，平面β的一个法向量n ＝(－1，－1，－1)，则不重合的两个平面α与β的位置关系是_______________．8．已知点P 是平行四边形ABCD 所在的平面外一点，如果AB →＝(2，－1，－4)，AD →＝(4,2,0)，AP →＝(－1,2，－1)．对于结论：①AP ⊥AB ；②AP ⊥AD ；③AP →是平面ABCD 的法向量；④AP →∥BD →.其中正确的是________．9.如图，正方体ABCD-A 1B 1C 1D 1的棱长为1，E ，F 分别是棱BC ，DD 1上的点，如果B 1E ⊥平面ABF ，则CE 与DF 的和的值为________．*10.如图，圆锥的轴截面SAB 是边长为2的等边三角形，O 为底面中心，M 为SO 中点，动点P 在圆锥底面内(包括圆周)．若AM ⊥MP ，则点P 形成的轨迹长度为________．11．如图所示，已知直三棱柱ABC —A 1B 1C 1中，△ABC 为等腰直角三角形，∠BAC ＝90°，且 AB ＝AA 1，D ，E ，F 分别为B 1A ，C 1C ，BC 的中点．求证： (1)DE ∥平面ABC ；(2)B 1F ⊥平面AEF .12．在平面四边形ABCD 中，AB ＝BD ＝CD ＝1，AB ⊥BD ，CD ⊥BD .将△ABD 沿BD 折起，使得平面ABD ⊥平面BCD ，如图所示．(1)求证：AB ⊥CD ；(2)若M 为AD 中点，求直线AD 与平面MBC 所成角的正弦值．*13.如图，长方体ABCD —A 1B 1C 1D 1中，AB ＝2，BC ＝CC 1＝1，点P 是CD 上的一点，PC ＝λPD . (1)若A 1C ⊥平面PBC 1，求λ的值；(2)设λ1＝1，λ2＝3所对应的点P 为P 1，P 2，二面角P 1—BC 1—P 2的大小为θ，求cos θ的值．立体几何中向量方法1、判断下列结论是否正确(请在括号中打“√”或“×”) (1)平面的单位法向量是唯一确定的．( × ) (2)若两平面的法向量平行，则两平面平行．( √ ) (3)若两直线的方向向量不平行，则两直线不平行．( √ )(4)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角．( × )(5)两异面直线夹角的范围是(0，π2]，直线与平面所成角的范围是[0，π2]，二面角的范围是[0，π]．( √ )(6)若二面角α－a －β的两个半平面α，β的法向量n 1，n 2所成角为θ，则二面角α－a －β的大小是π－θ.( × )2、已知A (1,0,0)，B (0,1,0)，C (0,0,1)，则下列向量是平面ABC 法向量的是( ) A ．(－1,1,1)B ．(1，－1,1)C ．(－33，－33，－33) D ．(33，33，－33) 答案 C解析 设n ＝(x ，y ，z )为平面ABC 的法向量， 则⎩⎪⎨⎪⎧n ·AB →＝0，n ·AC →＝0，化简得⎩⎪⎨⎪⎧－x ＋y ＝0，－x ＋z ＝0，∴x ＝y ＝z .故选C.3、如图，在空间直角坐标系中有直三棱柱ABC －A 1B 1C 1，CA ＝CC 1＝2CB ，则直线BC 1与直线AB 1所成角的余弦值为( ) A.55B.53C.56D.54答案 A解析 设CA ＝2，则C (0,0,0)，A (2,0,0)，B (0,0,1)，C 1(0,2,0)，B 1(0,2,1)，可得向量AB 1→＝(－2,2,1)，BC 1→＝(0,2，－1)，由向量的夹角公式得cos 〈AB 1→，BC 1→〉＝0＋4－14＋4＋1×0＋4＋1＝15＝55，故选A. 4、设u ，v 分别是平面α，β的法向量，u ＝(－2,2,5)，当v ＝(3，－2,2)时，α与β的位置关系为________；当v ＝(4，－4，－10)时，α与β的位置关系为________． 答案 α⊥β α∥β解析 当v ＝(3，－2,2)时，u ·v ＝(－2,2,5)·(3，－2,2)＝0⇒α⊥β. 当v ＝(4，－4，－10)时，v ＝－2u ⇒α∥β.5、如图所示，在正方体ABCD －A 1B 1C 1D 1中，O 是底面正方形ABCD 的中心，M 是D 1D 的中点，N 是A 1B 1的中点，则直线ON ，AM 的位置关系是________．答案 垂直解析 以A 为原点，分别以AB →，AD →，AA 1→所在直线为x ，y ，z 轴，建立空间直角坐标系，设正方体棱长为1，则A (0,0,0)，M (0,1，12)，O (12，12，0)，N (12，0,1)，AM →·ON →＝(0,1，12)·(0，－12，1)＝0， ∴ON 与AM 垂直． 无题型一 利用空间向量证明平行问题例1如图所示，平面P AD ⊥平面ABCD ，ABCD 为正方形，△P AD 是直角三角形，且P A ＝AD ＝2，E ，F ，G 分别是线段P A ，PD ，CD 的中点．求证：PB ∥平面EFG . 证明 ∵平面P AD ⊥平面ABCD ，ABCD 为正方形， △P AD 是直角三角形，且P A ＝AD ，∴AB ，AP ，AD 两两垂直，以A 为坐标原点，建立如图所示的空间直角坐标系Axyz ， 则A (0,0,0)，B (2，0,0)，C (2,2,0)，D (0,2,0)，P (0，0,2)，E (0,0,1)，F (0,1,1)，G (1，2,0)． ∴PB →＝(2,0，－2)，FE →＝(0，－1,0)，FG →＝(1,1，－1)， 设PB →＝sFE →＋tFG →，即(2,0，－2)＝s (0，－1,0)＋t (1,1，－1)， ∴⎩⎪⎨⎪⎧t ＝2，t －s ＝0，－t ＝－2，解得s ＝t ＝2，∴PB →＝2FE →＋2FG →，又∵FE →与FG →不共线，∴PB →，FE →与FG →共面． ∵PB ⊄平面EFG ，∴PB ∥平面EFG . 引申探究本例中条件不变，证明平面EFG ∥平面PBC . 证明 ∵EF →＝(0,1,0)，BC →＝(0,2,0)， ∴BC →＝2EF →，∴BC ∥EF .又∵EF ⊄平面PBC ，BC ⊂平面PBC ， ∴EF ∥平面PBC ，同理可证GF ∥PC ，从而得出GF ∥平面PBC . 又EF ∩GF ＝F ，EF ⊂平面EFG ，GF ⊂平面EFG ， ∴平面EFG ∥平面PBC . 【同步练习】1、正方体ABCD －A 1B 1C 1D 1中，M ，N 分别是C 1C ，B 1C 1的中点．求证：MN ∥平面A 1BD . 证明 如图所示，以D 为坐标原点，DA ，DC ，DD 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系． 设正方体的棱长为1，则M (0,1，12)，N (12，1,1)，D (0,0,0)，A 1(1,0,1)，B (1,1,0)，于是MN →＝(12，0，12)，DA 1→＝(1,0,1)，DB →＝(1,1,0)．设平面A 1BD 的法向量为n ＝(x ，y ，z )，则n ·DA 1→＝0，且n ·DB →＝0，得⎩⎪⎨⎪⎧x ＋z ＝0，x ＋y ＝0.取x ＝1，得y ＝－1，z ＝－1. 所以n ＝(1，－1，－1)．又MN →·n ＝(12，0，12)·(1，－1，－1)＝0，所以MN →⊥n .又MN ⊄平面A 1BD ，所以MN ∥平面A 1BD . 题型二 利用空间向量证明垂直问题例2 如图，在多面体ABC －A 1B 1C 1中，四边形A 1ABB 1是正方形，AB ＝AC ，BC ＝2AB ，B 1C 1綊12BC ，二面角A 1－AB －C 是直二面角．求证：(1)A 1B 1⊥平面AA 1C ；(2)AB 1∥平面A 1C 1C .证明 (1)∵二面角A 1－AB －C 是直二面角，四边形A 1ABB 1为正方形，∴AA 1⊥平面BAC .又∵AB ＝AC ，BC ＝2AB ，∴∠CAB ＝90°，即CA ⊥AB ，∴AB ，AC ，AA 1两两互相垂直．建立如图所示的空间直角坐标系，点A 为坐标原点，设AB ＝2，则A (0,0,0)，B 1(0,2,2)，A 1(0,0,2)，C (2,0,0)，C 1(1,1,2)，∴A 1B 1→＝(0,2,0)，A 1A →＝(0,0，－2)，AC →＝(2,0,0)．设平面AA 1C 的一个法向量n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·A 1A →＝0，n ·AC →＝0，即⎩⎪⎨⎪⎧ －2z ＝0，2x ＝0，即⎩⎪⎨⎪⎧ x ＝0，z ＝0，取y ＝1，则n ＝(0,1,0)．∴A 1B 1→＝2n ，即A 1B 1→∥n .∴A 1B 1⊥平面AA 1C .(2)易知AB 1→＝(0,2,2)，A 1C 1→＝(1,1,0)，A 1C →＝(2,0，－2)，设平面A 1C 1C 的一个法向量m ＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧m ·A 1C 1→＝0，m ·A 1C →＝0，即⎩⎪⎨⎪⎧x 1＋y 1＝0，2x 1－2z 1＝0，令x 1＝1，则y 1＝－1，z 1＝1，即m ＝(1，－1,1)．∴AB 1→·m ＝0×1＋2×(－1)＋2×1＝0，∴AB 1→⊥m .又AB 1⊄平面A 1C 1C ，∴AB 1∥平面A 1C 1C .【同步练习】1、如图，在四棱锥P －ABCD 中，底面ABCD 是边长为a 的正方形，侧面P AD ⊥底面ABCD ，且P A ＝PD ＝22AD ，设E ，F 分别为PC ，BD 的中点． (1)求证：EF ∥平面P AD ；(2)求证：平面P AB ⊥平面PDC .证明 (1)如图，取AD 的中点O ，连接OP ，OF .因为P A ＝PD ，所以PO ⊥AD .因为侧面P AD ⊥底面ABCD ，平面P AD ∩平面ABCD ＝AD ，所以PO ⊥平面ABCD .又O ，F 分别为AD ，BD 的中点，所以OF ∥AB .又ABCD 是正方形，所以OF ⊥AD .因为P A ＝PD ＝22AD ，所以P A ⊥PD ，OP ＝OA ＝a 2. 以O 为原点，OA ，OF ，OP 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，则A (a 2，0,0)，F (0，a 2，0)，D (－a 2，0,0)，P (0,0，a 2)，B (a 2，a,0)，C (－a 2，a,0)． 因为E 为PC 的中点，所以E (－a 4，a 2，a 4)．易知平面P AD 的一个法向量为OF →＝(0，a 2，0)， 因为EF →＝(a 4，0，－a 4)， 且OF →·EF →＝(0，a 2，0)·(a 4，0，－a 4)＝0， 所以OF ⊥EF ，又因为EF ⊄平面P AD ，所以EF ∥平面P AD .(2)因为P A →＝(a 2，0，－a 2)，CD →＝(0，－a,0)， 所以P A →·CD →＝(a 2，0，－a 2)·(0，－a,0)＝0， 所以P A ⊥CD .又P A ⊥PD ，PD ∩CD ＝D ，PD ⊂平面PDC ，CD ⊂平面PDC ，所以P A ⊥平面PDC .又P A ⊂平面P AB ，所以平面P AB ⊥平面PDC .1．直线的方向向量与平面的法向量的确定(1)直线的方向向量：在直线上任取一非零向量作为它的方向向量．(2)平面的法向量可利用方程组求出：设a ，b 是平面α内两不共线向量，n 为平面α的法向量，则求法向量的方程组为⎩⎪⎨⎪⎧n ·a ＝0，n ·b ＝0. 2．用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ，与平面α共面的两个不共线向量v 1和v 2，则l ∥α或l ⊂α⇔存在两个实数x ，y ，使v ＝x v 1＋y v 2.(3)设直线l 的方向向量为v ，平面α的法向量为u ，则l ∥α或l ⊂α⇔v ⊥u .(4)设平面α和β的法向量分别为u 1，u 2，则α∥β⇔u 1∥u 2.3．用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2＝0.(2)设直线l 的方向向量为v ，平面α的法向量为u ，则l ⊥α⇔v ∥u .(3)设平面α和β的法向量分别为u 1和u 2，则α⊥β⇔u 1⊥u 2⇔u 1·u 2＝0.4．两条异面直线所成角的求法设a ，b 分别是两异面直线l 1，l 2的方向向量，则l 1与l 2所成的角θ a 与b 的夹角β 范围 (0，π2] [0，π] 求法cos θ＝|a ·b ||a ||b | cos β＝a ·b |a ||b | 5.设直线l 的方向向量为a ，平面α的法向量为n ，直线l 与平面α所成的角为θ，a 与n 的夹角为β，则sin θ＝|cos β|＝|a ·n ||a ||n |. 6．求二面角的大小(1)如图①，AB ，CD 分别是二面角α－l －β的两个面内与棱l 垂直的直线，则二面角的大小θ＝〈AB →，CD →〉．(2)如图②③，n 1，n 2分别是二面角α－l －β的两个半平面α，β的法向量，则二面角的大小θ满足|cos θ|＝|cos 〈n 1，n 2〉|，二面角的平面角大小是向量n 1与n 2的夹角(或其补角)．题型三 利用空间向量求空间角命题点1 求直线和平面所成的角例3 如图1，在Rt △ACB 中，∠C ＝90°，BC ＝3，AC ＝6，D ，E 分别是AC ，AB 上的点，且DE ∥BC ，DE ＝2，将△ADE 沿DE 折起到△A 1DE 的位置，使A 1C ⊥CD ，如图2.(1)求证：A 1C ⊥平面BCDE ；(2)若M 是A 1D 上的点，试确定点M 的位置，使得直线CM 与平面A 1BE 所成角的正弦值为51428. (1)证明 因为∠C ＝90°，DE ∥BC ，所以BC ⊥CD ，BC ⊥A 1D ，因为CD ∩A 1D ＝D ，CD ⊂平面A 1CD ，A 1D ⊂平面A 1CD ，所以BC ⊥平面A 1CD ，因为A 1C ⊂平面A 1CD ，所以BC ⊥A 1C ，DE ⊥A 1C ，又A 1C ⊥CD ，CD ∩BC ＝C ，CD ∩DE ＝D ，DE ∥BC ，所以A 1C ⊥平面BCDE .(2)解 以C 为原点，以CB ，CD ，CA 1所在直线为x 轴，y 轴，z 轴建立空间直角坐标系(图略)，因为AD AC ＝DE CB，所以AD ＝4，CD ＝2，A 1C ＝23， 所以A 1(0,0,23)，B (3,0,0)，E (2,2,0)，D (0,2,0)，A 1E →＝(2,2，－23)，BE →＝(－1,2,0)，DA 1→＝(0，－2,23)．设M 点的坐标为(0，y 0，z 0)，DM →＝λDA 1→，则⎩⎨⎧ y 0－2＝－2λ，z 0＝23λ，所以CM →＝(0,2－2λ，23λ)， 设平面A 1BE 的一个法向量n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ n ·A 1E →＝0，n ·BE →＝0，即⎩⎨⎧2x ＋2y －23z ＝0，－x ＋2y ＝0， 令x ＝2，则y ＝1，z ＝3，即n ＝(2,1，3)．设直线CM 与平面A 1BE 所成角为θ，则sin θ＝|2－2λ＋6λ|(2－2λ)2＋12λ2·12＋22＋3＝51428， 即|2＋4λ|16λ2－8λ＋4＝57，解得λ＝34或13， 所以M 为线段A 1D (靠近点A 1)四分之一处的点或三分之二处的点．命题点2 求二面角例4 已知点E ，F 分别在正方体ABCD －A 1B 1C 1D 1的棱BB 1，CC 1上，且B 1E ＝2EB ，CF ＝2FC 1，则平面AEF 与平面ABCD 所成的二面角的正切值为________．答案 23 解析 如图，建立空间直角坐标系Dxyz ， 设DA ＝1，由已知条件得A (1,0,0)，E (1,1，13)，F (0,1，23)，AE →＝(0,1，13)，AF →＝(－1,1，23)，设平面AEF 的法向量为n ＝(x ，y ，z )，平面AEF 与平面ABCD 所成的二面角为θ，由图知θ为锐角，由⎩⎪⎨⎪⎧ n ·AE →＝0，n ·AF →＝0，得⎩⎨⎧ y ＋13z ＝0，－x ＋y ＋23z ＝0.令y ＝1，则z ＝－3，x ＝－1，即n ＝(－1,1，－3)，取平面ABCD 的法向量为m ＝(0,0，－1)，则cos θ＝|cos 〈n ，m 〉|＝31111，tan θ＝23. 【同步练习】1、如图，四棱锥P-ABCD 中，P A ⊥底面ABCD ，AD ∥BC ，AB ＝AD ＝AC ＝3，P A ＝BC ＝4，M 为线段AD 上一点，AM ＝2MD ，N 为PC 的中点．(1)证明MN ∥平面P AB ；(2)求直线AN 与平面PMN 所成角的正弦值．(1)证明 由已知得AM ＝23AD ＝2. 取BP 的中点T ，连接AT ，TN ，由N 为PC 中点知TN ∥BC ，TN ＝12BC ＝2. 又AD ∥BC ，故TN 綊AM ，四边形AMNT 为平行四边形，于是MN ∥AT .因为AT ⊂平面P AB ，MN ⊄平面P AB ，所以MN ∥平面P AB .(2)解 取BC 的中点E ，连接AE .由AB ＝AC 得AE ⊥BC ，从而AE ⊥AD ，AE ＝AB 2－BE 2＝AB 2－⎝⎛⎭⎫BC 22＝ 5. 以A 为坐标原点，AE →的方向为x 轴正方向，建立如图所示的空间直角坐标系Axyz .由题意知，P (0,0,4)，M (0,2,0)，C (5，2,0)，N ⎝⎛⎭⎫52，1，2，PM →＝(0,2，－4)，PN →＝⎝⎛⎭⎫52，1，－2，AN →＝⎝⎛⎭⎫52，1，2. 设n ＝(x ，y ，z )为平面PMN 的法向量，则 ⎩⎪⎨⎪⎧ n ·PM →＝0，n ·PN →＝0，即⎩⎪⎨⎪⎧2y －4z ＝0，52x ＋y －2z ＝0，可取n ＝(0,2,1)． 于是|cos 〈n ，AN →〉|＝|n ·AN →||n ||A N →|＝8525. 设AN 与平面PMN 所成的角为θ，则sin θ＝8525， ∴直线AN 与平面PMN 所成角的正弦值为8525. 2、如图1所示，正△ABC 的边长为4，CD 是AB 边上的高，E ，F 分别是AC 和BC 边的中点，现将△ABC 沿CD 翻折成直二面角A －DC －B ，如图2所示．(1)试判断直线AB 与平面DEF 的位置关系，并说明理由；(2)求二面角E －DF －C 的余弦值；(3)在线段BC 上是否存在一点P ，使AP ⊥DE ？证明你的结论．规范解答解 (1)AB ∥平面DEF ，理由如下：在△ABC 中，由E ，F 分别是AC ，BC 中点，得EF ∥AB .又AB ⊄平面DEF ，EF ⊂平面DEF ，∴AB ∥平面DEF .[2分](2)以D 为原点，建立如图所示的空间直角坐标系，则A (0,0,2)，B (2,0,0)，C (0,23，0)，E (0，3，1)，F (1，3，0)，[3分]易知平面CDF 的法向量为DA →＝(0,0,2)，设平面EDF 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ DF →·n ＝0，DE →·n ＝0，即⎩⎨⎧x ＋3y ＝0，3y ＋z ＝0，取n ＝(3，－3，3)， cos 〈DA →，n 〉＝DA →·n |DA →|·|n |＝217， ∴二面角E －DF －C 的余弦值为217.[8分] (3)设P (x ，y,0)，则AP →·DE →＝3y －2＝0，∴y ＝233. 又BP →＝(x －2，y,0)，PC →＝(－x,23－y,0)，∵BP →∥PC →，∴(x －2)(23－y )＝－xy ，∴3x ＋y ＝2 3.[10分] 把y ＝233代入上式得x ＝43，∴P (43，233，0)， ∴BP →＝13BC →， ∴在线段BC 上存在点P (43，233，0)，使AP ⊥DE .[14分] 一、证明垂直问题的方法(1)利用已知的线面垂直关系构建空间直角坐标系，准确写出相关点的坐标，从而将几何证明转化为向量运算．其中灵活建系是解题的关键．(2)其一证明直线与直线垂直，只需要证明两条直线的方向向量垂直；其二证明线面垂直，只需证明直线的方向向量与平面内不共线的两个向量垂直即可，当然 ，也可证直线的方向向量与平面的法向量平行；其三证明面面垂直：①证明两平面的法向量互相垂直；②利用面面垂直的判定定理，只要能证明一个平面内的一条直线的方向向量为另一个平面的法向量即可．二、利用向量法求空间角的方法(1)先求出直线的方向向量和平面的法向量，将求空间角转化为求两个向量的夹角．(2)利用数量积求向量的夹角，然后根据和所求角的关系得到空间角，但要注意所求角的大小．1．若平面α，β的法向量分别是n 1＝(2，－3,5)，n 2＝(－3,1，－4)，则( )A ．α∥βB ．α⊥βC ．α，β相交但不垂直D ．以上答案均不正确 答案 C解析 ∵n 1·n 2＝2×(－3)＋(－3)×1＋5×(－4)≠0，∴n 1与n 2不垂直，且不共线．∴α与β相交但不垂直．2．已知平面α内有一点M (1，－1,2)，平面α的一个法向量为n ＝(6，－3,6)，则下列点P 中，在平面α内的是( )A ．P (2,3,3)B ．P (－2,0,1)C ．P (－4,4,0)D ．P (3，－3,4) 答案 A解析 逐一验证法，对于选项A ，MP →＝(1,4,1)，∴MP →·n ＝6－12＋6＝0，∴MP →⊥n ，∴点P 在平面α内，同理可验证其他三个点不在平面α内． 3．若AB →＝λCD →＋μCE →，则直线AB 与平面CDE 的位置关系是( )A ．相交B ．平行C ．在平面内D ．平行或在平面内答案 D解析 ∵AB →＝λCD →＋μCE →，∴AB →、CD →、CE →共面，∴AB 与平面CDE 平行或在平面CDE 内．4．设u ＝(－2,2，t )，v ＝(6，－4,4)分别是平面α，β的法向量．若α⊥β，则t 等于( )A ．3B ．4C ．5D ．6答案 C解析 ∵α⊥β，则u ·v ＝－2×6＋2×(－4)＋4t ＝0，∴t ＝5.5．如图所示，在正方体ABCD －A 1B 1C 1D 1中，棱长为a ，M ，N 分别为A 1B 和AC 上的点，A 1M ＝AN ＝2a 3，则MN 与平面BB 1C 1C 的位置关系是( ) A ．斜交 B ．平行C ．垂直D ．MN 在平面BB 1C 1C 内 答案 B解析 建立如图所示的空间直角坐标系，由于A 1M ＝AN ＝2a 3， 则M (a ，2a 3，a 3)，N (2a 3，2a 3，a )，MN →＝(－a 3，0，2a 3)． 又C 1D 1⊥平面BB 1C 1C ，所以C 1D 1→＝(0，a,0)为平面BB 1C 1C 的一个法向量．因为MN →·C 1D 1→＝0，所以MN →⊥C 1D 1→，又MN ⊄平面BB 1C 1C ，所以MN ∥平面BB 1C 1C .6．在正方体ABCD －A 1B 1C 1D 1中，点E 为BB 1的中点，则平面A 1ED 与平面ABCD 所成的锐二面角的余弦值为( )A.12B.23C.33D.22答案 B解析 以A 为原点建立如图所示的空间直角坐标系Axyz ，设棱长为1，则A 1(0,0,1)，E (1,0，12)，D (0,1,0)， ∴A 1D →＝(0,1，－1)，A 1E →＝(1,0，－12)． 设平面A 1ED 的一个法向量为n 1＝(1，y ，z )，则有⎩⎪⎨⎪⎧ A 1D →·n 1＝0，A 1E →·n 1＝0， 即⎩⎪⎨⎪⎧ y －z ＝0，1－12z ＝0，∴⎩⎪⎨⎪⎧y ＝2，z ＝2.即n 1＝(1,2,2)． ∵平面ABCD 的一个法向量为n 2＝(0,0,1)，∴cos 〈n 1，n 2〉＝23×1＝23， 即所成的锐二面角的余弦值为23. 7．已知平面α内的三点A (0,0,1)，B (0,1,0)，C (1,0,0)，平面β的一个法向量n ＝(－1，－1，－1)，则不重合的两个平面α与β的位置关系是_______________．答案 α∥β解析 设平面α的法向量为m ＝(x ，y ，z )，由m ·AB →＝0，得x ·0＋y －z ＝0⇒y ＝z ，由m ·AC →＝0，得x －z ＝0⇒x ＝z ，取x ＝1，∴m ＝(1,1,1)，m ＝－n ，∴m ∥n ，∴α∥β.8．已知点P 是平行四边形ABCD 所在的平面外一点，如果AB →＝(2，－1，－4)，AD →＝(4,2,0)，AP →＝(－1,2，－1)．对于结论：①AP ⊥AB ；②AP ⊥AD ；③AP →是平面ABCD 的法向量；④AP →∥BD →.其中正确的是________．答案 ①②③解析 ∵AB →·AP →＝0，AD →·AP →＝0，∴AB ⊥AP ，AD ⊥AP ，则①②正确．又AB →与AD →不平行，∴AP →是平面ABCD 的法向量，则③正确．∵BD →＝AD →－AB →＝(2,3,4)，AP →＝(－1,2，－1)，∴BD →与AP →不平行，故④错误．9.如图，正方体ABCD-A 1B 1C 1D 1的棱长为1，E ，F 分别是棱BC ，DD 1上的点，如果B 1E ⊥平面ABF ，则CE 与DF 的和的值为________．答案 1解析 以D 1为原点，D 1A 1，D 1C 1，D 1D 所在直线分别为x ，y ，z 轴建立空间直角坐标系，设CE ＝x ，DF ＝y ，则易知E (x,1,1)，B 1(1,1,0)，F (0,0,1－y )，B (1,1,1)，∴B 1E →＝(x －1,0,1)，∴FB →＝(1,1，y )，∵B 1E ⊥平面ABF ，∴FB →·B 1E →＝(1,1，y )·(x －1，0,1)＝0⇒x ＋y ＝1.*10.如图，圆锥的轴截面SAB 是边长为2的等边三角形，O 为底面中心，M 为SO 中点，动点P 在圆锥底面内(包括圆周)．若AM ⊥MP ，则点P 形成的轨迹长度为________．答案 72解析 由题意可知，建立空间直角坐标系，如图所示．则A (0，－1,0)，B (0,1,0)，S (0,0，3)，M (0,0，32)，设P (x ，y,0)， ∴AM →＝(0,1，32)，MP →＝(x ，y ，－32)，即y ＝34， ∴点P 的轨迹方程为y ＝34. 根据圆的弦长公式，可得点P 形成的轨迹长度为2 1－(34)2＝72. 11．如图所示，已知直三棱柱ABC —A 1B 1C 1中，△ABC 为等腰直角三角形，∠BAC ＝90°，且AB ＝AA 1，D ，E ，F 分别为B 1A ，C 1C ，BC 的中点．求证：(1)DE ∥平面ABC ；(2)B 1F ⊥平面AEF .证明 (1)以A 为坐标原点，AB ，AC ，AA 1所在直线为x 轴，y 轴，z 轴，建立如图所示空间直角坐标系Axyz ，令AB ＝AA 1＝4，则A (0,0,0)，E (0,4,2)，F (2,2,0)，B (4,0,0)，B 1(4,0,4)．取AB 中点为N ，连接CN ，则N (2,0,0)，C (0,4,0)，D (2,0,2)，∴DE →＝(－2,4,0)，NC →＝(－2,4,0)，∴DE →＝NC →，∴DE ∥NC ，又∵NC ⊂平面ABC ，DE ⊄平面ABC .故DE ∥平面ABC .(2)B 1F →＝(－2,2，－4)，EF →＝(2，－2，－2)，AF →＝(2,2,0)．B 1F →·EF →＝(－2)×2＋2×(－2)＋(－4)×(－2)＝0，B 1F →·AF →＝(－2)×2＋2×2＋(－4)×0＝0.∴B 1F →⊥EF →，B 1F →⊥AF →，即B 1F ⊥EF ，B 1F ⊥AF ，又∵AF ∩EF ＝F ，AF ⊂平面AEF ，EF ⊂平面AEF ，∴B 1F ⊥平面AEF .12．在平面四边形ABCD 中，AB ＝BD ＝CD ＝1，AB ⊥BD ，CD ⊥BD .将△ABD 沿BD 折起，使得平面ABD ⊥平面BCD ，如图所示．(1)求证：AB ⊥CD ；(2)若M 为AD 中点，求直线AD 与平面MBC 所成角的正弦值．(1)证明 ∵平面ABD ⊥平面BCD ，平面ABD ∩平面BCD ＝BD ，AB ⊂平面ABD ，AB ⊥BD ，∴AB ⊥平面BCD .又CD ⊂平面BCD ，∴AB ⊥CD .(2)解 过点B 在平面BCD 内作BE ⊥BD ，如图所示．由(1)知AB ⊥平面BCD ，BE ⊂平面BCD ，BD ⊂平面BCD .∴AB ⊥BE ，AB ⊥BD .以B 为坐标原点，分别以BE →，BD →，BA →的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系．依题意，得B (0,0,0)，C (1,1,0)，D (0,1,0)，A (0,0,1)，M (0，12，12)， 则BC →＝(1,1,0)，BM →＝(0，12，12)，AD →＝(0,1，－1)． 设平面MBC 的法向量n ＝(x 0，y 0，z 0)，则⎩⎪⎨⎪⎧ n ·BC →＝0，n ·BM →＝0，即⎩⎪⎨⎪⎧ x 0＋y 0＝0，12y 0＋12z 0＝0， 取z 0＝1，得平面MBC 的一个法向量n ＝(1，－1,1)． 设直线AD 与平面MBC 所成角为θ，则sin θ＝|cos 〈n ，AD →〉|＝|n ·AD →||n ||AD →|＝63， 即直线AD 与平面MBC 所成角的正弦值为63. *13.如图，长方体ABCD —A 1B 1C 1D 1中，AB ＝2，BC ＝CC 1＝1，点P 是CD 上的一点，PC ＝λPD .(1)若A 1C ⊥平面PBC 1，求λ的值；(2)设λ1＝1，λ2＝3所对应的点P 为P 1，P 2，二面角P 1—BC 1—P 2的大小为θ，求cos θ的值． 解 方法一 (1)∵A 1C ⊥BC 1，若A 1C ⊥PB ，则A 1C ⊥平面PBC 1，只需A 1C ⊥PB 即可，在矩形ABCD 中，CP BC ＝BC AB ，解得CP ＝12，PD ＝32，λ＝13. (2)过点C 作CH ⊥BC 1交BC 1于点H ，连接P 1H ，P 2H (图略)，则∠P 1HP 2就是所求二面角的一个平面角θ.∵P 1C ＝1，P 2C ＝32，CH ＝22， ∴tan ∠P 1HC ＝2，tan ∠P 2HC ＝32， tan θ＝tan(∠P 2HC －∠P 1HC )＝28， 所求余弦值为46633. 方法二 (1)建立如图所示空间直角坐标系Oxyz ，则B (1,2,0)，C 1(0,2,1)，A 1(1,0,1)，C (0,2,0)，设P (0，21＋λ，0)， 则A 1C →＝(－1,2，－1)，BC 1→＝(－1,0,1)，BP →＝(－1，21＋λ－2,0)， 若A 1C ⊥平面PBC 1，则⎩⎪⎨⎪⎧ A 1C →·BP →＝0，A 1C →·BC 1→＝0，即⎩⎪⎨⎪⎧ 1＋41＋λ－4＝0，1＋0－1＝0，解得λ＝13. (2)由P 1(0,1,0)，P 2(0，12，0)， 得BP 1→＝(－1，－1,0)，BC 1→＝(－1,0,1)，BP 2→＝(－1，－32，0)． 设平面BC 1P 1与平面BC 1P 2的法向量分别是n 1，n 2，由⎩⎪⎨⎪⎧ n 1·BP 1→＝0，n 1·BC 1→＝0，得n 1＝(1，－1,1)， 由⎩⎪⎨⎪⎧ n 2·BP 2→＝0，n 2·BC 1→＝0，得n 2＝(3，－2,3)， ∴cos θ＝|n 1·n 2||n 1||n 2|＝4233＝46633.。

指数函数判断下列结论是否正确(请在括号中打“√”或“×”) (1)n a n ＝(na )n ＝a .( )(2)分数指数幂m na 可以理解为mn个a 相乘．( )(3)(－1)24＝(－1)12＝－1.( ) (4)函数y ＝a －x 是R 上的增函数．( ) (5)函数21x y a +=(a >1)的值域是(0，＋∞)．( )(6)函数y ＝2x －1是指数函数．( )无题型一 指数幂的运算 例1 化简下列各式：(1)[(0.06415)－2.5]23－3338－π0； (2)a 43－8a 13b4b 23＋23ab ＋a23÷(a23-－23b a )×a ·3a 25a ·3a.化简(14)12-·(4ab －1)3(0.1)－1·(a 3·b －3)12＝________. 题型二 指数函数的图象及应用例2 (1)已知实数a ，b 满足等式2 017a ＝2 018b ，下列五个关系式：①0<b <a ；②a <b <0；③0<a <b ；④b <a <0；⑤a ＝b .其中不可能成立的关系式有( )A．1个B．2个C．3个D．4个(2)已知函数f(x)＝|2x－1|，a<b<c且f(a)>f(c)>f(b)，则下列结论中，一定成立的是()A．a<0，b<0，c<0 B．a<0，b≥0，c>0C．2－a<2c D．2a＋2c<2(1)已知函数f(x)＝a x－b的图象如图所示，则函数g(x)＝ax＋b的图象可能是()(2)若曲线|y|＝2x＋1与直线y＝b没有公共点，则b的取值范围是________．题型三指数函数的性质及应用命题点1指数函数单调性的应用例3(1)下列各式比较大小正确的是()A．1.72.5>1.73B．0.6－1>0.62C．0.8－0.1>1.250.2D．1.70.3<0.93.1(2)设函数f (x )＝⎩⎪⎨⎪⎧(12)x －7，x <0，x ，x ≥0，若f (a )<1，则实数a 的取值范围是________．命题点2 复合函数的单调性例4 (1)已知函数f (x )＝22x m-(m 为常数)，若f (x )在区间[2，＋∞)上是增函数，则m 的取值范围是________．(2)函数f (x )＝⎝⎛⎭⎫12221x x -+-的单调减区间为_____________________________________． 引申探究函数f (x )＝142x x +-的单调增区间是________．例5 (1)函数y ＝⎝⎛⎭⎫14x －⎝⎛⎭⎫12x ＋1在区间[－3,2]上的值域是________．(2)如果函数y ＝a 2x ＋2a x －1(a >0，且a ≠1)在区间[－1,1]上的最大值是14，则a 的值为________．(1)已知函数f (x )＝⎩⎪⎨⎪⎧－(12)x ，a ≤x ＜0，－x 2＋2x ，0≤x ≤4的值域是[－8,1]，则实数a 的取值范围是( )A ．(－∞，－3]B ．[－3,0)C ．[－3，－1]D ．{－3}(2)已知函数f (x )＝2x －12x ，函数g (x )＝⎩⎪⎨⎪⎧f (x )，x ≥0，f (－x )，x <0，则函数g (x )的最小值是________．1．分数指数幂(1)我们规定正数的正分数指数幂的意义是m na ＝na m (a >0，m ，n ∈N *，且n >1)．于是，在条件a >0，m ，n ∈N *，且n >1下，根式都可以写成分数指数幂的形式．正数的负分数指数幂的意义与负整数指数幂的意义相仿，我们规定m na-＝1m na(a >0，m ，n ∈N *，且n >1).0的正分数指数幂等于0；0的负分数指数幂没有意义．(2)有理数指数幂的运算性质：a r a s ＝a r ＋s ，(a r )s ＝a rs ，(ab )r ＝a r b r ，其中a >0，b >0，r ，s ∈Q . 2．指数函数的图象与性质典例 已知函数y ＝b ＋22x xa+(a ，b 为常数，且a >0，a ≠1)在区间[－32，0]上有最大值3，最小值52，则a ，b 的值分别为________．1．已知函数f (x )＝a x －2＋2的图象恒过定点A ，则A 的坐标为( ) A ．(0,1) B ．(2,3) C ．(3,2) D ．(2,2)2．已知a ＝(35)13-，b ＝(35)14-，c ＝(32)34-，则a ，b ，c 的大小关系是( )A ．c <a <b ．a <b <c C ．b <a <c．c <b <a3．计算：⎝⎛⎭⎫3213-×⎝⎛⎭⎫－760＋814×42________. 4．函数y ＝8－23－x (x ≥0)的值域是________． 1．设2x ＝8y＋1,9y ＝3x －9，则x ＋y 的值为( )A ．18B ．21C ．24D ．27 2．函数f (x )＝2|x －1|的图象是( )3．已知a ＝40.2，b ＝0.40.2，c ＝0.40.8，则( ) A ．a >b >c B ．a >c >b C ．c >a >bD ．b >c >a4．已知f (x )＝3x －b (2≤x ≤4，b 为常数)的图象经过点(2,1)，则f (x )的值域为( ) A ．[9,81] B ．[3,9] C ．[1,9]D ．[1，＋∞)5．若函数f (x )＝2x ＋12x －a 是奇函数，则使f (x )＞3成立的x 的取值范围为( )A ．(－∞，－1)B ．(－1,0)C ．(0,1)D ．(1，＋∞)*6.已知g (x )＝ax ＋1，f (x )＝⎩⎪⎨⎪⎧2x －1，0≤x ≤2，－x 2，－2≤x <0，对任意x 1∈[－2,2]，存在x 2∈[－2,2]，使g (x 1)＝f (x 2)成立，则a 的取值范围是( ) A ．[－1，＋∞) B ．[－1,1] C ．(0,1]D ．(－∞，1]7．设函数f (x )＝⎩⎪⎨⎪⎧e x －1，x <1，x 13，x ≥1，则使得f (x )≤2成立的x 的取值范围是________．8．若直线y ＝2a 与函数y ＝|a x －1|(a >0且a ≠1)的图象有两个公共点，则a 的取值范围是________． 9．已知y ＝f (x )是定义在R 上的奇函数且当x ≥0时，f (x )＝－14x ＋12x ，则此函数的值域为________．10．当x ∈(－∞，－1]时，不等式(m 2－m )·4x －2x <0恒成立，则实数m 的取值范围是________． 11．已知函数f (x )＝(23)|x |－a .(1)求f (x )的单调区间；(2)若f (x )的最大值等于94，求a 的值．12．已知函数f (x )＝2431()3ax x -+.(1)若a ＝－1，求f (x )的单调区间； (2)若f (x )有最大值3，求a 的值．*13.已知函数f (x )＝14x －λ2x －1＋3(－1≤x ≤2)．(1)若λ＝32，求函数f (x )的值域；(2)若函数f (x )的最小值是1，求实数λ的值．指数函数判断下列结论是否正确(请在括号中打“√”或“×”)(1)nan＝(na)n＝a.(×)(2)分数指数幂可以理解为mn个a相乘．(×)(3)(－1) ＝(－1) ＝－1.(×)(4)函数y＝a－x是R上的增函数．(×)(5)函数(a>1)的值域是(0，＋∞)．(×)(6)函数y＝2x－1是指数函数．(×)无题型一指数幂的运算例1化简下列各式：(1)[(0.064 )－2.5] －3338－π0；(2)a －8a b4b ＋23ab＋a ÷(a －23ba)×a•3a25a•3a.解(1)原式＝{[(641 000) ] } －(278) －1＝[(410)3] －[(32)3] －1＝52－32－1＝0.(2)原式＝a [ a 3－2b 3] a 2＋a •2b ＋2b 2÷a －2b a×a•a a •a＝a (a －2b )×aa －2b ×a a＝a ×a×a ＝a2.思维升华(1)指数幂的运算首先将根式、分数指数幂统一为分数指数幂，以便利用法则计算，还应注意：①必须同底数幂相乘，指数才能相加；②运算的先后顺序．(2)当底数是负数时，先确定符号，再把底数化为正数．(3)运算结果不能同时含有根号和分数指数，也不能既有分母又含有负指数．化简(14) •4ab－130.1－1•a3•b－3＝________.答案85解析原式＝2×23•a •b 10•a •b ＝21＋3×10－1＝85.题型二指数函数的图象及应用例2(1)已知实数a，b满足等式2 017a＝2 018b，下列五个关系式：①0<b<a；②a<b<0；③0<a<b；④b<a<0；⑤a＝b.其中不可能成立的关系式有()A．1个B．2个C．3个D．4个(2)已知函数f(x)＝|2x－1|，a<b<c且f(a)>f(c)>f(b)，则下列结论中，一定成立的是()A．a<0，b<0，c<0 B．a<0，b≥0，c>0C．2－a<2c D．2a＋2c<2答案(1)B(2)D解析(1)如图，观察易知，a，b的关系为a<b<0或0<b<a或a＝b＝0.(2)作出函数f(x)＝|2x－1|的图象，如图，∵a<b<c且f(a)>f(c)>f(b)，结合图象知，0<f(a)<1，a<0，c>0，∴0<2a<1.∴f(a)＝|2a－1|＝1－2a<1，∴f(c)<1，∴0<c<1.∴1<2c<2，∴f(c)＝|2c－1|＝2c－1，又∵f(a)>f(c)，∴1－2a>2c－1，∴2a＋2c<2，故选D.思维升华(1)已知函数解析式判断其图象一般是取特殊点，判断所给的图象是否过这些点，若不满足则排除．(2)对于有关指数型函数的图象问题，一般是从最基本的指数函数的图象入手，通过平移、伸缩、对称变换而得到．特别地，当底数a与1的大小关系不确定时应注意分类讨论．(3)有关指数方程、不等式问题的求解，往往利用相应的指数型函数图象，数形结合求解．(1)已知函数f(x)＝ax－b的图象如图所示，则函数g(x)＝ax＋b的图象可能是()(2)若曲线|y|＝2x＋1与直线y＝b没有公共点，则b的取值范围是________．答案(1)A(2)[－1,1]解析(1)由f(x)的单调性知0<a<1，又x＝0时，a－b>1，x＝1时，a1－b<1，∴0<b<1，对照图象知g(x)的图象可能是A.(2)曲线|y|＝2x＋1与直线y＝b的图象如图所示，由图象可知：如果|y|＝2x＋1与直线y＝b没有公共点，则b应满足的条件是b∈[－1,1]．题型三指数函数的性质及应用命题点1指数函数单调性的应用例3(1)下列各式比较大小正确的是()A．1.72.5>1.73 B．0.6－1>0.62C．0.8－0.1>1.250.2 D．1.70.3<0.93.1(2)设函数f(x)＝12x－7，x<0，x，x≥0，若f(a)<1，则实数a的取值范围是________．答案(1)B(2)(－3,1)解析(1)选项B中，∵y＝0.6x是减函数，∴0.6－1>0.62.(2)当a<0时，不等式f(a)<1可化为(12)a－7<1，即(12)a<8，即(12)a<(12)－3，∴a>－3.又a<0，∴－3<a<0.当a≥0时，不等式f(a)<1可化为a<1.∴0≤a<1，综上，a的取值范围为(－3,1)．命题点2复合函数的单调性例4(1)已知函数f(x)＝2 (m为常数)，若f(x)在区间[2，＋∞)上是增函数，则m的取值范围是________．(2)函数f(x)＝12 的单调减区间为_____________________________________．答案(1)(－∞，4](2)(－∞，1]解析(1)令t＝|2x－m|，则t＝|2x－m|在区间[m2，＋∞)上单调递增，在区间(－∞，m2]上单调递减．而y＝2t为R上的增函数，所以要使函数f(x)＝2 在[2，＋∞)上单调递增，则有m2≤2，即m≤4，所以m的取值范围是(－∞，4]．(2)设u＝－x2＋2x＋1，∵y＝12u在R上为减函数，∴函数f(x)＝的减区间即为函数u＝－x2＋2x＋1的增区间．又u＝－x2＋2x＋1的增区间为(－∞，1]，∴f(x)的减区间为(－∞，1]．引申探究函数f(x)＝的单调增区间是________．答案[0，＋∞)解析设t＝2x，则y＝t2－2t的单调增区间为[1，＋∞)，令2x≥1，得x≥0，∴函数f(x)＝的单调增区间是[0，＋∞)．命题点3函数的值域(或最值)例5(1)函数y＝14x－12x＋1在区间[－3,2]上的值域是________．(2)如果函数y＝a2x＋2ax－1(a>0，且a≠1)在区间[－1,1]上的最大值是14，则a的值为________．答案(1)34，57(2)13或3解析(1)令t＝12x，因为x∈[－3,2]，所以t∈14，8，故y＝t2－t＋1＝t－122＋34.当t＝12时，ymin＝34；当t＝8时，ymax＝57.故所求函数的值域为34，57.(2)令ax＝t，则y＝a2x＋2ax－1＝t2＋2t－1＝(t＋1)2－2.当a>1时，因为x∈[－1,1]，所以t∈[1a，a]，又函数y＝(t＋1)2－2在1a，a上单调递增，所以ymax＝(a＋1)2－2＝14，解得a＝3(负值舍去)．当0<a<1时，因为x∈[－1,1]，所以t∈[a，1a]，又函数y＝(t＋1)2－2在[a，1a]上单调递增，则ymax＝(1a＋1)2－2＝14，解得a＝13(负值舍去)．综上，a＝3或a＝13.思维升华(1)在利用指数函数性质解决相关综合问题时，要特别注意底数a的取值范围，并在必要时进行分类讨论．(2)与指数函数有关的指数型函数的定义域、值域(最值)、单调性、奇偶性的求解方法，要化归于指数函数来解．(1)已知函数f(x)＝－12x，a≤x＜0，－x2＋2x，0≤x≤4的值域是[－8,1]，则实数a的取值范围是()A．(－∞，－3] B．[－3,0)C．[－3，－1] D．{－3}(2)已知函数f(x)＝2x－12x，函数g(x)＝f x，x≥0，f－x，x<0，则函数g(x)的最小值是________．答案(1)B(2)0解析(1)当0≤x≤4时，f(x)∈[－8,1]，当a≤x＜0时，f(x)∈[－(12)a，－1)，所以[－12a，－1)[－8,1]，即－8≤－12a＜－1，即－3≤a＜0，所以实数a的取值范围是[－3,0)．(2)当x≥0时，g(x)＝f(x)＝2x－12x为单调增函数，所以g(x)≥g(0)＝0；当x<0时，g(x)＝f(－x)＝2－x－12－x为单调减函数，所以g(x)>g(0)＝0，所以函数g(x)的最小值是0.1．分数指数幂(1)我们规定正数的正分数指数幂的意义是＝nam(a>0，m，n∈N*，且n>1)．于是，在条件a>0，m，n∈N*，且n>1下，根式都可以写成分数指数幂的形式．正数的负分数指数幂的意义与负整数指数幂的意义相仿，我们规定＝1 (a>0，m，n∈N*，且n>1).0的正分数指数幂等于0；0的负分数指数幂没有意义．(2)有理数指数幂的运算性质：aras＝ar＋s，(ar)s＝ars，(ab)r＝arbr，其中a>0，b>0，r，s∈Q. 2．指数函数的图象与性质y＝ax a>1 0<a<1图象定义域(1)R值域(2)(0，＋∞)性质(3)过定点(0,1)(4)当x>0时，y>1；当x<0时，0<y<1 (5)当x>0时，0<y<1；当x<0时，y>1(6)在(－∞，＋∞)上是增函数(7)在(－∞，＋∞)上是减函数典例已知函数y＝b＋(a，b为常数，且a>0，a≠1)在区间[－32，0]上有最大值3，最小值52，则a，b的值分别为________．错解展示解析令t＝x2＋2x＝(x＋1)2－1，∵－32≤x≤0，∴－1≤t≤0.∵1a≤at≤1，∴b＋1a≤b＋at≤b＋1，由b＋1a＝52，b＋1＝3，得a＝2，b＝2.答案2,2现场纠错解析令t＝x2＋2x＝(x＋1)2－1，∵x∈[－32，0]，∴t∈[－1,0]．①若a>1，函数f(x)＝at在[－1,0]上为增函数，∴at∈[1a，1]，b＋∈[b＋1a，b＋1]，依题意得b＋1a＝52，b＋1＝3，解得a＝2，b＝2.②若0<a<1，函数f(x)＝at在[－1,0]上为减函数，∴at∈[1，1a]，则b＋∈[b＋1，b＋1a]，依题意得b＋1a＝3，b＋1＝52，解得a＝23，b＝32.综上①②，所求a，b的值为a＝2，b＝2或a＝23，b＝32. 答案2,2或23，32纠错心得与指数函数、对数函数的单调性有关的问题，要对底数进行讨论. 1．已知函数f(x)＝ax－2＋2的图象恒过定点A，则A的坐标为() A．(0,1) B．(2,3) C．(3,2) D．(2,2)答案 B解析由a0＝1知，当x－2＝0，即x＝2时，f(2)＝3，即图象必过定点(2,3)．2．已知a＝(35) ，b＝(35) ，c＝(32) ，则a，b，c的大小关系是()A．c<a<b ．a<b<cC．b<a<c ．c<b<a答案 D解析∵y＝(35)x是减函数，∴(35) >(35) >(35)0，即a>b>1，又c＝(32) <(32)0＝1，∴c<b<a.3．计算：32 ×－760＋8 ×42－＝________.答案 2解析原式＝23 ×1＋2 ×2 －23 ＝2.4．函数y＝8－23－x(x≥0)的值域是________．答案[0,8)解析∵x≥0，∴－x≤0，∴3－x≤3，∴0<23－x≤23＝8，∴0≤8－23－x<8，∴函数y＝8－23－x的值域为[0,8)．1．设2x＝8y＋1,9y＝3x－9，则x＋y的值为()A．18 B．21 C．24 D．27答案 D解析∵2x＝8y＋1＝23(y＋1)，∴x＝3y＋3，∵9y＝3x－9＝32y，∴x－9＝2y，解得x＝21，y＝6，∴x＋y＝27.2．函数f(x)＝2|x－1|的图象是()答案 B解析∵|x－1|≥0，∴f(x)≥1，排除C、D.又x＝1时，|f(x)|min＝1，排除A.故选B.3．已知a＝40.2，b＝0.40.2，c＝0.40.8，则()A．a>b>c B．a>c>bC．c>a>b D．b>c>a答案 A解析由0.2<0.8，底数0.4<1知，y＝0.4x在R上为减函数，所以0.40.2>0.40.8，即b>c.又a＝40.2>40＝1，b＝0.40.2<1，所以a>b.综上，a>b>c.4．已知f(x)＝3x－b(2≤x≤4，b为常数)的图象经过点(2,1)，则f(x)的值域为() A．[9,81] B．[3,9]C．[1,9] D．[1，＋∞)答案 C解析由f(x)过定点(2,1)可知b＝2，因为f(x)＝3x－2在[2,4]上是增函数，所以f(x)min＝f(2)＝1，f(x)max＝f(4)＝9.故选C.5．若函数f(x)＝2x＋12x－a是奇函数，则使f(x)＞3成立的x的取值范围为() A．(－∞，－1) B．(－1,0)C．(0,1) D．(1，＋∞)答案 C解析∵f(x)为奇函数，∴f(－x)＝－f(x)，即2－x＋12－x－a＝－2x＋12x－a，整理得(a－1)(2x＋1)＝0，∴a＝1，∴f(x)＞3即为2x＋12x－1＞3，当x>0时，2x－1>0，∴2x＋1>3•2x－3，解得0<x<1；当x<0时，2x－1<0，∴2x＋1<3•2x－3，无解．∴x的取值范围为(0,1)．*6.已知g(x)＝ax＋1，f(x)＝2x－1，0≤x≤2，－x2，－2≤x<0，对任意x1∈[－2,2]，存在x2∈[－2,2]，使g(x1)＝f(x2)成立，则a的取值范围是()A．[－1，＋∞) B．[－1,1]C．(0,1] D．(－∞，1]答案 B解析由题意可得g(x)，x∈[－2,2]的值域为f(x)，x∈[－2,2]的值域的子集．经分析知f(x)，x∈[－2,2]的值域是[－4,3]，当a＝0时，g(x)＝1，符合题意；当a>0时，g(x)，x∈[－2,2]的值域是[－2a＋1,2a＋1]，所以－2a＋1≥－4，2a＋1≤3，则0<a≤1；当a<0时，g(x)，x∈[－2,2]的值域是[2a＋1，－2a＋1]，所以2a＋1≥－4，－2a＋1≤3，则－1≤a<0.综上可得－1≤a≤1.7．设函数f(x)＝ex－1，x<1，x ，x≥1，则使得f(x)≤2成立的x的取值范围是________．答案(－∞，8]解析当x<1时，由ex－1≤2，得x≤1＋ln 2，∴x<1时恒成立；当x≥1时，由x ≤2，得x≤8，∴1≤x≤8.综上，符合题意的x的取值范围是(－∞，8]．8．若直线y＝2a与函数y＝|ax－1|(a>0且a≠1)的图象有两个公共点，则a的取值范围是________．答案(0，12)解析(数形结合法)由图象可知0<2a<1，∴0<a<12.9．已知y＝f(x)是定义在R上的奇函数且当x≥0时，f(x)＝－14x＋12x，则此函数的值域为________．答案[－14，14]解析设t＝12x，当x≥0时，2x≥1，∴0<t≤1，f(t)＝－t2＋t＝－(t－12)2＋14.∴0≤f(t)≤14，故当x≥0时，f(x)∈[0，14]．∵y＝f(x)是定义在R上的奇函数，∴当x≤0时，f(x)∈[－14，0]．故函数的值域为[－14，14]．10．当x∈(－∞，－1]时，不等式(m2－m)•4x－2x<0恒成立，则实数m的取值范围是________．答案(－1,2)解析原不等式变形为m2－m<12x，因为函数y＝12x在(－∞，－1]上是减函数，所以12x≥12－1＝2，当x∈(－∞，－1]时，m2－m<12x恒成立等价于m2－m<2，解得－1<m<2.11．已知函数f(x)＝(23)|x|－a.(1)求f(x)的单调区间；(2)若f(x)的最大值等于94，求a的值．解(1)令t＝|x|－a，则f(x)＝(23)t，不论a取何值，t在(－∞，0]上单调递减，在[0，＋∞)上单调递增，又y＝(23)t是单调递减的，因此f(x)的单调递增区间是(－∞，0]，单调递减区间是[0，＋∞)．(2)由于f(x)的最大值是94，且94＝(23)－2，所以g(x)＝|x|－a应该有最小值－2，即g(0)＝－2，从而a＝2.12．已知函数f(x)＝.(1)若a＝－1，求f(x)的单调区间；(2)若f(x)有最大值3，求a的值．解(1)当a＝－1时，f(x)＝，令t＝－x2－4x＋3，由于t在(－∞，－2)上单调递增，在(－2，＋∞)上单调递减，而y＝13t在R上单调递减，所以f(x)在(－∞，－2)上单调递减，在(－2，＋∞)上单调递增，即函数f(x)的单调递增区间是(－2，＋∞)，单调递减区间是(－∞，－2)．(2)令g(x)＝ax2－4x＋3，则f(x)＝13g(x)，由于f(x)有最大值3，所以g(x)应有最小值－1，因此必有a>0，3a－4a＝－1，解得a＝1，即当f(x)有最大值3时，a的值为1.*13.已知函数f(x)＝14x－λ2x－1＋3(－1≤x≤2)．(1)若λ＝32，求函数f(x)的值域；(2)若函数f(x)的最小值是1，求实数λ的值．解(1)f(x)＝14x－λ2x－1＋3＝(12)2x－2λ•(12)x＋3(－1≤x≤2)．设t＝(12)x，得g(t)＝t2－2λt＋3(14≤t≤2)．当λ＝32时，g(t)＝t2－3t＋3＝(t－32)2＋34(14≤t≤2)．所以g(t)max＝g(14)＝3716，g(t)min＝g(32)＝34.所以f(x)max＝3716，f(x)min＝34，故函数f(x)的值域为[34，3716]．(2)由(1)得g(t)＝t2－2λt＋3＝(t－λ)2＋3－λ2(14≤t≤2)．①当λ≤14时，g(t)min＝g(14)＝－λ2＋4916，令－λ2＋4916＝1，得λ＝338>14，不符合，舍去；②当14<λ≤2时，g(t)min＝g(λ)＝－λ2＋3，令－λ2＋3＝1，得λ＝2(λ＝－2<14，不符合，舍去)；③当λ>2时，g(t)min＝g(2)＝－4λ＋7，令－4λ＋7＝1，得λ＝32<2，不符合，舍去．综上所述，实数λ的值为2.。

精心整理集合的含义与表示__________________________________________________________________________________1、2、3、1，2，32二、集合中元素的特性：1、确定性：设A 是一个给定的集合，x 是某一具体的对象，则x 或者是A 的元素，或者不是A 的元素，二者必居其一，不能模棱两可．2、互异性：对于一个给定的集合，它的任意两个元素是不能相同的。

集合中相同的元素只能算是一个。

如方程0122=+-x x 有两个重根121==x x ，其解集只能记为{}1，而不能记为{}1,1。

3、无序性：集合中的元素是不分顺序的．如{},a b 和{},b a 表示同一个集合． 特别提醒：集合和点的坐标是不同的概念，在平面直角坐标系中，点（l ，0）和点（0，l ）表示不同的两个点，而集合｛1，0｝和｛0，1｝表示同一个集合。

三、元素与集合的关系： a a a 素，就说a 不属于A ，记作A a ∉。

特别提醒：1、“属于”号∈与“不属于”号∉，使用时不可反过来写，“A －6”与“A 8”的写法是错误的；2、根据集合中元素的确定性，a A ∈或a A ∉，这两种情况必有一种成立；3、集合和元素是两个不同的概念，它们之间是个体与整体的关系，并且这种关系是相对的。

如：集合{}1A =相对于集合{}{}{}{}1,2,3B =而言，A 是B 的一个元素；元素与集合之间不存在大小与相等的关系，如2与{}3，只能是{}23∉，不能写成{}23≠。

4、符号∈和∉是表示元素和集合之间关系的，不能用来表示集合之间的关系，如：{}1∈{}1,2的写法是错误的，而{}{}{}{}11,2∈的写法是正确的。

四、集合的分类：按照集合中元素的个数是有限还是无限，集合可分为：有限集和无限集。

（1）有限集：含有有限个元素的集合；（2）无限集：含有无限个元素的集合（3）空集：特别地，不含任何元素的集合叫做空集，记作∅．空集是个特殊的集合，空集归入有限集。

直线与圆、圆与圆的位置关系判断下列结论是否正确(请在括号中打“√”或“×”)(1)如果两个圆的方程组成的方程组只有一组实数解，则两圆外切．()(2)如果两圆的圆心距小于两圆的半径之和，则两圆相交．()(3)从两圆的方程中消掉二次项后得到的二元一次方程是两圆的公共弦所在的直线方程．()(4)过圆O：x2＋y2＝r2上一点P(x0，y0)的圆的切线方程是x0x＋y0y＝r2.()(5)过圆O：x2＋y2＝r2外一点P(x0，y0)作圆的两条切线，切点分别为A，B，则O，P，A，B四点共圆且直线AB的方程是x0x＋y0y＝r2.()无题型一直线与圆的位置关系的判断例1(1)已知点M(a，b)在圆O：x2＋y2＝1外，则直线ax＋by＝1与圆O的位置关系是() A．相切B．相交C．相离D．不确定(2)圆x2＋y2－2x＋4y＝0与直线2tx－y－2－2t＝0(t∈R)的位置关系为()A．相离B．相切C．相交D．以上都有可能过点A(3，1)的直线l与圆x2＋y2＝1有公共点，则直线l的斜率的取值范围是() A．[－1,1]B．[0，3]C．[0,1]D．[－3，3]题型二圆与圆的位置关系例2(1)已知圆M：x2＋y2－2ay＝0(a＞0)截直线x＋y＝0所得线段的长度是22，则圆M与圆N：(x－1)2＋(y－1)2＝1的位置关系是()A ．内切B ．相交C ．外切D ．相离(2)如果圆C ：x 2＋y 2－2ax －2ay ＋2a 2－4＝0与圆O ：x 2＋y 2＝4总相交，那么实数a 的取值范围是______________________．已知两圆x 2＋y 2－2x －6y －1＝0和x 2＋y 2－10x －12y ＋m ＝0.(1)m 取何值时两圆外切； (2)m 取何值时两圆内切；(3)求m ＝45时两圆的公共弦所在直线的方程和公共弦的长． 题型三 直线与圆的综合问题 命题点1 求弦长问题例3已知直线l ：mx ＋y ＋3m －3＝0与圆x 2＋y 2＝12交于A ，B 两点，过A ，B 分别做l 的垂线与x 轴交于C ，D 两点，若|AB |＝23，则|CD |＝________. 命题点2 直线与圆相交求参数范围例4 已知过点A (0,1)且斜率为k 的直线l 与圆C ：(x －2)2＋(y －3)2＝1交于M ，N 两点． (1)求k 的取值范围；(2)若OM →·ON →＝12，其中O 为坐标原点，求|MN |. 命题点3 直线与圆相切的问题例5 已知圆C ：(x －1)2＋(y ＋2)2＝10，求满足下列条件的圆的切线方程． (1)与直线l 1：x ＋y －4＝0平行； (2)与直线l 2：x －2y ＋4＝0垂直； (3)过切点A (4，－1)．(1)过三点A (1,3)，B (4,2)，C (1，－7)的圆交y 轴于M 、N 两点，则|MN |等于( )A ．2 6B ．8C ．4 6D ．10(2)若直线x cos θ＋y sin θ－1＝0与圆(x －1)2＋(y －sin θ)2＝116相切，且θ为锐角，则该直线的斜率是( )A ．－33 B ．－ 3 C.33D. 3 1．判断直线与圆的位置关系常用的两种方法(1)几何法：利用圆心到直线的距离d 和圆半径r 的大小关系． d <r ⇔相交；d ＝r ⇔相切；d >r ⇔相离． (2)代数法：――――→判别式Δ＝b 2－4ac⎩⎪⎨⎪⎧>0⇔相交；＝0⇔相切；<0⇔相离.2．圆与圆的位置关系设圆O 1：(x －a 1)2＋(y －b 1)2＝r 21(r 1>0)， 圆O 2：(x －a 2)2＋(y －b 2)2＝r 22(r 2>0).【知识拓展】1．圆的切线方程常用结论(1)过圆x 2＋y 2＝r 2上一点P (x 0，y 0)的圆的切线方程为x 0x ＋y 0y ＝r 2.(2)过圆(x －a )2＋(y －b )2＝r 2上一点P (x 0，y 0)的圆的切线方程为(x 0－a )(x －a )＋(y 0－b )(y －b )＝r 2. (3)过圆x 2＋y 2＝r 2外一点M (x 0，y 0)作圆的两条切线，则两切点所在直线方程为x 0x ＋y 0y ＝r 2. 2．圆与圆的位置关系的常用结论(1)两圆的位置关系与公切线的条数：①内含：0条；②内切：1条；③相交：2条；④外切：3条；⑤外离：4条．(2)当两圆相交时，两圆方程(x 2，y 2项系数相同)相减便可得公共弦所在直线的方程． 一、与圆有关的最值问题典例1 (1)已知点A ，B ，C 在圆x 2＋y 2＝1上运动，且AB ⊥BC .若点P 的坐标为(2,0)，则|P A →＋PB →＋PC →|的最大值为( ) A ．6 B ．7 C ．8 D ．9(2)过点(2，0)引直线l 与曲线y ＝1－x 2相交于A 、B 两点，O 为坐标原点，当△AOB 的面积取最大值时，直线l 的斜率等于( ) A.33 B ．－33 C ．±33D ．－ 3 二、直线与圆的综合问题典例2 (1)已知直线l ：x ＋ay －1＝0(a ∈R )是圆C ：x 2＋y 2－4x －2y ＋1＝0的对称轴，过点A (－4，a )作圆C 的一条切线，切点为B ，则|AB |等于( ) A ．2 B ．4 2 C ．6 D ．210(2)在平面直角坐标系中，A ，B 分别是x 轴和y 轴上的动点，若以AB 为直径的圆C 与直线2x ＋y －4＝0相切，则圆C 面积的最小值为( ) A.45π B.34π C ．(6－25)πD.54π 1．圆(x －1)2＋(y ＋2)2＝6与直线2x ＋y －5＝0的位置关系是( ) A ．相切 B ．相交但直线不过圆心 C ．相交过圆心D ．相离2．圆x 2＋y 2－2x －8y ＋13＝0的圆心到直线ax ＋y －1＝0的距离为1，则a 等于( ) A ．－43 B ．－34C. 3 D ．23．若点A ，B 为圆(x －2)2＋y 2＝25上的两点，点P (3，－1)为弦AB 的中点，则弦AB 所在的直线方程为________．4．已知圆C 1：(x －2)2＋(y －3)2＝1，圆C 2：(x －3)2＋(y －4)2＝9，M ，N 分别是圆C 1，C 2上的动点，P 为x 轴上的动点，则|PM |＋|PN |的最小值为_____．1．平行于直线2x ＋y ＋1＝0且与圆x 2＋y 2＝5相切的直线的方程是( ) A ．2x ＋y ＋5＝0或2x ＋y －5＝0 B ．2x ＋y ＋5＝0或2x ＋y －5＝0 C ．2x －y ＋5＝0或2x －y －5＝0 D ．2x －y ＋5＝0或2x －y －5＝02．若点A (1,0)和点B (4,0)到直线l 的距离依次为1和2，则这样的直线有( ) A ．1条 B ．2条 C ．3条 D ．4条3．若圆C 1：x 2＋y 2－2ax ＋a 2－9＝0(a ∈R )与圆C 2：x 2＋y 2＋2by ＋b 2－1＝0(b ∈R )内切，则ab 的最大值为( )A. 2 B ．2 C ．4 D ．2 24．过点P (3,1)作圆C ：(x －1)2＋y 2＝1的两条切线，切点分别为A ，B ，则直线AB 的方程为( ) A ．2x ＋y －3＝0 B ．2x －y －3＝0 C ．4x －y －3＝0D ．4x ＋y －3＝05．若直线l ：y ＝kx ＋1(k <0)与圆C ：x 2＋4x ＋y 2－2y ＋3＝0相切，则直线l 与圆D ：(x －2)2＋y 2＝3的位置关系是( ) A ．相交 B ．相切 C ．相离 D ．不确定6．已知圆C ：x 2＋(y －3)2＝4，过A (－1,0)的直线l 与圆C 相交于P ，Q 两点，若|PQ |＝23，则直线l 的方程为( )A ．x ＝－1或4x ＋3y －4＝0B ．x ＝－1或4x －3y ＋4＝0C ．x ＝1或4x －3y ＋4＝0D ．x ＝1或4x ＋3y －4＝07．设直线y ＝x ＋2a 与圆C ：x 2＋y 2－2ay －2＝0相交于A ，B 两点，若|AB |＝23，则圆C 的面积为________．8．过点(1，2)的直线l 将圆(x －2)2＋y 2＝4分成两段弧，当劣弧所对的圆心角最小时，直线l 的斜率k ＝________.9．已知点A (1－m,0)，B (1＋m ，0)，若圆C ：x 2＋y 2－8x －8y ＋31＝0上存在一点P 使得P A →·PB →＝0，则正实数m 的最小值为________．10．在平面直角坐标系xOy中，圆C的方程为x2＋y2－8x＋15＝0，若直线y＝kx－2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值是________．11．已知圆C：x2＋y2＋2x－4y＋1＝0，O为坐标原点，动点P在圆C外，过P作圆C的切线，设切点为M.(1)若点P运动到(1,3)处，求此时切线l的方程；(2)求满足条件|PM|＝|PO|的点P的轨迹方程．12．圆O1的方程为x2＋(y＋1)2＝4，圆O2的圆心坐标为(2,1)．(1)若圆O1与圆O2外切，求圆O2的方程；(2)若圆O1与圆O2相交于A，B两点，且|AB|＝22，求圆O2的方程．*13已知直线l：4x＋3y＋10＝0，半径为2的圆C与l相切，圆心C在x轴上且在直线l的右上方．(1)求圆C的方程；(2)过点M(1,0)的直线与圆C交于A，B两点(A在x轴上方)，问在x轴正半轴上是否存在定点N，使得x轴平分∠ANB？若存在，请求出点N的坐标；若不存在，请说明理由．直线与圆、圆与圆的位置关系判断下列结论是否正确(请在括号中打“√”或“×”)(1)如果两个圆的方程组成的方程组只有一组实数解，则两圆外切．(×)(2)如果两圆的圆心距小于两圆的半径之和，则两圆相交．(×)(3)从两圆的方程中消掉二次项后得到的二元一次方程是两圆的公共弦所在的直线方程．(×)(4)过圆O：x2＋y2＝r2上一点P(x0，y0)的圆的切线方程是x0x＋y0y＝r2.(√)(5)过圆O：x2＋y2＝r2外一点P(x0，y0)作圆的两条切线，切点分别为A，B，则O，P，A，B四点共圆且直线AB的方程是x0x＋y0y＝r2.(√)无题型一直线与圆的位置关系的判断例1(1)已知点M(a，b)在圆O：x2＋y2＝1外，则直线ax＋by＝1与圆O的位置关系是() A．相切B．相交C．相离D．不确定(2)圆x2＋y2－2x＋4y＝0与直线2tx－y－2－2t＝0(t∈R)的位置关系为()A．相离B．相切C．相交D．以上都有可能答案(1)B(2)C解析(1)因为M(a，b)在圆O：x2＋y2＝1外，所以a2＋b2>1，而圆心O到直线ax＋by＝1的距离d＝|a·0＋b·0－1|a2＋b2＝1a2＋b2<1.所以直线与圆相交．(2)直线2tx－y－2－2t＝0恒过点(1，－2)，∵12＋(－2)2－2×1＋4×(－2)＝－5<0，∴点(1，－2)在圆x 2＋y 2－2x ＋4y ＝0内．直线2tx －y －2－2t ＝0与圆x 2＋y 2－2x ＋4y ＝0相交， 故选C.思维升华 判断直线与圆的位置关系的常见方法 (1)几何法：利用d 与r 的关系． (2)代数法：联立方程之后利用Δ判断．(3)点与圆的位置关系法：若直线恒过定点且定点在圆内，可判断直线与圆相交． 上述方法中最常用的是几何法，点与圆的位置关系法适用于动直线问题．过点A (3，1)的直线l 与圆x 2＋y 2＝1有公共点，则直线l 的斜率的取值范围是( )A ．[－1,1]B ．[0，3]C ．[0,1]D ．[－3，3]答案 B解析 设直线l 的方程为y －1＝k (x －3)，则圆心到直线l 的距离d ＝|3k －1|1＋k 2，因为直线l 与圆x 2＋y 2＝1有公共点，所以d ≤1，即|3k －1|1＋k 2≤1，得0≤k ≤ 3. 题型二 圆与圆的位置关系例2 (1)已知圆M ：x 2＋y 2－2ay ＝0(a ＞0)截直线x ＋y ＝0所得线段的长度是22，则圆M 与圆N ：(x －1)2＋(y －1)2＝1的位置关系是( ) A ．内切 B ．相交 C ．外切 D ．相离(2)如果圆C ：x 2＋y 2－2ax －2ay ＋2a 2－4＝0与圆O ：x 2＋y 2＝4总相交，那么实数a 的取值范围是______________________．答案(1)B(2)(－22，0)∪(0,22)解析(1)∵圆M：x2＋(y－a)2＝a2(a>0)，∴圆心坐标为M(0，a)，半径r1为a，圆心M到直线x＋y＝0的距离d＝|a|2，由几何知识得⎝⎛⎭⎫|a|22＋(2)2＝a2，解得a＝2.∴M(0,2)，r1＝2.又圆N的圆心坐标N(1,1)，半径r2＝1，∴|MN|＝(1－0)2＋(1－2)2＝2，r1＋r2＝3，r1－r2＝1.∴r1－r2＜|MN|＜r1＋r2，∴两圆相交，故选B.(2)圆C的标准方程为(x－a)2＋(y－a)2＝4，圆心坐标为(a，a)，半径为2. 依题意得0<a2＋a2<2＋2，∴0<|a|<2 2.∴a∈(－22，0)∪(0,22)．思维升华判断圆与圆的位置关系时，一般用几何法，其步骤是(1)确定两圆的圆心坐标和半径长；(2)利用平面内两点间的距离公式求出圆心距d，求r1＋r2，|r1－r2|；(3)比较d，r1＋r2，|r1－r2|的大小，写出结论．已知两圆x2＋y2－2x－6y－1＝0和x2＋y2－10x－12y＋m＝0.(1)m取何值时两圆外切；(2)m取何值时两圆内切；(3)求m ＝45时两圆的公共弦所在直线的方程和公共弦的长．解 两圆的标准方程分别为(x －1)2＋(y －3)2＝11，(x －5)2＋(y －6)2＝61－m ， 圆心分别为M (1,3)，N (5,6)，半径分别为11和61－m . (1)当两圆外切时，(5－1)2＋(6－3)2＝11＋61－m ， 解得m ＝25＋1011.(2)当两圆内切时，因为定圆的半径11小于两圆圆心间距离5， 故只有61－m －11＝5，解得m ＝25－1011. (3)两圆的公共弦所在直线方程为(x 2＋y 2－2x －6y －1)－(x 2＋y 2－10x －12y ＋45)＝0，即4x ＋3y －23＝0，所以公共弦长为2(11)2－(|4×1＋3×3－23|42＋32)2＝27.题型三 直线与圆的综合问题 命题点1 求弦长问题例3已知直线l ：mx ＋y ＋3m －3＝0与圆x 2＋y 2＝12交于A ，B 两点，过A ，B 分别做l 的垂线与x 轴交于C ，D 两点，若|AB |＝23，则|CD |＝________. 答案 4解析 设AB 的中点为M ，由题意知，圆的半径R ＝23，|AB |＝23，所以|OM |＝3，解得m ＝－33，由⎩⎨⎧x －3y ＋6＝0，x 2＋y 2＝12解得A (－3，3)，B (0，23)，则AC 的直线方程为y －3＝－3(x ＋3)， BD 的直线方程为y －23＝－3x ，令y ＝0，解得C (－2,0)，D (2,0)，所以|CD |＝4.命题点2 直线与圆相交求参数范围例4 已知过点A (0,1)且斜率为k 的直线l 与圆C ：(x －2)2＋(y －3)2＝1交于M ，N 两点． (1)求k 的取值范围；(2)若·＝12，其中O 为坐标原点，求|MN |. 解 (1)由题设，可知直线l 的方程为y ＝kx ＋1， 因为l 与C 交于两点，所以|2k －3＋1|1＋k 2<1. 解得4－73<k <4＋73.所以k 的取值范围为⎝⎛⎭⎪⎫4－73，4＋73.(2)设M (x 1，y 1)，N (x 2，y 2)．将y ＝kx ＋1代入方程(x －2)2＋(y －3)2＝1，整理得 (1＋k 2)x 2－4(1＋k )x ＋7＝0. 所以x 1＋x 2＝4(1＋k )1＋k 2，x 1x 2＝71＋k 2. ·＝x 1x 2＋y 1y 2＝(1＋k 2)x 1x 2＋k (x 1＋x 2)＋1＝4k (1＋k )1＋k 2＋8. 由题设可得4k (1＋k )1＋k 2＋8＝12，解得k ＝1，所以l 的方程为y ＝x ＋1.故圆心C 在l 上，所以|MN |＝2. 命题点3 直线与圆相切的问题例5 已知圆C ：(x －1)2＋(y ＋2)2＝10，求满足下列条件的圆的切线方程． (1)与直线l 1：x ＋y －4＝0平行； (2)与直线l 2：x －2y ＋4＝0垂直； (3)过切点A (4，－1)．解 (1)设切线方程为x ＋y ＋b ＝0， 则|1－2＋b |2＝10，∴b ＝1±25，∴切线方程为x ＋y ＋1±25＝0. (2)设切线方程为2x ＋y ＋m ＝0， 则|2－2＋m |5＝10，∴m ＝±52，∴切线方程为2x ＋y ±52＝0. (3)∵k AC ＝－2＋11－4＝13，∴过切点A (4，－1)的切线斜率为－3，∴过切点A (4，－1)的切线方程为y ＋1＝－3(x －4)， 即3x ＋y －11＝0.思维升华 直线与圆综合问题的常见类型及解题策略(1)处理直线与圆的弦长问题时多用几何法，即弦长的一半、弦心距、半径构成直角三角形． (2)圆的切线问题的处理要抓住圆心到直线的距离等于半径，从而建立关系解决问题．(1)过三点A (1,3)，B (4,2)，C (1，－7)的圆交y 轴于M 、N 两点，则|MN |等于( )A ．2 6B ．8C ．4 6D ．10(2)若直线x cos θ＋y sin θ－1＝0与圆(x －1)2＋(y －sin θ)2＝116相切，且θ为锐角，则该直线的斜率是( )A ．－33 B ．－ 3 C.33D. 3 答案 (1)C (2)A解析 (1)由已知，得＝(3，－1)，＝(－3，－9)， 则·＝3×(－3)＋(－1)×(－9)＝0， 所以⊥，即AB ⊥BC ，故过三点A 、B 、C 的圆以AC 为直径， 得其方程为(x －1)2＋(y ＋2)2＝25， 令x ＝0，得(y ＋2)2＝24，解得y 1＝－2－26，y 2＝－2＋26， 所以|MN |＝|y 1－y 2|＝46，选C.(2)依题意得，圆心到直线的距离等于半径， 即|cos θ＋sin 2θ－1|＝14，|cos θ－cos 2θ|＝14，所以cos θ－cos 2θ＝14或cos θ－cos 2θ＝－14(不符合题意，舍去)．由cos θ－cos 2θ＝14，得cos θ＝12，又θ为锐角，所以sin θ＝32，故该直线的斜率是－cos θsin θ＝－33，故选A.1．判断直线与圆的位置关系常用的两种方法(1)几何法：利用圆心到直线的距离d 和圆半径r 的大小关系． d <r ⇔相交；d ＝r ⇔相切；d >r ⇔相离． (2)代数法：――――→判别式Δ＝b 2－4ac⎩⎪⎨⎪⎧>0⇔相交；＝0⇔相切；<0⇔相离.2．圆与圆的位置关系设圆O 1：(x －a 1)2＋(y －b 1)2＝r 21(r 1>0)， 圆O 2：(x －a 2)2＋(y －b 2)2＝r 22(r 2>0).【知识拓展】1．圆的切线方程常用结论(1)过圆x 2＋y 2＝r 2上一点P (x 0，y 0)的圆的切线方程为x 0x ＋y 0y ＝r 2.(2)过圆(x －a )2＋(y －b )2＝r 2上一点P (x 0，y 0)的圆的切线方程为(x 0－a )(x －a )＋(y 0－b )(y －b )＝r 2.(3)过圆x2＋y2＝r2外一点M(x0，y0)作圆的两条切线，则两切点所在直线方程为x0x＋y0y＝r2.2．圆与圆的位置关系的常用结论(1)两圆的位置关系与公切线的条数：①内含：0条；②内切：1条；③相交：2条；④外切：3条；⑤外离：4条．(2)当两圆相交时，两圆方程(x2，y2项系数相同)相减便可得公共弦所在直线的方程．考点分析与圆有关的最值问题及直线与圆相结合的题目是近年来高考高频小考点．与圆有关的最值问题主要表现在求几何图形的长度、面积的最值，求点到直线的距离的最值，求相关参数的最值等方面．解决此类问题的主要思路是利用圆的几何性质将问题转化；直线与圆的综合问题主要包括弦长问题，切线问题及组成图形面积问题，解决方法主要依据圆的几何性质．一、与圆有关的最值问题典例1(1)已知点A，B，C在圆x2＋y2＝1上运动，且AB⊥BC.若点P的坐标为(2,0)，则|＋＋|的最大值为()A．6 B．7 C．8 D．9(2)过点(2，0)引直线l与曲线y＝1－x2相交于A、B两点，O为坐标原点，当△AOB的面积取最大值时，直线l的斜率等于()A.33B．－33C．±33D．－ 3解析(1)∵A，B，C在圆x2＋y2＝1上，且AB⊥BC，∴AC为圆的直径，故＋＝2＝(－4,0)，设B(x，y)，则x2＋y2＝1且x∈[－1,1]，＝(x－2，y)，∴＋＋＝(x－6，y)．故|＋＋|＝－12x＋37，∴当x＝－1时有最大值49＝7，故选B.(2)∵S△AOB＝12|OA||OB|sin∠AOB＝12sin∠AOB≤12.当∠AOB ＝π2时，△AOB 面积最大．此时O 到AB 的距离d ＝22. 设AB 方程为y ＝k (x －2)(k <0)， 即kx －y －2k ＝0.由d ＝|2k |k 2＋1＝22得k ＝－33.(也可k ＝－tan ∠OPH ＝－33)．答案 (1)B (2)B 二、直线与圆的综合问题典例2 (1)已知直线l ：x ＋ay －1＝0(a ∈R )是圆C ：x 2＋y 2－4x －2y ＋1＝0的对称轴，过点A (－4，a )作圆C 的一条切线，切点为B ，则|AB |等于( ) A ．2 B ．4 2 C ．6 D ．210(2)在平面直角坐标系中，A ，B 分别是x 轴和y 轴上的动点，若以AB 为直径的圆C 与直线2x ＋y －4＝0相切，则圆C 面积的最小值为( ) A.45π B.34π C ．(6－25)πD.54π 解析 (1)由于直线x ＋ay －1＝0是圆C ：x 2＋y 2－4x －2y ＋1＝0的对称轴，∴圆心C (2,1)在直线x ＋ay －1＝0上，∴2＋a －1＝0，∴a ＝－1，∴A (－4，－1)． ∴|AC |2＝36＋4＝40.又r ＝2，∴|AB |2＝40－4＝36. ∴|AB |＝6.(2)∵∠AOB ＝90°，∴点O 在圆C 上． 设直线2x ＋y －4＝0与圆C 相切于点D ，则点C 与点O 间的距离等于它到直线2x ＋y －4＝0的距离，∴点C 在以O 为焦点，以直线2x ＋y －4＝0为准线的抛物线上，∴当且仅当O ，C ，D 共线时，圆的直径最小为|OD |.又|OD |＝|2×0＋0－4|5＝45， ∴圆C 的最小半径为25， ∴圆C 面积的最小值为π(25)2＝45π.答案 (1)C (2)A1．圆(x －1)2＋(y ＋2)2＝6与直线2x ＋y －5＝0的位置关系是( ) A ．相切 B ．相交但直线不过圆心 C ．相交过圆心 D ．相离答案 B解析 由题意知圆心(1，－2)到直线2x ＋y －5＝0的距离d ＝|2×1－2－5|22＋1＝5<6且2×1＋(－2)－5≠0，所以直线与圆相交但不过圆心．2．圆x 2＋y 2－2x －8y ＋13＝0的圆心到直线ax ＋y －1＝0的距离为1，则a 等于( )A ．－43B ．－34 C. 3 D ．2答案 A解析 由圆的方程x 2＋y 2－2x －8y ＋13＝0，得圆心坐标为(1,4)，由点到直线的距离公式得d ＝|1×a ＋4－1|1＋a 2＝1，解得a ＝－43.3．若点A ，B 为圆(x －2)2＋y 2＝25上的两点，点P (3，－1)为弦AB 的中点，则弦AB 所在的直线方程为________． 答案 x －y －4＝0解析 设圆心为M ，则M (2,0)，∴k MP ＝－1， ∴直线AB 的斜率为1，∴直线AB 方程为y ＋1＝x －3，即x －y －4＝0.4．已知圆C 1：(x －2)2＋(y －3)2＝1，圆C 2：(x －3)2＋(y －4)2＝9，M ，N 分别是圆C 1，C 2上的动点，P 为x 轴上的动点，则|PM |＋|PN |的最小值为_____． 答案 52－4解析 圆C 1关于x 轴对称的圆C 1′的圆心为C 1′(2，－3)，半径不变，圆C 2的圆心为(3,4)，半径r ＝3，|PM |＋|PN |的最小值为圆C 1′和圆C 2的圆心距减去两圆的半径，所以|PM |＋|PN |的最小值为(3－2)2＋(4＋3)2－1－3＝52－4.1．平行于直线2x ＋y ＋1＝0且与圆x 2＋y 2＝5相切的直线的方程是( ) A ．2x ＋y ＋5＝0或2x ＋y －5＝0 B ．2x ＋y ＋5＝0或2x ＋y －5＝0 C ．2x －y ＋5＝0或2x －y －5＝0 D ．2x －y ＋5＝0或2x －y －5＝0答案 A解析 设所求直线方程为2x ＋y ＋c ＝0，依题有|0＋0＋c |22＋12＝5，解得c ＝±5，所以所求直线方程为2x＋y ＋5＝0或2x ＋y －5＝0，故选A.2．若点A (1,0)和点B (4,0)到直线l 的距离依次为1和2，则这样的直线有( ) A ．1条 B ．2条 C ．3条 D ．4条 答案 C解析 如图，分别以A ，B 为圆心，1,2为半径作圆．依题意得，直线l 是圆A 的切线，A 到l 的距离为1，直线l 也是圆B 的切线，B 到l 的距离为2，所以直线l 是两圆的公切线，共3条(2条外公切线，1条内公切线)．3．若圆C 1：x 2＋y 2－2ax ＋a 2－9＝0(a ∈R )与圆C 2：x 2＋y 2＋2by ＋b 2－1＝0(b ∈R )内切，则ab 的最大值为( )A. 2 B ．2 C ．4 D ．2 2 答案 B解析 圆C 1：x 2＋y 2－2ax ＋a 2－9＝0(a ∈R )． 化为(x －a )2＋y 2＝9，圆心坐标为(a,0)，半径为3.圆C 2：x 2＋y 2＋2by ＋b 2－1＝0(b ∈R )，化为x 2＋(y ＋b )2＝1，圆心坐标为(0，－b )，半径为1， ∵圆C 1：x 2＋y 2－2ax ＋a 2－9＝0(a ∈R )与圆C 2：x 2＋y 2＋2by ＋b 2－1＝0(b ∈R )内切， ∴a 2＋b 2＝3－1，即a 2＋b 2＝4，ab ≤12(a 2＋b 2)＝2.∴ab 的最大值为2.4．过点P (3,1)作圆C ：(x －1)2＋y 2＝1的两条切线，切点分别为A ，B ，则直线AB 的方程为( )A ．2x ＋y －3＝0B ．2x －y －3＝0C ．4x －y －3＝0D ．4x ＋y －3＝0答案 A解析 如图所示，由题意知：AB ⊥PC ，k PC ＝12，∴k AB ＝－2，∴直线AB 的方程为y －1＝－2(x －1)，即2x ＋y －3＝0.5．若直线l ：y ＝kx ＋1(k <0)与圆C ：x 2＋4x ＋y 2－2y ＋3＝0相切，则直线l 与圆D ：(x －2)2＋y 2＝3的位置关系是( )A ．相交B ．相切C ．相离D ．不确定答案 A解析 因为圆C 的标准方程为(x ＋2)2＋(y －1)2＝2，所以其圆心坐标为(－2,1)，半径为2，因为直线l 与圆C 相切．所以|－2k －1＋1|k 2＋1＝2，解得k ＝±1，因为k <0，所以k ＝－1，所以直线l 的方程为x ＋y －1＝0.圆心D (2,0)到直线l 的距离d ＝|2＋0－1|2＝22<3，所以直线l 与圆D 相交． 6．已知圆C ：x 2＋(y －3)2＝4，过A (－1,0)的直线l 与圆C 相交于P ，Q 两点，若|PQ |＝23，则直线l 的方程为( ) A ．x ＝－1或4x ＋3y －4＝0B ．x ＝－1或4x －3y ＋4＝0C ．x ＝1或4x －3y ＋4＝0D ．x ＝1或4x ＋3y －4＝0答案 B解析 当直线l 与x 轴垂直时，易知x ＝－1，符合题意；当直线l 与x 轴不垂直时，设直线l 的方程为y ＝k (x ＋1)，由|PQ |＝23，得圆心C 到直线l 的距离 d ＝|－k ＋3|k 2＋1＝1，解得k ＝43， 此时直线l 的方程为y ＝43(x ＋1)． 故所求直线l 的方程为x ＝－1或4x －3y ＋4＝0.7．设直线y ＝x ＋2a 与圆C ：x 2＋y 2－2ay －2＝0相交于A ，B 两点，若|AB |＝23，则圆C 的面积为________．答案 4π解析 圆C ：x 2＋y 2－2ay －2＝0，即C ：x 2＋(y －a )2＝a 2＋2，圆心为C (0，a )，C 到直线y ＝x ＋2a的距离d ＝|0－a ＋2a |2＝|a |2.又由|AB |＝23，得⎝⎛⎭⎫2322＋⎝⎛⎭⎫|a |22＝a 2＋2，解得a 2＝2，所以圆的面积为π(a 2＋2)＝4π.8．过点(1，2)的直线l 将圆(x －2)2＋y 2＝4分成两段弧，当劣弧所对的圆心角最小时，直线l 的斜率k ＝________.答案22 解析 ∵(1－2)2＋(2)2＝3<4，∴点(1，2)在圆(x －2)2＋y 2＝4的内部．当劣弧所对的圆心角最小时，圆心(2,0)与点(1，2)的连线垂直于直线l . ∵2－01－2＝－2，∴所求直线l 的斜率k ＝22. 9．已知点A (1－m,0)，B (1＋m ，0)，若圆C ：x 2＋y 2－8x －8y ＋31＝0上存在一点P 使得·＝0，则正实数m 的最小值为________．答案 4解析 圆C ：(x －4)2＋(y －4)2＝1，由已知P A ⊥PB ，设AB 的中点为M (1，0)， ∴|PM |＝12|AB |＝m ， 又|MC |＝5，r ＝1，∴4≤|PM |≤6，∴正实数m 的最小值为4.10．在平面直角坐标系xOy 中，圆C 的方程为x 2＋y 2－8x ＋15＝0，若直线y ＝kx －2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，则k 的最大值是________．答案 43解析 圆C 的标准方程为(x －4)2＋y 2＝1，圆心为(4,0)．由题意知(4,0)到kx －y －2＝0的距离应不大于2， 即|4k －2|k 2＋1≤2.整理，得3k 2－4k ≤0.解得0≤k ≤43. 故k 的最大值是43.11．已知圆C ：x 2＋y 2＋2x －4y ＋1＝0，O 为坐标原点，动点P 在圆C 外，过P 作圆C 的切线，设切点为M .(1)若点P 运动到(1,3)处，求此时切线l 的方程；(2)求满足条件|PM |＝|PO |的点P 的轨迹方程．解 把圆C 的方程化为标准方程为(x ＋1)2＋(y －2)2＝4，∴圆心为C (－1,2)，半径r ＝2.(1)当l 的斜率不存在时，此时l 的方程为x ＝1，C 到l 的距离d ＝2＝r ，满足条件．当l 的斜率存在时，设斜率为k ，得l 的方程为y －3＝k (x －1)，即kx －y ＋3－k ＝0， 则|－k －2＋3－k |1＋k 2＝2，解得k ＝－34. ∴l 的方程为y －3＝－34(x －1)， 即3x ＋4y －15＝0.综上，满足条件的切线l 的方程为x ＝1或3x ＋4y －15＝0.(2)设P (x ，y )，则|PM |2＝|PC |2－|MC |2＝(x ＋1)2＋(y －2)2－4，|PO |2＝x 2＋y 2，∵|PM |＝|PO |，∴(x ＋1)2＋(y －2)2－4＝x 2＋y 2，整理，得2x －4y ＋1＝0，∴点P的轨迹方程为2x－4y＋1＝0.12．圆O1的方程为x2＋(y＋1)2＝4，圆O2的圆心坐标为(2,1)．(1)若圆O1与圆O2外切，求圆O2的方程；(2)若圆O1与圆O2相交于A，B两点，且|AB|＝22，求圆O2的方程．解(1)圆O1的圆心坐标为(0，－1)，半径r1＝2，圆O2的圆心坐标为(2,1)，圆心距为|O1O2|＝(2－0)2＋(1＋1)2＝22，由两圆外切知，所求圆的半径为r2＝22－2，圆O2的方程为(x－2)2＋(y－1)2＝12－8 2.(2)由题意知，圆心O1到AB的距离为22－(2)2＝2，当圆心O2到AB的距离为22－2＝2时，圆O2的半径r2＝(2)2＋(2)2＝2，此时圆O2的方程为(x－2)2＋(y－1)2＝4.当圆心O2到AB的距离为22＋2＝32时，圆O2的半径r2′＝(32)2＋(2)2＝25，此时圆O2的方程为(x－2)2＋(y－1)2＝20.综上知，圆O2的方程为(x－2)2＋(y－1)2＝4或(x－2)2＋(y－1)2＝20.*13已知直线l：4x＋3y＋10＝0，半径为2的圆C与l相切，圆心C在x轴上且在直线l的右上方．(1)求圆C 的方程；(2)过点M (1,0)的直线与圆C 交于A ，B 两点(A 在x 轴上方)，问在x 轴正半轴上是否存在定点N ，使得x 轴平分∠ANB ？若存在，请求出点N 的坐标；若不存在，请说明理由．解 (1)设圆心C (a,0)(a >－52)， 则|4a ＋10|5＝2⇒a ＝0或a ＝－5(舍)． 所以圆C 的方程为x 2＋y 2＝4.(2)当直线AB ⊥x 轴时，x 轴平分∠ANB .当直线AB 的斜率存在时，设直线AB 的方程为y ＝k (x －1)，N (t,0)，A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧x 2＋y 2＝4，y ＝k (x －1)，得(k 2＋1)x 2－2k 2x ＋k 2－4＝0， 所以x 1＋x 2＝2k 2k 2＋1，x 1x 2＝k 2－4k 2＋1. 若x 轴平分∠ANB ，则k AN ＝－k BN ⇒y 1x 1－t ＋y 2x 2－t＝0 ⇒k (x 1－1)x 1－t ＋k (x 2－1)x 2－t＝0 ⇒2x 1x 2－(t ＋1)(x 1＋x 2)＋2t ＝0⇒2(k 2－4)k 2＋1－2k 2(t ＋1)k 2＋1＋2t ＝0⇒t ＝4， 所以当点N 为(4,0)时，能使得∠ANM ＝∠BNM 总成立．。

高三数学三角函数-图像与性质学生姓名授课日期教师姓名授课时长本讲义目的在于让同学从根本上了解三角函数的图像与性质，了解图像变换与解析式变换之间的对应关系，利用图像解决与三角函数有关的问题，并在此基础上发散思维，解决三角函数与其他知识融合的综合问题。

知识点一：由图像写解析式，突破识图难点；由性质写解析式，达到对条件的全面理解。

知识点二：通过解决图象与性质融合的新题目，既积累解题经验，又消除“怕新”“怕繁”的心理，提升思维品质与解题能力，适应各种变化。

知识点三：通过结合图象解决与三角函数有关的问题（如方程、不等式），发展用图象思考问题的能力。

知识点四：通过建立三角函数模型，体验建模的程序，发展应用意识和能力。

知识点五：通过解决三角函数与其他知识融合的综合问题，感悟知识之间的联系，体验解题过程的复杂性，发展综合运用能力。

【题目来源】【题目】 已知定义域为R 的函数（）（）ωϕ=+f x Asin x （A ＞0，ω＞0）的一段图象如图所示．（1）求（）f x 的解析式；（2）若3?（），（）（）（）==g x cos x h x f x g x ，求函数h （x ）的单调递增区间．【难度系数】3【题目来源】【题目】 求下列函数的最小正周期(1))23πsin(x y -=；(2))4π2πtan(+=x y ；x y 2cos )3(2=；(4)y ＝2sin 2x ＋2sin x cos x ；(5)y ＝｜sin x ｜． 【难度系数】3【题目来源】 【题目】（2000全国，5）函数y ＝－xc os x 的部分图象是（ ）【难度系数】2【题目来源】【题目】 已知函数（）（）φω=+f x Asin x （A>0，ω>0，x ∈R ）在一个周期内的图象如图所示，求直线y =f （x ）图象的所有交点的坐标。

【难度系数】3【题目来源】【题目】如下图弹簧挂着的小球作上下振动,时间t(s)与小球对于平衡位置(即静止时状态)的高度h(cm)之间的关系式是,t∈[0,+∞). 画出这个函数在长度为一个周期的闭区间上的简图,回答下列问题.(1)小球开始振动的位置在哪里?(2)小球最高､最低点与平衡位置的距离分别为多少?(3)经过多长时间小球往复振动一次(即周期是多少)?(4)小球每1 s能往复振动多少次?【难度系数】3【题目来源】【题目】[变式题]:如下图,单摆从某点开始来回摆动,离开平衡位置O的距离s cm和时间t s的函数关系式为), 那么单摆来回摆动一次所需的时间为( )A.2π sB.π sC.0.5 sD.1 s【难度系数】2试题演练【题目来源】【题目】得到2()3y tan x π=-的图象,只要将y=tan2x 的图象( )A.向左平移3π个单位 B.向右平移3π个单位C.向左平移6π个单位D.向右平移6π个单位【难度系数】2【题目来源】【题目】若A ､B 是锐角△ABC 的两个内角,则点P(cosB-sinA,sinB-cosA)在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 【难度系数】3【题目来源】 【题目】如下图,表示电流强度I 与时间t 的关系为I=Asin(ωt+φ)(A>0,ω>0)在一个周期内的图象,则该函数的解析式为( )A.I=300sin(50πt+3π)B.I=300sin(50πt-3π)C.I=300sin(100πt+3π)D.I=300sin(100πt- 3π)【难度系数】3【题目来源】【题目】函数y ＝sin(x ＋ϕ)的图象(部分)如图所示，则和ϕ的取值是( )A ．3π,1==ϕωB ．3π,1-==ϕω C ．6π,21==ϕωD ．6π,21-==ϕω【难度系数】3【题目来源】【题目】在△ABC 中．Sin 2A≤sin 2B+sin 2C-sinBsinC ．则A 的取值范围是 （ ） A ．06]（，π B ．[),6ππ C ．(0,]3π D ．[,)3ππ【难度系数】3【题目来源】 【题目】在△ABC 中，内角A ，B ，C 所对的边分别是a,b,c ，已知8b=5c ，C=2B ，则cosC=（ ） A.725 B. -725 C. ±725D. 2425【难度系数】3【题目来源】 【题目】设当θ=x 时，函数()2＝－f x sinx cosx 取得最大值，则θcos = ( )D.5【难度系数】3【题目来源】 【题目】 函数y sin()cos()26ππ=+-x x 的最大值为（ ）【难度系数】3【题目来源】 【题目】已知函数()(2)ϕ=+f x sin x ，其中ϕ为实数，若()|()|6π≤f x f 对x∈R 恒成立，且()()2ππ>f f ，则f(x)的单调递增区间是（ ） A.() ,k [k ]36ππππ-+∈k ZB. () ,k [k ]2πππ+∈k Z C. ()2 ,k 3[k ]6ππππ++∈k Z D. ()[k 2 ,k ]2πππ-∈k Z【难度系数】3【题目来源】 【题目】设函数()()()ϕϕωω=+++f x sin x cos x ，|)0,|2(πϕω><的最小正周期为π，且f(-x)=f(x),则（ ） A.y=f(x) 在(0,)2π单调递减B. y=f(x)在(,43)ππ单调递减 C. y=f(x)在(0,)2π单调递增D. y=f(x)在(3,44)ππ单调递增 【难度系数】3【题目来源】 【题目】A.1[25,4] B.1[23,4] C.[01,2] D.[0,2] 【难度系数】3【题目来源】 【题目】【难度系数】3【题目来源】 【题目】A ．22－1 B ．22＋1 C ．1－22D ．－1－22 【难度系数】3【题目来源】 【题目】（1）已知f （x ）的定义域为［0，1］，求f （cosx ）的定义域； （2）求函数y=lgsin （cosx ）的定义域；分析：求函数的定义域：（1）要使0≤cosx ≤1，（2）要使sin （cosx ）＞0，这里的cosx 以它的值充当角。

§1.3函数的基本性质1.3.1单调性与最大(小)值第1课时函数的单调性学习目标1.了解函数的单调区间、单调性等概念.2.会划分函数的单调区间，判断单调性.3.会用定义证明函数的单调性.知识点一增函数与减函数的定义设函数f(x)的定义域为I：(1)如果对于定义域I内某个区间D上的任意两个自变量的值x1，x2，当x1<x2时，都有f(x1)<f(x2)，那么就说函数f(x)在区间D上是增函数.(2)如果对于定义域I内某个区间D上的任意两个自变量的值x1，x2，当x1<x2时，都有f(x1)>f(x2)，那么就说函数f(x)在区间D上是减函数.思考(1)所有的函数在定义域上都具有单调性吗？(2)在增函数和减函数定义中，能否把“任意x1，x2∈D”改为“存在x1，x2∈D”？答案(1)不是.(2)不能.知识点二函数的单调区间如果函数y＝f(x)在区间D上是增函数或减函数，那么就说函数y＝f(x)在这一区间具有(严格的)单调性，区间D叫做y＝f(x)的单调区间.特别提醒：(1)函数单调性关注的是整个区间上的性质，单独一点不存在单调性问题，所以单调区间的端点若属于定义域，则该点处区间可开可闭，若区间端点不属于定义域则只能开.(2)单调区间D⊆定义域I.(3)遵循最简原则，单调区间应尽可能大.1.如果f(x)在区间[a，b]和(b，c]上都是增函数，则f(x)在区间[a，c]上是增函数.(×)2.函数f(x)为R上的减函数，则f(－3)>f(3).(√)3.若函数y＝f(x)在定义域上有f(1)<f(2)，则函数y＝f(x)是增函数.(×)4.若函数y＝f(x)在区间D上是增函数，则函数y＝－f(x)在区间D上是减函数.(√)题型一利用图象判断函数单调性例1(1)如图是定义在区间[－5,5]上的函数y＝f(x)，根据图象说出函数的单调区间，以及在每一单调区间上，它是增函数还是减函数？考点 求函数的单调区间 题点 求函数的单调区间解 y ＝f (x )的单调区间有[－5，－2)，[－2,1)，[1,3)，[3,5]，其中y ＝f (x )在区间[－5，－2)，[1,3)上是减函数，在区间[－2,1)，[3,5]上是增函数. (2)函数y ＝1x －1的单调递减区间是________.答案 (－∞，1)，(1，＋∞)解析 y ＝1x －1的图象可由y ＝1x 的图象向右平移一个单位得到，如图，∴单调减区间是(－∞，1)，(1，＋∞).反思感悟 函数的单调性是在定义域内的某个区间上的性质，单调区间是定义域的子集；当函数出现两个以上单调区间时，单调区间之间可用“，”分开，不能用“∪”，可以用“和”来表示；在单调区间D 上函数要么是增函数，要么是减函数，不能二者兼有.跟踪训练1(1)函数y＝f(x)，x∈[－4,4]的图象如图所示，则函数f(x)的所有单调递减区间为()A.[－4，－2]B.[1,4]C.[－4，－2]和[1,4]D.[－4，－2]∪[1,4]答案 C(2)函数y＝|x2－2x－3|的图象如图所示，试写出它的单调区间，并指出单调性.考点求函数的单调区间题点求函数的单调区间解y＝|x2－2x－3|的单调区间有(－∞，－1]，[－1,1]，[1,3]，[3，＋∞)，其中单调递减区间是(－∞，－1]，[1,3]；单调递增区间是[－1,1]，[3，＋∞).题型二函数单调性的证明例2求证：函数f(x)＝x＋1x在[1，＋∞)上是增函数.考点 函数的单调性的判定与证明 题点 定义法证明具体函数的单调性证明 设x 1，x 2是[1，＋∞)上的任意实数，且1≤x 1<x 2，则f (x 1)－f (x 2)＝x 1＋1x 1－⎝⎛⎭⎫x 2＋1x 2 ＝(x 1－x 2)＋⎝⎛⎭⎫1x 1－1x 2＝(x 1－x 2)＋x 2－x 1x 1x 2 ＝(x 1－x 2)⎝⎛⎭⎫1－1x 1x 2＝(x 1－x 2)⎝⎛⎭⎫x 1x 2－1x 1x 2. ∵1≤x 1<x 2，∴x 1－x 2<0,1<x 1x 2， ∴x 1x 2－1x 1x 2>0，故(x 1－x 2)⎝⎛⎭⎫x 1x 2－1x 1x 2<0，即f (x 1)－f (x 2)<0，即f (x 1)<f (x 2).∴f (x )＝x ＋1x在区间[1，＋∞)上是增函数.反思感悟 定义法证明或判断函数单调性的四个步骤跟踪训练2 利用定义判断f (x )＝2xx ＋3在区间(0，＋∞)上的单调性.解 任取x 1，x 2∈(0，＋∞)且x 1<x 2，则 f (x 2)－f (x 1)＝2x 2x 2＋3－2x 1x 1＋3＝2[x 2(x 1＋3)－x 1(x 2＋3)](x 1＋3)(x 2＋3)＝6(x 2－x 1)(x 1＋3)(x 2＋3).因为x 1<x 2，且x 1，x 2∈(0，＋∞)， 所以x 2－x 1>0，x 1＋3>0，x 2＋3>0， 所以f (x 2)－f (x 1)>0，所以f (x )＝2xx ＋3在区间(0，＋∞)上是增函数.题型三 函数单调性的应用例3 已知函数f (x )＝x 2＋2(a －1)x ＋2在区间(－∞，4]上是减函数，求实数a 的取值范围. 解 f (x )＝x 2＋2(a －1)x ＋2的开口方向向上，对称轴为x ＝1－a ， ∵f (x )＝x 2＋2(a －1)x ＋2在区间(－∞，4]上是减函数， ∴4≤1－a ， ∴a ≤－3，∴a 的取值范围是(－∞，－3]. 延伸探究1.若f (x )＝x 2＋2(a －1)x ＋2的单调减区间为(－∞，4]，则a 的值是什么？ 解 ∵f (x )＝x 2＋2(a －1)x ＋2的单调减区间为(－∞，1－a ]， ∴1－a ＝4， ∴a ＝－3.2.若f (x )＝x 2＋2(a －1)x ＋2在区间[2,4]上单调，则a 的取值范围是什么？ 解 ∵f (x )＝x 2＋2(a －1)x ＋2在区间[2,4]上单调， ∴二次函数的对称轴x ＝1－a 一定不在区间(2,4)内， ∴1－a ≤2或1－a ≥4， 即a ≥－1或a ≤－3，∴a 的取值范围为(－∞，－3]∪[－1，＋∞).3.若y ＝f (x )是定义在(－1,1)上的减函数，且f (1－a )<f (2a －1)，求a 的取值范围. 解 f (1－a )<f (2a －1)等价于 ⎩⎪⎨⎪⎧－1<1－a <1，－1<2a －1<1，1－a >2a －1，解得0<a <23，即所求a 的取值范围是⎩⎨⎧⎭⎬⎫a |0<a <23.反思感悟 函数单调性的应用(1)函数单调性定义的“双向性”：利用定义可以判断、证明函数的单调性，反过来，若已知函数的单调性可以确定函数中参数的取值范围.(2)若一个函数在区间[a ，b ]上是单调的，则此函数在这一单调区间内的任意子集上也是单调的.1.函数y ＝f (x )在区间[－2,2]上的图象如图所示，则此函数的增区间是( )A.[－2,0]B.[0,1]C.[－2,1]D.[－1,1]考点 求函数的单调区间 题点 求函数的单调区间 答案 C2.函数y ＝6x 的减区间是( )A.[0，＋∞)B.(－∞，0]C.(－∞，0)，(0，＋∞)D.(－∞，0)∪(0，＋∞)答案 C3.函数y＝x2－6x的单调递减区间是()A.(－∞，2]B.[2，＋∞)C.[3，＋∞)D.(－∞，3]答案 D解析y＝x2－6x的开口方向向上，对称轴为x＝3.所以其单调递减区间是(－∞，3].4.下列说法中正确的是()A.定义在(a，b)上的函数f(x)，若存在x1，x2∈(a，b)，使得当x1<x2时有f(x1)<f(x2)，则f(x)在(a，b)上为增函数B.定义在(a，b)上的函数f(x)，若有无穷多对x1，x2∈(a，b)，使得当x1<x2时有f(x1)<f(x2)，则f(x)在(a，b)上为增函数C.若f(x)在区间A上为减函数，在区间B上也为减函数，则f(x)在A∪B上也为减函数D.若f(x)在区间I上为增函数且f(x1)<f(x2)(x1，x2∈I)，则x1<x2答案 D5.若函数y＝f(x)在R上单调递减，且f(2m)>f(1＋m)，则实数m的取值范围是__________. 答案(－∞，1)解析由2m<1＋m得m<1.1.证明函数的单调性时要注意以下几点(1)用定义证明函数单调性时，易忽视x1，x2的任意性.(2)要证明f(x)在[a，b]上不是单调函数，只要举出一个反例即可.2.判断函数的单调性可用定义法、直接法、图象法，而函数单调性的证明现在只能用定义证明.3.已知函数单调性求参数的范围时，要树立两种意识：一是等价转化意识：如f(x)在D上递增，则f(x1)<f(x2)⇔x1<x2.二是数形结合意识：如处理一(二)次函数及反比例函数中的含参数的范围问题.一、选择题1.如图是定义在区间[－5,5]上的函数y＝f(x)，则下列关于函数f(x)的说法错误的是()A.函数在区间[－5，－3]上单调递增B.函数在区间[1,4]上单调递增C.函数在区间[－3,1]∪[4,5]上单调递减D.函数在区间[－5,5]上没有单调性答案 C解析单调区间不能用“∪”连接.2.下列函数中，在区间(0,2)上为增函数的是()A.y ＝3－xB.y ＝x 2＋1C.y ＝1xD.y ＝－|x ＋1|答案 B解析 y ＝x 2＋1在(0,2)上是增函数. 3.函数y ＝|x ＋2|在区间[－3,0]上( )A.递减B.递增C.先减后增D.先增后减答案 C解析 因为y ＝|x ＋2|＝⎩⎪⎨⎪⎧x ＋2，x ≥－2，－x －2，x <－2.作出y ＝|x ＋2|的图象， 如图所示，易知在[－3，－2)上为减函数，在[－2,0]上为增函数.4.已知函数f (x )是R 上的增函数，A (0，－1)，B (3,1)是其图象上的两点，那么－1<f (x )<1的解集是( )A.(－3,0)B.(0,3)C.(－∞，－1]∪[3，＋∞)D.(－∞，0]∪[1，＋∞)考点 函数单调性的应用题点 利用单调性解抽象函数不等式答案 B解析 由已知f (0)＝－1，f (3)＝1，∴－1<f (x )<1，即f (0)<f (x )<f (3).又∵f (x )在R 上单调递增，∴0<x <3，∴－1<f (x )<1的解集为(0,3).5.函数f (x )＝－x 2＋2(a －3)x ＋1在区间[－2，＋∞)上单调递减，则实数a 的取值范围是( )A.(－∞，－1]B.(－∞，1]C.[－1，＋∞)D.[1，＋∞) 答案 B解析 二次函数开口向下，对称轴为x ＝a －3，∴a －3≤－2，∴a ≤1.6.已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋4x ，x ≥0，4x －x 2，x <0，若f (4－a )>f (a )，则实数a 的取值范围是( ) A.(－∞，2)B.(2，＋∞)C.(－∞，－2)D.(－2，＋∞)考点 函数单调性的应用 题点 利用单调性解抽象函数不等式答案 A解析 画出f (x )的图象(图略)可判断f (x )在R 上单调递增，故f (4－a )>f (a )⇔4－a >a ，解得a <2.7.已知四个函数的图象如图所示，其中在定义域内具有单调性的函数是( )考点 函数的单调性的概念题点 函数单调性概念的理解答案 B解析 对于A ，存在x 1∈(0,1)，f (x 1)>f (1)，A 不对；对于C ，存在x 1>1，f (x 1)<f (1)，C 不对；对于D ，存在x 1＝－1，x 2＝1，f (x 1)<f (x 2)，D 不对；只有B 完全符合单调性定义.8.已知函数y ＝ax 和y ＝－b x在(0，＋∞)上都是减函数，则函数f (x )＝bx ＋a 在R 上是( )A.减函数且f (0)<0B.增函数且f (0)<0C.减函数且f (0)>0D.增函数且f (0)>0答案 A 解析 因为y ＝ax 和y ＝－b x在(0，＋∞)上都是减函数， 所以a <0，b <0，f (x )＝bx ＋a 为减函数且f (0)＝a <0，故选A.二、填空题9.已知函数f (x )＝⎩⎪⎨⎪⎧2x ＋1，x ≥1，5－x ，x <1，则f (x )的单调递减区间是________. 答案 (－∞，1)解析 当x ≥1时，f (x )是增函数，当x <1时，f (x )是减函数，所以f (x )的单调递减区间为(－∞，1).10.如果二次函数f (x )＝x 2－(a －1)x ＋5在区间⎝⎛⎭⎫12，1上是增函数，则实数a 的取值范围为________.答案 (－∞，2]解析 因为二次函数f (x )＝x 2－(a －1)x ＋5的图象的对称轴为直线x ＝a －12，又函数f (x )在区间⎝⎛⎭⎫12，1上是增函数，所以a －12≤12，解得a ≤2. 11.已知f (x )是定义在区间[－1,1]上的增函数，且f (x －2)<f (1－x )，则x 的取值范围是________. 考点 函数单调性的应用题点 利用单调性解抽象函数不等式答案 ⎣⎡⎭⎫1，32 解析 由题意，得⎩⎪⎨⎪⎧ －1≤x －2≤1，－1≤1－x ≤1，x －2<1－x ，解得1≤x <32， 故满足条件的x 的取值范围是⎣⎡⎭⎫1，32. 三、解答题12.求函数y ＝－x 2＋2|x |＋3的单调递增区间.考点 求函数的单调区间题点 求函数的单调区间解 ∵y ＝－x 2＋2|x |＋3＝⎩⎪⎨⎪⎧－x 2＋2x ＋3，x ≥0，－x 2－2x ＋3，x <0.函数图象如图所示，∴函数y ＝－x 2＋2|x |＋3的单调递增区间是(－∞，－1]和[0,1].13.证明：函数f (x )＝x 2－1x在区间(0，＋∞)上是增函数. 证明 任取x 1，x 2∈(0，＋∞)，且x 1<x 2，则f (x 1)－f (x 2)＝x 21－1x 1－x 22＋1x 2＝(x 1－x 2)·⎝⎛⎭⎫x 1＋x 2＋1x 1x 2. 因为0<x 1<x 2，所以x 1－x 2<0，x 1＋x 2＋1x 1x 2>0. 所以f (x 1)－f (x 2)<0，即f (x 1)<f (x 2).所以函数f (x )＝x 2－1x在区间(0，＋∞)上是增函数.14.若f (x )＝－x 2＋2ax 与g (x )＝a x ＋1在区间[1,2]上都是减函数，则a 的取值范围是____________.考点 函数单调性的应用 题点 已知二次函数单调性求参数范围答案 (0,1]解析 由f (x )＝－x 2＋2ax 在[1,2]上是减函数可得a ≤1.由g (x )＝a x ＋1在[1,2]上是减函数可得a >0.∴0<a ≤1.15.设f (x )是定义在(0，＋∞)上的函数，满足条件：(1)f (xy )＝f (x )＋f (y )；(2)f (2)＝1；(3)在(0，＋∞)上是增函数.如果f (2)＋f (x －3)≤2，求x 的取值范围.解 ∵f (xy )＝f (x )＋f (y )，∴令x ＝y ＝2，得f (4)＝f (2)＋f (2)＝2f (2).又f (2)＝1，∴f (4)＝2.∵f (2)＋f (x －3)＝f (2(x －3))＝f (2x －6)，∴f (2x －6)≤2＝f (4)，即f (2x －6)≤f (4).∵f (x )是定义在(0，＋∞)上的增函数，∴⎩⎪⎨⎪⎧ x －3＞0，2x －6≤4，解得3＜x ≤5.故x 的取值范围为(3,5].。