高中数学专题讲义-线性规划

初学讲义之高中数学二十五线性规划一、直线分割平面1.1 直线的两边学习线性规划前，先要补充学习一块坐标几何的内容如上图所示，中间的黑色线直线的函数为：y=x，写成方程为x-y=0由于直线是向两头无限延伸的，可以认为它把整个平面分为3个部分：直线本身(黑)、左(红)、右(蓝)可以叫左右，也可以叫上下，都一样。

其实平面上任何一条直线都可以把平面分成这三部分。

现在我们简单了解一下两边的情况。

1.2 直线的平移在学习一次函数时，已经学过函数的平移，这里直接用结论对直线y=x，如果把它变成y=(x-a)，就是向右平移a个单位（若a＜0就是向左）如果把它变成y=x+b，就是向上平移b个单位（若b＜0就是向下）对上面的两个平移，如果我们令a=-b，那么平移后得到的函数是相同的，都是y=x+b也就是说当a=-b时，向右平移a和向上平移b的结果是相同的现在具体令a=-b=2，我们来分别平移：如上图，黑色直线为y=x，红色直线为y=x-2首先按照向右平移，也就是橙色的箭头，变成y=(x-2)原来的(0,0)就被平移到了(2,0)，类似的，直线上的其他点(x_{0},y_{0})都平移到了 (x_{0}+2,y_{0})再来向上（下）平移，也就是粉色的箭头，变成y=x+(-2)原来的(0,0)就被平移到了(0,-2)，类似的，直线上的其他点(x_{0},y_{0})都平移到了 (x_{0},y_{0}-2)虽然翻译的方向不同，但结果是一样的。

上面是用一次函数表示直线，下面用方程来表现会更加直观：原直线：x-y=0新直线：x-y-a=0当a＞0时，直线向右（或下）平移当a＜0时，直线向左（或上）平移直线向右（或下）前进的过程中，扫过了全部的半个平面直线向左（或上）前进的过程中，扫过了全部的另外半个平面1.3 确定在哪边我们对新直线方程x-y-a=0变个形：a=x-y也就是说，直线右边（或下边）的所有点，都是a＞0的，也就是x-y＞0直线左边（或上边）的所有点，都是a＜0的，也就是x-y＜0因此直线x-y=0将平面分为3个部分，这3部分的点分别满足：x-y=0x-y＞0x-y＜0分别对应直线上（黑色），直线右边或下边（蓝色），直线左边或上边（红色）对任何直线都是如此1.4 举例再举2个其他的例子：例1：2x+3y-6=0它也把直线分为3个部分为了找到对应关系，随便代入某个点即可，比如在直线左侧的最简单的（0,0）：2*0+3*0-6=-6＜0因此对该直线，符合2x+3y-6＜0的点在左侧（或下侧），符合2x+3y-6＞0的点在右侧（或上侧）例2：-2x+3y+6=0代入在左侧的（0,0）：-2*0+3*0+6=6＞0因此对该直线，符合-2x+3y+6＞0的点在左侧（或上侧），符合-2x+3y+6＜0的点在右侧（或右侧）要注意的是从上面两个例子可以看出：1、对每条直线，“＞和＜“与“右还是左（下还是上）”的对应关系需要单独确定2、“上下”和“左右”通常也没有对应关系，只是为了方便的叫法1.5 围出一个多边形现在我们在一个坐标系内同时画上上面三条直线：x-y=0（红）2x+3y-6=0（绿）-2x+3y+6=0（蓝）这三条直线把平面分为好几个部分（懒得数了），中间围出一个三角形（阴影部分）那么这个阴影部分该如何表示呢？很简单，随便取个点，分别代入3条边试出不等号即可为方便运算，就取（2,0）吧，0越多越好，整数越多越好：代入x-y：2-0=2＞0代入2x+3y-6：2*2+3*0-6=-2＜0代入-2x+3y+6：-2*2+3*0+6=2＞0因此阴影部分的点可以用下面这个不等式组来表示：x-y＞02x+3y-6＜0-2x+3y+6＞0（此处左边应有大括号{，由于输入法原因无法实现）1.5.2 再加条直线再加条直线看看：x-y=0（红）2x+3y-6=0（绿）-2x+3y+6=0（蓝）x+y+2=0（黄）这下围出了四边形，也有三角形，和其他开放的图形如果想要知道此时阴影部分四边形点的特征，再加上第四条黄色的直线的不等式即可：还是代入(2,0)：2+0+2=4＞0因此中间阴影四边形中点的坐标符合：x-y＞02x+3y-6＜0-2x+3y+6＞0x+y+2＞0如果您想包含边界，只需将大于号和小于号更改为大于或等于号和小于或等于号。

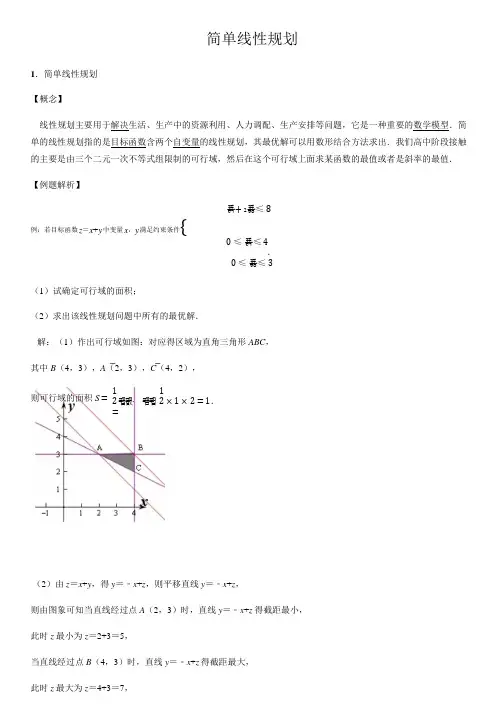
简单线性规划1．简单线性规划【概念】线性规划主要用于解决生活、生产中的资源利用、人力调配、生产安排等问题，它是一种重要的数学模型．简单的线性规划指的是目标函数含两个自变量的线性规划，其最优解可以用数形结合方法求出．我们高中阶段接触的主要是由三个二元一次不等式组限制的可行域，然后在这个可行域上面求某函数的最值或者是斜率的最值．【例题解析】푥+2푦≤8例：若目标函数z＝x+y 中变量x，y 满足约束条件{0≤푥≤4．0≤푦≤3（1）试确定可行域的面积；（2）求出该线性规划问题中所有的最优解．解：（1）作出可行域如图：对应得区域为直角三角形ABC，其中B（4，3），A（2，3），C（4，2），则可行域的面积S =12퐵퐶⋅퐴퐵=12×1×2=1．（2）由z＝x+y，得y＝﹣x+z，则平移直线y＝﹣x+z，则由图象可知当直线经过点A（2，3）时，直线y＝﹣x+z 得截距最小，此时z 最小为z＝2+3＝5，当直线经过点B（4，3）时，直线y＝﹣x+z 得截距最大，此时z 最大为z＝4+3＝7，1/ 5故该线性规划问题中所有的最优解为（4，3），（2，3）这是高中阶段接触最多的关于线性规划的题型，解这种题一律先画图，把每条直线在同一个坐标系中表示出来，然后确定所表示的可行域，也即范围；最后通过目标函数的平移去找到它的最值．【典型例题分析】题型一：二元一次不等式（组）表示的平面区域典例 1：若不等式组所表示的平面区域被直线y＝kx+分为面积相等的两部分，则k 的值是（）7343A．3B．7C．3D．44 4分析：画出平面区域，显然点（0，）在已知的平面区域内，直线系过定点（0，），结合图形寻找直线平分平33面区域面积的条件即可．解答：不等式组表示的平面区域如图所示．由于直线y＝kx +44过定点（0，）．因此只有直线过AB 中点时，直线y＝kx +3343能平分平面区域．15因为A（1，1），B（0，4），所以AB 中点D（，）．22当y＝kx +4155过点（，）时，3222=푘2+43，所以k =73．答案：A．点评：二元一次不等式（组）表示平面区域的判断方法：直线定界，测试点定域．注意不等式中不等号有无等号，无等号时直线画成虚线，有等号时直线画成实线．测试点可以选一个，也可以选多个，若直线不过原点，则测试点常选取原点．题型二：求线性目标函数的最值2/ 5典例 2：设x，y 满足约束条件：，求z＝x+y 的最大值与最小值．分析：作可行域后，通过平移直线l0：x+y＝0 来寻找最优解，求出目标函数的最值．解答：先作可行域，如图所示中△ABC 的区域，且求得A（5，2）、B（1，1）、C（1，），作出直线l0：x+y＝0，再将直线l0 平移，当l0 的平行线l1 过点B 时，可使z＝x+y 达到最小值；当l0 的平行线l2 过点A 时，可使z＝x+y达到最大值．故z min＝2，z max＝7．点评：（1）线性目标函数的最大（小）值一般在可行域的顶点处取得，也可能在边界处取得．（2）求线性目标函数的最优解，要注意分析线性目标函数所表示的几何意义，明确和直线的纵截距的关系．题型三：实际生活中的线性规划问题典例 3：某农户计划种植黄瓜和韭菜，种植面积不超过 50 亩，投入资金不超过 54 万元，假设种植黄瓜和韭菜的产量、成本和售价如下表：年产量/亩年种植成本/亩每吨售价黄瓜 4 吨 1.2 万元0.55 万元韭菜 6 吨0.9 万元0.3 万元为使一年的种植总利润（总利润＝总销售收入﹣总种植成本）最大，那么黄瓜和韭菜的种植面积（单位：亩）分别为（）A．50，0 B．30，20 C．20，30 D．0，50分析：根据线性规划解决实际问题，要先用字母表示变量，找出各量的关系列出约束条件，设出目标函数，转化为线性规划问题．3/ 5푥+푦≤50解析设种植黄瓜x 亩，韭菜y 亩，则由题意可知{1.2푥+0.9푦≤54푥，푦∈푁+求目标函数z＝x+0.9y 的最大值，根据题意画可行域如图阴影所示．当目标函数线l 向右平移，移至点A（30，20）处时，目标函数取得最大值，即当黄瓜种植 30 亩，韭菜种植 20 亩时，种植总利润最大．故答案为：B点评：线性规划的实际应用问题，需要通过审题理解题意，找出各量之间的关系，最好是列成表格，找出线性约束条件，写出所研究的目标函数，转化为简单的线性规划问题，再按如下步骤完成：（1）作图﹣﹣画出约束条件所确定的平面区域和目标函数所表示的平行直线系中过原点的那一条l；（2）平移﹣﹣将l 平行移动，以确定最优解的对应点A 的位置；（3）求值﹣﹣解方程组求出A 点坐标（即最优解），代入目标函数，即可求出最值．题型四：求非线性目标函数的最值푦典例 4：（1）设实数x，y 满足，则푥的最大值为．→（2）已知O 是坐标原点，点A（1，0），若点M（x，y）为平面区域上的一个动点，则|푂퐴+→푂푀|的最小值是．分析：与二元一次不等式（组）表示的平面区域有关的非线性目标函数的最值问题的求解一般要结合给定代数式的几何意义来完成．푦3解答：（1）푥表示点（x，y）与原点（0，0）连线的斜率，在点（1，）处取到最大值．24/ 5→（2）依题意得，푂퐴+→→푂푀=（x+1，y），|푂퐴+→푂푀| =(푥+1)2+푦2可视为点（x，y）与点（﹣1，0）间的距离，在坐标平面内画出题中的不等式组表示的平面区域，结合图形可知，在该平面区域内的点中，由点（﹣1，0）向→直线x+y＝2 引垂线的垂足位于该平面区域内，且与点（﹣1，0）的距离最小，因此|푂퐴+→푂푀|的最小值是|―1+0―2|2=322．332故答案为：（1）（2）．22点评：常见代数式的几何意义有（1）푥2+푦2表示点（x，y）与原点（0，0）的距离；（2）(푥―푎)2+(푦―푏)2表示点（x，y）与点（a，b）之间的距离；푦（3）푥表示点（x，y）与原点（0，0）连线的斜率；푦―푏（4）푥―푎表示点（x，y）与点（a，b）连线的斜率．【解题方法点拨】1．画出平面区域．避免失误的重要方法就是首先使二元一次不等式标准化．푧푧2．在通过求直线的截距푏的最值间接求出z 的最值时，要注意：当b＞0 时，截距푏取最大值时，z 也取最大值；截푧푧푧距푏取最小值时，z 也取最小值；当b＜0 时，截距푏取最小值时，z 取最大值．푏取最大值时，z 取最小值；截距5/ 5。

高一数学辅导讲义第7讲----简单的线性规划问题【知识与技能】一、二元一次不等式表示平面区域:1、二元一次不等式0>++C By Ax （或<0）在平面直角坐标系中表示直线0=++C By Ax 某一侧所有点组成的平面区域，不包括边界；2、二元一次不等式0≥++C By Ax （或≤0）在平面直角坐标系中表示直线0=++C By Ax 某一侧所有点组成的平面区域且包括边界。

注意：作图时,不包括边界画成虚线;包括边界画成实线.二、判断二元一次不等式表示哪一侧平面区域的方法:直线定界、特殊点定域三、利用图解法解决线性规划问题的一般步骤：1、作出可行域 ；2、作出目标函数的等值线；3、求出最终结果：在可行域中平移移动目标函数等值线，从图中能判断问题有惟一最优解，或者是有无穷最优解，或者无最优解。

四、线性规划解决常见问题：1、求给定可行域的最优解（包括最大、小值及最优整数解）2、求给定可行域的面积3、给出可行域的最优解，求目标函数中参数的范围【题型分类精讲】题型一、二元一次不等式（组）表示的平面区域的有关问题1、不等式组⎪⎩⎪⎨⎧≤+≥+≥43430y x y x x 所表示的平面区域的面积等于( )A 、23B 、32C 、34D 、43 2、设二元一次不等式组⎪⎩⎪⎨⎧≤-+≥+-≥-+0142080192y x y x y x 所表示的平面区域为M ，使函数)1,0(≠>=a a a y x(a ＞0,a ≠1)的图象过区域M 的a 的取值范围是 ( )A 、［1,3］B 、［2,10］ C.［2,9］ D.［10,9］题型二、利用线性规划求最大值、最小值3、若实数x,y 满足不等式组330,230,10,x y x y x y +-≥⎧⎪--≤⎨⎪-+≥⎩则y x +的最大值为（ ）A 、9B 、 157C 、1D 、7154、已知点P （x ，y ）在不等式组⎪⎩⎪⎨⎧≥-+≤-≤-022,01,02y x y x 表示的平面区域上运动，则z ＝x-y 最大值？题型三、含有字母系数的线性规划问题：5、若不等式组⎪⎪⎩⎪⎪⎨⎧≤+≥≤+≥-ay x y y x y x 0220表示的平面区域是一个三角形，则a 的范围是( ) A 、34≥a B 、10≤<a C 、341≤≤a D 、3410≥≤<a a 或 题型四、线性规划的最优解问题6、设y x 、满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x ，若目标函数)0,0(>>+=b a by ax z 的最大值为12，则ba 32+的最大值为（ ） A 、625 B 、38 C 、311 D 、4 题型五、利用线性规划解决实际问题7、某加工厂用某原料由甲车间加工出A 产品，由乙车间加工出B 产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A 产品，每千克A 产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克B 产品，每千克B 产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工，每天甲、乙车间耗费工时总和不得超过480小时，甲、乙两车间每天总获利最大的生产计划为（ ）A 、甲车间加工原料10箱，乙车间加工原料60箱B 、甲车间加工原料15箱，乙车间加工原料55箱C 、甲车间加工原料18箱，乙车间加工原料50箱D 、甲车间加工原料40箱，乙车间加工原料30箱。

3.4.2 简单线性规划1. 相关定义：(1)线性规划问题：求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题。

(2)可行解：满足线性约束条件的解叫做可行解。

(3)可行域：由所有可行解组成的集合叫做可行域。

(4)最优解：分别使目标函数取得最大值和最小值的可行解叫做最优解。

2. 线性规划问题的求解步骤：(1)先设出决策变量，找出约束条件和线性目标函数；(2)作出相应的图象（注意特殊点与边界）(3)利用图象，在线性约束条件下找出决策变量，使线性目标函数达到最大（小）值；在在求线性目标函数的最大（小）值时，直线往右（左）平移则值随之增大（小），这样就可以在可行域中确定最优解。

注：①对线性目标函数中的符号一定要注意：当时，当直线过可行域且在y 轴截距最大时，值最大，在y 轴截距最小时，值最小；当时，当直线过可行域且在y 轴截距最大时，值最小，在y 轴截距最小时，值最大。

②如果可行域是一个多边形，那么一般在其顶点处使目标函数取得最大或最小值，最优解一般就是多边形的某个顶点。

例1：设满足约束条件：，分别求下列目标函数的的最大值与最小值：(1)； (2)；(3)（是整数）； （4）； （5） 示中的区域，且【解析】先作可行域，如下图所求得、、),(y x ny mx z +=0=+ny mx By Ax z +=B 0>B z z 0<B z z y x ,⎪⎩⎪⎨⎧≥≤+-≤-1255334x y x y x y x z 106+=y x z -=2y x z -=2y x ,22y x +=ω1+=x y ωABC ∆)2,5(A)1,1(B )522,1(C(1)作出直线，再将直线平移，当的平行线过点B 时，可使达到最小值；当的平行线过点A 时，可使达到最大值。

故，(2)同上，作出直线，再将直线平移，当的平行线过点C 时，可使达到最小值；当的平行线过点A 时，可使达到最大值。

微专题43线性规划——作图与求解一、基础知识1、有关术语：（1）线性拘束条件：对于变量 x,y的一次不等式（或方程）组（2）可行解：知足线性拘束条件的解x,y3）可行域：全部可行解构成的会合4）目标函数：对于x,y的函数分析式5）最优解：是目标函数获得最大值或最小值的可行解2、怎样在直角坐标系中作出可行域：1）先作出围成可行域的直线，利用“两点独一确立一条直线”可选用直线上的两个特别点（比方坐标轴上的点），以便快速做出直线2）怎样判断知足不等式的地区位于直线的哪一侧：一条曲线（或直线）将平面分红若干地区，则在同一地区的点，所知足不等式的不等号方向同样，因此可用特别值法，利用特别点判断其能否切合不等式，假如切合，则该特别点所在地区均切合该不等式，详细来说有以下三种状况：①竖直线x a或水平线y b：可经过点的横（纵）坐标直接进行判断②一般直线y kx bkb 0：可代入0,0点进行判断，若切合不等式，则原点所在地区即为不等式表示地区，不然则为另一半地区。

比如：不等式x 2y 3 0，代入 0,0切合不等式，则x 2y 3 0所表示地区为直线x 2y 3 0的右下方③过原点的直线y kxk 0：没法代入 0,0，可代入座标轴上的特别点予以解决，或许利用象限进行判断。

比如：y x：直线y x穿过一、三象限，二、四象限分居直线双侧。

考虑第四象限的点x 0,y 0，因此必有y x，因此第四象限所在地区含在 y x表示的区域之中。

（3）在作可行域时要注意界限能否可以取到：对于拘束条件界限不可以取值时，在图像中界限用虚线F x,y0（或F x,y0）表示；对于拘束条件F x,y0（或F x,y0）界限能取值时，在图像中界限用实线表示3、利用数形联合追求最优解的一般步骤（1）依据拘束条件，在平面直角坐标系中作出可行域所代表的地区（2）确立目标函数z在式子中的几何意义，常有的几何意义有：（设a,b为常数）①线性表达式——与纵截距有关：比如zaxa zby，则有y x，进而z的取值与b b动直线的纵截距有关，要注意b的符号，若b0，则z的最大值与纵截距最大值有关；若b0，则z的最大值与纵截距最小值有关。