9750利用CASTEP模拟计算实例1

CASTEP 计算理论总结XBAPRSCASTEP 特点是适合于计算周期性结构，对于非周期性结构一般要将特定的部分作为周期性结构，建立单位晶胞后方可进行计算。

CASTEP 计算步骤可以概括为三步：首先建立周期性的目标物质的晶体；其次对建立的结构进行优化，这包括体系电子能量的最小化和几何结构稳定化。

最后是计算要求的性质，如电子密度分布(Electron density distribution)，能带结构(Band structure)、状态密度分布(Densityof states)、声子能谱(Phonon spectrum)、声子状态密度分布(DOS of phonon)，轨道群分布(Orbitalpopulations)以及光学性质(Optical properties)等。

本文主要将就各个步骤中的计算原理进行阐述，并结合作者对计算实践经验，在文章最后给出了几个计算事例，以备参考。

CASTEP 计算总体上是基于DFT ，但实现运算具体理论有：离子实与价电子之间相互作用采用赝势来表示；超晶胞的周期性边界条件；平面波基组描述体系电子波函数；广泛采用快速fast Fourier transform (FFT) 对体系哈密顿量进行数值化计算；体系电子自恰能量最小化采用迭带计算的方式；采用最普遍使用的交换-相关泛函实现DFT 的计算，泛函含概了精确形式和屏蔽形式。

一， CASTEP 中周期性结构计算优点与MS 中其他计算包不同，非周期性结构在CASTEP 中不能进行计算。

将晶面或非周期性结构置于一个有限长度空间方盒中，按照周期性结构来处理，周期性空间方盒形状没有限制。

之所以采用周期性结构原因在于：依据Bloch 定理，周期性结构中每个电子波函数可以表示为一个波函数与晶体周期部分乘积的形式。

他们可以用以晶体倒易点阵矢量为波矢一系列分离平面波函数来展开。

这样每个电子波函数就是平面波和，但最主要的是可以极大简化Kohn-Sham 方程。

提示： CASTAP计算所需时间随原子数平方的增加而增加。 因此，建议是用最小的初晶胞来描述体系，可使用 Build\Symmetry\Primitive Cell菜单选项来转换成初晶
CASTEP的任务
计算设置：合适的3D模型文件一旦确定，必须选择计算类型 和相关参数，例如，对于动力学计算必须确定系综和参数， 包括温度，时间步长和步数。选择运行计算的磁盘并开始 CASTEP作业。 结果分析：计算完成后，相关的CASTEP作业的文档返回用户， 在项目面板适当位置显示。这些文档进一步处理能获得所需 的观察量如光学性质。 CASTAP中选择一项任务 1 从模块面板（Module Explorer)选择CASTAP\Calculation 2 选择设置表 3 从任务列表中选择所要求的任务
晶胞分子晶体表面纳米结构聚合物等2458锐钛矿tio1112558pt110co2x1碳纳米管tio纳米棒2658materialstudio晶体结构模型建立建立方铅矿pbs晶体结构模型实验15步骤1查晶体结构数据如icsdpdf数据库2通过软件建模如materialstudio中模块visualizerdiamond2758castep使用2858castep是特别为固体材料学而设计的一个现代的量子力学基本程序其使用了密度泛函dft平面波赝势方法进行第一原理量子力学计算以探索如半导体陶瓷金属矿物和沸石等材料的晶体和表面性质
密度泛函理论
赝势(pseudo potential) 赝势就是把离子实的 内部势能用假想的势能 取代真实的势能，但在 求解波动方程时，不改 变能量本征值和离子实 之间区域的波函数。模 守恒赝势NCP (Norm Conserving Pseudopotential) 和 超软赝势 USPP(Ultrasoft Pseudoptential)

Z的坐标值应为1.39 Å，此既为原子层间的距离。 注意：一个fcc(110)体系，do 可通过下列公式得到： .
在弛豫表面之前，如果仅仅是只需要弛豫表面，我们必需要束 缚住内部Pd原子。
不包括最高层的Pd原子，按住SHIFT键选中所有的Pd原子。从菜 单栏中选中Modify | Constraints，勾选上Fix fractional position。关闭对话框。
注意， 此时表 面垂直 于z轴， 习惯。
在3D Viewer上单击右键，选择Display Style选项，选择 Line，则从结构图上可清楚看到O－ABC。记住相对方位，恢 复显示位Ball and Stick。
转动晶格，使z轴垂直于屏幕。打开Display Style 对话框，选择 Lattice 标签，将Display style 由 Default 改为 Original。关闭对话 框。
选择Properties标签，选中 Density of states。把k-point set改 为Gamma，勾选Calculate PDOS 选项。按下Run按钮。
出现如下对话框，选择No。
出现如下信息，表示CO优化成功。 查看OC的原子坐标，与实验值有差异。
从菜单栏中选择File | Save Project，然后在选中Window | Close All。我们可以进行下一步操作。 4．构造Pd(110)面 下面我们将要用到从Pd bulk中获得的Pd优化结构。 在Pd bulk/Pd CASTEPGeomOpt文档中打开Pd.xsd。
现 在 显 示 的 是 一 个 空 3D 模 型 文 档 。 我 们 可 以 使 用 Build Crystal工具来创建一个空晶格单元，然后在上面添加CO分子。

CASTEP 也支援較傳統電子之平衡狀態的恢復，它用到了對總能的極小化。電子波函數是以平面波基底來表 示並且展開係數會被變化以便達到最小的總能。此一極小化可利用每個波函數被獨立的最佳化的 band-by-band 的技術，或允許同時更新所有波函數的 all-band 方法來達成(只有 all-band 方式支援 USP 的使用)。此一方式用了如 Payne 等人所提出的預先調節式的共軛梯度技術。
註解
雖然 CASTEP 主要是用於大尺度的週期性系統，他也可以被應用在以超晶格建力起來的缺陷表面介面與分 子，更進一步的資訊請參照 42 頁的”非週期系統”已獲的更進一步的資訊。
CASTEP 模組允許你使用含有彈性的分子模型工具，Cerius2 模型環境所提供的進階的 GUI 來產生與設定模 型以便研究，定義你要進行計算工作的形式，並且在本地端的機器或遠端的機器執行它。
所有的膺勢都是採用可分離的 Kleinman-Bylander 形式上。norm-conserving potential 能夠在實空間或 是倒空間的波函數來使用；實空間的方法提供了對於系統而言比較好的 scalability。Ultrasoft 位勢目 前只可以在倒置空間中使用(提醒您注意，實空間實作的好處在此一情況下是比較小的)。
前言
CASTEP 的理論基礎是電荷密度泛函理論在局域電荷密度近似或是梯度修正的版本，這是由 Perdew 和 Wang 所發展的 GGA。DFT 所描述的電子氣體交互作用被認為是對大部分的狀況都是夠精確的，並且他是唯一能實 際有效分析週期性系統的理論方法。請看第三章一般理論來或的更進一步的 DFT 理論。
这几天在学习用 Material studio 软件包中 CASTEP 模块进行 DFT 计算，找到一个 CASTEP 模块的详细说明， 不敢独享！ CASTEP 前言

模型选定我们在进行材料物理模拟所需要做的第一步 (也是很重要的一步) 是模型的选定或建构。

CASTEP 虽然内建了很多功能来预测晶胞参数 (边长，夹角) 与原子位置，但仍然仰赖使用者告诉它 "要进行计算的系统是什么"。

在选定模型时，我们需切记如果系统内原子太多或是超晶胞体积太大，则计算量都会以平面波数的 3 次方增加到计算机难以负荷或使用者难以等待的程度，因此，我时时应考虑设计出一个足以表现出我们所想要研究的物理，而却又能使所有采用的超晶胞越少越好的模型。

如果研究上涉及到一系列原子数不同的大小系统需要做计算，最好能先计算小结构，不要一开始就送入大结构到计算机中。

如果要模拟的系统是含有杂质，则单位晶胞必须进一步放大成超晶胞以便使化学成分里的分数变成整数，因此晶胞会变得很大。

在某些特殊的情况，相互取代的元素种类是很类似的，(即在化学行为上类似)，则下一个版本的CASTEP会提供一种叫做虚拟晶体近似 (Virtural Crystal Approximation，VCA) 的方法，则模型里面的原子就可以指定成如0.3A元素加0.7B元素这种样子，因此总可以以最小晶胞来做计算的模型。

但这种方法的精确度通常只适用于合金材料，故要小心使用。

模型的选定有许多人为抉择会含在里面，例如表面计算的层数，因此有些情况也需要进行所谓的收敛性测试。

赝势选择选单VpsMS接口（界面）的设定是选用USP优先于NCP，USP有加速计算与减少内存使用的效果，其精确度也与NCP (norm-conserving potential) 相当。

至于什么时候使用NC呢 (就是在poseudopotential 选项中那些延伸文件名是 .recpot者)，使用到NCP的场合有：1.某些CASTEP计算的功能尚未支持到USP，因此需要选用NCP。

2.为了要与已经发展的文献比较或进行验证3.对计算的结果存疑者，能提供『多一种选择』( 注：至于延伸档名是*.psp者也是属于norm-conserving的一种，是TMpotential，在文献上也常被使用，但所需的截止动能较高，因此计算代价较大。

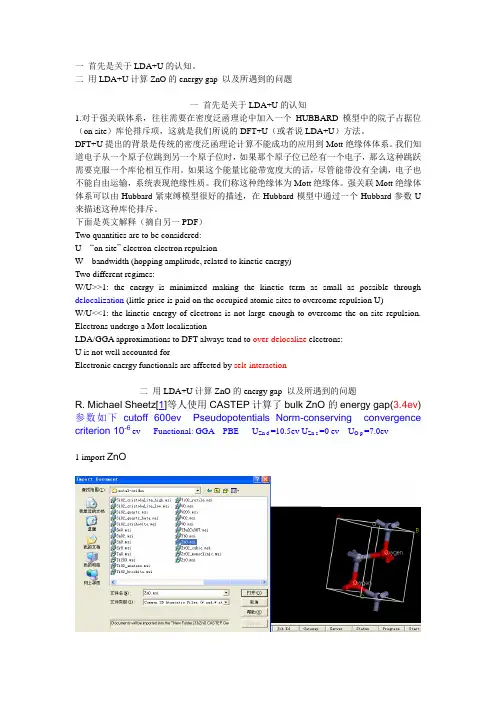
一首先是关于LDA+U的认知。

二用LDA+U计算ZnO的energy gap 以及所遇到的问题一首先是关于LDA+U的认知1.对于强关联体系，往往需要在密度泛函理论中加入一个HUBBARD模型中的院子占据位（on site）库伦排斥项，这就是我们所说的DFT+U（或者说LDA+U）方法。

DFT+U提出的背景是传统的密度泛函理论计算不能成功的应用到Mott绝缘体体系。

我们知道电子从一个原子位跳到另一个原子位时，如果那个原子位已经有一个电子，那么这种跳跃需要克服一个库伦相互作用。

如果这个能量比能带宽度大的话，尽管能带没有全满，电子也不能自由运输，系统表现绝缘性质。

我们称这种绝缘体为Mott绝缘体。

强关联Mott绝缘体体系可以由Hubbard紧束缚模型很好的描述，在Hubbard模型中通过一个Hubbard参数U 来描述这种库伦排斥。

下面是英文解释（摘自另一PDF）Two quantities are to be considered:U “on site” electron-electron repulsionW bandwidth (hopping amplitude, related to kinetic energy)Two different regimes:W/U>>1: the energy is minimized making the kinetic term as small as possible through delocalization (little price is paid on the occupied atomic sites to overcome repulsion U)W/U<<1: the kinetic energy of electrons is not large enough to overcome the on-site repulsion. Electrons undergo a Mott localizationLDA/GGA approximations to DFT always tend to over-delocalize electrons:U is not well accounted forElectronic energy functionals are affected by selt-interaction二用LDA+U计算ZnO的energy gap 以及所遇到的问题R. Michael Sheetz[1]等人使用CASTEP计算了bulk ZnO的energy gap(3.4ev) 参数如下cutoff 600ev Pseudopotentials Norm-conserving convergence criterion 10-6 ev Functional: GGA PBE U Zn d =10.5ev U Zn s =0 ev U O p =7.0ev1 import ZnO2 对bulk ZnO 结构优化（还没有选LDA+U，为了下面比较）结果分析我们可以看到band gap is 0.269ev 与3.4ev 相差很大3. 选上LDA+U 看看结果如何。

关于CASTEPCASTEP是特别为固体材料学而设计的一个现代的量子力学基本程序，其使用了密度泛函(DFT）平面波赝势方法，进行第一原理量子力学计算，以探索如半导体，陶瓷，金属，矿物和沸石等材料的晶体和表面性质。

典型的应用包括表面化学，键结构，态密度和光学性质等研究， CASTEP也可用于研究体系的电荷密度和波函数的3D形式。

此外， CASTEP可用于有效研究点缺陷（空位，间隙和置换杂质）和扩展缺陷（如晶界和位错）的性质。

Material Studio使用组件对话框中的CASTEP选项允许准备，启动，分析和监测CASTEP 服役工作。

计算：允许选择计算选项（如基集，交换关联势和收敛判据），作业控制和文档控制。

分析：允许处理和演示CASTEP计算结果。

这一工具提供加速整体直观化以及键结构图，态密度图形和光学性质图形。

CASTEP的任务CASTEP计算是要进行的三个任务中的一个，即单个点的能量计算，几何优化或分子动力学。

可提供这些计算中的每一个以便产生特定的物理性能。

性质为一种附加的任务，允许重新开始已完成的计算以便产生最初没有提出的额外性能。

在CASTEP计算中有很多运行步骤，可分为如下几组：* 结构定义：必须规定包含所感兴趣结构的周期性的3D模型文件，有大量方法规定一种结构：可使用构建晶体（Build Crystal)或构建真空板(Build Vacuum Stab)来构建，也可从已经存在的的结构文档中引入，还可修正已存在的结构。

注意： CASTEP仅能在3D周期模型文件基础上进行计算，必须构建超单胞，以便研究分子体系。

提示： CASTEP计算所需时间随原子数平方的增加而增加。

因此，建议是用最小的初晶胞来描述体系，可使用Build\Symmetry\Primitive Cell菜单选项来转换成初晶胞。

* 计算设置：合适的3D模型文件一旦确定，必须选择计算类型和相关参数，例如，对于动力学计算必须确定系综和参数，包括温度，时间步长和步数。

CASTAP几何优化任务
CASTAP几何优化任务允许改善结构的几何，获得稳定结构或 多晶型物。通过一个迭代过程来完成这项任务，迭代过程中调整原 子坐标和晶胞参数使结构的总能量最小化。 CASTAP几何优化是基于减小计算力和应力的数量级，直到小 于规定的收敛误差。也可能给定外部应力张量来对拉应力，压应力 和切应力等作用下的体系行为模型化。在这些情况下反复迭代内部 应力张量直到与所施加的外 部应力相等。 几何优化处理产生的模 型结构与真实结构紧密相似。 利用CASTAP计算的晶格参 数精度列于右图。
CASTAP的任务
CASTAP计算是要进行的三个任务中的计算中的每一个以便产 生特定的物理性能。性质为一种附加的任务，允许重新开始已完成 的计算以便产生最初没有提出的额外性能。 在CASTAP计算中有很多运行步骤，可分为如下几组： 结构定义：必须规定包含所感兴趣结构的周期性的3D模型文 件，有大量方法规定一种结构：可使用构建晶体（Build Crystal)或 构建真空板(Build Vacuum Stab)来构建，也可从已经存在的的结构 文档中引入，还可修正已存在的结构。
AlAs的原胞
下面我们将要优化它的几何结构。
把Task改为Geometry Optimization ，把Quality改为Fine。 优 化当中的默认设置是优化原子坐标.尽管如此,在本例中我们不仅要 优化原子坐标也要优化晶格.
按下Task右侧的More...按钮， 选中Optimize Cell。关闭对话框. 当我们改变Quality时,其他的参数也会有所改变来反映Quality的 改变。 选择Properties标签，可从中指定我们想要计算的属性。选中Band structure和Density of states。另外，我们也可以具体指明job control选项，例如实时更新等。 选择Job Control标签，选中More...按钮。在CASTEP Job Control Options对话框中，把Update 的时间间隔改为30秒。关闭对话框。 按下Run按钮，关闭对话框。 几秒钟之后，在Project Explorer中出现一个新的文件，它包含所 有的运行结果。一个工作日志窗口也会出现，它包含工作的运行状

CASTEP 计算理论总结XBAPRSCASTEP 特点是适合于计算周期性结构，对于非周期性结构一般要将特定的部分作为周期性结构，建立单位晶胞后方可进行计算。

CASTEP 计算步骤可以概括为三步：首先建立周期性的目标物质的晶体；其次对建立的结构进行优化，这包括体系电子能量的最小化和几何结构稳定化。

最后是计算要求的性质，如电子密度分布(Electron density distribution)，能带结构(Band structure)、状态密度分布(Densityof states)、声子能谱(Phonon spectrum)、声子状态密度分布(DOS of phonon)，轨道群分布(Orbitalpopulations)以及光学性质(Optical properties)等。

本文主要将就各个步骤中的计算原理进行阐述，并结合作者对计算实践经验，在文章最后给出了几个计算事例，以备参考。

CASTEP 计算总体上是基于DFT ，但实现运算具体理论有：离子实与价电子之间相互作用采用赝势来表示；超晶胞的周期性边界条件；平面波基组描述体系电子波函数；广泛采用快速fast Fourier transform (FFT) 对体系哈密顿量进行数值化计算；体系电子自恰能量最小化采用迭带计算的方式；采用最普遍使用的交换-相关泛函实现DFT 的计算，泛函含概了精确形式和屏蔽形式。

一， CASTEP 中周期性结构计算优点与MS 中其他计算包不同，非周期性结构在CASTEP 中不能进行计算。

将晶面或非周期性结构置于一个有限长度空间方盒中，按照周期性结构来处理，周期性空间方盒形状没有限制。

之所以采用周期性结构原因在于：依据Bloch 定理，周期性结构中每个电子波函数可以表示为一个波函数与晶体周期部分乘积的形式。

他们可以用以晶体倒易点阵矢量为波矢一系列分离平面波函数来展开。

这样每个电子波函数就是平面波和，但最主要的是可以极大简化Kohn-Sham 方程。

CASTEP计算理论总结+实例分析CASTEP 计算理论总结XBAPRSCASTEP 特点就是适合于计算周期性结构,对于非周期性结构一般要将特定的部分作为周期性结构,建立单位晶胞后方可进行计算。

CASTEP 计算步骤可以概括为三步:首先建立周期性的目标物质的晶体;其次对建立的结构进行优化,这包括体系电子能量的最小化与几何结构稳定化。

最后就是计算要求的性质,如电子密度分布(Electron density distribution),能带结构(Band structure)、状态密度分布(Density of states)、声子能谱(Phonon spectrum)、声子状态密度分布(DOS of phonon),轨道群分布(Orbital populations)以及光学性质(Optical properties)等。

本文主要将就各个步骤中的计算原理进行阐述,并结合作者对计算实践经验,在文章最后给出了几个计算事例,以备参考。

CASTEP 计算总体上就是基于DFT,但实现运算具体理论有:离子实与价电子之间相互作用采用赝势来表示;超晶胞的周期性边界条件;平面波基组描述体系电子波函数;广泛采用快速fast Fourier transform (FFT) 对体系哈密顿量进行数值化计算;体系电子自恰能量最小化采用迭带计算的方式;采用最普遍使用的交换-相关泛函实现DFT 的计算,泛函含概了精确形式与屏蔽形式。

一， CASTEP 中周期性结构计算优点与MS 中其她计算包不同,非周期性结构在CASTEP 中不能进行计算。

将晶面或非周期性结构置于一个有限长度空间方盒中,按照周期性结构来处理,周期性空间方盒形状没有限制。

之所以采用周期性结构原因在于:依据Bloch 定理,周期性结构中每个电子波函数可以表示为一个波函数与晶体周期部分乘积的形式。

她们可以用以晶体倒易点阵矢量为波矢一系列分离平面波函数来展开。

这样每个电子波函数就就是平面波与,但最主要的就是可以极大简化Kohn-Sham 方程。

此文档中的信息包括： *输入的应变和计算出的应力的总结 *每一种应变模式线性拟合和拟合质量的计算结果 *给定对称性下计算出的应力与弹性常数之间的对应 *弹性常数Cij和弹性柔量Sij的表格 *导出量：体积模量和其倒数、压缩系数、杨氏模量、 Poisson比、 Lame 常数(用于模拟各向同性介质)
3 弹性常数文件的描述 对于这种点阵类型，需要考虑两种应变模式(本教程只计算了一种)。对
选 中 CASTEP Calculation 对 话框中的Setup标签，把Task 设置改为Energy。
选择Electronic标签， 按下More…按钮，显 示出CASTEP Electronic Options对话 框。选择SCF标签，勾 选上Fix occupancy。 关闭CASTEP Electronic Options对话 框。
CASTEP Calculation 对 话 框。
几何优化的默认值不包括对单胞的优化。 在Setup标签上，把Task从Energy改为 Geometry Optimization，把Functional改为 LDA。
在CASTEP Geometry Optimization 对 话 框 中 ， 按 下 More... 按 钮 ， 勾 选 上 Optimize Cell。
选 中 Electronic 标 签 ， 把 Energy cutoff 设 置 为 Ultra-fine ， 把 SCF tolerance设置为 Ultra-fine，把kpoint set 设 置 为 Coarse 以 及 把 Pseudo-potentials 设 置 为 Normconserving。
现在，我们使用先前的计算结果来创建声子色散图。
从 Materials Studio 的 菜 单 栏 中 选 择 Modules | CASTEP | Analysis 。 从 属 性 列 表 中 选 择 Phonon dispersion 。 确 定 Results file 选 择 框 中 显 示 的 是Ge_PhononDisp.castep。

利用CASTEP模拟计算实例一，计算本征半导体硅的能带结构和状态密度等性质计算过程分为三个步骤：首先是建立硅的晶体结构计算模型，这个可以在MS物质结构数据库中调用即可。

在计算时为了节省时间，减少计算量将硅的普通的晶体转化为原胞结构，一个原胞中包含9个原子。

节下来是对晶体原胞结构进行几何结构优化，当然其中也含盖了对体系总能量的最小化。

结构优化过程中的两个图表文档分别表示了优化步骤中体系能量的变化和收敛精度，判断收敛是否成功就要查看最终完成计算后，能量的收敛精度是否达到了事前的设定值。

最后是计算性质，在计算状态密度时可以计算不同原子各个轨道按照角动量分布的偏态密度（PDOS），当体系是自旋极化时，偏态密度（PDOS）中包含了体系多数自旋(majority spin)和少数自旋(minority spin)的偏态密度（PDOS）。

光学性质的计算是模拟中的一个难点，从目前发表的文献来看，影响光学性质计算的因素很多（见光学计算原理部分，对此有详细描述），在研究体系有充足实验数据的条件下，可以对能带采用“剪刀”的工具对能带带隙进行刚性的调整，获得与实验结果符合较好的结论。

但对于初学者而言，这个工具一般是不推荐使用的。

作者对于硅的计算完全按照上述方案完成。

详细的计算结果和计算方法见本文所附带的专门文章。

二，搀杂半导体InP性质计算第三主族和第五主族元素之间形成的半导体，目前越来越受到的重视，在纳米材料中，各种纳米电子器件如场效应晶体管，半导体纳米量子阱，纳米量子点激光器等均广泛采用了诸如AlAS InP等材料，本文对InP能带结构、状态密度以及光学性质进行了计算。

计算步骤与前文描述相同。

详细结果见文章二。

三，FeS2性质计算二硫化亚铁是一种受到广泛研究的窄带隙的半导体，其能带带隙为0.95eV。

肖奇等人也采用CASTEP 对二硫化亚铁整体状态密度和（100）晶面双层超结构状态密度的计算结果进行了对比，发现了表面态对状态密度峰的分裂。

重要的一点现在我们来到 property 这里，刚 刚在 setup 选项里面选了 tasks 的 energy， 那么在 property 里进可以进一步指定我要 附加计算哪一些特性： 比如说
能带结构 density of state 光学性质 有与趣可以试试不同种类计算。注意，phonon dispersion 跟 phonon density of state相当耗时 间， pc 机有可能需要计算三两天甚至一两 周，看你不同的晶胞大小；其它都还算是比 较不会太费时。 现在为了示范光学计算，只选择能带结构， 态密度跟optical property ，其中态密度这个 部份我进一步还要选择要求计算投影态密 度，projected density of state ，那这个其它的 就用默认值。
10 / 111
NCHC CASTEP 教材
查看运行状态 根据刚才所选，电子结构算完后接着进行能带以及光学计算；另外，提交任务
后关掉materials studio的图形界面，程序还继续在远程或本机后台跑。可以安全的退 出materials studio的图形界面；同时，不关的话就会消耗一个license。这个job设置了 medium需要时间较长，用了330这个精确度对于一些初步的具有学术探讨价值的一 些物理量是已经不错了。打入”机器名:18888”，可以看到目前你正在运行的任务。
11 / 111
NCHC CASTEP 教材
从上面可以看到holon提交了作业G15EA，现在在running；选进去以后可以看得 见目前正在进行计算的castep 文件，如果我点进去的话它会因为application的定义没 有设好而要求我要选择下载或开启，我刚刚选择了开启，刚刚那个单纯做电子结构 计算的已经在七十几秒时结束，那另外属于能带结构计算的部份我也把它开启，能 带结构的计算也是另外一个七十几秒结束，那光学计算可能现在正在进行，你们可 以从上面看到名称有optics的这些就是光学计算。 结束计算

CASTE计算理论总结XBAPRSCASTEP寺点是适合于计算周期性结构，对于非周期性结构一般要将特定的部分作为周期性结构，建立单位晶胞后方可进行计算。

CASTER算步骤可以概括为三步：首先建立周期性的目标物质的晶体；其次对建立的结构进行优化，这包括体系电子能量的最小化和几何结构稳定化。

最后是计算要求的性质，如电子密度分布(Electron density distribution) ，能带结构(Band structure)、状态密度分布(Densityof states)、声子能谱(Pho non spectrum)、声子状态密度分布(DOS of pho non)，轨道群分布(Orbital populations) 以及光学性质(Optical properties) 等。

本文主要将就各个步骤中的计算原理进行阐述，并结合作者对计算实践经验，在文章最后给出了几个计算事例，以备参考。

CASTEP十算总体上是基于DFT,但实现运算具体理论有：离子实与价电子之间相互作用采用赝势来表示；超晶胞的周期性边界条件；平面波基组描述体系电子波函数；广泛采用快速fast Fourier tran sform (FFT) 对体系哈密顿量进行数值化计算；体系电子自恰能量最小化采用迭带计算的方式；采用最普遍使用的交换-相关泛函实现DFT的计算，泛函含概了精确形式和屏蔽形式。

一，CASTEF中周期性结构计算优点与MS中其他计算包不同，非周期性结构在CASTEF中不能进行计算。

将晶面或非周期性结构置于一个有限长度空间方盒中，按照周期性结构来处理，周期性空间方盒形状没有限制。

之所以采用周期性结构原因在于：依据Bloch定理，周期性结构中每个电子波函数可以表示为一个波函数与晶体周期部分乘积的形式。

他们可以用以晶体倒易点阵矢量为波矢一系列分离平面波函数来展开。

这样每个电子波函数就是平面波和，但最主要的是可以极大简化Kohn-Sham方程。

CASTEP 计算理论总结XBAPRSCASTEP 特点就是适合于计算周期性结构,对于非周期性结构一般要将特定的部分作为周期性结构,建立单位晶胞后方可进行计算。

CASTEP 计算步骤可以概括为三步:首先建立周期性的目标物质的晶体;其次对建立的结构进行优化,这包括体系电子能量的最小化与几何结构稳定化。

最后就是计算要求的性质,如电子密度分布(Electron density distribution),能带结构(Band structure)、状态密度分布(Density of states)、声子能谱(Phonon spectrum)、声子状态密度分布(DOS of phonon),轨道群分布(Orbital populations)以及光学性质(Optical properties)等。

本文主要将就各个步骤中的计算原理进行阐述,并结合作者对计算实践经验,在文章最后给出了几个计算事例,以备参考。

CASTEP 计算总体上就是基于DFT,但实现运算具体理论有:离子实与价电子之间相互作用采用赝势来表示;超晶胞的周期性边界条件;平面波基组描述体系电子波函数;广泛采用快速fast Fourier transform (FFT) 对体系哈密顿量进行数值化计算;体系电子自恰能量最小化采用迭带计算的方式;采用最普遍使用的交换-相关泛函实现DFT 的计算,泛函含概了精确形式与屏蔽形式。

一， CASTEP 中周期性结构计算优点与MS 中其她计算包不同,非周期性结构在CASTEP 中不能进行计算。

将晶面或非周期性结构置于一个有限长度空间方盒中,按照周期性结构来处理,周期性空间方盒形状没有限制。

之所以采用周期性结构原因在于:依据Bloch 定理,周期性结构中每个电子波函数可以表示为一个波函数与晶体周期部分乘积的形式。

她们可以用以晶体倒易点阵矢量为波矢一系列分离平面波函数来展开。

这样每个电子波函数就就是平面波与,但最主要的就是可以极大简化Kohn-Sham 方程。

密度泛函理论
Hohenberg-Kohn第一定理指出体了以基态密度为变量，将体系能 量最小化之后就得到了基态能量。 根据以上两定理，将薛定谔方程转变为Kohn-Sham 方程
密度函数
电子与原子核间的库仑势
电子间的库仑势
交换关联势 （未知）
密度泛函理论 LDA和GGA近似 Kohn-Sham方程原则是精确的，但遗憾 的是交换关联势是未知的。要进行具体计 算，就必须使用近似方法求出交换关联势。 常用的近似方法有局域密度近似(Local Density Approximation)和广义梯度近 似(Generalized Gradient Approximation),在某些情况下，广义梯 度近似改善了局域密度近似的计算结果， 但它并不总是优于局域密度近似。
提示： CASTAP计算所需时间随原子数平方的增加而增加。 因此，建议是用最小的初晶胞来描述体系，可使用 Build\Symmetry\Primitive Cell菜单选项来转换成初晶
CASTEP的任务
计算设置：合适的3D模型文件一旦确定，必须选择计算类型 和相关参数，例如，对于动力学计算必须确定系综和参数， 包括温度，时间步长和步数。选择运行计算的磁盘并开始 CASTEP作业。 结果分析：计算完成后，相关的CASTEP作业的文档返回用户， 在项目面板适当位置显示。这些文档进一步处理能获得所需 的观察量如光学性质。 CASTAP中选择一项任务 1 从模块面板（Module Explorer)选择CASTAP\Calculation 2 选择设置表 3 从任务列表中选择所要求的任务
密度泛函理论 基组(basis set) 求解Kohn-Sham方程，选取适当的基组， 将波函数对其展开，将方程求解转化为线 性代数问题。 一般选用如下基组展开:

欢迎访问，平面点位的坐标计算坐标正算（1）计算公式设测站点平面坐标为（X0,Y0），测站至待定点的平距为D，方位角为a，按下列坐标正算公式计算待定点的坐标为：X=X0+DcosaY=Y0+Dsina程序标识符规定如下：A,B------测站点平面坐标；C---------观测方位角；D---------观测平距；X,Y------待定点平面坐标；程序：（以下用-代表箭头指向）Fix 4：”X0=”?→A：”Y0=”?→B↵Lbl 1：”ALFA=”?→C：”DIST=”?→D：”X=”：A+cos(c) ◢”Y=”：B+Dsin（c）◢Goto 1 ↵欢迎访问，坐标反算（1）计算公式按两个已知点A,B 的平面坐标Xa ，Ya, Xb,Yb,计算两点间的距离D 和方位角a ，又称为“坐标反算”，计算公式为A=arctanYb Ya Xb Xa --（）（）程序中的标识符规定如下： A,B,C,D ——A,B 点的平面坐标； E,F ——A,B 点的坐标增量； R ——AB 的方位角； S ——AB 的平距。

欢迎访问，（2）程序Fix4：“XA=”?→A：“YA=”？→B↵Lbl1：“XB=”？→C：“YB=”？→D：C-A→E；D-B→F：→S：tan-1（F/E）→R↵If E〈0：ThenR+180→R：Goto2：IfEnd：F〈0⇒R+360—R↵Lbl2：“DIST=”：S◢“ALFA=”：R◢Goto1↵测边交会（1）计算公式设A，B为已知点，其平面坐标为Xa,Ya,Xb,Yb,P为待定点，观测平距D A(a),D B(b).从P点作AB（c）边的垂线，交AB于D点，设AD=e,PD=f.用下式计算辅助线段e,f的长度和待定点P的平面坐标：e=（a2+c2-b2）/2c f=x=xA+ecosaAB+fsinaABy=yA+esinaAB-fcosaAB欢迎访问，程序中的标识符规定如下：A,B,C,D——已知点A,B的平面坐标;P,Q——测边交会的观测边长；X,Y——待定点P的平距坐标。