工程力学(教案)单辉祖 第八章 轴向拉伸与压缩
- 格式:doc
- 大小:318.86 KB
- 文档页数:6


轴向拉伸与压缩教学教案第一章:轴向拉伸与压缩概念介绍教学目标:1. 让学生理解轴向拉伸与压缩的基本概念。
2. 让学生了解轴向拉伸与压缩的物理现象及其在实际中的应用。
教学内容:1. 轴向拉伸与压缩的定义。
2. 轴向拉伸与压缩的物理现象。
3. 轴向拉伸与压缩的应用实例。
教学方法:1. 采用讲授法,讲解轴向拉伸与压缩的基本概念及其物理现象。
2. 通过实物展示或图片,使学生更直观地了解轴向拉伸与压缩的应用实例。
教学评估:1. 通过课堂提问,检查学生对轴向拉伸与压缩概念的理解程度。
2. 通过布置课后作业,让学生巩固所学内容。
第二章:轴向拉伸与压缩的基本理论教学目标:1. 让学生掌握轴向拉伸与压缩的基本理论。
2. 让学生了解轴向拉伸与压缩的计算方法。
教学内容:1. 轴向拉伸与压缩的基本力学原理。
2. 轴向拉伸与压缩的计算方法。
教学方法:1. 采用讲授法,讲解轴向拉伸与压缩的基本力学原理。
2. 通过示例,让学生了解轴向拉伸与压缩的计算方法。
教学评估:1. 通过课堂提问,检查学生对轴向拉伸与压缩基本理论的理解程度。
2. 通过布置课后作业,让学生巩固所学内容。
第三章:轴向拉伸与压缩的实验研究教学目标:1. 让学生了解轴向拉伸与压缩实验的原理。
2. 培养学生进行实验操作和数据处理的能力。
教学内容:1. 轴向拉伸与压缩实验的原理。
2. 轴向拉伸与压缩实验的操作步骤。
3. 实验数据的处理方法。
教学方法:1. 采用实验教学法,让学生亲身体验轴向拉伸与压缩实验。
2. 通过实验操作和数据处理,使学生更好地理解轴向拉伸与压缩的物理现象。
教学评估:1. 通过实验报告,评估学生对轴向拉伸与压缩实验原理的理解程度。
2. 通过实验操作和数据处理的评价,培养学生进行实验的能力。
第四章:轴向拉伸与压缩在工程中的应用教学目标:1. 让学生了解轴向拉伸与压缩在工程中的应用。
2. 培养学生解决实际问题的能力。
教学内容:1. 轴向拉伸与压缩在工程中的应用实例。


《材料力学》课程教案1(一)轴向拉伸或压缩时的变形教学安排 ● 新课引入工程当中的构件要满足强度、刚度和稳定性的要求。
之前学习了轴向拉伸或压缩时杆的内力,应力,也就是强度问题。
今天转而讨论刚度问题。
工程当中构件因不满足刚度要求而失效的例子比比皆是,所谓刚度就是构件抵抗变形的能力,即一根杆件在设计好了之后,在正常的使用情况下,不能发生太大的弹性变形。
要想限制变形,首先应计算出变形。
如何计算?● 新课讲授一、纵向变形 (一)实验:杆件在受轴向拉伸时,在产生纵向变形的同时也产生横向变形。
纵向尺寸有所增大,横向尺寸有所减少。
思考:如图所示,杆件的纵向变形(axial deformation )的大小? 实验结论:F l ∝∆、l l ∝∆、A l 1∝∆AlF l ⋅∝∆⇒ 需引入比例常数,方可写成等式。
比例常数? (二)推导:杆件原长为l ,受轴向拉力F 之后,杆件长度由l 变成l 1,杆件纵向的绝对变形l l l -=∆1。
为了消除杆件长度对变形的影响,引入应变的概念ε。
当变形是均匀变形时,应变等于平均应变等于单位长度上的变形量,因此l l∆=ε。
学过的有关于ε的知识,即拉伸压缩的胡克定律(Hook’s law ):当应力不超过材料的比例极限时,应力与应变成正比,写成表达式即:εσ⋅=E )(p σσ<,σ(stress),ε(strain)。
杆件横截面上的应力:AF A F N ==σ 将应力和应变两式代入胡克定律中,得到:l lE AF ∆⋅=结论:纵向变形l ∆的表达式:EAFll =∆ )(p σσ< ——胡克定律(重点)含义:①E ——弹性模量,反映材料软硬的程度。
单位MPa 。
②在应力不超过比例极限时,杆件的伸长量l ∆与拉力F 成正比,与杆件的原长l 成正比,与弹性模量E 和横截面积A 成反比。
EA ——抗拉刚度,EA 越大,变形越小。
③两个胡克定律,一个是描述应力和应变的关系,一个是表示力和变形的关系,但本质上都是一样的。
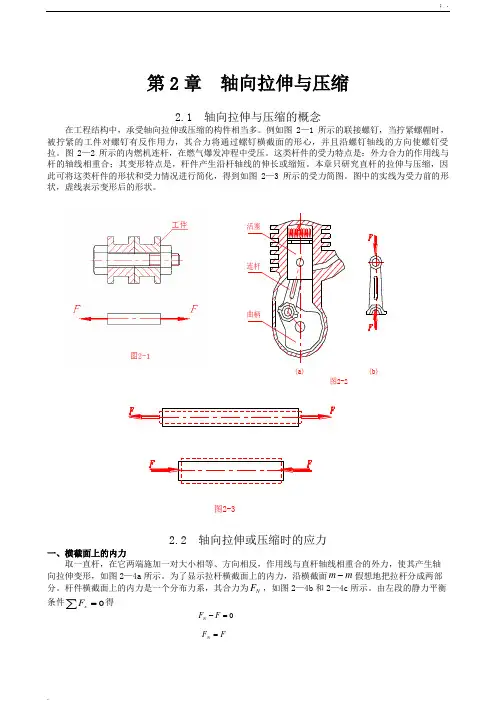
第2章 轴向拉伸与压缩2.1 轴向拉伸与压缩的概念在工程结构中,承受轴向拉伸或压缩的构件相当多。
例如图2—1所示的联接螺钉,当拧紧螺帽时,被拧紧的工件对螺钉有反作用力,其合力将通过螺钉横截面的形心,并且沿螺钉轴线的方向使螺钉受拉。
图2—2所示的内燃机连杆,在燃气爆发冲程中受压。
这类杆件的受力特点是:外力合力的作用线与杆的轴线相重合;其变形特点是,杆件产生沿杆轴线的伸长或缩短。
本章只研究直杆的拉伸与压缩,因此可将这类杆件的形状和受力情况进行简化,得到如图2—3所示的受力简图。
图中的实线为受力前的形状,虚线表示变形后的形状。
2.2 轴向拉伸或压缩时的应力一、横截面上的内力取一直杆,在它两端施加一对大小相等、方向相反,作用线与直杆轴线相重合的外力,使其产生轴向拉伸变形,如图2—4a 所示。
为了显示拉杆横截面上的内力,沿横截面m m -假想地把拉杆分成两部分。
杆件横截面上的内力是一个分布力系,其合力为N F ,如图2—4b 和2—4c 所示。
由左段的静力平衡条件∑=0x F 得0=-F F N FF N =活塞连杆曲柄图2-2(a)(b)图2-3因为外力F 的作用线与杆轴线相重合,所以内力合力N F 的作用线也一定与杆轴线相重合,故称NF 为轴力(normal force )。
为了使左右两段同一截面上的轴力,不仅大小相等而且正负符号也相同,必须联系变形,对轴力的符号作如下规定:使杆产生拉伸变形的轴力为正,产生压缩变形的轴力为负。
二、横截面上的应力仅仅知道杆件横截面上的轴力并不能解决杆的强度问题。
例如,两根材料相同而横截面面积不同的直杆,受到同样大小的轴向拉力作用,两杆横截面上的轴力也相同。
当轴向拉力逐渐增大时,横截面面积小的直杆,必定先被拉断。
这说明杆件强度不仅与轴力大小有关,而且与横截面面积有关。
所以必须用横截面上的应力来度量杆件的强度。
在拉(压)杆横截面上,与轴力N F 相对应的是正应力σ。
要确定该应力的大小,必须了解σ在横截面上的分布规律。



第八章轴向拉伸与压缩课型:新知课教学目标:1.掌握轴向拉压的概念;2.掌握轴力的计算和轴力图的绘制方法;3.掌握低碳钢Q235的应力应变图及其拉伸过程的四个阶段;4.熟记工作应力、极限应力和许用应力的概念及其关系式;5.掌握拉压杆的强度条件;!6.掌握弹性模量和泊松比的概念及其计算;重点:1. 轴力的计算和轴力图的绘制方法。
2. 低碳钢Q235的应力应变图及其拉伸过程的四个阶段。
3. 工作应力、极限应力和许用应力的概念及其关系式。
难点:1. 圣维南原理;2. 低碳钢Q235的应力应变图及其拉伸过程的四个阶段;3. 利用拉压杆的强度条件,解决一些强度问题。
教学手段、方法:结合应用实例进行理论讲授。
,教具:课件、板书教学过程:§8-1 引言作用线沿杆件轴线的载荷称为轴向载荷;以轴向伸长或缩短为主要特征的变形形式,称为轴向拉压;以轴向拉压为主要变形的杆件,称为拉压杆。
~§轴力与轴力图1、截面法求内力:(1) 假想沿m-m横截面将杆切开;(2) 留下左半段或右半段;(3) 将弃去部分对留下部分的作用用内力代替; (4) 对留下部分写平衡方程求出内力即轴力的值。
2、轴力:截面上的内力,由于外力的作用线与杆件的轴线重合,内力的作用线也与杆件的轴线重合。
所以称为轴力。
3、轴力正负号:拉为正、压为负。
4、轴力图:轴力沿杆件轴线的变化。
§ 拉压杆的应力与圣维南原理杆件的强度不仅与轴力有关,还与横截面面积有关。
必须用应力来比较和判断杆件的强度。
在拉(压)杆的横截面上,与轴力FN 对应的应力是正应力 。
根据连续性假设,横截面上到处都存在着内力。
于是得静力关系:N AF dA σ=⎰、观察变形:横向线ab 、cd 仍为直线,且仍垂直于杆轴线,只是分别平行移至a ’b ’、c ’d ’。
平面假设—变形前原为平面的横截面,变形后仍保持为平面且仍垂直于轴线。
从平面假设可以判断:(1)所有纵向纤维伸长相等;(2)因材料均匀,故各纤维受力相等;(3)内力均匀分布,各点正应力相等,为常量。



第八章轴向拉伸与压缩
课型:新知课
教学目标:
1.掌握轴向拉压的概念;
2.掌握轴力的计算和轴力图的绘制方法;
3.掌握低碳钢Q235的应力应变图及其拉伸过程的四个阶段;
4.熟记工作应力、极限应力和许用应力的概念及其关系式;
5.掌握拉压杆的强度条件;
6.掌握弹性模量和泊松比的概念及其计算;
重点:1. 轴力的计算和轴力图的绘制方法。
2. 低碳钢Q235的应力应变图及其拉伸过程的四个阶段。
3. 工作应力、极限应力和许用应力的概念及其关系式。
难点:1. 圣维南原理;
2. 低碳钢Q235的应力应变图及其拉伸过程的四个阶段;
3. 利用拉压杆的强度条件,解决一些强度问题。
教学手段、方法:结合应用实例进行理论讲授。
教具:课件、板书
教学过程:
§8-1 引言
作用线沿杆件轴线的载荷称为轴向载荷;以轴向伸长或缩短为主要特征的变形形式,称为轴向拉压;以轴向拉压为主要变形的杆件,称为拉压杆。
§8.2 轴力与轴力图
1、截面法求内力:
(1) 假想沿m-m横截面将杆切开;
(2) 留下左半段或右半段;
(3) 将弃去部分对留下部分的作用用内力代替;
(4) 对留下部分写平衡方程求出内力即轴力的值。
2、轴力:截面上的内力
由于外力的作用线与杆件的轴线重合,内力的作用线也与杆件的轴线重合。
所以称为轴力。
3、轴力正负号:
拉为正、压为负。
4、轴力图:轴力沿杆件轴线的变化。
§8.3 拉压杆的应力与圣维南原理
杆件的强度不仅与轴力有关,还与横截面面积有关。
必须用应力来比较和判断杆件的强度。
在拉(压)杆的横截面上,与轴力FN 对应的应力是正应力 。
根据连续性假设,横截面上到处都存在着内力。
于是得静力关系:N A
F dA σ=
⎰
观察变形:横向线ab 、cd 仍为直线,且仍垂直于杆轴线,只是分别平行移至a ’b ’、c ’d ’。
平面假设—变形前原为平面的横截面,变形后仍保持为平面且仍垂直于轴线。
从平面假设可以判断:
(1)所有纵向纤维伸长相等;
(2)因材料均匀,故各纤维受力相等;
(3)内力均匀分布,各点正应力相等,为常量。
横截面上的正应力σ计算公式:N
F A
σ=
正应力σ和轴力FN 同号。
即拉应力为正,压应力为负。
圣维南原理
力作用于杆端的分布方式,只影响杆端局部范围的应力分布,影响区的轴向范围约离杆端1~2个杆的横向尺寸。
§8.4 材料在拉伸与压缩时的力学性能
材料在拉伸时的力学性能:低碳钢Q235应力应变图
一 、四个阶段
1、弹性阶段ob 胡克定律
E σε=
P σ—比例极限 E —弹性模量(GN/m2)tan E σ
αε
=
= 2、屈服阶段bc (失去抵抗变形的能力)
s σ—屈服极限
3、强化阶段ce (恢复抵抗变形的能力)
b σ—强度极限
4、局部径缩阶段ef
两个塑性指标: 断后伸长率 100100%l l l δ-=
⨯ 断面收缩率 01
100%A A A ψ-=⨯ 5%δ≥为塑性材料 5%δ<为脆性材料。
低碳钢的2030%δ≈—,60%ψ≈为塑性材料。
二、卸载定律及冷作硬化
1、弹性范围内卸载、再加载 变形完全消失,--e σ弹性极限
2、过弹性范围卸载、再加载
在硬化阶段d 点逐渐减小载荷,卸载过程如图中dd ’所示,该直线与oa 几乎平行。
线段dd ’代表应力减小至零时残留的应变,即塑性应变或残余应变。
材料的比例极限增高,延伸率降低,称之为冷作硬化或加工硬化。
三、其它材料拉伸时的力学性质
对于没有明显屈服阶段的塑性材料,用名义屈服极限σp0.2来表示。
四、 塑性材料(低碳钢)的压缩
拉伸与压缩在屈服阶段以前完全相同。
脆性材料的抗拉与抗压性质不完全相同,压缩时的强度极限远大于拉伸时的强度极限。
§8.5 应力集中的概念
由于截面急剧变化所引起的应力局部增大现象,称为应力集中。
常见的油孔、沟槽等均有构件尺寸突变,突变处将产生应力集中现象。
应力集中程度用应力集中因数K 表示,其定义为max K σσ
=
1、形状尺寸的影响:
尺寸变化越急剧、角越尖、孔越小,应力集中的程度越严重。
2、材料的影响:
应力集中对塑性材料的影响不大;应力集中对脆性材料的影响严重,应特别注意。
§8.6 失效、许用应力和强度条件
一、失效与许用应力
前述试验表明,当正应力达到强度极限b σ,会引起断裂;当正应力达到屈服应力s σ时,将产生屈服或出现显著塑性变形。
构件工作时发生断裂或显著塑性变形,一般都是不容许的。
根据这类情况,通常将强度极限与屈服应力统称为材料的极限应力,并用u σ表示。
根据分析计算所得构件的应力,称为工作应力。
对于由一定材料制成的具体构件,工作应力的最大容许值,称为材料的许用应力,用[]σ表示。
许用应力和极限应力的关系:
[]u
n
σσ=
其中,n 为安全因数,对于塑性材料,按屈服应力所规定的安全因数s n ,通常取1.5~2.2;对于脆性材料,按强度极限所规定的安全因数b n ,通常取为3.0~5.0,甚至更大。
二、强度条件
为了保证拉压杆在工作时不致因强度不够而被破坏,杆内的最大工作应力max σ不得超过材料的许用应力[]σ,即要求
[]max N
F A
σσ=
≤ 上述判据为拉压杆的强度条件。
利用上述条件,可以解决以下几类强度问题。
1、强度校核:[]max N
F A
σσ=≤ 2、设计截面:[]
N
F A σ≥
3、确定许可载荷:[]N F A σ≤
§8.7 胡克定律与拉压杆的变形
杆件沿轴线方向的变形为杆的轴向变形;垂直轴线方向的变形称为杆的横向变形。
一、拉压杆的轴向变形与胡克定律
轴向拉压试验表明,在比例极限内,正应力与正应变成正比,E σε=
上述关系称为胡克定律。
比例系数E 称为材料的弹性模量,其值随材料而异,并由试验确定。
弹性模量的单位通常为GPa 。
二、拉压杆的横向变形与泊松比
试验表明,轴向拉伸时,杆沿轴向伸长,其横向尺寸减小,轴向压缩时,杆沿轴向缩短,其横向尺寸则增大,即横向正应变'ε与轴向正应变ε恒为异号。
在比例极限内,横向正应变与轴向正应变成正比。
将横向正应变与轴向正应变之比的绝对值用μ来表示,则由上述试验可知,
''εεμεε
=
=-
比例系数μ称为泊松比,在比例极限内,泊松比μ是一个常数。
对于大多数各项同性材料,00.5μ<<。
§8-9 连接部分的强度计算
拉压杆与其他构件之间,或一般构件与构件之间,常采用销钉、耳片或螺栓等连接,本节介绍连接件的强度计算。
一、剪切与剪切强度条件
假设切应力在剪切面(m-m 截面)上是均匀分布的, 得实用切应力计算公式:
s
F A
τ=
切应力强度条件:[]s
F A
ττ=
≤ []τ为许用切应力,常由实验方法确定。
塑性材料:[]()[]0.50.7τσ=- 脆性材料:[]()[]0.8 1.0τσ=-
二、挤压与挤压强度条件
在外力作用下,销钉与孔直接接触,接触面上的应力称为挤压应力。
假设应力在挤压面上是均匀分布的,得实用挤压应力公式
bs
bs bs
F A σ=
*注意挤压面面积的计算
(1)接触面为平面 Abs —实际接触面面积 (2)接触面为圆柱面 Abs —直径投影面面积
S F m
m
F
F
F
m
m F
S
F m
m。