当前位置：文档之家 › 勾股定理-说课课件(一)

勾股定理-说课课件(一)

  • 格式：ppt
  • 大小：838.00 KB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

勾股定理(说课课件)

勾股定理(说课课件)

Sa+Sb=Sc
C
c弦
a2+b2=c2
猜想:两直角边a、b与斜边c 之间的关系？
证法一：赵爽弦图
c
a
(1) c c
b
(2) (b-a)2 (3) (2) c
c
(3)
2
a2+b2－2ab = c2－2ab
(4)
1 c 4 ab (b a) 2 2
可得：a2 + Байду номын сангаас2 = c2
证法二： 毕达哥拉斯证法
c
b
a
设计意图：这样的板书比较简洁，但可 以呈现重点难点，强化学生记忆。
⑴若a=6 ， c=10 ，则b=____
⑵若a=5 ，b=12 ，则c=____
⑶ 若 c=25 ， b=15 ，则a=____
1.求下列图中表示边的未知数x、y、z的值.
144 81 144 169 ② 625
z
576
①
③
2.求下列直角三角形中未知边的长:
5
比 一 比 看 看 谁 算 得 快 ！
授课人：张碧云
一、说教材 二、说教法学法 三、说教学过程
一.说教材
（一） 地位和作用
本节课是人教版八年级数学下册第十七章第 一节勾股定理第一课时的内容。 勾股定理是学生在已经掌握了直角三角形的 有关性质的基础上进行学习的，它是直角三角形 的一条非常重要的性质，是几何中最重要的定理 之一，它揭示了一个三角形三条边之间的数量关 系，它可以解决直角三角形中的计算问题，是解 直角三角形的主要根据之一，在实际生活中用途 很大。
布置作业
必做题：
P28 习题：1、2
选做题： 这是由两个边长分别为1、2 的正方形连在一起的“L”型 纸片，你能否只剪两刀就能 将所得图形拼成一个正方形？

最新初中数学说课获奖：《勾股定理》(1)优秀ppt课件

最新初中数学说课获奖：《勾股定理》(1)优秀ppt课件
怎样得到正方形C 的面积？ 与同伴交流交流。
（图中每个小方格代表1平方厘米）
10
为了分散难点
（1）我制作一个表格，让学生完成这个表格，目的是学生在探究中更具有 方向性
图2-1
A的面积(单位 B的面积(单位 C的面积(单位
长度)
长度)
长度)
图2-2
A、B、C面积 关系
直角三角形三 边关系
11
为了分散难点 （2）学生在独立探究的基础上，进行小组合作，此时，留给学生充分的时间思考和交流， 教师参与小组活动，针对不同认识水平的学生引导其不同的方法.
3
一、教 材 分 析 3、教材的重点、难点： 难点：利用面积法探索勾股定理和用拼图的方法验证勾股定理 确立原因：八年级学生已具备一定的分析与归纳能力，初步掌握了探索图形性质的基本方法， 但是学生对利用割补方法和利用面积计算证明几何命题的意识和能力不够，对于如何将图形 与数有机结合起来还很陌生。
突破难点的 策略：（1）对于利用面积法探索勾股定理，通过小组合作，留给学生充分的时间 交流，采用分割或补全两种方法分散难点；
22
五 板书设计：
屏幕
§18、1、勾股定理 1、知识点
文字叙述 数学语言

抢答题 例题
23
六：教学设计说明
1.本节课是定理课：根据学生的知识结构，我采用的教学流程体现了 知识发生，形成，和发展的过程，让学生充分体会到观察、猜想、归纳、 验证的思想和数形结合的思想。
2.本节课最大的亮点是：始终把学生的探索与验证活动放在首位，让 学生以一个创造者或发明者的身份去探索知识，从而形成自觉实践的习 惯，达到我的教学目的。
12
这是用“补”的方法
C
A A

勾股定理 说课课件(一)

勾股定理 说课课件(一)

教学目标
【知识与技能目标】1、了解勾股定理的文化背景，体验勾理的探索过程，了 解利用拼图验证勾股定理的方法。 2、了解勾股定理的内容。 3、能利用已知两边求直角三角形另一边的长。 【能力与方法目标】1、通过拼图活动，体验数学思维的严谨性，发展形象思维。 2、在探索活动中，学会与人合作，并能与他人交流思维的 过程和探索的结果。
课后习题16.1 1.必做题: 复习巩固 练习 综合运用 习题1.2.3. 2.选做题: 了解勾股定理的多种证明方法.
(根据自己的知识能力掌握情况选择完成.)
如果直角三角形两直角边分别为a、b,
板 书 设 计 ：
斜边为c，那么
c a
┏
b
a2+b2=c2
直角三角形两直角边的平方和 等于斜边的平方.
在我国，把直角三角形的这一个 特佂叫做勾股定理
2、时间分配
1、创设情境
2、实验操作
2分钟
10分钟
3、归纳验证
4、问题解决
10分钟
10分钟
5、课堂小结
6、推荐作业
6分钟
2分钟
A
B
C
A、B、C的面积有什么关系？
SA+SB=SC
直角三角形三边有什么关系？ 两直边的平方和等于斜边的平方
设：直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系？
A a
B b
SA+SB=SC
c
C
a2+b2=c2
如果直角三角形两直角边分别为a、b,
斜边为c，那么
c a
┏
b
a2+b2=c2
勾 股 世 界
我国是最早了解勾股定理的国 家之一。早在三千多年前，周 朝数学家商高就提出，将一根 直尺折成一个直角，如果勾等 于三，股等于四，那么弦就等 于五，即“勾三、股四、弦 五”，它被记载于我国古代著 名的数学著作《周髀算经》中。

《勾股定理》PPT(第1课时)

《勾股定理》PPT(第1课时)
由上面的例子，我们猜想：
命题1 如果直角三角形的两条直角边长分别为a,b，斜边 长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
ac
b
课程讲授
1 勾股定理
下面让我们跟着以前的数学家们用拼图法来证明这一猜想.
c b a
b-a
证明：∵S大正方形＝c2， S小正方形＝(b-a)2,
∴S大正方形＝4S三角形＋S小正方形，
课程讲授 2 勾股定理与图形面积
归纳：与直角三角形三边相连的正方形、半圆及 正多边形、圆都具有相同的结论：两直角边上图 形面积的和等于斜边上图形的面积．本例考查了 勾股定理及半圆面积的求法，解答此类题目的关 键是仔细观察所给图形，面积与边长、直径有平 方关系，就很容易联想到勾股定理．
课程讲授Biblioteka 2 勾股定理与图形面积定有a2+b2=c2.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
课程讲授
1 勾股定理
几何语言： ∵在Rt△ABC中 ，∠C=90°，
B ac
∟
∴a2+b2=c2（勾股定理）.
C
勾股定理揭示了直角三角形三边之间的关系.
bA
课程讲授 1 勾股定理
例 在Rt△ABC中，∠C＝90°，AB＝10 cm， BC＝8 cm，求AC的长．
（1）正方形P的面积是 1 平方厘米； （2）正方形Q的面积是 1 平方厘米； （3）正方形R的面积是 2 平方厘米.
AR P
CQ B
上面三个正方形的面积之间有什么关系？ SP+SQ=SR
（图中每一格代表一平方厘米）
课程讲授 1 勾股定理
直角三角形ABC三边长度之间存在什么关系吗？ SP=AC2 SQ=BC2 SR=AB2 AC2+BC2=AB2

18.1q勾股定理说课课件

18.1q勾股定理说课课件
B c a C
b-a b
A
赵 爽 弦 图
（拼图验证） （2）仿照课本中赵爽的思路，只剪两刀，将边长 为a、b的两个连体正方形，拼成一个新的正方形？
C
c b
b- a a
b
a
b-a
C
b
a
b-a
M a
P
b
N
图18.1-3（1）
图18.1-3（2）
图18.1-3（3）
（3）怎样根据拼图活动的结果证明勾股定理呢？
一．了解历史 ：赵爽弦图 四．反馈练习 二．图形探究→猜想→证明 1. 三．勾股定理： 2. 如果直角三角形两直角边长 3. 分别是a,b,斜边长是c,那么 五．小结 六．作业 2 2 2
a b c
谢
谢
教学设计说明
为了让学生在学习过程中自我发现勾股定理，本节课从
探究等腰直角三角形三边的关系入手，自然过渡到探究一
般直角三角形，引导学生去观察、思考、探索、发现，进 而得到勾股定理．学生再通过小组合作，讨论交流，验证 勾股定理.从而经历知识产生、形成和发展的过程，提高学 生的思维能力.
板书设计
18.1勾股定理（一）
五、实践应用→拓展提高
活动5 ．（1）求出下列直角三角形中未知 边的长度.
A 10 B 15
B 6
C
A
8 C
（2） 试一试：剪四个与图1完全相同的直角三角形， 然后将它们拼成如图2所示的图形. 大正方形的面积可以表示为____, 又可以表示为____. 对比两种表示方法，看看能不能得到勾股定理的结论.
七、布置作业→巩固加深
活动7．作业 （1）（必做题）：习题18.1 第1, 7题. （2）（选做题）阅读课本“阅读与思考”，了解 勾股定理的多种证法．

勾股定理说课PPT课件

勾股定理说课PPT课件
观察猜测 动手操作 交流讨论 归纳总结
教学程序设计
教学流程图
回顾小结深化新知 学以致用拓展新知 学生活动验证新知 拼图验证归纳新知 观察特例发现新知 创设情境引入新课
《 勾股定理》说课
《 勾股定理》说课
教学程序设计
第一环节 创设情境 引入新课
赵爽弦图 中国——赵爽
北京欢迎您！
18.1勾股定理（1）
勾股命定题理1： 如果直角三角形的两直角边长分别为
, a，斜b 边长为 ，那c 么 a2 b2 c2.
勾
弦
c
a
股bΒιβλιοθήκη 股世界两千两多千多年年前前，，古古希希腊有腊个有哥拉个毕达哥拉斯 学斯学派派，，他他们们首首先发先现发了勾现股了定勾理，股因定此 理，因此在 在国国外外人人们们通通常常称勾称股勾定理股为定毕理达哥为拉毕斯 达哥拉斯定 定理理。。为为了了纪纪念念毕达毕哥达拉斯哥学拉派斯，1学95派5 ，1955年 年希希腊腊曾曾经经发发行行了一了枚一纪念枚票纪。念邮票。
结论：
a2 b2 c2
a
b c
a
c
b
(a b)2 c2 4 1 ab 2
a2 b2 c2
《 勾股定理》说课
教学程序设计
第五环节 学以致用 拓展新知
基础训练
1、分别求出图中A、B的面积
A
81
144
B 196
289
基础训练
2 .求出下列直角三角形中未知边的长度.
A
A
B
17
3 C4
B
《 勾股定理》说课
教学程序设计
第四环节 学生活动 验证新知
动y动=手0
尝试用下面四个全等的直角三角形围成一个 正方形，然后通过面积分割法和整体计算法分别 求出正方形的的面积，看看你有什么发现。

《勾股定理》PPT优质课件(第1课时)

《勾股定理》PPT优质课件(第1课时)

A． 3
B．3
C． 5
D．5
E
课堂检测
基础巩固题
1. 若一个直角三角形的两直角边长分别为9和12，则斜边的
长为（ C）
A.13
B.17
C. 15
D.18
2.若一个直角三角形的斜边长为17，一条直角边长为15，则
另一直角边长为（ A ）
A.8
B.40
C.50
D.36
3.在Rt△ABC中，∠C=90°，若a︰b=3︰4，c=100，则 a= _6_0___，b = __8_0___.
课堂检测
4．如图，所有的四边形都是正方形，所有的三角形都是直角三角 形，其中最大的正方形的边长为7cm,则正方形A，B，C，D的面 积之和为_____4_9_____cm2 ．
C D
B A
7cm
课堂检测
能力提升题
在Rt△ABC中，AB＝4，AC＝3，求BC的长.
解：本题斜边不确定，需分类讨论：
当AB为斜边时，如图，BC 42 32 7;
形，拼成一个新的正方形.
探究新知 剪、拼过程展示：
b
a ca
朱实
b 朱实 黄实朱实
c 〓b
ba
朱实
a
M a P bb
N
探究新知 “赵爽弦图”
c
朱实
b
朱实
黄实 朱实
a
朱实
证明：∵S大正方形＝c2， S小正方形＝(b-a)2,
∴S大正方形＝4·S三角形＋S小正方形，
探究新知
毕达哥拉斯证法：请先用手中的四个全等的直角三角形按图 示进行拼图，然后分析其面积关系后证明吧.
因此设a=x,c=2x,根据勾股定理建立方程得 (2x)2-x2=152，

17.1.1勾股定理说课课件

17.1.1勾股定理说课课件

C
S正方形c
1 = 5 -4× 2 ×2×3
2
C A
B
图1-3
=13（面积单位）
把C“补”成边长为5的 正方形面积减去4个直 角三角形的面积。
议 一 议
3．三个正方形A，B，
A的面积 B的面积 C的面积 图1-2 图1-3
16 4
9 9
25 13
C面积之间有什么关系？
A B
图1-2
C
SA+SB=SC
2002年在北京召开国际数学家大会
这就是本届大会 会徽的图案． 你听说过勾股定理吗？
这个图案是我国汉代数学家 赵爽在证明勾股定理时用到的， 被称为“赵爽弦图”．
勾股定理
在我国古代，人们将直角三角形中的短的直角边叫做 勾，长的直角边叫做股，斜边叫做弦．根据我国古算书 《周髀算经》记载，在约公元前1100年，人们已经知道， 如果勾是三，股是四，那么弦是五，后来人们进一步发现 并证明了直角三角形三边之间的关系：两条直角边的平方 和等于斜边的平方。这就是勾股定理。
用赵爽弦图证明勾股定理
通过这些实际操作，学生进行一步加深 c 对数形结合的理解，拼图也会产生感性 b 认识，也为论证勾股定理做好准备。 利用分组讨论，加强合作意识。 a 1、经历所拼图形与多媒体展示图形的 联系与区别。 b a 2、加强数学严密教育。从而更好地理 解代数与图形相结合 。 2+b2=c2
的证明方法已有几百种之多．下面我们就
依据科学理论的证实：
我国汉代的数学家赵爽指出：四个全等的直 角三角形如下拼成一个中空的正方形，由大正方 形的面积等于小正方形的面积与4个直角三角形 的面积和得：
直角三角形两直角边的平方和等于 斜边的平方.

勾股定理第一课时PPT课件

勾股定理第一课时PPT课件
58厘米
a
5、如图将长为5.41米的梯子AC斜靠在墙上,BC长 为2.16米,求梯子上端A到墙的底端B的距离AB(精确 到0.01米)
分析：先把实际问题转化成数学问题。 求：AB的长。
解：在Rt⊿ABC中，∠ABC = 90º， BC = 2.16 ， CA = 5.41 根据勾股定理得： AB = AC 2 BC 2 5.412 2.162 4.96（米）
两直边的平方和等于斜边的平方
同学们，我们也来 观察图中的地面， 看看你能发现什么？ 是否和大哲学家有 同样的发现呢？
你能发 现图中 的等腰 直角三 角形有 什么性 质吗？
A B C
观察 & 发现
C A
B
（1）观察图形 正方形A中含有 9 ___个小方格即A的 9 面积是位面积-----正方形B中含有 个小方格，即B的 9 面积是__ 个单位 9 面积-----正方形C中含 有 18 个小方格， 18 即C的面积是____ 个单位面积。
勾股定理
如果直角三角形两直角边分别为a，b，斜边 为c，那么 a2 + b2 = c2 即直角三角形两直角边的平方和等于斜边的平方.
2+ a 2 c
2 b
2 =c
b 股 2 - a2 =b2 c 在西方又称毕达哥拉斯定理！
2 =a2 b
勾a
弦
c
想一想：
1、已知：a＝3， b＝4，求c c 2、已知： c ＝10，a＝6，求b b 3、已知： c ＝13，a＝5，求阴影部分面积 4 、小明妈妈买了一部29英寸 c （74厘米）的电视机.小明量了电 a 视机的屏幕后，发现屏幕只有58 厘米长和46厘米宽，他觉得一定 是售货员搞错了.你同意他的想法 46厘米 吗？你能解释这是为什么吗？

【数学课件】勾股定理1课件

【数学课件】勾股定理1课件

a
c
你能证明这个 命题是正确的
命题吗？
b
命题：如果直角三角形的两直角边长分别 为a、b，斜边长为c，那么a2+b2=c2。
赵爽的证法：赵爽弦图证明勾股定理
bc
c b
a
a
a
等积变换
= a 2 b 2
c 2 数形结合思想
定理：经过证明被确认为 正确的命题叫做定理。
勾股定理：如果直角三角形的两直
角边长分别为ａ、ｂ，斜边为ｃ，那 么a2+b2=c2。
最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——（前苏联）苏霍姆林斯基 6、教育不是注满一桶水，而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的，但其果实是甜的。——亚里士多德 9、教育的目的，是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——（前苏联）苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美，人的关系的美而看到的精神的高尚、善良和诚实，并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知，而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品，就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心，这种道德上的自勉。要是儿童自己不求上进，不知自勉，任何教育者就都不能在他的身
b2 =c2-a2 b= c2-a2
c a2 b2
C

勾股定理说课课件

勾股定理说课课件

数形欣赏： 数形欣赏：
B A C D
8
送给你们一棵“美丽勾股树” 送给你们一棵“美丽勾股树”，所有的正方形都是以 直角三角形的边为边，其中最大的正方形的边长为8cm, 直角三角形的边为边，其中最大的正方形的边长为 求正方形A， ， ， 的面积之和 的面积之和。 求正方形 ，B，C，D的面积之和。
板书设计
b
c
b
c
b
c
b
c
a
a
a
a
幻灯片 12
赵爽弦图 思考：能否用两种方法表示大正方形面积？ c a b c b a b
1 (b − a) + 4 × ab = c 2 2
2
幻灯片 11
}
b − 2ab+ a + 2ab= c
2 2
2
a +b = c
2 2
2
a
分享成果： 分享成果：
勾 股 世 界
两千多年前， 两千多年前 ， 两千多年前，古希腊有个毕达哥拉斯 两千多年前，古希腊有个哥拉 斯学派， 他们首先发现了勾股定理， 斯学派， 他们首先发现了勾股定理 学派，他们首先发现了勾股定理， 学派，他们首先发现了勾股定理，因此 ，因此在 在国外人们通常称勾股定理为毕达哥拉斯 国外人们通常称勾股定理称为毕达哥拉斯 定理。为了纪念毕达哥拉斯学派， 定理。为了纪念毕达哥拉斯学派，1955 定理。为了纪念毕达哥拉斯学派， 定理。为了纪念毕达哥拉斯学派，1955 年希腊曾经发行了一枚纪念票。 年希腊曾经发行了一枚纪念票。 年希腊曾经发行了一枚纪念邮票。 年希腊曾经发行了一枚纪念邮票。 国家之一。早在三千多年前， 国家之一。早在三千多年前， 我国是最早了解勾股定理的 国家之一。早在三千多年前， 国家之一。早在三千多年前， 国家之一。早在三千多年前， 国家之一。早在三千多年前，周 国家之一。早在三千多年前， 国家之一。早在三千多年前， 朝数学家商高就提出， 朝数学家商高就提出，将一根直 国家之一。早在三千多年前， 国家之一。早在三千多年前， 尺折成一个直角，如果勾等于三， 尺折成一个直角，如果勾等于三， 国家之一。早在三千多年前， 国家之一。早在三千多年前， 股等于四，那么弦就等于五， 股等于四，那么弦就等于五，即 国家之一。早在三千多年前， 国家之一 、股四、弦五” 勾三、股四、弦五” “勾三。早在三千多年前， ，它被记 国家之一。早在三千多年前， 国家之一。早在三千多年前， 载于我国古代著名的数学著作 国家之一。 国家之一。早在三千多年前 周髀算经》 《周髀算经》中。

勾股定理说课稿ppt课件

勾股定理说课稿ppt课件

（二）学情分析
八年级学生已初步具有几何图形的 观察，几何证明的理论思维能力。希 望老师预设便于他们进行观察的几何 环境，给他们发表自己见解和表现自 己才华的机会，希望老师满足他们的 创造愿望，让他们实际操作，使他们 获得施展自己创造才能的机会。
580 630
（三）教学方法
数学是一门培养人的思维,发展人的思维的重要学 科,因此,在教学中,要展现获取知识和方法的思维过 程, 针对八年级学生的知识结构和心理特征，本节 课采取引导探索法，由浅入深，由特殊到一般地提 出问题。以导为主,采用设疑的形式，让学生通过观 察、分析、讨论、操作、归纳，理解定理，提高学 生动手操作能力，以及分析问题和解决问题的能力。 5 使学生得到获得新知的成功感受，从而激发学生钻 m 研新知。并利用教具与多媒体进行教学。
2m
活动2、探索勾股定理
探究一（观察特例→发现新知）
{问题一}：在图中你能发现哪些基本图形？ {问题二}：与等腰直角三角形相邻的正方形面积之间 有怎样的关系？ {问题三}：如图，每个小方格的面积为1个单位，你能 写出正方形A、Ｂ、Ｃ的面积吗？ {问题四}：由此你可以得出等腰直角三角形三边存在着一种怎样特殊的数量关 系吗？ 学生在独立探究的基础上观察图片，计算面积，分组交流， 猜想和归纳。 教师参与学生小组活动，指导，倾听学生交流。 设计意图：通过讲传说故事来激发学生学习兴趣，引导学生进入学习状态。 学生会很积极的投入到探索这个问题的实践中。 “问题是思维的起点”，通过层层设问，引导学生发现新知。由正方形的面 积等于边长的平方归纳出：等腰直角三角形两条直角边的平方和等于斜边的平 方。 {问题五}：等腰直角三角形三边具有这样的特殊关系，那么一般的直角三角形 呢？
B
Ｂ
350 A

勾股定理说课(完整版)PPT课件

勾股定理说课(完整版)PPT课件

教学目标
（1）、知识与技能： 理解勾股定理的两种 证明方法——毕达哥拉斯证法和赵爽的弦图 证法；应用勾股定理解决简单的直角三角形 三边计算问题 （2）、过程与方法：通过对直角三角形三边 关系的猜想验证，经历从特殊到一般的探索 过程，发展合情推理，体会数形结合的思想 （3）、情感态度与价值观：在勾股定理的探 索过程中感受数学文化的内涵，增进数学学 习的信心
2、直角ABC的一条直角边a=10,斜边 c=26，则b=
( 24 )。
３、已知：∠C＝90°，a=6， a：b＝3：4， 求b和c。
c=10 b=8
ac
b
1.说一说本节课我有哪些收获? 2.本节课我还有哪些疑惑?
-
作业
必做题：课本69页第一题。 选做题：收集有关勾股定理的其它 证明方法，下节课展示、交流。
图2
4
9
13
图2
C
A
B
图3
图3
9 25 34
A、B、 C面积 关系
直角三 角形三 边关系
sA+sB=sC
两直角边的平方和 等于斜边的平方
ac
结论
b
直角三角形两直角边的平方和等于斜边的平方．
是不是所有的直角三角形都具有这样的特点呢？ 这就需要我们对一个一般的直角三角形进行证 明．到目前为止，对这个命题的证明方法已有几百 种之多．下面我们就来看一看我国数学家赵爽是怎 样证明这个命题的．
教学重点、难点
重点：探究并理解勾股定理 难点：探索勾股定理的验证方法
教法 分析
平行线的性质是学生对图形性质的第一 次系统研究，对于研究过程和研究方法都 是陌生的，所以学生需要在老师的引导下 类比研究平行线的判定的过程来构建平行 线的性质的研究过程。

鲁教版七年级上册数学《勾股定理》说课课件(共20张PPT)

鲁教版七年级上册数学《勾股定理》说课课件(共20张PPT)

a2 b2 c2
（六）盘点收获——谈一谈
学生谈体会. 补充：勾股定理又叫“毕达哥拉 斯”“百牛”“驴桥”定理，数学家华罗 庚建议发射勾股定理的图形与“外星人” 交流等.
【作业布置】
推荐1、收集勾股定理的其它证明方法.
推荐2、利用几何画板探究锐角和钝角三角形 是否也满足勾股定理所说的特点.
板书设计
本节课意在使学生经历勾股定理的发现过程，所以课堂上 尽可能的展示学生的发现，教师要做得仅仅是问题的激发者、 有序探究的组织者、学生错误的澄清者和多角度思考的促进者， 最终使师生成为“数学学习的共同体”.
谢谢聆听
Swire Beverages
20
①通过探究学习体 验解决问题方法的 多样性，培养学生 合作交流的意识和 探索精神; ②通过 了解勾股定理的历 史背景，感受数学 文化，激发学习热 情.
重点难点
教学重点：探索和证明勾股定理 教学难点：勾股定理的发现过程
学情分析
知识学习的必要性
几何定理的学习，学生往 往只重视应用，忽视探索、研 究、发现定理的过程，这样必 然会导致对知识一知半解，知 其然，却不知所以然.通过本 节课的学习，纠正学生的学习 误区，使学生在探索活动中真 正收获到知识、技能和方法.
欣赏图片说一说 探索发现猜一猜 归纳总结写一写 大胆质疑画一画 动手动脑拼一拼 盘点收获谈一谈
SⅠ+ SⅡ= S
学
a2 b2 c2
生 活
勾股定理… 动
区
设计反思
这节课是一节几何定理探索课，在设计时，我依据课程 标准、教材特点、遵循学生的认知规律，由浅入深、由特殊到 一般的提出问题，把学生置于问题的提出过程；通过合作探究， 把学生置于结论的发现过程；最后，通过猜想证明，把学生置 于知识体系的构建过程.

勾股定理第一课时说课课件

勾股定理第一课时说课课件

P
P Q
C R C R
Q
用了“补”的方法 用了“割”的方法 如图，小方格的边长为1. 你能求出正方形R的面积吗？
观察所得到的各组数据，你有什么发现？ P a Q b
SP+SQ=SR
c
R
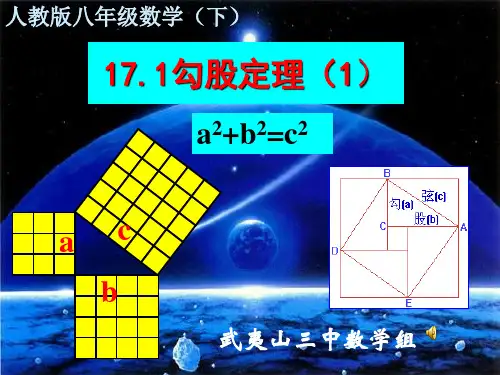
a2+b2=c2
猜想:两直角边a、b与斜边c 之间的关系？
命题1 直角三角形，两个直角边的平方 和等于斜边的平方。
勾 股 世 界
两千多年前，古希腊有个哥拉 两千多年前，古希腊有个毕达哥拉斯 斯学派，他们首先发现了勾股定理，因此 学派，他们首先发现了勾股定理，因此在 在国外人们通常称勾股定理为毕达哥拉斯 国外人们通常称勾股定理为毕达哥拉斯定 定理。为了纪念毕达哥拉斯学派， 1955 理。为了纪念毕达哥拉斯学派， 1955年 年希腊曾经发行了一枚纪念票。 希腊曾经发行了一枚纪念邮票。
应用知识 回归生活
2. 填空题：
1) 在直角三角形中，两条直角边 2+b2 2 a 分别为a,b, 斜边为c，则c =____ 2) 在RT△ABC中∠C=90°, 5 ⑴若a=4,b=3,则c=____
12 ⑵若c=13,b=5,则a=____
15 ⑶ 若 c=17,a=8,则b=____
应用知识 回归生活
一般地提出问题。 引导学生自主探索，合作交
流，这种教学理念反映了时代精神，有利于提
高学生的思维能力，能有效地激发学生的思维
积极性和创造性。
教材分析
教法分析
学法分析
过程分析
设计说明
在教师的组织引导下，采用自主探索、合作 交流的研讨式学习方式，让学生思考问题，获取 知识，掌握方法，逐步培养学生动口、动手、动 脑的能力，使学生真正成为学习的主体。体现了 以学生发展为本的新课改精神。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

拼图展示
赵爽弦图
思考：大正方形面积怎么求？
c
a c
a
b
b
1 2 (b a) 4 ab c 2
2
b 2ab a 2ab c
2 2
2
结论：
a b c
2 2
2
勾股定理
直角三角形两直角边的平方和等于 斜边的平方.
弦
c
勾a ┏
股
b
a2+b2=c2
练习一
A 81 144 1、求下图中字母A、B所代 表的正方形的面积 2、求出下图中直角三角形 中未知边的长度
（二）观察特例→发现新知
Hale Waihona Puke A C毕达哥拉斯（公元前572—前 497年），古希腊著名的哲学 家、数学家、天文学家.
B
观察并思考：毕达哥拉斯发现些什么？ 等腰直角三角形两条直角边的平方和等于斜边的平方 正方形A、B的面积之和等于大正方形C的面积. 即 a 2 b2 c 2 .
（三）深入探究→交流归纳
教法和学法分析

数学是一门培养人的思维，发展人的思维的重 要学科，因此在教学中，不仅要使学生“知其 然”，而且还要使学生“知其所以然”。针对 八年级学生的认知结构和心理特征，本节课选 择“引导探索法”，由浅到深，由特殊到一般 的提出问题,引导学生自主探索，合作交流。 培养学生“动手”、“动脑”、“动口”的习 惯与能力，使学生真正成为学习的主人。
例1
课堂训练
例2
学生板演
a2 b2 c2
时间分配
1、创设情境
2、实验操作
2分钟
10分钟
3、归纳验证
4、问题解决
10分钟
10分钟
5、课堂小结
6、推荐作业
6分钟
2分钟
设计理念
各位老师，我这堂课的设计理念是： 围绕一个核心：以人为本，把更多的人文精神融 入课堂； 突出一个重心：以学生为重心，创设激情，设疑 激趣，变学会为会学。优化配置“教师主导、学生 主体”的教学模式，在积极愉悦的课堂氛围中实现 教学相长。
猜一猜：等腰直角三角形有上述性质，一般的直 角三角形也有这个性质吗？
B
A的面积 (单位 面积)
B的面积 (单位 面积)
C的面积 (单位 面积)
A
C
图1 A、B、 C 面积 关系 直角三 角形三 边关系
4
9
13
sA+sB=sC
两直角边的平方和等 于斜边的平方．
图1
命题
如果直角三角形的两直角边长 分别为 a， ，斜边长为 c ，那 b 2 2 2 么 a b c .
教学程序设计
教学流程图
创 设 情 境 探 索 新 知 实 验 操 作 获 取 新 知 归 纳 验 证 完 善 新 知 问 题 解 决 应 用 新 知 课 堂 小 结 巩 固 新 知
推 荐 作 业 拓 展 新 知
（一）情景导入某超市为方便顾客购物要建一传送电梯，已
知楼高4米，电梯底部距楼底10米，请问传送电梯的履带需多长?
c a
b
归纳验证
对于定理的证明，是本堂课的难点，所以我采取 四人小组进行分组讨论，让学生尝试解决。学生讨论 时，教师巡回指导。如果有些学生感到困难，可以进 行适当点拨, 在这一环节中，学生充分讨论，各抒己见 ，充分暴露其思维过程。通过学生的互相讨论，激发 学生的思维活动，可以发现一些解题的方法。 学生代表上台展示拼图结果,对学生的表现及时给 予肯定和鼓励。
18.1 勾股定理
说课内容
学情 分析 教材 分析 教法 分析 学法 分析
教学程 序设计
说
设计 理念
教材分析
教材地位作用
勾股定理是学生在已经掌握了直角三角形有关性 质的基础上进行学习的，它是直角三角形的一条 非常重要的性质，是几何中最重要的定理之一， 它揭示了直角三角形三条边之间的数量关系，为 理解并掌握勾股定理的内容和证明，能够灵 以后学习解直角三角形奠定基础,另外其在实际生 活运用勾股定理进行计算。
课堂小结
1、这节课我的收获是——； 2、我最感兴趣的地方是—； 3、我想进一步研究的问题是—— —。
作业
1、习题18.1第2、3、4、5题 2、通过查找、翻阅有关证明勾股定理 的多种方法的资料，写一篇以勾股定理 为主体的小论文 。
板书设计
18.1 勾股定理
勾股定理：
拼图展示区
直角三角形两直角边a、b的 平方和等于斜边c的平方：
学情分析
(1)学生的认知基础：八年级学生已具备一定的分析与归 纳能力，但对于勾股定理的得出，首先需要学生通过动手 操作，在观察的基础上，大胆猜想数学结论，而这需要学 生具备一定的分析、归纳的思维方法和运用数学的思想意 识，但学生在这一方面的可预见性和耐挫折能力并不是很 成熟，因此比较困难。 (2)学生年龄心理特点：八年级的学生在心理与生理方面 已经日趋成熟，对待事物的看法有一定的个性见解，表现 欲强，思维敏捷。
教学目标
• 知识与能力目标： • •
教学重点、难点
在探索勾股定理的过程中，让学生经历“观察-猜 活中应用也很普遍。 过程与方法目标： 想-归纳-验证”的数学过程，并体会数形结合和 通过介绍中国古代勾股方面的成就，激发学 从特殊到一般的思想方法。 情感态度与价值观： 生热爱祖国和热爱祖国悠久文化的思想感情， 培养学生的民族自豪感和钻研精神。 【教学重点】勾股定理的证明与运用 【教学难点】用面积法等方法证明勾股定理
A
B 625 400 C 6 B 12 B 25
A
7 C
练习二
1、直角三角形中，两直角边长分别是3和4，则第 三边长是———； 2、△ABC中，∠B＝90度，∠ C＝30度，AC=4， 则AB=———； 3、暴风雨后，一棵小树从B处折断，小树顶部C落 到离小树底部A点4米远处，已知小树高8米，则小 树是在距A多少米处断裂的？