一次移动平均法和一次指数平滑法线性二次移动平均法培训课件
- 格式:ppt
- 大小:294.00 KB
- 文档页数:30


•平均预测法原理
-随机因素对数据的影响,通过对数据的平均或平滑消除后,呈现出事物的本质规律
•算术平均
-简单平均、加权平均、几何平均
几何平均
•概念:几何平均数是一个统计的概念,某一变量的几何平均值定义为:
移动平均法
原理:
通过对历史数据的移动平均,消除随机因素影响,建立模型,进而预测。
一次移动平均法、二次移动平均法
一次移动平均法
指数平滑法
•移动平均法存在着以下不足:
-丢失历史数据。
对历史数据平等对待。
•方法
-一次指数平滑法。
二次指数平滑法。



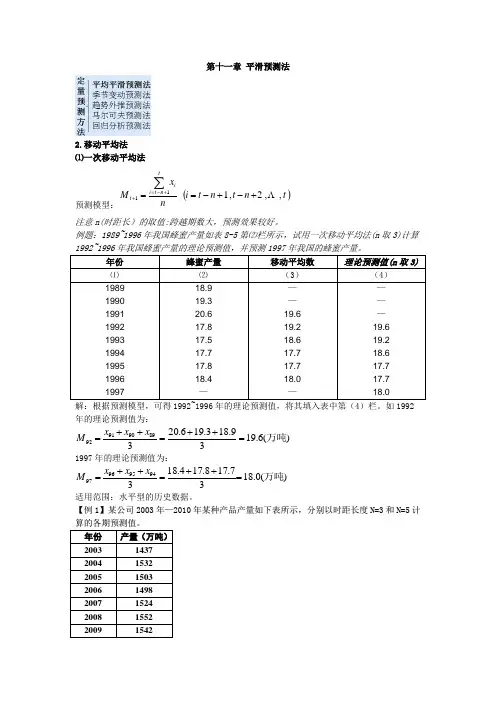
第十一章 平滑预测法2.移动平均法⑴一次移动平均法预测模型:()t n t n t i nx M tn t i it ,,2,111 +-+-==∑+-=+注意n(时距长)的取值:跨越期数大,预测效果较好。
例题:1989~1996年我国蜂蜜产量如表8-5第⑵栏所示,试用一次移动平均法(n 取3)计算1992~1996年我国蜂蜜产量的理论预测值,并预测1997年我国的蜂蜜产量。
年份 蜂蜜产量 移动平均数 理论预测值(n 取3)⑴ ⑵ (3) (4) 1989 1990 1991 1992 1993 1994 1995 1996 199718.9 19.3 20.6 17.8 17.5 17.7 17.8 18.4 —— — 19.6 19.2 18.6 17.7 17.7 18.0 —— — — 19.6 19.2 18.6 17.7 17.7 18.0解:根据预测模型,可得1992~1996年的理论预测值,将其填入表中第(4)栏。
如1992年的理论预测值为:)(6.1939.183.196.20389909192万吨=++=++=x x x M 1997年的理论预测值为:)(0.1837.178.174.183********万吨=++=++=x x x M适用范围:水平型的历史数据。
【例1】某公司2003年—2010年某种产品产量如下表所示,分别以时距长度N =3和N =5计算的各期预测值。
年份 产量(万吨)2003 1437 2004 1532 2005 1503 2006 1498 2007 1524 2008 1552 200915422010 1632 年份 产量(万吨)预测值(N=3)预测值(N=5) 2003 1437 2004 1532 2005 1503 2006 1498 2007 1524 2008 1552 2009 1542 2010 16322011年份 产量(万吨) 预测值(N=3) 预测值(N=5)2003 1437 2004 1532 2005 15032006 1498 1491 2007 1524 15112008 1552 1508 1499 2009 1542 1525 1522 2010 16321539 1524 201115751550⑵二次移动平均法预测模型:T b a Y t t T t +=+ˆ式中:T t Y +ˆ为t+T 期预测值,t 为本期,at 和 bt 为参数()t t t t t t M M M M M a ''-'=''-'+'=2()t t t M M n b ''-'-=12t M '和t M ''分别为一次移动平均数和二次移动平均数∑+-=='t n t i i t x n M 11 ∑+-==''tn t i i t M n M 11适用范围:斜坡型历史数据 例:某省1995~2004年人均卷烟消费量如表第⑵栏所示,试用二次移动平均法计算2000~2004年我国人均卷烟消费量的理论预测值,并预测2005年的卷烟消费量(时据长度=3)。


移动平均法and指数平滑法感谢:⼀、移动平均法(Moving average , MA)移动平均法⼜称滑动平均法、滑动平均模型。
⽤处:⼀组最近的实际数据值->[预测]->未来⼀期或⼏期内公司产品需求量/公司产能。
分类:简单移动平均和加权移动平均思想:根据时间序列资料,逐项推移,依次计算包含⼀定项数的序时平均值,以反映长期趋势。
好处:时间序列数值受周期变动和随机波动影响起伏较⼤,不容易显⽰事件发展趋势, MA可以消除这些因素影响。
(⼀)简单移动平均法各个元素的权重相等。
公式如下:Ft=(At-1 + At-2 + At-3 + ... + At-n) / n[简单的滑动窗⼝](⼆)加权移动平均法加权移动平均给固定跨越期限内的每个变量值以不同的权重。
其原理是:历史各期产品需求的数据信息对预测未来期内的需求量的作⽤不⼀样。
Ft=w1At-1 + w2At-2 + w3At-3 + ... + wnAt-n⼆、指数平滑法(Exponential Smoothing, ES)指数平滑法认为时间序列的态势具有稳定性或规则性,所以时间序列可被合理地顺势推延;他认为最近的过去态势,在某种程度上会持续到最近的未来,所以将较⼤的权数放在最近的资料。
指数平滑法是⽣产预测中常⽤的⼀种⽅法,⽤于中短期经济发展趋势预测,所有预测⽅法中指数平滑⽤得最多。
简单的全期平均法:全部平均。
移动平均法:不考虑较远期数据,并在加权移动平均法中给予近期资料更⼤权重。
指数平滑法:兼容全期平均和移动平均所长,不舍弃过去的数据,仅给予逐渐减弱的影响程度,即随着数据的远离,赋予逐渐收敛为零的权数。
指数平滑法在移动平均法基础上发展起来的⼀种时间序列分析预测法,通过计算指数平滑值,配合⼀定的时间序列预测模型对现象的未来进⾏预测。
任⼀期的指数平滑值都是本期实际观察值与前⼀期指数平滑的加权平均。
(⼀)指数平滑法的公式S_t = a \c dot y_t + (1-a)S_{t-1}S_t:时间t的平滑值y_t: 时间t的实际值S_t-1: 时间t-1的平滑值a--平滑常数,取值范围[0, 1](⼆)指数平滑的预测公式根据平滑次数不同,指数平滑法分为:⼀次指数平滑法、⼆次指数平滑法和三次指数平滑法等(1)⼀次指数平滑y_t+1(predict) = a* y_t(actual) + (1-a) * y_t(predict)(2)⼆次指数平滑预测yt+m=(2+am/(1-a))yt'-(1+am/(1-a))yt=(2yt'-yt)+m(yt'-yt) a/(1-a)其中yt= ayt-1'+(1-a)yt-1,就是⼀次指数平滑的再平滑。



第五章1.一次指数平滑法与一次移动平滑法相比,其优点是什么指数平滑法实际上是从移动算数平滑法演变而来的,优点是不需要保留较多的历史数据,只要有最近一期的实际观测值和这期的预测误差,就可以对未来进行预测。
2.在何种情况下,宜采用线性二次移动平均法或线性二次指数平滑法如果时间序列具有明显的线性变化趋势,则不宜采用一次移动平均法及一次指数平滑法来预测,宜采用二次移动平均法或线性二次指数平滑法来预测。
3.线性二次指数平滑法优于二次移动平均法之处在哪里二次指数平滑是对一次指数平滑值再进行一次平滑,它是用平滑值对时序存在的线性趋势进行修正。
线性二次指数平滑法只利用三个数据值和一个 值就可以计算这种方法可以使过去观察值的权数减少。
4.线性二次指数平滑法包含哪两种方法,各有什么特点布朗单一参数线性指数平滑法其基本原理与线性二次移动平均法相似。
当时间序列有趋势存在时,一次和二次指数平滑都落后于实际值,将一次和二次平滑值之差加在一次平滑值上,则可对趋势进行修正。
布朗单一参数线性指数平滑法,它适用于对具有线性变化趋势的时序进行短期预测。
霍尔特双参数线性指数平滑法其基本原理与布朗线性指数平滑法相似,只是它不用二次指数平滑,而是趋势直线进行平滑。
由于他可以用不同的参数对原序列的趋势进行平滑,因此具有很大的灵活性。
5.在何种情况下,宜采用二次曲线指数平滑法有的时间序列虽然有增加或减少的趋势,但不一定是线性的,可能按二次曲线的形状增加而减少。
对于这种非线性增长的时间序列,从用二次曲线指数平滑法可能要比线性指数平滑法更为有效。
6.温特线性和季节性指数平滑法有什么特点这种方法可以同时修正时间序列数据的季节性和倾向性,因此,它能对于对既有倾向性变通趋势又有季节性变动的时间序列进行预测。
指数平滑法指数平滑法是美国人R.G. Brown 所创,是从移动平均法发展而来的。
可以说是移动平均法的一种变形。
其特点是预测时所需的资料少,计算方便。
利用指数平滑法进行预测,就是对不规则的时间序列数据加以平滑,从而获得其变化规律和趋势,以此对未来的经济数据进行推断和预测。
根据平滑次数的不同,有一次指数平滑、二次指数平滑及高次指数平滑,但高次指数平滑很少使用,下面主要介绍一次指数平滑法和二次指数平滑法。
1.一次指数平滑法一次指数平滑法是根据前期的实测数和预测数,以加权因子为权数,进行加权平均,来预测未来时间趋势的方法。
一次指数平滑法计算公式为:式中,―― 时期t 的实测值;―― 时期t 的预测值;―― 平滑系数,又称加权因子,取值范围为。
将的表达式逐次代入中,展开整理后,得:从上式中可以看出,一次指数平滑法实际上是以为权数的加权移动平均法。
由于k越大,越小,所以越是远期的实测值对未来时期平滑值的影响就越小。
在展开式中,最后一项为初始平滑值,在通常情况下可用最初几个实测值的平均值来代替,或直接可用第 1 时期的实测值来代替。
从上式可以看出,新预测值是根据预测误差对原预测值进行修正得到的。
的大小表明了修正的幅度。
值愈大,修正的幅度愈大,值愈小,修正的幅度愈小。
因此,值既代表了预测模型对时间序列数据变化的反应速度,又体现了预测模型修匀误差的能力。
在实际应用中,值是根据时间序列的变化特性来选取的。
若时间序列的波动不大,比较平稳,则应取小一些,如0.1 ~ 0.3 ;若时间序列具有迅速且明显的变动倾向,则应取大一些,如 0.6 ~ 0.9 。
实质上,是一个经验数据,通过多个值进行试算比较而定,哪个值引起的预测误差小,就采用哪个。
2.二次指数平滑法一次指数平滑法只适用于水平型时间序列模式的预测,而不适用于呈斜坡型线性趋势历史数据的预测。
因为,对于明显呈斜坡型的历史数据,即使取值很大,仍会产生较大的系统误差。
因此,对于此类数据变动趋势的预测,应对一次指数平滑法进行改进,可以用二次指数平滑法进行预测。
二次移动平均法一、一次移动平均法公式:为第t+1期预测值;为第t 期一次移动平均值;为第t 期的观测值;n 为数据的个数,也是移动的平均期数。
各组数据的移动平均值在数值上和下一期预测值的数值相等。
二、二次移动平均法:定义 :是对时间序列的一次移动平均值再进行第二次移动平均,利用一次移动平均值和二次移动平均值构成时间序列的最后一个数据为依据建立线性预测模型进行预测。
二次移动平均值的公式:Y t +Y t-1+…+Y t-n+1M t (1)=nM t (1)+ M t-1(1)+…+ M t-n+1(1)M t (2)=nM t (1)为第t 期的一次移动平均值;M t (2)为第t 期的二次移动平均值;n 为计算移动平均值的跨越期。
二次移动平均预测法的预测模型为: F t+T =a t +b t Ta t =2M t(1)- M t (2)b t = (M t (1)-M t (2)) T 为向未来预测的期数;a t 为截距,即第t 期现象的基础水平;b t 为斜率,即第t 期现象单位时间的变化量。
①② ③④ 2 n-1⑤ ⑥一次移动平均值和二次平均值并不是直接运用于预测,只是用以求出线性预测模型的平滑系数和修正滞后偏差。
(区别于一次移动平均法各组数据的移动平均值在数值上和下一期预测值的数值相等。
)三、例题(P131 例4—4)四、总结:1、一次移动平均值和二次平均值并不是直接运用于预测,只是用以求出线性预测模型的平滑系数。
2、在观察期内各期估计值a、b值是变化的,而在预测期各预测值的a、b值是一致的,即最后一个观察期的a、b值。
3、二次移动平均法解决了一次移动平均法只能向未来预测一期问题。
4二次移动平均法解决了一次移动平均法不能用于有明显趋势变动的市场现象时间序列。
五、补充问题对例题(P131 例4—4)数据的进一步分析。
远方。